The Influence of Colloidal Properties of Carbon Black on Static and Dynamic Mechanical Properties of Natural Rubber
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Shore A Hardness, Tensile to Break, and Cyclic Tensile Tests
2.3. Dynamic Strain Sweep Characterization
3. Results and Discussion
3.1. Compound Dispersion Index
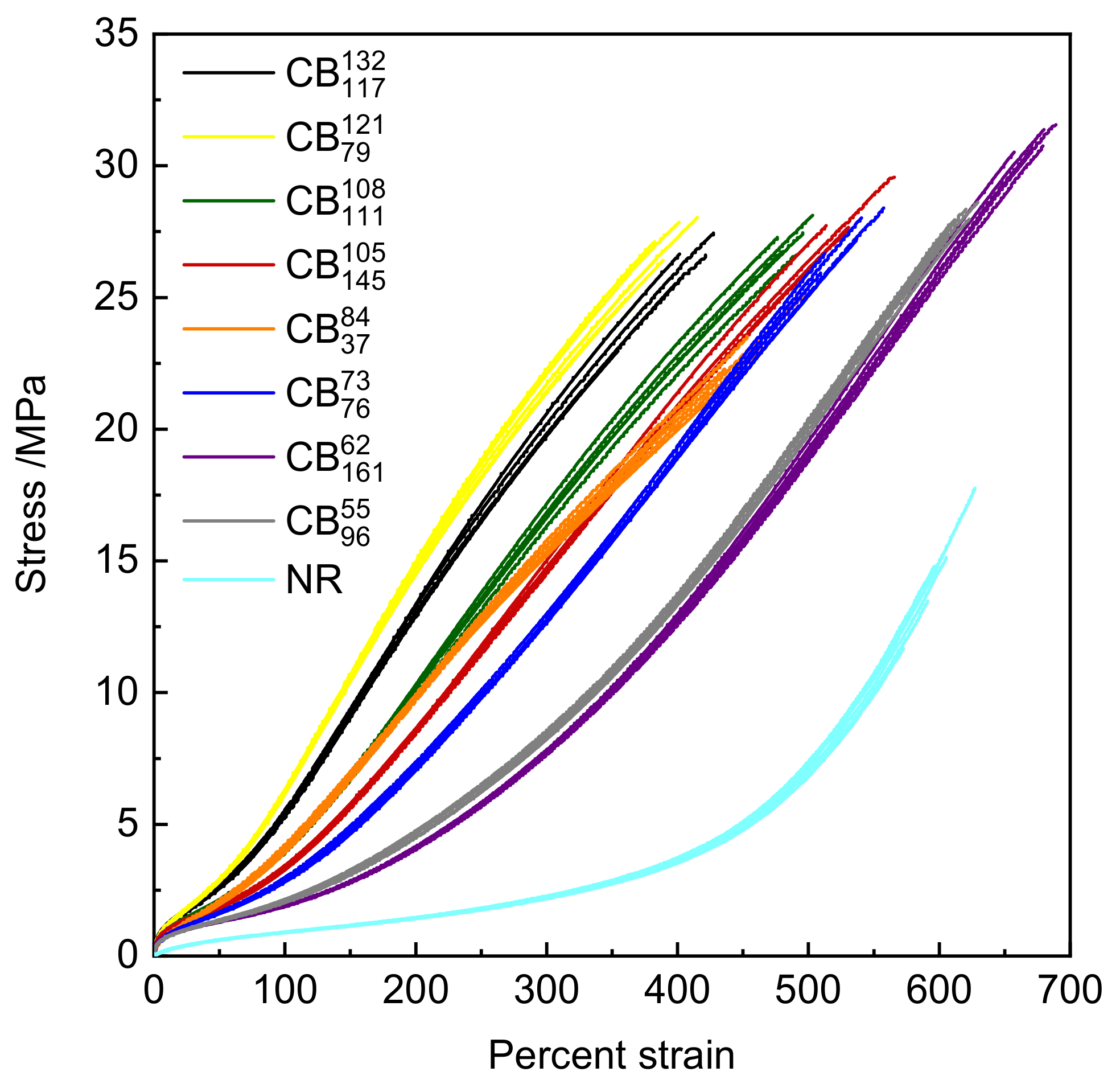
3.2. Tensile Stress Strain and Shore A Hardness Measurements
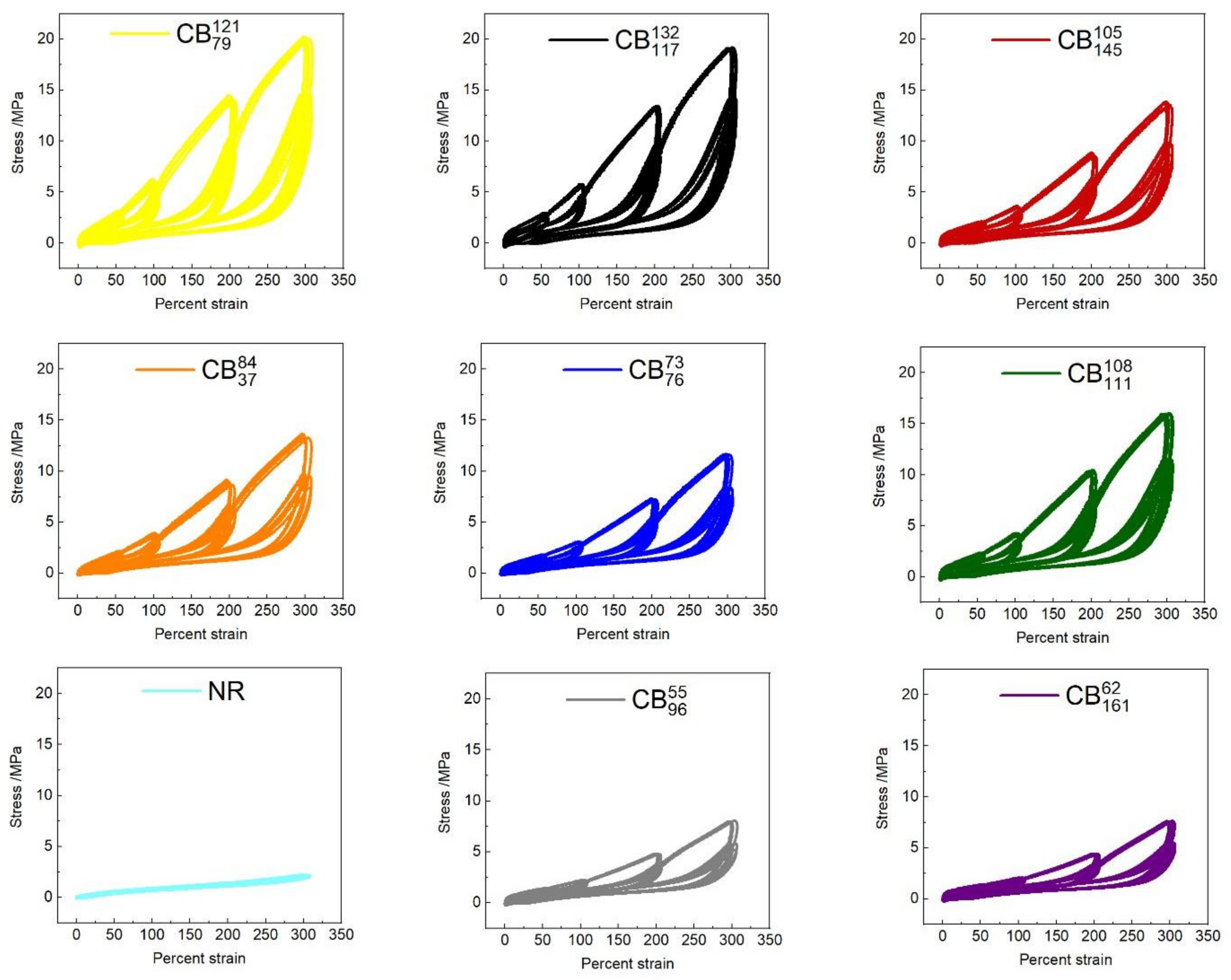
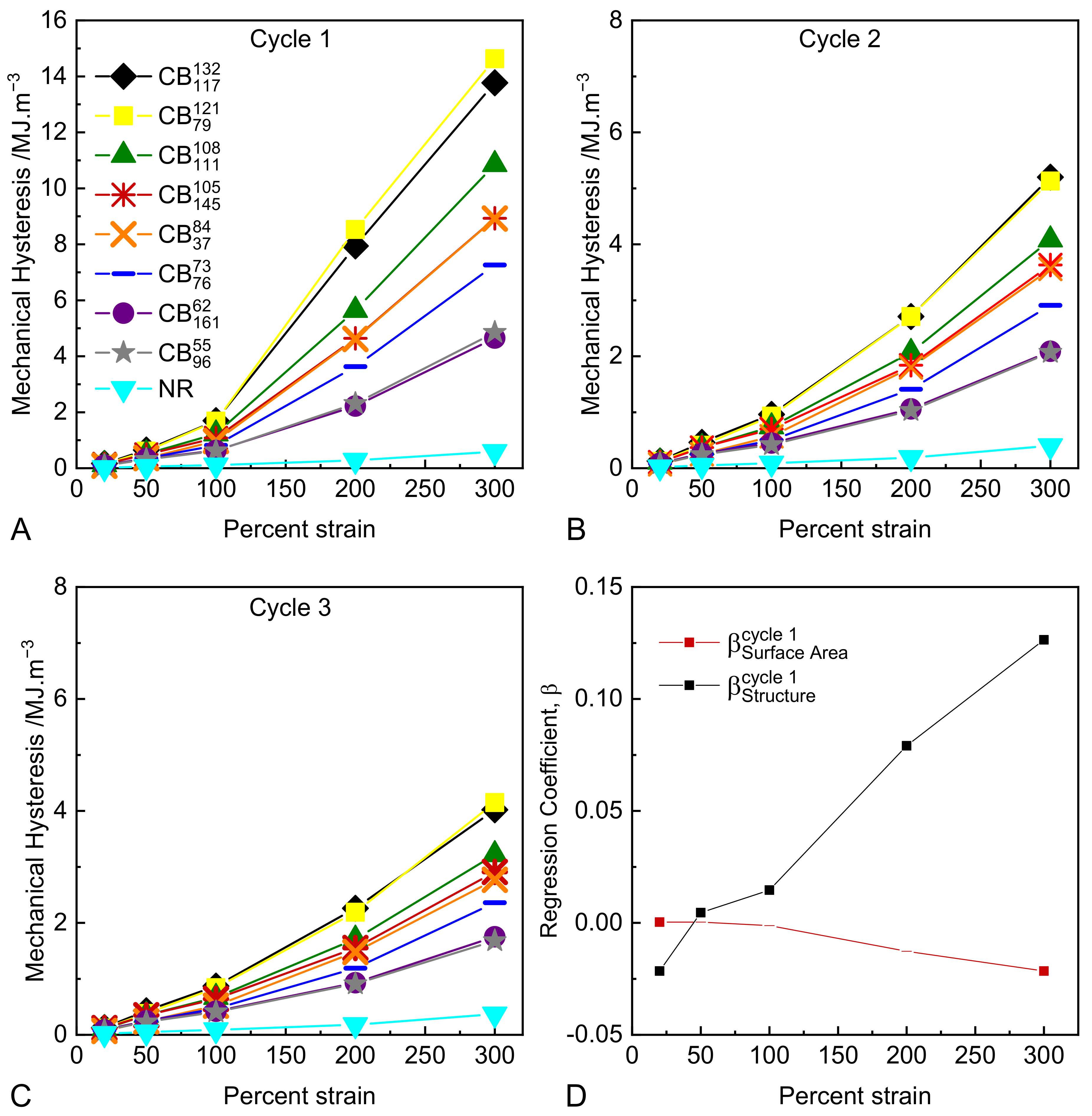
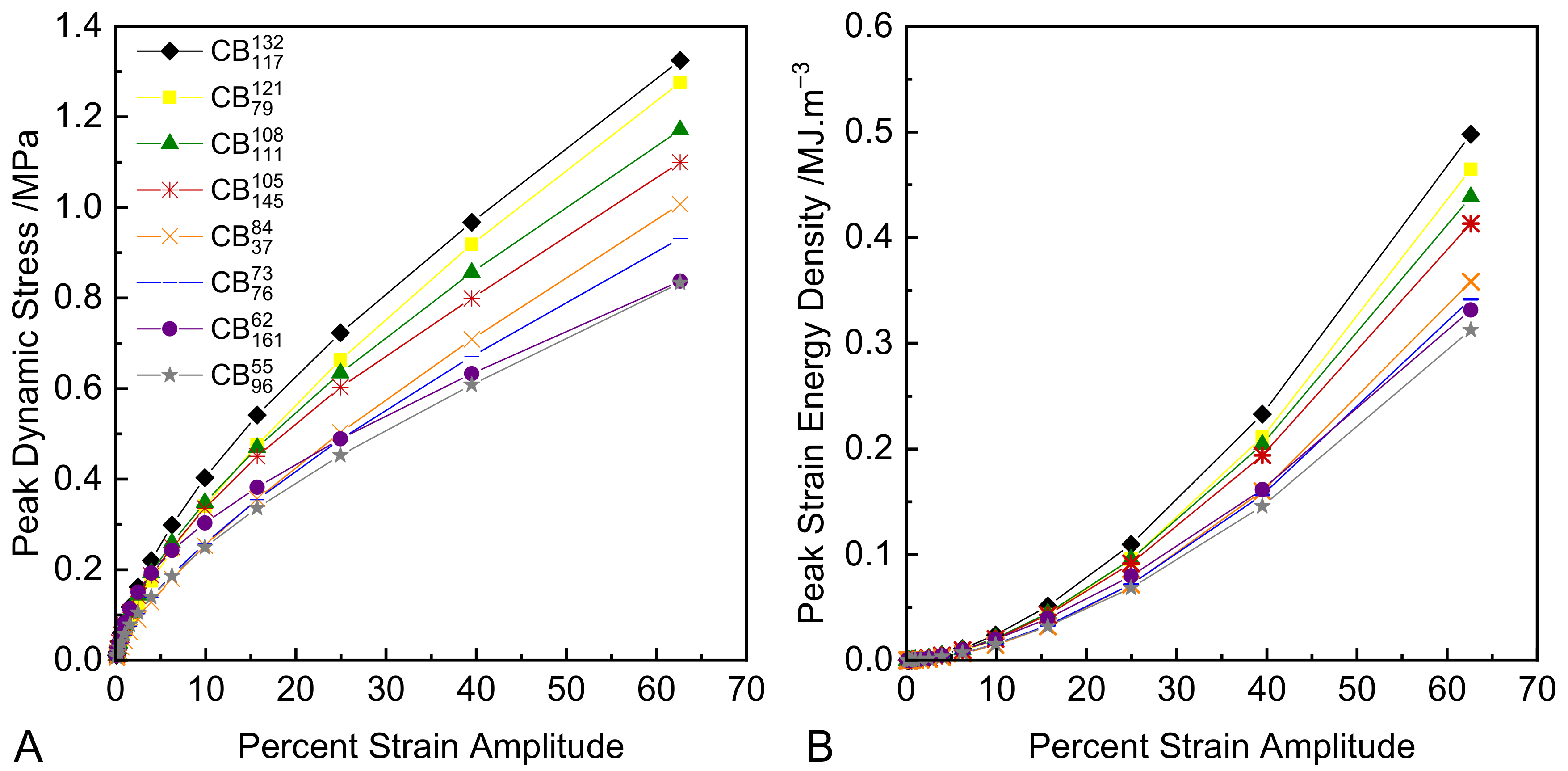
3.3. Cyclic Tensile Tests
- At a practical level, the degree of mechanical hysteresis (and therefore softening) of a rubber compound at a fixed strain level scales with the virgin modulus of the compound at that strain. All other parameters being equal (such as CB volume fraction, polymer type, and crosslink density), this modulus is determined by the structure of the CB in the formulation [45].
- At a microstructural level, the strong correlation between hysteresis and CB structure provides several hints as to the origin of the Mullins-type hysteresis and softening. It suggests that the hysteretic energy dissipation at these large strains is isolated in the rubber matrix and arises due to strain amplification/matrix overstrain, as opposed to hysteretic polymer–particle surface slippage and/or hysteretic breakup of flocculated aggregate clusters, which have been proposed in the literature. Note that strain amplification as described by hydrodynamic-type equations is independent of CB particle size/surface area, which is consistent with our observations [10,11,12]. In these experiments, specimens have been cycled to specified strain levels. Harwood, Mullins, and Payne [23] conducted highly relevant experiments where specimens were cycled to specified stress levels. Under these conditions, the resulting mechanical hysteresis values were found to be identical for a wide range of CB reinforced and gum NR compounds. These findings are consistent with our results in the sense that they can both be explained if we assume that energy dissipation occurring at these large strains is isolated predominantly in the overstrained rubber matrix.
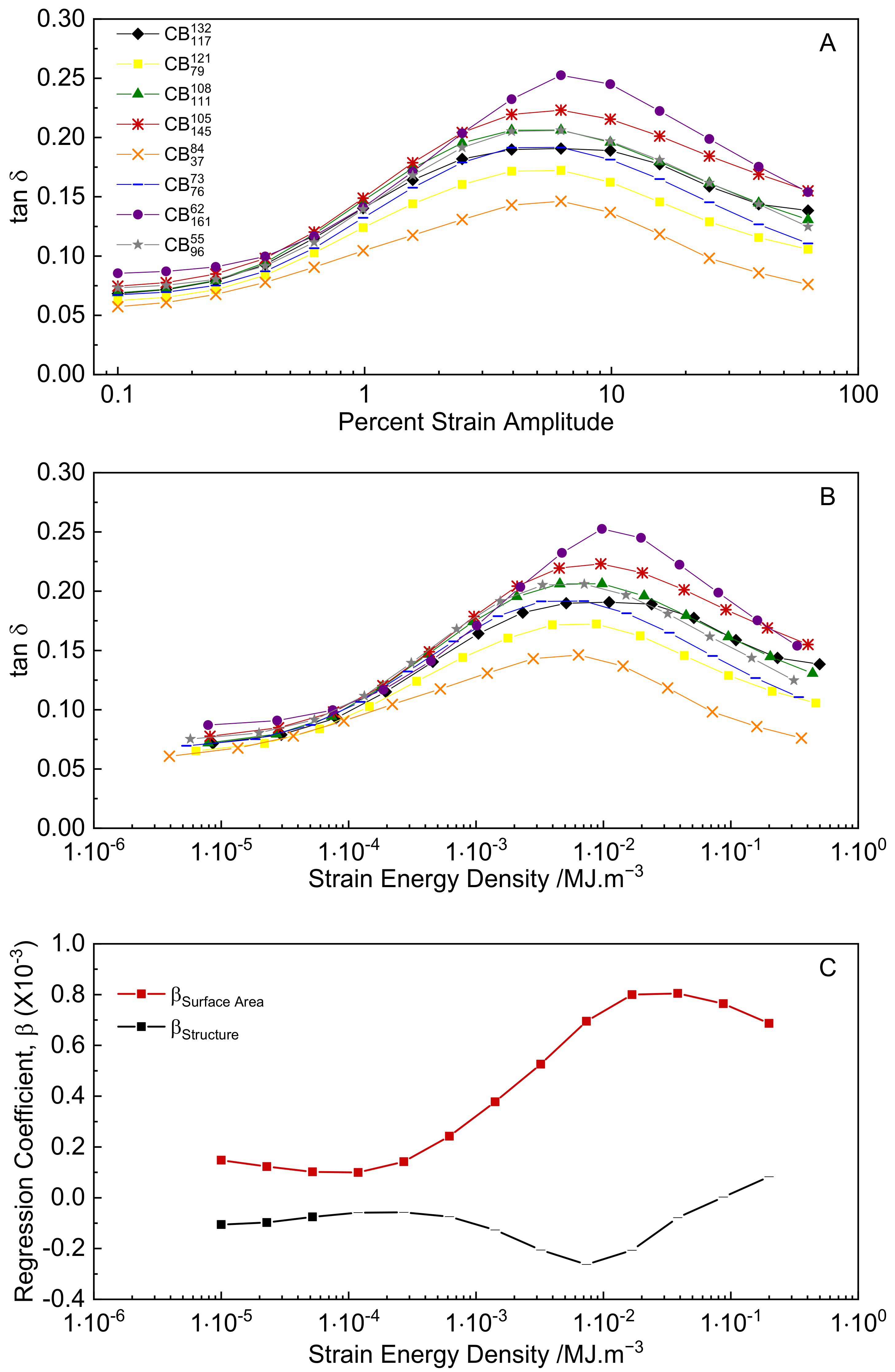
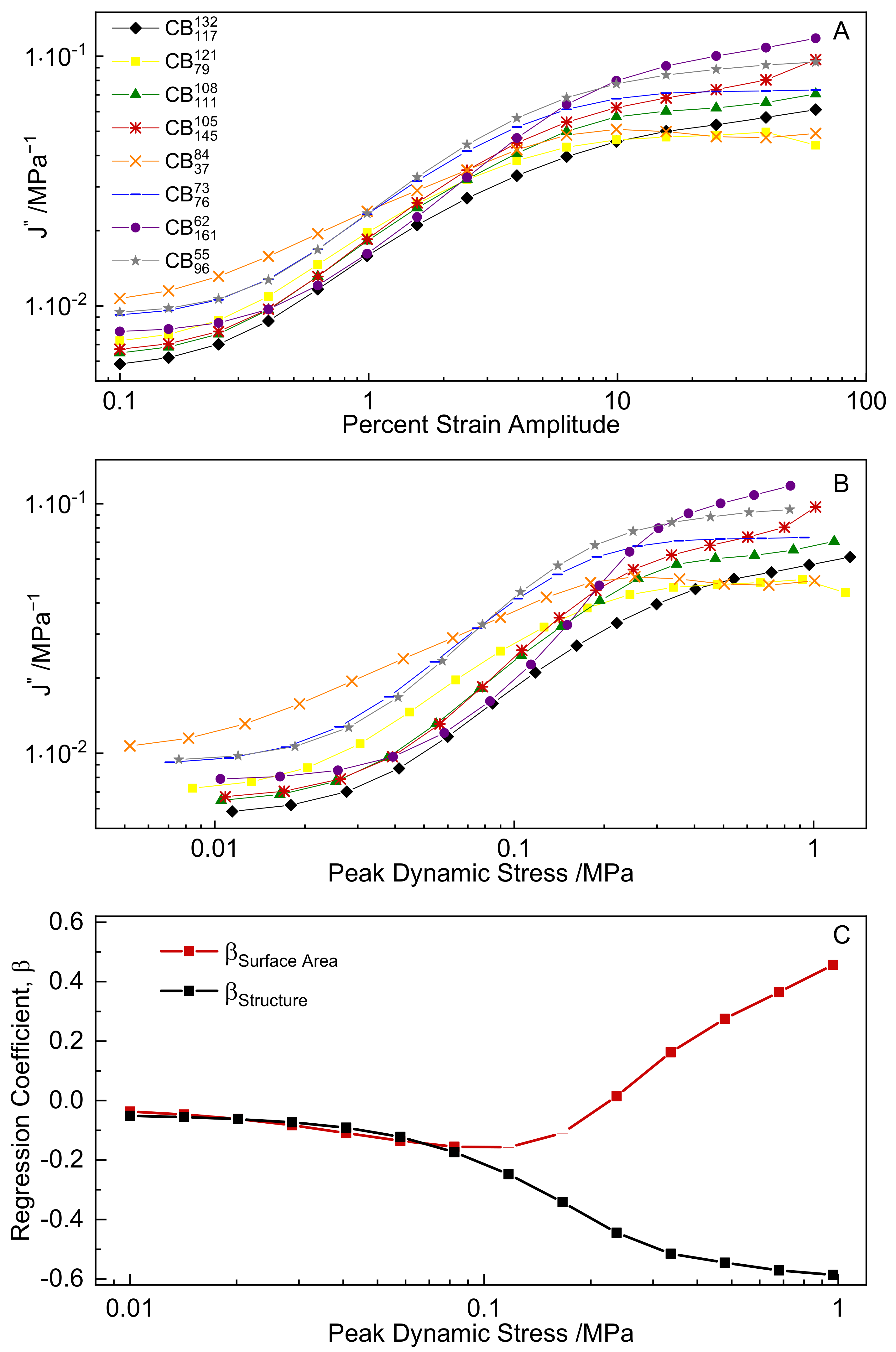
3.4. Dynamic Strain Sweeps
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dannenberg, E.M. Bound Rubber and Carbon Black Reinforcement. Rubber Chem. Technol. 1986, 59, 512–524. [Google Scholar] [CrossRef]
- Dannenberg, E.M. Carbon Black Dispersion and Reinforcement. Rubber Chem. Technol. 1952, 25, 843–857. [Google Scholar] [CrossRef]
- Dannenberg, E.M. The Effects of Surface Chemical Interactions on the Properties of Filler-Reinforced Rubbers. Rubber Chem. Technol. 1975, 48, 410–444. [Google Scholar] [CrossRef]
- Donnet, J.-B. Black and White Fillers and Tire Compound. Rubber Chem. Technol. 1998, 71, 323–341. [Google Scholar] [CrossRef]
- Kraus, G. Interactions of Elastomers and Reinforcing Fillers. Rubber Chem. Technol. 1965, 38, 1070–1114. [Google Scholar] [CrossRef]
- Kraus, G. Mechanical losses in carbon-black-filled rubbers. In Chemistry and Technology of Rubber, Proceeding of the International Rubber Conference, Paris, France, 2–4 June 1982; Vidal, A., Donnet, J.-B., Eds.; John Wiley & Sons: New York, NY, USA, 1984; pp. 75–93. [Google Scholar]
- Medalia, A.I. Heat Generation in Elastomer Compounds: Causes and Effects. Rubber Chem. Technol. 1991, 64, 481–492. [Google Scholar] [CrossRef]
- Medalia, A.I. Effect of Carbon Black on Dynamic Properties of Rubber Vulcanizates. Rubber Chem. Technol. 1978, 51, 437–523. [Google Scholar] [CrossRef]
- Wang, M.-J. Effect of polymer-filler and filler-filler interactions on dynamic properties of filled vulcanizates. Rubber Chem. Technol. 1998, 71, 520–589. [Google Scholar] [CrossRef]
- Smallwood, H.M. Limiting Law of the Reinforcement of Rubber. J. Appl. Phys. 1944, 15, 758. [Google Scholar] [CrossRef]
- Guth, E. Theory of Filler Reinforcement. J. Appl. Phys. 1945, 16, 20–25. [Google Scholar] [CrossRef]
- Allegra, G.; Raos, G.; Vacatello, M. Theories and simulations of polymer-based nanocomposites: From chain statistics to reinforcement. Prog. Polym. Sci. 2008, 33, 683–731. [Google Scholar] [CrossRef]
- Domurath, J.; Saphiannikova, M.; Heinrich, G. The Concept of Hydrodynamic Amplification in Filled Elastomers; KGK Rubberpoint: Heidelberg, Germany, 2017; pp. 40–43. [Google Scholar]
- Payne, A.R.; Whittaker, R.E. Low Strain Dynamic Properties of Filled Rubbers. Rubber Chem. Technol. 1971, 44, 440–478. [Google Scholar] [CrossRef]
- Randall, A.M.; Robertson, C.G. Linear-nonlinear dichotomy of the rheological response of particle-filled polymers. J. Appl. Polym. Sci. 2014, 131, 40818. [Google Scholar] [CrossRef]
- Tunnicliffe, L.B. Thixotropic flocculation effects in carbon black–reinforced rubber: KINETICS and thermal activation. Rubber Chem. Technol. 2021, 94, 298–323. [Google Scholar] [CrossRef]
- Merabia, S.; Sotta, P.; Long, D.R. A Microscopic Model for the Reinforcement and the Nonlinear Behavior of Filled Elastomers and Thermoplastic Elastomers (Payne and Mullins Effects). Macromolecules 2008, 41, 8252–8266. [Google Scholar] [CrossRef]
- Mujtaba, A.; Keller, M.; Ilisch, S.; Radusch, H.-J.; Beiner, M.; Thurn-Albrecht, T.; Saalwächter, K. Detection of Surface-Immobilized Components and Their Role in Viscoelastic Reinforcement of Rubber–Silica Nanocomposites. ACS Macro Lett. 2014, 3, 481–485. [Google Scholar] [CrossRef]
- Mullins, L. Effect of Stretching on the Properties of Rubber. Rubber Chem. Technol. 1948, 21, 281–300. [Google Scholar] [CrossRef]
- Mullins, L. Softening of Rubber by Deformation. Rubber Chem. Technol. 1969, 42, 339–362. [Google Scholar] [CrossRef]
- Diani, J.; Fayolle, B.; Gilormini, P. A review on the Mullins effect. Eur. Polym. J. 2009, 45, 601–612. [Google Scholar] [CrossRef] [Green Version]
- Plagge, J.; Lang, A. Filler-polymer interaction investigated using graphitized carbon blacks: Another attempt to explain reinforcement. Polymer 2021, 218, 123513. [Google Scholar] [CrossRef]
- Harwood, J.; Mullins, L.; Payne, A. Stress softening in natural rubber vulcanizates. Part II. Stress softening effects in pure gum and filler loaded rubbers. J. Appl. Polym. Sci. 1965, 9, 3011–3021. [Google Scholar] [CrossRef]
- Huang, M.; Tunnicliffe, L.B.; Thomas, A.G.; Busfield, J.J. The glass transition, segmental relaxations and viscoelastic behaviour of particulate-reinforced natural rubber. Eur. Polym. J. 2015, 67, 232–241. [Google Scholar] [CrossRef]
- Robertson, C.; Roland, C.M. Glass Transition and Interfacial Segmental Dynamics in Polymer-Particle Composites. Rubber Chem. Technol. 2008, 81, 506–522. [Google Scholar] [CrossRef]
- Bueche, F. Mullins effect and rubber-filler interaction. J. Appl. Polym. Sci. 1961, 5, 271–281. [Google Scholar] [CrossRef]
- Kraus, G. Mechanical losses in carbon-black filled rubbers. J. Appl. Polym. Sci. Appl. Polym. Symp. 1984, 39, 75. [Google Scholar]
- Heinrich, G.; Klüppel, M. Recent advancces in the theory of filler networking in elastomers, in Filled elastomers drug delivery systems. In Advances in Polymer Science; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Goöritz, D.; Raab, H.; Froöhlich, J.; Maier, P.G. Surface Structure of Carbon Black and Reinforcement. Rubber Chem. Technol. 1999, 72, 929–945. [Google Scholar] [CrossRef]
- Goeritz, D.; Hofmann, R.W.P.; Bissem, H.H. Mobility of adsorbed polymer chains. Rubber Chem. Technol. 2010, 83, 323–330. [Google Scholar] [CrossRef]
- ASTM D3849; Standard Test method for Carbon Black-Morphological Characterization of Carbon Black Using electron Microscopy. ASTM International: West Conschohocken, PA, USA, 2016.
- ASTM D6556; Standard Test Method for Carbon Black—Total and External Surface area by Nitrogen Adsorption. ASTM International: West Conschohocken, PA, USA, 2019.
- ASTM D2414; Standard Test Method for Carbon Black Oil Absorption Number (OAN). ASTM International: West Conschohocken, PA, USA, 2019.
- ASTM D3493; Standard Test Method for Carbon Black—Oil Absoprtion Number of Compressed Sample (COAN). ASTM International: West Conschohocken, PA, USA, 2019.
- Medalia, A.I. Morphology of aggregates. VI. Effective volume of aggregates of carbon black from electron microscopy;application to vehicle absorption and to die swell of filled rubber. J. Colloid Interface Sci. 1970, 32, 115–131. [Google Scholar] [CrossRef]
- Medalia, A.I. Effective Degree of Immobilization of Rubber Occluded within Carbon Black Aggregates. Rubber Chem. Technol. 1972, 45, 1171–1194. [Google Scholar] [CrossRef]
- Wang, M.-J.; Wolff, S.; Tan, E.-H. Filler-elastomer interactions. Part VIII. The role of the distance between filler aggregates in the dynamic properties of filled vulcanizates. Rubber Chem. Technol. 1993, 66, 178–195. [Google Scholar] [CrossRef]
- Robertson, C.G.; Hardman, N.J. Nature of Carbon Black Reinforcement of Rubber: Perspective on the Original Polymer Nanocomposite. Polymers 2021, 13, 538. [Google Scholar] [CrossRef]
- ASTM D2663; Standard Test Methods for Carbon Black—Dispersion in Rubber. ASTM International: West Conschohocken, PA, USA, 2019.
- ASTM D2240; Standard Test Method for Rubber Property—Durometer Hardness. ASTM International: West Conschohocken, PA, USA, 2017.
- ASTM D412; Standard Test Methods for Vulcanized Rubber and Thermoplastic Elastomers—Tension. ASTM International: West Conschohocken, PA, USA, 2002.
- Klüppel, M. The Role of Disorder in Filler Reinforcement of Elastomers on Various Length Scales. In Filler-Reinforced Elastomers Scanning Force Microscopy; Advances in Polymer Science; Springer: Berlin/Heidelberg, Germany, 2003; pp. 1–86. [Google Scholar] [CrossRef]
- Kraus, G. A Carbon Black Structure-Concentration Equivalence Principle. Application to Stress-Strain Relationships of Filled Rubbers. Rubber Chem. Technol. 1971, 44, 199–213. [Google Scholar] [CrossRef]
- Robertson, C.G.; Tunnicliffe, L.B.; Maciag, L.; Bauman, M.A.; Miller, K.; Herd, C.R.; Mars, W.V. Characterizing Distributions of Tensile Strength and Crack Precursor Size to Evaluate Filler Dispersion Effects and Reliability of Rubber. Polymers 2020, 12, 203. [Google Scholar] [CrossRef] [Green Version]
- Kyei-Manu, W.A.; Tunnicliffe, L.B.; Plagge, J.; Herd, C.R.; Akutagawa, K.; Pugno, N.M.; Busfield, J.J.C. Thermomechanical Characterization of Carbon Black Reinforced Rubbers During Rapid Adiabatic Straining. Front. Mater. 2021, 8, 421. [Google Scholar] [CrossRef]
- Hyun, K.; Wilhelm, M.; Klein, C.O.; Cho, K.S.; Nam, J.G.; Ahn, K.H.; Lee, S.J.; Ewoldt, R.; McKinley, G. A review of nonlinear oscillatory shear tests: Analysis and application of large amplitude oscillatory shear (LAOS). Prog. Polym. Sci. 2011, 36, 1697–1753. [Google Scholar] [CrossRef]
- Xiong, W.; Wang, X. Nonlinear responses of carbon black-filled polymer solutions to forced oscillatory shear. J. Non-Newtonian Fluid Mech. 2020, 282, 104319. [Google Scholar] [CrossRef]
- Xiong, W.; Wang, X. Linear-nonlinear dichotomy of rheological responses in particle-filled polymer melts. J. Rheol. 2018, 62, 171–181. [Google Scholar] [CrossRef]
- Futamura, S. Deformation Index—Concept for Hysteretic Energy-Loss Process. Rubber Chem. Technol. 1991, 64, 57–64. [Google Scholar] [CrossRef]
- Futamura, S. Analysis of Ice- and Snow Traction of Tread Material. Rubber Chem. Technol. 1996, 69, 648–653. [Google Scholar] [CrossRef]



| Component | Loading/Parts per Hundred Rubber (phr) | Manufacturer of Component |
|---|---|---|
| NR—SMR CV-60 | 100 | Herman Weber & Co. |
| Carbon Black | 50 | Birla Carbon |
| Zinc Oxide | 5 | Akrochem |
| Stearic Acid | 3 | PMC Biogenix |
| Anti-ozonant/Antioxidant | 3 | Americas International |
| Micro-wax | 2 | Strahl & Pitsch |
| Sulphur | 2.5 | R.E. Carroll |
| TBBS *-75 | 0.8 | Akrochem |
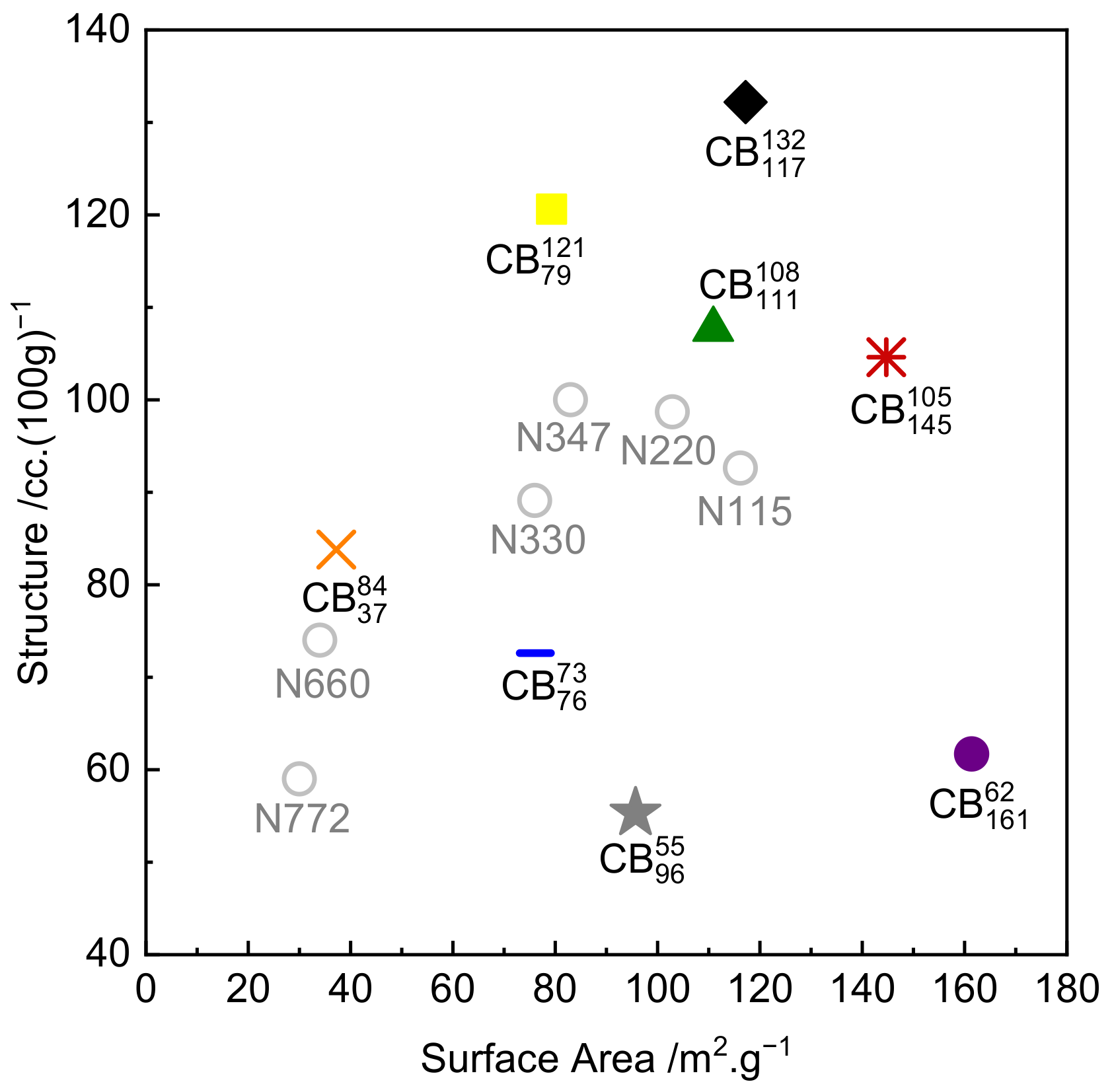
| Carbon Black/ Compound Code | Structure (COAN)/ cc.(100 g)−1 | Surface Area (STSA)/ m2·g−1 | Carbon Black Commercial Name | Corresponding Compound Dispersion Index |
|---|---|---|---|---|
| Unfilled NR | NA | NA | NA | NA |
| 132 | 117 | BC2005 | 99.3 | |
| 105 | 145 | BC2115 | 98.8 | |
| 121 | 79 | BC2013 | 98.8 | |
| 108 | 111 | N234 | 99.4 | |
| 73 | 76 | N326 | 98.0 | |
| 55 | 96 | Raven 1200 | 90.2 | |
| 62 | 161 | Raven 2000 | 81.5 | |
| 84 | 37 | N550 | 98.7 |
| Compound Code | 300% Modulus /MPa | Percent Elongation at Break | Tensile Strength /MPa | Shore A Hardness /Shore A |
|---|---|---|---|---|
| Unfilled NR | 2.23 | 598 | 14.6 | 41.6 |
| 19.89 | 402 | 26.6 | 74.8 | |
| 14.58 | 530 | 27.7 | 70.8 | |
| 21.76 | 389 | 27.1 | 74.6 | |
| 16.69 | 491 | 27.3 | 71.5 | |
| 12.77 | 536 | 27.2 | 66.7 | |
| 8.33 | 620 | 28.0 | 63.7 | |
| 7.82 | 679 | 30.8 | 64.4 | |
| 15.38 | 461 | 23.1 | 66.1 |
| Regression Parameter | 300% Modulus /MPa | Tensile Strength /MPa | Percent Elongation at Break | Shore A Hardness/Shore A |
|---|---|---|---|---|
| 3.52 | 24.79 | 671.32 | 54.33 | |
| 0.1657 | −0.0232 | −3.1103 | 0.1545 | |
| COAN p | 3.47 × 10−5 | 0.1881 | 1.20 × 10−6 | 7.28 × 10−5 |
| −0.0404 | 0.0444 | 1.2572 | 0.0047 | |
| STSA p | 0.0049 | 0.0091 | 1.91 × 10−5 | 0.6330 |
| Adjusted R2 | 0.97 | 0.71 | 0.99 | 0.95 |
| Deformation Mode | Dynamic Deformation Conditions | Static Deformation Conditions |
|---|---|---|
| Strain control |
|
|
| Stress control | Low Stress Levels
Medium-Large Stress Levels
|
|
| Strain energy control |
|
|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kyei-Manu, W.A.; Herd, C.R.; Chowdhury, M.; Busfield, J.J.C.; Tunnicliffe, L.B. The Influence of Colloidal Properties of Carbon Black on Static and Dynamic Mechanical Properties of Natural Rubber. Polymers 2022, 14, 1194. https://doi.org/10.3390/polym14061194
Kyei-Manu WA, Herd CR, Chowdhury M, Busfield JJC, Tunnicliffe LB. The Influence of Colloidal Properties of Carbon Black on Static and Dynamic Mechanical Properties of Natural Rubber. Polymers. 2022; 14(6):1194. https://doi.org/10.3390/polym14061194
Chicago/Turabian StyleKyei-Manu, William Amoako, Charles R. Herd, Mahatab Chowdhury, James J. C. Busfield, and Lewis B. Tunnicliffe. 2022. "The Influence of Colloidal Properties of Carbon Black on Static and Dynamic Mechanical Properties of Natural Rubber" Polymers 14, no. 6: 1194. https://doi.org/10.3390/polym14061194
APA StyleKyei-Manu, W. A., Herd, C. R., Chowdhury, M., Busfield, J. J. C., & Tunnicliffe, L. B. (2022). The Influence of Colloidal Properties of Carbon Black on Static and Dynamic Mechanical Properties of Natural Rubber. Polymers, 14(6), 1194. https://doi.org/10.3390/polym14061194







