The Role of Structure in Polymer Rheology: Review
Abstract
:1. Introduction
2. The Cox–Merz Rule as a Reflection of the Viscoelastic Origin on Non-Linear Rheology
3. Thixotropy—The Most Evident Reflection of Structure Transformation
4. Yielding—Structure Breakdown Leading to Solid-to-Liquid Transition
5. Solid Particles in Polymeric Liquids—Basic Model of Multicomponent Media
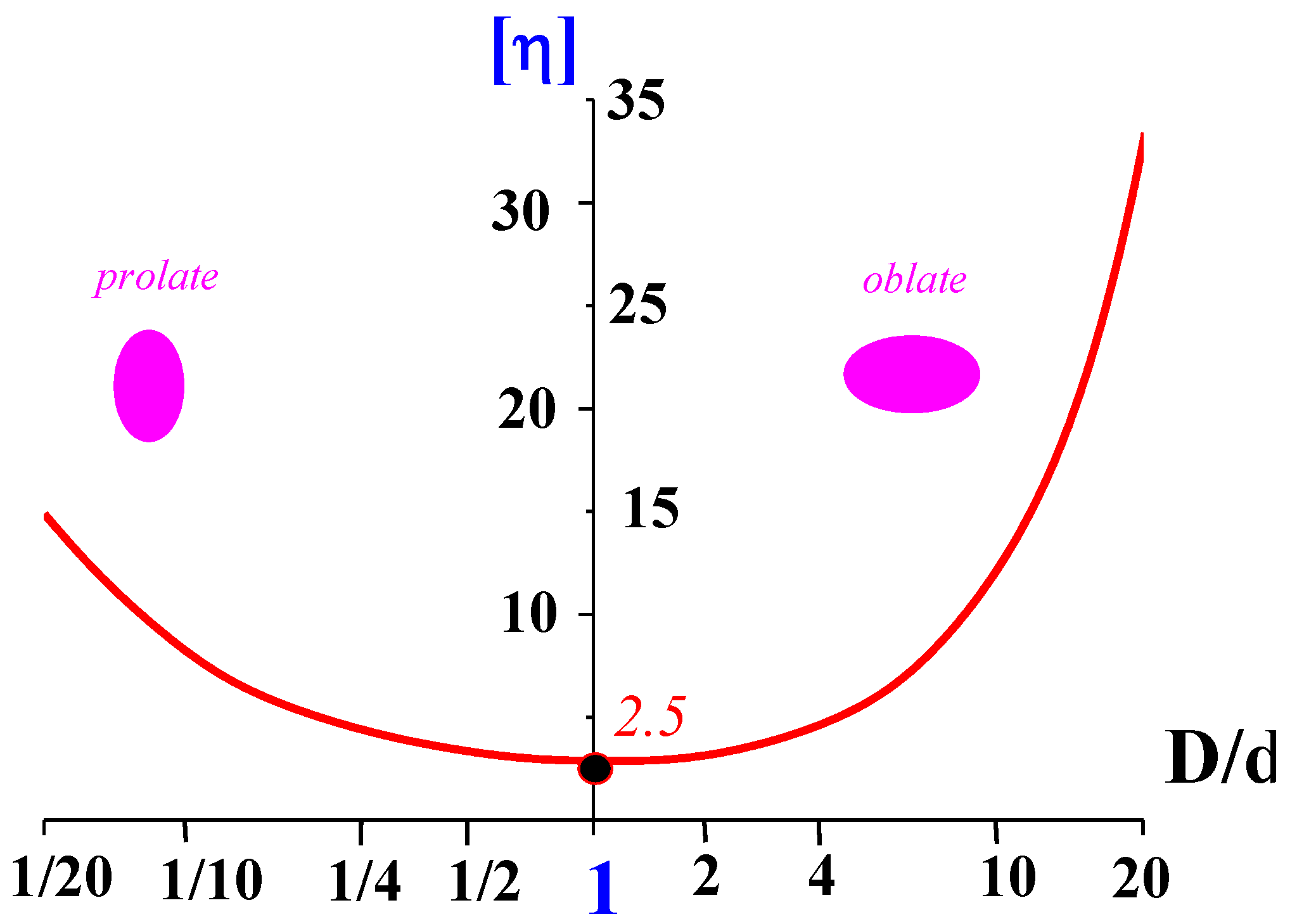
5.1. A Single Particle in a Liquid Matrix
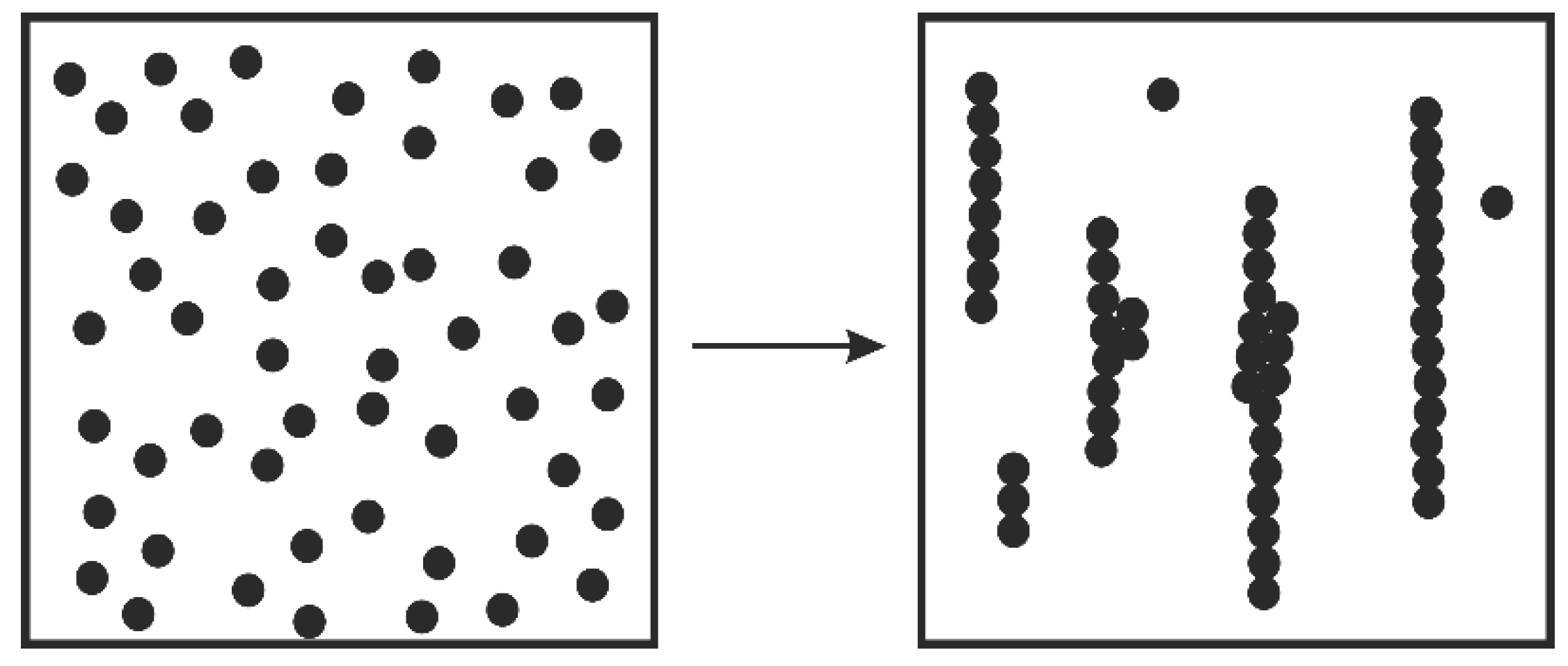
5.2. Self-Assembling in Filled Polymeric Liquids
6. Shear-Induced Structure Formation in Polymer Melts and Blends
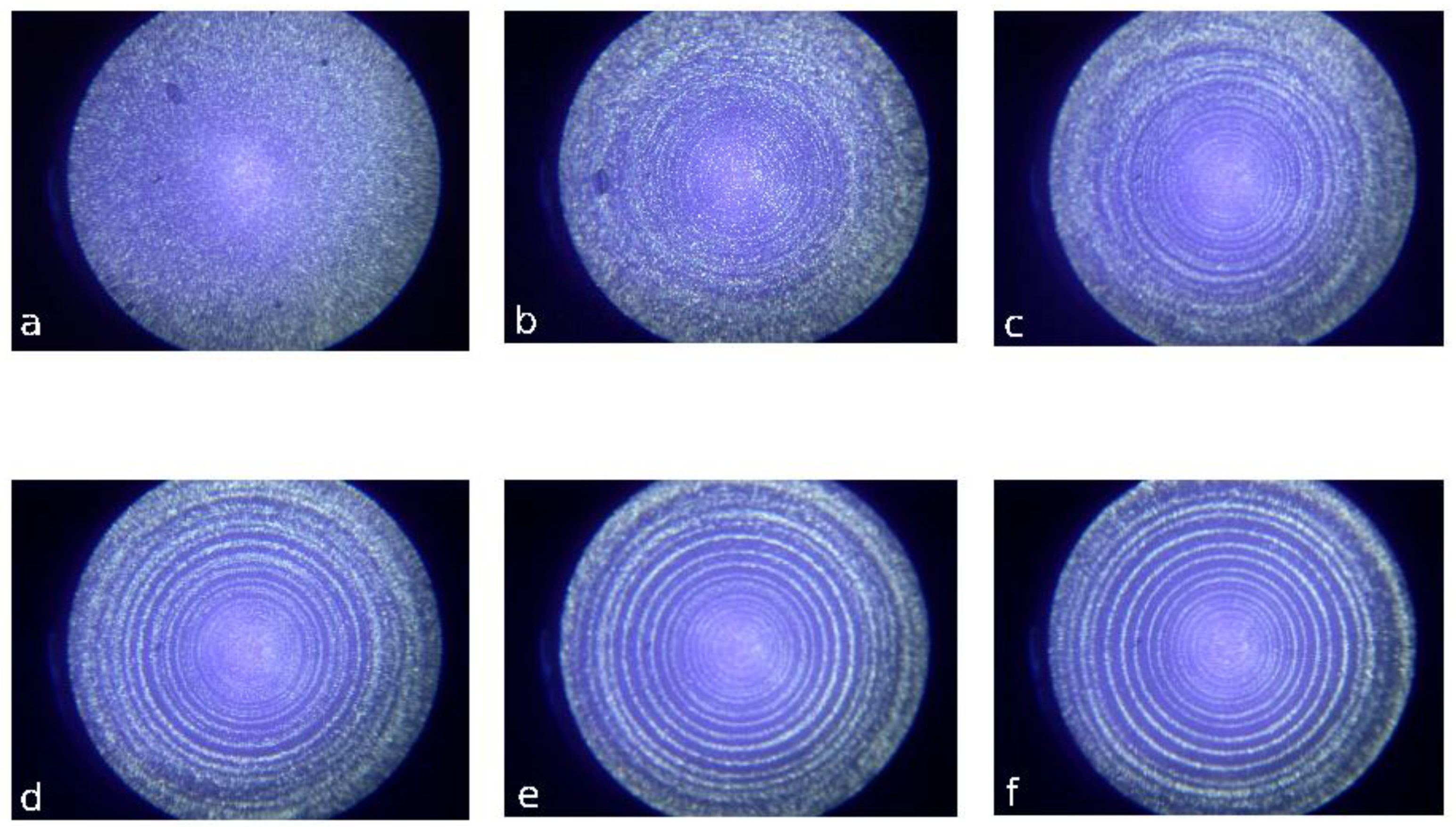
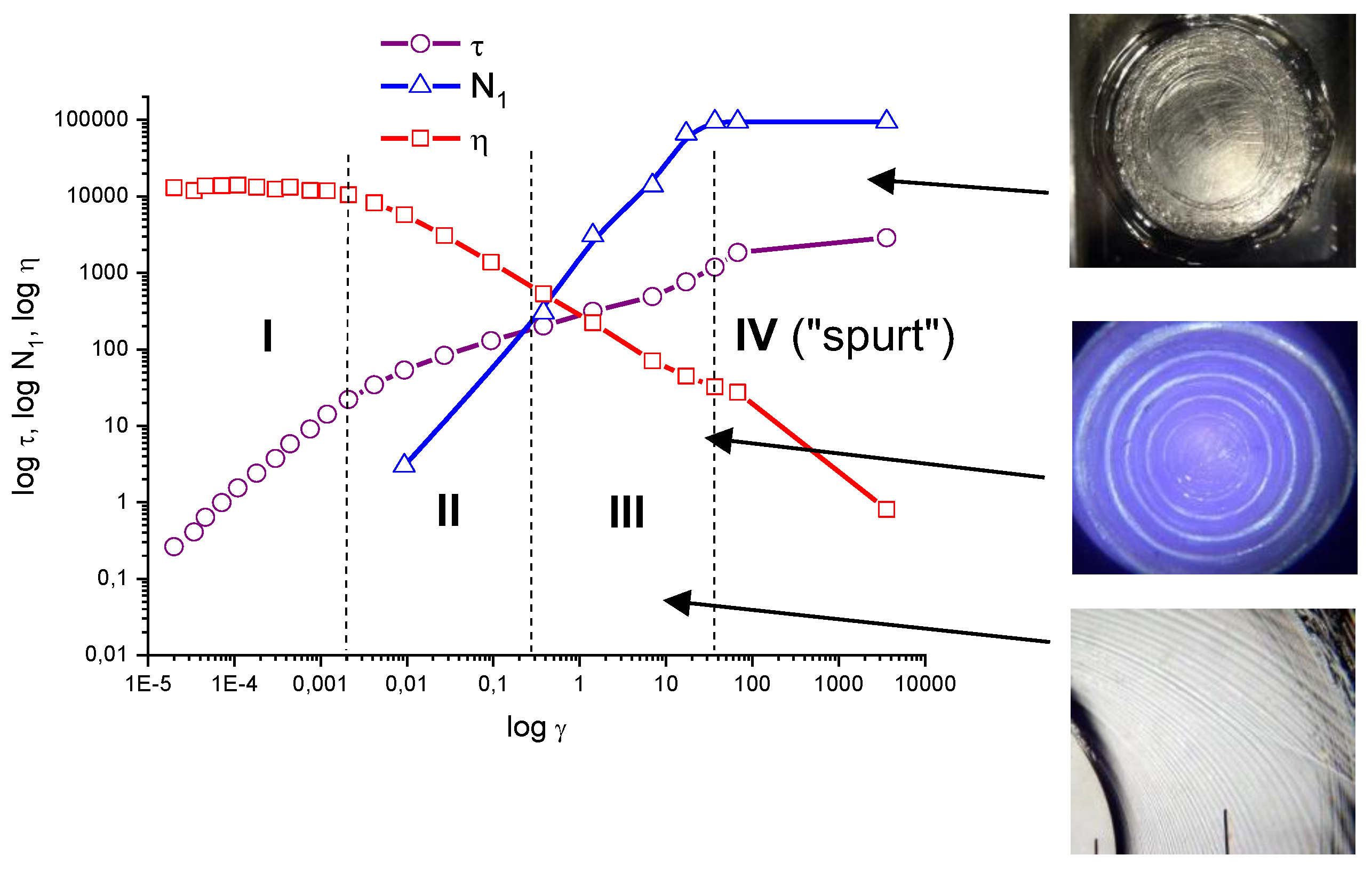
6.1. Shear-Induced Self-Assembling in Polymer Melts
6.2. Layered Flow in Polymer Mixtures
7. Deformation-Induced Structure Effects in Solutions
7.1. Main Experimental Observations
7.2. Theoretical Argumentations
Conclusions and Challenges
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Barnes, H.A.; Hutton, J.F.; Walters, K. An Introduction to Rheology; Elsevier Science Publishers B.V.: Amsterdam, The Netherlands, 1989; ISBN 0-444-87140-3. [Google Scholar]
- Malkin, A.Y. Non-linearity in rheology—An essay of classification. Rheol. Acta 1995, 34, 27–39. [Google Scholar] [CrossRef]
- Mewis, J.; Wagner, N.J. Thixotropy. Adv. Coll. Interface Sci. 2009, 147–148, 214–227. [Google Scholar] [CrossRef]
- Ferry, J.D. Viscoelastic Properties of Polymers, 3rd ed.; Wiley: New York, NY, USA, 1980; ISBN 978-0-471-04894-7. [Google Scholar]
- Cox, W.P.; Merz, E.H. Correlation of dynamic and steady-flow viscosities. J. Polym. Sci. 1958, 28, 619–622. [Google Scholar] [CrossRef]
- Winter, H.H. Three views of viscoelasticity for Cox–Merz materials. Rheol. Acta 2009, 48, 241–243. [Google Scholar] [CrossRef]
- Rathner, R.; Roland, W.; Albrecht, H.; Ruemer, F.; Miethlinger, J. Applicability of the Cox-Merz Rule to High-Density Polyethylene Materials with Various Molecular Masses. Polymers 2021, 13, 1218. [Google Scholar] [CrossRef] [PubMed]
- Malkin, A.Y. Non-Newtonian viscosity in steady-state shear flows. J. Non-Newton. Fluid Mech. 2013, 192, 48–65. [Google Scholar] [CrossRef] [Green Version]
- Wagner, H.M. Zur Netzwerktheorie von Polymer-Schmelzen. Rheol. Acta 1979, 18, 33–50. [Google Scholar] [CrossRef]
- Malkin, A.Y.; Semakov, A.V. Macro-modeling of entanglements. In Proceedings of the 7-th Annual European Rheology Conference AERC-2011, Suzdal, Russia, 4–8 May 2011. [Google Scholar]
- Malkin, A.Y.; Petrie, C.J.S. Some conditions for rupture of polymer liquids in extension. J. Rheol. 1997, 41, 1–25. [Google Scholar] [CrossRef]
- Malkin, A.Y.; Arinstein, A.; Kulichikhin, V.G. Polymer extension flows and instabilities. Prog. Polym. Sci. 2014, 39, 959–978. [Google Scholar] [CrossRef]
- Larson, R.G. The Structure and Rheology of Complex Fluids; Oxford University Press: New York, NY, USA, 1999; ISBN 0-19-512197-X. [Google Scholar]
- Andrade, R.J.; Maia, J.M. A study on the flow, failure, and rupture mechanisms of low-density polyethylene in controlled-stress uniaxial extensional flow. J. Rheol. 2011, 55, 925–937. [Google Scholar] [CrossRef]
- Huang, Q.; Hassager, O. Polymer liquids fracture like solids. Soft Matter 2017, 13, 3470–3474. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhu, X.; Wang, S.-Q. Mechanisms for different failure modes in startup extension. Tensile (rupture-like) failure and necking. J. Rheol. 2013, 57, 223–248. [Google Scholar] [CrossRef]
- Rasmussen, H.K.; Wingstrand, S.L.; Hassager, O. On the universality in the extensional rheology of monodisperse polymer melts and oligomer dilutions thereof. Rheol. Acta 2019, 58, 333–340. [Google Scholar] [CrossRef]
- Feng, Y.; Liu, J.; Wang, S.-Q.; Ntetsikas, K.; Avgeropoulos, A.; Kostas, M.; Mays, J. Exploring rheological responses to uniaxial stretching of various entangled polyisoprene melts. J. Rheol. 2019, 63, 763–771. [Google Scholar] [CrossRef]
- Matsumiya, Y.; Watanabe, H. Non-Universal Features in Uniaxially Extensional Rheology of Linear Polymer Melts and Concentrated Solutions: A Review. Prog. Polym. Sci. 2021, 112, 101325. [Google Scholar] [CrossRef]
- Huang, Q.; Mangnus, M.; Alvarez, N.J.; Koopmans, R.; Hassager, O. A new look at extensional rheology of low-density polyethylene. Rheol. Acta 2016, 55, 343–350. [Google Scholar] [CrossRef] [Green Version]
- Huang, Q.; Ahn, J.; Parisi, D.; Chang, T.; Hassager, O.; Panyukov, S.; Rubinstein, M.; Vlassopoulos, D. Unexpected Stretching of Entangled Ring Macromolecules. Phys. Rev. Lett. 2019, 122, 208001. [Google Scholar] [CrossRef] [Green Version]
- Wagner, M.H.; Narimissa, E.; Huang, Q. On the origin of brittle fracture of entangled polymer solutions and melts. J. Rheol. 2018, 62, 221–233. [Google Scholar] [CrossRef]
- Wang, S.-Q. Letter to the Editor: Melt rupture unleashed by few chain scission events in fully stretched strands. J. Rheol. 2018, 63, 105–107. [Google Scholar] [CrossRef]
- Wagner, M.H.; Narimissa, E.; Huang, Q. Response to “Letter to the Editor: Melt rupture unleashed by few chain scission events in fully stretched strands”. J. Rheol. 2019, 63, 419–421. [Google Scholar] [CrossRef]
- Wanger, M.H.; Narimissa, E.; Shalid, T. Elongational viscosity and brittle fracture of bidisperse blends of a high and several low molecular mass polystyrenes. Rheol. Acta 2021, 60, 603–617. [Google Scholar] [CrossRef]
- Larson, R. Constitutive equations for thixotropic fluids. J. Rheol. 2015, 59, 595–611. [Google Scholar] [CrossRef]
- Larson, R.; Wei, Y. A review of thixotropy and its rheological modeling. J. Rheol. 2019, 63, 477–501. [Google Scholar] [CrossRef]
- Agarwal, M.; Sharma, S.; Shankar, V.; Joshi, Y.M. Distinguishing thixotropy from viscoelasticity. J. Rheol. 2021, 65, 663–680. [Google Scholar] [CrossRef]
- Joishi, Y.M. Thixotropy, nonmonotonic stress relaxation, and the second law of thermodynamics. J. Rheol. 2022, 66, 111. [Google Scholar] [CrossRef]
- Coussot, P.; Nguyen, Q.D.; Huynh, H.T.; Bonn, D. Viscosity bifurcation in thixotropic, yielding fluids. J. Rheol. 2002, 46, 573–589. [Google Scholar] [CrossRef] [Green Version]
- Skvortsov, I.Y.; Malkin, A.Y.; Kulichikhin, V.G. Self-Oscillations Accompanying Shear Flow of Colloidal and Polymeric Systems. Reality and Instrumental Effects. Colloid J. 2019, 8, 176–186. [Google Scholar]
- Bagusat, F.; Böhme, B.; Schiller, P.; Mögel, H.-J. Shear induced periodic structure changes in concentrated alumina suspensions at constant shear rate monitored by FBRM. Rheol. Acta 2005, 44, 313–318. [Google Scholar] [CrossRef]
- Godfrin, P.D.; Valadez-Pérez, N.E.; Castañeda-Priego, R.; Wagner, N.J.; Lin, Y. Generalized phase behavior of cluster formation in colloidal dispersions with competing interactions. Soft Matter 2014, 10, 5061–5071. [Google Scholar] [CrossRef]
- de Souza Mendes, P.R.; Thompson, R.L. A critical overview of elasto-viscoplastic thixotropic modeling. J. Non. Newton. Fluid Mech. 2012, 187–188, 8–15. [Google Scholar] [CrossRef]
- Mujumdar, A.; Beris, A.N.; Metzner, A.B. Transient phenomena in thixotropic systems. J. Non-Newton. Fluid Mech. 2002, 101, 157–178. [Google Scholar] [CrossRef]
- Ewoldt, R.H.; McKinley, G.H. Mapping thixo-elasto-visco-plastic behavior. Rheol. Acta 2017, 56, 195–210. [Google Scholar] [CrossRef]
- Bharadwaj, N.A.; Ewoldt, R.H. The general low-frequency prediction for asymptotically-nonlinear material functions in oscillatory shear. J. Rheol. 2014, 58, 891–910. [Google Scholar] [CrossRef]
- Wei, Y.; Solomon, M.J.; Larson, R.G. Quantitative nonlinear thixotropic model with stretched exponential response in transient shear flows. J. Rheol. 2016, 60, 1301–1315. [Google Scholar] [CrossRef]
- Wei, Y.; Solomon, M.J.; Larson, R.G. A multimode structural kinetics constitutive equation for the transient rheology of thixotropic elasto-viscoplastic fluids. J. Rheol. 2018, 62, 321–342. [Google Scholar] [CrossRef]
- Wei, Y.; Solomon, M.J.; Larson, R.G. Letter to the Editor: Modeling the nonmonotonic time-dependence of viscosity bifurcation in thixotropic yield-stress fluids. J. Rheol. 2019, 53, 673–675. [Google Scholar] [CrossRef]
- Dimitriou, C.J.; McKinley, G.H. A comprehensive constitutive law for waxy crude oil: A thixotropic yield stress fluid. Soft Matter 2014, 10, 6619–6644. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fraggedakis, D.; Dimakopoulos, Y.; Tsamopoulos, J. Yielding the Yield Stress Analysis: A thorough comparison of recently proposed Elasto-Visco-Plastic (EVP) fluid models. J. Non-Newton. Fluid Mech. 2006, 236, 104–122. [Google Scholar] [CrossRef]
- Varchanis, S.; Makrigiorgos, G.; Moschopoulos, P.; Dimakopoulos, Y.; Tsamopoulos, J. Modeling the rheology of thixotropic elasto-visco-plastic materials. J. Rheol. 2019, 63, 609–639. [Google Scholar] [CrossRef]
- Metzger, B.; Pham, P.; Butler, J.E. Irreversibility and chaos: Role of lubrication interactions in sheared suspensions. Phys. Rev. E 2013, 87, 052304. [Google Scholar] [CrossRef] [Green Version]
- Coussot, P.; Malkin, A.Y.; Overlez, G. Introduction: Yield stress—Or 100 years of rheology. Rheol. Acta 2017, 56, 161–162. [Google Scholar] [CrossRef] [Green Version]
- Malkin, A.; Kulichikhin, V.; Ilyin, S. A modern look on yield stress fluids. Rheol. Acta 2017, 56, 177–188. [Google Scholar] [CrossRef]
- Masalova, I.; Fabrice, K.K.; Tschilumbu, N.N.; George, N.; Malkin, A.Y. Emulsification of highly concentrated emulsions—A criterion of shear stability. J. Rheol. 2018, 62, 781–790. [Google Scholar] [CrossRef]
- Malkin, A.Y. Rheology of filled polymers. In Filled Polymers I Science and Technology; Springer: Heidelberg, Germany, 1990; Volume 96, pp. 69–97. ISSN 0065-3195. [Google Scholar]
- Møller, P.C.F.; Mewis, J.; Bonn, D. Yield stress and thixotropy: On the difficulty of measuring yield stresses in practice. Soft Matter 2006, 2, 274–283. [Google Scholar] [CrossRef] [PubMed]
- Masalova, I.; Malkin, A.Y.; Foudazi, R. Yield stress of emulsions and suspensions as measured in steady shearing and in oscillations. Appl. Rheol. 2008, 18, 44790–44791. [Google Scholar] [CrossRef]
- Owens, C.E.; Hart, A.J.; McKinley, G.H. Improved rheometry of yield stress fluids using bespoke fractal 3D printed vanes. J. Rheol. 2020, 64, 643–662. [Google Scholar] [CrossRef] [Green Version]
- De Kee, D. Yield stress measurement techniques: A review. Phys. Fluids 2021, 33, 111301. [Google Scholar] [CrossRef]
- Uhlherr, H.T.; Guo, J.; Tiu, C.; Zhang, X.-M.; Zhou, J.Z.-Q.; Fang, T.-N. The shear-induced solid–liquid transition in yield stress materials with chemically different structures. J. Non-Newton. Fluid Mech. 2005, 125, 101–119. [Google Scholar] [CrossRef]
- Caton, F.; Baravian, C. Plastic behavior of some yield stress fluids: From creep to long-time yield. Rheol. Acta 2008, 47, 601–607. [Google Scholar] [CrossRef]
- Masalova, M.; Taylor, E.; Kharatiyan, E.; Malkin, A.Y. Rheopexy in highly concentrated emulsions. J. Rheol. 2005, 49, 839–849. [Google Scholar] [CrossRef]
- Malin, A.Y.; Isayev, A.I. Rheology: Concepts, Methods, and Applications, 4th ed.; ChemTec Publ.: Toronto, ON, Canada, 2022. [Google Scholar]
- Møller, P.C.F.; Fall, A.; Bonn, D. Origin of apparent viscosity in yield stress fluids below yielding. Europhys. Lett. 2009, 87, 38004. [Google Scholar] [CrossRef] [Green Version]
- Richards, J.A.; Guy, B.M.; Blanco, E.; Hermes, M.; Poy, G.; Poon, W.C.K. The role of friction in the yielding of adhesive non-Brownian suspensions. J. Rheol. 2020, 64, 405–412. [Google Scholar] [CrossRef] [Green Version]
- Jung, G.; Fielding, S.M. Wall slip and bulk yielding in soft particle suspensions. J. Rheol. 2021, 65, 199–212. [Google Scholar] [CrossRef]
- Barnes, H.A.; Walters, K. The yield stress myth? Rheol. Acta 1985, 24, 323–326. [Google Scholar] [CrossRef]
- Barnes, H.A. The “Yield Stress Myth?’ Paper—21 Years On. Appl. Rheol. 2007, 17, 43110-1. [Google Scholar] [CrossRef]
- Dinkgreve, M.; Denn, M.M.; Bonn, D. “Everything flows?”: Elastic effects on startup flows of yield-stress fluids. Rheol. Acta 2017, 56, 189–194. [Google Scholar] [CrossRef] [Green Version]
- Pal, R. Rheology of high internal phase ratio emulsions. Food Hydrocoll. 2006, 20, 997–1005. [Google Scholar] [CrossRef]
- Thompson, R.L.; de Souza Mendes, P.R. Rheological material functions at yielding. J. Rheol. 2020, 64, 615–623. [Google Scholar] [CrossRef]
- Malkin, A.Y.; Masalova, I. Shear and normal stresses in flow of highly concentrated emulsions. J. Non-Newton. Fluid Mech. 2007, 147, 65–68. [Google Scholar] [CrossRef]
- Dimitriou, C.J.; McKinley, G.H. A canonical framework for modeling elasto-viscoplasticity in complex fluids. J. Non-Newton. Fluid Mech. 2019, 265, 116–132. [Google Scholar] [CrossRef]
- de Cagny, H.; Fazilat, M.; Habibi, M.; Denn, M.M.; Bonn, D. The yield normal stress. J. Rheol. 2019, 63, 285–290. [Google Scholar] [CrossRef] [Green Version]
- Yang, K.; Liu, Z.; Wang, J.; Yu, W. Stress bifurcations in large avplitudes oscillatory shear of yield stress fluids. J. Rheol. 2018, 62, 89–106. [Google Scholar] [CrossRef]
- Zhang, X.; Fadoul, O.; Lorenceau, E.; Coussot, P. Yielding and flow of soft-jammed systems in elongation. Phys. Rev. Lett. 2018, 120, 048001. [Google Scholar] [CrossRef]
- Ovarlez, G.; Barra, Q.; Coussot, P. Three-dimensional jamming and flows of soft glassy materials. J. Nat. Mater. 2010, 9, 115–119. [Google Scholar] [CrossRef] [PubMed]
- Thompson, R.L.; Sica, P.; Mendes, P.R. de Souza. The yield stress tensor. J. Non-Newton. Fluid Mech. 2018, 261, 211–219. [Google Scholar] [CrossRef]
- Louvet, N.; Bonn, D.; Kellay, H. Nonuniversality in the Pinch-Off of Yield Stress Fluids: Role of Nonlocal Rheology. Phys. Rev. Lett. 2014, 113, 218302. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vermant, J.; Van Puyvelde, P.; Moldenaers, P.; Mewis, J.; Fuller, G.G. Anisotropy and Orientation of the Microstructure in Viscous Emulsions during Shear Flow. Langmuir 1998, 14, 1612–1617. [Google Scholar] [CrossRef]
- Jackson, N.E.; Tucker, C.L., III. A model for large deformation of an ellipsoidal droplet with interfacial tension. J. Rheol. 2003, 47, 659–682. [Google Scholar] [CrossRef]
- Caggioni, M.; Trappe, V.; Spicer, P.T. Variations of the Herschel–Bulkley exponent reflecting contributions of the viscous continuous phase to the shear rate-dependent stress of soft glassy materials. J. Rheol. 2020, 64, 413–422. [Google Scholar] [CrossRef] [Green Version]
- Gilbert, D.; Valette, R.; Lemaire, E. Impact of particle stiffness on shear-thinning of non-Brownian suspensions. J. Rheol. 2022, 66, 161. [Google Scholar] [CrossRef]
- Khabaz, F.; Liu, T.; Cloitre, M.; Bonnecaze, R.T. Shear-induced ordering and crystallization of jammed suspensions of soft particles glasses. Phys. Rev. Fluids 2017, 2, 093301. [Google Scholar] [CrossRef]
- Malkin, A.Y. Shear-induced transitions in colloidal and polymeric liquids. Adv. Colloid Interface Sci. 2021, 290, 102381. [Google Scholar] [CrossRef] [PubMed]
- Pasquino, R.; Snijkers, F.; Grizzuti, N.; Vermant, J. The effect of particle size and migration on the formation of flow-induced structures in viscoelastic suspensions. Rheol. Acta 2010, 49, 993–1001. [Google Scholar] [CrossRef]
- Mirsepassi, A.; Rajaram, B.; Mohraz, A.; Dunn-Rankin, D. Particle chaining and chain dynamics in viscoelastic liquids. J. Non-Newton. Fluid Mech. 2012, 179–180, 1–8. [Google Scholar] [CrossRef]
- Pasquino, R.; Snijkers, F.; Grizzuti, N.; Vermant, J. Directed self-assembly of spheres into a two dimensional colloidal crystal by viscoelastic stresses. Langmuir 2010, 26, 3016–3019. [Google Scholar] [CrossRef]
- Kulichikhin, V.G.; Semakov, A.V.; Karbushev, V.V.; Platé, N.A.; Picken, S.J. The chaos-to-order transition in critical modes of shearing for polymer and nanocomposite melts. Polym. Sci. Ser. A 2009, 51, 1303. [Google Scholar] [CrossRef]
- Huang, P.; Hu, H.; Joseph, D. Direct simulation of the sedimentation of elliptic particles in Oldroyd-B fluids. J. Fluid Mech. 1998, 362, 297–326. [Google Scholar] [CrossRef] [Green Version]
- Van Loon, S.; Fransaer, J.; Clasen, C.; Vermant, J. String formation in sheared suspensions in rheologically complex media: The essential role of shear thinning. J. Rheol. 2014, 58, 237–252. [Google Scholar] [CrossRef] [Green Version]
- Pignon, F.; Magnin, A.; Piau, J.-M. Thixotropic behavior of clay dispersions: Combinations of scattering and rheometric techniques. J. Rheol. 1998, 42, 1349–1373. [Google Scholar] [CrossRef]
- Hipp, J.B.; Richards, J.J.; Wagner, N.J. Direct measurements of the microstructural origin of shear-thinning in carbon black suspensions. J. Rheol. 2021, 65, 145–157. [Google Scholar] [CrossRef]
- Papkov, S.P.; Kulichikhin, V.G.; Kalmykova, V.D.; Malkin, A.Y. Rheological properties of anisotropic poly(para-benzamide) solutions. J. Polym. Sci. Polym. Phys. Ed. 1974, 12, 1753–1770. [Google Scholar] [CrossRef]
- Kwolek, S.L.; Morgan, P.W.; Schaefgen, J.M.; Gurlich, L.W. ACS Polym. Preprints 1976, 17, 53–58. [Google Scholar]
- Malkin, A.Y.; Vasil’eva, N.V.; Belousova, T.A.; Kulichikhin, V.G. Viscosity anisotropy in lyotropic liquid crystals of poly-p-benzamide. Colloid J. USSR 1979, 41, 162–163. [Google Scholar]
- Makarova, V.V.; Tolstykh, M.Y.; Picken, S.J.; Mendes, E.; Kulichikhin, V.G. Rheology-Structure interrelationships of hydroxypropylcellulose liquid crystal solutions and their nanocomposites under flow. Macromolecules 2013, 46, 1144–1157. [Google Scholar] [CrossRef]
- Kawabata, H.; Nishiura, D.; Sakaguchi, H.; Tatsumi, Y. Self-organized domain microstructures in a plate-like particle suspension subjected to rapid simple shear. Rheol. Acta 2013, 52, 1–21. [Google Scholar] [CrossRef]
- Monsenti, A.; Peña, A.A.; Pasquali, P. Vorticity Alignment and Negative Normal Stresses in Sheared Attractive Emulsions. Phys. Rev. Lett. 2004, 92, 058303. [Google Scholar] [CrossRef] [Green Version]
- Bian, X.; Litvinov, S.; Ellero, M.; Wagner, N.J. Hydrodynamic shear thickening of particulate suspension under confinement. J. Non-Newton. Fluid Mech. 2014, 213, 39–40. [Google Scholar] [CrossRef]
- Rathee, V.; Blair, D.; Urbach, J.S. Localized transient jamming in discontinuous shear thickening. J. Rheol. 2020, 64, 299–308. [Google Scholar] [CrossRef] [Green Version]
- Sohn, I.S.; Rajagopalan, R. Microrheology of model quasi-hard sphere dispersions. J. Rheol. 2004, 48, 117–142. [Google Scholar] [CrossRef]
- Carotenuto, C.; Rexha, G.; Martone, R.; Minale, M. The microstructural change causing the failure of the Cox-Merz rule in Newtonian suspensions: Experiments and simulations. Rheol. Acta 2021, 60, 309–325. [Google Scholar] [CrossRef]
- Li, B.; Guo, Y.; Steeman, P.; Bulters, M.; Yu, W. Shear-induced breakdown and agglomeration in nanoparticles filled polymer: The shift of phase boundary and kinetics. J. Rheol. 2021, 65, 291–310. [Google Scholar] [CrossRef]
- O’Brien, V.T.; Mackley, M.E. Shear and elongation flow properties of kaolin suspensions. J. Rheol. 2002, 46, 557. [Google Scholar] [CrossRef]
- Lee, Y.S.; Wagner, N.J. Shear thickening in concentrated suspensions is due to the formation of jamming cluster. Rheol. Acta 2003, 42, 199–208. [Google Scholar] [CrossRef]
- Egres, R.G.; Wagner, N.J. The rheology and microstructure of acicular precipitated calcium carbonate colloidal suspensions through shear and thickening transition. J. Rheol. 2005, 49, 719–746. [Google Scholar] [CrossRef] [Green Version]
- Malkin, A.Y.; Kulichilhin, V.G. Shear Thickening and Dynamic Glass Transition of Concentrated Suspensions. State of the Problem. Colloid J. 2016, 78, 1–8. [Google Scholar] [CrossRef]
- Mari, R.; Seto, R.; Morris, J.F.; Denn, M.M. Shear thickening, frictionless and frictional rheologies in non-Brownian suspensions. J. Rheol. 2014, 58, 1693–1724. [Google Scholar] [CrossRef] [Green Version]
- Malkin, A.Y.; Mityukov, A.V.; Kotomin, S.V.; Shabeko, A.A.; Kulichikhin, V.G. Elasticity and plasticity of highly concentrated non-colloidal suspensions in shear. J. Rheol. 2020, 64, 469–478. [Google Scholar] [CrossRef]
- Mityukov, A.V.; Govorov, V.A.; Malkin, A.Y.; Kulichikhin, V.G. Rheology of Highly Concentrated Suspensions with a Bimodal Size Distribution of Solid Particles for Powder Injection Molding. Polymers 2021, 13, 2709. [Google Scholar] [CrossRef] [PubMed]
- Azzurri, F.; Alfonso, C.C. Insightes into formation and relaxation of shear induced nucleation precursors in isotactic polystyrene. Macromolecules 2008, 41, 1377–1383. [Google Scholar] [CrossRef]
- Mortensen, K.; Theunissen, E.; Kleppinger, R.; Almdal, K.; Reynaers, H. Shear-Induced Morphologies of Cubic Ordered Block Copolymer Micellar Networks Studied by in Situ Small-Angle Neutron Scattering and Rheology. Macromolecules 2002, 35, 7773–7781. [Google Scholar] [CrossRef]
- Zhao, Y.; Matsubo, G.; Ito, H. Shear-induced crystallization and rheological behavior of syndiotactic polystyrene. J. Mater. Res. 2012, 27, 1372–1378. [Google Scholar] [CrossRef]
- Wang, J.; Bai, J.; Zhang, Y.; Fang, H.; Wang, Z. Shear-induced enhancements of crystallization kinetics and morphological transformation for long chain branched polylactides with different branching degrees. Sci. Rep. 2016, 6, 26560. [Google Scholar] [CrossRef] [PubMed]
- Chang, B.; Schneider, K.; Lu, B.; Vogel, R.; Zheng, G.; Heinrich, G. Accelerating shear-induced crystallization and enhancing crystal orientation of isotactic-polypropylene via nucleating agent self-assembly. Polymer 2018, 158, 213–222. [Google Scholar] [CrossRef]
- Chen, J.; Schneider, K.; Heinrich, G. In-Situ Synchrotron X-ray Study on the Structure Variation of Morphology-Identified Injection-Molded β-Nucleated iPP under Tensile Deformation. Polymers 2021, 13, 3730. [Google Scholar] [CrossRef] [PubMed]
- Jalali, A.; Shahbikian, S.; Huneault, M.A.; Elkoun, S. Effect of molecular weight on the shear-induced crystallization of poly(lactic acid). Polymer 2017, 112, 393–401. [Google Scholar] [CrossRef]
- Jariyavidyanont, K.; Mallardo, S.; Cerruti, P.; Di Lorenzo, M.L.; Boldi, R.; Rhoades, A.M.; Androsch, R. Shear-induced crystallization of polyamide 11. Rheol. Acta 2021, 60, 231–240. [Google Scholar] [CrossRef]
- Nébouy, M.; de Almeida, A.; Chazeau, L.; Baeza, G.P. Modeling shear-induced crystallization in startup flow: The case of segmented copolymers. J. Rheol. 2019, 63, 837–850. [Google Scholar] [CrossRef]
- Fusco, C.; Dieudonné-George, P.; Baeza, G.P. Flow-induced crystallization of a multiblock copolymer under large amplitude oscillatory shear: Experiments and modeling. J. Rheol. 2021, 65, 405–418. [Google Scholar] [CrossRef]
- Liu, X.; Yu, W. Weak shear-induced slowdown in crystallization of less-entangled poly(ε-caprolactone). Macromolecules 2021, 54, 3347–3357. [Google Scholar] [CrossRef]
- Liu, C.; Zhang, J.; Zhang, Z.; Huang, S.; Chen, Q.; Colby, R.H. Shear-Induced Oriented Crystallization for Isotactic Poly(1-butene) and Its Copolymer with Ethylene. Macromolecules 2020, 53, 3071–3081. [Google Scholar] [CrossRef]
- Graham, R.S. Understanding flow-induced crystallization in polymers: A perspective on the role of molecular simulations. J. Rheol. 2019, 63, 203–214. [Google Scholar] [CrossRef]
- Nicholson, D.A.; Rutledge, G.C. An assessment of models for flow-enhanced nucleation in an n-alkane melt by molecular simulation. J. Rheol. 2019, 63, 465–475. [Google Scholar] [CrossRef]
- Janeschitz-Kriegl, H. Some remarks on flow induced crystallization in polymer melts. J. Rheol. 2013, 57, 1057–1964. [Google Scholar] [CrossRef]
- Hu, Y.H. Steady-state shear banding in entangled polymers? J. Rheol. 2010, 54, 1307–1324. [Google Scholar] [CrossRef]
- Agimelen, O.S.; Olmsted, P. Apparent Fracture in Polymeric Fluids Under Step Shear. Phys. Rev. Lett. 2012, 110, 204503. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, X.; Wang, S.-Q. Strain localization during squeeze of entangled polymer melts under constant force. J. Rheol. 2018, 62, 491–499. [Google Scholar] [CrossRef]
- Lerouge, S.; Olmsted, P.D. Non-local Effects in Shear Banding of Polymeric Flows. Front. Phys. 2020, 7, 246. [Google Scholar] [CrossRef]
- Zhang, J.; Lodge, T.P.; Macosko, C.W. Interfacial slip reduced polymer-polymer adhesion during coextrusion. J. Rheol. 2006, 50, 41–57. [Google Scholar] [CrossRef]
- Lee, P.C.; Park, H.E.; Morse, D.C.; Macosko, C.W. Polymer-polymer interfacial slip in multilayered films. J. Rheol. 2009, 53, 893–915. [Google Scholar] [CrossRef]
- Malkin, A.Y.; Patlazhan, V.A. Wall slip for complex liquids—Phenomenon and its causes. Adv. Coll. Interface Sci. 2018, 257, 42–57. [Google Scholar] [CrossRef] [PubMed]
- Jordan, A.M.; Lee, B.; Kim, K.; Ludtke, E.; Lhost, O.; Jaffer, S.A.; Bates, F.; Macosko, C.W. Rheology of polymer multilayers: Slip in shear, hardening in extension. J. Rheol. 2019, 63, 751–761. [Google Scholar] [CrossRef]
- Li, Z.; Olah, A.; Baer, E. Micro- and nano-layered processing of new polymeric systems. Prog. Polym. Sci. 2020, 102, 101–210. [Google Scholar] [CrossRef]
- Tsebrenko, M.V.; Danilova, G.P.; Malkin, A.Y. Fracture of ultrafine fibers in the flow of non-Newtonian polymers. J. Non-Newt. Fluid Mech. 1989, 31, 1–26. [Google Scholar] [CrossRef]
- Malkin, A.Y.; Gumennyi, I.V.; Aliev, A.D.; Chalykh, A.E.; Kulichikhin, V.G. Molecular motion in mixtures of polymer melts in a capillary flow. J. Mol. Liquids 2021, 344, 117919. [Google Scholar] [CrossRef]
- Isayev, A.I.; Modic, M. Self-Reinforced melt processible polymer composites: Extrusion, compression, and injection molding. Polym. Compos. 1987, 8, 158–175. [Google Scholar] [CrossRef]
- Kulichikhin, V.G.; Plate, Ν.A. Blend composites based on liquid crystal thermoplasts. Polym. Sci. USSR 1991, 33A, 1–37. [Google Scholar] [CrossRef]
- Peterson, J.D.; Fredrickson, G.H.; Leal, L.G. Shear induced demixing in bidisperse and polydisperse polymer blends: Predictions from a multifluid model. J. Rheol. 2020, 64, 1391–1408. [Google Scholar] [CrossRef]
- Schreiber, H.P. Component redistribution in extrusion of polyethylene compounds. J. Appl. Polym. Sci. 1974, 18, 2501–2508. [Google Scholar] [CrossRef]
- Sommer, D.E.; Favaloro, A.J.; Pipes, R.B. Coupling anisotropic viscosity and fiber orientation in applications to squeeze flow. J. Rheol. 2018, 52, 669–679. [Google Scholar] [CrossRef]
- Matsuo, T.; Pavan, A.; Peterlin, A.; Turner, D.T. Time-dependent changes of viscosity in dilute polymer solutions. J. Colloid Interface Sci. 1967, 24, 241–251. [Google Scholar] [CrossRef]
- Malkin, A.Y.; Kulichikhin, V.G.; Polyakova, M.Y.; Zuev, K.V.; Govorov, V.A. Unexpected rheological behavior of solutions of aromatic polyamide in transient physical states. Phys. Fluids 2020, 32, 073107. [Google Scholar] [CrossRef]
- Ghannam, M.T.; Selim, Y.E.; Zekri, A.Y.; Esmail, N. Thixotropic Assessment of Some Enhanced Oil Recovery used Polymers. Int. J. Eng. Res. Technol. 2020, 9, 1683–1693. Available online: https://www.ijert.org/thixotropic-assessment-of-some-enhanced-oil-recovery-used-polymers (accessed on 23 February 2022).
- Valenti, G.; Alfonso, C.; Ciferri, A.; Giordani, P.; Marrucci, G. Solution Spinning of a Semirigid Chain Polymer Forming Ultrahigh Modulus Fibers. J. Appl. Polym. Sci. 1981, 26, 3643–3655. [Google Scholar] [CrossRef]
- Münstedt, H.; Starý, Z. Steady states in extensional flow of strain hardening polymer melts and the uncertainties of their determination. J. Rheol. 2013, 57, 1065–1077. [Google Scholar] [CrossRef]
- Bach, A.; Rasmussen, H.K.; Hassager, O. Extensional viscosity for polymer melts measured in the filament stretching rheometer. J. Rheol. 2003, 47, 429–441. [Google Scholar] [CrossRef] [Green Version]
- Malkin, A.Y.; Subbotin, A.V.; Kulichilkin, V.G. Stability of polymer jets in extension: Physicochemical and rheological mechanisms, Russ. Chem. Rev. 2020, 89, 811–828. [Google Scholar] [CrossRef]
- Datta, S.S.; Ardekani, A.M.; Arratia, P.E.; Beris, A.N.; Bischofberger, I.; McKinley, G.H.; Eggers, J.G.; López-Aguilar, J.E.; Fielding, S.M.; Frishman, A.; et al. Perspectives on viscoelastic flow instabilities and elastic turbulence. arXiv, 2021; arXiv:2108.09841. [Google Scholar]
- Oliveira, M.S.N.; McKinley, G.H. Iterated stretching and multiple beads-on-a-string phenomena in dilute solutions of highly extensible flexible polymers. Phys. Fluids 2005, 17, 071704. [Google Scholar] [CrossRef] [Green Version]
- Tirtaatmadja, V.; McKinley, G.H.; Cooper-White, J.J. Drop formation and breakup of low viscosity elastic fluids: Effects of molecular weight and concentration. Phys. Fluids 2006, 18, 043101. [Google Scholar] [CrossRef] [Green Version]
- Bhat, P.P.; Appathurai, S.; Harris, M.T.; Pasquali, M.; McKinley, G.H.; Basaran, O.A. Formation of beads-on-a-string structures during break-up of viscoelastic filaments. Nat. Phys. 2010, 6, 625–631. [Google Scholar] [CrossRef] [Green Version]
- Wagner, C.; Amarouchene, Y.; Bonn, D.; Eggers, J. Droplet Detachment and Satellite Bead Formation in Viscoelastic Fluids. Phys. Rev. Lett. 2005, 95, 164504. [Google Scholar] [CrossRef] [Green Version]
- Sattler, R.; Wagner, C.; Eggers, J. Blistering Pattern and Formation of Nanofibers in Capillary Thinning of Polymer Solutions. Phys. Rev. Lett. 2008, 100, 164502. [Google Scholar] [CrossRef]
- Sattler, R.; Gier, S.; Eggers, J.; Wagner, C. The final stages of capillary break-up of polymer solutions. Phys. Fluids 2012, 24, 023101. [Google Scholar] [CrossRef]
- Kulichikhin, V.G.; Malkin, A.Y.; Semakov, A.V.; Skvortsov, I.Y.; Arinstein, A. Liquid Filament Instability due to Stretch-Induced Phase Separation in Polymer Solutions. Liquid Filament Instability. Eur. Phys. J. E 2014, 37, 10. [Google Scholar] [CrossRef] [PubMed]
- Semakov, A.V.; Kulichikhin, V.G.; Tereshin, A.K.; Antonov, S.V.; Malkin, A.Y. On the nature of phase separation of polymer solutions at high extension rates. J. Polym. Sci. Part B Polym. Phys. 2015, 53, 559–565. [Google Scholar] [CrossRef]
- Kulichikhin, V.G.; Skvortsov, I.Y.; Mironova, M.I.; Ozerin, A.N.; Kurkin, T.S.; Berkovich, A.K.; Frenkin, E.I.; Malkin, A.Y. From polyacrylonitrile, its solutions and filaments to carbon fibers. II. Spinning PAN-precursors and their thermal treatment. Adv. Polym. Technol. 2016, 36, 21761. [Google Scholar] [CrossRef]
- Hoyle, D.M.; Fielding, S.M. Necking after extensional filament stretching of complex fluids and soft solids. J. Non-Newton. Fluid Mech. 2017, 247, 132–145. [Google Scholar] [CrossRef] [Green Version]
- Hassager, O.; Wang, Y.; Huang, Q. Extensional rheometry of model liquids: Simulations of filament stretching. Phys. Fluids 2022, 33, 123108. [Google Scholar] [CrossRef]
- Karim, A.M.; Suszynski, W.J.; GrifÞth, W.B.; Pujari, S.; Francis, L.F.; Carvalho, M.S. Effect of viscoelasticity on stability of liquid curtain. J. Non-Newton. Fluid Mech. 2018, 257, 83–94. [Google Scholar] [CrossRef]
- Bazzi, M.S.; Carvalho, M.S. Effect of viscoelasticity on liquid sheet rupture. J. Non-Newton Fluid Mech. 2019, 264, 107–116. [Google Scholar] [CrossRef]
- Semakov, A.V.; Kulichikhin, V.G.; Malkin, A.Y. Self-organization of polymeric fluids in strong stress fields. Adv. Condens. Matter Phys. 2015, 2015, 172862. [Google Scholar] [CrossRef] [Green Version]
- Semakov, A.V.; Skvortsov, I.Y.; Kulichikhin, V.G.; Malkin, A.Y. From Capillary to Elastic Instability of Jets of Polymeric Liquids: Role of the Entanglement Network of Macromolecules. JETP Lett. 2015, 101, 690–692. [Google Scholar] [CrossRef]
- Kibbelaar, H.V.M.; Deblais, A.; Burla, F.; Koenderink, G.H.; Velikov, K.P.; Bonn, D. Capillary thinning of elastic and viscoelastic threads: From elastocapillarity to phase separation. Phys. Rev. Fluids 2020, 5, 092001. [Google Scholar] [CrossRef]
- Deblais, A.; Velikov, K.P.; Bonn, D. Pearling Instabilities of a Viscoelastic Thread. Phys. Rev. Lett. 2018, 120, 194501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cromer, M.; Villet, M.C.; Fredrickson, G.H.; Leal, L.G.; Sepanyan, R.; Bulters, M.J. Concentration fluctuations in polymer solutions under extensional flow. J. Rheol. 2013, 57, 1211–1235. [Google Scholar] [CrossRef]
- Peterson, J.D.; Cromer, M.; Fredrickson, G.H.; Leal, L.G. Shear banding predictions for the two-fluid Rolie-Poly model. J. Rheol. 2016, 60, 927–951. [Google Scholar] [CrossRef]
- Peterson, J.D.; Fredrickson, G.H.; Leal, L.G. Does shear induced demixing resemble a thermodynamically driven instability? J. Rheol. 2019, 63, 335–359. [Google Scholar] [CrossRef]
- Likhtman, A.E.; Graham, R.S. Simple constitutive equation for linear polymer melts derived from molecular theory: Rolie–Poly equation. J. Non-Newton. Fluid Mech. 2003, 114, 1–12. [Google Scholar] [CrossRef]
- Boudara, V.A.H.; Peterson, J.D.; Leal, L.G.; Read, D.J. Nonlinear rheology of polydisperse blends of entangled linear polymers: Rolie-Double-Poly models. J. Rheol. 2019, 63, 71–91. [Google Scholar] [CrossRef] [Green Version]
- Narimissa, E.; Wagner, M.H. Review on tube model based constitutive equations for polydisperse linear and long-chain branched polymer melts. J. Rheol. 2019, 63, 361–375. [Google Scholar] [CrossRef]
- Dinic, J.; Sharma, V. Macromolecular relaxation, strain, and extensibility determine elastocapillary thinning and extensional viscosity of polymer solutions. Proc. Natl. Acad. Sci. USA 2019, 116, 8766–8774. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Subbotin, A.V.; Skvortsov, I.Y.; Kuzin, M.S.; Gerasimenko, P.S.; Kulichikhin, V.G.; Malkin, A.Y. The shape of a falling jet formed by concentrated polymer solutions. Phys. Fluids 2021, 33, 083108. [Google Scholar] [CrossRef]
- Ardekani, A.M.; Sharma, V.; Mckinley, G.H. Dynamics of bead formation, filament thinning and breakup in weakly viscoelastic jets. J. Fluid Mech. 2010, 665, 46–56. [Google Scholar] [CrossRef] [Green Version]
- Clasen, C.; Plog, J.P.; Kulicke, W.-M.; Owens, M.; Macosko, C.; Scriven, L.E.; Verani, M.; McKinley, G.H. How dilute are dilute solutions in extensional flows? J. Rheol. 2006, 50, 849–881. [Google Scholar] [CrossRef] [Green Version]
- Malkin, A.Y.; Semakov, A.V.; Skvortsov, I.Y.; Zatonskikh, P.; Kulichikhin, V.G.; Subbotin, A.V.; Semenov, A.N. Spinnability of dilute polymer solutions. Macromolecules 2017, 50, 8231–8244. [Google Scholar] [CrossRef]
- Semenov, A.N.; Subbotin, A.V. Hierarchical structure formation in unentangled polymer solutions under extension. AIP Conf. Proc. 2016, 1736, 020086. [Google Scholar]
- Prabhakar, R.; Gadkari, S.; Gopesh, T.; Shaw, M.J. Influence of stretching induced self-concentration and self-dilution on coil-stretch hysteresis and capillary thinning of unentangled polymer solutions. J. Rheol. 2016, 60, 345–366. [Google Scholar] [CrossRef]
- Prabhakar, R.; Sasmal, C.; Nguyen, D.A.; Sridhar, T.; Prakash, J.R. Effect of stretching-induced changes in hydrodynamic screening on coil-stretch hysteresis of unentangled polymer solutions. Phys. Rev. Fluids 2017, 2, 011301(R). [Google Scholar] [CrossRef] [Green Version]
- Subbotin, A.V.; Semenov, A.N. Phase Separation in Dilute Polymer Solutions at High-Rate Extension. J. Polym. Sci. Part B Polym. Phys. 2016, 54, 1066–1073. [Google Scholar] [CrossRef]
- Semenov, A.N.; Subbotin, A.V. Phase Separation Kinetics in Unentangled Polymer Solutions Under High-Rate Extension. J. Polym. Sci. Part B Polym. Phys. 2017, 55, 623–637. [Google Scholar] [CrossRef]
- Subbotin, A.V.; Semenov, A.N. Phase Separation in Polymer Solutions under Extension. Polym. Sci. Ser. C 2018, 60, 106–117. [Google Scholar] [CrossRef]
- Subbotin, A.V.; Semenov, A.N. Capillary-induced Phase Separation in Ultrathin Jets of Rigid-chain Polymer Solutions. JETP Lett. 2020, 111, 55–61. [Google Scholar] [CrossRef]
- Subbotin, A.V.; Semenov, A.N. Multiple droplets formation in ultrathin bridges of rigid rod dispersions. J. Rheol. 2020, 64, 13–27. [Google Scholar] [CrossRef]













Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kulichikhin, V.G.; Malkin, A.Y. The Role of Structure in Polymer Rheology: Review. Polymers 2022, 14, 1262. https://doi.org/10.3390/polym14061262
Kulichikhin VG, Malkin AY. The Role of Structure in Polymer Rheology: Review. Polymers. 2022; 14(6):1262. https://doi.org/10.3390/polym14061262
Chicago/Turabian StyleKulichikhin, Valery G., and Alexander Ya. Malkin. 2022. "The Role of Structure in Polymer Rheology: Review" Polymers 14, no. 6: 1262. https://doi.org/10.3390/polym14061262
APA StyleKulichikhin, V. G., & Malkin, A. Y. (2022). The Role of Structure in Polymer Rheology: Review. Polymers, 14(6), 1262. https://doi.org/10.3390/polym14061262






