Impact of the Liquid Crystal Order of Poly(azomethine-sulfone)s on the Semiconducting Properties
Abstract
:1. Introduction
2. Materials and Methods
3. Results
- −
- is nonmultifractal time, an affine parameter of the movement curves of the entities found in the complex system;
- −
- is the multifractal spatial coordinate;
- −
- is the velocity field at a differentiable scale resolution;
- −
- is the velocity field at a nondifferentiable scale resolution;
- −
- is the scale resolution;
- −
- is a constant coefficient associated with the multifractal–nonmultifractal scale transition;
- −
- is the state density;
- −
- is the state function with the amplitude and phase ;is the scalar specific multifractal potential, which quantifies the multifractalization degree of the movement curves in the complex system;
- −
- is the singularity spectrum of order where is the fractal dimension of the movement curves of the complex system entities. This spectrum allows the identification of universality classes in the complex system dynamics, even when attractors have different aspects, and it also allows the identification of areas in which the dynamics can be characterized by a specific fractal dimension.
- −
- the velocity field at a nondifferentiable scale:
- −
- the specific multifractal force field:
- −
- conductivity at differentiable scale resolutions:
- −
- conductivity at nondifferentiable scale resolutions:
- −
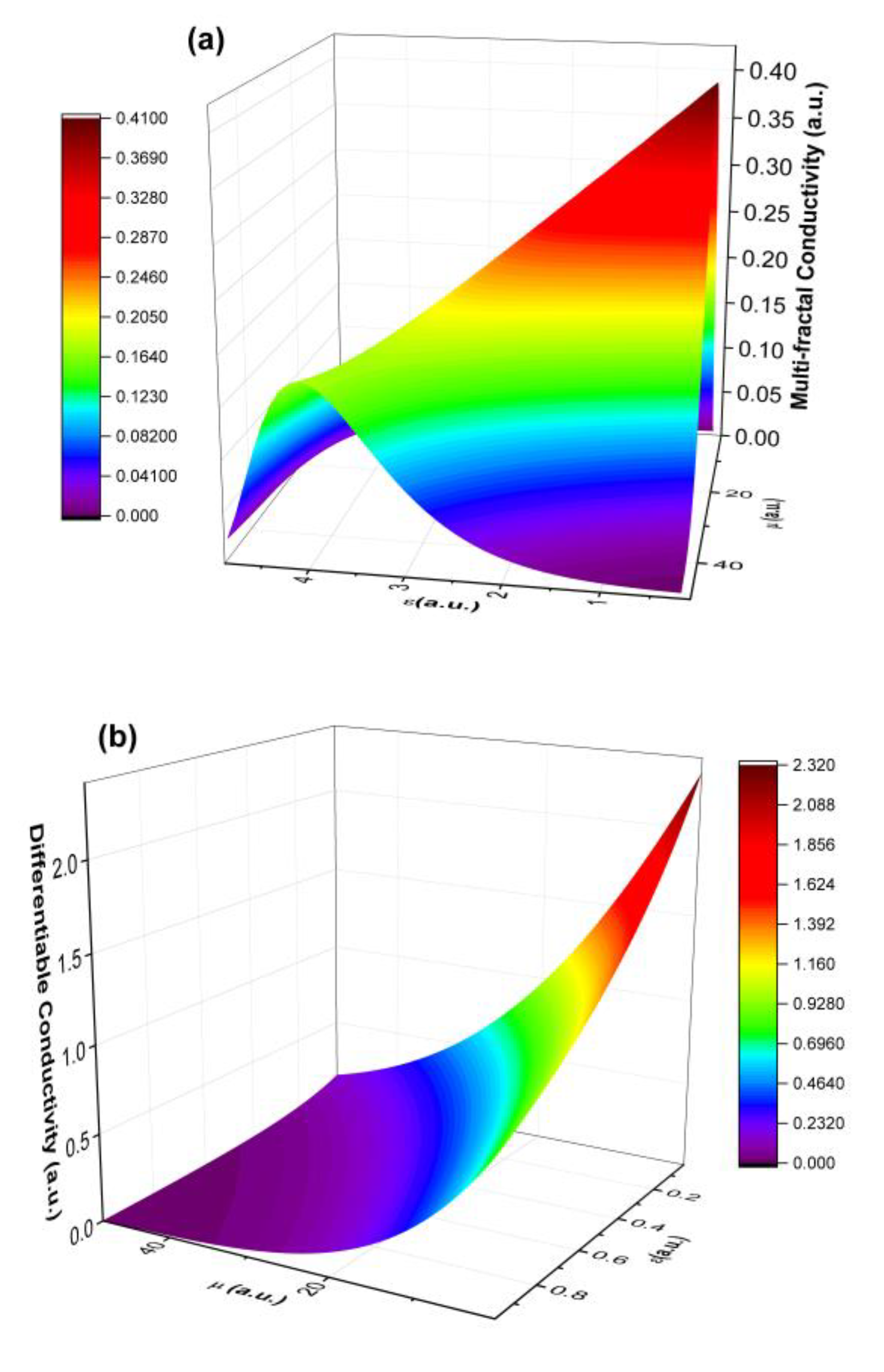
- conductivity at global scale resolutions:
- −
- conductivity at differentiable scale resolutions:
- −
- conductivity at nondifferentiable scale resolutions:
- −
- conductivity at global scale resolutions:
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bronstein, H.; Nielsen, C.B.; Schroeder, B.C.; McCulloch, I. The role of chemical design in the performance of organic semiconductors. Nat. Rev. Chem. 2020, 4, 66–77. [Google Scholar] [CrossRef]
- Bendrea, A.D.; Cianga, L.; Cianga, I. Progress in the Field of Conducting Polymers for Tissue Engineering Applications. J. Biomat. Appl. 2011, 26, 3–84. [Google Scholar] [CrossRef] [PubMed]
- Ramanavicius, S.; Ramanavicius, A. Conducting Polymers in the Design of Biosensors and Biofuel Cells. Polymers 2021, 13, 49. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.; Ozlu, B.; Eom, T.; Martin, D.C.; Shim, B.S. Electrically conducting polymers for bio-interfacing electronics: From neural and cardiac interfaces to bone and artificial tissue biomaterials. Biosens. Bioelectron. 2020, 170, 112620. [Google Scholar] [CrossRef]
- Silva, A.C.d.; Torresi, S.I.C.d. Advances in Conducting, Biodegradable and Biocompatible Copolymers for Biomedical Applications. Front. Mater. 2019, 6, 98. [Google Scholar] [CrossRef] [Green Version]
- Li, G.; Yu, K.; Noordijk, J.; Meeusen-Wierts, M.H.; Gebben, B.; Lohuis, P.A.M.; Schotman, A.H.M.; Bernaerts, K. Hydrothermal polymerization towards fully biobased polyazomethines. Chem. Commun. 2020, 56, 9194–9197. [Google Scholar] [CrossRef] [PubMed]
- Lei, T.; Guan, M.; Liu, J.; Lin, H.C.; Pfattner, R.; Shaw, L.; McGu, A.F. Biocompatible and totally disintegrable semiconducting polymer for ultrathin and ultralightweight transient electronics. Proc. Natl. Acad. Sci. USA 2017, 114, 5107–5112. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bolduc, A.; Ouahabi, A.A.; Mallet, C.; Skene, W.G. Insight into the isoelectronic character of azomethines and vinylenes using representative models—A spectroscopic and electrochemical study. J. Org. Chem. 2013, 78, 9258–9269. [Google Scholar] [CrossRef] [PubMed]
- Zabulica, A.; Balan, M.; Belei, D.; Sava, M.; Simionescu, B.C.; Marin, L. Novel luminescent phenothiazine-based Schiff bases with tuned morphology. Synthesis, structure, photophysical and thermotropic characterization. Dye. Pigment. 2013, 96, 686–698. [Google Scholar] [CrossRef]
- Katariya, K.D.; Nakum, K.J.; Hagar, M. New fluorinated azo/Schiff base liquid crystals: Synthesis, characterization, mesomorphic study and DFT calculations. Liq. Cryst. 2021, 48, 1–15. [Google Scholar] [CrossRef]
- He, Q.Q.; Lan, Y.; Quan, Y.Y.; Li, C.Y.; Liu, Y.P.; Wang, X.J.; Jia, Y.G.; Tian, M.; Yao, D.S. The influence of the structure of terminal groups and cores on the properties of schiff base star-shaped liquid crystals. Liq. Cryst. 2021, 48, 1309–1320. [Google Scholar] [CrossRef]
- Zhang, L.; Zhao, K.; Li, H.; Zhang, T.; Liu, D.; Han, Y. Liquid crystal ordering on conjugated polymers film morphology for high performance. J. Polym. Science Polym. Phys. 2019, 57, 1572–1591. [Google Scholar] [CrossRef] [Green Version]
- Marin, L.; Timpu, D.; Cozan, V.; Rusu, G.I.; Airinei, A. Solid State Properties of Thin Films of New Copoly(azomethine-sulfone)s. J. Appl. Polym. Sci. 2011, 120, 1720–1728. [Google Scholar] [CrossRef]
- Ciobanu, M.; Cozan, V.; Bruma, M. Aromatic polysulfones used in sensor applications. Rev. Adv. Mat. Sci. 2009, 22, 89–96. [Google Scholar]
- Jiang, Q.; Zhang, Q.; Wu, X.; Wu, L.; Lin, J.H. Exploring the Interfacial Phase and π–π Stacking in Aligned Carbon Nanotube/Polyimide Nanocomposites. Nanomaterials 2020, 10, 1158. [Google Scholar] [CrossRef] [PubMed]
- Li, J.-L.; Yin, J.-H.; Ji, T.; Feng, Y.; Liu, Y.-Y.; Zhao, H.; Li, Y.-P.; Zhu, C.; Yue, D.; Su, B.; et al. Microstructure evolution effect on high-temperature thermal conductivity of LDPE/BNNS investigated by in-situ SAXS. Mat. Lett. 2020, 234, 74–78. [Google Scholar] [CrossRef]
- Mombrú, D.; Romero, M.; Faccio, R.; Castiglioni, J.; Mombrú, A.W. In situ growth of ceramic quantum dots in polyaniline host via water vapor flow diffusion as potential electrode materials for energy applications. J. Solid State Chem. 2017, 250, 60–67. [Google Scholar] [CrossRef]
- Khan, I.; Mohan, S.D.; Belbut, M.; Kamma-Lorger, C.S.; Mateus, A.; Mitchell, G.R. Multiscale structure evolution in electrically conductive nanocomposites studied by SAXS. Proc. Manufact. 2017, 12, 79–88. [Google Scholar] [CrossRef]
- Ailincai, D.; Dorobanțu, A.M.; Dima, B.; Irimiciuc, S.A.; Lupașcu, C.; Agop, M.; Orzan, O. Poly(vinyl alcohol boric acid)-Diclofenac Sodium Salt Drug Delivery Systems: Experimental and Theoretical Studies. J. Immun. Res. 2020, 2020, 3124304. [Google Scholar] [CrossRef] [PubMed]
- Ailincai, D.; Agop, M.; Marinas, I.C.; Zala, A.; Irimiciuc, S.A.; Dobreci, L.; Petrescu, T.C.; Volovat, C. Theoretical model for the diclofenac release from PEGylated chitosan hydrogels. Drug Deliv. 2021, 28, 261–271. [Google Scholar] [CrossRef] [PubMed]
- Iftime, M.M.; Irimiciuc, S.A.; Agop, M.; Angheloiu, M.; Ochiuz, L.; Vasincu, D. A Theoretical Multifractal Model for Assessing Urea Release from Chitosan Based Formulations. Polymers 2020, 12, 1264. [Google Scholar] [CrossRef] [PubMed]
- Destri, S.; Porzio, W.; Bertini, F. Synthesis and characterization of new azomethine derivatives exhibiting liquid crystalline properties. Liq. Cryst. 2009, 36, 21–32. [Google Scholar]
- Sivaranjini, B.; Umadevi, S.; Khan, R.K.; Pratibha, R.; Dekshinamoorthy, A.; Vijayaraghavan, S.; Ganesh, V. Planar and Vertical Alignment of Rod-like and Bent-core Liquid Crystals Using Functionalized Indium Tin Oxide Substrates. Liq. Cryst. 2021, 41, 1–15. [Google Scholar] [CrossRef]
- Manabe, A.; Bremer, M.; Kraska, M. Ferroelectric nematic phase at and below room temperature. Liq. Cryst. 2021, 48, 1079–1086. [Google Scholar] [CrossRef]
- Marin, L.; Bejan, A.; Ailincai, D.; Belei, D. Poly(azomethine-phenothiazine)s with efficient emission in solid state. Eur. Polym. J. 2017, 95, 127–137. [Google Scholar] [CrossRef]
- Macanas, J.; Palacio, L.; Pradanos, P.; Hernandez, A.; Munoz, M. Atomic force microscopy as a suitable technique for surface characterization of activated composite membranes for metal ion facilitated transport. Appl. Phys. A. 2006, 84, 277–284. [Google Scholar] [CrossRef]
- Tan, D.Q. Differentiation of roughness and surface defect impact on dielectric strength of polymeric thin films. IET Nanodielectr. 2020, 3, 28–31. [Google Scholar] [CrossRef]
- Popovici, D.; Diaconu, A.; Rotaru, A.; Marin, L. Microwave-Assisted Synthesis of an Alternant Poly(fluorene-oxadiazole). Synthesis, Properties, and White Light-Emitting Devices. Polymers 2019, 11, 1562. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Dong, H.; Jiang, L.; Hu, W. Organic semiconductor crystals. Chem. Soc. Rev. 2018, 47, 422–500. [Google Scholar] [CrossRef]
- Nasrin, L.; Nasir, A.K.; Yoshizawa, A.; Ghosh, S.; Rahman, M. Nematic—cybotactic nematic phase transition in a liquid crystal: A dielectric spectroscopic study. Mater. Res. Express 2019, 6, 115105. [Google Scholar] [CrossRef]
- Marin, L.; Zabulica, A.; Sava, M. Symmetric Liquid Crystal Dimers Containing a Luminescent Mesogen: Synthesis, Mesomorphic Behavior, and Optical Properties. Soft Mater. 2013, 11, 32–39. [Google Scholar] [CrossRef]
- Schliemann, J. Ballistic side jump motion of electrons and holes in semiconductor quantum wells. Phy. Rev. B Cond. Matt. 2006, 75, 045304. [Google Scholar] [CrossRef] [Green Version]
- Cobzeanu, B.M.; Irimiciuc, S.; Vaideanu, D.; Grigorovici, A.; Popa, O. Possible dynamics of polymer chains by means of a Ricatti’s procedure-an exploitation for drug release at large time intervals. Mat. Plast. 2017, 54, 531–534. [Google Scholar] [CrossRef]
- Agop, M.; Mercheș, I. Operational Procedures Describing Physical Systems; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Merches, I.; Agop, M. Differentiability and Fractality in Dynamics of Physical Systems; World Scientific: Hackensack, NJ, USA, 2016. [Google Scholar]
- Agop, M.; Păun, V.P. On the New Perspectives of Fractal Theory: Fundaments and Application; Romanian Academy Publishing House: Bucharest, Romania, 2017. [Google Scholar]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dumbravă, O.; Popovici, D.; Vasincu, D.; Popa, O.; Ochiuz, L.; Irimiciuc, Ș.-A.; Agop, M.; Negură, A. Impact of the Liquid Crystal Order of Poly(azomethine-sulfone)s on the Semiconducting Properties. Polymers 2022, 14, 1487. https://doi.org/10.3390/polym14071487
Dumbravă O, Popovici D, Vasincu D, Popa O, Ochiuz L, Irimiciuc Ș-A, Agop M, Negură A. Impact of the Liquid Crystal Order of Poly(azomethine-sulfone)s on the Semiconducting Properties. Polymers. 2022; 14(7):1487. https://doi.org/10.3390/polym14071487
Chicago/Turabian StyleDumbravă, Oana, Dumitru Popovici, Decebal Vasincu, Ovidiu Popa, Lăcrămioara Ochiuz, Ștefan-Andrei Irimiciuc, Maricel Agop, and Anca Negură. 2022. "Impact of the Liquid Crystal Order of Poly(azomethine-sulfone)s on the Semiconducting Properties" Polymers 14, no. 7: 1487. https://doi.org/10.3390/polym14071487
APA StyleDumbravă, O., Popovici, D., Vasincu, D., Popa, O., Ochiuz, L., Irimiciuc, Ș.-A., Agop, M., & Negură, A. (2022). Impact of the Liquid Crystal Order of Poly(azomethine-sulfone)s on the Semiconducting Properties. Polymers, 14(7), 1487. https://doi.org/10.3390/polym14071487








