Convertible Thermal Meta-Structures via Hybrid Manufacturing of Stereolithography Apparatus 3D Printing and Surface Metallization for Thermal Flow Manipulation
Abstract
1. Introduction
2. Fundamental Design Theory of Thermal Meta-Structures
2.1. The Transformation Thermotics Theory
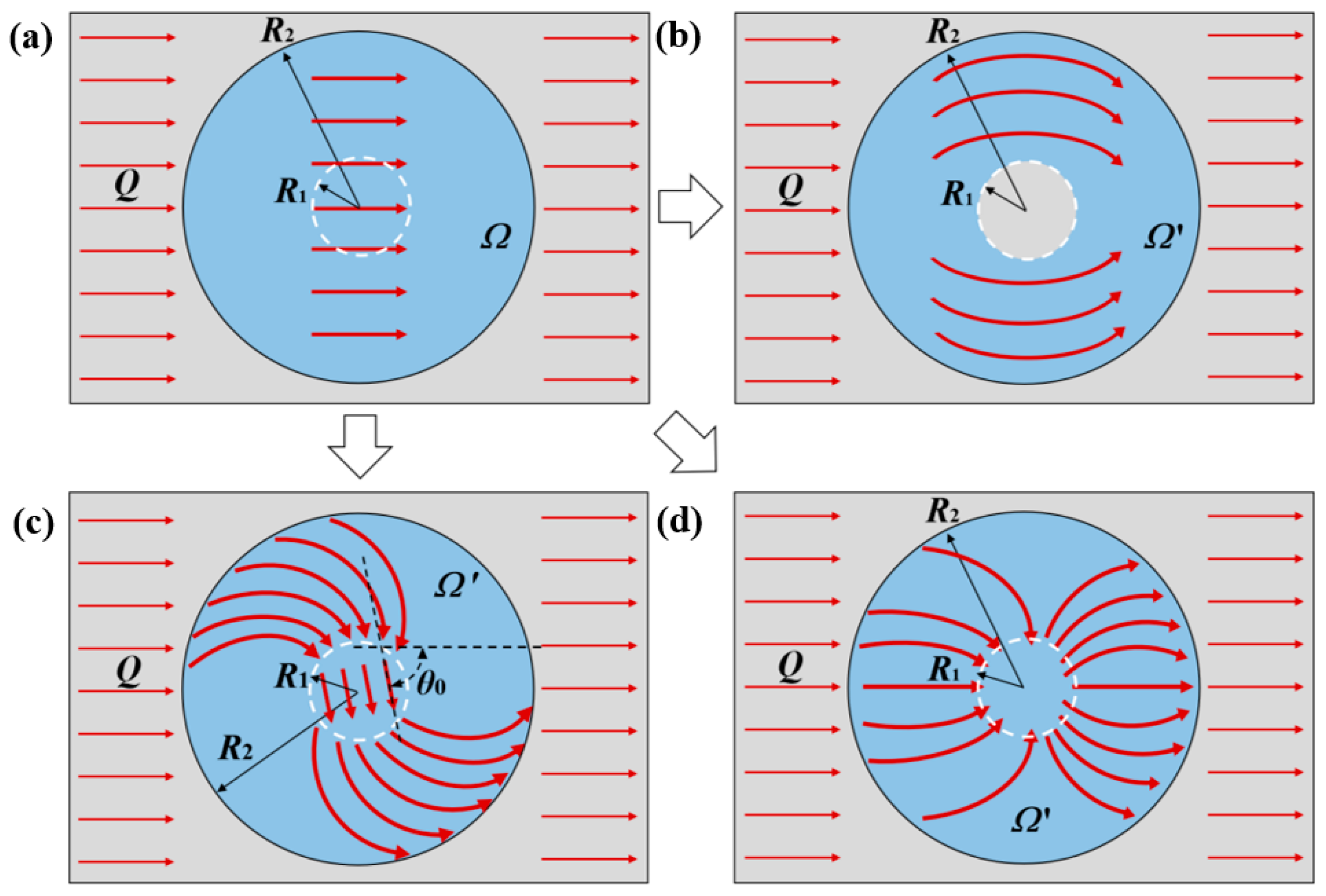
2.2. Application of the Transformation Thermotics on Thermal Cloak Meta-Structure
2.3. Application of the Transformation Thermotics on Thermal Rotation Meta-Structure
2.4. Application of the Transformation Thermotics on Thermal Concentration Meta-Structure
3. Methods
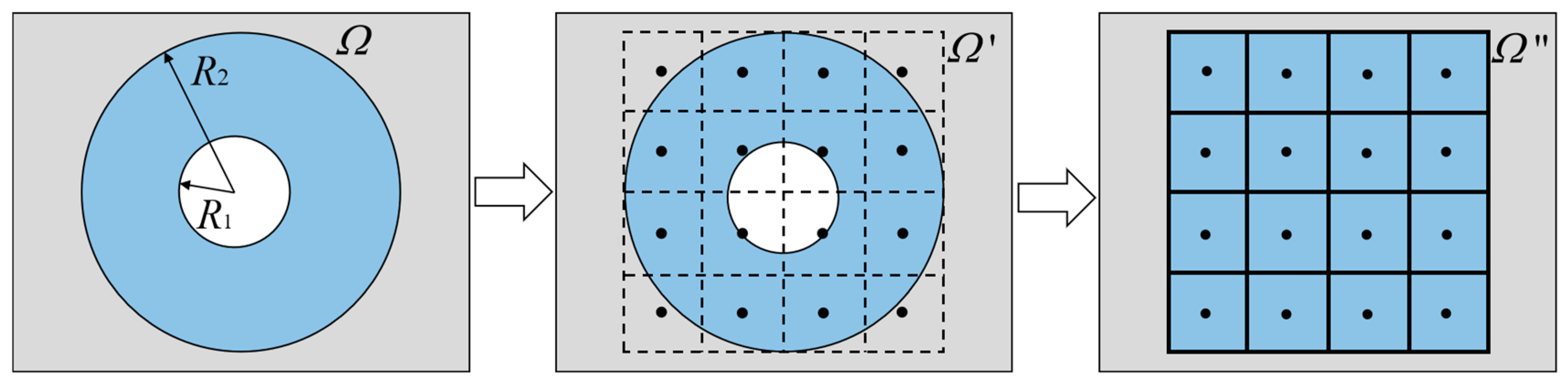
3.1. Design and Numerical Simulation Analysis
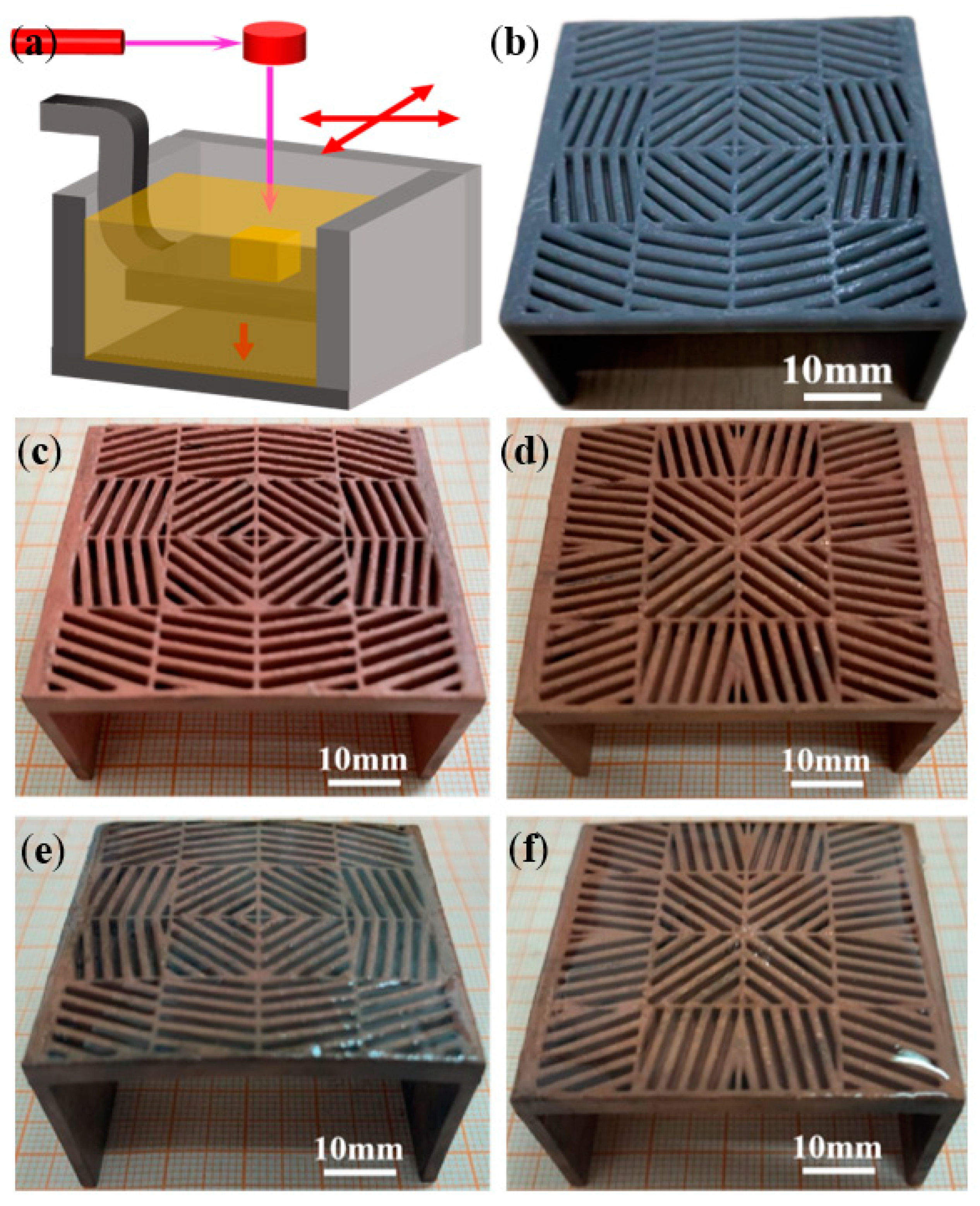
3.2. Hybrid Manufacturing via SLA 3D Printing and Surface Metallization
- The 3D models of modules to compose several thermal meta-structural devices were imported to the SLA printing process software system and then printed using a 25 μm layer thickness and a 250 mW laser power. The as-printed solid parts were cleaned using alcohol to remove the uncured liquid resin from their surface.
- The as-printed and air-dried resin modules were electrolessly plated to prepare a Cu-containing conductive layer on the surface as an intermediate and conductive layer for subsequent electroplating since the as-printed solid resin was not conducive. Silicon–oxygen coupling agent acetone solution was used for the initial surface activation of the as-printed solid resin, aiming to enhance the adhesion of Cu ions on the resin surface. Then, the parts were soaked in the electroless plating solution, which contained CuSO4, HCHO, C4O0H4KNa, and NaOH, for Cu ions attaching to the resin surface and undergoing a reduction reaction at a set temperature of 30°, according to a non-catalytic reaction, causing Cu2O particles to be reduced: 2Cu2+ + HCHO + 5OH− → 2HCOO− + 3H2O + Cu2O. Then, the Cu2O was further reduced to particulate copper, according to a reaction: Cu2O + 2HCHO + 2OH− → 2Cu + 2HCOO− + H2 + H2O. The duration of the electroless plating of Cu on the resin modules was 30 min.
- Next, Cu electroplating was performed on the module parts containing the electroless-plated conductive layer of Cu to obtain a thicker and denser metal Cu thermal conductive layer on their surface. The main reagent components of the professional Cu electroplating solution, including NaKC4H4O6, K2HPO4, and K6[Cu(P2O7)2], was employed in a lab-used electrolyzer. An electroplating instrument, including DC stabilized power supply, a Harlem tank, and the heater was utilized for plating Cu at room temperature. The pH value of the plating solution was tailored as 7. The current density for electroplating was determined as 0.5 A/dm2. The duration of the Cu electroplating was 45 min.
- After the surface plating of Cu was conducted, a PDMS liquid was configured and poured into the grooves of the modules. The PDMS played the role of heat insulation and packaging. Subsequently, the module parts with liquid PDMS were placed in a room-temperature environment for 24 h to cure.
- The multiple modules with a solid resin, Cu surface layer, and cured solid PDMS were arranged in different patterns to assemble and compose meta-structural devices with several thermal-flow manipulative forms, including thermal cloak, thermal rotation, thermal concentration, and thermal dispersion.
3.3. Thermal Testing Verification
4. Convertible Thermal Meta-Structural Design
5. Results and Discussion
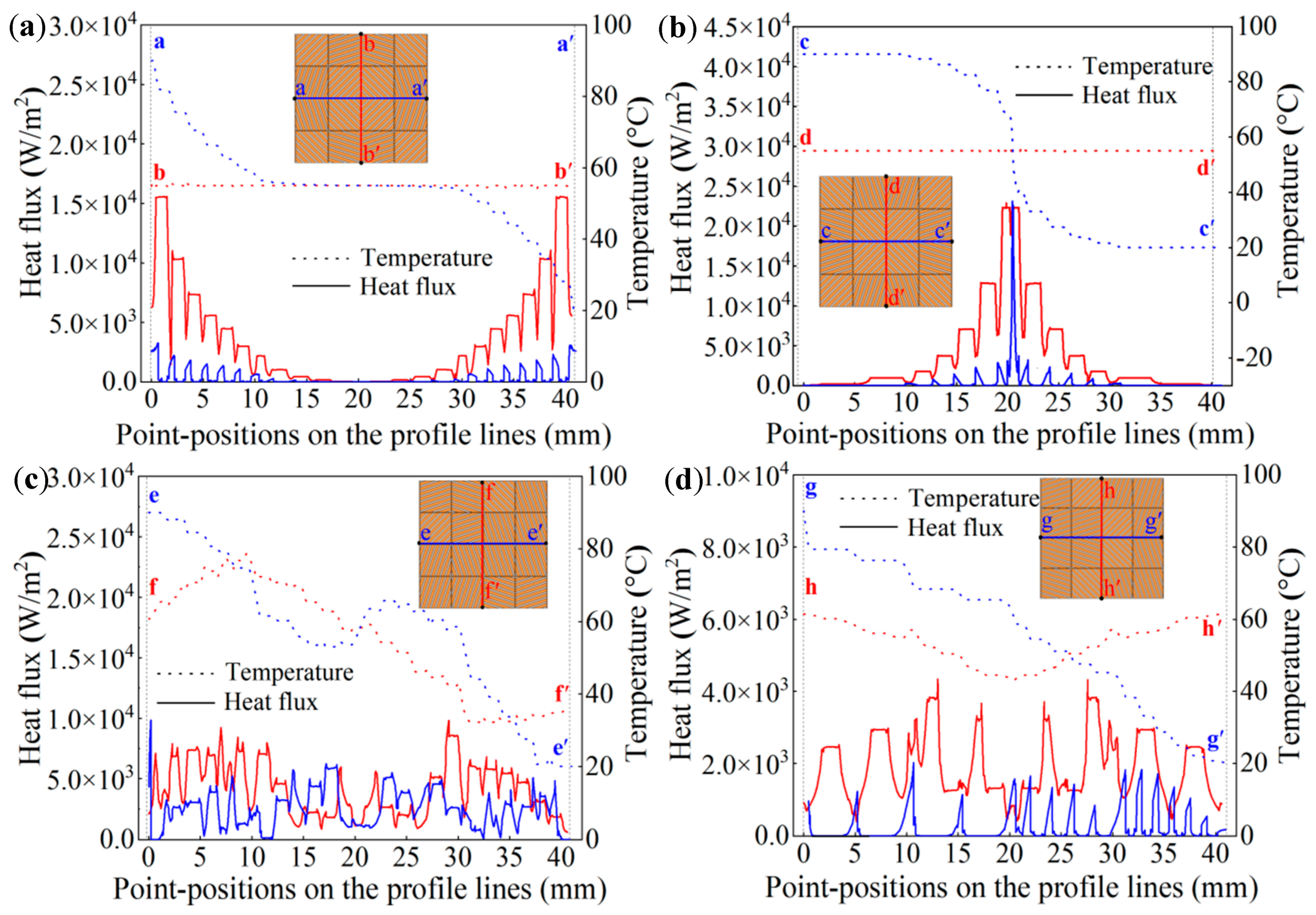
5.1. Thermal Simulation Analysis of the Meta-Structures
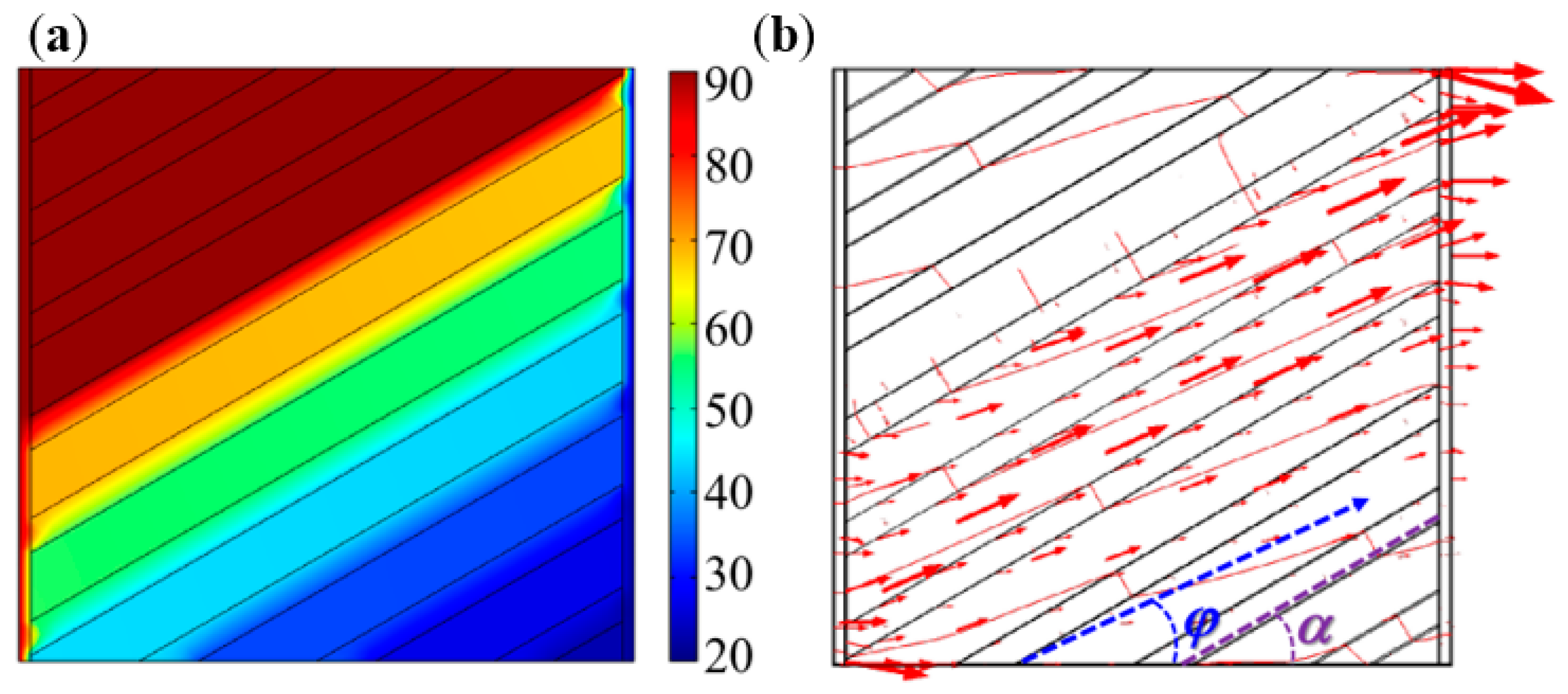
5.2. Fabrication and Thermal Testing Results of the Meta-Structures
5.3. Engineering Advantages of Hybrid-Fabricated Convertible Thermal Meta-Structures
6. Conclusions
- (1)
- Using multiple dispersed square unit modules to replace the annular region of the thermal meta-structure exhibited different thermal flow functions, including thermal cloak, concentration, rotation, and dispersion, through the unique geometric design of the heat-flow transfer direction on each module. By rotating each square unit module at a specific angle and arranging the modules, the convertibility among different thermal manipulation functions was achieved.
- (2)
- Thermal simulations and plotted temperature and heat flux change curves of the thermal meta-structures indicated that the convertible thermal meta-structure had a solid ability to change the directions of heat flows. It was also verified in the experimental thermal tests of artificially fabricated thermal cloak and concentration meta-structural devices.
- (3)
- The convertible thermal meta-structure devices with good geometric accuracy were successfully fabricated via a hybrid manufacturing path of “SLA 3D printing—electroless plating of Cu—electroplating of Cu—PDMS packaging”. A uniform copper layer with a high thermal conductivity was achieved on the SLA-printed solid resin part to act as heat conduction elements in the modules. The proposed hybrid manufacturing method can exhibit a high geometric accuracy, a relatively low cost, and a pronounced convenience of mass manufacturing for thermal meta-structural devices.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Pendry, J.B.; Schurig, D.; Smith, D.R. Controlling Electromagnetic Fields. Science 2006, 312, 1780–1782. [Google Scholar] [CrossRef] [PubMed]
- Schurig, D.; Mock, J.J.; Justice, B.J.; Cummer, S.A.; Pendry, J.B.; Starr, A.F.; Smith, D.R. Metamaterial Electromagnetic Cloak at Microwave Frequencies. Science 2006, 314, 977–980. [Google Scholar] [CrossRef] [PubMed]
- Leonhardt, U. Optical Conformal Mapping. Science 2006, 312, 1777–1780. [Google Scholar] [CrossRef] [PubMed]
- Schittny, R.; Kadic, M.; Bückmann, T.; Wegener, M. Invisibility cloaking in a diffusive light scattering medium. Science 2014, 345, 427–429. [Google Scholar] [CrossRef]
- Li, J.; Pendry, J.B. Hiding under the Carpet: A New Strategy for Cloaking. Phys. Rev. Lett. 2008, 101, 203901. [Google Scholar] [CrossRef]
- Yang, T.; Bai, X.; Gao, D.; Wu, L.; Li, B.; Thong, J.T.L.; Qiu, C.-W. Invisible Sensors: Simultaneous Sensing and Camouflaging in Multiphysical Fields. Adv. Mater. 2015, 27, 7752–7758. [Google Scholar] [CrossRef]
- Liu, M.; Mei, Z.L.; Ma, X.; Cui, T.J. Dc illusion and its experimental verification. Appl. Phys. Lett. 2012, 101, 051905. [Google Scholar] [CrossRef]
- Hu, R.; Zhou, S.; Li, Y.; Lei, D.-Y.; Luo, X.; Qiu, C.-W. Illusion thermotics. Adv. Mater. 2018, 30, 1707237. [Google Scholar] [CrossRef]
- Zhou, S.; Hu, R.; Luo, X. Thermal illusion with twinborn-like heat signatures. Int. J. Heat Mass Transf. 2018, 127, 607–613. [Google Scholar] [CrossRef]
- Liu, Z.; Lee, H.; Xiong, Y.; Sun, C.; Zhang, X. Far-Field Optical Hyperlens Magnifying Sub-Diffraction-Limited Objects. Science 2007, 315, 1686. [Google Scholar] [CrossRef]
- Li, J.; Fok, L.; Yin, X.; Bartal, G.; Zhang, X. Experimental demonstration of an acoustic magnifying hyperlens. Nat. Mater. 2009, 8, 931–934. [Google Scholar] [CrossRef]
- Fan, C.Z.; Gao, Y.; Huang, J.P. Shaped graded materials with an apparent negative thermal conductivity. Appl. Phys. Lett. 2008, 92, 251907. [Google Scholar] [CrossRef]
- Shen, X.; Huang, J. Thermally hiding an object inside a cloak with feeling. Int. J. Heat Mass Transf. 2014, 78, 1–6. [Google Scholar] [CrossRef]
- Qin, J.; Luo, W.; Yang, P.; Wang, B.; Deng, T.; Han, T. Experimental demonstration of irregular thermal carpet cloaks with natural bulk material. Int. J. Heat Mass Transf. 2019, 141, 487–490. [Google Scholar] [CrossRef]
- Liu, Y.; Guo, W.; Han, T. Arbitrarily polygonal transient thermal cloaks with natural bulk materials in bilayer configurations. Int. J. Heat Mass Transf. 2017, 115, 1–5. [Google Scholar] [CrossRef]
- Ji, Q.; Qi, Y.; Liu, C.; Meng, S.; Liang, J.; Kadic, M.; Fang, G. Design of thermal cloaks with isotropic materials based on machine learning. Int. J. Heat Mass Transf. 2022, 189, 122716. [Google Scholar] [CrossRef]
- Zhu, Z.; Ren, X.; Sha, W.; Xiao, M.; Hu, R.; Luo, X. Inverse design of rotating metadevice for adaptive thermal cloaking. Int. J. Heat Mass Transf. 2021, 176, 121417. [Google Scholar] [CrossRef]
- Ji, Q.; Chen, X.; Liang, J.; Laude, V.; Guenneau, S.; Fang, G.; Kadic, M. Designing thermal energy harvesting devices with natural materials through optimized microstructures. Int. J. Heat Mass Transf. 2021, 169, 120948. [Google Scholar] [CrossRef]
- Sun, T.; Wang, X.; Yang, X.; Meng, T.; He, R.; Wang, Y. Design of thermal cloak and concentrator with interconnected structure. Int. J. Heat Mass Transf. 2022, 187, 122568. [Google Scholar] [CrossRef]
- Zhang, X.; He, X.; Wu, L. Experimental investigation of thermal architected metamaterials for regulating transient heat transfer. Int. J. Heat Mass Transf. 2022, 193, 122960. [Google Scholar] [CrossRef]
- Li, Y.; Shen, X.; Wu, Z.; Huang, J.; Chen, Y.; Ni, Y.; Huang, J. Temperature-Dependent Transformation Thermotics: From Switchable Thermal Cloaks to Macroscopic Thermal Diodes. Phys. Rev. Lett. 2015, 115, 195503. [Google Scholar] [CrossRef]
- Han, T.; Yue, X.; Wen, K.; Nangong, J. Monolayer thermal meta-device with switching functions. Int. J. Heat Mass Transf. 2022, 186, 122498. [Google Scholar] [CrossRef]
- Xu, L.; Huang, J. Controlling thermal waves with transformation complex thermotics. Int. J. Heat Mass Transf. 2020, 159, 120133. [Google Scholar] [CrossRef]
- Han, T.; Bai, X.; Thong, J.T.L.; Li, B.; Qiu, C.-W. Full Control and Manipulation of Heat Signatures: Cloaking, Camouflage and Thermal Metamaterials. Adv. Mater. 2014, 26, 1731–1734. [Google Scholar] [CrossRef]
- Xu, L.; Yang, S.; Huang, J. Thermal theory for heterogeneously architected structure: Fundamentals and application. Phys. Rev. E 2018, 98, 052128. [Google Scholar] [CrossRef]
- Su, Y.; Li, Y.; Yang, T.; Han, T.; Sun, Y.; Xiong, J.; Wu, L.; Qiu, C.-W. Path-Dependent Thermal Metadevice beyond Janus Functionalities. Adv. Mater. 2020, 33, e2003084. [Google Scholar] [CrossRef]
- Narayana, S.; Sato, Y. Heat Flux Manipulation with Engineered Thermal Materials. Phys. Rev. Lett. 2012, 108, 214303. [Google Scholar] [CrossRef]
- Schittny, R.; Kadic, M.; Guenneau, S.; Wegener, M. Experiments on Transformation Thermodynamics: Molding the Flow of Heat. Phys. Rev. Lett. 2013, 110, 195901. [Google Scholar] [CrossRef]
- Peralta, I.; Fachinotti, V.D.; Álvarez Hostos, J.C. A Brief Review on Thermal Metamaterials for Cloaking and Heat Flux Manipulation. Adv. Eng. Mater. 2019, 22, 1901034. [Google Scholar] [CrossRef]
- Deng, T.; Li, B.; Xuan, F. Additive manufactured thermal metamaterial devices for manipulating heat flow: Geometric configuration design and SLM-assisted fabrication. Eng. Res. Express 2021, 3, 025038. [Google Scholar] [CrossRef]
- Charles, A.; Elkaseer, A.; Paggi, U.; Thijs, L.; Hagenmeyer, V.; Scholz, S. Down-facing surfaces in laser powder bed fusion of Ti6Al4V: Effect of dross formation on dimensional accuracy and surface texture. Addit. Manuf. 2021, 46, 102148. [Google Scholar] [CrossRef]
- Yang, T.; Liu, T.; Liao, W.; Wei, H.; Zhang, C.; Chen, X.; Zhang, K. Effect of processing parameters on overhanging surface roughness during laser powder bed fusion of AlSi10Mg. J. Manuf. Process. 2020, 61, 440–453. [Google Scholar] [CrossRef]
- Sadeqi, A.; Nejad, H.R.; Owyeung, R.E.; Sonkusale, S. Three dimensional printing of metamaterial embedded geometrical optics (MEGO). Microsyst. Nanoeng. 2019, 5, 16. [Google Scholar] [CrossRef]
- Guenneau, S.; Amra, C.; Veynante, D. Transformation thermodynamics: Cloaking and concentrating heat flux. Opt. Express 2012, 20, 8207–8218. [Google Scholar] [CrossRef]
- Nan, C.-W.; Birringer, R.; Clarke, D.; Gleiter, H. Effective thermal conductivity of particulate composites with interfacial thermal resistance. J. Appl. Phys. 1997, 81, 6692–6699. [Google Scholar] [CrossRef]
- Slovick, B.A.; Yu, Z.G.; Krishnamurthy, S. Generalized effective-medium theory for metamaterials. Phys. Rev. B 2014, 89, 115118. [Google Scholar] [CrossRef]
- Li, J.; Li, Y.; Wang, W.; Li, L.; Qiu, C.-W. Effective medium theory for thermal scattering off rotating structures. Opt. Express 2020, 28, 25894–25907. [Google Scholar] [CrossRef]
- Wang, M.; Pan, N. Predictions of effective physical properties of complex multiphase materials. Mater. Sci. Eng. R Rep. 2008, 63, 1–30. [Google Scholar] [CrossRef]


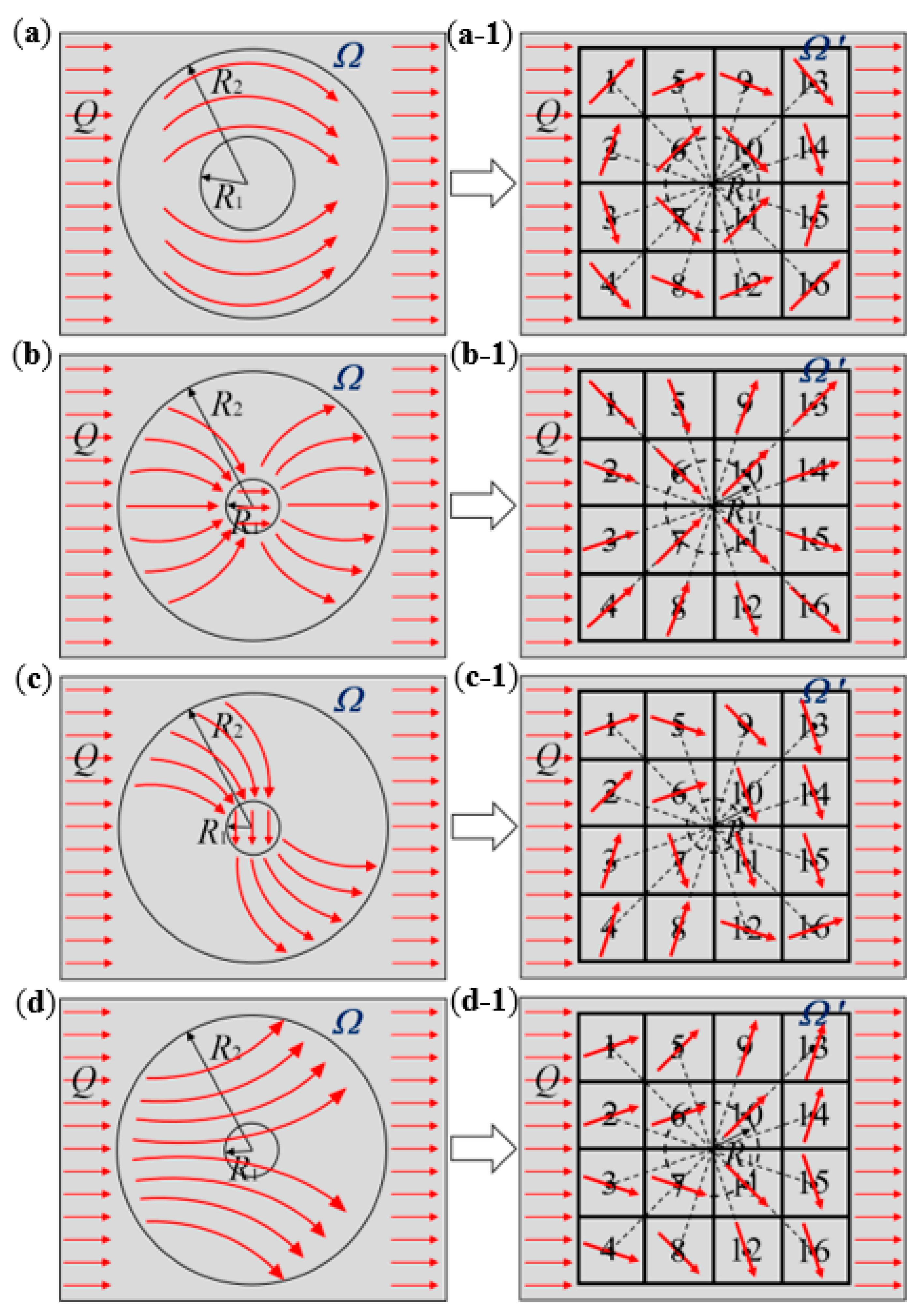

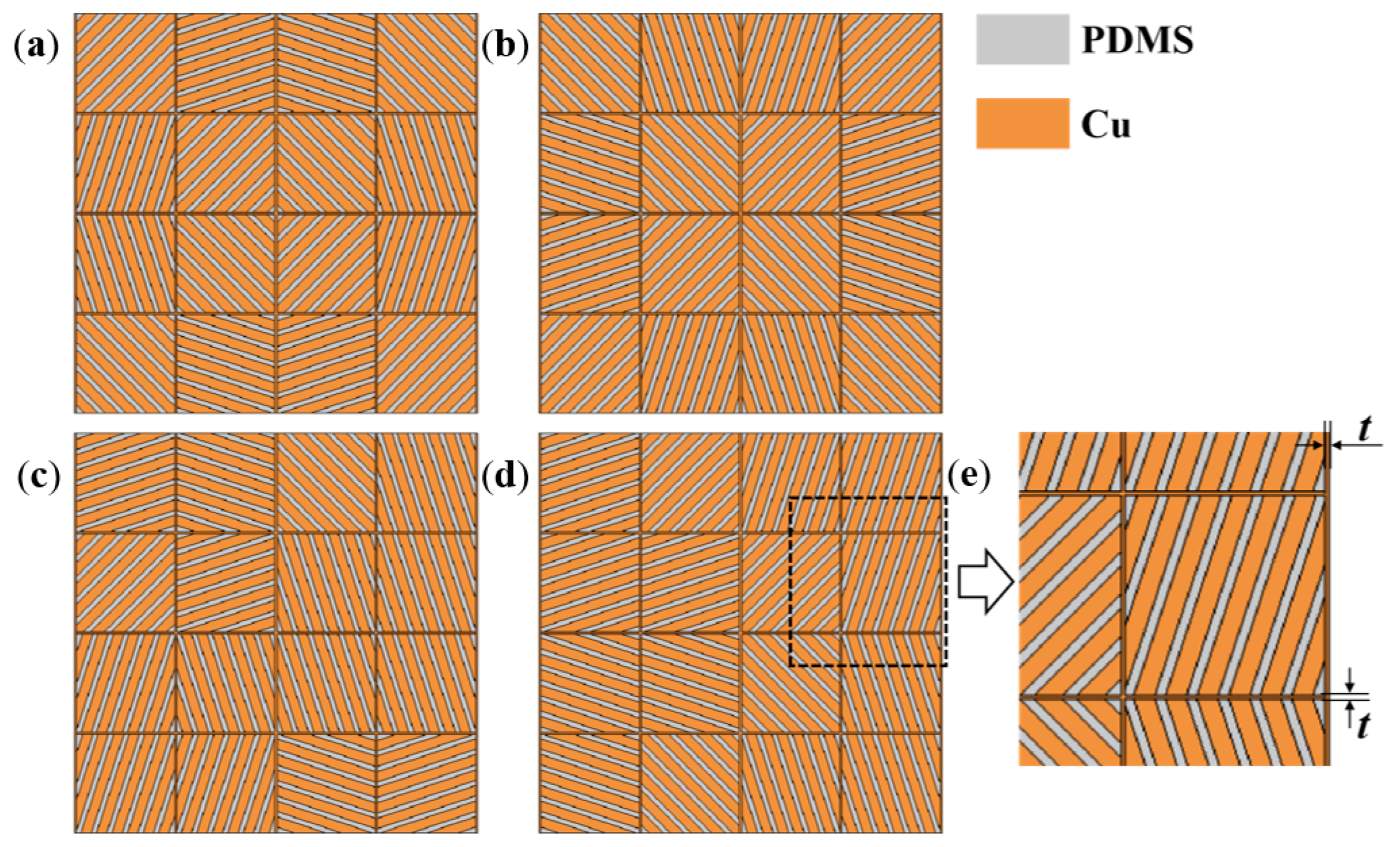

| Module No. in TClM. | Module φ in TClM | Module No. in TCoM | Module φ in TCoM | Module No. in TRoM | Module φ in TRoM | Module No. in TDiM | Module φ in TDiM |
|---|---|---|---|---|---|---|---|
| No. 1 | 45° | No. 1 | −45° | No. 1 | 18.4° | No. 1 | 18.4° |
| No. 2 | 71.6° | No. 2 | −18.4° | No. 2 | 45° | No. 2 | 18.4° |
| No. 3 | −71.6° | No. 3 | 18.4° | No. 3 | 71.6° | No. 3 | −18.4° |
| No. 4 | −45° | No. 4 | 45° | No. 4 | 71.6° | No. 4 | −18.4° |
| No. 5 | 18.4° | No. 5 | −71.6° | No. 5 | −18.4° | No. 5 | 45° |
| No. 6 | 45° | No. 6 | −45° | No. 6 | 18.4° | No. 6 | 18.4° |
| No. 7 | −45° | No. 7 | 45° | No. 7 | −71.6° | No. 7 | −18.4° |
| No. 8 | −18.4° | No. 8 | 71.6° | No. 8 | 71.6° | No. 8 | −45° |
| No. 9 | −18.4° | No. 9 | 71.6° | No. 9 | −45° | No. 9 | 71.6° |
| No. 10 | −45° | No. 10 | 45° | No. 10 | −71.6° | No. 10 | 45° |
| No. 11 | 45° | No. 11 | −45° | No. 11 | −71.6° | No. 11 | −45° |
| No. 12 | 18.4° | No. 12 | −71.6° | No. 12 | −18.4° | No. 12 | −71.6° |
| No. 13 | −45° | No. 13 | 45° | No. 13 | −71.6° | No. 13 | 71.6° |
| No. 14 | −71.6° | No. 14 | 18.4° | No. 14 | −71.6° | No. 14 | 71.6° |
| No. 15 | 71.6° | No. 15 | −18.4° | No. 15 | −71.6° | No. 15 | −71.6° |
| No. 16 | 45° | No. 16 | −45° | No. 16 | 18.4° | No. 16 | −71.6° |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, B.; Zhang, J.; Deng, T.; Ren, F. Convertible Thermal Meta-Structures via Hybrid Manufacturing of Stereolithography Apparatus 3D Printing and Surface Metallization for Thermal Flow Manipulation. Polymers 2023, 15, 174. https://doi.org/10.3390/polym15010174
Li B, Zhang J, Deng T, Ren F. Convertible Thermal Meta-Structures via Hybrid Manufacturing of Stereolithography Apparatus 3D Printing and Surface Metallization for Thermal Flow Manipulation. Polymers. 2023; 15(1):174. https://doi.org/10.3390/polym15010174
Chicago/Turabian StyleLi, Bo, Jianrui Zhang, Tianxiang Deng, and Facai Ren. 2023. "Convertible Thermal Meta-Structures via Hybrid Manufacturing of Stereolithography Apparatus 3D Printing and Surface Metallization for Thermal Flow Manipulation" Polymers 15, no. 1: 174. https://doi.org/10.3390/polym15010174
APA StyleLi, B., Zhang, J., Deng, T., & Ren, F. (2023). Convertible Thermal Meta-Structures via Hybrid Manufacturing of Stereolithography Apparatus 3D Printing and Surface Metallization for Thermal Flow Manipulation. Polymers, 15(1), 174. https://doi.org/10.3390/polym15010174






