Evaluation of Deformation for Steel Fiber Concrete Beams with BFRP Tendons Eroded by Seawater under Cyclic Loading
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials Properties
2.1.1. Concrete
2.1.2. FRP Bars
2.1.3. Simulated Seawater Solution
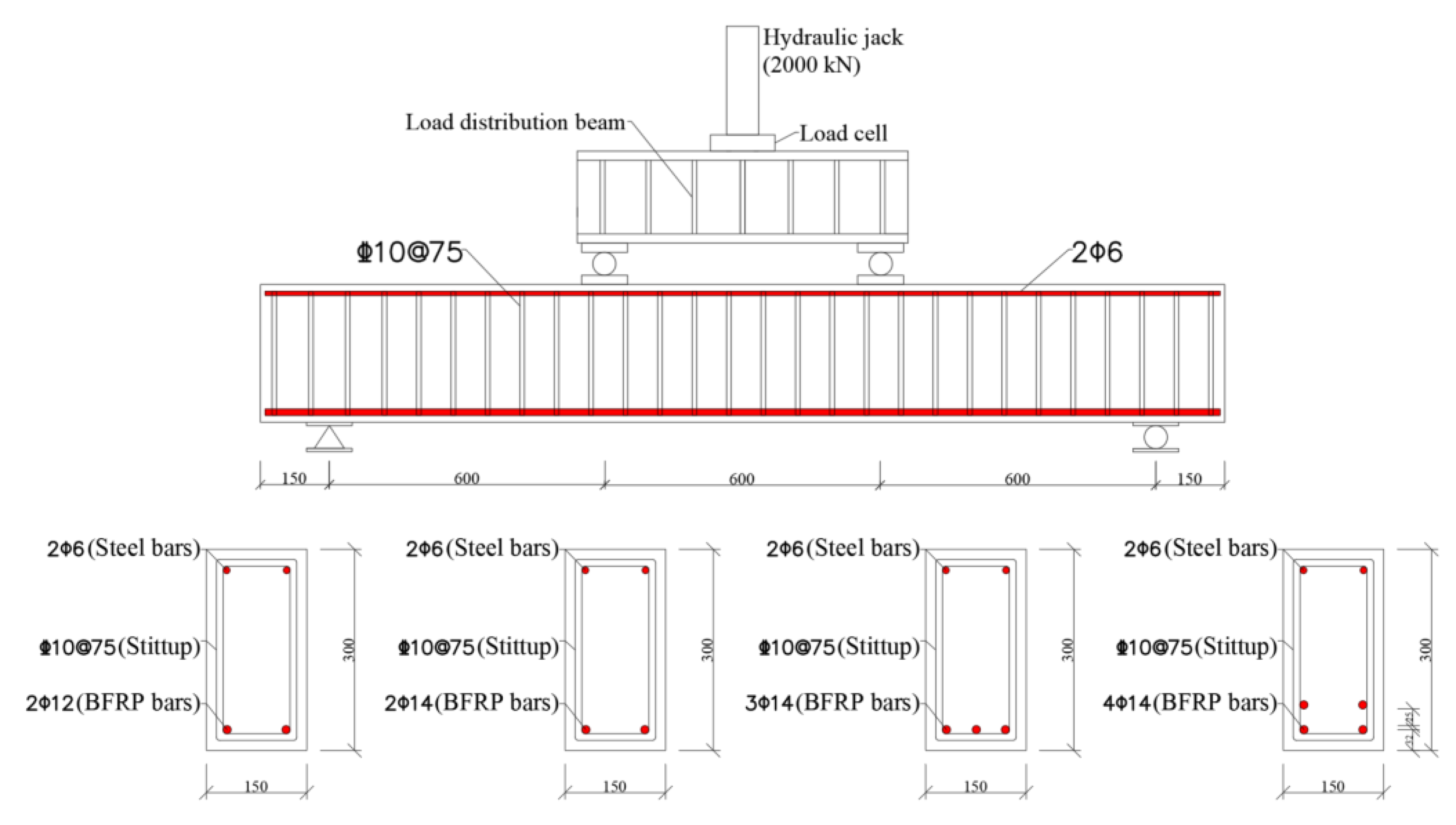
2.2. Specimen Design
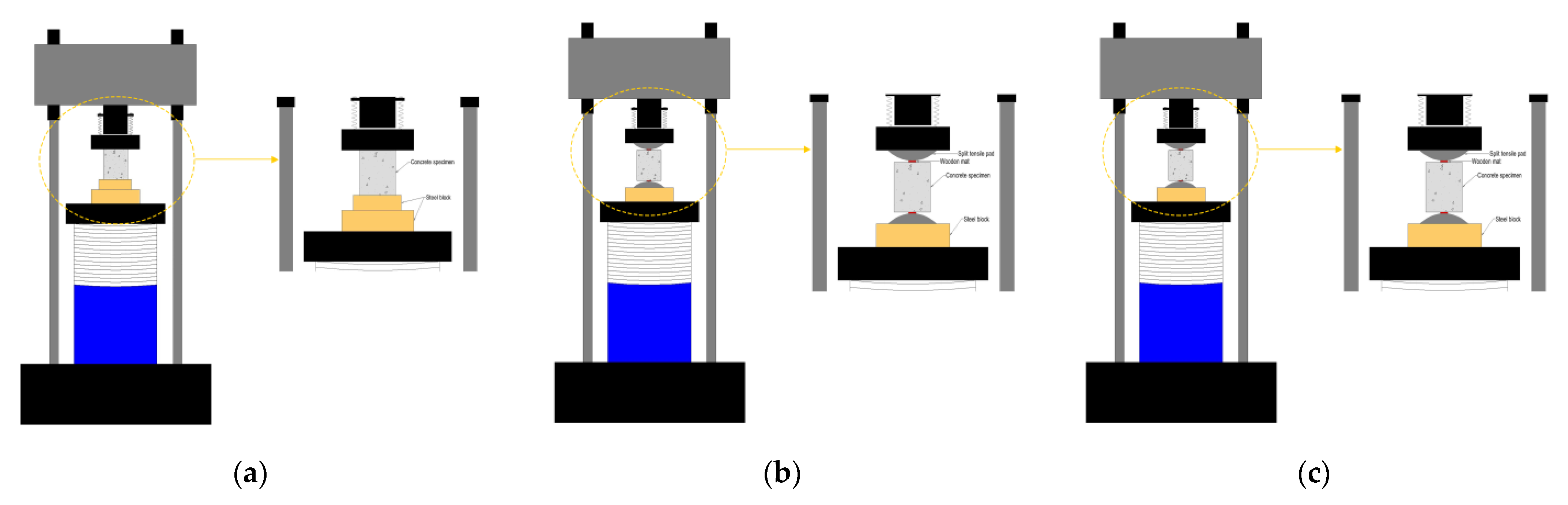
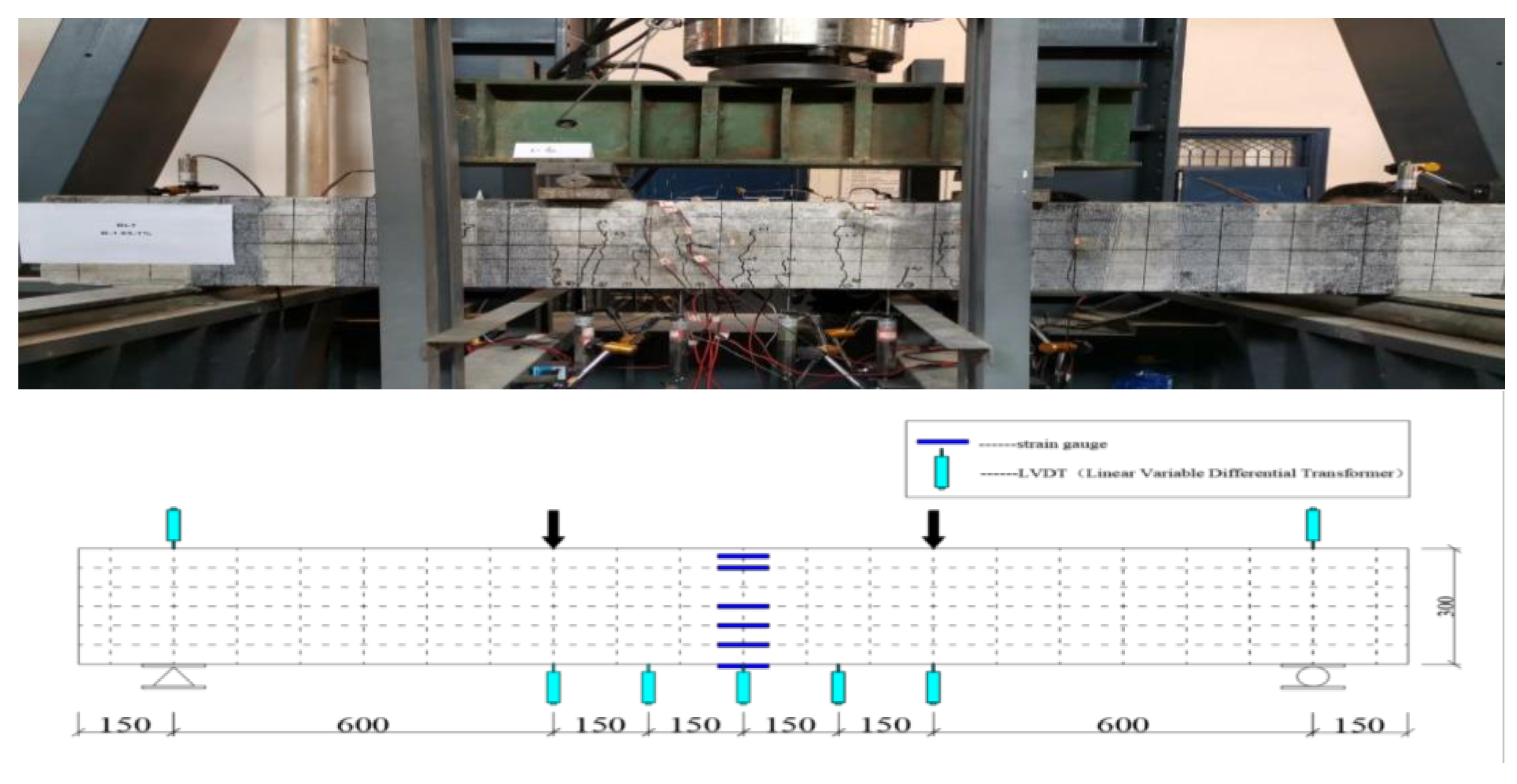
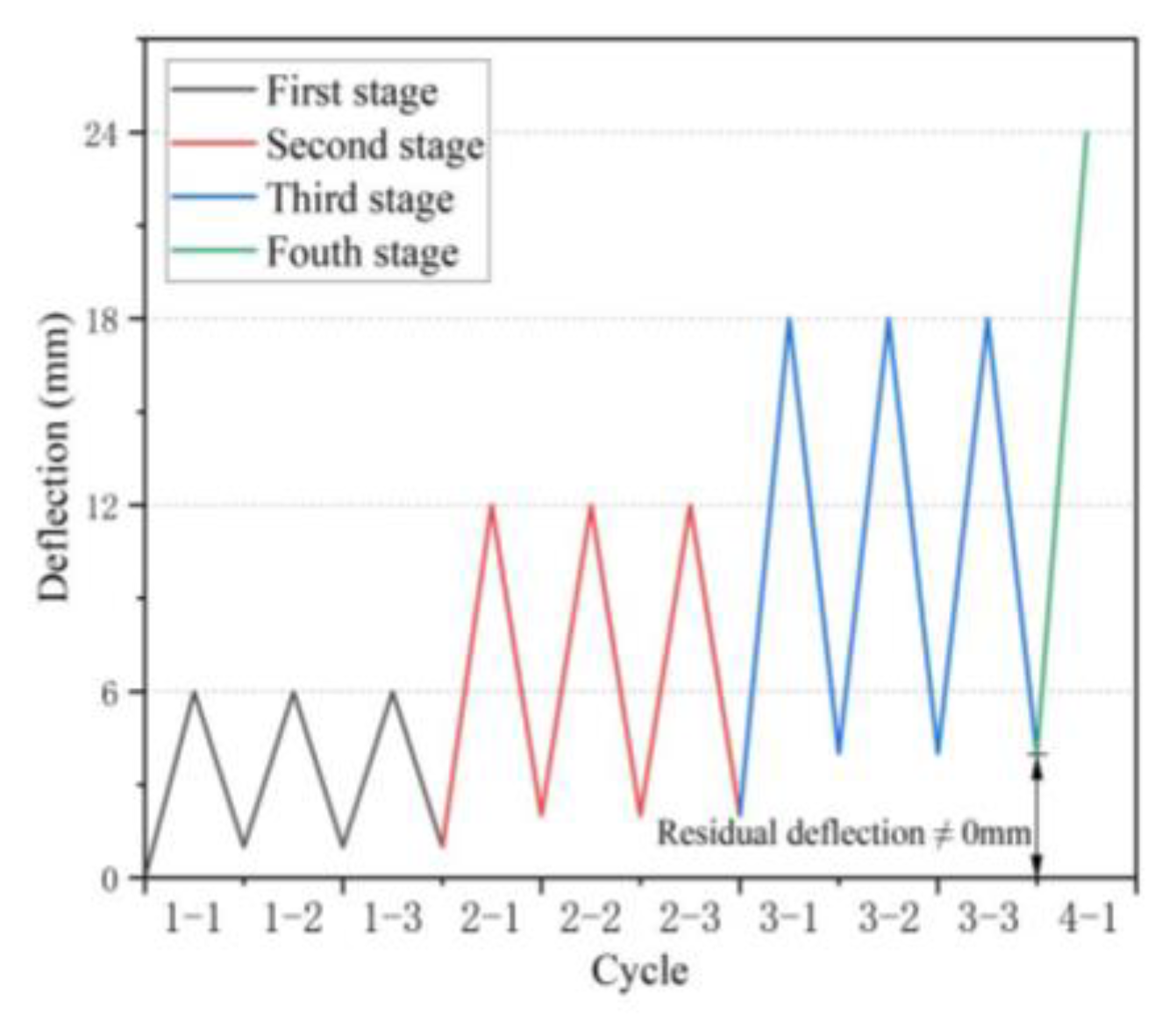
2.3. Test Setup and Instrumentation
3. Results and Discussion
3.1. Cracking Moment
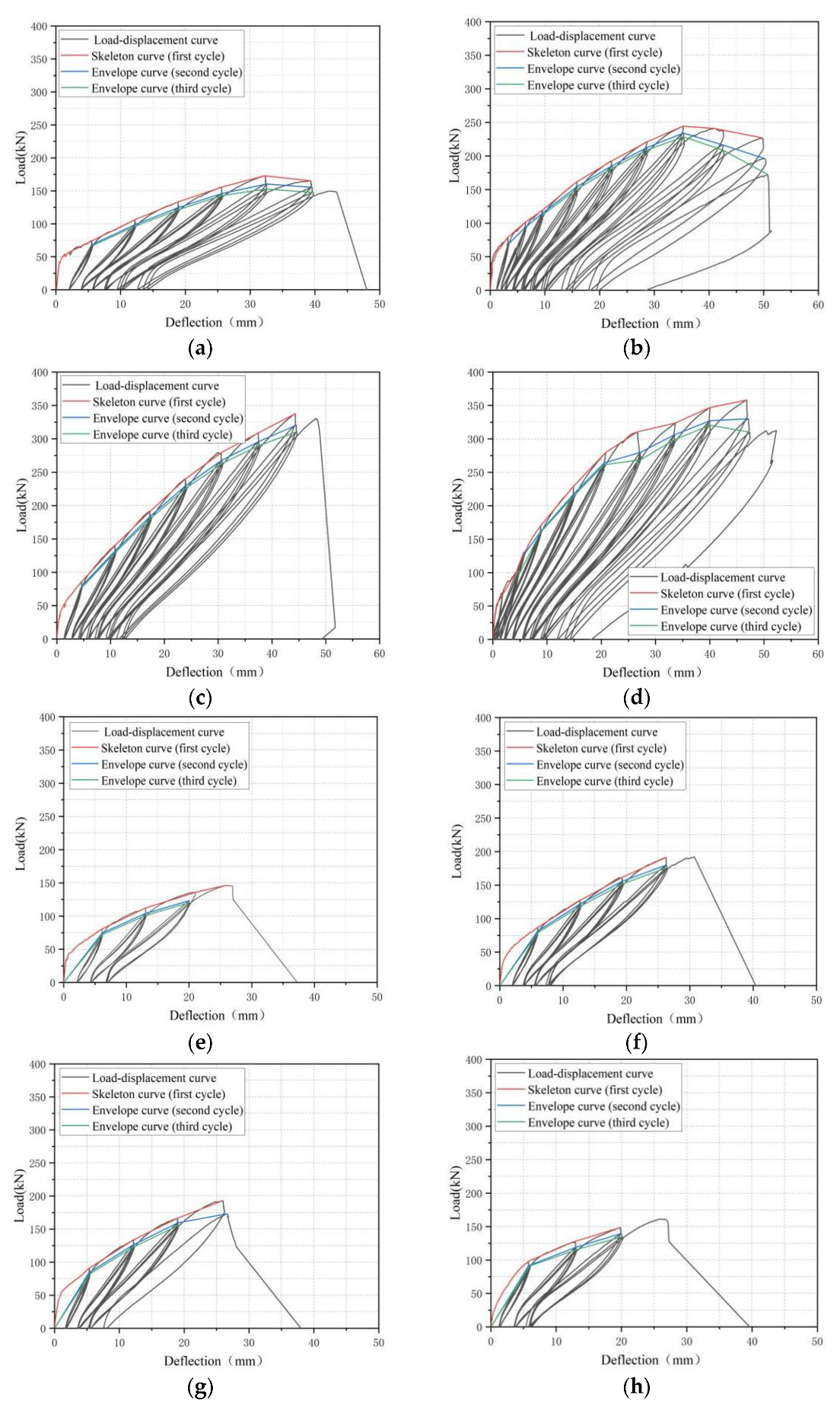
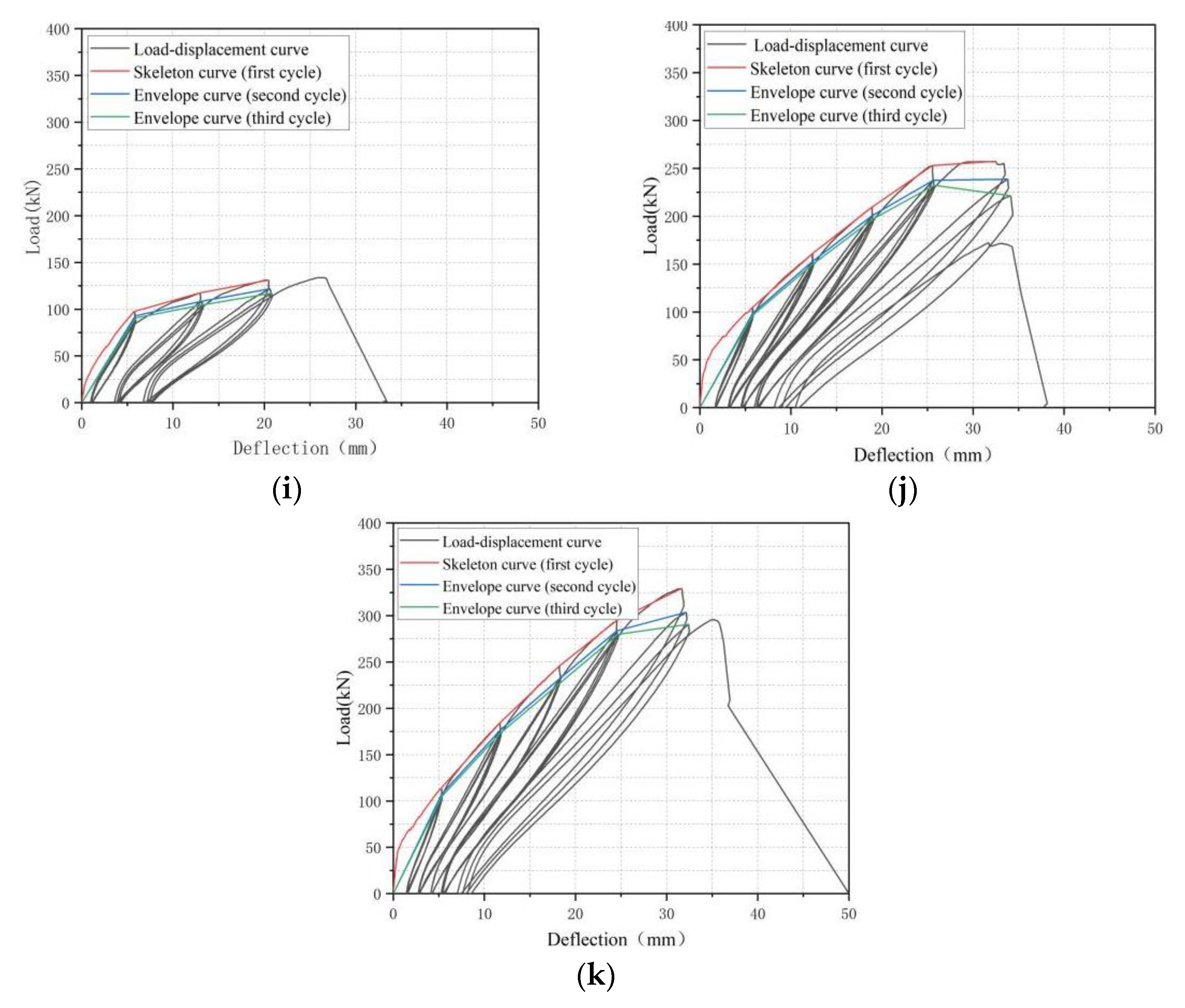
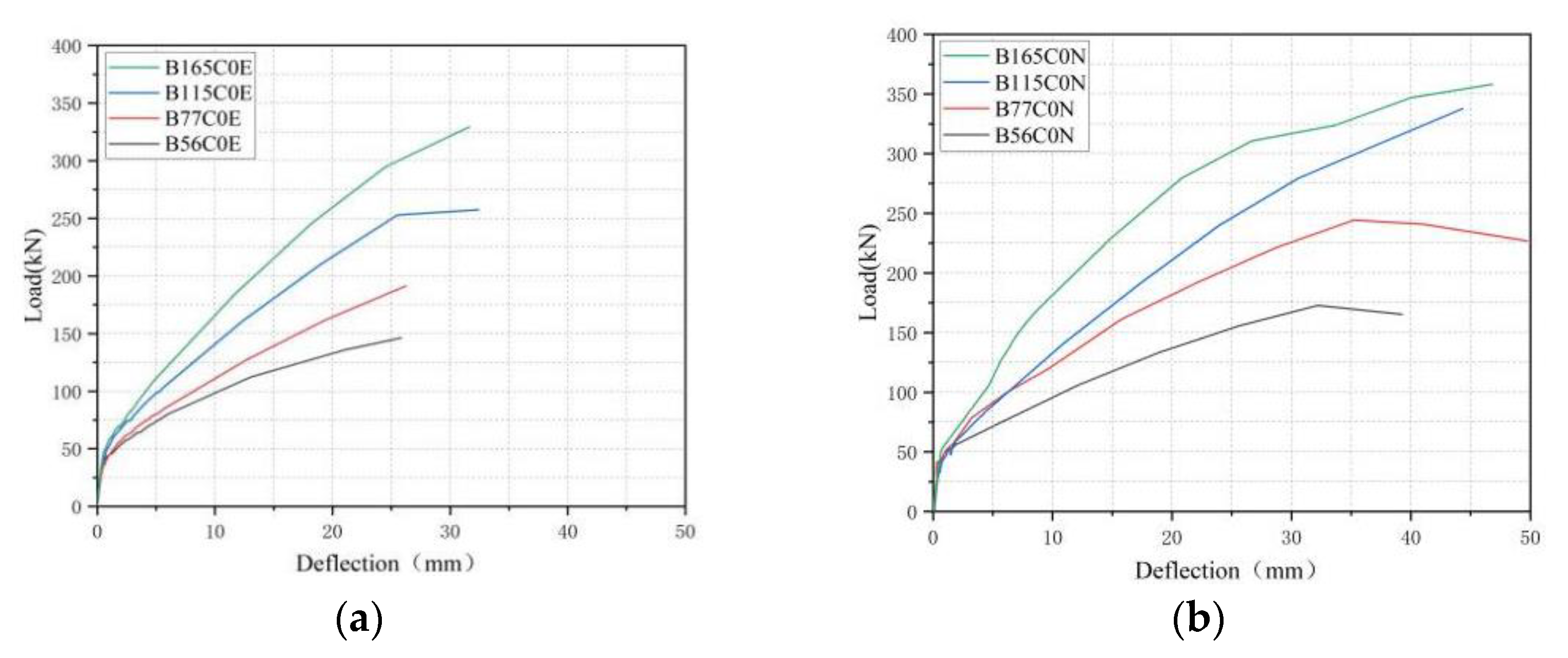
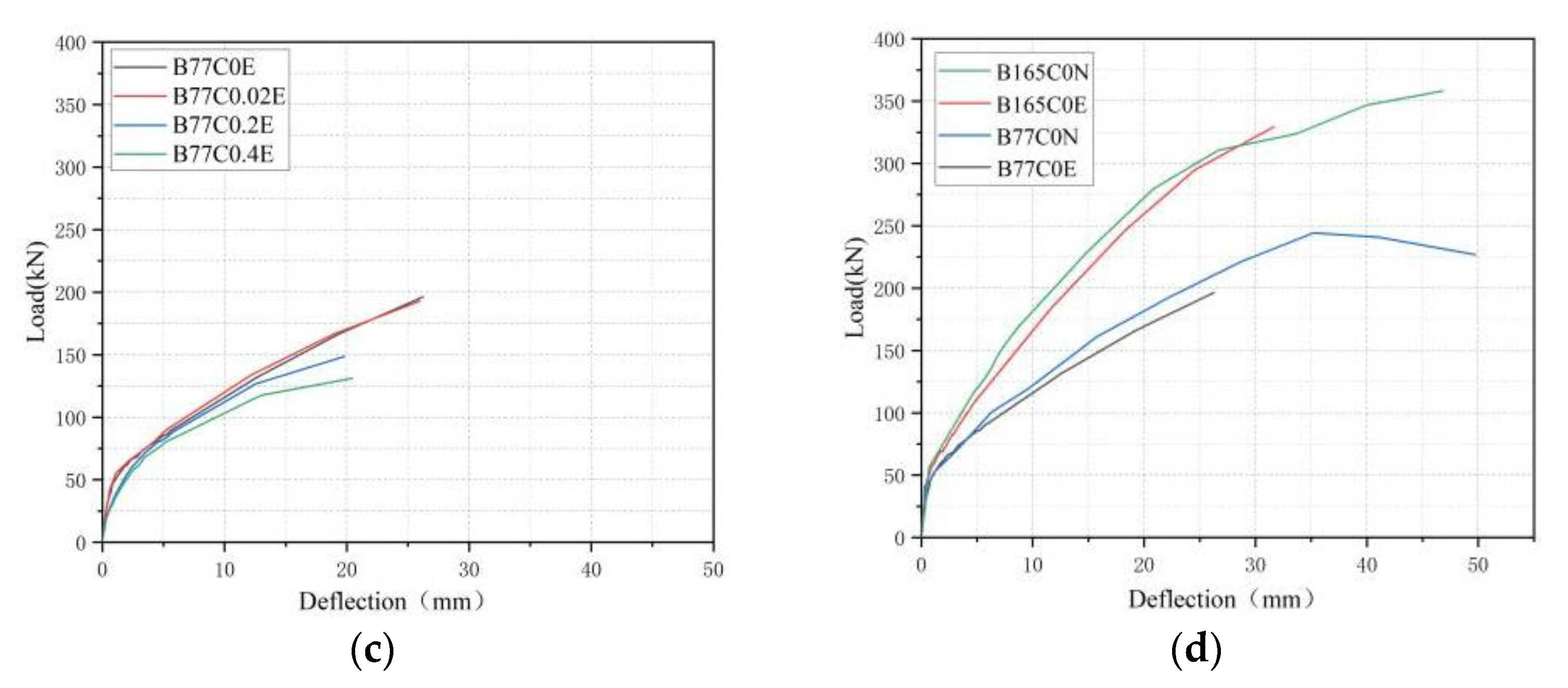
3.2. Load-Deflection Curves
3.3. Skeleton Curves
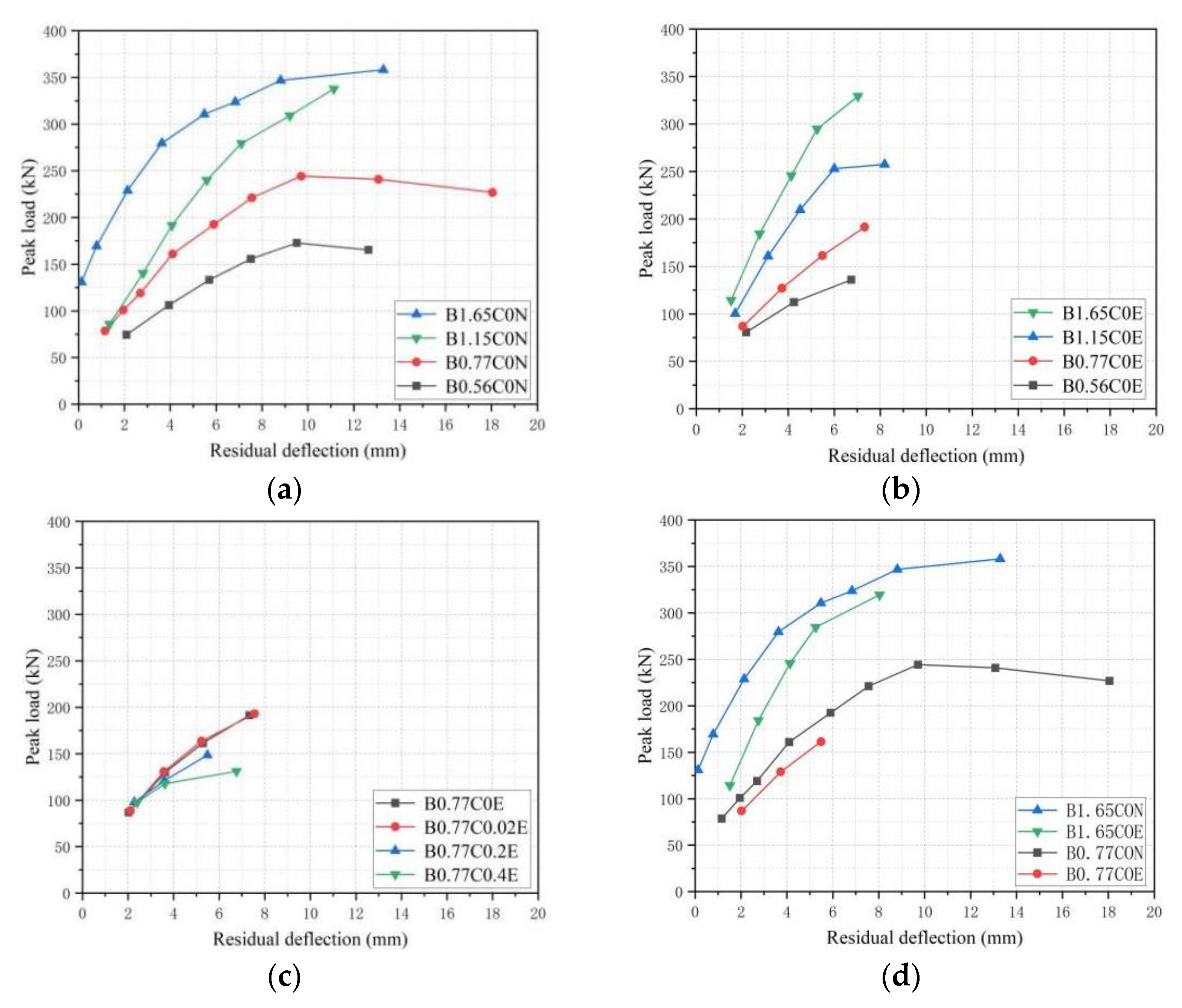
3.4. Residual Deflection
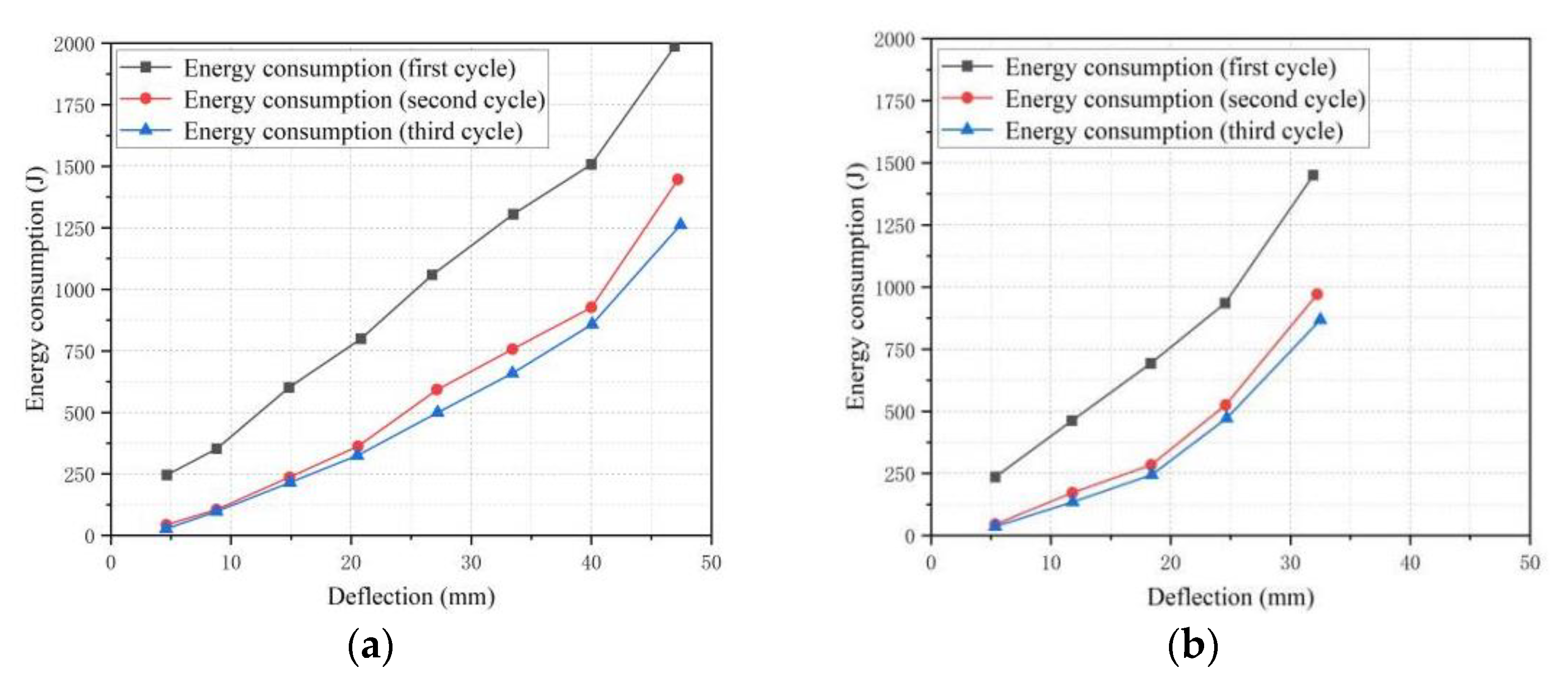
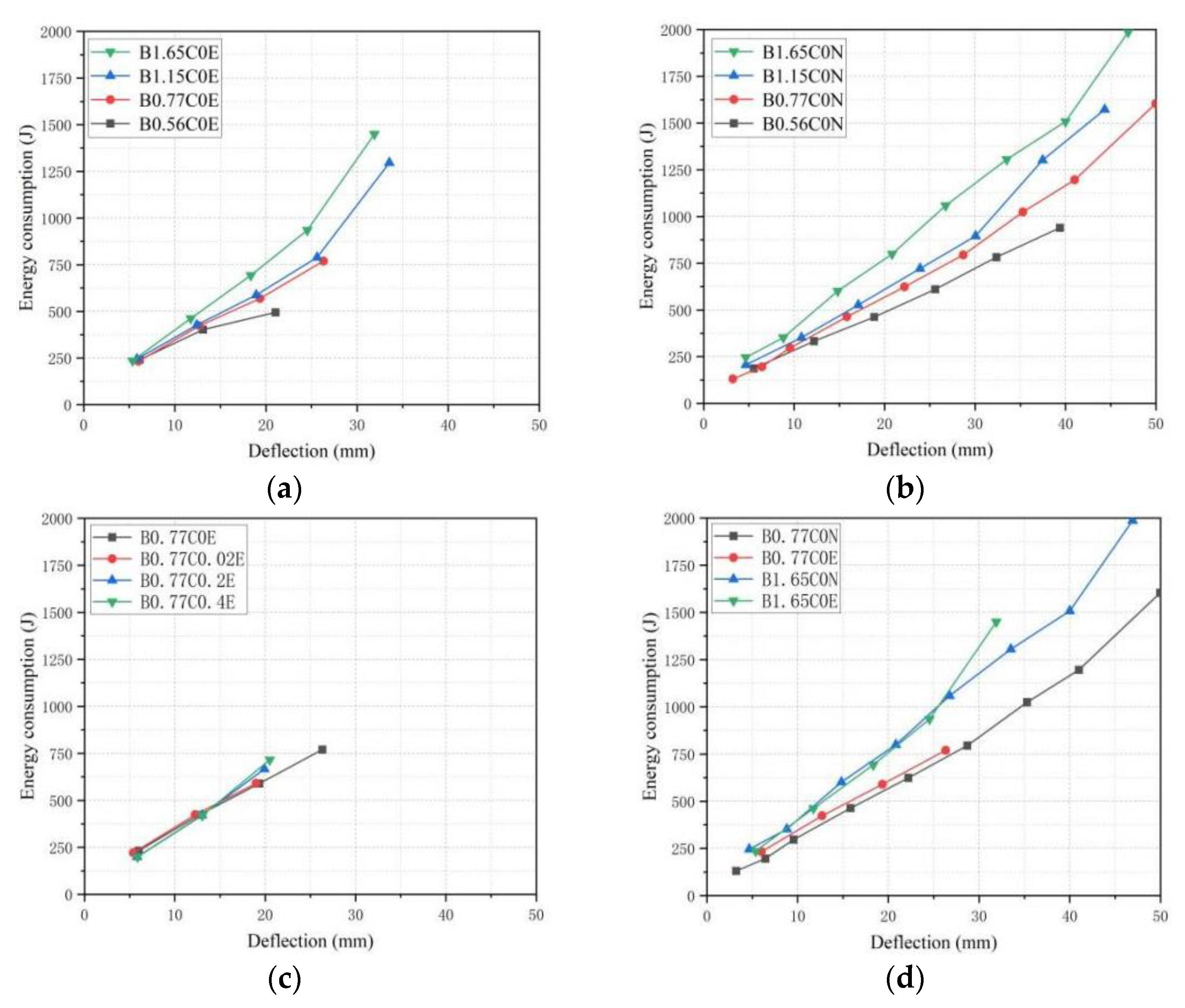
3.5. Energy Consumption Capacity
4. Comparison of Experimental Results with Model Predictions
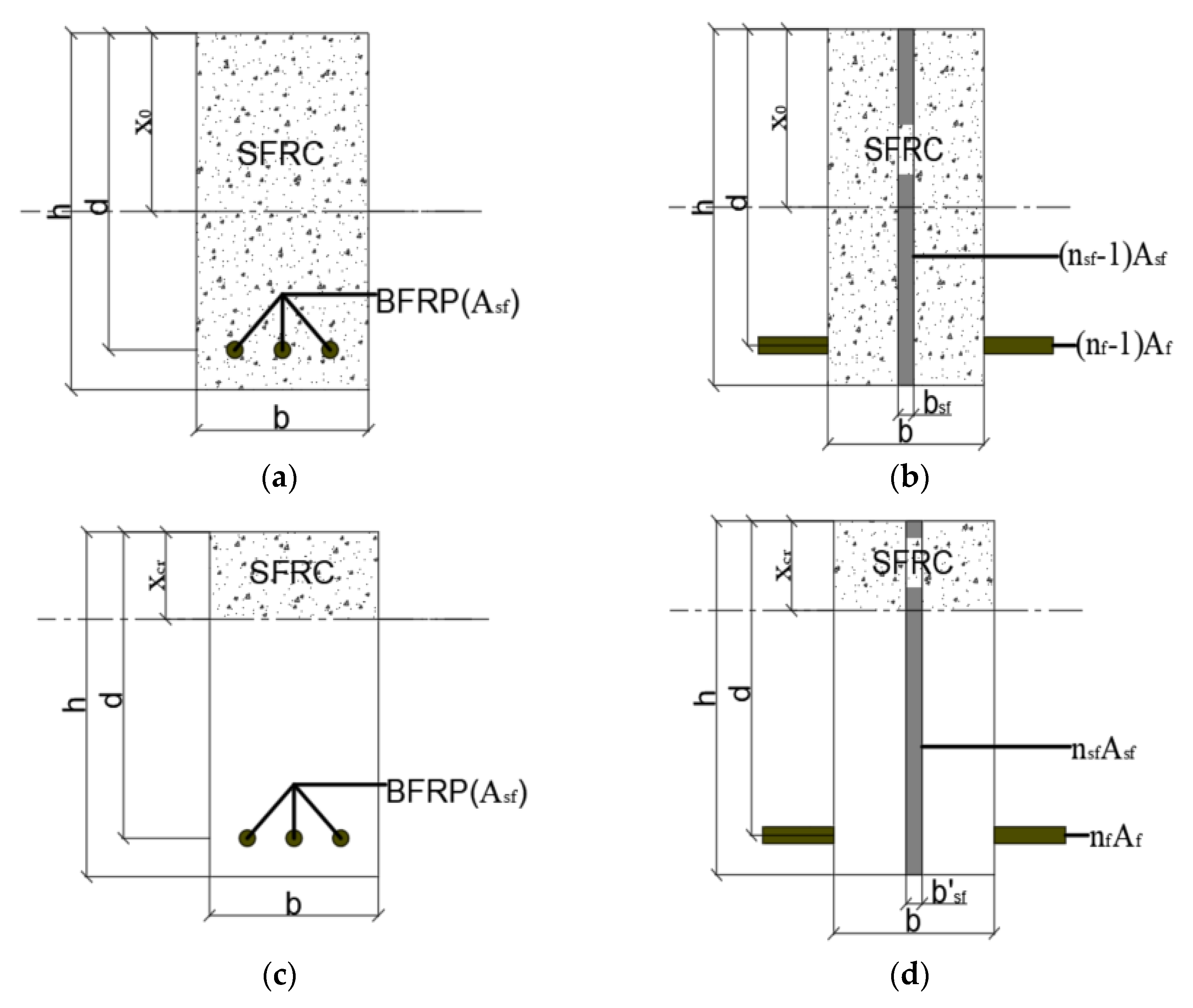
4.1. Theoretical Calculation Models of FRP-RC Beam Deflection
4.2. New Calculation Method of Deflection
5. Conclusions
- The cracking load of BFRP-SFRC beams was independent of the BFRP reinforcement ratios, at the same time, the seawater erosion had little effect on the cracking load after one year. The cracking load was mainly related to the tensile strength of concrete;
- The load–deflection curves of BFRP-SFRC beams show bilinear growth. With the increase in the loading and unloading cycles, the peak load and energy consumption of the tested beams decreased, while the residual deflection increased, and the impact of loading and unloading cycles on the flexural performances of the BFRP-SFRC beams enhanced with the increase of displacement;
- High BFRP reinforcement ratios were conducive to increasing the stiffness and total energy consumption, reducing the deformation and the residual deflection of the test beams. The peak load and energy consumption of BFRP-SFRC beams after seawater erosion decreased, but the stiffness change was not obvious under the same displacement;
- The contribution of steel fibers to the stiffness of the beams was ignored at the after cracking when using the current effective moment of inertia model to calculate the moment of inertia of the BFRP-SFRC beams. Considering the pre-splitting treatment, seawater erosion and the strain-hardening behavior of steel fibers after cracking, a new deflection evaluation model of BFRP-SFRC beams was established, whose results were closer to the experimental values than those of other available models.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Jiang, W.-Q.; Shen, X.-H.; Hong, S.; Wu, Z.-Y.; Liu, Q.-F. Binding capacity and diffusivity of concrete subjected to freeze-thaw and chloride attack: A numerical study. Ocean Eng. 2019, 186, 106093. [Google Scholar] [CrossRef]
- Kwan, W.H.; Ramli, M. Indicative performance of fiber reinforced polymer (FRP) encased beam in flexure. Constr. Build. Mater. 2013, 48, 780–788. [Google Scholar] [CrossRef]
- Vedernikov, A.; Minchenkov, K.; Gusev, S.; Sulimov, A.; Zhou, P.; Li, C.; Xian, G.; Akhatov, I.; Safonov, A. Effects of the Pre-Consolidated Materials Manufacturing Method on the Mechanical Properties of Pultruded Thermoplastic Composites. Polymers 2022, 14, 2246. [Google Scholar] [CrossRef]
- Wu, G.; Wang, X.; Wu, Z.; Dong, Z.; Xie, Q. Degradation of basalt FRP bars in alkaline environment. Sci. Eng. Compos. Mater. 2014, 22, 649–657. [Google Scholar] [CrossRef]
- Andreea, S.; Maurizio, G.; Kypros, P. Mechanical Characterization of Basalt FRP Rebars and Long-Term Strength Predictive Model. J. Compos. Constr. 2015, 19, 04014037. [Google Scholar]
- Benmokrane, B.; Elgabbas, F.; Ahmed, E.A.; Cousin, P. Characterization and Comparative Durability Study of Glass/Vinylester, Basalt/Vinylester, and Basalt/Epoxy FRP Bars. J. Compos. Constr. 2015, 19, 04015008. [Google Scholar] [CrossRef]
- Lv, B. Durability Study of BFRP Bars and Their Reinforced Concrete Beam Immersed in Seawater. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2016. (In Chinese). [Google Scholar]
- Wang, Z.; Zhao, X.-L.; Xian, G.; Wu, G.; Raman, R.S.; Al-Saadi, S.; Haque, A. Long-term durability of basalt- and glass-fibre reinforced polymer (BFRP/GFRP) bars in seawater and sea sand concrete environment. Constr. Build. Mater. 2017, 139, 467–489. [Google Scholar] [CrossRef]
- Wang, Z.; Zhao, X.L.; Xian, G.; Wu, G.; Raman, R.S.; Al-Saadi, S. Durability study on interlaminar shear behaviour of basalt-, glass-and carbon-fibre reinforced polymer (B/G/CFRP) bars in seawater sea sand concrete environment. Constr. Build. Mater. 2017, 156, 985–1004. [Google Scholar] [CrossRef]
- Benmokrane, B.; Robert, M.; Mohamed, H.M.; Ali, A.H.; Cousin, P. Durability Assessment of Glass FRP Solid and Hollow Bars (Rock Bolts) for Application in Ground Control of Jurong Rock Caverns in Singapore. J. Compos. Constr. 2017, 21, 06016002. [Google Scholar] [CrossRef]
- Duo, Y.; Liu, X.; Liu, Y.; Tafsirojjaman, T.; Sabbrojjaman, M. Environmental impact on the durability of FRP reinforcing bars. J. Build. Eng. 2021, 43, 102909. [Google Scholar] [CrossRef]
- Ahmed, A.; Guo, S.; Zhang, Z.; Shi, C.; Zhu, D. A review on durability of fiber reinforced polymer (FRP) bars reinforced seawater sea sand concrete. Constr. Build. Mater. 2020, 256, 119484. [Google Scholar] [CrossRef]
- Wang, H.; Belarbi, A. Flexural durability of FRP bars embedded in fiber-reinforced-concrete. Constr. Build. Mater. 2013, 44, 541–550. [Google Scholar] [CrossRef]
- Chen, C.; Chen, J.; Zhou, Y.; Sui, L.; Hu, B. Design of ductile H-anchorage for strengthening reinforced concrete beams with prestressed FRP. Constr. Build. Mater. 2021, 307, 124883. [Google Scholar] [CrossRef]
- Altun, F.; Haktanir, T.; Ari, K. Effects of steel fiber addition on mechanical properties of concrete and RC beams. Constr. Build. Mater. 2006, 21, 654–661. [Google Scholar] [CrossRef]
- Aoude, H.; Belghiti, M.; Cook, W.D.; Mitchell, D. Response of Steel Fiber-Reinforced Concrete Beams with and without Stirrups. ACI Struct. J. 2012, 109, 359–367. [Google Scholar] [CrossRef]
- Yang, J.-M.; Min, K.-H.; Shin, H.-O.; Yoon, Y.-S. Effect of steel and synthetic fibers on flexural behavior of high-strength concrete beams reinforced with FRP bars. Compos. Part B Eng. 2012, 43, 1077–1086. [Google Scholar] [CrossRef]
- Zhu, H.; Li, Z.; Wen, C.; Cheng, S.; Wei, Y. Prediction model for the flexural strength of steel fiber reinforced concrete beams with fiber-reinforced polymer bars under repeated loading. Compos. Struct. 2020, 250, 112609. [Google Scholar] [CrossRef]
- Xian, G.; Li, H.; Su, X. Water absorption and hygrothermal ageing of ultraviolet cured glass-fiber reinforced acrylate composites. Polym. Compos. 2012, 33, 1120–1128. [Google Scholar] [CrossRef]
- Wu, G.; Dong, Z.-Q.; Wang, X.; Zhu, Y.; Wu, Z.-S. Prediction of Long-Term Performance and Durability of BFRP Bars under the Combined Effect of Sustained Load and Corrosive Solutions. J. Compos. Constr. 2015, 19, 04014058. [Google Scholar] [CrossRef]
- GB/T14684-2011; Sand for Construction. General Administration of Quality Supervision. Inspection and Quarantine of PR China: Beijing, China, 2011.
- GB175-2007; General Administration of Quality Supervision. Common Portland Cement. Inspection and Quarantine of PR China: Beijing, China, 2007.
- Issa, M.S.; Metwally, I.M.; Elzeiny, S.M. Influence of fibers on flexural behavior and ductility of concrete beams reinforced with GFRP rebars. Eng. Struct. 2011, 33, 1754–1763. [Google Scholar] [CrossRef]
- JG/T 472–2015; Steel Fibre Reinforced Concrete. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2015.
- GB/T 50081-2019; Standard for Methods of Concrete Physical and Mechancial Properties. General Administration of Quality Supervision, Inspection and Quarantine of PR China: Beijing, China, 2019.
- ACI Committee 440. 3R-12; Guide Test Methods for Fiber Reinforced Polymer (FRP) Composites for Reinforcing or Strengthening Concrete and Masonry Structures. American Concrete Institute: Farmington Hills, MI, USA, 2012.
- ACI Committee 440. 1R-15; Guide for the Design and Construction of Concrete Reinforced with FRP Bars. American Concrete Institute: Farmington Hills, MI, USA, 2015.
- Sun, X.; Fang, X.; Guan, L. Mechanics of Materials 1; Higher Education Press: Beijing, China, 2019. [Google Scholar]
- ACI Committee 440. 1R-03; Guide for the Design and Construction of Concrete Reinforced with FRP Bars. American Concrete Institute: Farmington Hills, MI, USA, 2003.
- Ammash, H.K.; Hemzah, S.A.; Al-Ramahee, M.A. Unified Advanced Model of Effective Moment of Inertia of Reinforced Concrete Members. Int. J. Appl. Eng. Res. 2018, 13, 557–563. [Google Scholar]
- Branson, D.E. Deformation of Concrete Structures; McGraw-Hill: New York, NY, USA, 1977; p. 537. [Google Scholar]
- ACI Committee 318-19; Build Code Requirements for Structural Concrete. American Concrete Institute: Farmington Hills, MI, USA, 2019.
- Zhu, H.; Cheng, S.; Gao, D.; Neaz, S.M.; Li, C. Flexural behavior of partially fiber-reinforced high-strength concrete beams reinforced with FRP bars. Constr. Build. Mater. 2018, 161, 587–597. [Google Scholar] [CrossRef]
- Danying, G. Basic Theory of Steel Fibre Reinforced Concrete; Scientific and Technical Documentation Press: Beijing, China, 1994. [Google Scholar]
- Ming, Z. Fatigue Performance and Calculation Method of Steel Fiber Reinforced High-Strength Concrete Beams; Zhengzhou University: Zhengzhou, China, 2015. [Google Scholar]
- Toutanji, H.A.; Saafi, M. Flexural Behavior of Concrete Beams Reinforced with Glass Fiber-Reinforced Polymer (GFRP) Bars. ACI Struct. J. 2000, 97, 712–719. [Google Scholar] [CrossRef]
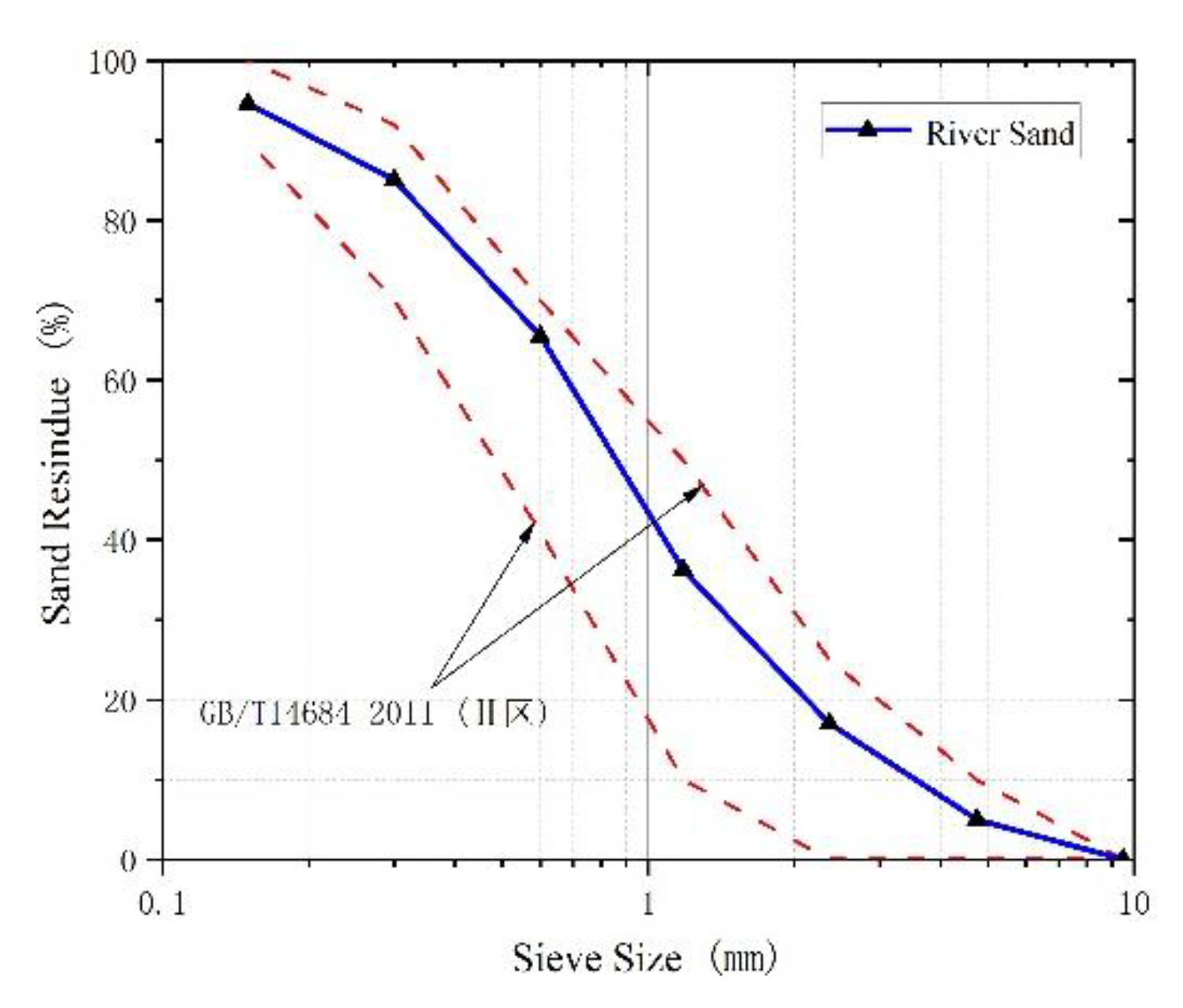




| Water | Cement | Coarse Aggregate | Sand | Steel Fiber | Water-Reducers |
|---|---|---|---|---|---|
| 164 | 529 | 1026 | 706 | 78.5 | 5.82 |
| df (mm) | Af (mm²) | Mechanical Properties of BFRP Bars | |||
|---|---|---|---|---|---|
| Before Seawater Erosion | After Seawater Erosion (365 d) | ||||
| ffu (MPa) | Ef (GPa) | ffu (MPa) | Ef (GPa) | ||
| 12 | 113.1 | 1034.1 | 43.26 | 926.9 | 39.4 |
| 14 | 153.9 | 1025.6 | 41.79 | 910.8 | 38.2 |
| Kind | Content (g/L) | Kind | Content (g/L) |
|---|---|---|---|
| NaCl | 28.219 | MgCl2 | 2.392 |
| MgSO4 | 3.439 | CaCl2 | 1.234 |
| NaHCO3 | 0.256 | KCl | 0.764 |
| Series | Specimens | BFRP Reinforcement Ratios (%) | Pre-Crack Width (mm) | Environment | Actual Foundation Mechanical Properties of Concrete | |||
|---|---|---|---|---|---|---|---|---|
| Before Seawater Erosion | After Seawater Erosion | |||||||
| fcu (MPa) | fc (MPa) | fcu (MPa) | fc (MPa) | |||||
| I | B0.56C0N | 0.56 | 0 | Nature | 48.13 | 60.16 | ||
| B0.77C0N | 0.77 | 0 | Nature | 52.45 | 74.99 | |||
| B1.15C0N | 1.15 | 0 | Nature | 65.18 | 81.47 | |||
| B1.65C0N | 1.65 | 0 | Nature | 61.18 | 76.47 | |||
| II | B0.56C0E | 0.56 | 0 | Seawater erosion | 64.58 | 41.45 | 77.24 | 55.16 |
| B0.77C0E | 0.77 | 0 | Seawater erosion | 74.99 | 54.45 | 87.50 | 65.62 | |
| B0.77C0.02E | 0.77 | 0.02 | Seawater erosion | 72.13 | 52.93 | 83.13 | 70.64 | |
| B0.77C0.2E | 0.77 | 0.2 | Seawater erosion | 66.98 | 50.69 | 81.69 | 65.71 | |
| B0.77C0.4E | 0.77 | 0.4 | Seawater erosion | 69.16 | 52.42 | 84.17 | 68.41 | |
| B1.15C0E | 1.15 | 0 | Seawater erosion | 69.31 | 53.84 | 83.37 | 63.12 | |
| B1.65C0E | 1.65 | 0 | Seawater erosion | 72.56 | 53.14 | 86.61 | 67.76 | |
| Average value | 65.15 | 59.27 | 83.39 | 65.20 | ||||
| Standard deviations | 8.39 | 12.67 | 3.38 | 5.03 | ||||
| Series | Specimens | Failure Mode | Mcr (kN) | Mu (kN·m) | Δmax (mm) |
|---|---|---|---|---|---|
| I | B0.56C0N | BFRP bars rupturing | 13.50 | 51.85 | 32.23 |
| B0.77C0N | BFRP bars rupturing | 14.10 | 73.28 | 35.23 | |
| B1.15C0N | Concrete crushing | 14.25 | 101.34 | 44.32 | |
| B1.65C0N | Concrete crushing | 15.00 | 101.43 | 46.83 | |
| II | B0.56C0E | BFRP bars rupturing | 10.65 | 43.80 | 20.06 |
| B0.77C0E | BFRP bars rupturing | 11.42 | 56.55 | 26.45 | |
| B0.77C0.02E | BFRP bars rupturing | — | 56.49 | 25.98 | |
| B0.77C0.2E | BFRP bars rupturing | — | 44.43 | 19.79 | |
| B0.77C0.4E | BFRP bars rupturing | — | 39.18 | 20.20 | |
| B1.15C0E | BFRP bars rupturing | 12.18 | 77.01 | 34.27 | |
| B1.65C0E | BFRP bars rupturing | 14.10 | 98.22 | 32.46 | |
| Average value | 13.15 | 67.60 | 30.71 | ||
| Standard deviations | 1.55 | 23.97 | 9.31 |
| Beams | Ft (kN) | Δt (mm) | ΔACI15 (mm) | ΔACI15 /Δt | ΔACI03 (mm) | ΔACI03 /Δt | ΔAmmash (mm) | ΔAmmash /Δt | Δc (mm) | Δc /Δt |
|---|---|---|---|---|---|---|---|---|---|---|
| B0.56C0N | 77.33 | 5.56 | 6.75 | 1.21 | 5.78 | 0.96 | 6.52 | 1.08 | 5.47 | 0.98 |
| B0.77C0N | 86.01 | 5.62 | 8.23 | 1.47 | 5.71 | 0.96 | 6.10 | 1.02 | 5.90 | 1.05 |
| B1.15C0N | 87.1 | 4.64 | 4.67 | 1.01 | 6.56 | 1.23 | 7.55 | 1.41 | 4.84 | 1.04 |
| B1.65C0N | 93.31 | 4.62 | 5.03 | 1.09 | 7.82 | 1.37 | 9.49 | 1.67 | 4.52 | 0.98 |
| B0.56C0E | 80.12 | 6.02 | 9.61 | 1.59 | 7.67 | 1.33 | 9.05 | 1.57 | 6.00 | 1.00 |
| B0.77C0E | 86.81 | 5.97 | 7.97 | 1.34 | 6.43 | 1.10 | 8.10 | 1.39 | 5.90 | 0.99 |
| B0.77C0.02E | 86.71 | 5.35 | 8.69 | 1.63 | 6.47 | 1.22 | 8.57 | 1.62 | 5.90 | 1.10 |
| B0.77C0.2E | 86.80 | 5.70 | 9.79 | 1.72 | 3.75 | 0.67 | 5.68 | 1.02 | 6.36 | 1.12 |
| B0.77C0.4E | 79.70 | 5.77 | 9.71 | 1.68 | 5.66 | 1.01 | 7.67 | 1.37 | 5.97 | 1.04 |
| B1.15C0E | 100.40 | 5.85 | 7.05 | 1.21 | 4.23 | 0.91 | 4.28 | 0.92 | 5.77 | 0.99 |
| B1.65C0E | 114.29 | 5.29 | 6.51 | 1.23 | 6.85 | 1.48 | 6.47 | 1.40 | 5.64 | 1.07 |
| Average value | 1.38 | 1.11 | 1.32 | 1.03 | ||||||
| Standard deviations | 0.25 | 0.24 | 0.26 | 0.05 | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, H.; Chen, Q.; Li, Z.; Zhang, Y.; Duan, W.; Li, Z. Evaluation of Deformation for Steel Fiber Concrete Beams with BFRP Tendons Eroded by Seawater under Cyclic Loading. Polymers 2023, 15, 62. https://doi.org/10.3390/polym15010062
Zhu H, Chen Q, Li Z, Zhang Y, Duan W, Li Z. Evaluation of Deformation for Steel Fiber Concrete Beams with BFRP Tendons Eroded by Seawater under Cyclic Loading. Polymers. 2023; 15(1):62. https://doi.org/10.3390/polym15010062
Chicago/Turabian StyleZhu, Haitang, Qun Chen, Zongze Li, Yin Zhang, Wencheng Duan, and Zemin Li. 2023. "Evaluation of Deformation for Steel Fiber Concrete Beams with BFRP Tendons Eroded by Seawater under Cyclic Loading" Polymers 15, no. 1: 62. https://doi.org/10.3390/polym15010062
APA StyleZhu, H., Chen, Q., Li, Z., Zhang, Y., Duan, W., & Li, Z. (2023). Evaluation of Deformation for Steel Fiber Concrete Beams with BFRP Tendons Eroded by Seawater under Cyclic Loading. Polymers, 15(1), 62. https://doi.org/10.3390/polym15010062







