Low Power Consuming Mode Switch Based on Hybrid-Core Vertical Directional Couplers with Graphene Electrode-Embedded Polymer Waveguides
Abstract
:1. Introduction
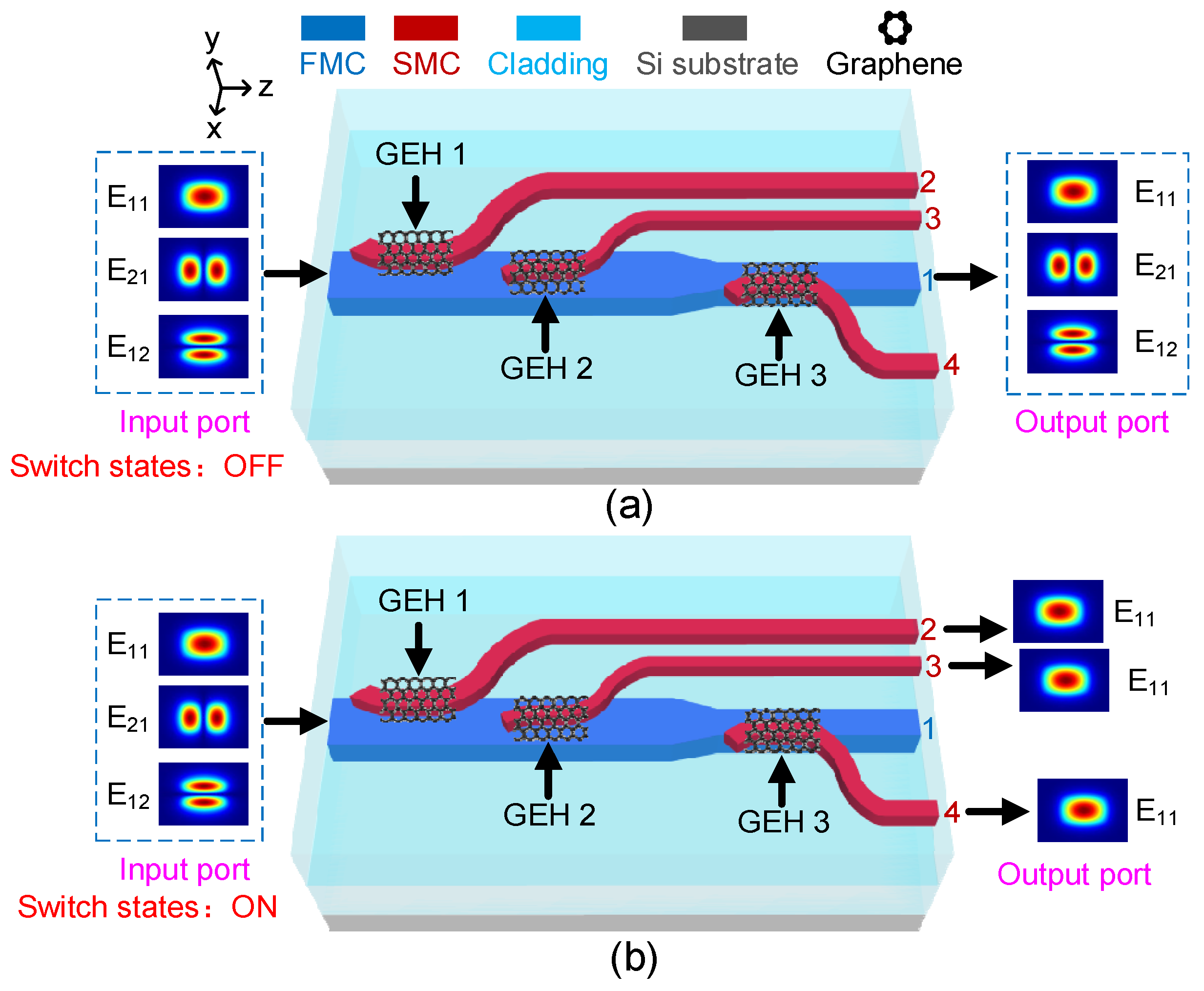
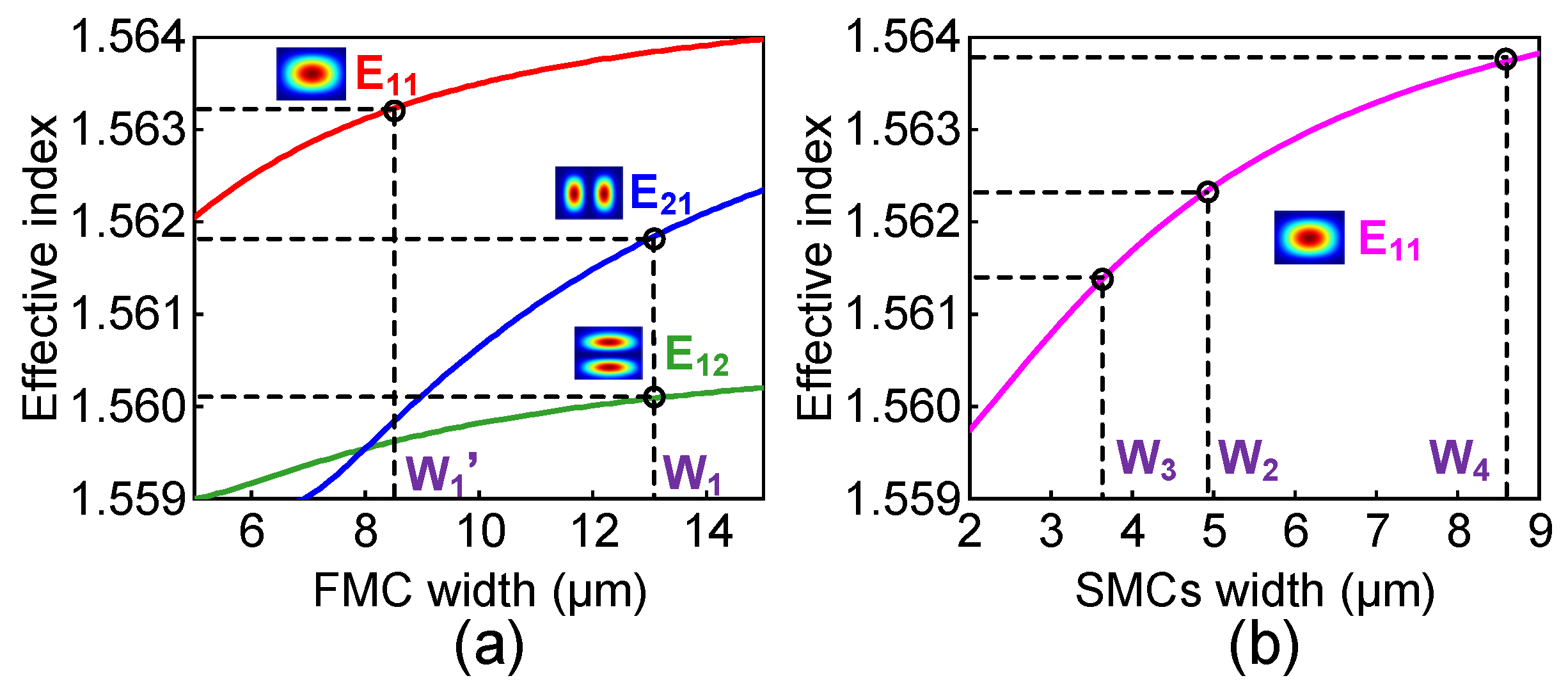
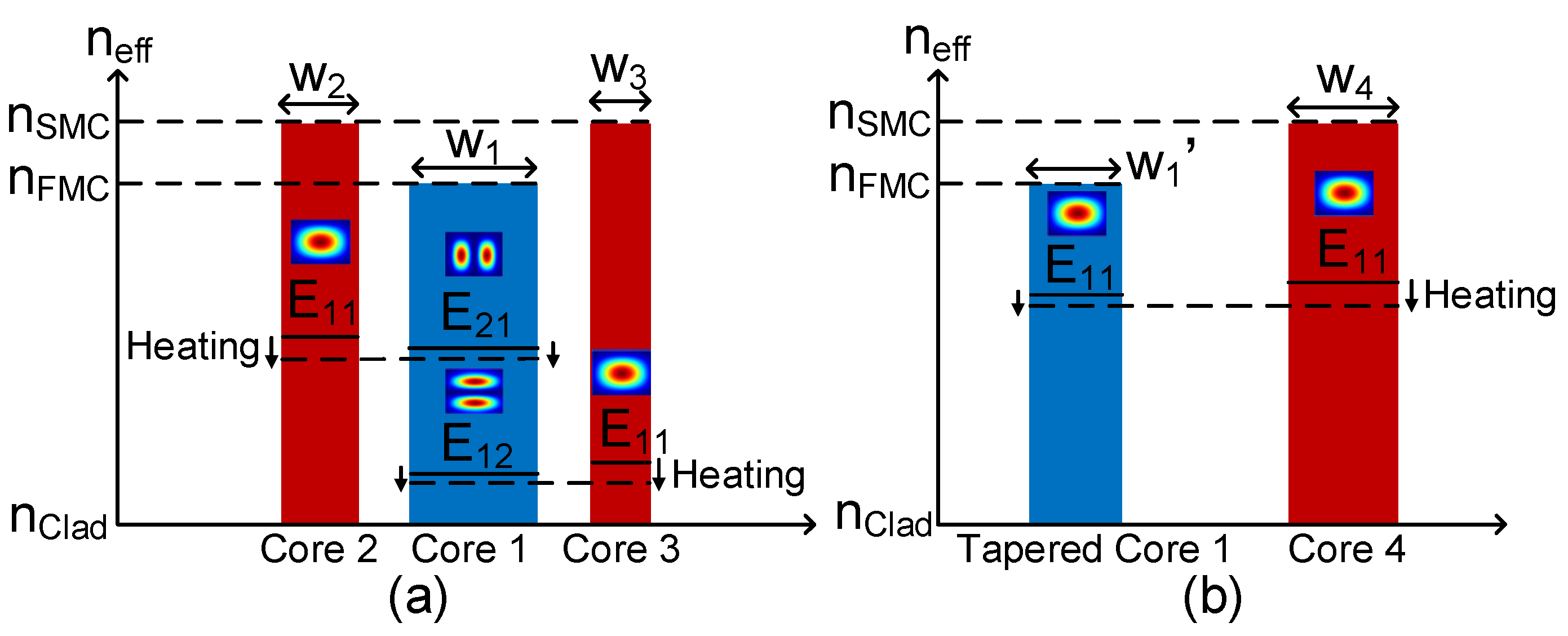
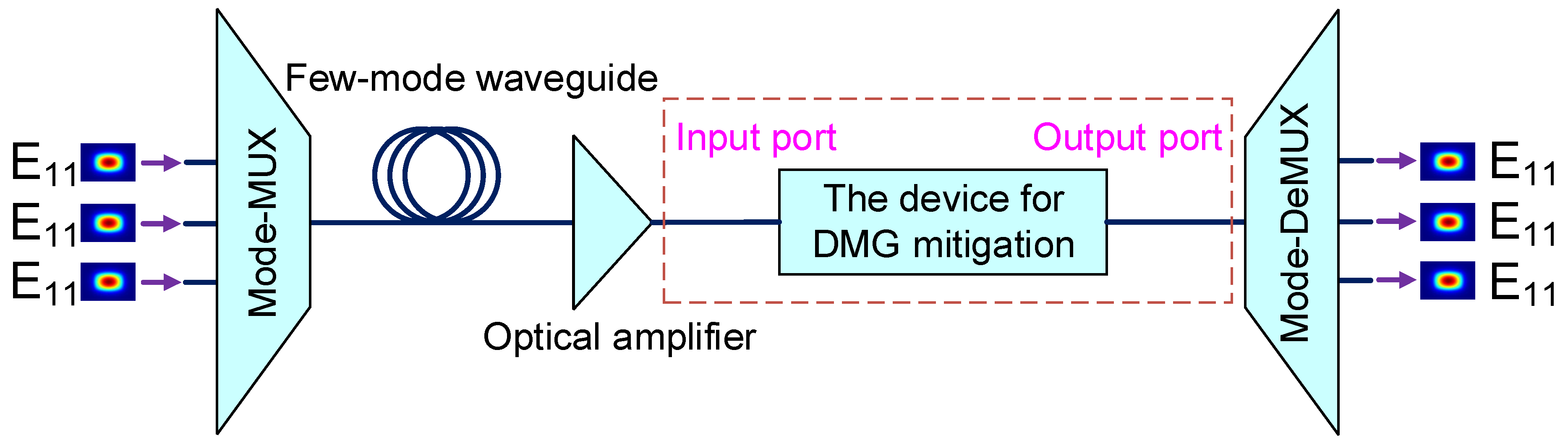
2. Operating Principle and Design
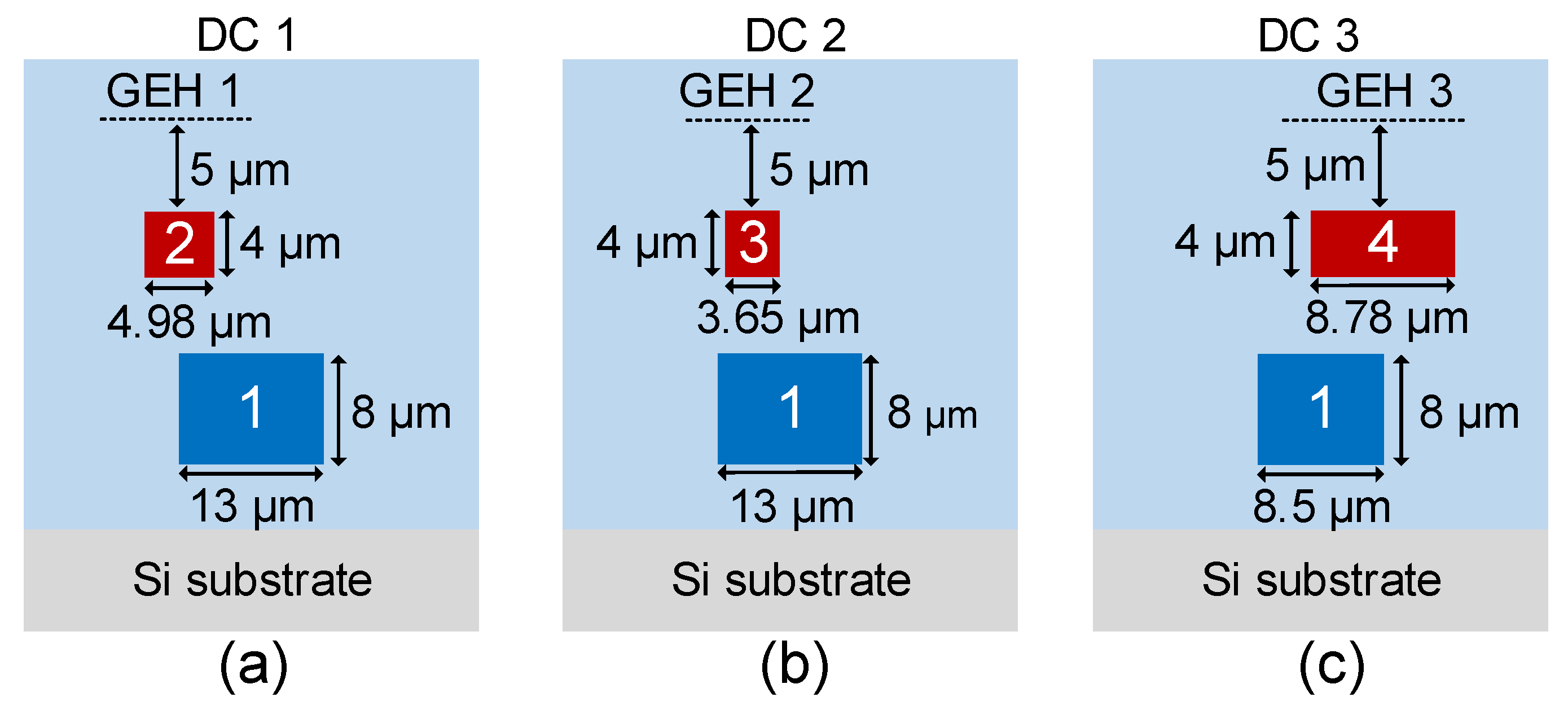
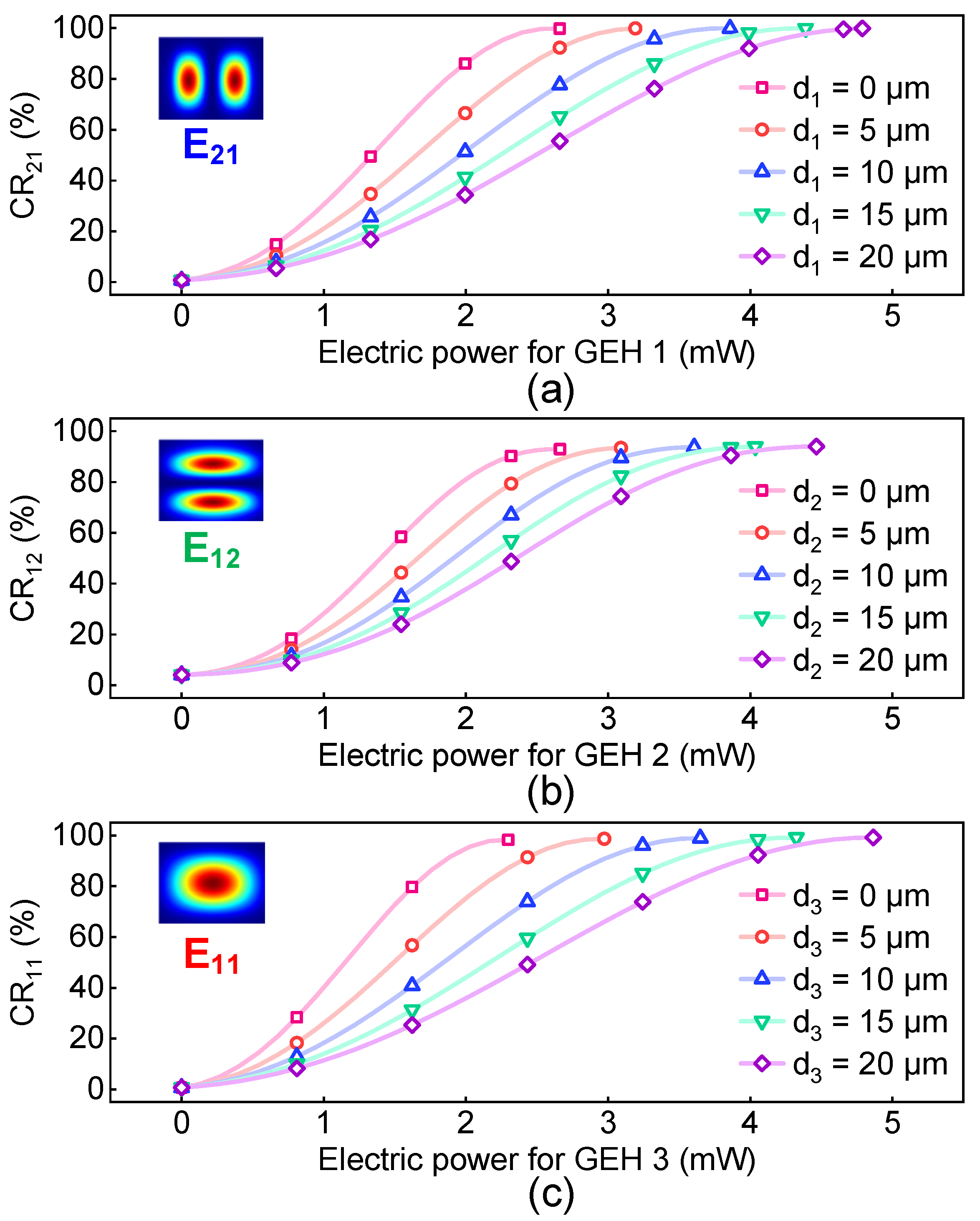
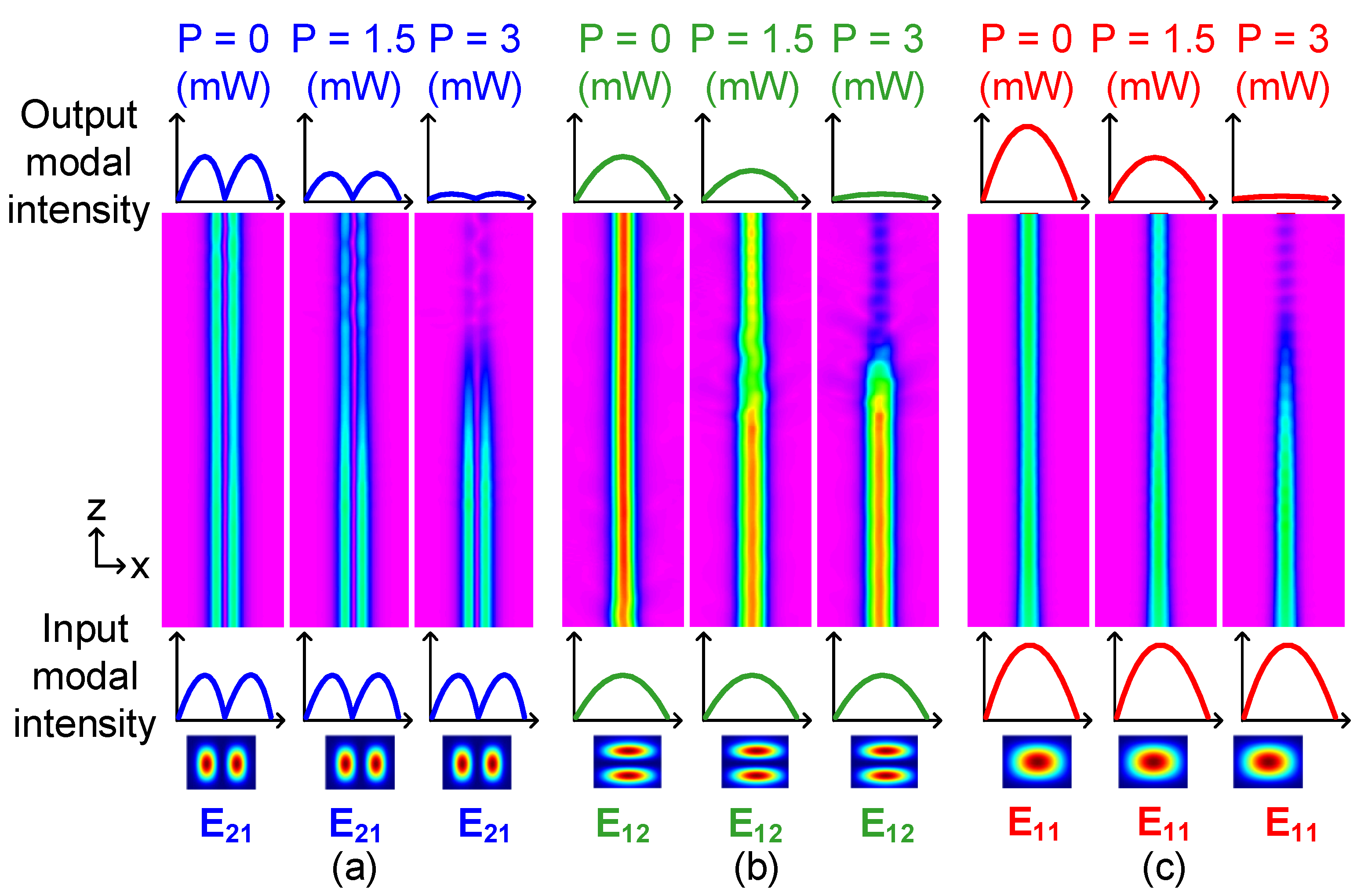
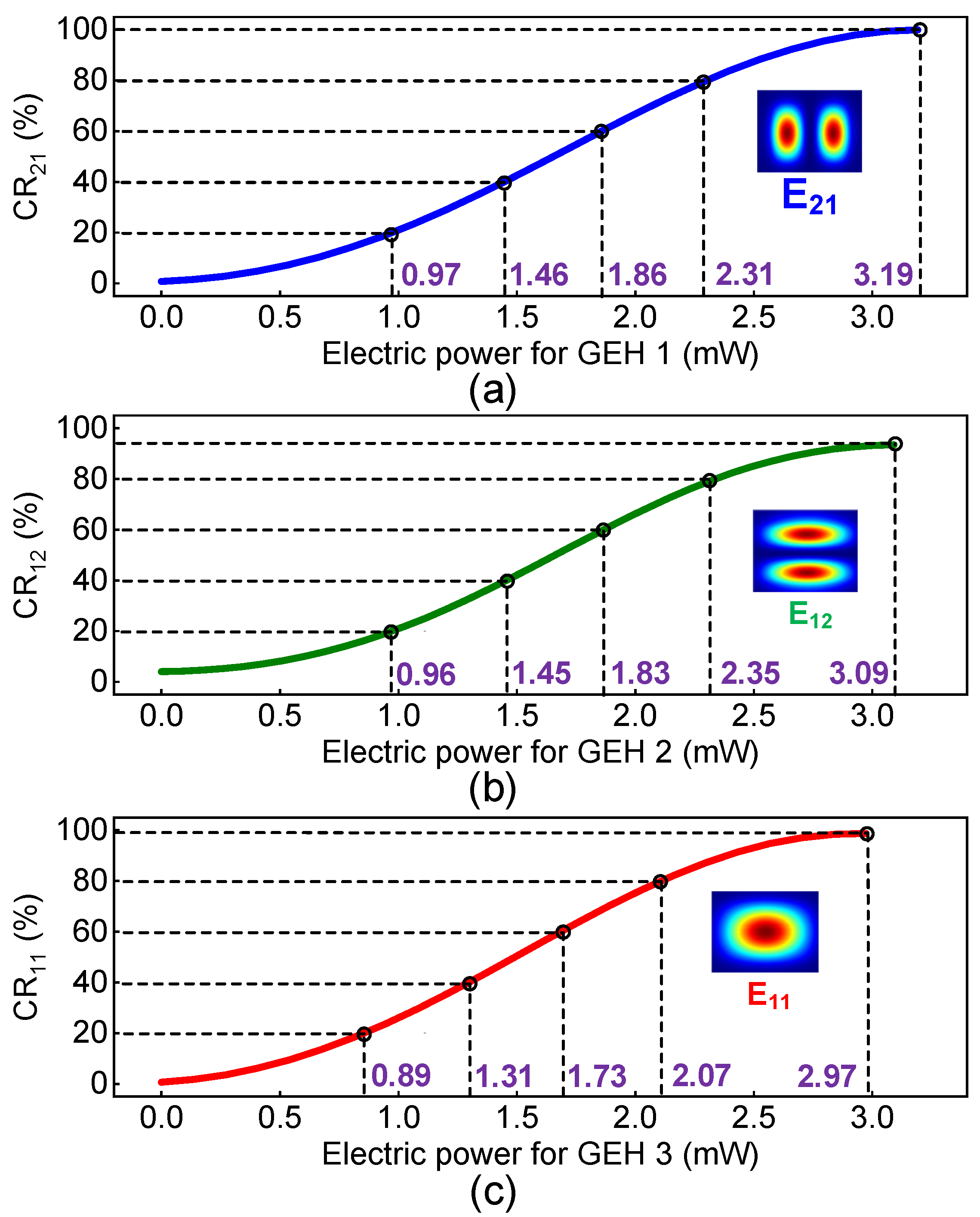
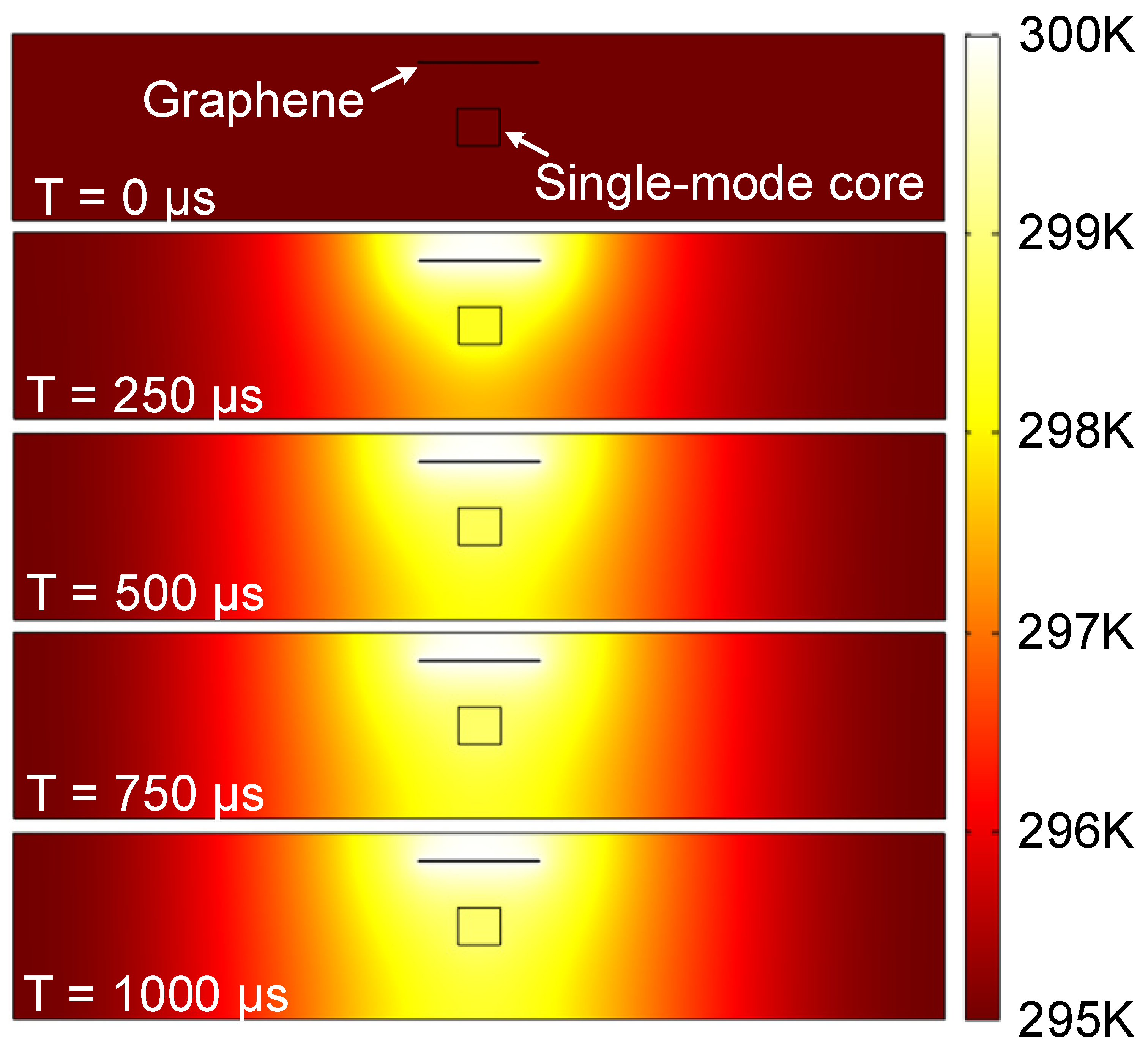
3. Simulation Results and Discussions
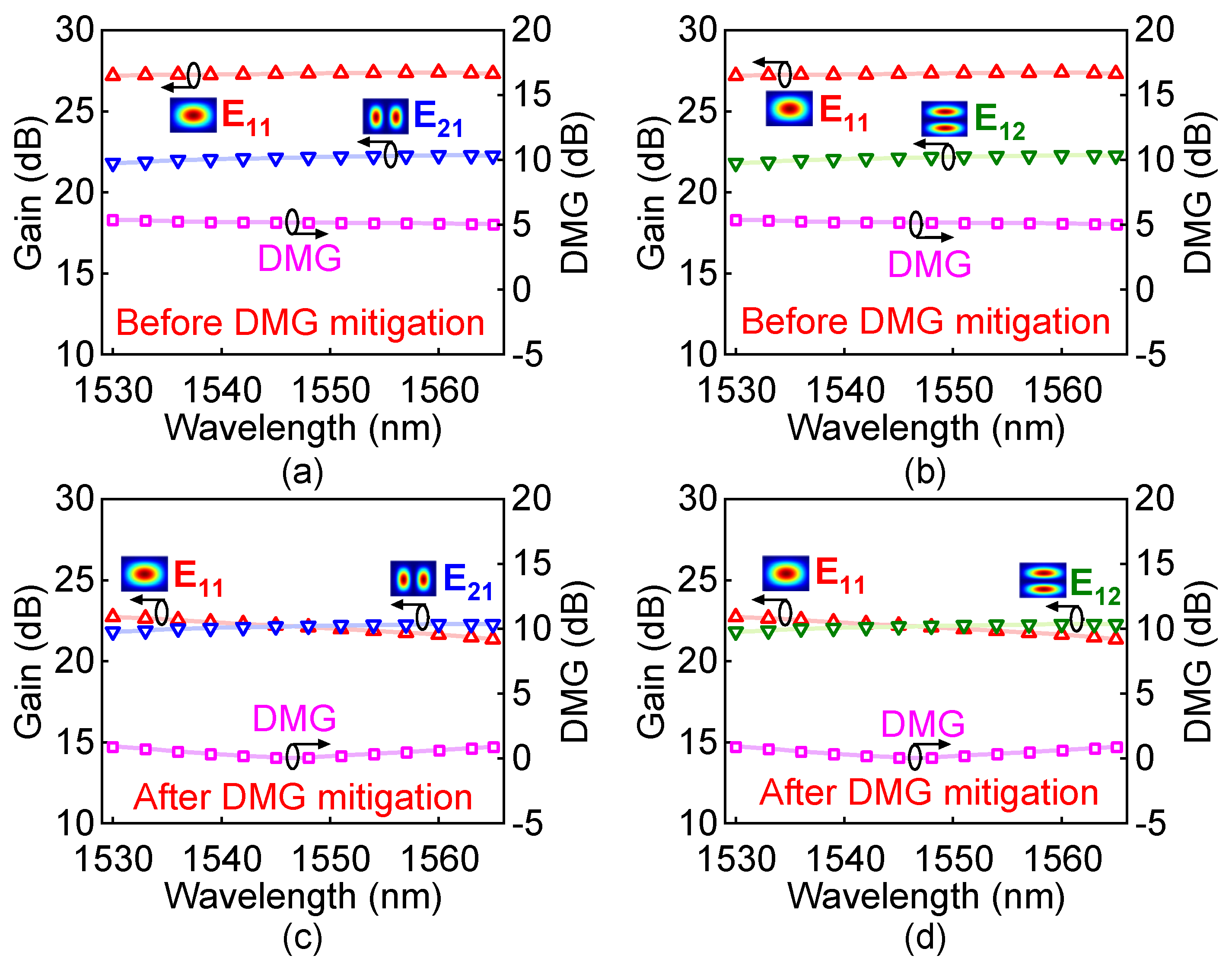
4. Application of Gain Equalization
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Richardson, D.J.; Fini, J.M.; Nelson, L.E. Space-division multiplexing in optical fibres. Nat. Photon. 2013, 7, 354–362. [Google Scholar] [CrossRef] [Green Version]
- Li, G.; Bai, N.; Zhao, N.; Xia, C. Space-division multiplexing: The next frontier in optical communication. Adv. Opti. Photon. 2014, 6, 413–487. [Google Scholar] [CrossRef] [Green Version]
- Winzer, P.J.; Neilson, D.T.; Chraplyvy, A.R. Fiber-optic transmission and networking: The previous 20 and the next 20 years [Invited]. Opt. Express 2018, 26, 24190–24239. [Google Scholar] [CrossRef] [PubMed]
- Puttnam, B.J.; Rademacher, G.; Luís, R.S. Space-division multiplexing for optical fiber communications. Optica 2021, 8, 1186–1203. [Google Scholar] [CrossRef]
- Li, C.; Liu, D.; Dai, D. Multimode silicon photonics. Nanophotonics 2019, 8, 227–247. [Google Scholar] [CrossRef]
- Han, X.; Jiang, Y.; Frigg, A.; Xiao, H.; Zhang, P.; Nguyen, T.G.; Boes, A.; Yang, J.; Ren, G.; Su, Y.; et al. Mode and polarization-division multiplexing based on silicon nitride loaded lithium niobate on insulator platform. Laser Photon. Rev. 2022, 16, 2100529. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Z.; Liu, Y.; Wang, X.; Guo, X.; Li, D.; Yao, Y.; Song, Q.; Du, J.; He, Z.; et al. Ultra-compact mode-division multiplexed photonic integrated circuit for dual polarizations. J. Lightw. Technol. 2021, 39, 5925–5932. [Google Scholar] [CrossRef]
- Zhao, W.; Liu, R.; Peng, Y.; Yi, X.; Chen, H.; Dai, D. High-performance silicon polarization switch based on a Mach–Zehnder interferometer integrated with polarization-dependent mode converters. Nanophotonics 2022, 11, 2293–2301. [Google Scholar] [CrossRef]
- Chang, P.H.; Lin, C.; Helmy, A.S. Integrated photonic functions using anisotropic 2D material structures. J. Lightw. Technol. 2021, 39, 7464–7471. [Google Scholar] [CrossRef]
- Douglass, G.; Dreisow, F.; Gross, S.; Withford, M.J. Femtosecond laser written arrayed waveguide gratings with integrated photonic lanterns. Opt. Express 2018, 26, 1497–1505. [Google Scholar] [CrossRef]
- Lu, Y.; Liu, W.; Chen, Z.; Jiang, M.; Zhou, Q.; Zhang, J.; Li, C.; Chai, J.; Jiang, Z. Spatial mode control based on photonic lanterns. Opt. Express 2021, 29, 41788–41797. [Google Scholar] [CrossRef]
- Chang, W.; Lu, L.; Ren, X.; Li, D.; Pan, Z.; Cheng, M.; Liu, D.; Zhang, M. Ultra-compact mode (de) multiplexer based on subwavelength asymmetric Y-junction. Opt. Express 2018, 26, 8162–8170. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.; Hashisaka, M.; Akiho, T.; Muraki, K.; Fujisawa, T. Quantized charge fractionalization at quantum Hall Y junctions in the disorder dominated regime. Nat. Commun. 2021, 12, 131. [Google Scholar] [CrossRef] [PubMed]
- Han, L.; Kuo, B.P.P.; Alic, N.; Radic, S. Ultra-broadband multimode 3dB optical power splitter using an adiabatic coupler and a Y-branch. Opt. Express 2018, 26, 14800–14809. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.X.; Younesi, M.; Chung, H.P.; Chiu, H.K.; GEISS, R.; Tseng, Q.H.; Setzpfandt, F.; Pertsch, T.; Chen, Y.H. Ultra-compact, broadband adiabatic passage optical couplers in thin-film lithium niobate on insulator waveguides. Opt. Express 2021, 29, 27362–27372. [Google Scholar] [CrossRef]
- Lin, B.; Sun, S.; Yang, K.; Zhu, M.; Gu, Y.; Yu, Q.; Wang, X.; Zhang, D. Polymer/silica hybrid 3D waveguide thermo-optic mode switch based on cascaded asymmetric directional couplers. Appl. Opt. 2021, 60, 6943–6949. [Google Scholar] [CrossRef]
- Thomaschewski, M.; Zenin, V.A.; Wolff, C.; Bozhevolnyi, S.I. Plasmonic monolithic lithium niobate directional coupler switches. Nat. Commun. 2020, 11, 748. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Chen, H.; Liu, L.; Shang, J.; Yu, L.; Li, K.; Dong, J.; Qiu, W.; Guan, H.; Lu, H.; et al. An optical switch based on electro-optic mode deflection in lithium niobate waveguide. IEEE Photon. Technol. Lett. 2020, 32, 1295–1298. [Google Scholar] [CrossRef]
- Chen, K.; Yan, J.; He, S.; Liu, L. Broadband optical switch for multiple spatial modes based on a silicon densely packed waveguide array. Opt. Lett. 2019, 44, 907–910. [Google Scholar] [CrossRef]
- Xiong, Y.; Priti, R.B.; Ladouceur, O.L. High-speed two-mode switch for mode-division multiplexing optical networks. Optica 2017, 4, 1098–1102. [Google Scholar] [CrossRef]
- Song, Q.Q.; Chen, K.X.; Hu, Z.F. Low-power broadband thermo-optic switch with weak polarization dependence using a segmented graphene heater. J. Lightw. Technol. 2020, 38, 1358–1364. [Google Scholar] [CrossRef]
- Gan, X.; Zhao, C.; Wang, Y.; Mao, D.; Fang, L.; Han, L.; Zhao, J. Graphene-assisted all-fiber phase shifter and switching. Optica 2015, 2, 468–471. [Google Scholar] [CrossRef]
- Chu, R.; Guan, C.; Bo, Y.; Liu, J.; Shi, J.; Yang, J.; Ye, P.; Li, P.; Yang, J.; Yuan, L. Graphene decorated twin-core fiber Michelson interferometer for all-optical phase shifter and switch. Opt. Lett. 2020, 45, 177–180. [Google Scholar] [CrossRef]
- Guo, T.; Gao, S.; Zeng, H.; Tang, L.; Qiu, C. All-optical control of a single resonance in a graphene-on-silicon nanobeam cavity using thermo-optic effect. J. Lightw. Technol. 2021, 39, 4710–4716. [Google Scholar] [CrossRef]
- Yang, Y.; Lv, J.; Lin, B.; Cao, Y.; Yi, Y.; Zhang, D. Graphene-assisted polymer waveguide optically controlled switch using first-order mode. Polymers 2021, 13, 2117. [Google Scholar] [CrossRef]
- Truong, C.D.; Hang, D.N.T.; Chandrahalim, H.; Trinh, M.T. On-chip silicon photonic controllable 2×2 four-mode waveguide switch. Sci. Rep. 2021, 11, 897. [Google Scholar] [CrossRef]
- Xie, Y.; Han, J.; Qin, T.; Ge, X.; Wu, X.; Liu, L.; Wu, X.; Yi, Y. Low power consumption hybrid-integrated thermo-optic switch with polymer cladding and silica waveguide core. Polymers 2022, 14, 5234. [Google Scholar] [CrossRef]
- Lin, B.; Sun, S.; Sun, X.; Lian, T.; Zhu, M.; Che, Y.; Wang, X.; Zhang, D. Dual-mode 2 × 2 thermo-optic switch based on polymer waveguide mach-zehnder interferometer. IEEE Photon. Technol. Lett. 2022, 34, 1317–1320. [Google Scholar] [CrossRef]
- Mikhailov, S.A.; Ziegler, K. New electromagnetic mode in graphene. Phys. Rev. Lett. 2007, 99, 016803. [Google Scholar] [CrossRef] [Green Version]
- Huang, Q.; Zhong, L.; Dong, J.; Xu, O.; Zheng, Z.; Huang, T.; Li, J.; Xiang, M.; Fu, S.; Qin, Y. All-optical light manipulation based on graphene-embedded side-polished fiber. Opt. Lett. 2022, 47, 1478–1481. [Google Scholar] [CrossRef]
- Huang, Q.; Ghimire, I.; Yang, J.; Fleer, N.; Chiang, K.S.; Wang, Y.; Gao, S.; Wang, P.; Banerjee, S.; Lee, H. Optical modulation in hybrid antiresonant hollow-core fiber infiltrated with vanadium dioxide phase change nanocrystals. Opt. Lett. 2020, 45, 4240–4243. [Google Scholar] [CrossRef] [PubMed]
- He, G.; Ji, L.; Gao, Y.; Liu, R.; Sun, X.; Yi, Y.; Wang, X.; Chen, C.; Wang, F.; Zhang, D. Low power 1×4 polymer/SiO2 hybrid waveguide thermo-optic switch. Opt. Commun. 2017, 402, 422–429. [Google Scholar] [CrossRef]
- Yan, Y.F.; Zheng, C.T.; Liang, L.; Meng, J.; Sun, X.Q.; Wang, F.; Zhang, D. Response-time improvement of a 2×2 thermo-optic switch with polymer/silica hybrid waveguide. Opt. Commun. 2012, 285, 3758–3762. [Google Scholar] [CrossRef]
- Xu, Q.; Jiang, M.; Niu, D.; Wang, X.; Wang, L.; Chiang, K.S.; Zhang, D. Fast and low-power thermo-optic switch based on organic-inorganic hybrid strip-loaded waveguides. Opt. Lett. 2018, 43, 5102–5105. [Google Scholar] [CrossRef] [PubMed]
- Sugawara, N.; Kudo, M.; Fujisawa, T.; Sakamoto, T.; Matsui, T.; Tsujikawa, K.; Nakajima, K.; Saitoh, K. 3-mode PLC-based mode dependent loss equalizer in MDM transmission. In Proceedings of the 2019 24th OptoElectronics and Communications Conference (OECC) and 2019 International Conference on Photonics in Switching and Computing (PSC), Fukuoka, Japan, 7–11 July 2019. Paper TuE2-2. [Google Scholar]
- Rademacher, G.; Luís, R.S.; Puttnam, B.J.; Eriksson, T.A.; Ryf, R.; Agrell, E.; Maruyama, R.; Aikawa, K.; Awaji, Y.; Furukawa, H.; et al. High capacity transmission with few-mode fibers. J. Lightw. Technol. 2019, 37, 425–432. [Google Scholar] [CrossRef] [Green Version]
- Arikawa, M.; Nakamura, K.; Hosokawa, K.; Hayashi, K. Long-haul WDM/SDM transmission over coupled 4-core fiber with coupled 4-Core EDFA and its mode dependent loss characteristics estimation. J. Lightw. Technol. 2022, 40, 1664–1671. [Google Scholar] [CrossRef]
- Fujisawa, T.; Mori, T.; Sakamoto, J.; Yamashita, Y.; Sakamoto, T.; Imada, R.; Ima, R.; Sato, T.; Watanabe, K.; Kasahara, R.; et al. Silica-PLC based mode-dependent-loss equalizer for two LP mode transmission. In Proceedings of the 2022 Optical Fiber Communications Conference and Exhibition (OFC), San Diego, CA, USA, 6–10 March 2022. Paper M4J.4. [Google Scholar]
- Bai, N.; Ip, E.; Wang, T.; Li, G. Multimode fiber amplifier with tunable modal gain using a reconfigurable multimode pump. Opt. Express 2011, 19, 16601–16611. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Zhang, M.; Jiang, M.; Lian, T.; Wang, F.; Zhang, D. Monolithic integrated waveguide device with dual functions of electro-optic modulation and optical amplification. Opt. Lett. 2021, 46, 3536–3539. [Google Scholar] [CrossRef]
- Huang, Q.; Wang, X.; Dong, J.; Zheng, Z.; Xu, O.; Fu, S.; Peng, D.; Li, J.; Qin, Y. Ultra-broadband LP11 mode converter with high purity based on long-period fiber grating and an integrated Y-junction. Opt. Express 2022, 30, 12751–12759. [Google Scholar] [CrossRef]

| NOA Polymer | Graphene | |
|---|---|---|
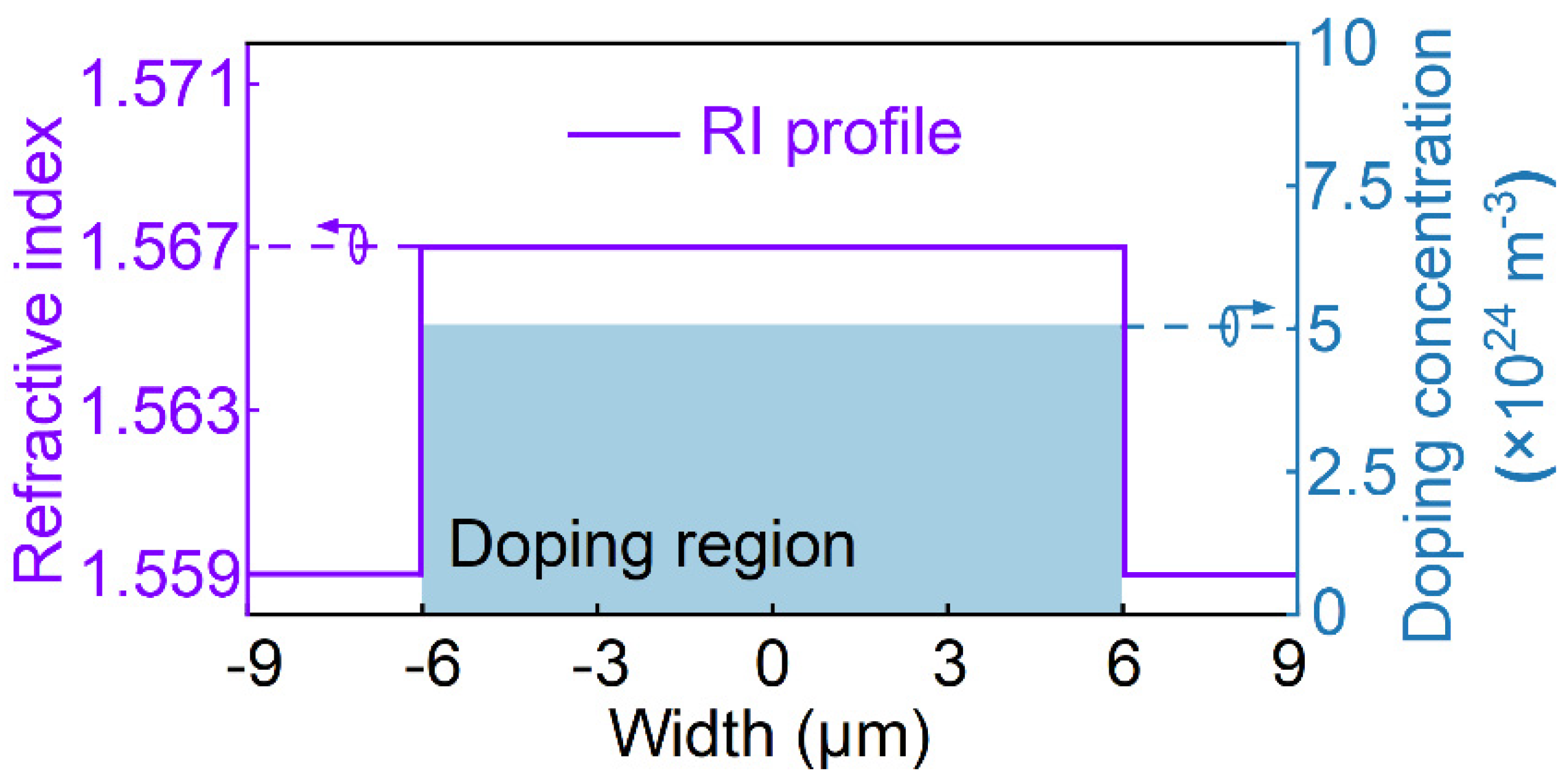
| Refractive index | 1.559/1.566/1.569 | 2.98 + 2.79i |
| Density ρ (kg·m−3) | 1200 | 1060 |
| Heat capacity at constant pressure Cp (J·kg−1·k−1) | 1420 | 740 |
| Thermal conductivity k (W·m−1·K−1) | 0.2 | 5300 |
| Thermo-optic coefficient (K−1) | −3 × 10−4 | Not applicable |
| The Core-Graphene Distance (µm) | 0 | 2 | 4 | 6 | |
|---|---|---|---|---|---|
| Core 2 | TE polarized | 1.52 × 10−4 | 2.00 × 10−5 | 2.88 × 10−6 | 4.38 × 10−7 |
| TM polarized | 1.08 × 10−6 | 1.26 × 10−7 | 1.69 × 10−8 | 2.46 × 10−9 | |
| Core 3 | TE polarized | 1.31 × 10−4 | 2.02 × 10−5 | 3.59 × 10−6 | 6.90 × 10−7 |
| TM polarized | 0.84 × 10−6 | 1.03 × 10−7 | 1.64 × 10−8 | 2.92 × 10−9 | |
| Core 4 | TE polarized | 1.72 × 10−4 | 1.94 × 10−5 | 2.27 × 10−6 | 2.72 × 10−7 |
| TM polarized | 1.33 × 10−6 | 1.46 × 10−7 | 1.68 × 10−8 | 1.98 × 10−9 | |
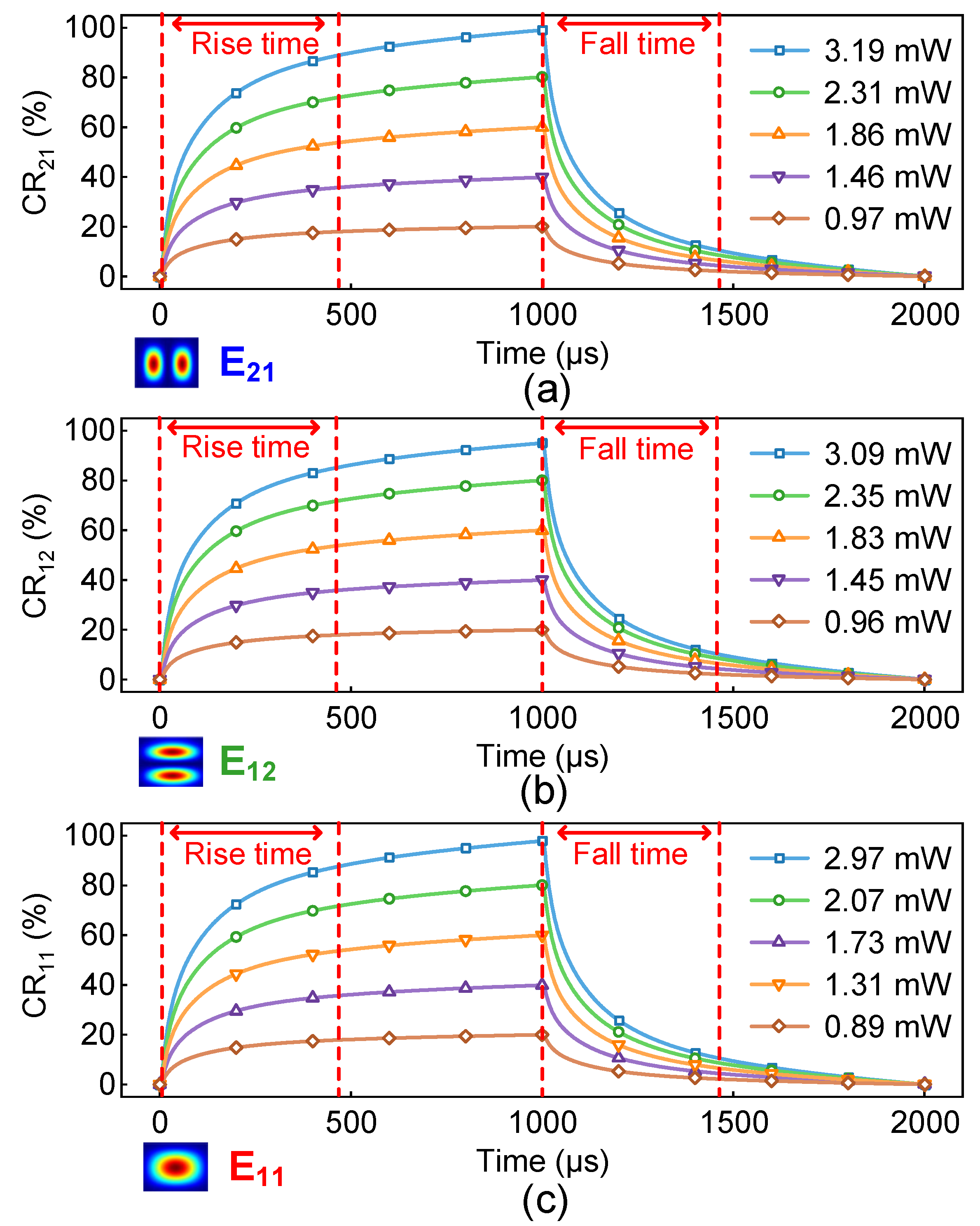
| CR (%) | 20 | 40 | 60 | 80 | Max * | |
|---|---|---|---|---|---|---|
| DC 1 | Rise time (µs) | 466 | 474 | 474 | 475 | 475 |
| Fall time (µs) | 491 | 495 | 484 | 486 | 482 | |
| DC 2 | Rise time (µs) | 477 | 477 | 473 | 475 | 476 |
| Fall time (µs) | 481 | 486 | 485 | 481 | 483 | |
| DC 3 | Rise time (µs) | 480 | 471 | 480 | 482 | 483 |
| Fall time (µs) | 492 | 498 | 492 | 489 | 487 | |
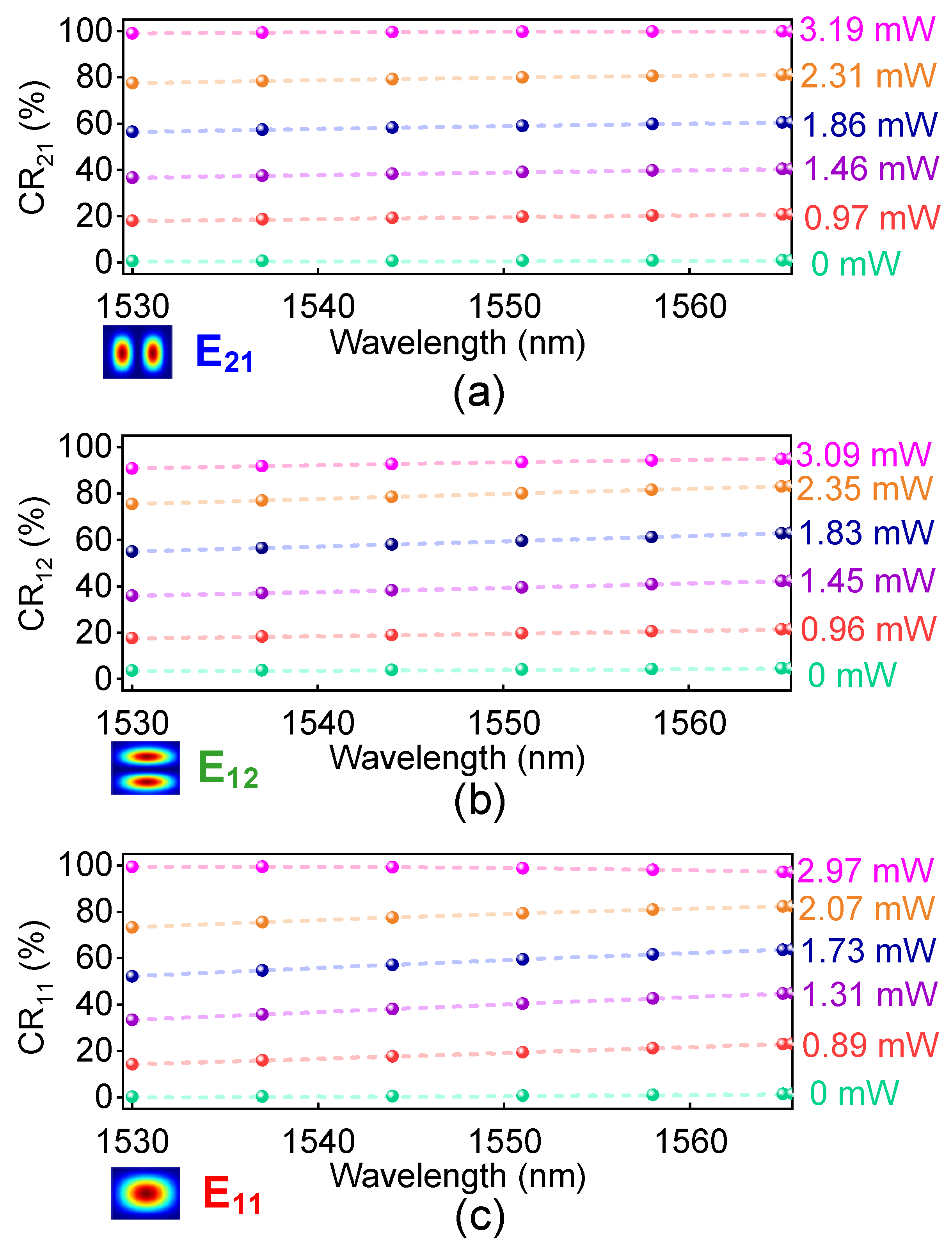
| References | Waveguide | Wavelength (nm) | PC 1 | RT 2 | FT 3 |
|---|---|---|---|---|---|
| [16] | Polymer/silica | 1530–1570 | 17.35 | 183 | 259 |
| [21] | Polymer | 1530–1605 | 3.12 | 980 | 520 |
| [25] | Polymer/silica/silicon | 980/1550 | 9.5 | 106 | 102 |
| [26] | Silica/silicon | 1525–1575 | 22.5 | 5.4 | 6.4 |
| [27] | Polymer/silica | 1550 | 5.96 | 121 | 329 |
| [28] | Polymer | 1530–1565 | 9.0 | 1200 | 1420 |
| This work | Polymer | 1530–1565 | 3.19 | 483 | 498 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhong, L.; Huang, Q.; Zhang, J.; Xu, O. Low Power Consuming Mode Switch Based on Hybrid-Core Vertical Directional Couplers with Graphene Electrode-Embedded Polymer Waveguides. Polymers 2023, 15, 88. https://doi.org/10.3390/polym15010088
Zhong L, Huang Q, Zhang J, Xu O. Low Power Consuming Mode Switch Based on Hybrid-Core Vertical Directional Couplers with Graphene Electrode-Embedded Polymer Waveguides. Polymers. 2023; 15(1):88. https://doi.org/10.3390/polym15010088
Chicago/Turabian StyleZhong, Lixi, Quandong Huang, Jiali Zhang, and Ou Xu. 2023. "Low Power Consuming Mode Switch Based on Hybrid-Core Vertical Directional Couplers with Graphene Electrode-Embedded Polymer Waveguides" Polymers 15, no. 1: 88. https://doi.org/10.3390/polym15010088
APA StyleZhong, L., Huang, Q., Zhang, J., & Xu, O. (2023). Low Power Consuming Mode Switch Based on Hybrid-Core Vertical Directional Couplers with Graphene Electrode-Embedded Polymer Waveguides. Polymers, 15(1), 88. https://doi.org/10.3390/polym15010088





