2.1. Laminate Configurations and Elastic-Bending Properties
For the definition of the stacking sequences of the specimens and their corresponding interface angles at the crack plane, it must be considered that a high mismatch angle can lead to a crack propagation that cannot be anticipated by the standard [
37], which would thus invalidate the test. Taking this into account, the orientation for the plies at the interfaces has been limited to a combination of seven angles: 0, ±15, ±30, and ±45. Nevertheless, the repetition of angles at the two interfaces is excluded, as the real interest of the analysis is when two different orientations are present at the delamination interface.
In their numerical investigation, Sebaey et al. [
47] concluded that for MD-DCB specimens of traditional composite laminates, the higher the flexural stiffness of the specimen arms, the higher the probability of obtaining a valid interlaminar fracture toughness characterization in mode I. However, in a previous study on unidirectional specimens with the same CF/PA composite as the one considered here [
17], stable and smooth crack onset and propagation was only obtained for thin specimens with 1.5 mm thick arms. Specimens with 2.5 mm thick arms showed rapid crack propagation, stick–slip effect, and crack branching, which invalidated the test.
The initial laminate configuration for the MD-DCB specimens considered a total of 24 plies, 12 per specimen beam, for a total thickness of 3 mm. The stacking sequence of each specimen beam is symmetrical and balanced, with the inside plies oriented at 0°. Thus, the stacking sequence of the specimen corresponds to [(±θ1/04)s//(±θ2/04)s], where // indicates the location of the interface. For a better identification, the following codification was used: L1_12_12_θ1_θ2, where L1 indicates the laminate series, the two ‘12’ numbers indicate the total number of plies in the bottom and top beams, respectively, and θ1 and θ2 denote the ply orientation of the layers adjacent to the interface, representing bottom and top, respectively.
During the propagation of an interlaminar crack in a DCB test, the uniformity of the energy release rate is favored using the minimization of two elastic parameters,
Bt and
Dc.
Dc indicates the curvature ascribable to longitudinal/transverse bending coupling, which should be less than 0.25 [
48,
49].
Bt indicates the skewness of the crack profile ascribable to bending/twisting coupling, which should be maintained as low as possible to ensure a symmetric crack front [
50,
51]. Hence,
Bt and
Dc depend on the bending stiffness matrix coefficients
Dij, and can be determined as
For this study, the laminate configuration of each DCB specimen was divided into three parts: the whole laminate (A), the lower arm (B), and the upper arm (T), as suggested by Prombut et al. [
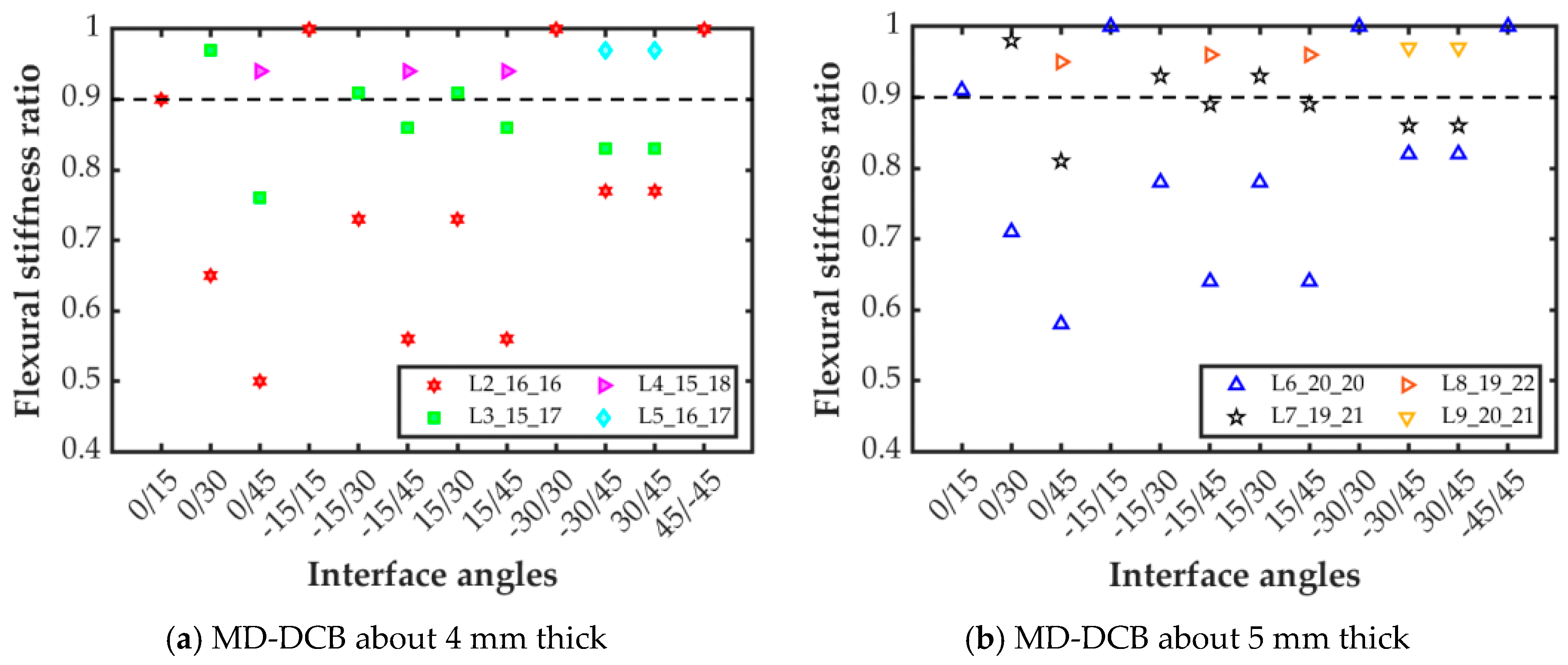
49]. The three parts should follow the same rules as the elastic, in order to achieve a symmetrical crack front. Moreover, we took into account that, in order to achieve mode I crack propagation, the opening of the two arms of the specimen should be symmetrical. Thus, the flexural stiffness of the two arms of the specimen should be as similar as possible. To verify this requirement, the flexural stiffness of the two arms of all the considered MD-DCB specimens were evaluated and compared, defining a flexural–stiffness ratio. This ratio corresponds to the ratio between the minimum flexural stiffness of the two arms divided by the maximum one. In this way, flexural–stiffness ratios close to one indicate similar flexural stiffness for both arms, and a high probability of symmetrical opening. Conversely, specimens with flexural–stiffness ratios lower than 0.9 should be avoided, as the probability of symmetrical opening is low.
The analysis of the
Bt parameter for all the L1_12_12_θ
1_θ
2 laminates, where θ
1 and θ
2 were varied according to the seven orientation angles previously described, determined to have a maximum value equal to 0.057 for the 45° plies. As expected, the lower the lamina orientation, the lower the value of
Bt. Considering that, while the value of this parameter should be as low as possible, no threshold value has been established, this elastic constant is not considered as decisive for assessing the DCB laminate configurations. Thus, only the bending/twisting parameter,
Dc, will be used to assess the appropriateness of the proposed DCB specimens.
Table 2 summarizes the results of the evaluation of the
Dc for the twelve pairs of interface angles for laminate L1.
As can be seen in
Table 2, half of the interface configurations did not fulfill the condition, and the value of
Dc was higher than the limit (0.25) in at least one beam of the specimen. Thus, a bending/twisting coupling could be expected during the test, and these laminate configurations were discarded. Thus, only L1 specimens with interfaces 0/15, 0/30, −15/15, −15/30, 15/30 and −30/30 were to be considered.
The analysis of the flexural stiffness of the 12 interfaces considered for laminate L1 (summarized in
Appendix A for conciseness reasons), reveals that the minimum value of the flexural–stiffness ratio for the valid interfaces was 0.56. This ratio is only higher than 0.9 for interfaces −15/15 and −30/30, with a ratio of one, and interface 0/15, with a ratio of 0.9. Consequently, there were only three interface configurations for laminate type L1 with symmetrical opening and low bending/coupling effects. For this reason, more laminate configurations were taken into account, in order to increase the number of suitable interface configurations. Following the suggestion of Sebaey et al. [
47], thicker specimens were considered by adding 0° plies in the cores of the laminates of each bending arm, to increase the bending stiffness.
Eight new MD-DCB laminate configurations were defined, keeping the same combinations of interface angles but increasing the number of plies of the laminates. In all the cases the stacking sequences considered for the beams of the specimens are balanced and symmetrical. However, to compensate for differences in stiffness between the two arms of the specimen due to the different orientations of the interface plies (in addition to ensuring a symmetrical opening), six of these configurations have been defined with one arm thicker than the other. These additional plies have not been included for all the combinations of interface angles, but only for those with lower flexural–stiffness ratios. The eight new stiffer laminate configurations are presented in
Table 3. As shown in the table, laminates L3_15_17, L4_15_18, L5_16_17, L7_19_21, L8_19_22, and L9_20_21 correspond to specimens with different beam thicknesses. In laminates L3 and L7, the total number of plies was the same as in laminates L2 and L6, 32 and 40 plies, respectively. In laminates L4, L5, L8 and L9, an additional 0° was added to one of the specimen beams.
All laminate configurations, from the more flexible L2_16_16_θ
1_θ
2 to the stiffer L9_20_21_θ
1_θ
2, fulfilled the criterion established for the bending/twisting parameter, namely,
Dc < 0.25. Moreover, the higher the bending flexural stiffness for each part of the specimen, the lower the value of the elastic parameter
Bt (see
Appendix A). Therefore, the assessment analysis focused on the ratio between the bending moduli of the specimen arms. Again, all laminate configurations with a flexural stiffness ratio equal to or higher than 0.9 were considered to be homogeneous flexural specimens. Flexural stiffness ratios below this value would result in specimens with unbalanced bending arms and asymmetric opening displacements, which would entail mixed-mode crack propagation. As shown in
Figure 1a, eight interface combinations for laminate L2 did not fulfill this criterion (red hexagram below the dashed black line in the figure). Although the ratio for interface 0/15 is right in the limit, it is taken to be valid. Thus, these eight interface configurations are reevaluated by transferring one 0° ply from the stiffer specimen beam to the other one, which corresponds to laminate L3_15_17_θ
1_θ
2. With this laminate configuration, three out of these eight interfaces fulfilled the flexural–stiffness ratio criterion (green squares above the dashed black line in the figure). For further improvement of the flexural stiffness ratio, an additional 0° layer was added to the specimen beam with the lowest flexural stiffness. So, these two new laminate configurations were taken into account: laminate L4_15_18_θ
1_θ
2 for interfaces 0/45 and ±15/45, and laminate L5_16_17_θ
1_θ
2 for interfaces ±30/45. As can be seen in
Figure 1a, with the inclusion of these alternative laminate configurations, the value of the flexural–stiffness ratio was above the 0.9 limit for all the considered interfaces, and similar opening displacements can be expected in both specimen beams.
The same procedure as that of the specimens which were approximately 4 mm thick (around 32 plies) was likewise followed for the specimens that were approximately 5 mm thick (laminates L6 to L9). As shown in
Figure 1, the flexural–stiffness ratio was higher for the thicker laminates (
Figure 1b) than for the thinner ones (
Figure 1a). However, the same eight interface configurations with a flexural–stiffness ratio lower than 0.9 for laminate L2 also do not fulfill the criterion for laminate L6. Again, transferring one of the plies from the stiffer beam to the more flexible one (laminate L7) served to achieve a flexural stiffness higher than 0.9 only for the same three interface configurations as for laminate L3. Adding an additional 0° layer to the more flexible arm of laminate L7, laminate L8, or laminate L9 ensured that all the interface combinations fulfilled the criterion on the flexural–stiffness ratio, as shown in the figure.
Table 4 summarizes the laminate configurations obtained for the different interface combinations considered during the numerical exploration campaign.
2.2. Finite Element Model
Before manufacturing and testing the MD-DCB specimens, different FE simulations were carried out to check if the interlaminar fracture toughness in multidirectional interfaces can be determined in the laminate and interface configurations selected in the previous section. The main objective of this numerical investigation was to ensure that the interlaminar crack propagates in the correct interface, and that there is no crack jumping or branching or any other form of damage.
The commercial FE software Abaqus/Standard 6.14 was used to model the proposed MD-DCB specimens based on the configuration indicated in the ISO-15024 [
37] standard. The actual length and width of the specimens considered were 175 mm and 22.5 mm, respectively, and each had a precrack of 50 mm. However, to reduce the computational time, the specimen length was reduced to 100 mm, not including those parts of the specimen which were either away from the crack tip or not loaded during the test. This did not affect the local stresses close to the delamination area and, thus, did not alter the obtained results. The model was divided in three parts: the precrack zone (50 mm); an uncracked zone (40 mm), in which the propagation of the crack is simulated; and a final zone, where the two specimen beams are bonded with a tie constraint (10 mm). The mesh was refined both in the crack tip zone, to properly simulate the interlaminar damage propagation, and near the specimen edges, to correctly capture the edge effects (see
Figure 2). The eight-node solid elements with incompatible modes C3D8I were used for all simulations. The beams of the specimens were modelled by defining one element of 0.125 mm in the thickness direction for each of the ±θ plies, and two central blocks to simulate the 0° layers, as shown in
Figure 2.
Cohesive elements were used for simulating the propagation of the crack, including the cohesive element formulated by Turon et al. [
52], and were then implemented by means of a user subroutine defined element (UEL). The cohesive elements had a negligible thickness of 1 μm. Both the cohesive element size and the entire delamination length were calculated according to what was indicated by Soto et al. [
53]. Considering the lack of interlaminar fracture toughness properties for multidirectional interfaces with this material system, the values of
GIc and
GIIc reported by Santos et al. [
17] (i.e., 1.7 and 2.3 J/m
2, respectively) were used for the modelling. The penalty stiffness was set as being equal to K
0 = 1 × 10
6 N/mm
3, which should be large enough to avoid altering the compliance of the assembly. Finally, the interfacial strength was σ
0 = 2.7 MPa. The ply elastic mechanical properties reported in
Table 1 were also used for the FE model.
2.2.1. LaRC04 Criterion for Matrix Cracking
For the investigation of crack jumping and crack branching during the propagation of the interlaminar crack, it was hypothesized that these two mechanisms were triggered using matrix cracking. Hence, the matrix tensile failure index was assessed using LaRC04 failure criteria [
54] along the simulation. Whenever the matrix tensile failure index reaches one around the delamination plane, it is considered that crack jumping will occur during the experimental test. The LaRC04 in-plane tensile matrix cracking failure criterion was implemented by means of the ABAQUS user output variable standard subroutine, UVARM. The matrix tensile failure presented by Pinho et al. [
54] corresponds to:
where
is the in situ transverse tensile strength,
is the material fracture toughness ratio
,
is the normal stress,
is the shear stress, and
is a nonlinear relationship parameter between shear stress and shear strain, which was taken to equal 5 × 10
−8, as it was by Sebaey et al. [
47].
Notice that no damage evolution is defined and, thus, the specimen always remains elastic.
2.2.2. Crack Front Assessment
During the propagation of an interlaminar crack, the shape of the crack front depends on the laminate stacking sequence and the interface angles. Multidirectional interfaces may result in a nonuniform distribution of the energy release rate and generate asymmetrical crack fronts [
46], which can also facilitate the migration of the crack to another interface planes. On the other hand, the crack propagation was experimentally measured on the specimen edge and the crack front was considered as a straight line along the specimen width. Such an assumption may not be reliable, especially for multidirectional composites with asymmetrical crack fronts. Hence, the elastic bending–twisting and bending–bending couplings may cause highly curved thumbnail-shaped delamination fronts.
In this study, the symmetry of the crack front was assessed by obtaining the out-of-plane stress distribution right ahead of the crack tip during the simulations, as can be schematically seen in
Figure 3. Then, the Out-Of-Symmetry (OOS) parameter defined by Sebaey et al. [
47] was determined according to the following procedure: (i) the crack opening (just behind the crack front, where the maximum out-of-plane stress is experienced) was measured and normalized with respect to its maximum value; (ii) a symmetry line was drawn at the specimens’ midwidth (see
Figure 3a); and (iii) the absolute value of the difference in the crack opening between each pair of equidistant nodes (node
i and
j) was labeled as the out of symmetry (OOS) coefficient. This procedure was repeated for all pair of nodes in the crack front, and the maximum value was reported as the OOS coefficient of the specimen.
The straightness of the crack front was quantified by defining the visual deviation
parameter as the difference between the relative crack position at the specimen edge and at the crack front mean line, as can be seen in see
Figure 3b. The
parameter was used to establish a quantitative comparison and discussion of the relative position of the crack front between the proposed specimen configurations.