4. Simulations of Rouse Modes
We now turn to simulations that actually examine the properties of Rouse modes.
Dynamic simulations of polymers are readily traced back to the work of Grest and Kremer [
10], who simulated a bead–spring model for a polymer chain, in which the beads are subject to independently fluctuating thermal forces, all bead pairs separated by less than a specified distance interact with a Lennard–Jones potential, and each bead’s motions are coupled to a heat bath that supplies a friction term and a thermal driving force. The interaction between bonded beads is represented with a finitely extensible (FENE) potential
where
is the distance between two beads,
k and
are simulational parameters, and the potential is set to zero for
. The above potential is not the harmonic potential used by Rouse, so strictly speaking, this simulation was not a test of the Rouse model. Single chains and rings containing 50–200 beads, and a 200-bead chain with no Lennard–Jones potentials, were examined. The diffusion coefficient, bead mean-square displacement, mean-square center-of-mass displacement, and static structure factor
were calculated. Comparisons were made with theoretical expectations. Chain motions for these single chains were found to be consistent with the Rouse model.
Kremer and Grest [
37] then reported their pioneering study of a melt of bead–spring polymers, covering from the short nonentangled (‘Rouse’) regime up to the highly entangled (‘reptation’) regime. In their molecular dynamics simulation, all beads exerted a purely repulsive Lennard–Jones potential and had a FENE bond between next neighbors along each polymer chain, and had a weak frictional force
and a corresponding thermal force. Systems with chain lengths
N from 5 to 400 beads and a total of 250 to 20,000 beads, corresponding to 16 to 100 chains, were studied. The nominal entanglement length was reported to be ≈35 beads, so these simulations included both unentangled and entangled systems. Static properties that were examined include the mean-square end-to-end distance, the radius of gyration, the static structure factor, and the mean-square amplitude of Rouse modes. These quantities show the expected scaling dependencies on
N. Time-dependencies of the mean-square displacements of single monomers, chain centers-of-mass, and monomers relative to the center of mass, of Rouse amplitudes, of scattering functions, and of chain motion relative to a primitive path were also analyzed. Here, we focus on the Rouse modes.
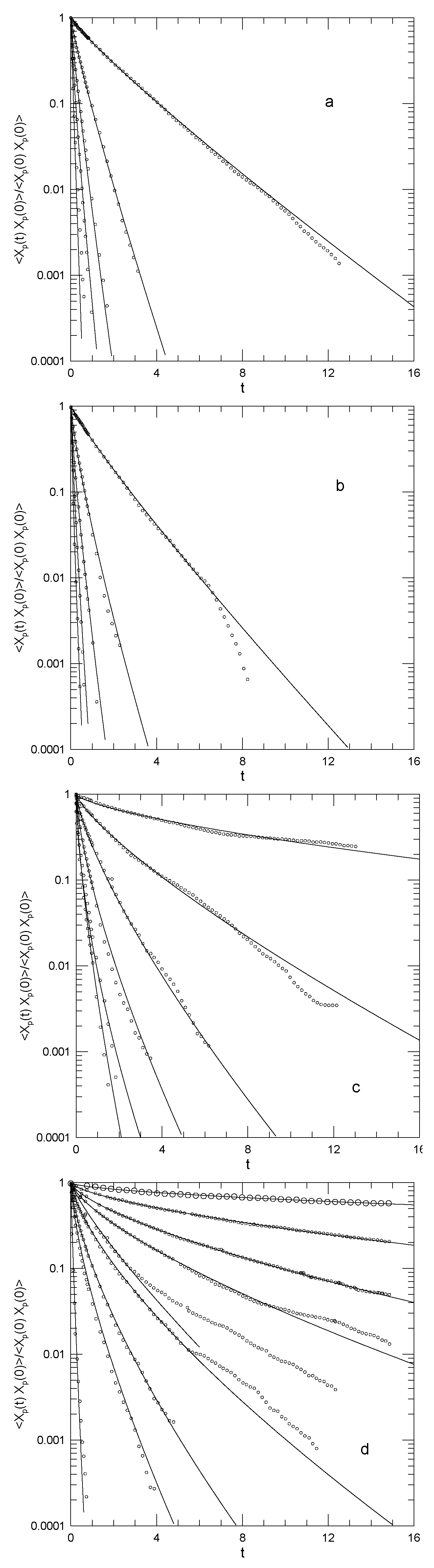
Kremer and Grest reported the normalized Rouse mode temporal autocorrelation functions
for chain lengths
and 200.
Figure 1 shows their results. Kremer and Grest interpreted these as clear single exponentials for the two shorter chains and two time scales for the longer chains. The figures show our fits to stretched exponentials in time. The relaxations are fit well by stretched exponentials. In these pioneering studies, for the two longer chains, at long times, the correlation functions show weak fluctuations on top of the stretched exponentials, making it difficult to determine
accurately. Kremer and Grest also evaluated
for
, finding that the static cross correlations vanish to within the noise in the simulations.
Figure 1.
Time autocorrelation functions from Kremer and Grest [
37] for Rouse mode amplitudes
for
(top to bottom) for melts of bead–spring linear polymers having
N of (
a) 20, (
b) 50, (
c) 100, and (
d) 200. Larger values of
p do not appear in all graphs; values of
p are listed in
Table 1. Circles represent the original simulations; solid lines are stretched exponentials.
Figure 1.
Time autocorrelation functions from Kremer and Grest [
37] for Rouse mode amplitudes
for
(top to bottom) for melts of bead–spring linear polymers having
N of (
a) 20, (
b) 50, (
c) 100, and (
d) 200. Larger values of
p do not appear in all graphs; values of
p are listed in
Table 1. Circles represent the original simulations; solid lines are stretched exponentials.
Tsalikis et al. [
13] report simulations of ring polymers. Their study is noteworthy for the range of chain parameters that were studied during the course of their simulations. A major focus of the work is comparison with Rouse model predictions for chain dynamics, but a considerable number of other parameters were also studied. These workers report an extended series of molecular dynamics simulations of 5, 10, and 20 kDa poly(ethylene oxide) ring polymers in the melt, corresponding to polymers having 120, 227, or 455 monomers. Simulations were made with a united atom force field [
38,
39] under isothermal/isobaric conditions, with
K and
atm. The force field parameters were expected to be sufficiently realistic for quantitative comparisons with experiments to be expected to be possible, as confirmed in the paper. For the largest polymer, the simulation cell contained more than 50,000 atoms, the simulation being extended to an equivalent of 2.2 μS.
In considering Tsalikis et al.’s findings on the applicability of the Rouse model to ring melts, one might say that the cup is half full or half empty. Tsalikis et al. chose to emphasize points, where their simulations clearly match the Rouse model predictions. Here, we emphasize the differences, points where the simulations do not match the Rouse model as applied to a ring polymer.
Tsalikis et al. use their simulation data to compute for their rings the mean-square Rouse amplitudes. Their interpretation of a Rouse model for rings predicts that the normalized amplitudes should be independent of mode number p and polymer bead count N. This prediction is rejected by Tsalikis et al.’s simulations: the normalized amplitudes depend on p, and at small p are smaller than predicted by the Rouse model. For the polymer, the normalized amplitude for is modestly more than half its value for the same polymer at large p. The range of smaller p-values for which the normalized amplitudes are below their large-p limit increases with increasing N, the increase in the range being approximately linear in N. However, for all N studied, the normalized amplitudes do appear to go to the same large-p limit, so the model is arguably valid for large p.
For each of their chain lengths and
and 12, Tsalikis et al. also report the time dependence of the time correlation functions
.
Figure 2 shows a sampling of their measurements (dots). The figure also shows our fits to stretched exponentials (solid lines) and to pure exponentials (dashed lines, obtained from fits to the initial slope). Here,
and
are fitting parameters. The correlation functions are normalized to unity at
. If
Figure 2 is examined, it is apparent that the relaxation of
is described well by a stretched exponential in time, except for a few of the largest-
t points, contrary to the Rouse model prediction that the relaxations should be simple exponentials.
The stretched exponential is characterized by
and
. Numerical values for the fitting parameters and the average decay rate
are seen in
Table 2. For each molecular weight,
increases nearly 40-fold between
and
.
is close to unity for the
polymer but about 0.8 for the two larger rings.
Tsalikis et al. calculate the normalized cross correlations
, Equation (
10), between the Rouse amplitudes. They observe that the cross correlations are not large;
is almost always less than 0.1. Before considering this result, we ask how large
is plausibly likely to be. If
, modes
p and
q are perfectly cross correlated; the value of one determines the value of the other. If one mode is cross correlated with several others,
for any pair of modes must be considerably less than unity. For example, if a given mode is equally cross correlated with
n other independent modes, then, at most, the
n modes completely determine the value of the given mode, in which case the cross correlations would be of typical size
. One might also ask how accurately
can be determined. If
lies within simulational error of zero, non-zero values for
are uninteresting.
Tsalikis et al. [
13] evaluated the relaxation of the correlation function
For a linear chain, is the end-to-end vector. Ring polymers have no ends, so is usefully defined to be a vector from a bead to another bead half-way around the ring. has two paths to relaxation. First, its magnitude fluctuates around its average value, contributing a relaxation; however, this process cannot relax the correlation function to zero. Second, as the dominant process, relaxes by chain reorientation. At long times, and cease to be correlated, so their cross-correlation function decays to zero. As shown by the original authors, follows a stretched exponential in time, with an average relaxation time that increases as , based on the three molecular weights studied. Tsalikis et al. compare the functional form of that they obtained from their simulations with predictions from the Rouse model. The Rouse predictions for the time dependencies, other than going to zero at a long time, do not resemble the simulation determinations of the time dependence of .
Other quantities studied by Tsalikis et al. [
13] include the intermolecular and intramolecular atom–atom radial distribution functions, which have the expected forms. Static structure factors were calculated and found to be in good agreement with experiment. The distributions of end-to-end distances of chain segments of different lengths were calculated as functions of the length of the segments. The distributions were generally not described by Gaussians, especially for the larger rings. In contrast, an initial assumption of the Rouse and Kirkwood–Riseman models is that the end-to-end distances have Gaussian distributions, an assumption leading to the potential of average force between pairs of linked beads. If the bead-to-bead distances do not have Gaussian distributions, the potential of the average force between them is not a Gaussian and does not correspond to a simple spring. Local dynamics were studied using the temporal autocorrelation functions of the torsion angles; the functions were described well with stretched exponentials in time. Finally, these authors asked how many other polymer chains a given chain typically interacts with. As a sensible approximation to this number, they calculated
, the average number of other chains that had their center of mass within the radius of gyration of the chain of interest. For their ring polymers,
was in the range 1.75–2.75. For linear chains having the same three molecular weights,
was in the range 8.5–9.5, with
increasing as the chain molecular weight was increased from 5 kDa to 20 kDa.
From the above, Tsalikis et al. concluded that the Rouse model is valid for their systems.
Papadopoulos et al. [
40] report united atom simulations of polyethylene oxide rings in the melt and in dilute solution in melts of three different linear polyethylene chains. Simulations used the modified TrAPPE force field [
38,
39] executed with GROMACS [
41] held at T = 413 K and 1 atmosphere. Comparison was made with simulated melts of the three linear chains and with experimental studies by Goosen et al. [
42] using nuclear spin echo spectroscopy. Goosen et al. concluded that the segmental dynamics of dilute rings in a melt of linear chains are primarily determined by the dynamics of the host polymers. The ring polymers contained 456 monomers, for a molecular weight of 20 kDa, while the linear polymers had molecular weights of 1.8, 10, and 20 kDa, corresponding to chain
N of 41, 228, and 456. Simulations included 8 rings and 72–720 linear chains with >
atoms in a simulation cell.
In addition to a series of other static and dynamics properties, Rouse amplitudes were used to compute and , the former for from 100 down to < and the latter for . For small p, the Rouse model predicts . For the ring melt and the blends, this result was confirmed for . For larger p, i.e., , deviates downward from the small-p predicted value, attaining at the largest p examined perhaps half the value expected from an extrapolation of small-p behavior.
Papadopoulos et al.’s determinations of the time correlation functions
appear in
Figure 3. They report their determinations as smooth curves, appearing in the figure here as dotted lines. We fit to stretched exponentials (solid lines) and show simple exponentials (dashed lines) where appropriate. There is one behavior for the ring melt and for dilute rings in the 1.8 kDa chain melt (
Figure 3a,b), and a somewhat different behavior for dilute rings in melts of the 10 and 20 kDa chains (
Figure 3c,d).
Our description of the relaxation functions is not entirely the same as that of Papadopolous et al. Numerical fits, leading to parameters seen in
Table 3, clarify issues visible in the figures. In the ring melt, and in dilute solution in the 1.8 kDa linear chains,
shows a stretched-exponential relaxation at earlier times, followed by a sharp transition to a simple-exponential relaxation at later times. The transition, which is especially prominent for
and
, occurs at earlier times and smaller values of
as
p is increased. For larger
p, the transition is more readily apparent in the solution of rings in the 1.8 kDa linear chain melt than in the ring melt. In contrast, for rings in dilute solution in the 10 kDa and 20 kDa melts,
for
and for
relaxes as a single stretched exponential out to the longest times observed. At larger
p,
fluctuates around the fitted stretched exponential. The transition between short and long time behavior is not seen in many other studies, so it appears to be worthy of further investigation.
Papadopolous et al. report integrated times for their four systems and the six smallest values of p. They report that scales approximately as , being several-fold larger for rings in melts of the larger-N linear polymers than for rings in their own melts. Note, however, that Papadopolous et al. found Gaussian distributions of distances between remote parts of the rings.
Kopf et al. [
14] demonstrate a novel simulational test of the Rouse model. They consider systems containing 16 to 25 chains of 10 to 150 beads, in which the forces between all pairs of chains are exactly identical, but in which the beads on some or all of the polymer chains are made 4 or 100 times as massive as the original ’light’ beads. The forces between the beads are the FENE potential and a truncated, purely repulsive bead–bead Lennard–Jones potential. From basic statistical mechanics, a change in bead mass should have no effect on the static properties of the chains in a melt, an outcome that was confirmed simulationally. In mixtures, increasing the mass of the heavier beads slows down the motions of the light-bead chains. Kopf et al. took advantage of the fact that they were doing molecular dynamics to calculate the velocity autocorrelation function through multiple oscillations out to long times. The frequency of the oscillations is relatively independent of the fraction of light or heavy polymers in the system, suggesting that the oscillations in the velocity autocorrelation function arise primarily from intramolecular interactions. The Rouse model remained accurate in light–heavy polymer mixtures. Rouse modes were found not to be cross correlated. Rouse time correlation functions decayed approximately exponentially in time. Contrary to the Rouse model, these simulations observed subdiffusion (mean-square center-of-mass displacement proportional to
) on shorter time scales. A nominal entanglement time was used to estimate a nominal tube diameter, which the authors also described as a characteristic length for slowing down the monomer motion. Their results indicated that the nominal tube diameter is independent of the monomer mass, implying that the tube diameter is a static rather than a dynamic quantity, consistent with topological pictures for entanglements.
We turn to Paul et al. [
43], who studied 40 to 120 chains of a C
100 polyethylene using atomistic molecular dynamics. Their simulations included both an explicit-atom model and also a unified atom model, in which each CH
2 group was treated as a single atom. The polymer was chosen to be long enough that it could reasonably be expected to show Gaussian behavior for its static chain statistics, yet short enough that its dynamics would be expected to have Rouse-like and not reptational behavior. The authors recognized that the assumption of Rouse-like behavior in unentangled melts required examination. A stochastic dynamics simulation was used to equilibrate the samples, while data were obtained using molecular dynamics. Static behavior was tested by calculating the static structure factor; good agreement between simulation and experiment was found. In addition to other dynamic studies, large-scale dynamic behavior was compared with expectations from the Rouse model.
The end-to-end vector reorientation time and the long-time self-diffusion coefficient are consistent with the same value for the segmental friction coefficient, these results being applicable ‘on time scales larger than the Rouse time’. However, contrary to the Rouse model, at times shorter than the Rouse time, the center-of-mass diffusion is subdiffusive, being proportional to or so. Static mean-square amplitudes of Rouse modes were calculated. For , the small-p Rouse model expectation was observed. For , the mean-square mode amplitudes decrease approximately as , not as . The equal-time cross-correlation functions () were found to vanish to “…within the error bars in the simulation”; they interpret this finding to imply that “…the Rouse modes are still good eigenmodes for a dynamic analysis…”, a claim that would also require that for and .
Paul et al. also calculated the temporal autocorrelation functions . A plot of correlation functions with and 3 finds that the three correlation functions decay nearly exponentially as , a single value of sufficing for all three values of p, with small deviations over the first quarter of the decay. For , the are markedly non-exponential. When plotted against , with increasing p, the decay more rapidly. The authors conclude that the Rouse model ‘…is at most applicable to a few largest scale eigenmodes’. They do, however, note that the self-diffusion coefficient and the rotational diffusion coefficient can be described self-consistently in terms of a single segmental friction factor.
These results were extended by Paul et al. [
23], who considered the single-chain intermediate structure factor
for unentangled polyethylene molecules in a melt, comparing results from neutron spin echo spectroscopy with results from atomistic and from united atom molecular dynamics simulations. They continued to study C
100 polyethylene, because the polymer is short enough not to be entangled and long enough to have Gaussian chain statistics. The corresponding Rouse model has two parameters, namely a bond strength revealed by the average segment length
b, and a monomer drag coefficient revealed by the chain center-of-mass diffusion coefficient
D, the latter determined both experimentally and from each of the two sets of simulations. The simulation values for
for the explicit-atom and unified-atom simulations are in agreement with the experiments over a factor of six in
q and two orders of magnitude in the scaled time
.
Having validated the accuracy of the simulations, Paul et al. then used the simulations to calculate the Rouse amplitudes, their time autocorrelation functions, and the implied by the Rouse modes. The predicted by the Rouse model only agrees with the simulations for a limited range of q () and times ≤ 4 nS. At larger q and separately at longer times, Rouse-model predictions of are significantly smaller than from the experiment or as calculated directly in the simulations. The authors note three marked deviations between the simulational results and the Rouse model: first, for times less than a time , diffusion is found by the simulations to be subdiffusive, with exponent 0.83, rather than diffusive; in contrast, Rouse-model chains exhibit diffusive center-of-mass motion at all times. Second, simulations find that only the lowest Rouse modes, , have relaxations that scale as ; for larger p, Paul et al. attribute deviations from behavior to non-Gaussian chain statistics at short distances. Third, in the simulations, each decays as a stretched exponential in time; the of the Rouse model all decay as pure exponentials.
Finally,
from the simulations, together with a Gaussian approximation
was used to calculate a mean-square center-of-mass displacement
. It should be emphasized that Doob’s theorem guarantees as a mathematical certainty that if the physical requirements leading to the Gaussian approximation are valid, then, as a mathematical certainty,
increases linearly in time. However, as found by Paul [
43], at short times, the calculated center-of-mass motion is subdiffusive, i.e.,
grows as
not as
. The Gaussian-approximation estimate of the mean-square displacement does agree with the simulations at long times
, at which the center-of-mass motion is diffusive. At times shorter than the Rouse time,
as determined by the simulation is considerably larger than
inferred from
and Equation (
23), showing that the Gaussian approximation is not valid in these systems at shorter times.
Several theoretical advances followed this work. Smith and Paul [
44] used quantum chemistry calculations to generate an improved set of force parameters for simulations of 1,4-polybutadiene. Harnau et al. [
45,
46] proposed that the experimental results of Paul et al. [
23] could be understood by replacing the Rouse model with a semiflexible chain model that takes into account chain stiffness. The semiflexible chain model with reasonable parameters agrees well with Paul et al.’s experimental and simulational determinations of
of the mean-square displacement of the central monomer as a function of time and of the Rouse-mode relaxation times.
Smith et al. [
47] present simulations of an unentangled C
100H
202 1,4-polybutadiene melt using a united atom, quantum chemistry-based potential, the focus of the work being to examine the presence of non-Gaussian displacement distributions of polymer beads in a melt. The single-chain intermediate structure factor
was determined from neutron spin-echo measurements and separately from molecular dynamics simulations using Smith and Paul’s [
44] united atom potential. For
Å
and times out to 17 nS, experimental and simulated values of
were in good agreement. The center-of-mass motion was diffusive at long times but subdiffusive
at times shorter than
nS. The simulated
was compared with predictions of the Rouse model and several of this model’s proposed modifications, finding that none of the models reproduced the simulations. Simulations were also used to calculate
, the correlation function vanishing for
, at least for
. Use of the simulated
in the Rouse form for
also did not lead to agreement of this modified Rouse model with experiment.
The authors observe that the Gaussian approximation for is only appropriate if the distribution of relative bead displacements , being the position of bead m at time t, is Gaussian at all times. To examine the consequences of this observation, they calculated using the Gaussian approximation and values of mean-square displacements obtained from their simulations, finding that this calculated was in good agreement with as predicted by the Rouse model but did not agree with as calculated directly from the simulation, thus showing the importance of non-Gaussian particle displacements. Smith et al. conclude that the non-Gaussian distribution of bead displacements is responsible for the observed failure of the Rouse model in polymer melts.
Two sorts of non-Gaussian behavior are possible here. The first is that the distribution of displacements for each bead separately could be non-Gaussian. The second is that the distributions of displacements of pairs of beads could be cross correlated. Thanks to the fluctuation–dissipation theorem, this latter possibility is equivalent to the statement that there are significant hydrodynamic interactions in polymer melts, a possibility that would only be surprising if the Rouse model were correct in polymer melts.
Harmandaris et al. [
48] made atomistic simulations of 24-, 78-, and 156-atom (mean length) linear polyethylene melts, finding a diffusion coefficient
D as well as the time autocorrelation functions of the polymer end-to-end vector and the Rouse mode amplitudes. Each autocorrelation function may be said to have a characteristic time
. The study was novel, in that the authors deliberately simulated polydisperse melts, having a polydispersity index near 1.09. From these quantities, nominal monomer friction factors were extracted. Initial chain configurations were equilibrated using the end-bridging Monte Carlo scheme [
49]. Molecular dynamics were executed using a sixth-order predictor–corrector model. The objectives of the study were to test the Rouse model and to take advantage of the polydispersity to examine the dynamics of chains having different lengths, all in the same melt. Potential energies included a Lennard–Jones potential between non-bonded atoms, bond-bending and torsional potentials, and a Fixman potential [
50] to keep the bond lengths constant. The 24- and 78-atom carbon models were simulated in both the NVE and NVT ensembles; the results agreed. The mean-square end-to-end distance
, radius of gyration, and intermolecular bead–bead static correlation functions from the molecular dynamics simulation and the end-bridging Monte Carlo simulation were found to agree, confirming the validity of the two simulations. Local dynamics as estimated with the torsion angle temporal autocorrelation function showed that local dynamics become slightly slower as the chain length is increased.
Harmandaris et al. [
48] calculated properties of the Rouse amplitudes
. The mean-square static amplitudes
decrease with the increasing
p, for the first two modes with the
dependence predicted by the Rouse model, and at larger
p much more rapidly, approximately as
. For
, the discrepancy between the simulation and the Rouse model approaches an order of magnitude. The temporal correlation functions
, at least for the 83- and 117-carbon chain systems, also do not agree with the Rouse model, namely they are not simple exponentials, and their relaxation times do not scale with time as
. On the other hand, for the end-to-end vector, the relaxation time of
calculated using the Rouse model and the relaxation time inferred from simulations of
agree well. From observations of the chain center-of-mass motion over long times, a chain diffusion coefficient
D and therefore a monomer friction factor
can be inferred. Contrary to the Rouse model,
depends on the chain length, increasing threefold from the shortest to the longest chains studied. However,
appears to reach an asymptotic value for the longer chains, those with
or so. Harmandaris et al. propose that
is therefore a lower limit, below which the Rouse model is inapplicable. These workers also calculated, from the diffusion coefficient, a zero-shear viscosity. The calculation was based on Rouse’s theory, which, in some other respects, does not describe the dynamics of these systems, but the calculated viscosity determined by
and the
mode does approximately follow Rouse model predictions.
Krushev et al. [
51] simulated melts of 1,4-polybutadiene. Their interest was to determine the effects of torsion barriers on molecular motions. To do this, they examined the static structure factor, Rouse mode amplitudes, Rouse–Rouse temporal autocorrelation functions, and the intermediate scattering function
. Their polymer melts incorporated 40 polymer chains, each with 29 or 30 subunits, all with united atom potentials, including a model with chains incorporating vinyl groups, a model with chains not incorporating vinyl groups, and a model with no vinyl groups and all rotational potentials set to zero. The three models have the same distribution for their radii of gyration.
Rouse mode amplitudes had, at most, weak cross correlations,
for
being less than 2% of
. The mode amplitudes
only followed the Rouse prediction
for
. At larger
p, the mean-square amplitude depended on good accuracy as
, which is the prediction for a freely rotating polymer [
52]. The calculated static structure factor was not affected by adding or deleting the torsion potential. The time correlation functions
showed stretched-exponential, not single-exponential, behavior for all
p that were studied over an adequate time range. Time correlation functions with and without torsion potentials were very nearly the same when plotted in reduced time units, in which the
time was identified as unit time, showing that chain stiffness arising from torsion potentials did not have a significant effect on the form of the relaxation of
.
The intermediate scattering function also did not follow the Rouse model predictions, namely the Rouse model predicts an over-rapid decay of at larger q, and underpredicts the degree of stretching of . is not significantly changed when torsional potentials are added or removed from the potential energy; the authors infer that observed deviations from Rouse behavior are not due to internal rotation barriers. The Rouse model calculation of agrees with the calculated from the simulation on using the Gaussian approximation and the measured mean-square displacement. Neither calculation agrees with the actual . Furthermore, the center of mass mean-square displacements are subdiffusive at short times. The authors conclude that the Rouse model assumption—that atomic motions are described by a joint Gaussian random process—is thus shown to be incorrect.
Padding and Briels [
53] reported simulations of twelve chains of a C
120H
242 polyethylene melt. They simulated four different starting points for their melt, molecules having united atom potential energies. The potential energy used by these authors was not the simple-harmonic bond-length potential of the Rouse model. Bond lengths and angles had harmonic potential energies; a torsion potential energy was present; unbonded (separated by four or more atoms in a single molecule) pairs of united atoms had a Lennard–Jones potential. A weak coupling to a bath held the temperature fixed. Melt starting chain configurations were created by gradual compression of a dilute system, in which only repulsive interatomic forces were present.
The time-dependent dynamic parameters that they obtained from their simulations include mean-square displacements, the end-to-end vector time autocorrelation function, the intermediate structure factor, and the stress tensor. A single set of numerical parameters for the number of segments N in a chain, for the diffusion coefficient D, and for the longest relaxation time , described most of the dynamic quantities that they calculated, but only over distances longer than a limiting length scale. This paper actually tested the relationships between N, D, , and the calculated dynamic parameters, as predicted by the Rouse model, but did not test the Rouse model itself (Rouse’s description of the internal dynamics of a polymer chain).
Here, the stress tensor was calculated as
where
is the velocity of atom (or center of mass)
i,
is the position of atom (or center of mass)
i, and
is the force exerted on atom (molecular center of mass)
i by atom (molecular center of mass)
j. The forces between two molecules can create a torque, an antisymmetric part of the stress tensor, on each molecule. The stress tensor was identified as leading to the zero-shear relaxation modulus via
where
is the symmetrized traceless part of
.
Padding and Briels concluded that there is a shortest length scale nm over which the Rouse model is valid in their simulations. The length scale manifests itself as the shortest Rouse-mode wavelength for which the model works, the shortest distance over which a mean-square displacement must occur before Rouse behavior is seen, and the shortest wavelength for which the simulated agrees with the model. Over shorter distances and times, matters become more complicated. Padding and Briels calculate for a series of wave vector magnitudes. At small q, only center-of mass diffusion is seen. At larger q, has contributions from polymer internal modes. At larger q, from the simulation, and calculated from the Rouse modes and the diffusion coefficient found at small q, do not agree. from the Rouse formula decays faster at long times than from the simulations, the discrepancy becoming larger at larger q. The short-distance internal chain modes are thus not the same as the internal modes predicted from the Rouse model. Similarly, measurements of mean-square displacements from simulations only agree with the Rouse model when mean-square displacements are greater than (1.1 nm). Finally, at short times, the simulated shear relaxation modulus “…does not behave Rouse-like at all…”, but corrections due to this issue at long times are limited in size.
In a further paper, Padding and Briels [
54] reported simulations of a heavily coarse-grained (one bead = 20 monomers, 120 chains in a simulation box) C
120 linear polyethylene that incorporated a complicated switchable scheme for enforcing chain uncrossability. The scheme could be turned off, leading to simulations of a melt, in which polymer chains could pass through each other. Interactions included non-bonded, bonded, and bending-angle contributions to the bead–bead potential of average force. Beads incorporated as many monomers as feasible without making the beads larger than a nominal tube radius. Padding and Briels calculated the mean-square displacements, both of single blobs and of the chain centers of mass. For the unentangled chains, mean-square displacements increased linearly with time. Adding the uncrossability constraint reduced the mean-square displacements and gave them a sublinear time dependence over a considerable time regime.
Padding and Briels [
54] calculated the time-dependent Rouse amplitudes and evaluated their time correlation functions. Fits were then made to stretched exponentials in time. Chains had six beads, so they only had five internal Rouse modes. When chain crossing was permitted, the time correlation functions were very nearly single exponentials. Adding chain crossing constraints and a bond bending potential led to appreciably non-exponential relaxations, the stretching parameter
falling from close to unity in the absence of chain crossing constraints or a bond bending potential to 0.77 for the three highest modes when the constraint and potential were added. The chain crossing constraint considerably increased the relaxation times of the
and
modes but did not increase substantially the relaxation times of the three higher-
p modes. Padding and Briels determined effective relaxation times
for their five modes. However, instead of calculating
from the stretched-exponential fitting parameters, the authors performed numerical integrals of the measured
curves. The Rouse relaxation rates, Equation (
16), were evaluated for each
p. In the Rouse model,
is independent of
p. In the presence of chain stiffness, and more dramatically in the presence of uncrossability,
was found to increase several-fold as
p was increased, the major change from the Rouse model being that, in the presence of chain stiffness and uncrossability,
is reduced for small
p. Finally, Padding and Briels [
54] calculated the system’s intermediate structure factor
for a series of values of
q. At small
q,
is relaxed by whole-body translational diffusion, a fit giving the polymer’s diffusion coefficient. In the presence of chain uncrossability and larger
q,
did not agree with the Rouse model predictions.
Padding and Briels [
20] further extended their work on polyethylene by making extended united atom simulations of melts of seven different polyethylenes, using 80 to 180 chains with 80 to 1000 carbon atoms coarse-grained into 4 to 50 blobs at 450 K and a density 0.761 g/cm
3. They stressed that the eliminated internal coordinates become thermal bath variables, and contributed to the motion of the blobs as unseen random thermal forces and a friction factor, which they treated as a scalar with no associated memory function. The paper considers a considerable list of different dynamic parameters. Here, we are only concerned with the behavior of the Rouse amplitudes. They calculated the Rouse amplitudes and their time correlation functions. On plotting
against
, values of
for all chain lengths
N superpose, but contrary to the Rouse model
is not independent of
; it instead falls off from slightly more than 3 to slightly more than 1 as
is reduced, i.e., as
p is increased. They interpret this non-Rouseian behavior as arising from their angular potential, which leads to some degree of chain stiffness.
Padding and Briels [
20] also calculated the Rouse–Rouse time correlation functions. Rouse modes at time zero are not cross correlated; they did not report what happens at later times. Rouse-mode temporal autocorrelation functions were found to decay as stretched exponentials in time. The stretching parameter
was close to 0.7 near
.
decreased to 0.55 or so near
, and then increased to near 0.7 at
. At larger
,
was nearly constant. The dependence of
on
was examined. For
,
is independent of
. For
, modestly above 1 and up to 3 or so,
. For
,
. Padding and Briels note, for the second and third regimes, that these dependencies are not in agreement with either the Rouse or the reptation model. Padding and Briels then propose that at large times
switches over from a stretched-exponential to a simple-exponential time dependence.
Abrams and Kremer [
55] studied a bead and spring polymer melt, the interest being the effects of varying the equilibrium bond length
relative to a nominal bead diameter
. In different simulations, the bead length was given 13 values in the range
. The model contained 80 freely jointed chains, each having 50 beads, at density 0.85
and nominal temperature
in natural units, so that
. Bonded beads were linked with a harmonic potential
,
ℓ being a bond length, with
k and
being simulational parameters. Non-bonded beads interacted with a truncated Lennard–Jones potential. The authors studied the time correlation functions of the Rouse amplitudes
and the mean-square displacements of the bead centers of mass.
Semi-log plots of the normalized as functions of a normalized time were presented for equaling 0.79, 0.97, and 1.24 and . For , the plots were nearly linear. The curvature increased with increasing . For the smallest , plots of for the different values of p nearly superpose. For larger , the curves spread out modestly from each other, though the dependence on p is hard to discern. Abrams and Kremer extracted from fits of to the early parts of the curves, and advanced from there to nominal friction factors . In doing this, they indicated that “…The Rouse model best describes the early phase of the decay of…” and described behavior at later times as “…subtle non-Rouse-like behavior …”, whose examination was deferred to a future study. The inferred values were presented as averages over p. As a function of , the averaged increases rapidly at larger . Abrams and Kremer also calculated the average number of other polymer beads within a distance of a bead of interest. That number increases, roughly from 0.4 to 1, over the observed range of .
Doxastakis et al. [
56] reported extensive atomistic and unified-atom simulations of melts of very short (40–115 atom) polyisoprenes, including 64 chains of C
80 polyisoprene, and compared with measurements from
13C NMR, quasielastic neutron scattering, the torsional correlation function from the simulation, dielectric relaxation spectroscopy, and polymer self-diffusion. Because these authors performed atomistic simulations, their simulations determined single-bond and few-atom motions that could be compared with
13C NMR and neutron scattering. Reasonable agreement between simulation and experimentally measured quantities, within the expected limits of accuracy of the simulations, was obtained. Dielectric relaxation measurements were interpreted in terms of a Kohlrausch–Williams–Watts function for a higher-frequency peak and Rouse normal modes for a lower-frequency peak. The Rouse fit showed some deviation from the experiment at higher frequencies. The mean-square amplitudes
of the Rouse modes only followed the theoretical
scaling for the first two or three modes; for larger
p, the measured amplitudes are smaller than the theoretical prediction. Plots of the simulated
against
should collapse onto a single line. If the
amplitude is normalized out, the plots come respectably close to doing so. However, at short times,
from the simulations fell well below a fit of the long-time
to a single exponential, especially for larger
p. The simulated time autocorrelation function for the chain end-to-end vector was at early times also smaller than expected from the Rouse model. Finally, on uniting the various theoretical and fitted treatments of chain end-to-end relaxation, very good agreement was obtained between the theoretical form and the simulations. The authors concluded that the Rouse model is sustained by their simulations for the quantities that they analyzed, a conclusion that neglects the issues they faithfully reported with the mode mean-square amplitudes.
Tsolou et al. [
11,
57,
58] report a series of molecular dynamics simulations of polybutadiene and polyethylene. Their first paper [
57] simulated
cis-1,4-polybutadiene based on a united atom description, in which hydrogen atoms were merged with the carbon atom to which they were bonded. Bonds were represented as Hookian springs with a finite rest length; bend and torsion angles had associated potential energies. Non-bonded atoms interacted with a non-truncated Lennard–Jones potential. Melt simulations were performed on monodisperse polymers with
N of 32 to 400 carbon atoms in systems containing more than 10,000 united atoms for times up to 600 nS. End-bridging Monte Carlo methods were used to create rapid equilibration; simulations were based on multiple-time-step molecular dynamics. The system was thermostatted to a constant temperature and pressure. A long series of static quantities were calculated, including the mean-square radius of gyration, mean-square end-to-end distance, characteristic ratio, specific volume as a function of chain length, density as a function of temperature, the intermolecular pair radial distribution function, and the static structure factor. For the last of these, the locations of the hydrogen atoms had to be backed out from the unified atom description.
Tsolou et al. [
57] also calculated dynamic quantities, including the time autocorrelation functions for the torsion angles and the chain end-to-end vector
. Efforts to fit
as a sum of Rouse modes were unsatisfactory; on the other hand,
was fit accurately with a single stretched exponential in
t. The nominal relaxation times from these fits increased with increasing polymer length
N, namely
with
a increasing from 2.1 for the shortest polymers to 2.8 for the longest polymers. The change in
a with increasing
N was not obviously discontinuous.
Tsolou et al. also determined the mean-square displacements of the chain centers-of-mass as functions of time, and inferred from the displacements the diffusion coefficient D. D depends on N approximately as a power law. Curiously, the slope of against is shallowest for intermediate values of N.
An algorithm was used to obtain a nominal primitive path for each polymer chain at a series of times. The primitive path from this algorithm is a smooth curve that follows the atomistic backbone. The diameter
a of the corresponding tube is
, which is considerably larger than the experimental
tube diameter reported [
59] for the same system.
a is much larger than the distance between neighboring polymer chains, showing that when a polymer chain attempts to move transversely to its primitive path and encounters another polymer chain, in general, it is able to continue to move in the same direction over considerable distances. The authors also computed the mean-square displacements
of the central beads of each chain.
appears to be a smooth curve that could be described as having sections that follow power laws
. However,
was never less than 0.4, so it never reached the
of the Rouse model. For
, the transition from an initial
down to
occurred at ≈
pS.
Calculations of the single-chain intermediate structure factor were made. The authors concluded that there is no q for which agrees with a fit to the Rouse model, including times shorter than a few nS. According to the authors, the tube-reptation model indicates that at times shorter than a few nS, polymer chains are supposed to be performing Rouse-like motion because they have not yet having encountered the walls of their tube. However, obtained from these simulations decays more slowly than does predicted by the Rouse model, using Rouse times calculated by fitting independently to the time correlation functions of the polymer end-to-end vector. The tube-reptation prediction does not match the simulations. Nonetheless, the authors were able to extract a nominal friction factor from the Rouse form for the diffusion coefficient, even though the Rouse model does not appear to describe the dynamics.
Tsolou et al. [
58] examined Rouse amplitudes and dynamic structure factors for simulated cis-1,4-polybutadiene melts. The simulations viewed 32 chains of a C
128 polymer as functions of the system’s temperature and pressure, at temperatures from 165 to 413 K and pressures from one atmosphere to 3.5 kbar. Simulation methods duplicated those in earlier papers by Tsolou et al. [
60,
61]. The authors first examined the time autocorrelation functions
of the Rouse mode amplitudes for
p having various values in the range
. The
were all found to decay as stretched exponentials in time, not the exponentials predicted by the Rouse model, leading to a set of values for
and
. The stretched exponentials were also characterized via their total correlation times
Tsolou et al. [
58] found that the
depends on temperature via a modified Vogel–Fulcher–Tamman equation,
Here,
T is the absolute temperature,
and
are fitting parameters, and
is a characteristic temperature. Over the range of temperatures that were examined in the simulations, the temperature dependencies of the
do not depend markedly on
p. Pressure dependencies of the
were obtained at temperatures 310 and 413 K. The
increases exponentially with increasing pressure
P. Viewed graphically, the effect of
P on
does not depend a great deal on
p. The authors define an activation volume for the
via
decreases roughly by two-fold between
and
, and for smaller
p is modestly smaller (by less than 10%) at the higher than at the lower temperature.
Tsolou et al. [
58] also calculated the single-chain intermediate structure factor [
57,
62]
in which
n and
m label two of the
N segments of a single chain,
q being the magnitude of the scattering vector and
being the distance between segments
n and
m at two times separated by
t.
was found to be described by a stretched exponential in
t. The stretching exponent
was reported to change with pressure and to decrease with increasing
q. The total correlation times for
were found to decrease with increasing
q and to increase exponentially with increasing pressure. The activation volumes
, as calculated from the pressure dependencies of these total correlation times, decrease with increasing
q.
Tsolou et al. [
58] calculated the single-chain incoherent scattering factor
, which differs from
in that in Equation (
29) the restriction
is forced.
decays as a stretched exponential in time.
was found to increase from ≈0.5 to ≈0.9 as
q was increased over the observed range. The total correlation time
decreased strongly with increasing
q. Lines to guide the eye, drawn as
for smaller
q and
at larger
q, are harmonious with the
q dependencies of
at multiple temperatures and a full range of pressures. The peculiar
exponent is an artifact of the stretched-exponential form
used to parameterize
. If the parameterization had instead been the rational alternative
then for smaller
q, the result would have been
, while for larger
q, the form
would have appeared as an approximant.
The Rouse model predicts that the relaxation time of the
mode should depend on
p as
. As the model also predicts that modes relax as simple exponentials in
t, not the stretched exponentials actually found, there is no theoretical basis for identifying the total correlation time with the Rouse time. Indeed,
is not independent of
p; it instead decreases by about 30% as
p is increased from 1 to 20. Tsolou et al. [
58] used this observation to estimate the longest relaxation time and hence a model-dependent zero-shear viscosity for the system. The inferred viscosity follows a Vogel–Fulcher–Tamman form.
Tsolou et al. [
11] simulated melts of ring polyethylenes containing 24–400 carbon atoms per ring at nominal temperature and pressure of 450 K and 1 atmosphere; simulation boxes contained 3000–20,000 united atoms. Simulations were made with a united atom model treating methylene units as single atoms, a harmonic bond-stretching potential, a harmonic-in-bond-angle bending potential, a bond-torsional potential, and a 12-6 Lennard–Jones potential for atoms separated by more than three bonds, using the r-RESPA algorithm [
63] for molecular dynamics. As two of a large number of properties (most not considered in this review), they calculated
and
. For
, the mean-square amplitude
increased linearly in
. At smaller
, the increase in
with increasing
was much more rapid than linear in
, contrary to any prediction of linear behavior at all
. The time correlation functions
were found to depend on
t as stretched exponentials in time, not the simple exponentials of the Rouse model. A comparison was made between a Rouse prediction
for small
p, and the
calculated from the time integral of
. The prediction was sustained for
. At smaller
,
decreases two-fold as
is reduced from 30 toward 1. Rouse model predictions for the time correlation function and its zero-time value are, therefore, confirmed only for larger values of
.
Bulacu and van der Giessen [
64] simulated the effect of bending and torsional potential energies on a polymer melt. Their systems included up to 1000 chains with
. Their polymer was a bead–spring model, with a 6-12 Lennard–Jones potential truncated at its minimum, bonds between beads represented with a FENE potential, a cosine harmonic bending potential
with
, and a coupled bending–torsion potential
The torsion potential refers to four beads in a row along a polymer, the two internal angles and formed by the two overlapping sets of three beads in a row, and the dihedral angle . The was determined by quantum calculations for n-butane as . Simulations used the velocity Verlet algorithm; the temperature was held steady with a heat bath’s random force and friction factor. and are stiffness coefficients.
Static properties examined include the mean-square end-to-end distance
and the radius of gyration
; these were calculated both for the entire chain and also for all of its sub-chains. With increasing chain stiffness,
was found. Histogram distributions of bond lengths, bending angles, and dihedral angles were reported. The bead–bead radial distribution functions, same chain, different chain, and all chains, were reported as linear plots. (Linear plots, while completely orthodox, can lose details of
. Whitford and Phillies previously showed that the range of
in a Lennard–Jones fluid is, at lower temperatures, much longer than is sometimes assumed [
65,
66] as was made apparent by plotting
against
r).
Dynamic properties studied include the polymer self-diffusion coefficient D, mean-square bead displacements, and . For the chain, D depends on the stiffness coefficients as and . D depends on N via a smaller-N and a larger-N power law. The authors determined the break between the two power laws by maximizing the sum of the regression coefficients in fits of the two laws to the data. With increasing chain stiffness, D is reduced. With increasing chain stiffness, for shorter chains, D depends more strongly on N, the transition from short-to long-chain behavior moves to larger N, and the N-dependence of D in the long-chain regime increases, finally attaining .
The authors remark that they do not expect the Rouse modes to be exact eigenmodes in their systems, but they still investigated . The dependence of mean-square Rouse amplitudes on p and the two chain stiffness parameters was examined for an polymer. While increasing has little effect on , for larger values of p, increasing considerably reduces by close to five-fold for . Time correlation functions were found to follow stretched exponentials in time, with and the mode relaxation time decreasing with increasing p and with an increase in chain stiffness.
Moreno and Colmenero [
26] reported an extended simulation of an A-B blend of bead–spring polymers. The polymers were all shorter than the known nominal entanglement length, which is approximately 32 monomer beads. Beads were connected by a FENE potential and a monomer–monomer potential
with
,
, and
= 1.6, 1.3, or 1, respectively, in units of
for
, or
, respectively, with a packing fraction 0.53 and a cutoff
. Temperatures ranged from 1.5 to 0.33 in different simulations. All chains were the same length, with
N between 4 and 21; systems contained 2000–4000 monomers. Dynamic asymmetry appeared because
differed between the two types of chain, with the A chains being larger and more numerous (70% of the total).
Moreno and Colmenero calculated the correlation functions . For , was found, which was taken to indicate that cross correlations between Rouse amplitudes are small. One notes that while the individual off-diagonal are small, for any p or q, there may be a respectably large number of them, so the total effect of the cross-correlations might not be negligible. The were found to be described by stretched exponentials in t. The stretching exponent depends weakly on p, tending to decrease with increasing p. Considering chains with , for the larger, more numerous A chains and , . For the smaller, less numerous B chains, with decreasing temperature, fell smoothly from 0.9 or so to 0.3 or so. That is, the relaxations are not the pure exponentials predicted by the Rouse model, but are closer to being single exponentials for the larger A chains, while being more remote from single exponentials for the B chains.
The two authors also considered how the measured scaled with . For the A chains, except for the shortest-wavelength modes, scales approximately as at all temperatures studied. For , these being the shortest wavelength modes, tended to be slightly larger than a scaling line prediction. For the smaller, less numerous B chains, a normalized scaled as , with at high temperature but increasing to at the smallest temperature studied. matches the reptation prediction , except, as the authors noted, they considered polymers that are too short to be entangled, indeed, polymers with as few as 4 monomer beads. For both chains, scaled as , which is not far from the Rouse value . For chains of length , the authors computed the mean-square displacement of the center beads of the B chains as a function of time at various temperatures. For times shorter than the Rouse time, there is at each temperature a region in which , with a y that decreases markedly as the temperature is lowered. However, as the authors note, the entanglement crossover is reached by making polymer chains long, while here a crossover with the same appearance is reached by increasing the dynamic asymmetry, the value of between two components, neither of which is entangled. The authors note suggestions that these anomalous diffusive behaviors arise because density fluctuations around each chain become slow, but slowness “may be induced by entanglement, but data reported here for the fast component suggest that this is not a necessary ingredient”. They emphasize that, with sufficient dynamic asymmetry, entanglement-like dynamics are observed, even for model bead–spring tetramers.
Brodeck et al. [
34] reported simulations of a polyethylene oxide melt and a comparison with inelastic neutron scattering studies. Simulations used Materials Studio 4.1 and Discover-3 (version 2005.1) with the COMPASS force field. In addition to potential energy terms reflecting bond stretching, bond bending, and bond torsion, their potential energy calculations include the coordinate cross-coupling terms known to be essential for calculating infrared and Raman frequencies. The polyethylene oxide oxygen has a significant partial charge, leading to Coulombic interactions. A Lennard–Jones 6–9 potential was used for the general non-bonded interaction. The simulation cell included five polymer chains, each composed of 43 monomer units in a
cubic cell at temperatures 400, 375, and 350 K. Brodeck et al. made a series of tests of implications of the Rouse model, finding that the available scattering data on this system all agree with predictions of the Rouse model, namely that (i) for q ≤ 0.6
, the characteristic relaxation time scales as
, (ii) the incoherent scattering function depends on time as
, at least for times longer than 2 pS, and (iii) the Rouse rate
from simulations agrees with the experiment.
The Rouse mode amplitudes , their mean-square values, and their temporal autocorrelation functions were determined for . A test of orthogonality found that was , except for some large mode numbers. For each p, was described well by a stretched exponential in time. For small p, followed the Rouse model behavior so that and the integrated average relaxation time each scaled as . For larger , decreased relative to an expected dependence, finally reaching perhaps 2/3 of the expected value, while, over the same range of p, fell to a quarter of its expected value. was never a simple exponential. For , the stretching exponent was as large as 0.9. With increasing p, falls, reaching a minimum of 0.7 or so for close to 1, and then increasing slightly as is reached. is weakly temperature dependent, especially at large p, increasing by a few percentage points as the temperature is increased.
Lahmar et al. [
67] extended the earlier work of Tzoumanekas et al. [
68] to consider the dynamics of their polymer model. In their model, individual beads represent 20-carbon backbone segments. Atomistic simulations were then used to determine the bead–bead nearest-neighbor-intrachain and interchain radial distribution functions and the three-bead angular distribution function. From these, the potentials of average force and thence, via an iterative process, the mean forces between polymer beads were determined. Bead motions were obtained using dissipative particle dynamics. Because the polymer beads are soft and can interpenetrate, a short range segmental repulsion force adequate to greatly reduce chain crossing was superposed. Chains with 6 to 40 beads, i.e., 120 to 800 carbon atoms in the backbone, were then examined. The center-of-mass diffusion coefficient was found to depend on chain length as
for the shortest chains and
for the longest chains, these values not being in agreement with the Rouse and reptation model predictions
and
, respectively, though the latter is in reasonable agreement with experiments on polymer melts. The end-to-end vector reorientation time also depends on the chain length, its short- and long-chain dependencies being in approximate agreement with Rouse and reptation model predictions.
Lahmar et al. [
67] examined the Rouse amplitude time correlation functions
, finding that these decay as stretched exponentials in time, not the pure exponentials required by the Rouse model. The stretching exponent
depends on
p and on the chain length. For chains that cannot cross,
was smallest for
p in the range
to
. The authors propose that this length scale corresponds to the length scale of the network mesh as discussed by Tzoumanekas et al. [
68]. For the longest chain studied,
,
decreased from 0.9 for the smallest and largest possible values of
p to
at its minimum. When chain-crossing constraints were removed,
was close to unity at small
p and decreased to 0.9 or so at large
p. The mode relaxation times do not scale with
N and
p as predicted by the Rouse model. In the absence of the segmental repulsion chain-crossing barrier, the mode relaxation times do not depend on chain length, but are slower than expected at large
p. In the presence of chain-crossing constraints, for large
N, the relaxation times only follow reptation model predictions for the first few values of
p. Lahmar et al. concluded that Rouse modes are not the system’s normal modes but did not claim that the system actually has normal modes of relaxation.
Perez-Aparicio et al. [
69] reported a molecular dynamics simulation of poly(ethylene-
alt-propylene) based on a coarse-grained bead and spring model. Their coarse-grained potentials were the bead–bead potentials of average force determined by comparison with simulations made on shorter chains using an atomistic potential, with a single coarse-grained bead representing ten monomers, about half of the nominal entanglement length. Coarse-grained chains containing between 5 and 30 beads, with 150 to 80 chains in a simulation cell, were then simulated. A coarse-grained friction factor
f was set so that the long-time mean-square center-of-mass displacement of the coarse-grained short chains matched the long-time mean-square center-of-mass displacement of the atomistic chains. The short-time mean-square center-of-mass and bead displacements of the coarse-grained and atomistic chains do not match, apparently because for the coarse-grained chains, a short-time frictional memory function is replaced with a simple friction factor.
The authors then studied chain dynamics by calculating the , which were found to follow stretched exponentials in time. The dependence of the mean-square amplitude , the stretching parameter , an average relaxation time , and a Rouse frequency on mode number p and chain length N were considered. is the inverse of a nominal time needed for a bead to diffuse through the length of a statistical segment. For p close to unity, relaxations were very nearly exponential, with . With increasing p, fell, declining to for in the range 2–3. At still larger p, increased again, reaching 0.95 or so for . For , and followed the Rouse model predictions; at smaller , and are both substantially smaller than the Rouse predictions. The authors indicate their simulations are unrealistic at very small , roughly , this regime being much narrower than the regime in which the Rouse behavior is not seen. The Rouse frequency depends strongly on , increasing perhaps fourfold as p is increased from 1 to its upper limiting value . When chains are allowed to pass through each other, the dependence of on p is reduced by approximately 50%, while the modest dependence of on N disappears. These features are not consistent with the hypothesis that the Rouse model provides a valid description of polymer dynamics in the melt.
Perez-Aparicio et al. [
69] repeat the warnings of Akkermans, Padding, and Briels [
20,
54,
70,
71] that the coarse-graining of atomic coordinates leads to friction forces, ‘random’ thermal forces, and can permit long polymer chains to pass through each other if appropriate precautions are not taken. The rigorous statistico-mechanical representation of coarse graining is provided by the Mori–Zwanzig formalism [
72], in which the complete set of atomic coordinates is partitioned between variables retained for study and variables described as
bath variables, the latter being subject to a thermal averaging process that removes them from further consideration. The Mori–Zwanzig coarse-graining process introduces to the equations of motion a set of random
thermal forces, a corresponding set of frictional forces that together with the thermal forces keep the system in thermal equilibrium, and a set of Mori memory kernels
that replace friction factors, namely
Here,
is a bead velocity at time
t. One could, in principle, use simulations to recover the Mori memory kernels
, as was done in a different class of systems by Phillies and Stott [
73,
74].
Perez-Aparicio et al. [
69] explore possible paths for uniting their simulations with the Rouse model. They note the possibility that the statistical segment length
b or the friction constant
f could depend on the mode so that a mode dependence of
b or
f might explain some of their results. In the context of the Rouse model,
b and
f are associated with individual bonds or beads, respectively, so it is unclear how a simple
p-dependent form of these variables could be interpreted, other than as a formal re-parameterization. However, each
samples
t with slightly different weightings for each time, and therefore represents a different averaging over a memory function
, thus providing a mechanism that would lead to formal
p dependencies of
b and
f. Some authors noted that united atom simulations show different short-time dynamics than do all-atom simulations. Failure to treat friction with a memory function
, as required by the Mori [
29,
30] formalism, rather than with a simple friction factor
f, would lead to this outcome. The extensive review by Jin et al. [
75] discusses current results on applying approximations to the Mori–Zwanzig formalism to molecular dynamics in the presence of united atoms or coarse graining.
Kalathi et al. [
17] reported simulations of melts of 500–2000 linear polymer chains, with individual chains containing between 10 and 500 beads. The objective was to analyze polymer motions in terms of Rouse modes, the hope being that the dynamics of longer- and shorter-wavelength (smaller and larger
p) Rouse modes would reveal the motions of longer and shorter chain segments. As a justification for the study, experimental and simulational evidence was cited for deviations from Rouse behavior at short distances and small times [
34,
76]. Temporal autocorrelation functions of Rouse amplitudes were found to decay as stretched exponentials in time, not the simple exponentials predicted by the Rouse model [
77], with mean-square amplitudes that fail to scale as
. Additionally, the stretching parameter
was previously found by Padding and Briels to depend on
p [
20,
54]. Finally, Kalathi et al. noted the result of Likhtman [
16] that Rouse modes are sometimes substantially cross correlated (
for
and
).
In Kalathi et al.’s simulations, the bead–spring Kremer–Grest model was used, with a finitely extensible nonlinear-elastic potential for bonded beads, a Lennard–Jones interaction between all pairs of unbonded beads, and a bending potential between linked segments along each chain. This potential energy keeps chains from passing through each other. In some simulations, the potential energy was modified to permit chain crossing, the modified potential energy being such as to not change chain static properties significantly, thus testing for effects arising from topological interactions. Rouse amplitude time correlation functions were evaluated for p as large as 24 and 4 values for the chain stiffness. Simulations were executed for sufficiently large t such that decayed to essentially zero. Except at the earliest times, where in some systems for small p the fitted curves pass above the data, their measurements were described well by stretched exponentials in time.
From the simulations, fails to be independent of , contrary to the prediction of the Rouse model. This product does approach the characteristic ratio asymptotically for small p. With decreasing , the product decreases slowly until reaches 15 or so; at smaller , this function decreases rapidly toward 0.5–0.8 at . The stretching parameter of also depends on , being roughly 0.9 at , decreasing to a minimum for , and then increasing to 0.75 or 0.8 for . The minimum in is found for , being an inferred entanglement length. also depends modestly on the bending constant in the force field.
Kalathi et al. reported results for a range of chain lengths, from to . At fixed , is independent of N for shorter chains, but for chains with and , the authors report that decreases markedly with increasing . also shows distinct behaviors for shorter and longer chains. For , simply increases as is increased. At larger N, shows a minimum at intermediate . Kalathi et al. reported the effective monomeric relaxation rate and the longest relaxation time. increases by ten- to thirty-fold between small and large p.
Removing the chain-crossing constraint considerably increases , especially for longer chains, eliminates the dependence of on chain length, and eliminates the dip in at intermediate . In the absence of the chain-crossing constraint, increases monotonically from 0.8 at smaller to near unity as , while the longest relaxation rate increased as for all chain lengths studied, rather than—in the presence of chain uncrossability—increasing more rapidly than at large N.
The central conclusion of Kalathi et al.’s simulations is that the Rouse amplitudes of their bead–spring polymers show one behavior if the chains are short and a different behavior if the chains are longer than some length , but the short chain–long chain difference disappears if the chains are enabled to pass through each other. However, removing the chain-crossing constraint does not replace the stretched-exponential time dependencies of with the simple-exponential time dependence of the Rouse model. Their results provide direct evidence for the contribution of topological interactions (chain-crossing constraints) to the dynamics of long polymers.
Hsu and Kremer [
78,
79] made molecular dynamics simulations of 1000 chains containing N = 500, 1000, or 2000 beads at volume fraction 0.85, using a novel scheme for equilibrating a large assembly of long chains [
80]. The chains were described by a bead–spring model [
37] with a FENE potential between bonded atoms, a Lennard–Jones potential between non-bonded atoms, and in different simulations, a bend-bonding constant
of 0 or 1.5. Molecular dynamics were executed using the ESPResSo++ package. Averaging, especially of the stress tensor
, was improved by making an ensemble as well as a time average, namely by averaging over ten independently generated equilibrated systems as well as an extended time average. The nominal distance
between the hypothesized entanglement points was estimated from primitive path analysis, and from Green–Kubo determinations of viscoelastic properties, to be 26–28 monomers, so the 1000-bead chain would nominally have contained three dozen entanglement lengths and proportionately more or less for the 2000 and 500 bead chains.
Hsu and Kremer [
78] first calculated static correlation functions, including the distribution functions for the end-to-end distance and the radius of gyration, the mean-square distance between pairs of polymer beads as a function of the distance between them along the chain, the bond–bond orientation correlation function, and the static structure factor
, thus identifying a good compromise value for the bond-bending constant. They then developed several dynamic properties, beginning with the time dependence of mean-square displacements of inner monomers, of inner monomers with respect to the center of mass, and of the center of mass itself. Comparison was made with power-law time dependencies. They made a primitive path analysis based on cooling the chains while holding the ends fixed, and computed the stress relaxation modulus from the stress tensor.
Hsu and Kremer [
79] advanced to study the
and
. For each
p,
was found to decay as a stretched exponential in
t, relaxations being longer lived at larger
. The deviation from a simple-exponential decay was smaller for large
, i.e., for small
p, and was less obvious at early times. For small
, say
, i.e.,
,
was found to be independent of the chain length. For larger
,
was seen to depend on
N,
decaying less rapidly for the longer chains. The parameters of the stretched exponential were found to depend on
. The stretching exponent
decreases from 0.8 or so at small
to a minimum near 0.5 for
near 25 or 80 (depending on the chain stiffness
), and then increases to 0.6 or so for large
. The location of the minimum in
is independent of the polymer length. The value of
for which
reaches its minimum is approximately the same as the value of
above which
begins to depend on
N. The average time constant
increases through eight orders of magnitude as
is increased from 1 to 1000. Hsu and Kremer compare
to power laws
, using asserted theoretical model values
for small
and
for large
. Regions where these predictions are approximately correct are indeed found, though, at large
,
tends to roll off to below the
power law curve. Hsu and Kremer propose that the stretched-exponential behavior arises as a crossover from Rouse behavior at early times to reptational behavior at longer times.
Finally, Hsu and Kremer [
79] discussed the coherent and incoherent structure factors
and
.
is the self part of the sum that defines
. Their analysis is based on the self part of the Gaussian approximation
where
is the mean-square displacement of bead
i during time
t. Hsu and Kremer report
and
as functions of time for a half-dozen values of
q. If the Gaussian approximation is correct, the latter quantity would be independent of
q. Contrariwise, if
has a pronounced
q-dependence, this quantity would be determined by the all moments
,
of the bead displacement, not just the mean-square bead displacement [
81]. Indeed, Hsu and Kremer reported that at short times,
is independent of
q, so at short times, the Gaussian approximation is correct and
gives the mean-square bead displacement.
At times longer than a hypothesized entanglement time , depends markedly on q, so in the hypothesized reptation regime, the Gaussian approximation fails, in which case does not reveal the mean-square displacement of the beads and does not provide a test of the existence of the proposed motional regime. The hypothesized power laws from the reptation model were drawn as tangent lines to some of the curves, transitions between the hypothesized motional regimes being estimated as points where the power-law lines intersect. From the estimated times, an estimate of the entanglement length was obtained, this length being approximately in agreement with estimated from primitive path analysis or from melt viscoelastic properties.
Goto et al. [
82] used the Kremer–Grest bead–spring model to study melts of linear and ring molecules. Their calculations incorporated 10,000 beads, linked in different simulations into molecules having between 5 and 400 linked beads, beads interacting via FENE, bending angle, and Lennard–Jones potentials. The temporal autocorrelation functions of the Rouse amplitudes were calculated. For each molecular weight and
p,
was found to be described well by a stretched exponential in time. The stretching exponent
, the mean-square amplitude
, and the relaxation time
were all found to depend on the mode number
p and the length
N of the polymer chain as functions of the unified variable
. For ring polymers,
was never larger than 0.8, with a local minimum of 0.7 near
, a return to 0.8 for
, and a tendency to decrease at larger
, contrary to the Rouse model prediction
at all
. For linear polymers,
was 0.85 at
, decreased to
for
, increased to 0.8 or so near
, and for
decreased again to 0.6 or so. According to the Rouse model, the normalized Rouse amplitude
should be a constant independent of
. For both rings and linear chains, in Goto et al.’s simulations, this quantity instead increases roughly five-fold between
and
; for ring polymers at
, this quantity clearly declines again with increasing
. The integrated relaxation time
increases with increasing
, approximately as a power law in
, the power being close to the Rouse model value 2 at smaller
and larger, especially for the linear polymers, at large
. Goto et al. described this
dependence as “
the deviation from the model behavior becomes remarkable…”. The exponent of the power law visibly increases smoothly with increasing
, without a sharp transition in its value at some
.
Goto et al. [
82] also examined
, the probability distributions for the displacement of single beads and for chain centers of mass. For ring polymers,
remains nearly Gaussian at all times. For linear polymers, at larger times,
deviates from the expected Gaussian form, becoming broader as
t increases. Characterizing the deviation from a simple Gaussian with a non-Gaussian parameter
,
for monomers in linear chains has a small short-time peak, roughly the same size for all chain lengths, and a long-time peak whose size increases perhaps linearly with the chain length. For monomers in ring polymers, only the small short-term peak is apparent.
Roh et al. [
12] simulated ring and linear polyethylenes that had short-chain branches spaced along their lengths. The polyethylene backbones each contained 400 carbon atoms, with 33 side chains, each being 5 carbon atoms in length; as a control, simulations were made of polymers having the same backbones but no side chains. Simulated systems contained 54–70 molecules held at constant temperature and pressure 450 K and 1 atm. Molecules interacted via TraPPE united atom potentials, motions being calculated with the r-RESPA algorithm [
83,
84,
85]. The addition of short chains to the polymers renders the molecules more compact.
Rouse mode amplitudes were computed. For linear chains, the equilibrium average was linear in for large , but, for , fell below the linear line. For ring polymers, had a linear dependence on , with a slight drop-off from that dependence in the limits of small or large . Roh et al. also examined the temporal autocorrelation functions . In all cases examined, deviated from a simple exponential decay, having instead the form of a stretched exponential in time. Writing the stretched exponential as , was found to scale as .
A few studies used very different bead–bead potential energies. Smith et al. [
86,
87] used a tangent hard-sphere polymer model, in which the bond length between adjoining spheres was allowed to vary over a narrow range. Their polymer chains had any of the 6 lengths between 8 and 192 spheres, at volume fractions 0.3, 0.4, or 0.45. Systems contained 32 or 64 chains in a cell with periodic boundary conditions. The simulations covered five orders of magnitude in time. Smith et al. studied the behavior of static and dynamic properties, including chain dimensions, Rouse amplitudes, chain mean-square displacements, fluctuations in the chain end-to-end vector’s length and orientation, evidence for knot formation, dynamic structure factors, and Rouse amplitude autocorrelation functions. Smith et al. asserted that reptation and the tube model predict that, at times shorter than the entanglement time, for chain segments shorter than the mean number of beads between two entanglements, the Rouse model should be applicable, but at long times, the Rouse mode relaxation rates should increase in proportion to the number of times that a typical chain is entangled.
From the amplitudes
of the Rouse mode, Smith et al. [
86,
87] calculated the normalized temporal correlation functions
. These were plotted against the reduced times
, where
p is the mode number and
N is the chain length. For a 32-bead polymer at volume fraction 0.3, the correlation functions are very nearly exponential. At the larger polymer concentrations, the higher-order modes (
) deviate from simple-exponential behavior, their relaxations being slower than exponential at long times, with relaxation rates scaling linearly in
. For a 192-bead polymer, relaxations are markedly non-exponential, the deviation from single exponential behavior being most notable at the largest polymer volume fraction. In contrast to the 32-bead polymer, for the 192-bead polymer, the non-exponential behavior is most prominent for small
p. Additionally, for the 192-bead polymers, the mode relaxation rates are not linear in
. At
, the correlation function for
gains a pronounced shoulder, after which it decays very rapidly toward zero. The Rouse model prediction of exponential decay of
is thus not sustained for longer polymer chains.
Smith et al. reported seeing Rouse behavior, based on the observations for shorter polymers and mean-square displacement proportional to at shorter times. Their D against N plot shows, for each polymer volume fraction, a smooth curve approaching a tangent to at small N and to at large N, though most of their points are in the intermediate transition region. At intermediate times, they found mean-square displacements or . behavior was not observed. They also noted an anomaly: Following a second regime in the mean-square displacements, they observed a small plateau in the time dependencies of the mean-square displacement and the end-to-end vector time correlation function. They proposed that the plateau corresponds to a time-scale separation between two types of entanglements, namely tight local knots and surrounding chains functioning as fixed obstacles.
Can Rouse coordinates and modes emerge naturally from an analysis of Brownian or molecular dynamics simulations? This question was approached by Wong and Choi [
88], who considered a non-linear bead–spring model, in which individual terms of the linked-bead potential have a form
Here,
k is a force constant,
is the position of bead
i, and
b is a constant. This potential energy term has a minimum when beads
i and
j are separated by the distance
b. In the original Rouse model,
; when in their rest positions, all beads of a Rouse chain are at the same location. For their Brownian dynamics simulations, Wong and Choi integrated their equations of motion with the Newton–Gauss method. Wong and Choi also made molecular dynamics simulations of chains in a melt, using the TraPPE [
84,
85] force field with GROMACS [
41] as an integrator. For the molecular dynamics simulations, individual chains had 30–73 beads, the number of chains being fixed at 40 for simulations of longer chains.
For each molecule and time step, Wong and Choi then calculated, separately along each Cartesian coordinate, the distance
for each bead
i from the chain center of mass. They then formed and averaged the
single-time correlation matrices
t here being the label on the
S time steps. Proper orthogonal decomposition was then used to obtain dominant eigenvectors of
. Simulations of single chains using Brownian dynamics and simulations of chain melts using molecular dynamics yielded similar forms for the eigenvectors of
. Wong and Choi examined linear, ring, and star polymers. The dominant eigenvectors of the linear polymer closely resemble the eigenvectors of the Rouse model.
The temporal autocorrelation functions of the eigenvectors were then evaluated, finding that the autocorrelation functions decay as stretched exponentials in time, with values of close to unity. For ring and star polymers, two or three, respectively, of the relaxations were found to be nearly degenerate in their relaxation times. The temporal cross-correlation functions were not evaluated. The integrated average relaxation time for the modes scales differently for the Brownian dynamics and the molecular dynamics simulations, namely for the Brownian dynamics simulations but for the molecular dynamics simulations.