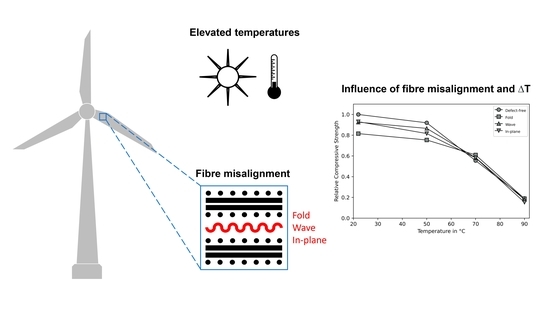
Effect of Fiber Misalignment and Environmental Temperature on the Compressive Behavior of Fiber Composites
Abstract
:1. Introduction
2. Materials and Methods
3. Experimental Results and Discussion
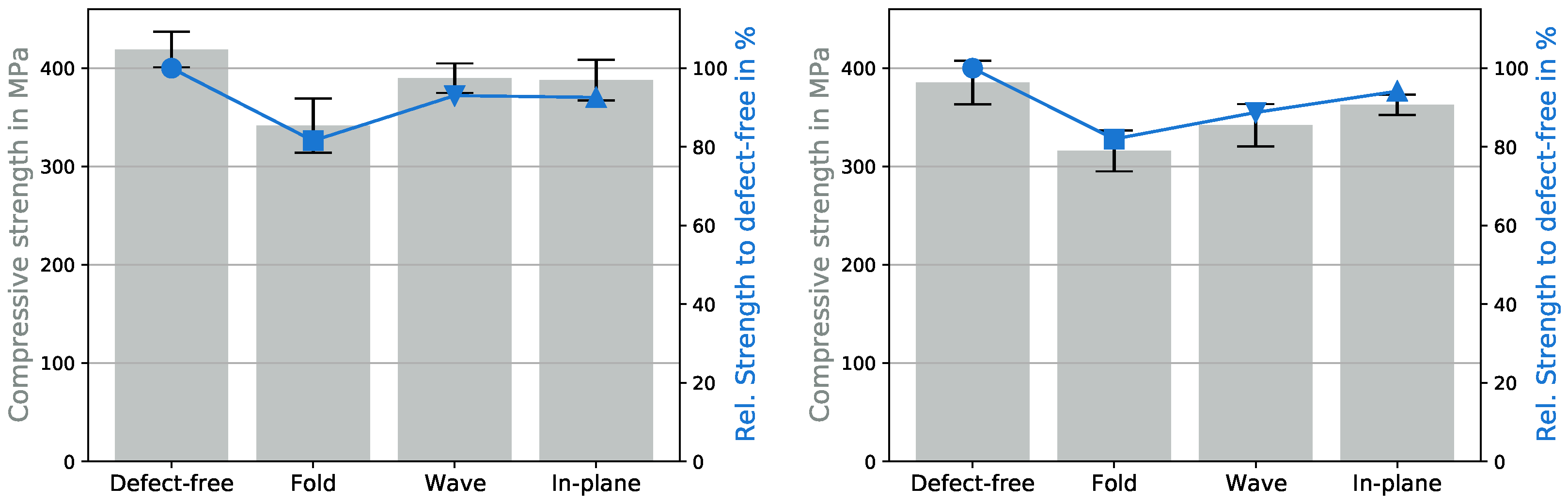
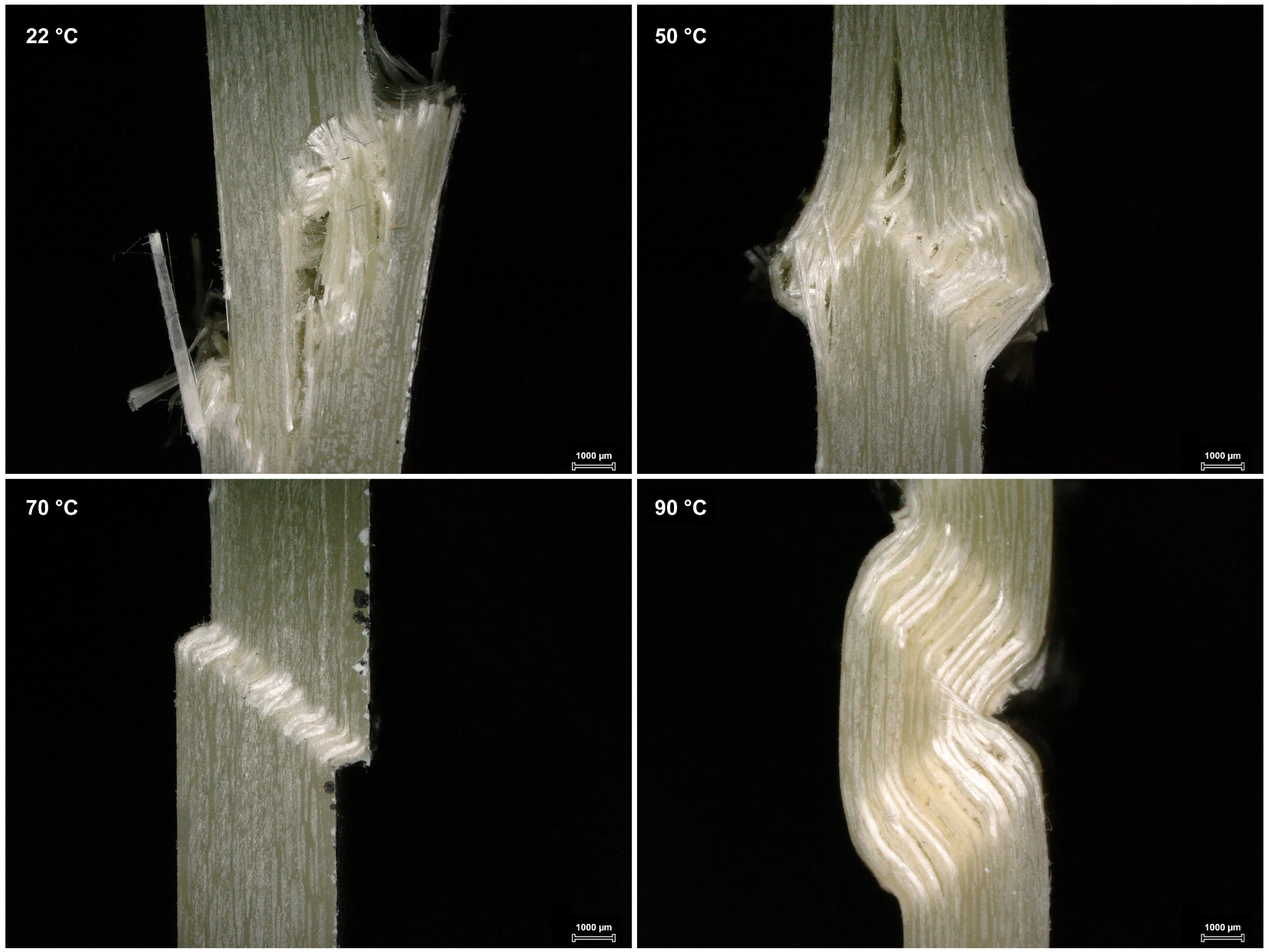
3.1. Damage Behavior Due to Defects
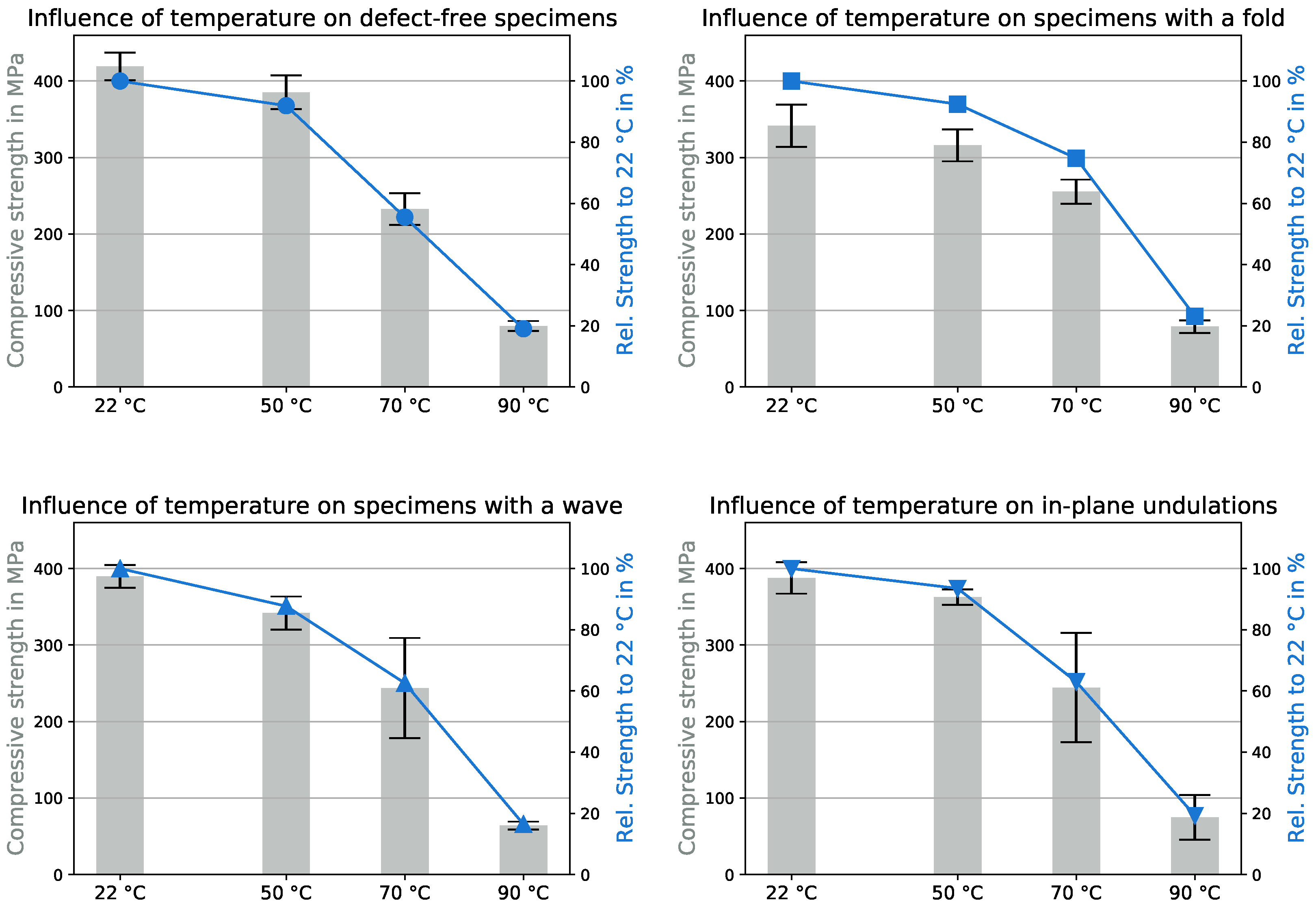
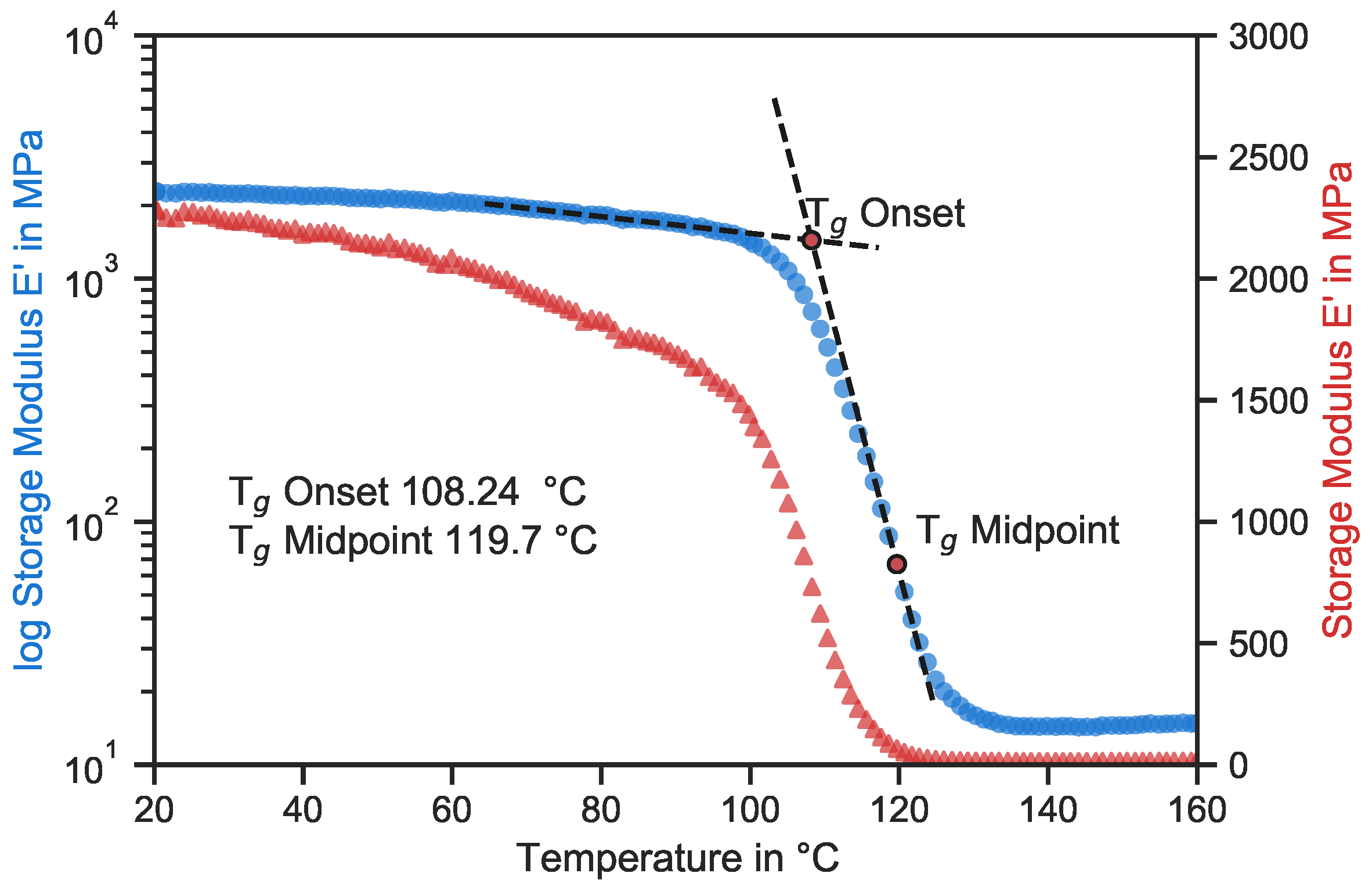
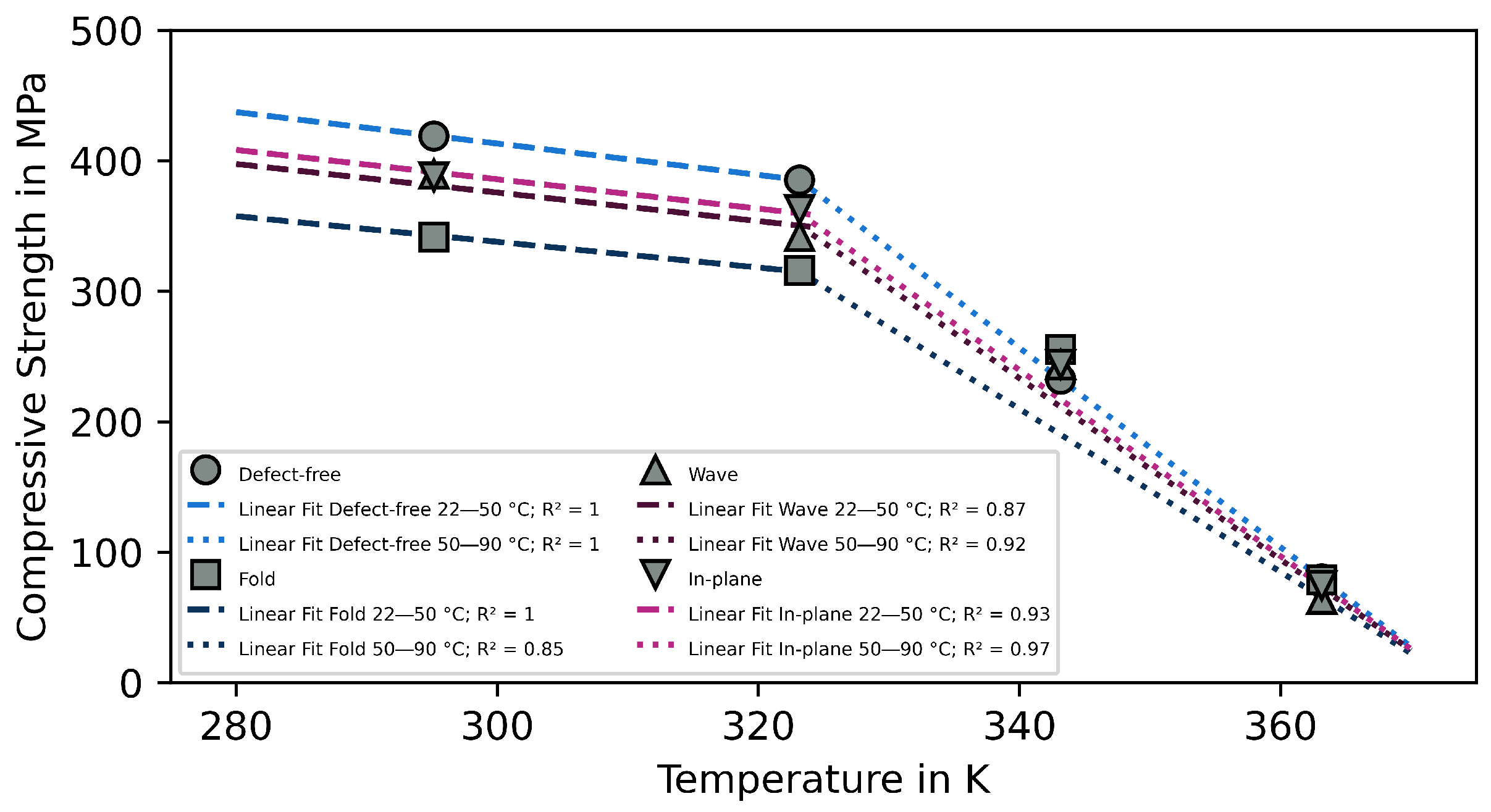
3.2. Influence of Temperature
3.3. Numerical Description
4. Conclusions
- (1)
- Defects had a significant impact on the mechanical behavior of GFRP, causing early failure, with a lower elongation and stresses. “Minor” misalignment led to a reduction in the UCS of at least 6%, already more than the relative amount of fibers contributed to the GFRP by this layer (4.3%). Whereby, the fold was particularly critical, leading to a reduction of 18%; therefore, this needs to be avoided in real-life applications;
- (2)
- Defects produce early failure but do not seem to change the occurring failure mode. The damage initiation and growth during the experiment were monitored via AE. The defect-free and defect-loaded specimens displayed a similar behavior, with only a little damage before failure. A deeper investigation of the damage initiation using microscopic images was not possible, due to the sudden failure and small amount of pre-damage of the specimens. Cyclic tests could provide a good opportunity to observe damage growth and the lifetime behavior of damage-loaded specimens;
- (3)
- In the context of environmental temperature, it is clear that temperature had a non-linear impact on the stiffness of the matrix, resulting in a non-linear effect on the UCSs of the tested specimens;
- (4)
- At higher temperatures, the mechanical behavior of the composites shifted from fiber-architecture-dominated to matrix-dominated. At 22 and 50 °C, the defects had a significant impact on the mechanical properties, but at 70 and 90 °C, the UCSs almost coincided. This was due to the fact that the less stiff matrix could no longer support the fibers against buckling and the maximum fiber strength had not been reached. This further stresses the importance of choosing a matrix material according to the environmental demands;
- (5)
- Describing the experimental data using a linear fit worked well for moderate temperatures, but due to the changing damage mode, it was difficult to make an accurate prediction at elevated temperatures.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| at 22 °C | at 50 °C | at 70 °C | at 90 °C | |
|---|---|---|---|---|
| Defect-free | MPa | MPa | MPa | MPa |
| Fold | MPa | MPa | MPa | MPa |
| Wave | MPa | MPa | MPa | MPa |
| In-plane | MPa | MPa | MPa | MPa |
References
- Pervaiz, M.; Panthapulakkal, S.; Sain, M.; Tjong, J. Emerging Trends in Automotive Lightweighting through Novel Composite Materials. Mater. Sci. Appl. 2016, 7, 26. [Google Scholar] [CrossRef] [Green Version]
- Wiser, R.; Rand, J.; Seel, J.; Beiter, P.; Baker, E.; Lantz, E.; Gilman, P. Expert elicitation survey predicts 37% to 49% declines in wind energy costs by 2050. Nat. Energy 2021, 6, 555–565. [Google Scholar] [CrossRef]
- Lawrence, J.M.; Hsiao, K.T.; Don, R.C.; Simacek, P.; Estrada, G.; Sozer, E.; Stadtfeld, H.C.; Advani, S.G. An approach to couple mold design and on-line control to manufacture complex composite parts by resin transfer molding. Compos. Part A Appl. Sci. Manuf. 2002, 33, 981–990. [Google Scholar] [CrossRef]
- Fasel, U.; Keidel, D.; Baumann, L.; Cavolina, G.; Eichenhofer, M.; Ermanni, P. Composite additive manufacturing of morphing aerospace structures. Manuf. Lett. 2020, 23, 85–88. [Google Scholar] [CrossRef]
- Luplow, T. Herausforderungen dickwandiger, duroplastischer Faser-Kunststoff-Verbunde in der Herstellung sowie mechanischen und zerstörungsfreien Prüfung—Ein Review. Z. Kunststofftechnik 2023, 1, 73–117. [Google Scholar] [CrossRef]
- Struzziero, G.; Teuwen, J. Residual Stresses Generation in Ultra-Thick Components for Wind Turbine Blades. Procedia CIRP 2019, 85, 8–12. [Google Scholar] [CrossRef]
- Thor, M.; Sause, M.G.R.; Hinterhölzl, R.M. Mechanisms of Origin and Classification of Out-of-Plane Fiber Waviness in Composite Materials—A Review. J. Compos. Sci. 2020, 4, 130. [Google Scholar] [CrossRef]
- Kunze, E.; Galkin, S.; Böhm, R.; Gude, M.; Kärger, L. The Impact of Draping Effects on the Stiffness and Failure Behavior of Unidirectional Non-Crimp Fabric Fiber Reinforced Composites. Materials 2020, 13, 2959. [Google Scholar] [CrossRef]
- Potter, K.; Khan, B.; Wisnom, M.; Bell, T.; Stevens, J. Variability, fibre waviness and misalignment in the determination of the properties of composite materials and structures. Compos. Part A Appl. Sci. Manuf. 2008, 39, 1343–1354. [Google Scholar] [CrossRef]
- Gower, M.R.L.; Shaw, R.M.; Broughton, W.R. Thick Composites: Part I: Mechanical Test Review, Part II: Cure Optimisation; NPL: Teddington, UK, 2008. [Google Scholar]
- Wisnom, M.R.; Atkinson, J.W. Fibre Waviness Generation and Measurement and Its Effect on Compressive Strength. J. Reinf. Plast. Compos. 2000, 19, 96–110. [Google Scholar] [CrossRef]
- Thor, M.; Mandel, U.; Nagler, M.; Maier, F.; Tauchner, J.; Sause, M.G.R.; Hinterhölzl, R.M. Numerical and experimental investigation of out-of-plane fiber waviness on the mechanical properties of composite materials. Int. J. Mater. Form. 2021, 14, 19–37. [Google Scholar] [CrossRef] [Green Version]
- Gigante, V.; Aliotta, L.; Phuong, V.T.; Coltelli, M.B.; Cinelli, P.; Lazzeri, A. Effects of waviness on fiber-length distribution and interfacial shear strength of natural fibers reinforced composites. Compos. Sci. Technol. 2017, 152, 129–138. [Google Scholar] [CrossRef]
- O’Donnell, J.; Chalivendra, V.; Hall, A.; Haile, M.; Nataraj, L.; Coatney, M.; Kim, Y. Electrical and shear constitutive response of conductive glass fibre/epoxy composites. Plast. Rubber Compos. 2020, 49, 108–115. [Google Scholar] [CrossRef]
- Lee, J.; Soutis, C. A study on the compressive strength of thick carbon fibre–epoxy laminates. Compos. Sci. Technol. 2007, 67, 2015–2026. [Google Scholar] [CrossRef] [Green Version]
- Boyer, R.; Padmapriya, N. Aircraft Materials. In Reference Module in Materials Science and Materials Engineering; Hashmi, S., Ed.; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar] [CrossRef]
- Morales, C.N.; Claure, G.; Emparanza, A.R.; Nanni, A. Durability of GFRP reinforcing bars in seawater concrete. Constr. Build. Mater. 2021, 270, 121492. [Google Scholar] [CrossRef]
- Guo, R.; Xian, G.; Li, F.; Li, C.; Hong, B. Hygrothermal resistance of pultruded carbon, glass and carbon/glass hybrid fiber reinforced epoxy composites. Constr. Build. Mater. 2022, 315, 125710. [Google Scholar] [CrossRef]
- Xian, G.; Guo, R.; Li, C.; Hong, B. Mechanical properties of carbon/glass fiber reinforced polymer plates with sandwich structure exposed to freezing-thawing environment: Effects of water immersion, bending loading and fiber hybrid mode. Mech. Adv. Mater. Struct. 2023, 30, 814–834. [Google Scholar] [CrossRef]
- Budiansky, B.; Fleck, N.A. Compressive failure of fibre composites. J. Mech. Phys. Solids 1993, 41, 183–211. [Google Scholar] [CrossRef]
- Fiedler, B.; Hobbiebrunken, T.; Hojo, M.; Schulte, K. Influence of stress state and temperature on the strength of epoxy resins. In Proceedings of the 11th International Conference on Fracture 2005, ICF11, Turin, Italy, 20–25 March 2005; pp. 2271–2275. [Google Scholar]
- Gibhardt, D.; Buggisch, C.; Meyer, D.; Fiedler, B. Hygrothermal Aging History of Amine-Epoxy Resins: Effects on Thermo-Mechanical Properties. Front. Mater. 2022, 9, 64. [Google Scholar] [CrossRef]
- Wang, J.; Potter, K.D.; Hazra, K.; Wisnom, M.R. Experimental fabrication and characterization of out-of-plane fiber waviness in continuous fiber-reinforced composites. J. Compos. Mater. 2012, 46, 2041–2053. [Google Scholar] [CrossRef]
- Nartey, M.; Zhang, T.; Gong, B.; Wang, J.; Peng, S.; Wang, H.; Peng, H.X. Understanding the impact of fibre wrinkle architectures on composite laminates through tailored gaps and overlaps. Compos. Part B Eng. 2020, 196, 108097. [Google Scholar] [CrossRef]
- Joyce, P.J.; Kugler, D.; Moon, T.J. A technique for characterizing process-induced fiber waviness in unidirectional composite laminates-using optical microscopy. J. Compos. Mater. 1997, 31, 1694–1727. [Google Scholar] [CrossRef]
- Joyce, P.J.; Moon, T.J. Compression strength reduction in composites with in-plane fiber waviness. ASTM Spec. Tech. Publ. 1998, 1330, 76–96. [Google Scholar]
- Kulkarni, P.; Mali, K.D.; Singh, S. An overview of the formation of fibre waviness and its effect on the mechanical performance of fibre reinforced polymer composites. Compos. Part A Appl. Sci. Manuf. 2020, 137, 106013. [Google Scholar] [CrossRef]
- Hamstad, M.A. A review: Acoustic emission, a tool for composite-materials studies. Exp. Mech. 1986, 26, 7–13. [Google Scholar] [CrossRef]
- Gao, Y.; Wang, J.; Song, X.; Ding, H.; Wang, H.; Bi, Y.; Ke, Y. Investigation on the compressive mechanical properties of ultra-thick CFRP laminates. Int. J. Mech. Sci. 2023, 241, 107966. [Google Scholar] [CrossRef]
- Elhajjar, R.F.; Shams, S.S. Compression testing of continuous fiber reinforced polymer composites with out-of-plane fiber waviness and circular notches. Polym. Test. 2014, 35, 45–55. [Google Scholar] [CrossRef]
- Mandell, J.; Samborsky, D.; Wang, L. Effects of fiber waviness on composites for wind turbine blades. In International SAMPE Symposium and Exhibition; SAMPE: Covina, CA, USA, 2003. [Google Scholar]
- Adams, D.O.; Bell, S.J. Compression strength reductions in composite laminates due to multiple-layer waviness. Compos. Sci. Technol. 1995, 53, 207–212. [Google Scholar] [CrossRef]
- Wang, B.; Uda, N.; Ono, K.; Nagai, H. Effect of micro in-plane fiber waviness on compressive properties of unidirectional fabric composites. J. Compos. Mater. 2018, 52, 2065–2074. [Google Scholar] [CrossRef]
- Mukhopadhyay, S.; Jones, M.I.; Hallett, S.R. Compressive failure of laminates containing an embedded wrinkle; experimental and numerical study. Compos. Part A Appl. Sci. Manuf. 2015, 73, 132–142. [Google Scholar] [CrossRef] [Green Version]
- Nimbal, S.S.; Banker, M.M.; Roopa, A.; Varughese, B.; Sundaram, R. Effect of Gap Induced Waviness on Compressive Strength of Laminated Composites. Mater. Today Proc. 2017, 4, 8355–8369. [Google Scholar] [CrossRef]
- Wisnom, M.R. Analysis of Shear Instability in Compression Due to Fibre Waviness. J. Reinf. Plast. Compos. 1993, 12, 1171–1189. [Google Scholar] [CrossRef]
- Nelson, J.W.; Riddle, T.W.; Cairns, D.S. Effects of defects in composite wind turbine blades—Part 1: Characterization and mechanical testing. Wind Energy Sci. 2017, 2, 641–652. [Google Scholar] [CrossRef] [Green Version]
- Drummer, J.; Gibhardt, D.; Körbelin, J.; Fiedler, B. General influence of the environmental temperature on the matrix strength under tensile and compressive loading—A comprehensive study on high performance matrices. Compos. Sci. Technol. 2022, 230, 109486. [Google Scholar] [CrossRef]
- Khaneghahi, M.H.; Najafabadi, E.P.; Bazli, M.; Vatani Oskouei, A.; Zhao, X.L. The effect of elevated temperatures on the compressive section capacity of pultruded GFRP profiles. Constr. Build. Mater. 2020, 249, 118725. [Google Scholar] [CrossRef]
- Bai, Y.; Keller, T. Delamination and kink-band failure of pultruded GFRP laminates under elevated temperatures and compression. Compos. Struct. 2011, 93, 843–849. [Google Scholar] [CrossRef]
- Körbelin, J. Damage Tolerance of High-Performance Composites. Ph.D. Thesis, TUHH Universitätsbibliothek, Hamburg, Germany, 2022. [Google Scholar]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Drummer, J.; Tafesh, F.; Fiedler, B. Effect of Fiber Misalignment and Environmental Temperature on the Compressive Behavior of Fiber Composites. Polymers 2023, 15, 2833. https://doi.org/10.3390/polym15132833
Drummer J, Tafesh F, Fiedler B. Effect of Fiber Misalignment and Environmental Temperature on the Compressive Behavior of Fiber Composites. Polymers. 2023; 15(13):2833. https://doi.org/10.3390/polym15132833
Chicago/Turabian StyleDrummer, Jonas, Felwa Tafesh, and Bodo Fiedler. 2023. "Effect of Fiber Misalignment and Environmental Temperature on the Compressive Behavior of Fiber Composites" Polymers 15, no. 13: 2833. https://doi.org/10.3390/polym15132833
APA StyleDrummer, J., Tafesh, F., & Fiedler, B. (2023). Effect of Fiber Misalignment and Environmental Temperature on the Compressive Behavior of Fiber Composites. Polymers, 15(13), 2833. https://doi.org/10.3390/polym15132833