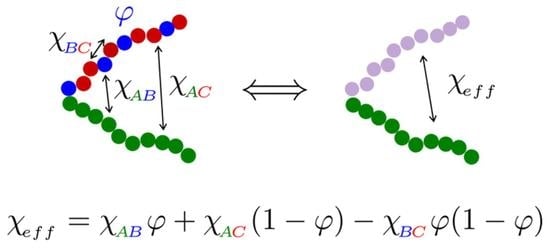
Effective Interaction between Homo- and Heteropolymer Block of Poly(n-butyl acrylate)-b-poly(methyl methacrylate-r-styrene) Diblock Copolymers
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
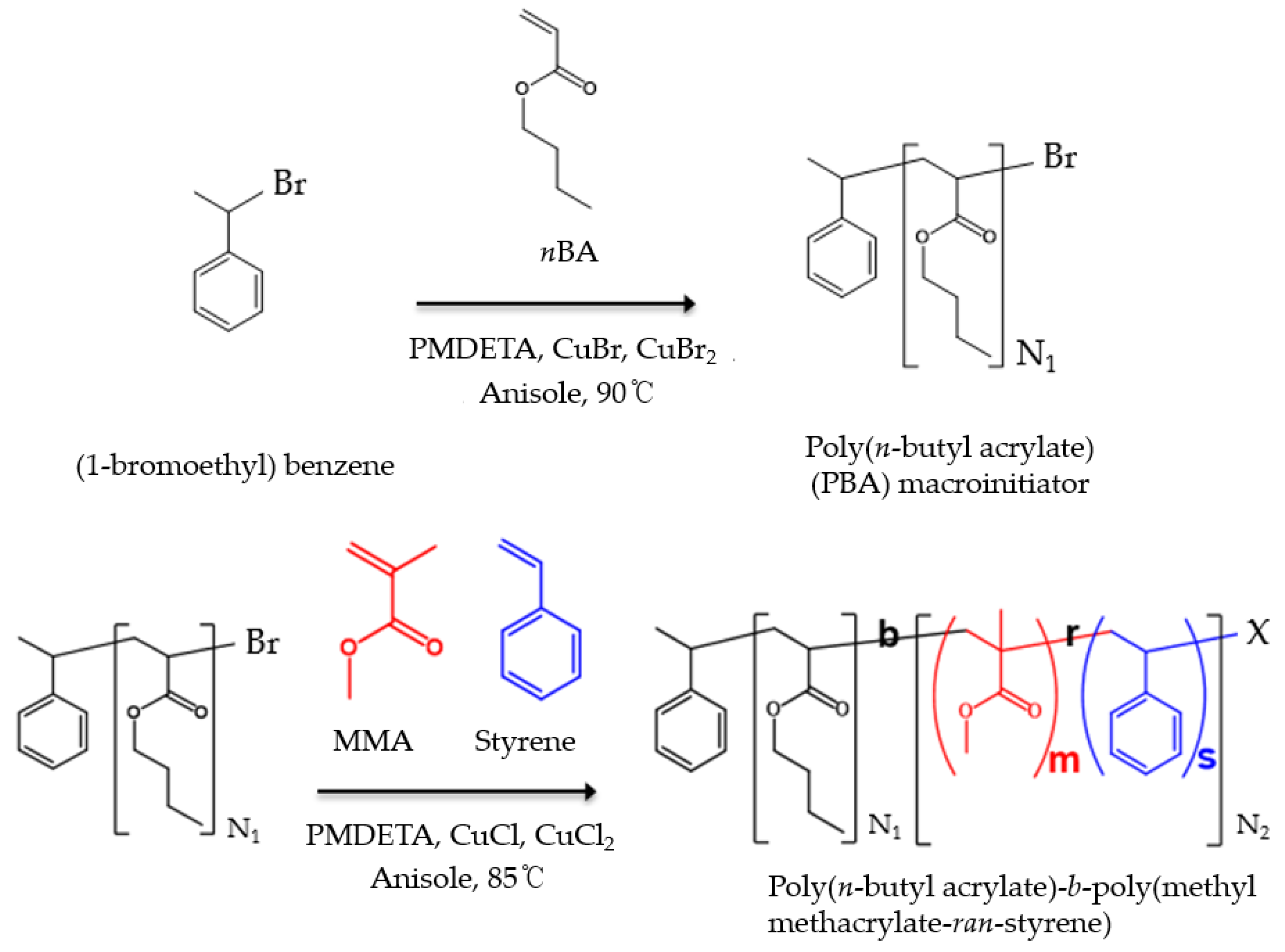
2.2. ATRP Synthesis
2.2.1. ATRP Synthesis of PBA Macroinitiator
2.2.2. ATRP Synthesis of PBA-b-P(MMA-r-S) Diblock Copolymer
2.2.3. Analytical Techniques
2.3. SAXS Measurements
2.4. Characterization of Diblock Copolymer
3. Results
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Braunecker, W.A.; Matyjaszewski, K. Controlled/living Radical Polymerization: Features, Developments, and Perspectives. Prog. Polym. Sci. 2007, 32, 93–146. [Google Scholar] [CrossRef]
- Tong, J.D.; Moineau, G.; Leclere, P.; Brédas, J.L.; Lazzaroni, R.; Jérôme, R. Synthesis, Morphology, and Mechanical Properties of Poly(methyl methacrylate)-b-poly(n-butyl acrylate)-b-poly(methyl methacrylate) Triblocks: Ligated Anionic Polymeri-zation vs Atom Transfer Radical Polymerization. Macromolecules 2000, 33, 470–479. [Google Scholar] [CrossRef]
- Destarac, M. Controlled Radical Polymerization: Industrial Stakes, Obstacles and Achievements. Macromol. React. Eng. 2010, 4, 165–179. [Google Scholar] [CrossRef]
- Holden, G.; Bishop, E.; Legge, N.R. Thermoplastic Elastomers. J. Polym. Sci. Part C Polym. Symp. 1969, 26, 37–57. [Google Scholar] [CrossRef]
- Holden, G.L.; Legge, N.R.; Quirk, R.P.; Schroeder, H.E. Thermoplastic Elastomers; Hanser: Munich, Germany, 1996. [Google Scholar]
- Fetters, L.J.; Morton, M. Synthesis and Properties of Block Polymers. I. Poly(α-methyl styrene)-b-polyisoprene-b-poly(α-methylstyrene). Macromolecules 1969, 2, 453–458. [Google Scholar] [CrossRef]
- Meng, S.; Kuchanov, S.I.; Xua, J.; Kyu, T. Collaborative Studies of Thermo-Oxidative Degradation of Styrene–Isoprene Diblock Copolymer. Polymer 2005, 46, 5580–5587. [Google Scholar] [CrossRef]
- Munteanu, S.B.; Brebu, M.; Vasile, C. Thermal and Thermo-Oxidative Behaviour of Butadiene-Styrene Copolymers with Different Architectures. Polym. Degrad. Stab. 2005, 89, 501–512. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, A.; Zhou, T.; Cao, X.; Xie, Z. A Study on Thermal Oxidation Mechanism of Styrene-Butadiene-Styrene Block Copolymer (SBS). Polym. Degrad. Stab. 2007, 92, 1682–1691. [Google Scholar] [CrossRef]
- Matyjaszewski, K. Atom Transfer Radical Polymerization (ATRP): Current Status and Future Perspectives. Macromolecules 2012, 45, 4015–4039. [Google Scholar] [CrossRef]
- Shipp, D.A.; Wang, J.L.; Matyjaszewski, K. Synthesis of Acrylate and Methacrylate Block Copolymers Using Atom Transfer Radical Polymerization. Macromolecules 1998, 31, 8005–8008. [Google Scholar] [CrossRef]
- Moineau, C.; Minet, M.; Teyssié, P.; Jérôme, R. Synthesis and Characterization of Poly(methyl methacrylate)-block-poly(n-butyl acrylate)-block-poly(methyl methacrylate) Copolymers by Two-Step Controlled Radical Polymerization (ATRP) Catalyzed by NiBr2(PPh3)2, 1. Macromolecules 1999, 32, 8277–8282. [Google Scholar] [CrossRef]
- Garcia, M.F.; de la Fuente, J.L.; Fernandez-Sanz, M.; Madruga, E.L. The Importance of Solvent Polar Character on the Synthesis of PMMA-b-PBA Block Copolymers by Atom Transfer Radical Polymerization. Polymer 2001, 42, 9405–9412. [Google Scholar] [CrossRef]
- Guillaneuf, Y.; Gigmes, D.; Marque, S.R.; Astolfi, P.; Greci, L.; Tordo, P.; Bertin, D. First Effective Nitroxide-Mediated Polymerization of Methyl Methacrylate. Macromolecules 2007, 40, 3108–3114. [Google Scholar] [CrossRef]
- Tran, T.A.; Leonardi, F.; Bourrigaud, S.; Gerard, P.; Derail, C. All Acrylic Block Copolymers Based on Poly(methyl methacrylate) and Poly(butyl acrylate): A Link between the Physico-Chemical Properties and the Mechanical Behaviour on Impact Tests. Polym. Test. 2008, 27, 945–950. [Google Scholar] [CrossRef]
- Lu, W.; Wang, Y.; Wang, W.; Cheng, S.; Zhu, J.; Xu, Y.; Hong, K.; Kang, N.-G.; Mays, J. All Acrylic-Based Thermoplastic Elastomers with High Upper Service Temperature and Superior Mechanical Properties. Polym. Chem. 2017, 8, 5741–5748. [Google Scholar] [CrossRef]
- Atkinson, R.L.; Monaghan, O.R.; Elsmore, M.T.; Topham, P.D.; Toolan, D.T.; Derry, M.J.; Taresco, V.; Stockman, R.A.; De Focatiis, D.S.; Irvine, D.J. RAFT Polymerisation of Renewable Terpene (Netha) Acrylates and the Convergent Synthesis of Methacrylate–Acrylate–Methacrylate Triblock Copolymers. Polym. Chem. 2021, 12, 3177–3189. [Google Scholar] [CrossRef]
- Bensabeh, N.; Jiménez-Alesanco, A.; Liblikas, I.; Ronda, J.C.; Cádiz, V.; Galià, M.; Vares, L.; Abián, O.; Lligadas, G. Biosourced All-Acrylic ABA Block Copolymers with Lactic Acid-Based Soft Phase. Molecules 2020, 25, 5740. [Google Scholar] [CrossRef]
- Atkinson, R.L.; Elsmore, M.; Smith, S.; Reynolds-Green, M.; Topham, P.D.; Toolan, D.T.; Derry, M.J.; Monaghan, O.; Taresco, V.; Irvine, D.J. Sustainable ABA Triblock Methacrylate Copolymers Incorporating Both High and Low Tg Terpene-Derived Monomers. Eur. Polym. J. 2022, 179, 111567–111576. [Google Scholar] [CrossRef]
- Awasthi, P.; Banerjee, S.S. Fused Deposition Modeling of Thermoplastic Elastomeric Materials: Challenges and Opportunities. Addit. Manuf. 2021, 46, 102177–102194. [Google Scholar] [CrossRef]
- Kim, H.J.; Jin, K.; Shim, J.; Dean, W.; Hillmyer, M.A.; Ellison, C.J. Sustainable Triblock Copolymers as Tunable and Degradable Pressure Sensitive Adhesives. ACS Sustain. Chem. Eng. 2020, 8, 12036–12044. [Google Scholar] [CrossRef]
- Dufour, B.; Koynov, K.; Pakula, T.; Matyjaszewski, K. PBA–PMMA 3-Arm Star Block Copolymer Thermoplastic Elastomers. Macromol. Chem. Phys. 2008, 209, 1686–1693. [Google Scholar] [CrossRef]
- Nese, A.; Mosnacek, J.; Juhari, A.; Yoon, J.A.; Koynov, K.; Kowalewski, T.; Matyjaszewski, K. Synthesis, Characterization, and Properties of Starlike Poly(n-butyl acrylate)-b-poly(methyl methacrylate) Block Copolymers. Macromolecules 2010, 43, 1227–1235. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Z.; Wang, X.; Wang, Z. The Synthesis of Bottlebrush Cellulose-Graft-Diblock Copolymer Elastomers via Atom Transfer Radical Polymerization Utilizing a Halide Exchange Technique. Chem. Commun. 2019, 55, 13904–13907. [Google Scholar] [CrossRef] [PubMed]
- Milner, S.T.; Witten, T.A. Bridging Attraction by Telechelic Polymers. Macromolecules 1992, 25, 5495–5503. [Google Scholar] [CrossRef]
- Lee, S.I.; Seo, M.G.; Huh, J.; Paik, H.J. Small-Angle X-ray Scattering Analysis on the Estimation of Interaction Parameter of Poly(n-butyl acrylate)-b-Poly(methyl methacrylate). Polymers 2022, 14, 5567. [Google Scholar] [CrossRef] [PubMed]
- Anastasiadis, S.H.; Gancarz, I.; Koberstein, J.T. Interfacial Tension of Immiscible Polymer Blends: Temperature and Molecular Weight Dependence. Macromolecules 1988, 21, 2980–2987. [Google Scholar] [CrossRef]
- Hewel, M.; Ruland, W. Microphase Separation Transition in Block Copolymer Melts. Makromol. Chem. Macromol. Symp. 1986, 4, 197–202. [Google Scholar] [CrossRef]
- Mori, K.; Hasegawa, H.; Hashimoto, T. Small-Angle X-Ray Scattering from Bulk Block Polymers in Disordered State. Estimation of χ-Values from Accidental Thermal Fluctuations. Polym. J. 1985, 17, 799–806. [Google Scholar] [CrossRef] [Green Version]
- Kim, K.W.; Kim, J.; Yun, Y.D.; Ahn, H.; Min, B.; Kim, N.H.; Rah, S.; Kim, H.Y.; Lee, C.S.; Seo, I.D. Small-Angle X-ray Scattering Beamline BL4C SAXS at Pohang Light Source II. Biodesign 2017, 5, 24–29. [Google Scholar]
- Rho, Y.; Kim, J.H.; Min, B.; Jin, K.S. Chemically Denatured Structures of Porcine Pepsin Using Small-Angle X-ray scattering. Polymers 2019, 11, 2104. [Google Scholar] [CrossRef] [Green Version]
- Ahn, S.; Seo, Y.; Kim, J.K.; Duan, C.; Zhang, L.; Li, W. Cylindrical to Lamellar Microdomain Transition upon Heating for a Linear Tetrablock Copolymer with Upper Critical Ordering Transition. Macromolecules 2019, 52, 9039–9044. [Google Scholar] [CrossRef]
- Bodycomb, J.; Yamaguchi, D.; Hashimoto, T. Observation of a Discontinuity in the Value of Im-1 at the Order-Disorder Tran-sition in Diblock Copolymer/Hornopolymer and Diblock Copolymer/Diblock Copolymer Blends. Polym. J. 1996, 28, 821–824. [Google Scholar] [CrossRef] [Green Version]
- Korobeinichev, O.P.; Paletsky, A.A.; Gonchikzhapov, M.B.; Glaznev, R.K.; Gerasimov, I.E.; Naganovsky, Y.K.; Shundrina, I.K.; Snegirev, A.Y.; Vinu, R. Kinetics of Thermal Decomposition of PMMA at Different Heating Rates and in a Wide Temperature Range. Thermochim. Acta. 2019, 671, 17–25. [Google Scholar] [CrossRef]
- Nikolaidis, A.K.; Achilias, D.S. Thermal Degradation Kinetics and Viscoelastic Behavior of Poly(Methyl Methacrylate)/ Organomodified Montmorillonite Nanocomposites Prepared via In Situ Bulk Radical Polymerization. Polymers 2018, 10, 491. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Teodorescu, M.; Mîndru, C.; Drăghici, C. Synthesis of poly(methyl methacrylate-co-styrene)-block-polysulfide-block-poly(methyl methacrylate-co-styrene) copolymers by free radical polymerization combined with oxidative coupling. Eur. Polym. J. 2006, 42, 2247–2253. [Google Scholar] [CrossRef]
- Roos, S.G.; Müller, A.H.; Matyjaszewski, K. Copolymerization of n-Butyl Acrylate with Methyl Methacrylate and PMMA Macromonomers: Comparison of Reactivity Ratios in Conventional and Atom Transfer Radical Copolymerization. Macromolecules 1999, 32, 8331–8335. [Google Scholar] [CrossRef] [Green Version]
- Bates, F.S.; Rosedale, J.H.; Fredrickson, G.H. Fluctuation Effects in a Symmetric Diblock Copolymer near the Order–Disorder Transition. J. Chem. Phys. 1990, 92, 6255–6270. [Google Scholar] [CrossRef]
- Abu-Sharkh, B.; AlSunaidi, A. Morphology and Conformation Analysis of Self-Assembled Triblock Copolymer Melts. Macromol. Theory Simul. 2006, 15, 507–515. [Google Scholar] [CrossRef]
- Sakamoto, N.; Hashimoto, T. Order-Disorder Transition of Low Molecular Weight Polystyrene-block-polyisoprene: 1. SAXS Analysis of Two Characteristic Temperatures. Macromolecules 1995, 28, 6825–6834. [Google Scholar] [CrossRef]
- Schwahn, D.; Willner, L. Phase Behavior and Flory-Huggins Interaction Parameter of Binary Polybutadiene Copolymer Mixtures with Different Vinyl Content and Molar Volume. Macromolecules 2002, 35, 239–247. [Google Scholar] [CrossRef] [Green Version]
- Russell, T.P.; Hjelm, R.P., Jr.; Seeger, P.A. Temperature Dependence of the Interaction Parameter of Polystyrene and Poly(methy1 methacrylate). Macromolecules 1990, 23, 890–893. [Google Scholar] [CrossRef]
- Zhao, Y.; Sivaniah, E.; Hashimoto, T. SAXS Analysis of the Order-Disorder Transition and the Interaction Parameter of Polystyrene-block-poly(methyl methacrylate). Macromolecules 2008, 41, 9948–9951. [Google Scholar] [CrossRef]
- Paul, D.R.; Barlow, J.W. A Binary Interaction Model for Miscibility of Copolymers in Blends. Polymer 1984, 25, 487–494. [Google Scholar] [CrossRef]
- Kambour, R.P.; Bendler, J.T.; Bopp, R.C. Phase Behavior of Polystyrene, Poly(2,6-Dimethyl-l,4-Phenylene Oxide), and Their Brominated Derivatives. Macromolecules 1983, 16, 753–757. [Google Scholar] [CrossRef]
- ten Brinke, G.; Challa, G.; Karasz, F.E.; MacKnight, W.J. Phase Behavior in Copolymer Blends: Poly(2,6-Dimethyl-1,4-Phenylene Oxide) and Halogen-Substituted Styrene Copolymers. Macromolecules 1983, 16, 1827–1832. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.; Nealey, P.F.; Bates, F.S. Decoupling Bulk Thermodynamics and Wetting Characteristics of Block Copolymer Thin Films. ACS Macro Lett. 2012, 1, 11–14. [Google Scholar] [CrossRef]
- Ren, Y.; Lodge, T.P.; Hillmyer, M.A. Synthesis, Characterization, and Interaction Strengths of Difluorocarbene-Modified Polystyrene-Polyisoprene Block Copolymers. Macromolecules 2000, 33, 866–876. [Google Scholar] [CrossRef]
- Loo, W.S.; Feng, H.; Ferron, T.J.; Ruiz, R.; Sunday, D.F.; Nealey, P.F. Determining Structure and Thermodynamics of A-b-(B-r-C) Copolymers. ACS Macro Lett. 2023, 12, 118–124. [Google Scholar] [CrossRef]

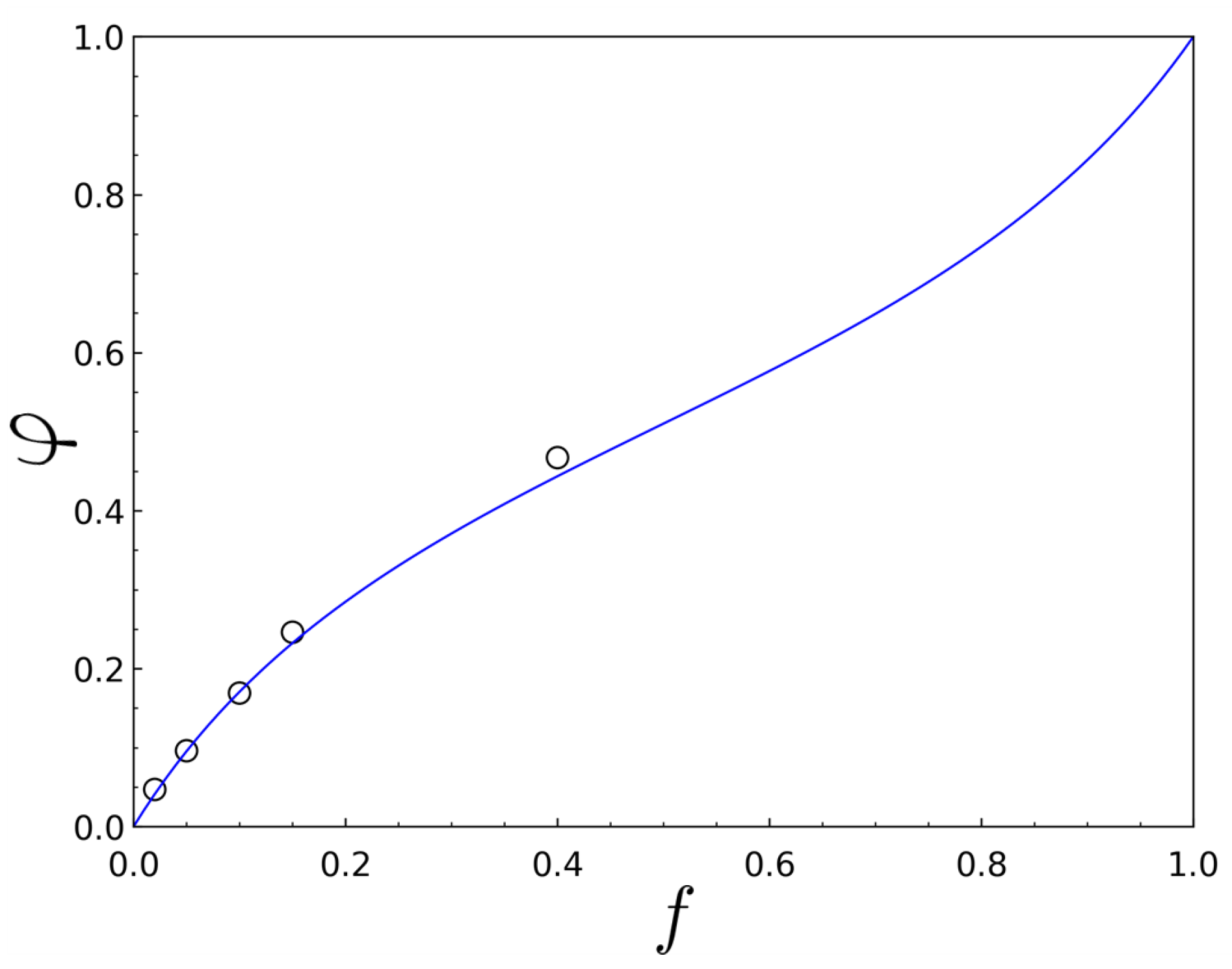



| Diblock Samples | Code | (kg/mol) (PDI) of PBA | (kg/mol) (PDI) of Diblock | |
|---|---|---|---|---|
| PBA-b-PMMA | BM | 12.5 (1.08) | 23.5 (1.15) | 0.0 |
| PBA-b-P(MMA-r-S 4.7) | B(MS | 12.5 (1.08) | 42.5 (1.15) | 0.047 |
| PBA-b-P(MMA-r-S 9.6) | B(MS | 12.5 (1.08) | 31.3 (1.13) | 0.096 |
| PBA-b-P(MMA-r-S 16.9) | B(MS | 12.5 (1.08) | 39.5 (1.16) | 0.169 |
| PBA-b-P(MMA-r-S 24.6) | B(MS | 12.5 (1.08) | 30.9 (1.17) | 0.246 |
| PBA-b-P(MMA-r-S 46.7) | B(MS | 17.1 (1.09) | 43.7 (1.17) | 0.467 |
| PBA-b-PMMA | BS | 28.0 (1.05) | 42.0 (1.06) | 1.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, S.-I.; Seo, M.-G.; Huh, J.; Paik, H.-j. Effective Interaction between Homo- and Heteropolymer Block of Poly(n-butyl acrylate)-b-poly(methyl methacrylate-r-styrene) Diblock Copolymers. Polymers 2023, 15, 2915. https://doi.org/10.3390/polym15132915
Lee S-I, Seo M-G, Huh J, Paik H-j. Effective Interaction between Homo- and Heteropolymer Block of Poly(n-butyl acrylate)-b-poly(methyl methacrylate-r-styrene) Diblock Copolymers. Polymers. 2023; 15(13):2915. https://doi.org/10.3390/polym15132915
Chicago/Turabian StyleLee, Sang-In, Min-Guk Seo, June Huh, and Hyun-jong Paik. 2023. "Effective Interaction between Homo- and Heteropolymer Block of Poly(n-butyl acrylate)-b-poly(methyl methacrylate-r-styrene) Diblock Copolymers" Polymers 15, no. 13: 2915. https://doi.org/10.3390/polym15132915
APA StyleLee, S. -I., Seo, M. -G., Huh, J., & Paik, H. -j. (2023). Effective Interaction between Homo- and Heteropolymer Block of Poly(n-butyl acrylate)-b-poly(methyl methacrylate-r-styrene) Diblock Copolymers. Polymers, 15(13), 2915. https://doi.org/10.3390/polym15132915