Comprehensive Kinetic Study of PET Pyrolysis Using TGA
Abstract
:1. Introduction
2. Materials and Procedures
2.1. The Proximate and Ultimate Analyses
2.2. TGA of PET
2.3. Derivation of the Kinetic Equations
2.4. Thermodynamic Parameter Analysis of PET Pyrolysis
3. Results and Discussion
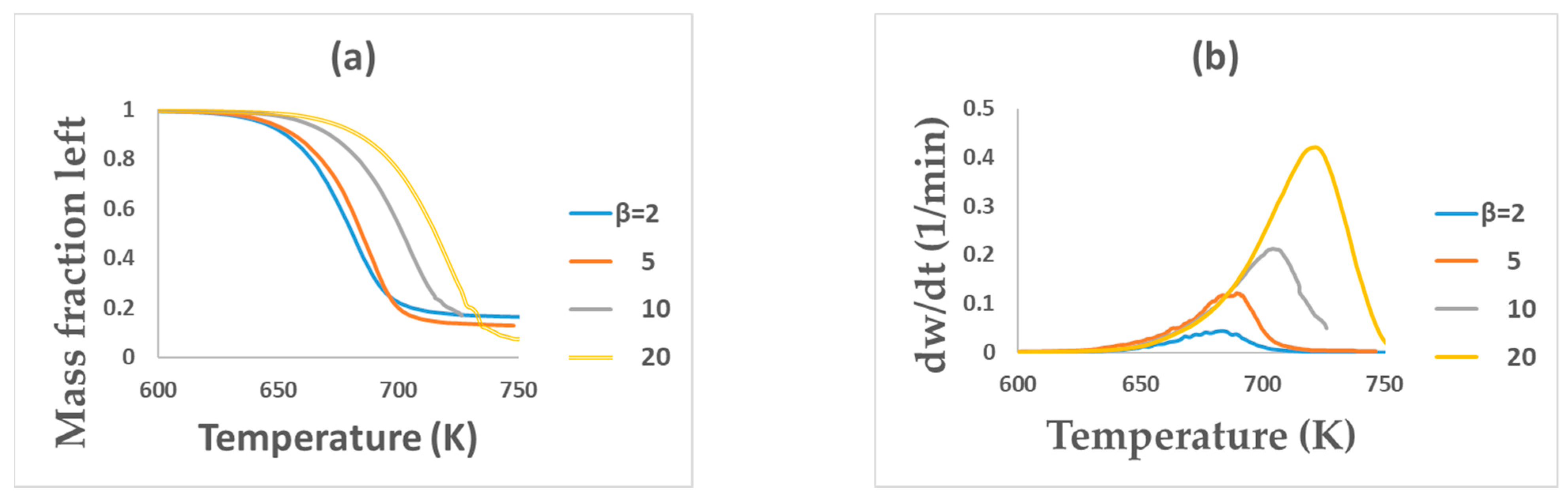
3.1. TGA of PET
3.2. Determination of Kinetic Parameters by Model-Free Methods
3.3. Determining the Kinetic Parameters by Model-Fitting Methods
3.4. Thermodynamic Parameter Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Martín-Gullón, I.; Esperanza, M.; Font, R. Kinetic model for the pyrolysis and combustion of poly-(ethylene terephthalate) (PET). J. Anal. Appl. Pyrolysis 2001, 58, 635–650. [Google Scholar] [CrossRef]
- Diaz-Silvarrey, L.S.; McMahon, A.; Phan, A.N. Benzoic acid recovery via waste poly(ethylene terephthalate) (PET) catalytic pyrolysis using sulphated zirconia catalyst. J. Anal. Appl. Pyrolysis 2018, 134, 621–631. [Google Scholar] [CrossRef] [Green Version]
- Moltó, J.; Font, R.; Conesa, J.A. Kinetic model of the decomposition of a PET fibre cloth in an inert and air environment. J. Anal. Appl. Pyrolysis 2007, 79, 289–296. [Google Scholar] [CrossRef]
- Çepelioğullar, Ö.; Pütün, A. Thermal and kinetic behaviors of biomass and plastic wastes in co-pyrolysis. Energy Convers. Manag. 2013, 75, 263–270. [Google Scholar] [CrossRef]
- Yang, J.; Miranda, R.; Roy, C. Using the DTG curve fitting method to determine the apparent kinetic parameters of thermal decomposition of polymers. Polym. Degrad. Stab. 2001, 73, 455–461. [Google Scholar] [CrossRef]
- Saha, B.; Maiti, A.K.; Ghoshal, A.K. Model-free method for isothermal and non-isothermal decomposition kinetics analysis of PET sample. Thermochim. Acta 2006, 444, 46–52. [Google Scholar] [CrossRef]
- Brems, A.; Baeyens, J.; Vandecasteele, C.; Dewil, R. Polymeric Cracking of Waste Polyethylene Terephthalate to Chemicals and Energy. Technol. Pap. 2011, 61, 721–731. [Google Scholar] [CrossRef]
- Diaz Silvarrey, L.S.; Phan, A.N. Kinetic study of municipal plastic waste. Int. J. Hydrogen Energy 2016, 41, 16352–16364. [Google Scholar] [CrossRef] [Green Version]
- Miandad, R.; Barakat, M.A.; Rehan, M.; Aburiazaiza, A.S.; Ismail, I.M.I.; Nizami, A.S. Plastic waste to liquid oil through catalytic pyrolysis using natural and synthetic zeolite catalysts. Waste Manag. 2017, 69, 66–78. [Google Scholar] [CrossRef]
- Dimitrov, N.; Krehula, L.K.; Siročić, A.P.; Hrnjak-Murgić, Z. Analysis of recycled PET bottles products by pyrolysis-gas chromatography. Polym. Degrad. Stab. 2013, 98, 972–979. [Google Scholar] [CrossRef]
- Chandrasekaran, S.R.; Kunwar, B.; Moser, B.R.; Rajagopalan, N.; Sharma, B.K. Catalytic thermal cracking of postconsumer waste plastics to fuels. 1. Kinetics and optimization. Energy Fuels 2015, 29, 6068–6077. [Google Scholar] [CrossRef]
- Ganeshan, G.; Shadangi, K.P.; Mohanty, K. Degradation Kinetic Study of Pyrolysis and Co-Pyrolysis of Biomass with Polyethylene Terephthalate (PET) Using Coats–Redfern Method. J. Therm. Anal. Calorim. 2018, 131, 1803–1816. [Google Scholar] [CrossRef]
- Osman, A.I.; Farrell, C.; Al-Muhtaseb, A.H.; Al-Fatesh, A.S.; Harrison, J.; Rooney, D.W. Pyrolysis kinetic modelling of abundant plastic waste (PET) and in-situ emission monitoring. Environ. Sci. Eur. 2020, 32, 112. [Google Scholar] [CrossRef]
- Das, P.; Tiwari, P. Thermal degradation study of waste polyethylene terephthalate (PET) under inert and oxidative environments. Thermochim. Acta 2019, 679, 178340. [Google Scholar] [CrossRef]
- Mishra, R.K.; Sahoo1, A.; Mohanty, K. Pyrolysis kinetics and synergistic effect in co-pyrolysis of Samanea saman seeds and polyethylene terephthalate using thermogravimetric analyser. Bioresour. Technol. 2019, 289, 121608. [Google Scholar] [CrossRef]
- Chowdhury, T.; Wang, Q. Study on Thermal Degradation Processes of Polyethylene Terephthalate Microplastics Using the Kinetics and Artificial Neural Networks Models. Processes 2023, 11, 496. [Google Scholar] [CrossRef]
- Dubdub, I.; Al-Yaari, M. Pyrolysis of mixed plastic waste: I. Kinetic study. Materials 2020, 13, 4912. [Google Scholar] [CrossRef] [PubMed]
- Dubdub, I.; Alhulaybi, Z. Catalytic Pyrolysis of PET Polymer Using Nonisothermal Thermogravimetric Analysis Data: Kinetics and Artificial Neural Networks Studies. Polymers 2023, 15, 70. [Google Scholar] [CrossRef]
- Koga, N.; Vyazovkin, S.; Burnham, A.K.; Favergeon, L.; Muravyev, N.V.; Perez-Maqueda, L.A.; Saggese, C.; Sánchez-Jiménez, P.E. ICTAC Kinetics Committee Recommendations for Analysis of Thermal Decomposition Kinetics. Thermochim. Acta 2023, 719, 179384. [Google Scholar] [CrossRef]
- Aboulkas, A.; El Harfi, K.; El Bouadili, A. Thermal degradation behaviors of polyethylene and polypropylene. Part I Pyrolysis kinetics and mechanisms. Energy Convers. Manag. 2010, 51, 1363–1369. [Google Scholar] [CrossRef]
- Dubdub, I. Kinetics Study of Polypropylene Pyrolysis by Non-Isothermal Thermogravimetric Analysis. Materials 2023, 16, 584. [Google Scholar] [CrossRef] [PubMed]
- Dhyani, V.; Kumar, J.; Bhaskar, T. Thermal Decomposition Kinetics of Sorghum Straw via Thermogravimetric Analysis. Bioresour. Technol. 2017, 245, 1122–1129. [Google Scholar] [CrossRef]
- Al-Salem, S.M.; Antelava, A.; Constantinou, A.; Manos, G.; Dutta, A. A review on thermal and catalytic pyrolysis of plastic solid waste (PSW). J. Environ. Manag. 2017, 197, 177–198. [Google Scholar] [CrossRef] [PubMed]
- Singh, R.K.; Ruj, B.; Sadhukhan, A.K.; Gupta, A. A TG-FTIR investigation on the co-pyrolysis of the waste HDPE, PP, PS and PET under high heating conditions. J. Energy Inst. 2020, 93, 1020–1035. [Google Scholar] [CrossRef]
- Damartzis, T.; Vamvuka, D.; Sfakiotakis, S.; Zabaniotou, A. Thermal degradation studies and kinetic modeling of cardoon (Cynara cardunculus) pyrolysis using thermogravimetric analysis (TGA). Bioresour. Technol. 2011, 102, 6230–6238. [Google Scholar] [CrossRef]
- Senneca, O.; Chirone, R.; Salatino, P. Oxidative pyrolysis of solid fuels. J. Anal. Appl. Pyrolysis 2004, 71, 959–970. [Google Scholar] [CrossRef]
- Girija, B.G.; Sailaja, R.R.N.; Madras, G. Thermal degradation and mechanical properties of PET blends. Polym. Degrad. Stab. 2005, 90, 147–153. [Google Scholar] [CrossRef]
- Enyoh, C.E.; Wang, Q. Combined Experimental and Molecular Dynamics Removal Processes of Contaminant Phenol from Simulated Wastewater by Polyethylene Terephthalate Microplastics. Environ. Technol. 2022, 1–20. [Google Scholar] [CrossRef]
- Xu, Y.; Chen, B. Investigation of Thermodynamic Parameters in the Pyrolysis Conversion of Biomass and Manure to Biochars Using Thermogravimetric Analysis. Bioresour. Technol. 2013, 146, 485–493. [Google Scholar] [CrossRef]





| Proximate Analysis, wt% | Ultimate Analysis, wt% | |||||
|---|---|---|---|---|---|---|
| Moisture | Volatile | Ash | C | H | N | O |
| 0.523 | 88.231 | 11.246 | 64.256 | 4.367 | 0 | 31.377 |
| Method | Equation | Integral (I) or Differential (D) | Plot | |
|---|---|---|---|---|
| FR | (3) | D | ||
| FWO | (4) | I | ||
| KAS | (5) | I | ||
| STK | (6) | I | ||
| DAEM | (7) | I | ||
| Method | Equation | |
|---|---|---|
| CR | (8) | |
| Criado | (9) | |
| Reaction Mechanism | Code | ||
|---|---|---|---|
| Reaction order models—first order | F1 | 1 − α | |
| Reaction order models—second order | F2 | ||
| Reaction order models—third order | F3 | ||
| Diffusion model—one dimension | D1 | ||
| Diffusion model—two dimensions | D2 | ||
| Diffusion model—three dimensions | D3 | ||
| Nucleation models—two dimensions | A2 | ||
| Nucleation models—three dimensions | A3 | ||
| Nucleation models—four dimensions | A4 | ||
| Geometrical contraction models—one dimension | R1 | 1 | |
| Geometrical contraction models—sphere | R2 | ||
| Geometrical contraction models—cylinder | R3 | ||
| Nucleation models—two-power law | P2 | ||
| Nucleation models—three-power law | P3 | ||
| Nucleation models—four-power law | P4 |
| Heating Rate K/min | This Work | Previous Work | References | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Onset (K) | Peak (K) | Final (K) | Mass Loss (%) | Onset (K) | Peak (K) | Final (K) | Mass Loss (%) | ||
| 2 | 620 | 680 | 690 | 80 | 623 | 667 | 694 | 100 | Osman et al. (2020) [13] |
| 5 | 650 | 685 | 710 | 85 | 658 623 | 700 673 | 723 733 | 80 80 | Das and Tiwari (2019) [14] Diaz Silvarrey and Phan (2016) [8] |
| 10 | 670 | 710 | 725 | 80 | 671 643 633 643 585 | 711 714 700 693 648 707 | 748 775 773 743 856 | 80 80 79.78 80 27.5 | Das and Tiwari (2019) [14] Yang et al. (2001) [5] Çepelioğullar and Pütün (2013) [4] Diaz Silvarrey and Phan (2016) [8] Mishra et al. (2019) [15] Chowdhury et al. (2023) [16] |
| 20 | 680 | 725 | 750 | 95 | 681 673 603 | 721 703 713 | 759 773 882 | 80 80 22.5 | Das and Tiwari (2019) [14] Diaz Silvarrey and Phan (2016) [8] Chowdhury et al. (2023) [16] |
| 30 | 661 | 672 716 | 878 | 27.5 | Mishra et al. (2019) [15] Chowdhury et al. (2023) [16] | ||||
| 40 | 690 698 693 | 733 748 723 | 783 798 803 | 80 82 80 | Das and Tiwari (2019) [14] Singh et al. (2020) [24] Diaz Silvarrey and Phan (2016) [8] | ||||
| 50 | 698 | 743 684 | 793 | 80 | Das and Tiwari (2019) [14] Mishra et al. (2019) [15] | ||||
| Conversion | FR | FWO | KAS | STK | DAEM | Average | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| E kJ mol−1 | R2 | E kJ mol−1 | R2 | E kJ mol−1 | R2 | E kJ mol−1 | R2 | E kJ mol−1 | R2 | E kJ mol−1 | R2 | |
| 0.1 | 213 | 0.8777 | 236 | 0.9005 | 225 | 0.8914 | 226 | 0.8918 | 225 | 0.8914 | 225 | 0.8899 |
| 0.2 | 214 | 0.8858 | 229 | 0.898 | 218 | 0.8882 | 218 | 0.8886 | 218 | 0.8882 | 219 | 0.8912 |
| 0.3 | 209 | 0.9033 | 227 | 0.9047 | 215 | 0.8952 | 216 | 0.8957 | 215 | 0.8952 | 216 | 0.8986 |
| 0.4 | 200 | 0.8421 | 224 | 0.9037 | 213 | 0.894 | 213 | 0.8944 | 213 | 0.894 | 213 | 0.8838 |
| 0.5 | 200 | 0.8342 | 221 | 0.8953 | 209 | 0.8846 | 210 | 0.895 | 209 | 0.8846 | 210 | 0.8727 |
| 0.6 | 204 | 0.8314 | 219 | 0.8848 | 207 | 0.8546 | 236 | 0.8551 | 236 | 0.8546 | 220 | 0.8571 |
| 0.7 | 199 | 0.7583 | 217 | 0.8725 | 205 | 0.8594 | 206 | 0.8599 | 205 | 0.8594 | 206 | 0.8340 |
| 0.8 | 190 | 0.7646 | 186 | 0.8366 | 197 | 0.8198 | 197 | 0.8206 | 197 | 0.8198 | 193 | 0.8104 |
| Average | 204 | 0.8372 | 220 | 0.8870 | 211 | 0.8734 | 215 | 0.8751 | 214 | 0.8734 | 212 | 0.8692 |
| References | E (kJ mol−1) | Method |
|---|---|---|
| Yang et al. (2001) [5] | 242 | Curve fitting |
| Senneca et al. (2004) [26] | 217 | FR |
| Girij et al. (2005) [27] | 227 208 236 | FR Ozawa Kissinger |
| Saha et al. (2006) [6] | 180–208 | VY |
| Das and Tiwari (2019) [14] | 203–355 | AIC |
| Osman et al. (2020) [13] | 165.6 166–180 165–195 | ASTME698 FWO FR |
| Mishra et al. (2019) [15] | 225.64 230.71 230.55 231.03 | FR KAS FWO STK |
| Reaction Mechanism | Code | PET2 | PET5 | ||||
|---|---|---|---|---|---|---|---|
| Ea kJ mol−1 | ln(A0) | R2 | Ea kJ mol−1 | ln(A0) | R2 | ||
| Reaction order models—first order | F1 | 246 | 41.3 | 0.9996 | 277 | 47.51 | 0.9999 |
| Reaction order models—second order | F2 | 286 | 48.81 | 0.9989 | 393 | 68.73 | 0.9988 |
| Reaction order models—third order | F3 | 330 | 57.01 | 0.998 | 533 | 94.14 | 0.9966 |
| Diffusion models—one dimension | D1 | 432 | 73.87 | 0.9997 | 384 | 65.65 | 0.9983 |
| Diffusion models—two dimensions | D2 | 454 | 77.43 | 0.9997 | 437 | 74.58 | 0.9992 |
| Diffusion models—three dimensions | D3 | 479 | 80.49 | 0.9997 | 500 | 84.55 | 0.9998 |
| Diffusion models—four dimensions | D4 | 465 | 77.45 | 0.9997 | 458 | 73.66 | 0.9995 |
| Nucleation models—two dimensions | A2 | 118 | 17.91 | 0.9995 | 133 | 21.51 | 0.9999 |
| Nucleation models—three dimensions | A3 | 75 | 9.82 | 0.9995 | 85 | 12.64 | 0.9999 |
| Nucleation models—four dimensions | A4 | 53 | 13.12 | 0.9994 | 61 | 12.93 | 0.9999 |
| Geometrical contraction models—one-dimension phase boundary | R1 | 210 | 34.49 | 0.9997 | 186 | 30.75 | 0.9982 |
| Geometrical contraction models—sphere | R2 | 228 | 39.11 | 0.9997 | 229 | 37.89 | 0.9995 |
| Geometrical contraction models—cylinder | R3 | 234 | 37.86 | 0.9997 | 244 | 40.34 | 0.9997 |
| Nucleation models—two-power law | P2 | 100 | 14.41 | 0.9996 | 88 | 12.91 | 0.998 |
| Nucleation models—three-power law | P3 | 63 | 11.74 | 0.9996 | 55 | 14.06 | 0.9977 |
| Nucleation models—four-power law | P4 | 44 | 14.6 | 0.9995 | 38 | 16.54 | 0.9973 |
| Reaction Mechanism | Code | PET10 | PET20 | ||||
| Ea kJ mol−1 | ln(A0) | R2 | Ea kJ mol−1 | ln(A0) | R2 | ||
| Reaction order models—first order | F1 | 264 | 45.05 | 0.9996 | 213 | 35.33 | 0.9999 |
| Reaction order models—second order | F2 | 373 | 64.5 | 0.9976 | 228 | 38.17 | 0.9996 |
| Reaction order models—third order | F3 | 503 | 87.72 | 0.9949 | 244 | 41.13 | 0.999 |
| Diffusion models—one dimension | D1 | 371 | 62.68 | 9996 | 408 | 67.96 | 1 |
| Diffusion models—two dimensions | D2 | 420 | 70.9 | 0.9999 | 417 | 69 | 1 |
| Diffusion models—three dimensions | D3 | 479 | 79.97 | 0.9999 | 427 | 69.3 | 1 |
| Diffusion models—four dimensions | D4 | 440 | 72.9 | 1 | 421 | 68.1 | 1 |
| Nucleation models—two dimensions | A2 | 127 | 20.58 | 0.9996 | 101 | 15.96 | 0.9999 |
| Nucleation models—three dimensions | A3 | 81 | 12.22 | 0.9996 | 63 | 14.57 | 0.9999 |
| Nucleation models—four dimensions | A4 | 58 | 14.37 | 0.9995 | 45 | 17.34 | 0.9999 |
| Geometrical contraction models—one-dimension phase boundary | R1 | 180 | 29.58 | 0.9996 | 198 | 32.62 | 1 |
| Geometrical contraction models—sphere | R2 | 219 | 36.12 | 1 | 205 | 33.27 | 1 |
| Geometrical contraction models—cylinder | R3 | 234 | 38.35 | 0.9999 | 208 | 33.32 | 1 |
| Nucleation models—two-power law | P2 | 84 | 12.63 | 0.9995 | 93 | 14.56 | 1 |
| Nucleation models—three-power law | P3 | 52 | 15.34 | 0.9994 | 58 | 15.37 | 1 |
| Nucleation models—four-power law | P4 | 36 | 17.67 | 0.9993 | 41 | 17.91 | 1 |
| Test No. | Ea kJ mol−1 | ln(A0) | R2 | Reaction Mechanism |
|---|---|---|---|---|
| PET2 | 246 | 41.3 | 0.9996 | Reaction order models—first order—F1 |
| PET5 | 277 | 47.51 | 0.9999 | Reaction order models—first order—F1 |
| PET10 | 264 | 45.05 | 0.9996 | Reaction order models—first order—F1 |
| PET20 | 213 | 35.33 | 0.9999 | Reaction order models—first order—F1 |
| Conversion | ln[A0 (min−1)] | |||||
|---|---|---|---|---|---|---|
| FR | FWO | KAS | STK | DAEM | Average | |
| 0.1 | 35.45 | 37.56 | 17.27 | 17.87 | 39.33 | 29.50 |
| 0.2 | 35.84 | 36.31 | 15.98 | 16.58 | 37.22 | 28.39 |
| 0.3 | 34.94 | 35.99 | 15.65 | 16.25 | 36.4 | 27.85 |
| 0.4 | 33.46 | 35.59 | 15.23 | 15.84 | 35.6 | 27.14 |
| 0.5 | 33.63 | 35.05 | 14.69 | 15.28 | 34.71 | 26.67 |
| 0.6 | 34.39 | 34.74 | 19.44 | 19.91 | 39.3 | 29.56 |
| 0.7 | 33.53 | 34.49 | 14.09 | 14.69 | 33.53 | 26.07 |
| 0.8 | 39.51 | 33.18 | 12.77 | 13.38 | 31.83 | 26.13 |
| Average | 35.09 | 35.36 | 15.64 | 16.23 | 35.99 | 27.66 |
| Heating Rates (K/min) | 2 | 5 | 10 | 20 |
|---|---|---|---|---|
| Kinetic Parameters | ||||
| Ea (kJ/mol) | 212 | |||
| A (min−1) | 1.29 × 1011 | |||
| Tp (K) | 680 | 685 | 710 | 725 |
| Thermodynamic Parameters | ||||
| ∆H (kJ/mol) | 206.34 | 206.3 | 206.1 | 206.00 |
| ∆G (kJ/mol) | 215.4 | 215.48 | 215.82 | 216.03 |
| ∆S (kJ/mol.K) | −0.01332 | −0.0134 | −0.01369 | −0.01383 |
| Potential Energy Barrier | ||||
| Ea–∆H (kJ/mol) * | 5.82 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alhulaybi, Z.; Dubdub, I. Comprehensive Kinetic Study of PET Pyrolysis Using TGA. Polymers 2023, 15, 3010. https://doi.org/10.3390/polym15143010
Alhulaybi Z, Dubdub I. Comprehensive Kinetic Study of PET Pyrolysis Using TGA. Polymers. 2023; 15(14):3010. https://doi.org/10.3390/polym15143010
Chicago/Turabian StyleAlhulaybi, Zaid, and Ibrahim Dubdub. 2023. "Comprehensive Kinetic Study of PET Pyrolysis Using TGA" Polymers 15, no. 14: 3010. https://doi.org/10.3390/polym15143010
APA StyleAlhulaybi, Z., & Dubdub, I. (2023). Comprehensive Kinetic Study of PET Pyrolysis Using TGA. Polymers, 15(14), 3010. https://doi.org/10.3390/polym15143010







