Sound Absorption of the Absorber Composed of a Shunt Loudspeaker and Porous Materials in Tandem
Abstract
1. Introduction
2. Models and Methods
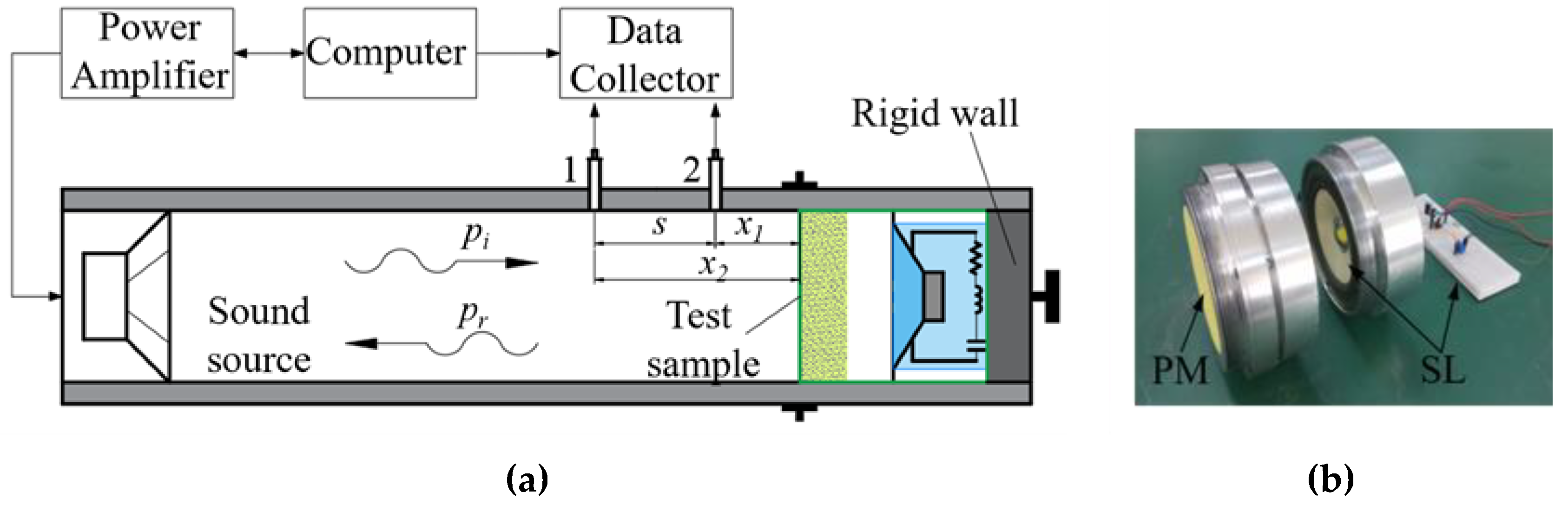
2.1. Experimental Measurement
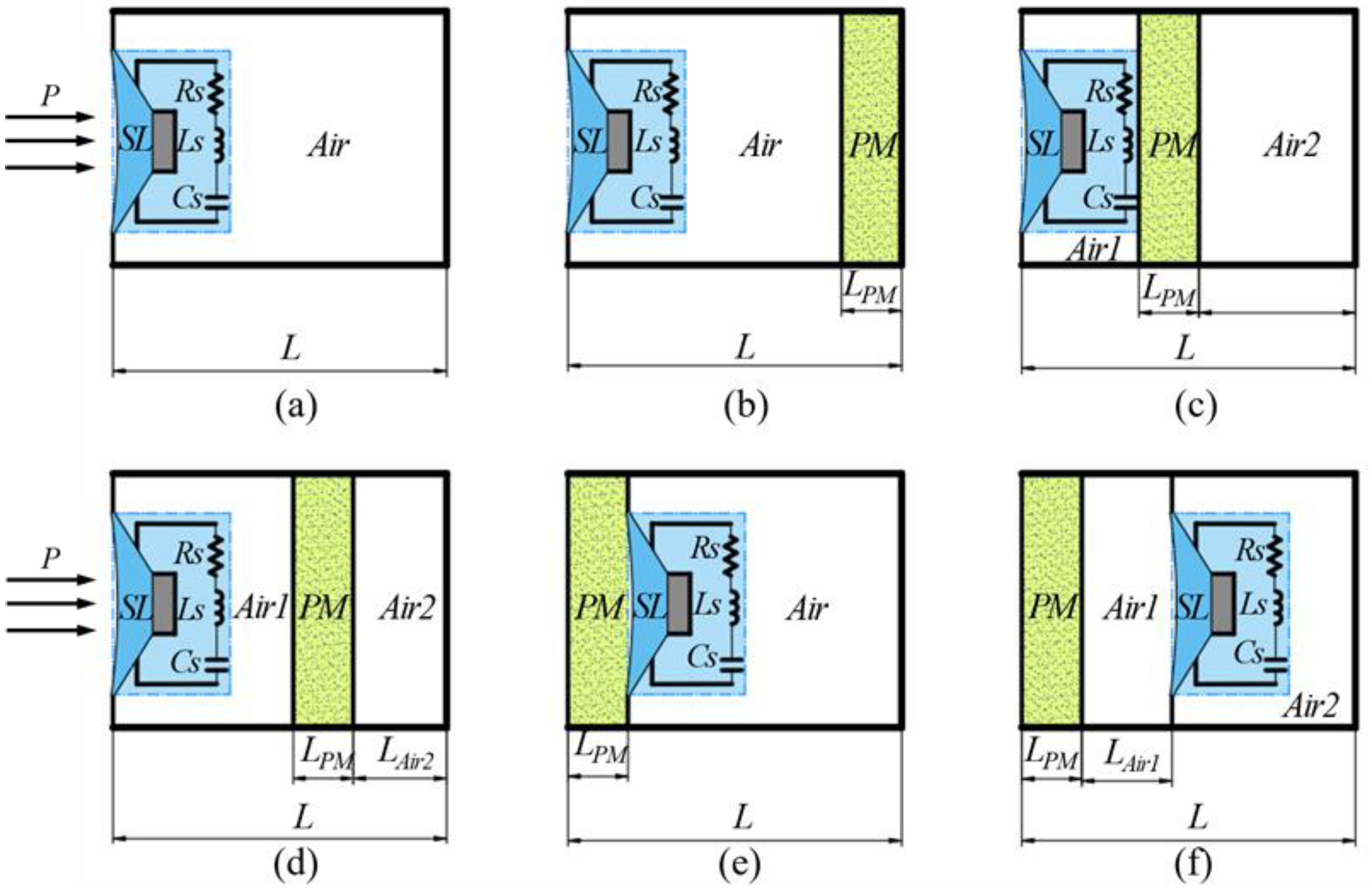
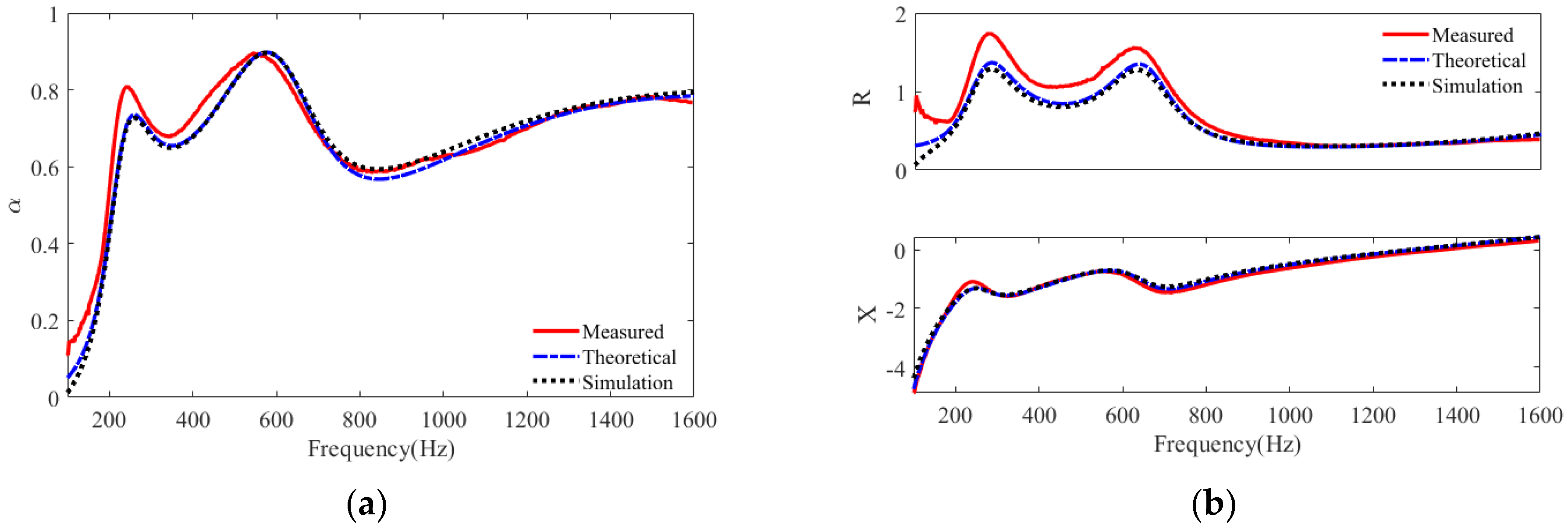
2.2. Model Building
3. Results and Discussion
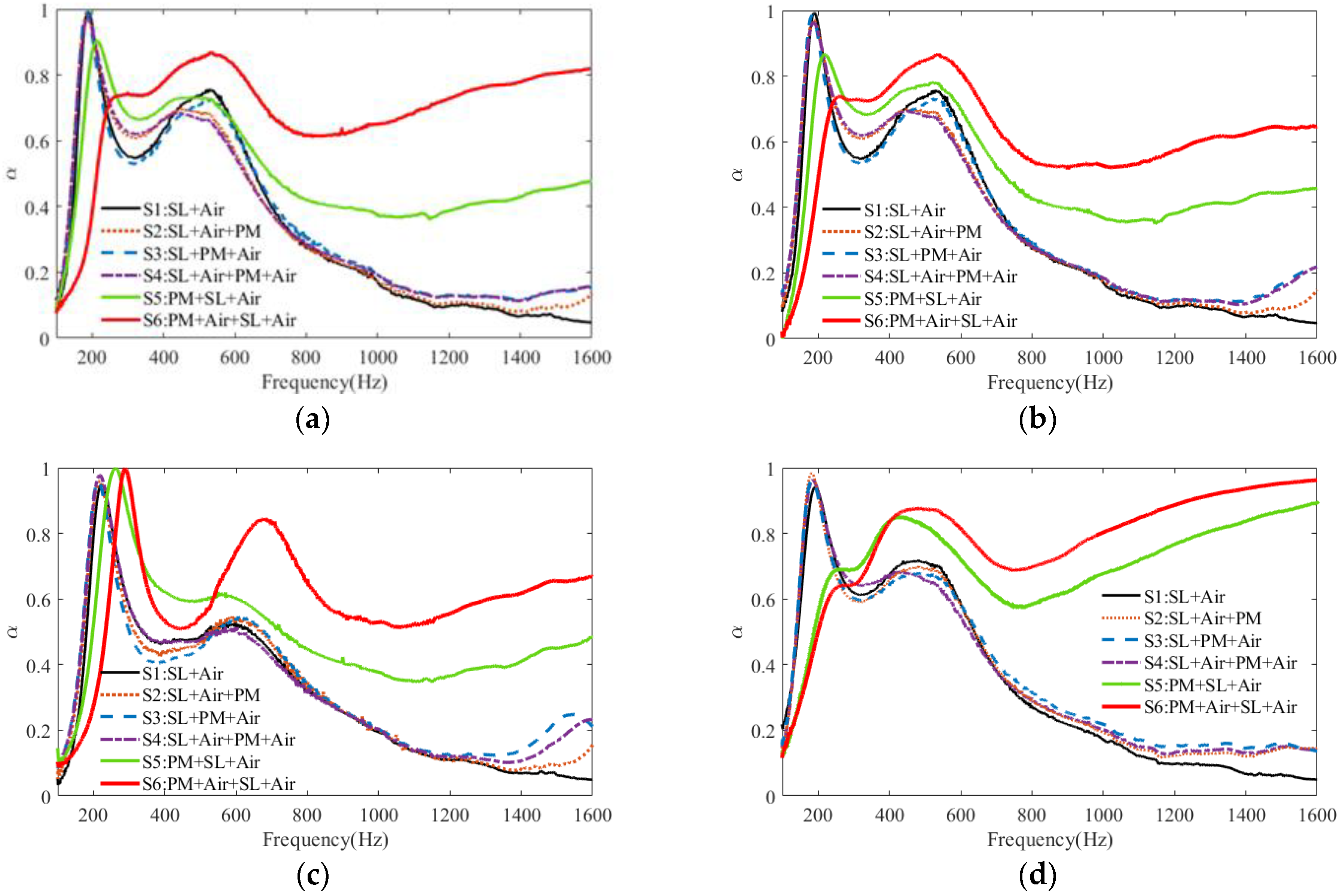
3.1. Analysis of the Sound Absorption Mechanism
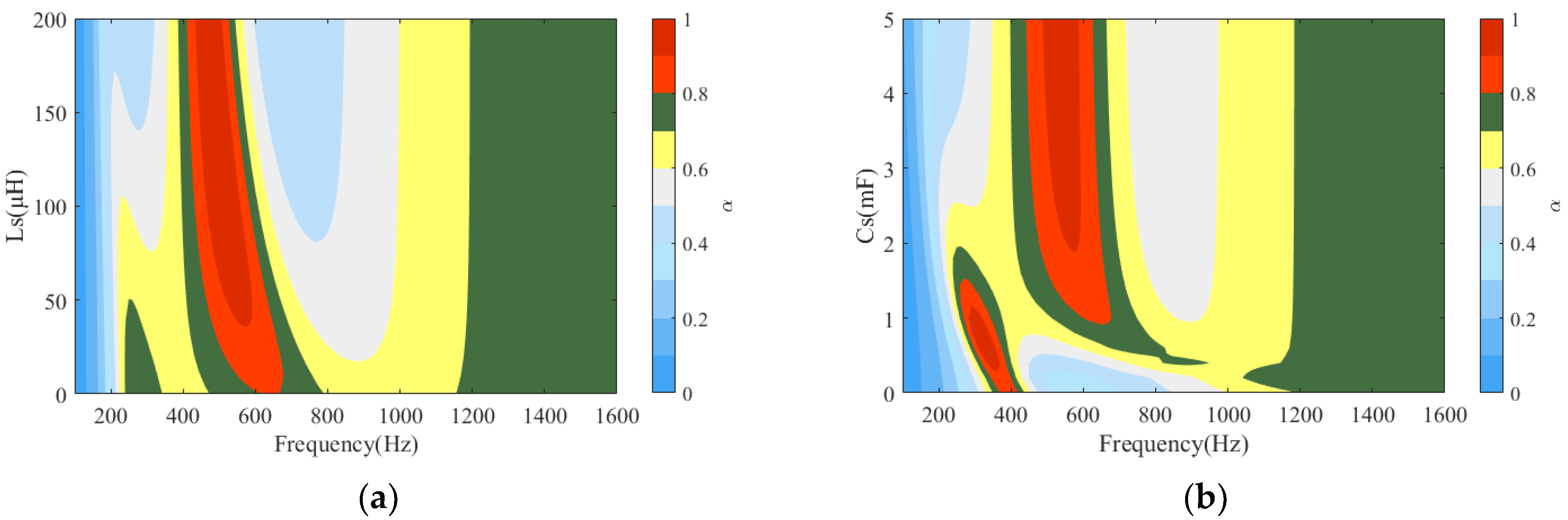
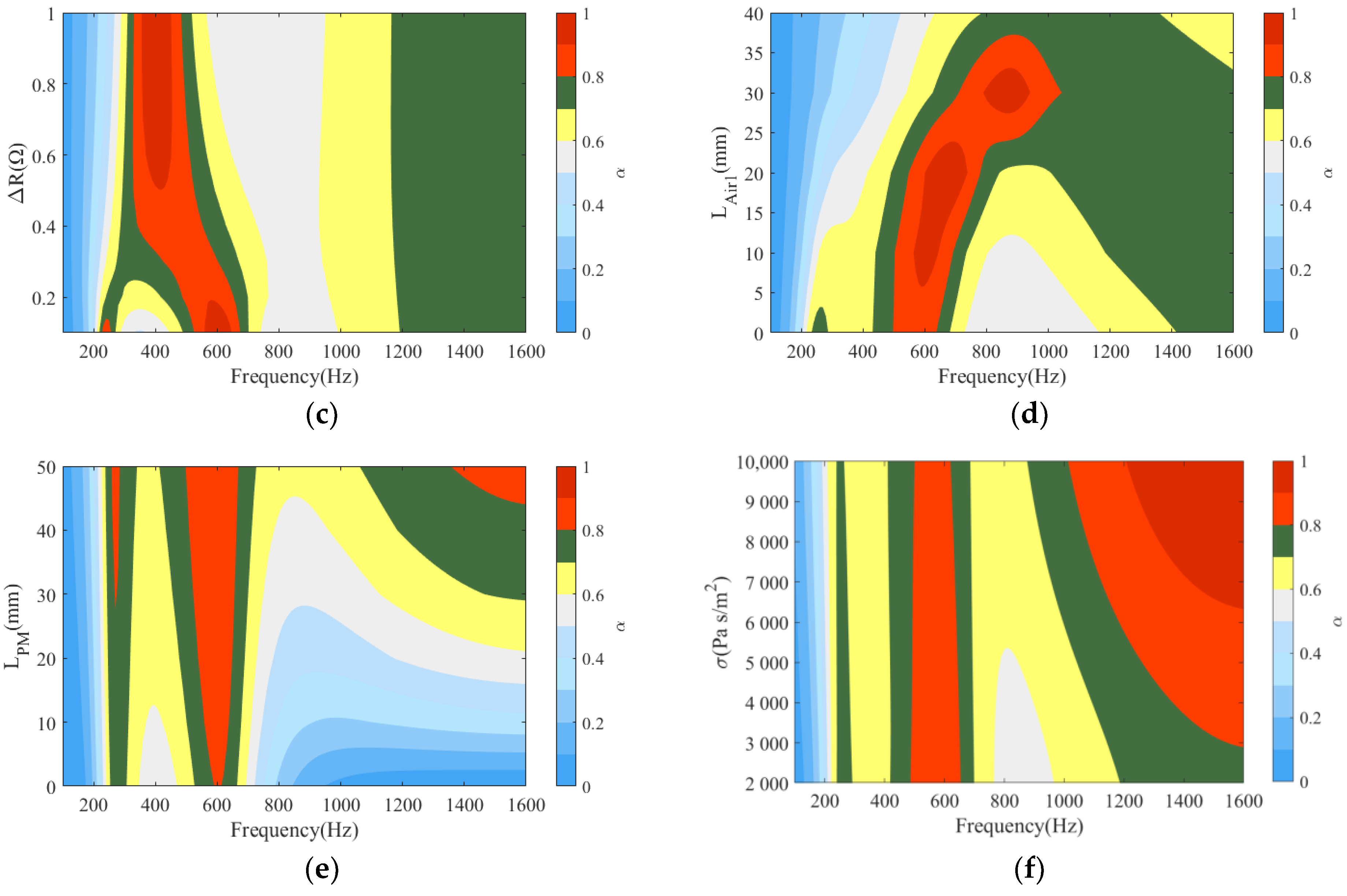
3.2. Influence of the Parameters on Sound Absorption
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, B.; Li, X. Noise transmission and absorption of lightweight structures: An overview and experience. In Proceedings of the 26th International Congress on Sound and Vibration, Montreal, QC, Canada, 7–11 July 2019. ICSV 26. [Google Scholar]
- Gao, N.; Zhang, Z.; Deng, J.; Guo, X.; Cheng, B.; Hou, H. Acoustic Metamaterials for Noise Reduction: A Review. Adv. Mater. Technol. 2022, 7, 2100698. [Google Scholar] [CrossRef]
- Maa, D.Y. Microperforated-panel wideband absorbers. Noise Control Eng. J. 1987, 29, 77–84. [Google Scholar] [CrossRef]
- Yang, M.; Sheng, P. Sound Absorption Structures: From Porous Media to Acoustic Metamaterials. Annu. Rev. Mater. Res. 2017, 47, 83–114. [Google Scholar] [CrossRef]
- Cao, L.; Fu, Q.; Si, Y.; Ding, B.; Yu, J. Porous materials for sound absorption. Compos. Commun. 2018, 10, 25–35. [Google Scholar] [CrossRef]
- Lissek, H. Shunt loudspeaker technique for use as acoustic liner. In Proceedings of the Internoise 2009: Innovations in Practical Noise Control, Ottawa, ON, Canada, 23–26 August 2009. [Google Scholar]
- Boulandet, R.; Lissek, H. Optimization of electroacoustic absorbers by means of designed experiments. Appl. Acoust. 2010, 71, 830–842. [Google Scholar] [CrossRef]
- Zhang, Y.; Chan, Y.J.; Huang, L. Thin broadband noise absorption through acoustic reactance control by electro-mechanical coupling without sensor. J. Acoust. Soc. Am. 2014, 135, 2738–2745. [Google Scholar] [CrossRef]
- Lissek, H.; Boulandet, R.; Fleury, R. Electroacoustic absorbers: Bridging the gap between shunt loudspeakers and active sound absorption. J. Acoust. Soc. Am. 2011, 129, 2968–2978. [Google Scholar] [CrossRef]
- Cerník, M.; Mokry, P. Sound reflection in an acoustic impedance tube terminated with a loudspeaker shunted by a negative impedance converter. Smart Mater. Struct. 2012, 21, 115016. [Google Scholar] [CrossRef]
- Zhang, Y.; Huang, L.; Zhang, Z. Tunable noise absorption by shhunted loudspeaker. In Proceedings of the International Congress on Sound & Vibration, Beijing, China, 13–17 July 2014. [Google Scholar]
- Zhang, Y.; Huang, L. Realization of Resonance of a Diaphragm at Any Desired Frequency. J. Mech. 2018, 34, 29–34. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, C.; Huang, L. Tuning of the acoustic impedance of a shunted electro-mechanical diaphragm for a broadband sound absorber. Mech. Syst. Signal Process. 2019, 126, 536–552. [Google Scholar] [CrossRef]
- Li, Z.; Li, X.; Liu, B. Optimization of Shunted Loudspeaker for Sound Absorption by Fully Exhaustive and Backtracking Algorithm. Appl. Sci. 2021, 11, 5574. [Google Scholar] [CrossRef]
- Tao, J.; Jiao, Q.; Qiu, X. A composite sound absorber with micro-perforated panel and shunted loudspeaker. J. Acoust. Soc. Am. 2013, 133, 3351. [Google Scholar] [CrossRef]
- Tao, J.; Jing, R.; Qiu, X. Sound absorption of a finite micro-perforated panel backed by a shunted loudspeaker. J. Acoust. Soc. Am. 2014, 135, 231–238. [Google Scholar] [CrossRef] [PubMed]
- Zhang, P.; Li, X.-H.; Gai, X.-L.; Wang, W.-J.; Li, X.-Y. Study on Low-frequency Sound Absorption Performance of Perforated Membrane and Loudspeaker Composed Structures. Noise Vib. Control 2022, 42, 221–231. [Google Scholar]
- Rivet, E.; Karkar, S.; Lissek, H. Multi-degree-of-freedom low-frequency electroacoustic absorbers through coupled resonators. Appl. Acoust. 2018, 132, 109–117. [Google Scholar] [CrossRef]
- Cong, C.; Tao, J.; Qiu, X. A Multi-Tone Sound Absorber Based on an Array of Shunted Loudspeakers. Appl. Sci. 2018, 8, 2484. [Google Scholar] [CrossRef]
- Cong, C.; Tao, J.; Qiu, X. Thin multi-tone sound absorbers based on analog circuit shunt loudspeakers. Noise Control Eng. J. 2018, 66, 496–504. [Google Scholar] [CrossRef]
- Zhang, P.; Cong, C.; Tao, J.; Qiu, X. Dual frequency sound absorption with an array of shunt loudspeakers. Sci. Rep. 2020, 10, 10806. [Google Scholar] [CrossRef]
- Li, X.; Cao, Z.; Li, Z.; Liu, B. Sound absorption of a shunt loudspeaker on a perforated plate. Appl. Acoust. 2022, 193, 108776. [Google Scholar] [CrossRef]
- Cao, Z.; Li, X.; Liu, B. Broadband sound absorption of a hybrid absorber with shunt loudspeaker and perforated plates. Appl. Acoust. 2023, 203, 109185. [Google Scholar] [CrossRef]
- ISO(10534-2); Acoustics–Determination of Sound Absorption Coefficient and Impedance in Impedance Tubes–Part 2: Transfer-Function Method. International Organization for Standardization: Geneva, Switzerland, 2001.
- Lee, D.H.; Kwon, Y.P. Estimation of the absorption performance of multiple layer perforated panel systems by transfer matrix method. J. Sound Vib. 2004, 278, 847–860. [Google Scholar] [CrossRef]
- Xin, F.; Ma, X.; Liu, X.; Zhang, C. A multiscale theoretical approach for the sound absorption of slit-perforated double porosity materials. Compos. Struct. 2019, 223, 110919. [Google Scholar] [CrossRef]
- Liu, Q.; Liu, X.; Zhang, C.; Xin, F. A novel multiscale porous composite structure for sound absorption enhancement. Compos. Struct. 2021, 276, 114456. [Google Scholar] [CrossRef]
- Rafique, F.; Wu, J.H.; Naqvi SM, A.; Ma, F. Enhanced wideband low-frequency sound absorption of a single-layer multiple parallel-arranged inhomogeneous microperforated panel absorber. Acoust. Aust. 2022, 50, 49–69. [Google Scholar] [CrossRef]
- Liu, Q.; Zhang, C. Broadband and low-frequency sound absorption by a slit-perforated multi-layered porous metamaterial. Eng. Struct. 2023, 281, 115743. [Google Scholar] [CrossRef]



| Group | Parameter | ||||||
|---|---|---|---|---|---|---|---|
| G1 | SL | (g) | (kg/s) | (mm/N) | (N/A) | (Ω) | (μH) |
| 2.711 | 0.448 | 0.626 | 1.339 | 3.77 | 72 | ||
| (Ω) | (μH) | (mF) | (m2) | ||||
| −3.57 | 26.62 | 1.842 | 0.0059 | ||||
| PM (Melamine) | (%) | Λ (μm) | Λ′ (μm) | LPM (mm) | |||
| 6883 | 99.6 | 179 | 318 | 1.05 | 20 | ||
| G2 | SL | (g) | (kg/s) | (mm/N) | (N/A) | (Ω) | (μH) |
| 2.711 | 0.448 | 0.626 | 1.339 | 3.77 | 72 | ||
| (Ω) | (μH) | (mF) | (m2) | ||||
| −3.57 | 26.62 | 1.842 | 0.0059 | ||||
| PM (Polyurethane) | (%) | Λ (μm) | Λ′ (μm) | LPM (mm) | |||
| 2368 | 98.45 | 185 | 206 | 1.06 | 30 | ||
| G3 | SL | (g) | (kg/s) | (mm/N) | (N/A) | (Ω) | (μH) |
| 2.711 | 0.448 | 0.626 | 1.339 | 3.77 | 72 | ||
| (Ω) | (μH) | (mF) | (m2) | ||||
| −3.63 | 14.66 | 1.17 | 0.0059 | ||||
| PM (Polyurethane) | (%) | Λ (μm) | Λ′ (μm) | LPM (mm) | |||
| 2368 | 98.45 | 185 | 206 | 1.06 | 30 | ||
| G4 | SL | (g) | (kg/s) | (mm/N) | (N/A) | (Ω) | (μH) |
| 2.711 | 0.448 | 0.626 | 1.339 | 3.77 | 72 | ||
| (Ω) | (μH) | (mF) | (m2) | ||||
| −3.57 | 34.85 | 1.97 | 0.0059 | ||||
| PM (Melamine) | (%) | Λ (μm) | Λ′ (μm) | LPM (mm) | |||
| 8102 | 99.36 | 102 | 146 | 1.02 | 40 | ||
| Mm (g) | Rm (kg/s) | Cm (mm/N) | BL (N/A) | (Ω) | (mH) | LPM (mm) | Sd (m2) |
|---|---|---|---|---|---|---|---|
| 2.711 | 0.448 | 0.626 | 1.339 | 0.2 | 28.5 | 40 | 0.0059 |
| (mF) | Λ (μm) | Λ′ (μm) | (%) | LAir1 (mm) | LAir2 (mm) | ||
| 1.795 | 2080 | 150 | 202 | 99.14 | 1.09 | 18 | 37 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Cao, Z.; Xu, L.; Liu, B. Sound Absorption of the Absorber Composed of a Shunt Loudspeaker and Porous Materials in Tandem. Polymers 2023, 15, 3051. https://doi.org/10.3390/polym15143051
Li X, Cao Z, Xu L, Liu B. Sound Absorption of the Absorber Composed of a Shunt Loudspeaker and Porous Materials in Tandem. Polymers. 2023; 15(14):3051. https://doi.org/10.3390/polym15143051
Chicago/Turabian StyleLi, Xin, Zhigang Cao, Lijun Xu, and Bilong Liu. 2023. "Sound Absorption of the Absorber Composed of a Shunt Loudspeaker and Porous Materials in Tandem" Polymers 15, no. 14: 3051. https://doi.org/10.3390/polym15143051
APA StyleLi, X., Cao, Z., Xu, L., & Liu, B. (2023). Sound Absorption of the Absorber Composed of a Shunt Loudspeaker and Porous Materials in Tandem. Polymers, 15(14), 3051. https://doi.org/10.3390/polym15143051






