A General Deep Learning Method for Computing Molecular Parameters of a Viscoelastic Constitutive Model by Solving an Inverse Problem
Abstract
:1. Introduction
2. Problem Setting
3. Methodology
3.1. DNN Representation of Molecular Constitutive Model
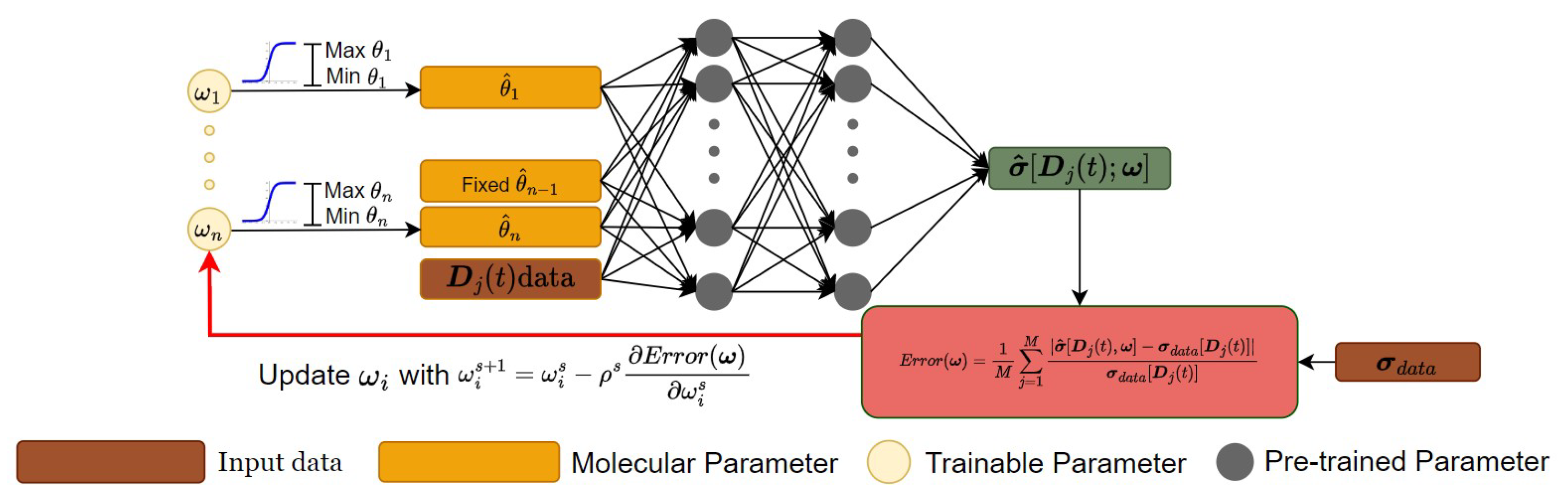
3.2. A DNN-Based Numerical Solver for Inversely Computing Molecular Parameters
4. Results and Discussion
4.1. Training DNNs for Modeling Entangled Polymer Solutions
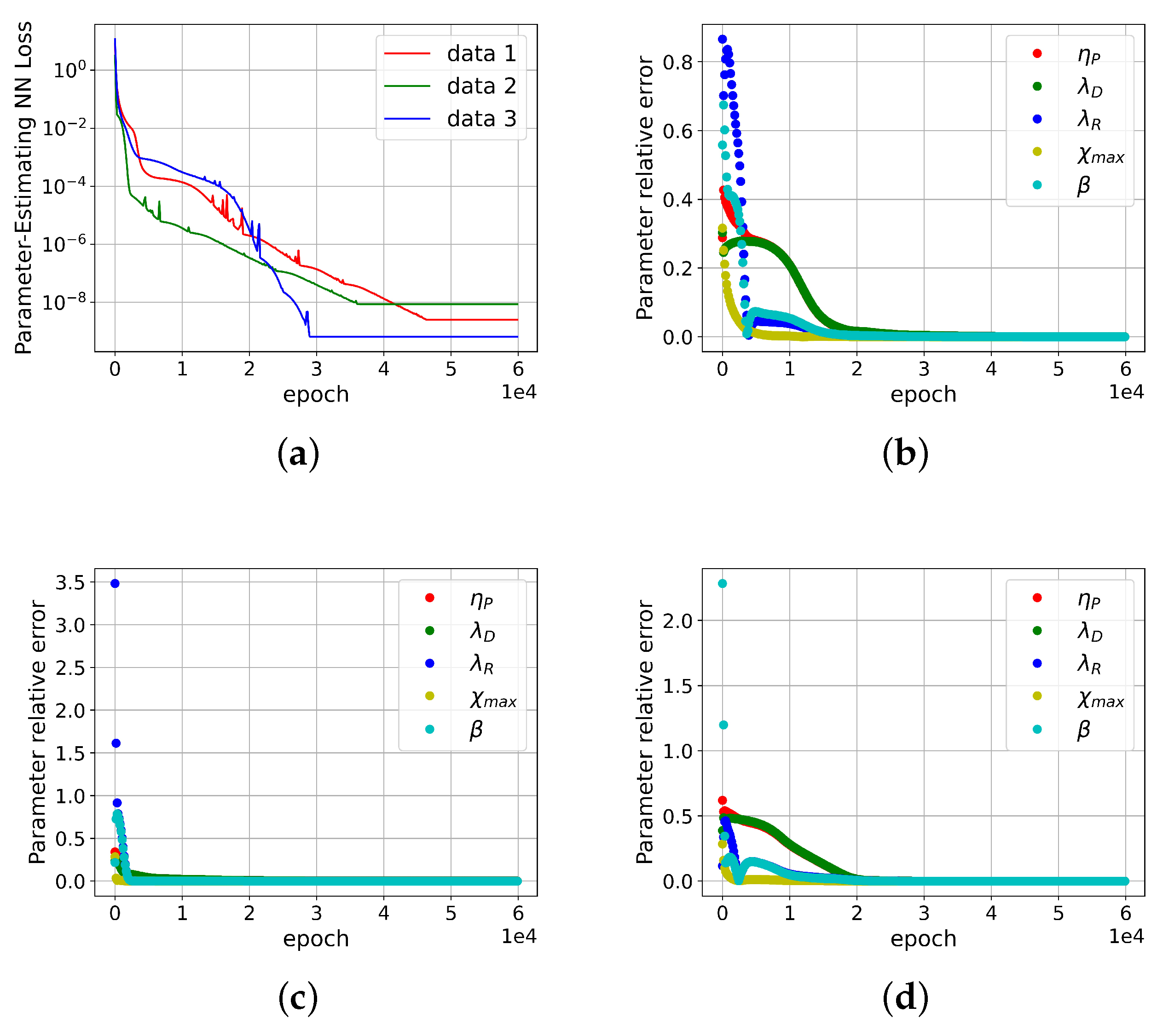
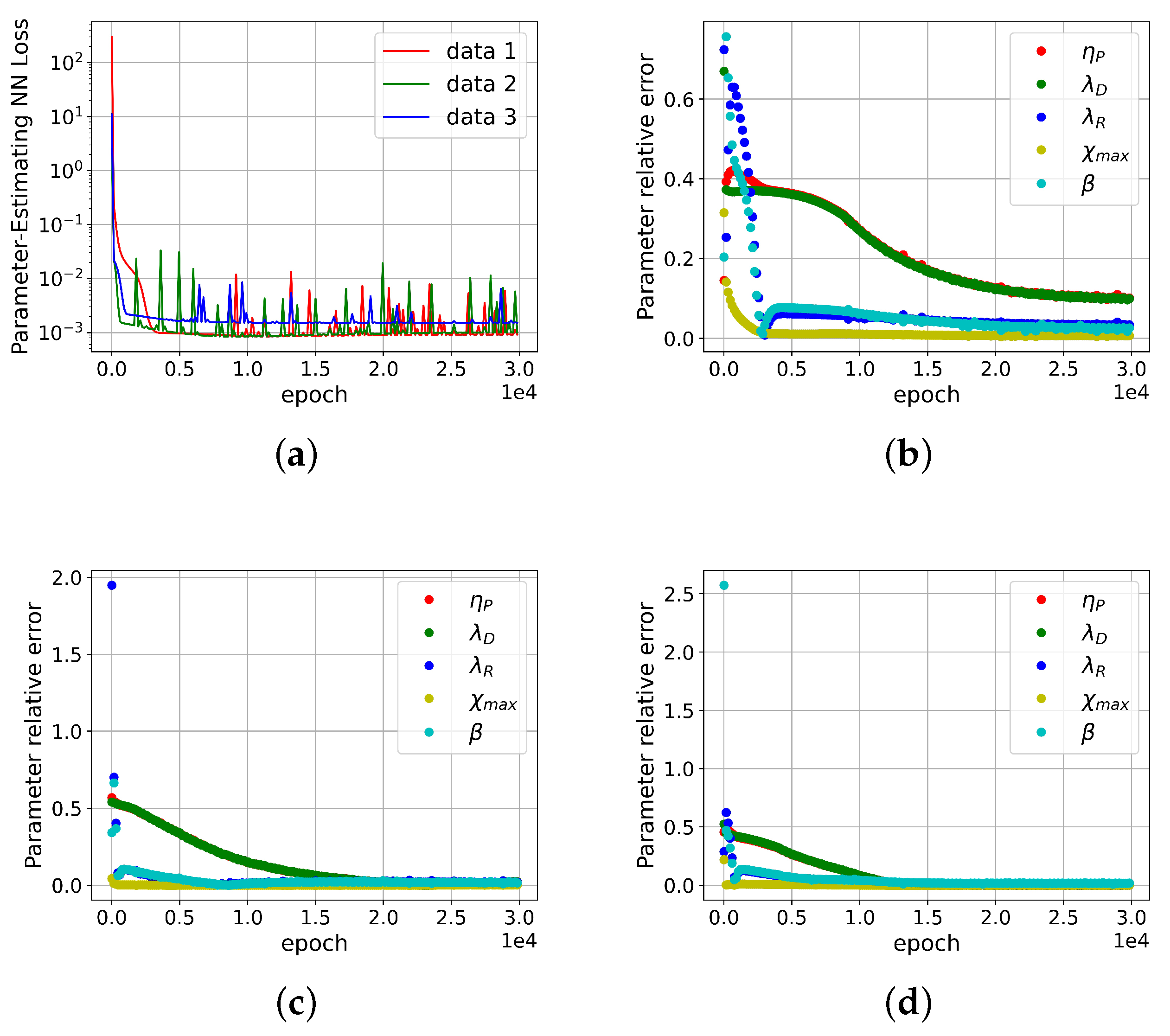
4.2. Validation of Convergence
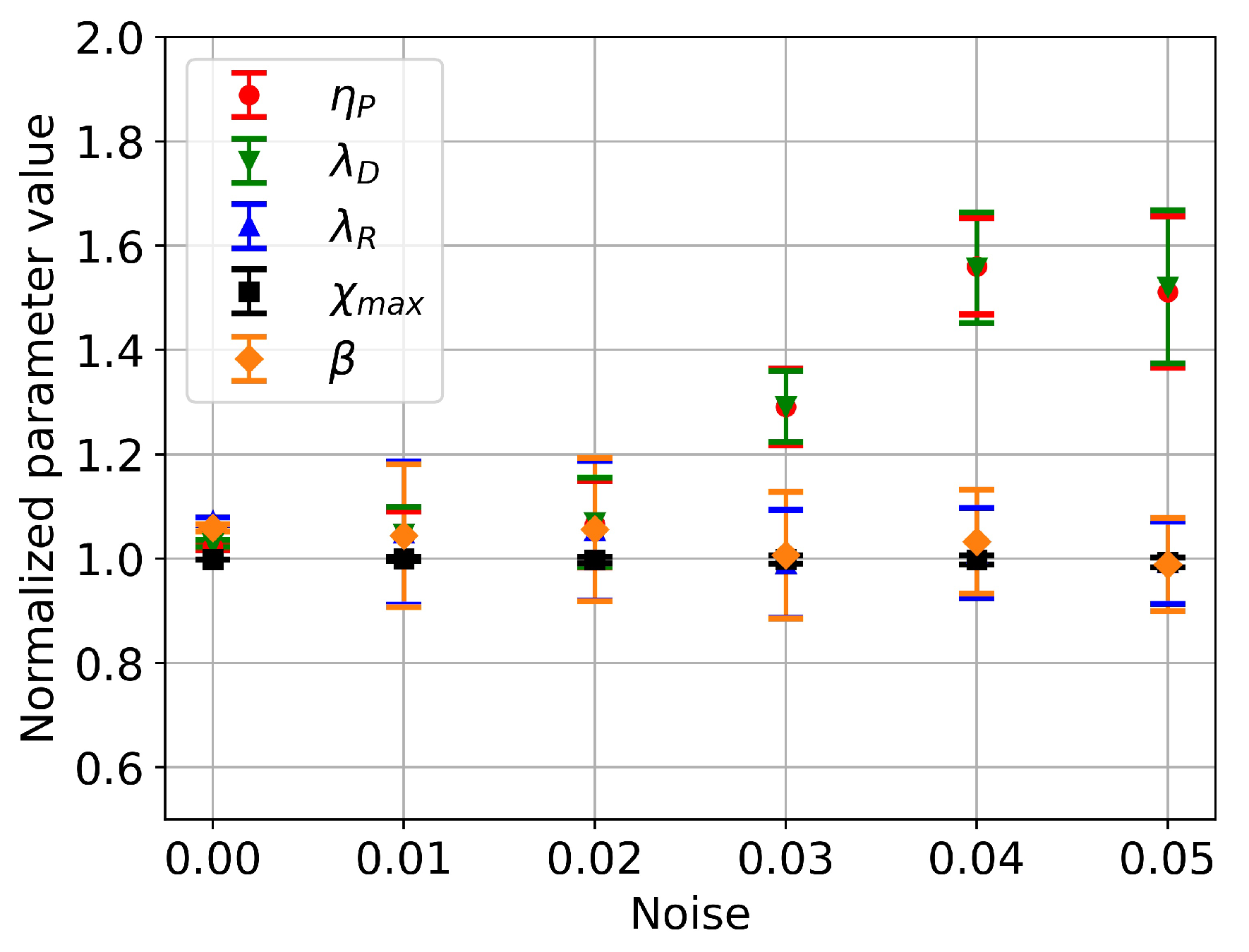
4.3. Effects of Input Data Noise
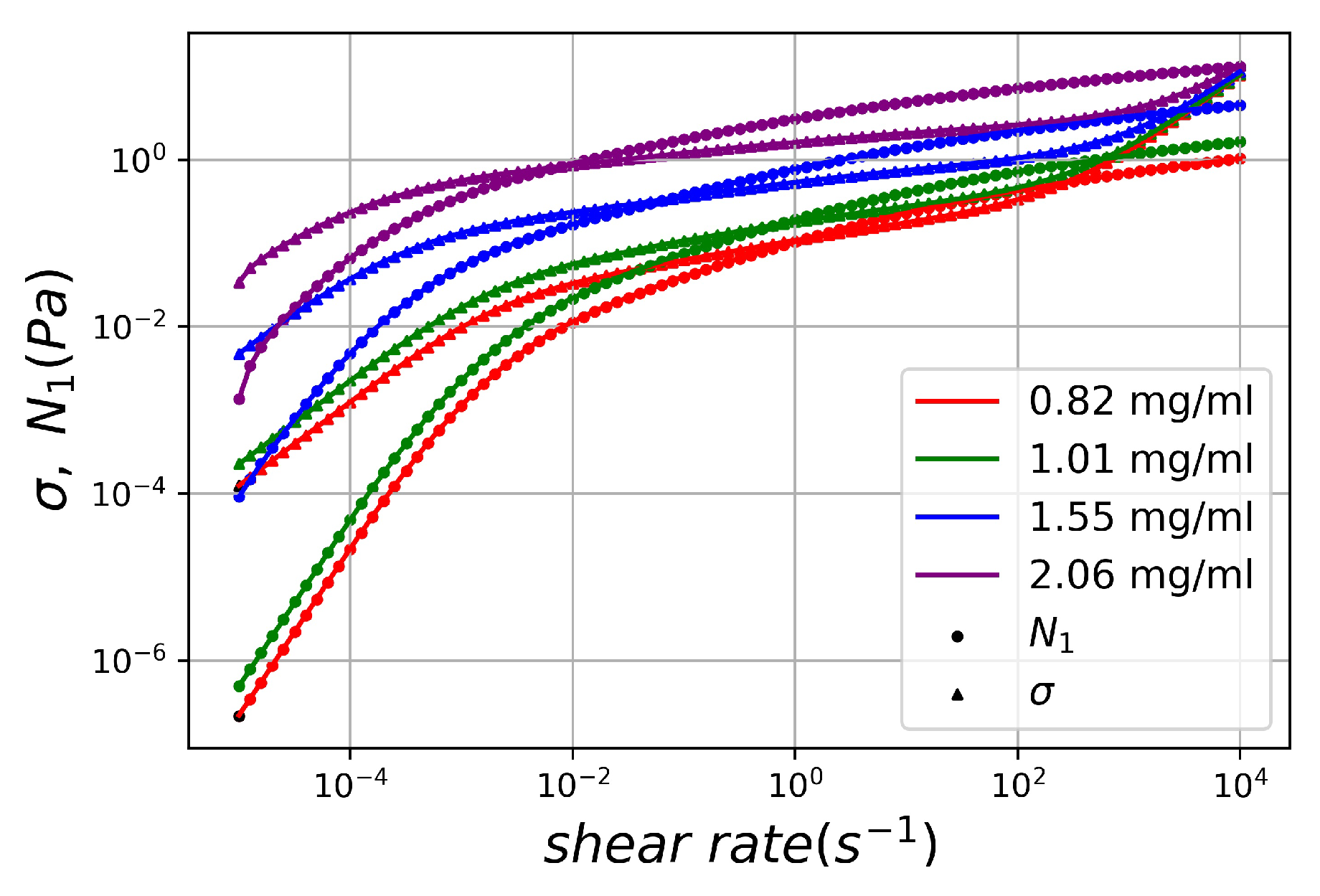
4.4. Validation by Completely Monodisperse Entangled Polymer Solution
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Groisman, A.; Steinberg, V. Elastic turbulence in a polymer solution flow. Nature 2000, 405, 53–55. [Google Scholar] [CrossRef] [PubMed]
- Groisman, A.; Steinberg, V. Efficient mixing at low Reynolds numbers using polymer additives. Nature 2001, 410, 905–908. [Google Scholar] [CrossRef] [PubMed]
- Groisman, A.; Steinberg, V. Elastic turbulence in curvilinear flows of polymer solutions. New J. Phys. 2004, 6, 29. [Google Scholar] [CrossRef]
- Howe, A.M.; Clarke, A.; Giernalczyk, D. Flow of concentrated viscoelastic polymer solutions in porous media: Effect of MW and concentration on elastic turbulence onset in various geometries. Soft Matter 2015, 11, 6419–6431. [Google Scholar] [CrossRef] [PubMed]
- Traore, B.; Castelain, C.; Burghelea, T. Efficient heat transfer in a regime of elastic turbulence. J. Non-Newton. Fluid Mech. 2015, 223, 62–76. [Google Scholar] [CrossRef]
- Abed, W.M.; Whalley, R.D.; Dennis, D.J.; Poole, R.J. Experimental investigation of the impact of elastic turbulence on heat transfer in a serpentine channel. J. Non-Newton. Fluid Mech. 2016, 231, 68–78. [Google Scholar] [CrossRef]
- Virk, P.S. Drag reduction fundamentals. AIChE J. 1975, 21, 625–656. [Google Scholar] [CrossRef]
- White, C.M.; Mungal, M.G. Mechanics and prediction of turbulent drag reduction with polymer additives. Annu. Rev. Fluid Mech. 2008, 40, 235–256. [Google Scholar] [CrossRef]
- Xi, L. Turbulent drag reduction by polymer additives: Fundamentals and recent advances. Phys. Fluids 2019, 31, 121302. [Google Scholar] [CrossRef]
- Doi, M.; Edwards, S.F.; Edwards, S.F. The Theory of Polymer Dynamics; Oxford University Press: Oxford, UK, 1988; Volume 73. [Google Scholar]
- Graham, R.S.; Likhtman, A.E.; McLeish, T.C.; Milner, S.T. Microscopic theory of linear, entangled polymer chains under rapid deformation including chain stretch and convective constraint release. J. Rheol. 2003, 47, 1171–1200. [Google Scholar] [CrossRef]
- Bent, J.; Hutchings, L.; Richards, R.; Gough, T.; Spares, R.; Coates, P.D.; Grillo, I.; Harlen, O.; Read, D.; Graham, R.; et al. Neutron-mapping polymer flow: Scattering, flow visualization, and molecular theory. Science 2003, 301, 1691–1695. [Google Scholar] [CrossRef] [PubMed]
- Iten, R.; Metger, T.; Wilming, H.; Del Rio, L.; Renner, R. Discovering physical concepts with neural networks. Phys. Rev. Lett. 2020, 124, 010508. [Google Scholar] [CrossRef] [PubMed]
- Öttinger, H.C. Stochastic processes, polymer dynamics, and fluid mechanics. In Stochastic Processes in Polymeric Fluids; Springer: Berlin/Heidelberg, Germany, 1996; pp. 1–15. [Google Scholar]
- Chen, N.; Majda, A.J. A new efficient parameter estimation algorithm for high-dimensional complex nonlinear turbulent dynamical systems with partial observations. J. Comput. Phys. 2019, 397, 108836. [Google Scholar] [CrossRef]
- Annaswamy, A.M.; Yu, S.H. /spl theta/-adaptive neural networks: A new approach to parameter estimation. IEEE Trans. Neural Netw. 1996, 7, 907–918. [Google Scholar] [CrossRef] [PubMed]
- Afkham, B.M.; Chung, J.; Chung, M. Learning regularization parameters of inverse problems via deep neural networks. Inverse Probl. 2021, 37, 105017. [Google Scholar] [CrossRef]
- Zaplotnik, J.; Pišljar, J.; Škarabot, M.; Ravnik, M. Neural networks determination of material elastic constants and structures in nematic complex fluids. Sci. Rep. 2023, 13, 6028. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Reyes, B.; Howard, A.A.; Perdikaris, P.; Tartakovsky, A.M. Learning unknown physics of non-Newtonian fluids. Phys. Rev. Fluids 2021, 6, 073301. [Google Scholar] [CrossRef]
- Xu, K.; Tartakovsky, A.M.; Burghardt, J.; Darve, E. Learning viscoelasticity models from indirect data using deep neural networks. Comput. Methods Appl. Mech. Eng. 2021, 387, 114124. [Google Scholar] [CrossRef]
- Mahmoudabadbozchelou, M.; Caggioni, M.; Shahsavari, S.; Hartt, W.H.; Em Karniadakis, G.; Jamali, S. Data-driven physics-informed constitutive metamodeling of complex fluids: A multifidelity neural network (mfnn) framework. J. Rheol. 2021, 65, 179–198. [Google Scholar] [CrossRef]
- Wang, J.; Zhu, B.; Hui, C.Y.; Zehnder, A.T. Determination of material parameters in constitutive models using adaptive neural network machine learning. J. Mech. Phys. Solids 2023, 177, 105324. [Google Scholar] [CrossRef]
- Niaki, M.H.; Ahangari, M.G.; Pashaian, M. A material-independent deep learning model to predict the tensile strength of polymer concrete. Compos. Commun. 2022, 36, 101400. [Google Scholar] [CrossRef]
- Schulte, R.; Karca, C.; Ostwald, R.; Menzel, A. Machine learning-assisted parameter identification for constitutive models based on concatenated loading path sequences. Eur. J. Mech. A/Solids 2023, 98, 104854. [Google Scholar] [CrossRef]
- Ivanov, A.S.; Nikolaev, K.G.; Novikov, A.S.; Yurchenko, S.O.; Novoselov, K.S.; Andreeva, D.V.; Skorb, E.V. Programmable soft-matter electronics. J. Phys. Chem. Lett. 2021, 12, 2017–2022. [Google Scholar] [CrossRef]
- Chen, Y.; Liang, X.; Kontogeorgis, G.M. Artificial neural network modeling on the polymer-electrolyte aqueous two-phase systems involving biomolecules. Sep. Purif. Technol. 2023, 306, 122624. [Google Scholar] [CrossRef]
- Likhtman, A.E.; Graham, R.S. Simple constitutive equation for linear polymer melts derived from molecular theory: Rolie–Poly equation. J. Non-Newton. Fluid Mech. 2003, 114, 1–12. [Google Scholar] [CrossRef]
- Kabanemi, K.K.; Hétu, J.F. Nonequilibrium stretching dynamics of dilute and entangled linear polymers in extensional flow. J. Non-Newton. Fluid Mech. 2009, 160, 113–121. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Hornik, K. Approximation capabilities of multilayer feedforward networks. Neural Netw. 1991, 4, 251–257. [Google Scholar] [CrossRef]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. Tensorflow: Large-scale machine learning on heterogeneous distributed systems. arXiv 2016, arXiv:1603.04467. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. Pytorch: An imperative style, high-performance deep learning library. Adv. Neural Inf. Process. Syst. 2019, 32. Available online: https://papers.nips.cc/paper_files/paper/2019/file/bdbca288fee7f92f2bfa9f7012727740-Paper.pdf (accessed on 29 June 2023).
- Banik, S.; Kong, D.; San Francisco, M.J.; McKenna, G.B. Monodisperse Lambda DNA as a Model to Conventional Polymers: A Concentration-Dependent Scaling of the Rheological Properties. Macromolecules 2021, 54, 8632–8654. [Google Scholar] [CrossRef]
- Fan, Y.-Q.; Lanzaro, A.; Yuan, X.-F. Universal concentration scaling on rheometric properties of polydisperse and high molecular weight polyacrylamide aqueous solutions. Chin. J. Polym. Sci. 2022, 40, 1432–1440. [Google Scholar] [CrossRef]
| Parameter | Variation Range (SI Unit) |
|---|---|
| Pa·s | |
| s | |
| s | |
| Neurons | 64 | 128 | 192 | 256 | |
|---|---|---|---|---|---|
| Hidden Layers | |||||
| 2 | 2.31% | 1.65% | 1.46% | 1.49% | |
| 3 | 2.34% | 1.45% | 1.41% | 1.43% | |
| 4 | 2.39% | 1.97% | 1.74% | 1.38% | |
| 5 | 2.61% | 1.56% | 1.33% | 1.54% | |
| 6 | 2.26% | 1.49% | 1.57% | 1.65% | |
| Concentration | 0.82 mg/mL | 1.01 mg/mL | 1.55 mg/mL | 2.06 mg/mL | |||||
|---|---|---|---|---|---|---|---|---|---|
| Parameter | Extracted | DNN Solution | Extracted | DNN Solution | Extracted | DNN Solution | Extracted | DNN Solution | |
| 12.4 | 12.53 ± 0.02 | 22.6 | 22.58 ± 0.02 | 474.4 | 474 ± 1 | 4811.7 | 4784.2 ± 0.4 | ||
| 87.0 | 88.00 ± 0.09 | 109.0 | 109.00 ± 0.01 | 1006.0 | 998 ± 4 | 4092.0 | 4095.10 ± 0.02 | ||
| 11.0 | 10.7 ± 0.1 | 14.0 | 13.00 ± 0.08 | 21.0 | 20.5 ± 0.2 | 29.0 | 31.70 ± 0.02 | ||
| 18.0 | 19 ± 2 | 18.0 | 17.2 ± 0.7 | 18.0 | 19 ± 1 | 18.0 | 17.500 ± 0.004 | ||
| 20.0 | 19.5 ± 0.3 | 13.0 | 12.20 ± 0.06 | 5.00 | 5.00 ± 0.05 | 1.0 | 1.000 ± 0.002 | ||
| 0.0076 | 0.0025 | 0.0017 | 0.005 | ||||||
| 0.0037 | 0.0017 | 0.0019 | 0.0035 | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, M.; Fan, Y.-Q.; Yuan, X.-F. A General Deep Learning Method for Computing Molecular Parameters of a Viscoelastic Constitutive Model by Solving an Inverse Problem. Polymers 2023, 15, 3592. https://doi.org/10.3390/polym15173592
Ye M, Fan Y-Q, Yuan X-F. A General Deep Learning Method for Computing Molecular Parameters of a Viscoelastic Constitutive Model by Solving an Inverse Problem. Polymers. 2023; 15(17):3592. https://doi.org/10.3390/polym15173592
Chicago/Turabian StyleYe, Minghui, Yuan-Qi Fan, and Xue-Feng Yuan. 2023. "A General Deep Learning Method for Computing Molecular Parameters of a Viscoelastic Constitutive Model by Solving an Inverse Problem" Polymers 15, no. 17: 3592. https://doi.org/10.3390/polym15173592
APA StyleYe, M., Fan, Y.-Q., & Yuan, X.-F. (2023). A General Deep Learning Method for Computing Molecular Parameters of a Viscoelastic Constitutive Model by Solving an Inverse Problem. Polymers, 15(17), 3592. https://doi.org/10.3390/polym15173592






