Reliability Study of Wood–Plastic Composites Based on Probabilistic Finite Elements
Abstract
:1. Introduction
2. Materials and Methods
3. Mechanical Property Test
4. Result and Discussion
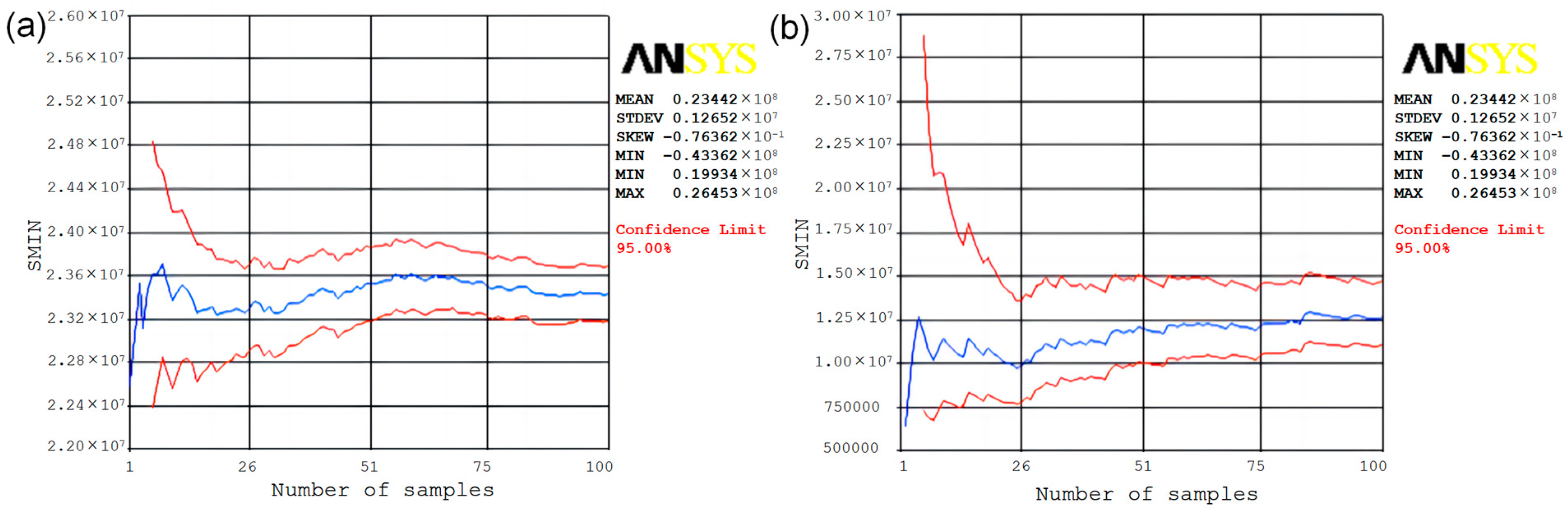
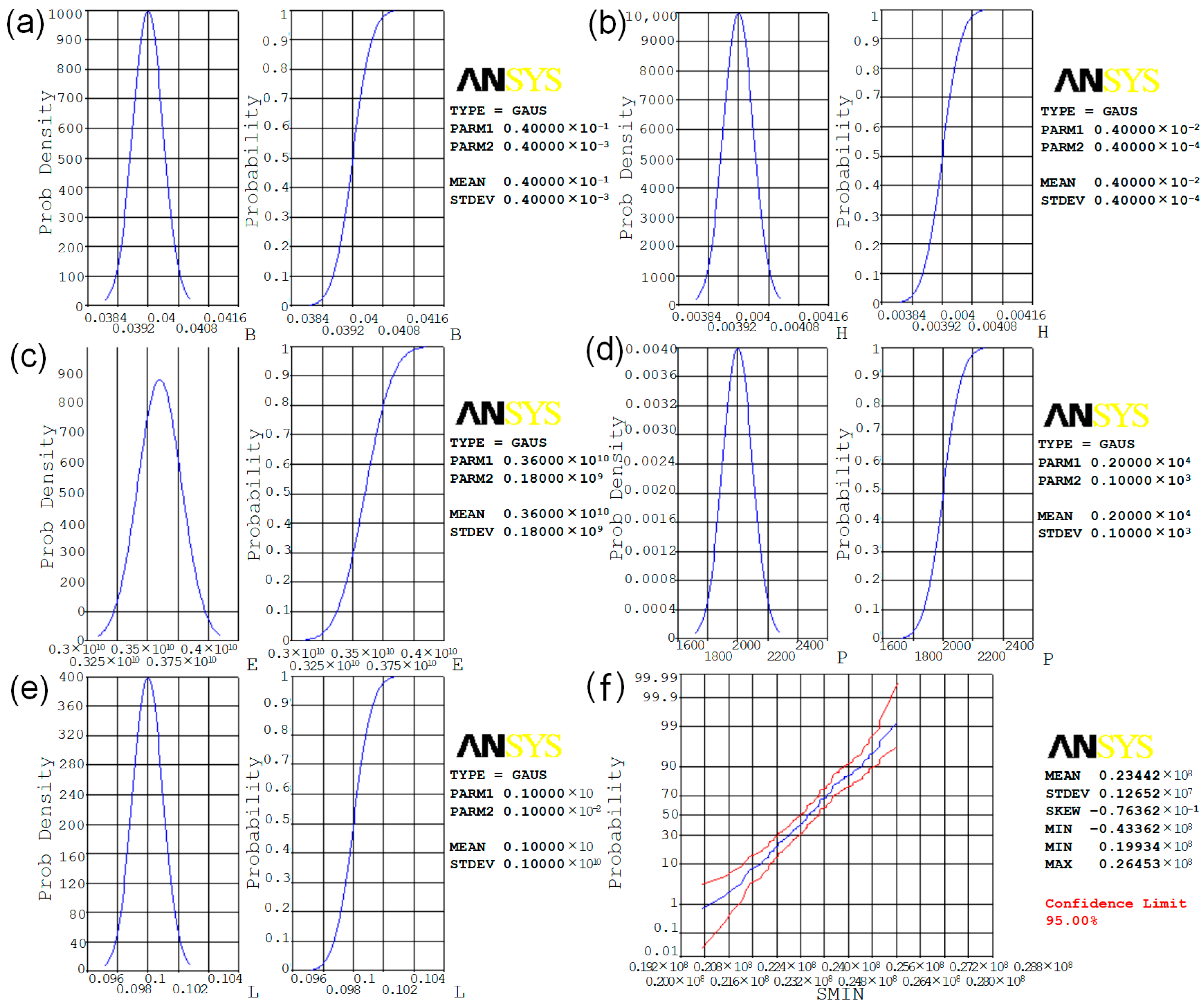
4.1. Finite Element Simulation of Wood–Plastic Composites
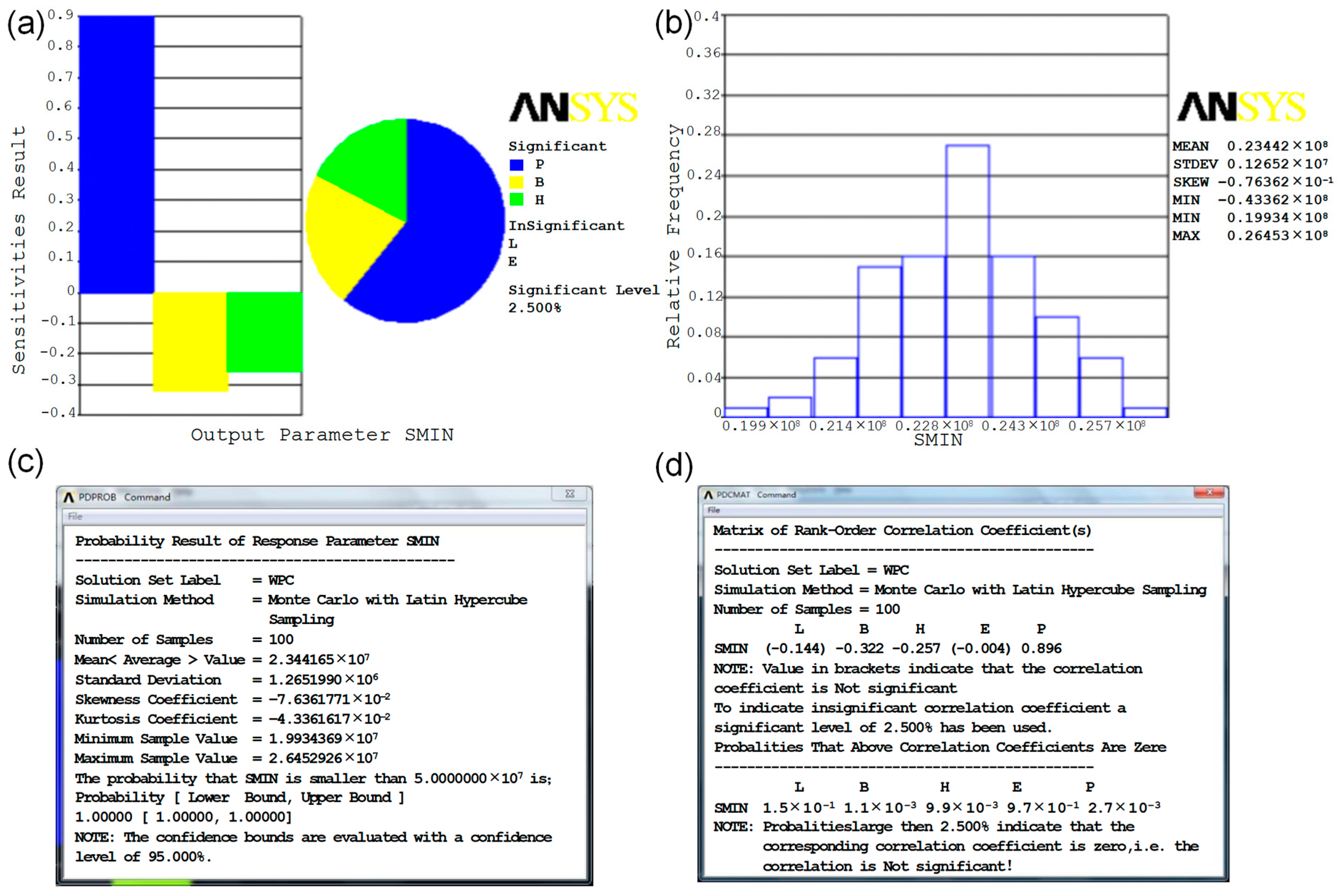
4.2. Simulation of the Influence of Process Parameters on Reliability
4.2.1. Simulation of the Effect of Wood Flour Content on the Reliability of Wood–Plastic Composites
4.2.2. Simulation of the Effect of Granulation Temperature on the Reliability of Wood–Plastic Composites
4.2.3. Simulation of the Effect of Coupling Agent Content on the Reliability of Wood–Plastic Composites
4.2.4. Simulation of the Effect of Screw Speed on the Reliability of Wood–Plastic Composites
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sobczak, L.; Brüggemann, O.; Putz, R.F. Polyolefin composites with natural fibers and wood-modification of the fiber/filler–matrix interaction. J. Appl. Polym. Sci. 2012, 127, 1–17. [Google Scholar] [CrossRef]
- Sobczak, L.; Lang, R.W.; Haider, A. Polypropylene composites with natural fibers and wood – General mechanical property profiles. Compos. Sci. Technol. 2012, 72, 550–557. [Google Scholar] [CrossRef]
- Alrubaie, M.A.A.; Lopez-Anido, R.A.; Gardner, D.J.; Tajvidi, M.; Han, Y. Experimental investigation of the hygrothermal creep strain of wood–plastic composite lumber made from thermally modifified wood. J. Thermoplast. Compos. Mater. 2019, 33, 1248–1268. [Google Scholar] [CrossRef]
- Alrubaie MA, A.; Lopez-Anido, R.A.; Gardner, D.J.; Tajvidi, M.; Han, Y. Modeling the hygrothermal creep behavior of wood plastic composite (WPC) lumber made from thermally modified wood. J. Thermoplast. Compos. Mater. 2019, 33, 1109–1124. [Google Scholar] [CrossRef]
- Daniel, A.V. Structural Performance of Wood Plastic Composite Sheet Piling. J. Mater. Civ. Eng. 2010, 12, 1235–1243. [Google Scholar]
- Gardner, D.; Han, Y. Towards Structural Wood-Plastic Composites: Technical Innovations. In Proceedings of the 6th Meeting of the Nordic-Baltic Network in Wood Material Science and Engineering (WSE), Tallinn, Estonia, 21–22 October 2010. [Google Scholar]
- Haiar, K.J. Performance and Design of Prototype Wood-Plastic Composite Sections; Washington State University: Pullman, WA, USA, 2000. [Google Scholar]
- Hamel, S.E. Modeling the Time-Dependent Flexural Response of Wood-Plastic Composite Materials; University of Wisconsin-Madison: Madison, WI, USA, 2011. [Google Scholar]
- Dan, M.F.; Recek, S. Reliability of fiber-reinforced composite laminate plates. Probabilistic Eng. Mech. 2003, 18, 119–137. [Google Scholar]
- Yang, H.S.; Qiao, P.; Wolcott, M.P. Fatigue characterization and reliability analysis of wood flour filled polypropylene composites. Polym. Compos. 2010, 31, 554–560. [Google Scholar] [CrossRef]
- Lin, S.C. Reliability predictions of laminated composite plates with random system parameters. Probabilistic Eng. Mech. 2000, 15, 327–338. [Google Scholar] [CrossRef]
- Yu, G.W. Nondestructive Testing and Reliability Analysis of Wood Plastic Plate; Northeast Forestry University: Harbin, China, 2013. [Google Scholar]
- Yu, G.W.; Hu, Y.C.; Gu, J.Y. Relativity Analysis between Dynamic and Static Modulus of Elasticity on Different Thickness Wood-Plastic Structural Plates. Appl. Mech. Mater. 2011, 121, 4254–4258. [Google Scholar] [CrossRef]
- Chen, N.Z.; Sun, H.H.; Soares, C.G. Reliability analysis of a ship hull in composite material. Compos. Struct. 2003, 62, 59–66. [Google Scholar] [CrossRef]
- Chen, N.Z.; Soares, C.G. Reliability assessment of post-buckling compressive strength of laminated composite plates and stiffened panels under axial compression. Int. J. Solids Struct. 2007, 44, 7167–7182. [Google Scholar] [CrossRef]
- Slaughter, A.E. Design and Fatigue of a Structural Wood-Plastic Composite; Washington State University: Pullman, WA, USA, 2004. [Google Scholar]
- Jiang, L.; Fu, J.; He, C. Reliability analysis of wood-plastic composites in simulated seawater conditions: Effect of iron oxide pigments. J. Build. Eng. 2020, 31, 101318. [Google Scholar] [CrossRef]
- Jiang, L.; Fu, J.; Liu, L. Seawater Degradation Resistance of Straw Fiber-reinforced Polyvinyl Chloride Composites. BioResources 2020, 15, 5305–5315. [Google Scholar] [CrossRef]
- Schirp, A.; Plinke, B.; Napolow, D. Effectiveness of organic and inorganic pigments for mass colouration of thermo-mechanical pulp used in wood–plastic composites. Eur. J. Wood Wood Prod. 2015, 73, 5–16. [Google Scholar] [CrossRef]
- Haque, M.M.U.; Goda, K.; Ogoe, S.; Sunaga, Y. Fatigue analysis and fatigue reliability of polypropylene/wood flour composites. Adv. Ind. Eng. Polym. Res. 2019, 2, 136–142. [Google Scholar] [CrossRef]
- Yang, H.S.; Qiao, P.; Wolcott, M.P. Flexural Fatigue and Reliability Analysis of Wood Flour/High-density Polyethylene Composites. J. Reinf. Plast. Compos. 2010, 29, 1295–1310. [Google Scholar] [CrossRef]
- ASTMD790; Standard Test Methods for Flexural Properties of Unreinforced and Reinforced Plastics and Electrical Insulating Materials. American Society for Testing and Materials: West Conshohocken, PA, USA, 2010.
- Wilczyński, K.; Buziak, K.; Wilczyński, K.J.; Lewandowski, A.; Nastaj, A. Computer Modeling for Single-Screw Extrusion of Wood–Plastic Composites. Polymers 2018, 10, 295. [Google Scholar] [CrossRef] [PubMed] [Green Version]
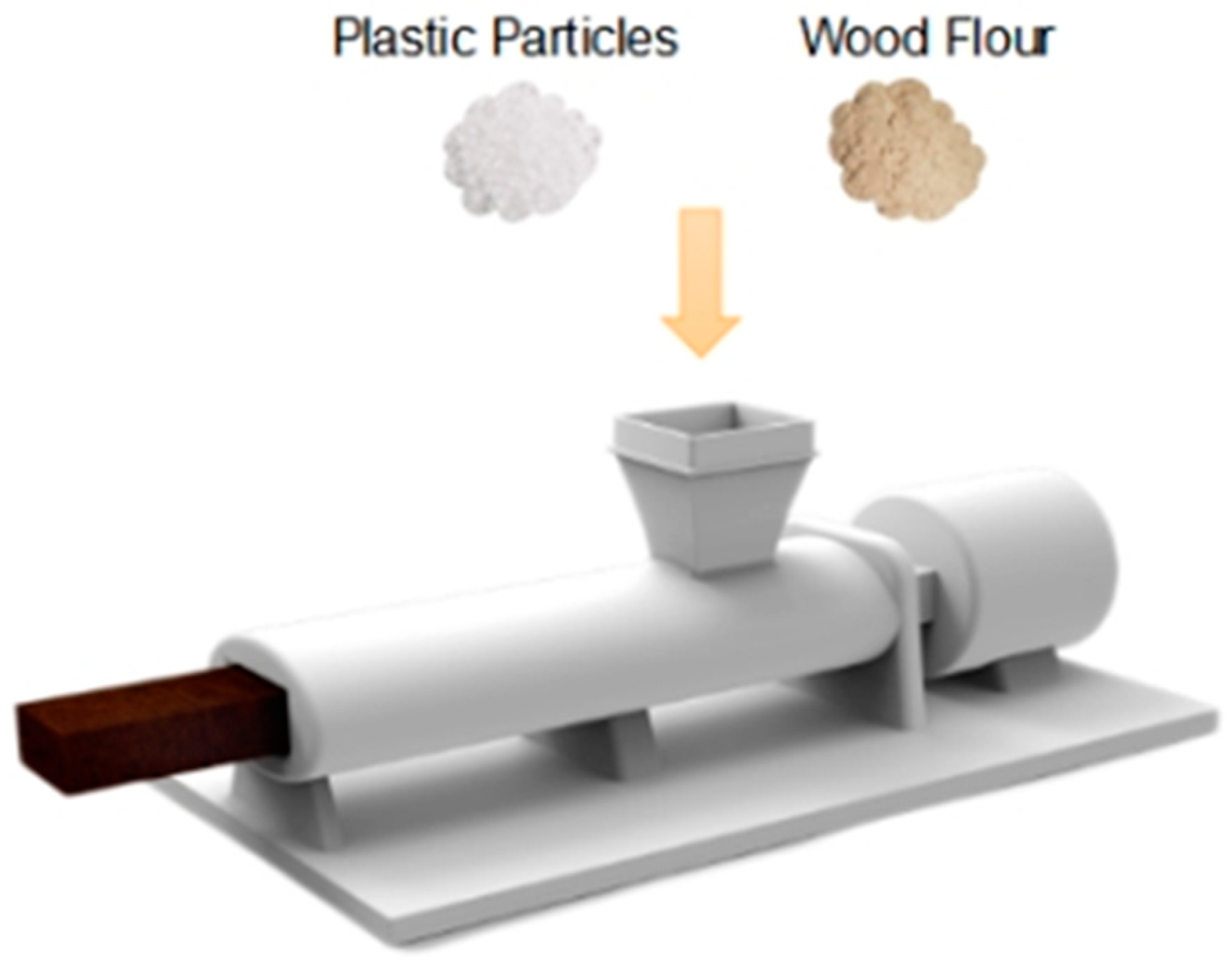
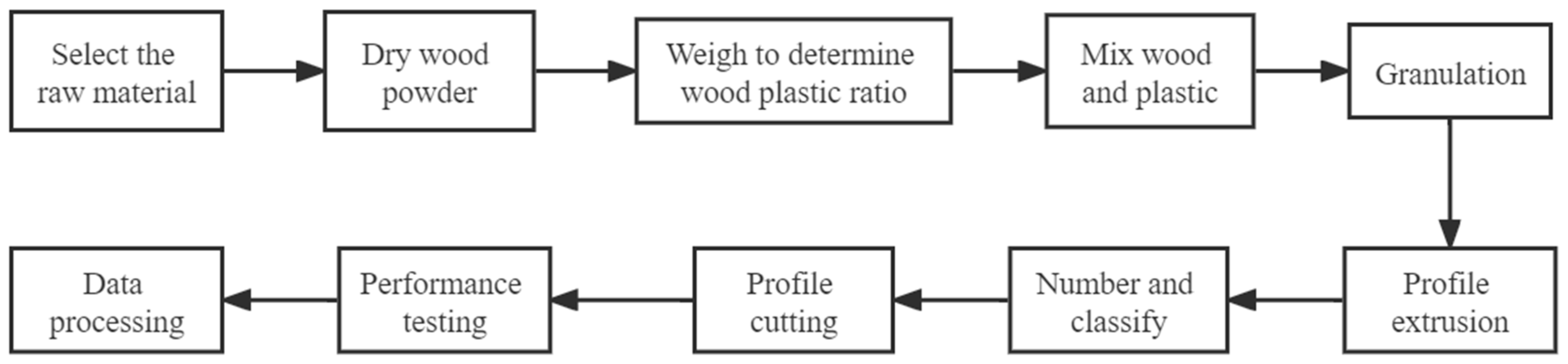


| Specimen Group | Wood Flour Content | Granulation Temperature (°C) | Coupling Agent Content | Screw Speed (r/min) |
|---|---|---|---|---|
| 1~5 | 30, 40, 50, 60, 70 | 140 | 3 | 120 |
| 6~10 | 30 | 130, 135, 140, 145, 150 | 3 | 120 |
| 11~15 | 40 | 140 | 1, 2, 3, 4, 5 | 120 |
| 16~20 | 50 | 140 | 3 | 60, 90, 120, 150, 180 |
| (a) The effect of wood flour content on reliability | ||||
| Specimen Number | Wood Flour Content /% | Modulus of Elasticity/Pa | Bending Strength /Pa | |
| Average Value | Standard Deviation | |||
| 1 | 30 | 2.2 × 109 | 1.1 × 108 | 4.2 × 107 |
| 2 | 40 | 3.6 × 109 | 1.8 × 108 | 5.0 × 107 |
| 3 | 50 | 4.9 × 109 | 2.5 × 108 | 5.6 × 107 |
| 4 | 60 | 4.8 × 109 | 2.4 × 108 | 6.5 × 107 |
| 5 | 70 | 4.4 × 109 | 2.2 × 108 | 6.0 × 107 |
| Distribution Type | - | Gaussian distribution | - | |
| (b) The effect of granulation temperature on reliability | ||||
| Specimen Number | Granulation Temperature/ °C | Modulus of Elasticity/Pa | Bending Strength /Pa | |
| Average Value | Standard Deviation | |||
| 6 | 130 | 2.0 × 109 | 1.0 × 108 | 4.0 × 107 |
| 7 | 135 | 2.5 × 109 | 1.25 × 108 | 5.5 × 107 |
| 8 | 140 | 3.0 × 109 | 1.5 × 108 | 5.2 × 107 |
| 9 | 145 | 2.4 × 109 | 1.2 × 108 | 5.3 × 107 |
| 10 | 150 | 2.8 × 109 | 1.4 × 108 | 5.8 × 107 |
| Distribution Type | - | Gaussian distribution | - | |
| (c) The effect of coupling agent content on reliability | ||||
| Specimen Number | Screw Speed r/min | Modulus of Elasticity/Pa | Bending Strength /Pa | |
| Average Value | Standard Deviation | |||
| 16 | 60 | 5.0 × 109 | 2.5 × 108 | 6.8 × 107 |
| 17 | 90 | 4.9 × 109 | 2.45 × 108 | 5.7 × 107 |
| 18 | 120 | 4.2 × 109 | 2.1 × 108 | 5.3 × 107 |
| 19 | 150 | 5.0 × 109 | 2.5 × 108 | 7.2 × 107 |
| 20 | 180 | 4.9 × 109 | 2.45 × 108 | 7.3 × 107 |
| Distribution Type | - | Gaussian distribution | - | |
| (d) The effect of rotation speed on reliability | ||||
| Specimen Number | Coupling Agent Content % | Modulus of Elasticity/Pa | Bending Strength /Pa | |
| Average Value | Standard Deviation | |||
| 11 | 1 | 3.4 × 109 | 1.7 × 108 | 5.0 × 107 |
| 12 | 2 | 3.6 × 109 | 1.8 × 108 | 5.0 × 107 |
| 13 | 3 | 4.0 × 109 | 2.0 × 108 | 7.0 × 107 |
| 14 | 4 | 3.8 × 109 | 1.9 × 108 | 6.7 × 107 |
| 15 | 5 | 3.6 × 109 | 1.8 × 108 | 6.5 × 107 |
| Distribution Type | - | Gaussian distribution | - | |
| Specimen Number | Wood Flour Content/% | Maximum Stress Mean Value/Pa | Bending Strength/Pa | Reliability/% | Safety Factor |
|---|---|---|---|---|---|
| 1 | 30 | 4.688 × 107 | 4.2 × 107 | 2.971 | 0.896 |
| 2 | 40 | 4.688 × 107 | 5.0 × 107 | 88.373 | 1.067 |
| 3 | 50 | 4.688 × 107 | 5.6 × 107 | 100 | 1.195 |
| 4 | 60 | 4.688 × 107 | 6.5 × 107 | 100 | 1.387 |
| 5 | 70 | 4.688 × 107 | 6.0 × 107 | 100 | 1.280 |
| Specimen Number | Granulation Temperature/°C | Maximum Stress Mean Value/Pa | Bending Strength/Pa | Reliability/% | Safety Factor |
|---|---|---|---|---|---|
| 6 | 130 | 4.690 × 107 | 4.0 × 107 | 0 | 0.853 |
| 7 | 135 | 4.690 × 107 | 5.2 × 107 | 96.890 | 1.109 |
| 8 | 140 | 4.690 × 107 | 5.3 × 107 | 98.480 | 1.130 |
| 9 | 145 | 4.690 × 107 | 5.5 × 107 | 99.059 | 1.173 |
| 10 | 150 | 4.690 × 107 | 5.8 × 107 | 100 | 1.237 |
| Specimen Number | Coupling Agent Content % | Maximum Stress Mean/Pa | Bending Strength/Pa | Reliability/% | Safety Factor |
|---|---|---|---|---|---|
| 11 | 1 | 4.690 × 107 | 5.0 × 107 | 92.362 | 1.066 |
| 12 | 2 | 4.690 × 107 | 5.0 × 107 | 92.362 | 1.066 |
| 13 | 3 | 4.690 × 107 | 5.3 × 107 | 100 | 1.493 |
| 14 | 4 | 4.690 × 107 | 5.5 × 107 | 100 | 1.429 |
| 15 | 5 | 4.690 × 107 | 5.8 × 107 | 100 | 1.386 |
| Specimen Number | Screw Speed/r/min | Maximum Stress Mean Value/Pa | Bending Strength/Pa | Reliability/% | Safety Factor |
|---|---|---|---|---|---|
| 16 | 60 | 4.690 × 107 | 6.8 × 107 | 100 | 1.450 |
| 17 | 90 | 4.690 × 107 | 5.7 × 107 | 100 | 1.215 |
| 18 | 120 | 4.690 × 107 | 5.3 × 107 | 98.480 | 1.130 |
| 19 | 150 | 4.690 × 107 | 7.2 × 107 | 100 | 1.535 |
| 20 | 180 | 4.690 × 107 | 7.3 × 107 | 100 | 1.557 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, L.; Wang, D.; Yan, J. Reliability Study of Wood–Plastic Composites Based on Probabilistic Finite Elements. Polymers 2023, 15, 312. https://doi.org/10.3390/polym15020312
Feng L, Wang D, Yan J. Reliability Study of Wood–Plastic Composites Based on Probabilistic Finite Elements. Polymers. 2023; 15(2):312. https://doi.org/10.3390/polym15020312
Chicago/Turabian StyleFeng, Li, Dejin Wang, and Jun Yan. 2023. "Reliability Study of Wood–Plastic Composites Based on Probabilistic Finite Elements" Polymers 15, no. 2: 312. https://doi.org/10.3390/polym15020312
APA StyleFeng, L., Wang, D., & Yan, J. (2023). Reliability Study of Wood–Plastic Composites Based on Probabilistic Finite Elements. Polymers, 15(2), 312. https://doi.org/10.3390/polym15020312







