Quality Control of Thermally Modified Western Hemlock Wood Using Near-Infrared Spectroscopy and Explainable Machine Learning
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
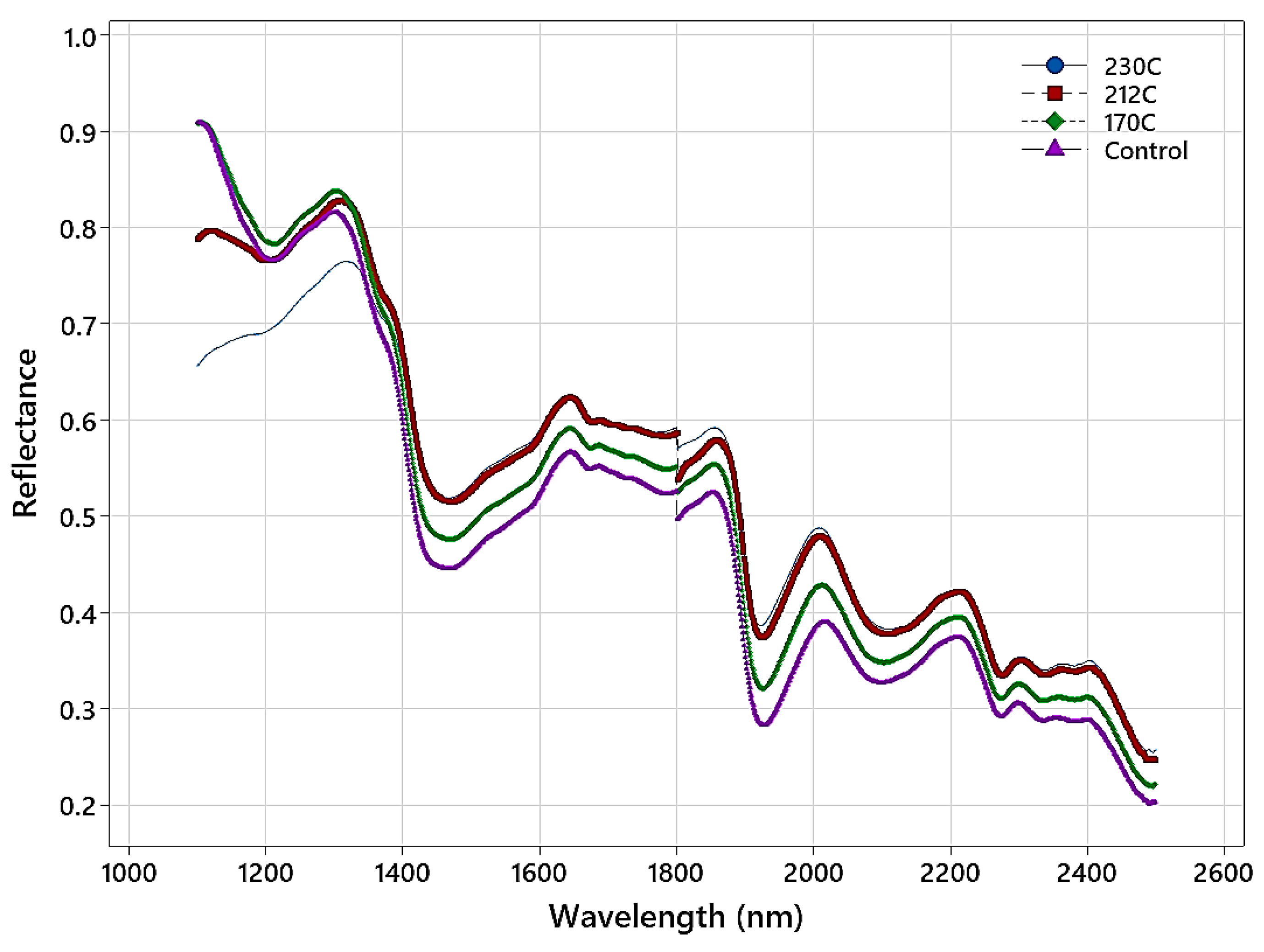
3.1. NIR Spectra and Color Features
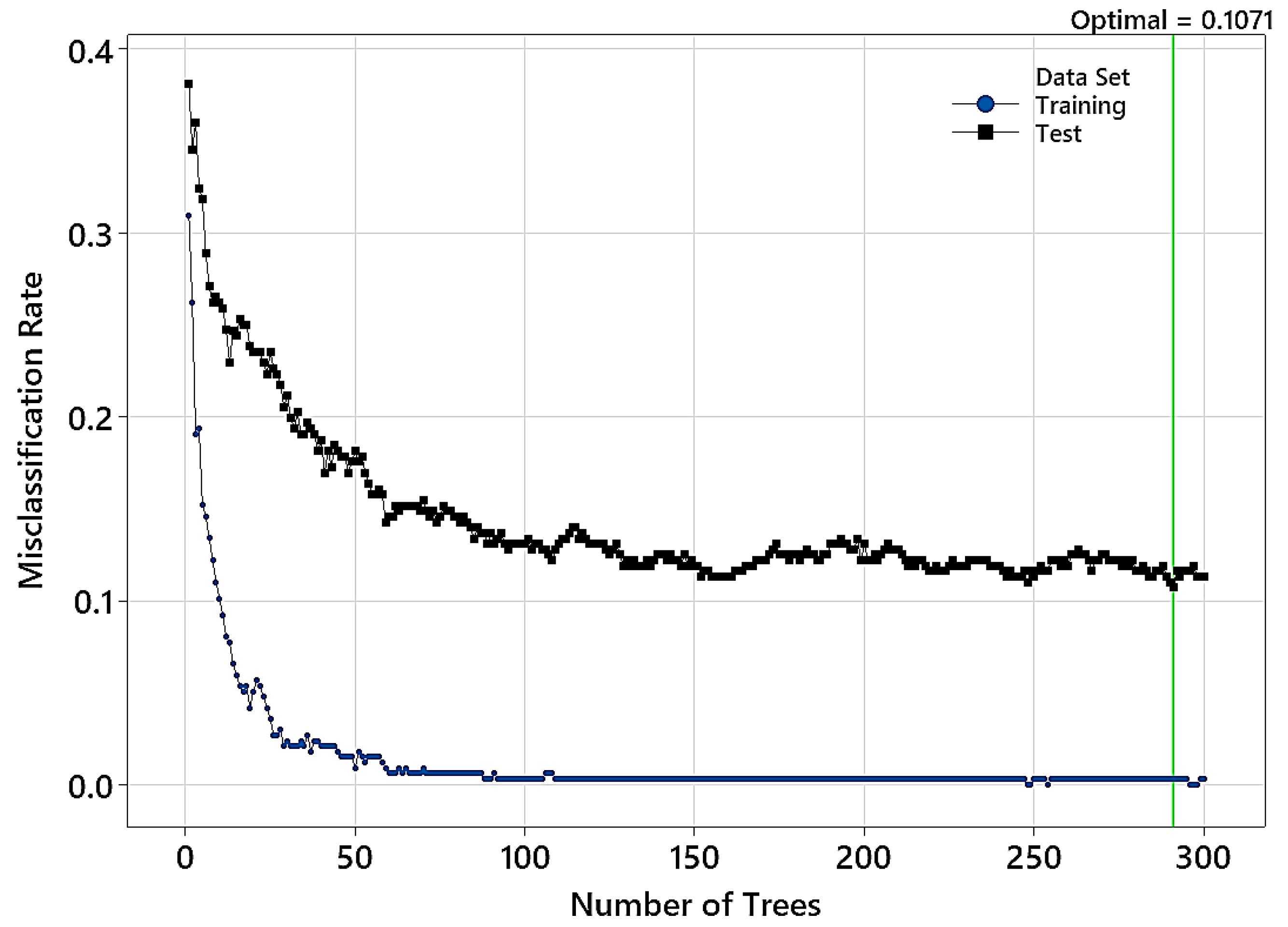
3.2. Binary Classification
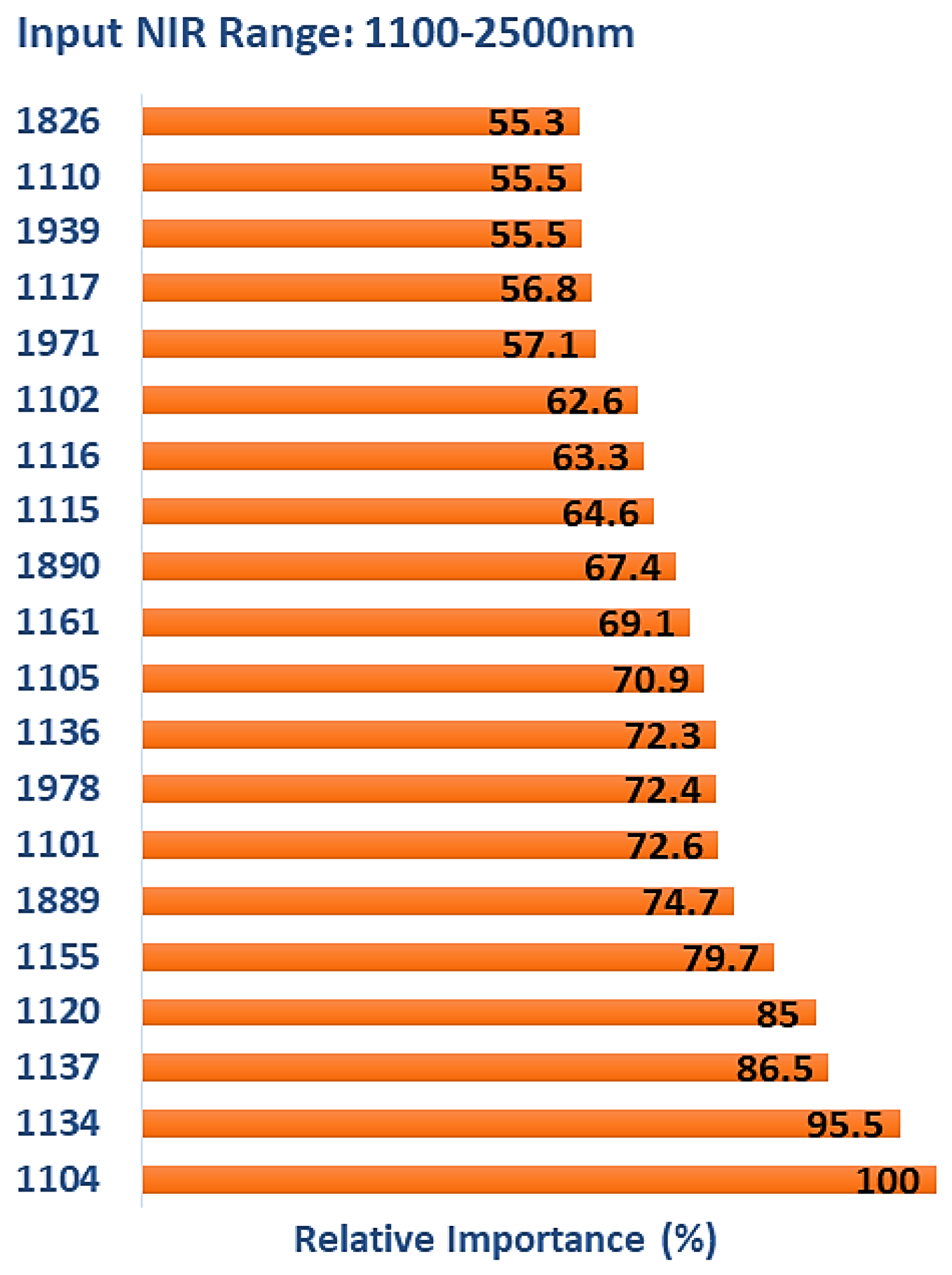
3.3. Multiclass Classification (1100–2500 nm)
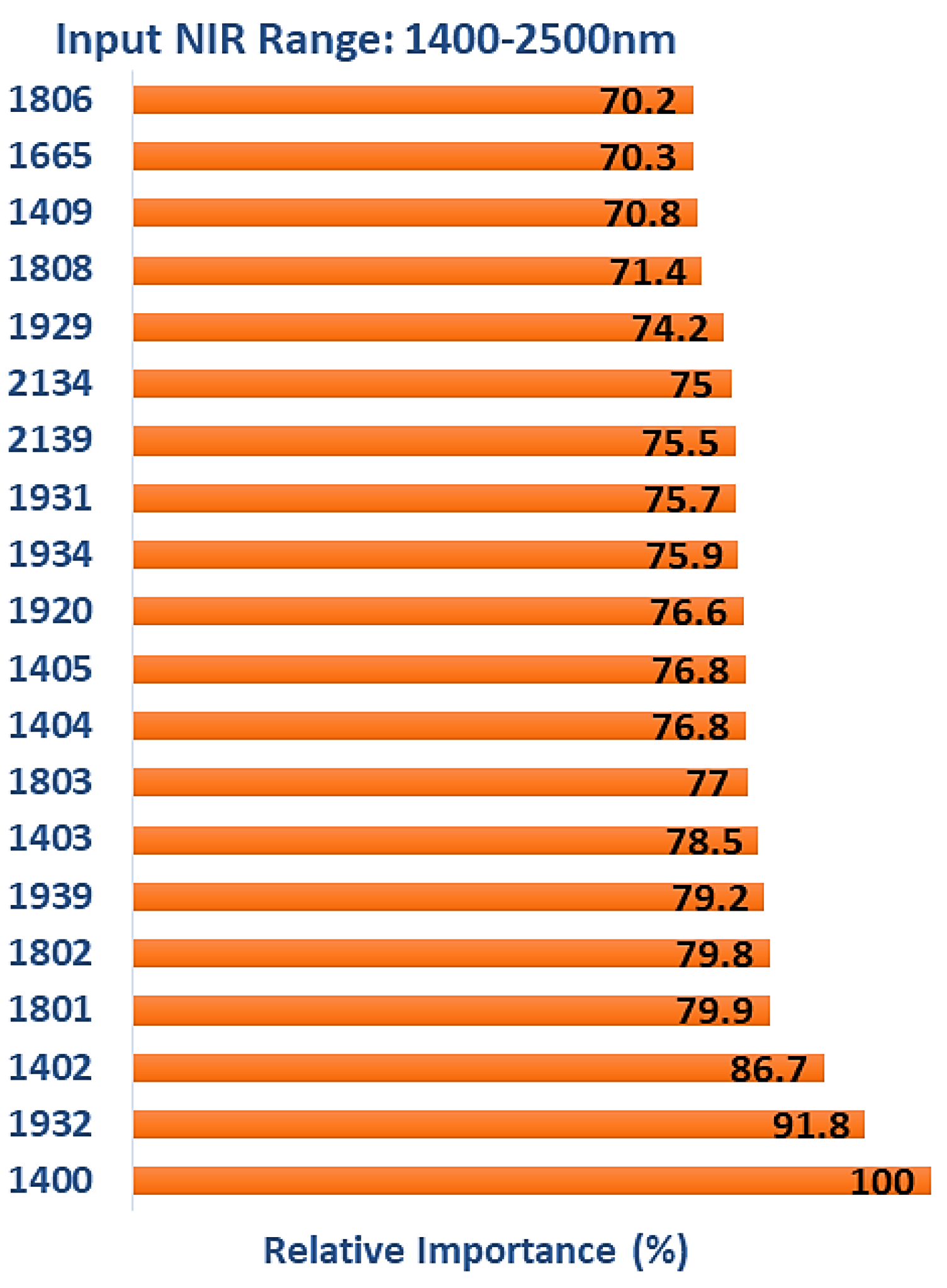
3.4. Multiclass Classification (1400–2500 nm)
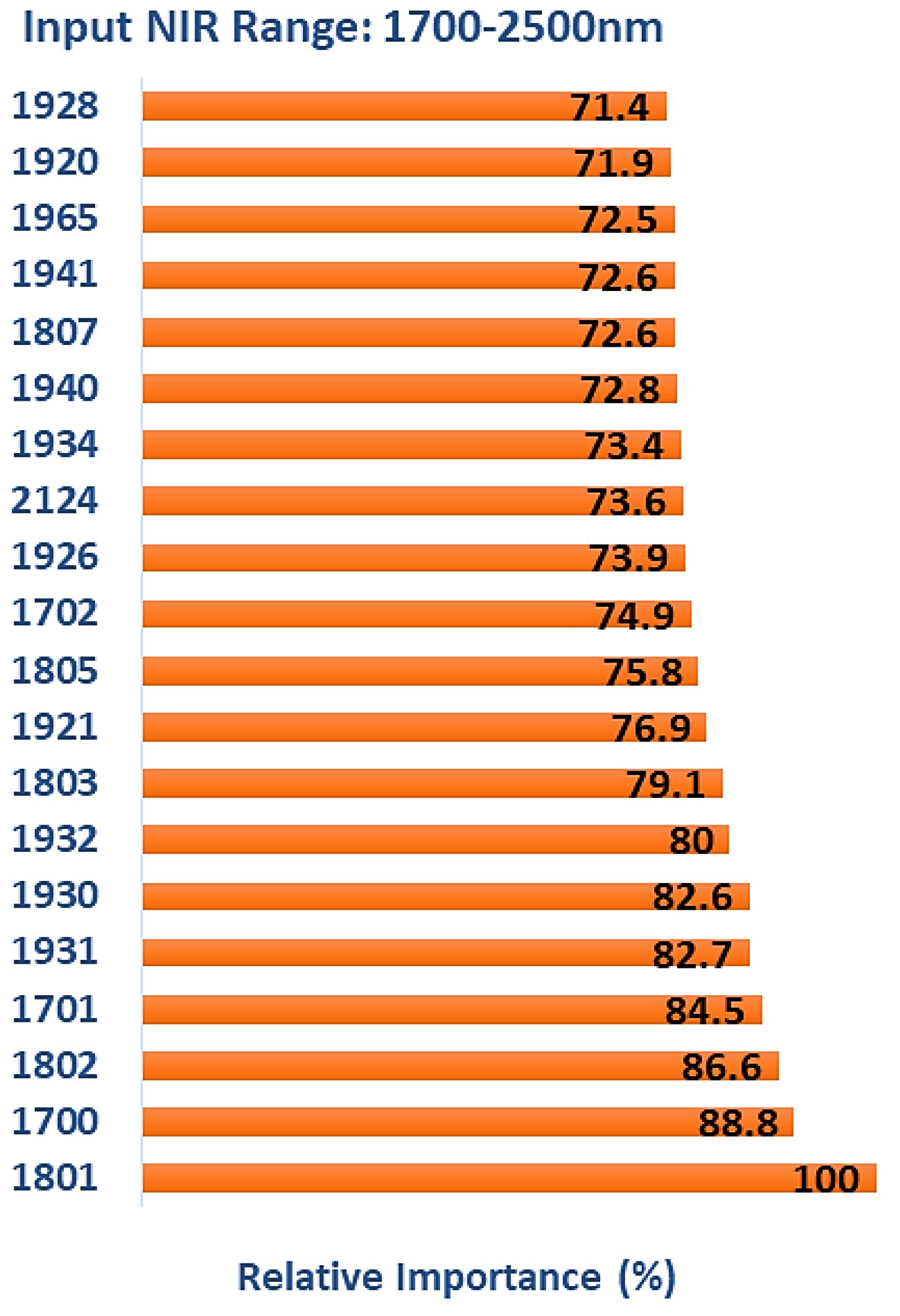
3.5. Multiclass Classification (1700–2500 nm)
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Esteves, B. Wood modification by heat treatment: A review. BioResources 2009, 4, 370–404. [Google Scholar] [CrossRef]
- Sandberg, D.; Kutnar, A.; Mantanis, G. Wood modification technologies-a review. Iforest-Biogeosci. For. 2017, 10, 895. [Google Scholar] [CrossRef]
- Haftkhani, A.R.; Abdoli, F.; Sepehr, A.; Mohebby, B. Regression and ANN models for predicting MOR and MOE of heat-treated fir wood. J. Build. Eng. 2021, 42, 102788. [Google Scholar] [CrossRef]
- Goli, G.; Negro, F.; Emmerich, L.; Militz, H. Thermal and chemical modification of wood–a combined approach for exclusive, high-demanding performance products. Wood Mater. Sci. Eng. 2023, 18, 58–66. [Google Scholar] [CrossRef]
- Wentzel, M.; González-Prieto, Ó.; Brischke, C.; Militz, H. Physico-Mechanical Properties of Thermally Modified Eucalyptus Nitens Wood for Decking Applications. Wood Ind. Drv. Ind. 2019, 70, 235–245. [Google Scholar] [CrossRef]
- Batista, D.; Wentzel, M.; Brischke, C.; Militz, H. Impact of Process Duration on Selected Physical Properties of Thermally Modified Eucalyptus Wood. In Proceedings of the 10th European Conference on Wood Modification, Nancy, France, 25–26 April 2022. [Google Scholar]
- Candelier, K.; Thevenon, M.-F.; Petrissans, A.; Dumarcay, S.; Gerardin, P.; Petrissans, M. Control of wood thermal treatment and its effects on decay resistance: A review. Ann. For. Sci. 2016, 73, 571–583. [Google Scholar] [CrossRef]
- Esteves, B. Improvement of technological quality of eucalypt wood by heat treatment in air at 170–200 °C. For. Prod. J. 2007, 57, 47–52. [Google Scholar]
- Cademartori, P.H.G.d.; Missio, A.L.; Mattos, B.D.; Gatto, D.A. Effect of thermal treatments on technological properties of wood from two Eucalyptus species. An. Acad. Bras. Ciências 2015, 87, 471–481. [Google Scholar] [CrossRef]
- Esteves, B.; Marques, A.V.; Domingos, I.; Pereira, H. Influence of steam heating on the properties of pine (Pinus pinaster) and eucalypt (Eucalyptus globulus) wood. Wood Sci. Technol. 2007, 41, 193–207. [Google Scholar] [CrossRef]
- Srinivas, K.; Pandey, K.K. Effect of heat treatment on color changes, dimensional stability, and mechanical properties of wood. J. Wood Chem. Technol. 2012, 32, 304–316. [Google Scholar] [CrossRef]
- Kesik, H.I.; Korkut, S.; Hiziroglu, S.; Sevik, H. An evaluation of properties of four heat treated wood species. Ind. Crops Prod. 2014, 60, 60–65. [Google Scholar] [CrossRef]
- Tiryaki, S.; Aydın, A. An artificial neural network model for predicting compression strength of heat treated woods and comparison with a multiple linear regression model. Constr. Build. Mater. 2014, 62, 102–108. [Google Scholar] [CrossRef]
- Tjeerdsma, B.; Boonstra, M.; Pizzi, A.; Tekely, P.; Militz, H. Characterisation of thermally modified wood: Molecular reasons for wood performance improvement. Holz Als Roh-Und Werkst. 1998, 56, 149–153. [Google Scholar] [CrossRef]
- Bourgois, J.; Guyonnet, R. Characterization and analysis of torrefied wood. Wood Sci. Technol. 1988, 22, 143–155. [Google Scholar] [CrossRef]
- Srinivas, K.; Pandey, K.K. Photodegradation of thermally modified wood. J. Photochem. Photobiol. B Biol. 2012, 117, 140–145. [Google Scholar] [CrossRef]
- Barcík, Š.; Gašparík, M.; Razumov, E.Y. Effect of temperature on the color changes of wood during thermal modification. Cellul. Chem. Technol 2015, 49, 789–798. [Google Scholar]
- Barcík, Š.; Gašparík, M.; Razumov, E.Y. Effect of thermal modification on the colour changes of oak wood. Wood Res. 2015, 60, 385–396. [Google Scholar]
- SAKA, S. Structure and chemical composition of wood as a natural composite material. In Recent Research on Wood and Wood-Based Materials; Elsevier: Amsterdam, The Netherlands, 1993; pp. 1–20. [Google Scholar]
- Tuong, V.M.; Li, J. Effect of heat treatment on the change in color. BioResources 2010, 5, 1257–1267. [Google Scholar] [CrossRef]
- Hon, D.N.; Shiraishi, N. Wood and Cellulosic Chemistry, Revised, and Expanded; CRC Press: Boca Raton, FL, USA, 2000. [Google Scholar]
- Chen, Y.; Fan, Y.; Gao, J.; Stark, N.M. The effect of heat treatment on the chemical and color change of black locust (Robinia pseudoacacia) wood flour. BioResources 2012, 7, 1157–1170. [Google Scholar] [CrossRef]
- Rowell, R.M. Chemical modification of wood: A short review. Wood Mater. Sci. Eng. 2006, 1, 29–33. [Google Scholar] [CrossRef]
- Nasir, V.; Nourian, S.; Zhou, Z.; Rahimi, S.; Avramidis, S.; Cool, J. Classification and characterization of thermally modified timber using visible and near-infrared spectroscopy and artificial neural networks: A comparative study on the performance of different NDE methods and ANNs. Wood Sci. Technol. 2019, 53, 1093–1109. [Google Scholar] [CrossRef]
- Willems, W.; Lykidis, C.; Altgen, M.; Clauder, L. Quality control methods for thermally modified wood: COST action FP0904 2010–2014: Thermo-hydro-mechanical wood behaviour and processing. Holzforschung 2015, 69, 875–884. [Google Scholar] [CrossRef]
- Riggio, M.; Anthony, R.W.; Augelli, F.; Kasal, B.; Lechner, T.; Muller, W.; Tannert, T. In situ assessment of structural timber using non-destructive techniques. Mater. Struct. 2014, 47, 749–766. [Google Scholar] [CrossRef]
- Patzelt, M.; Emsenhuber, G.; Stingl, R. Colour measurement as means of quality control of thermally treated wood. In Proceedings of the European Conference on Wood Modification, Gent, Belgium, 3–4 April 2003; pp. 213–218. [Google Scholar]
- van Blokland, J.; Nasir, V.; Cool, J.; Avramidis, S.; Adamopoulos, S. Machine learning-based prediction of internal checks in weathered thermally modified timber. Constr. Build. Mater. 2021, 281, 122193. [Google Scholar] [CrossRef]
- Nasir, V.; Nourian, S.; Avramidis, S.; Cool, J. Stress wave evaluation by accelerometer and acoustic emission sensor for thermally modified wood classification using three types of neural networks. Eur. J. Wood Wood Prod. 2019, 77, 45–55. [Google Scholar] [CrossRef]
- Nasir, V.; Nourian, S.; Avramidis, S.; Cool, J. Classification of thermally treated wood using machine learning techniques. Wood Sci. Technol. 2019, 53, 275–288. [Google Scholar] [CrossRef]
- Brischke, C.; Welzbacher, C.R.; Brandt, K.; Rapp, A.O. Quality control of thermally modified timber: Interrelationship between heat treatment intensities and CIE L* a* b* color data on homogenized wood samples. Holzforschung 2007, 61, 19–22. [Google Scholar] [CrossRef]
- Gonzalez-Pena, M.M.; Hale, M.D. Colour in thermally modified wood of beech, Norway spruce and Scots pine. Part 1: Colour evolution and colour changes. Holzforschung 2009, 63, 385–393. [Google Scholar] [CrossRef]
- Schnabel, T.; Zimmer, B.; Petutschnigg, A.; Schonberger, S. An approach to classify thermally modified hardwoods by color. For. Prod. J. 2007, 57, 105. [Google Scholar]
- Johansson, D.; Morén, T. The potential of colour measurement for strength prediction of thermally treated wood. Holz Als Roh-Und Werkst. 2006, 64, 104–110. [Google Scholar] [CrossRef]
- Bächle, H.; Zimmer, B.; Wegener, G. Classification of thermally modified wood by FT-NIR spectroscopy and SIMCA. Wood Sci. Technol. 2012, 46, 1181–1192. [Google Scholar] [CrossRef]
- Mao, K. Identifying critical variables of principal components for unsupervised feature selection. IEEE Trans. Syst. Man Cybern. Part B 2005, 35, 339–344. [Google Scholar] [CrossRef] [PubMed]
- Arrieta, A.B.; Díaz-Rodríguez, N.; Del Ser, J.; Bennetot, A.; Tabik, S.; Barbado, A.; García, S.; Gil-López, S.; Molina, D.; Benjamins, R. Explainable Artificial Intelligence (XAI): Concepts, taxonomies, opportunities and challenges toward responsible AI. Inf. Fusion 2020, 58, 82–115. [Google Scholar] [CrossRef]
- Schimleck, L.; Ayanleye, S.; Avramidis, S.; Nasir, V. A chemistry-based explainable machine learning model based on NIR spectra for predicting wood properties and understanding wavelength selection. Wood Mater. Sci. Eng. 2023, 1–12. [Google Scholar] [CrossRef]
- Burkart, N.; Huber, M.F. A survey on the explainability of supervised machine learning. J. Artif. Intell. Res. 2021, 70, 245–317. [Google Scholar] [CrossRef]
- Linardatos, P.; Papastefanopoulos, V.; Kotsiantis, S. Explainable ai: A review of machine learning interpretability methods. Entropy 2020, 23, 18. [Google Scholar] [CrossRef]
- Wojtas, M.; Chen, K. Feature importance ranking for deep learning. Adv. Neural Inf. Process. Syst. 2020, 33, 5105–5114. [Google Scholar]
- ASTM D2244-16; Standard Practice for Calculation of Color Tolerances and Color Differences from Instrumentally Measured Color Coordinates. ASTM International: West Conshohocken, PA, USA, 2016.
- Nasir, V.; Ali, S.D.; Mohammadpanah, A.; Raut, S.; Nabavi, M.; Dahlen, J.; Schimleck, L. Fiber Quality Prediction Using Nir Spectral Data: Tree-Based Ensemble Learning Vs. Deep Neural Networks. Wood Fiber Sci. 2023, 55, 100–115. [Google Scholar] [CrossRef]
- Sun, Y.; Lin, Q.; He, X.; Zhao, Y.; Dai, F.; Qiu, J.; Cao, Y. Wood species recognition with small data: A deep learning approach. Int. J. Comput. Intell. Syst. 2021, 14, 1451–1460. [Google Scholar] [CrossRef]
- Carty, D.M.; Young, T.M.; Zaretzki, R.L.; Guess, F.M.; Petutschnigg, A. Predicting and correlating the strength properties of wood composite process parameters by use of boosted regression tree models. For. Prod. J. 2015, 65, 365–371. [Google Scholar] [CrossRef]
- Somvanshi, M.; Chavan, P.; Tambade, S.; Shinde, S. A review of machine learning techniques using decision tree and support vector machine. In Proceedings of the 2016 International Conference on Computing Communication Control and Automation (ICCUBEA), Pune, India, 12–13 August 2016; pp. 1–7. [Google Scholar]
- Bikmukhametov, T.; Jäschke, J. Oil production monitoring using gradient boosting machine learning algorithm. Ifac-Pap. 2019, 52, 514–519. [Google Scholar] [CrossRef]
- Steinberg, D. CART: Classification and regression trees. In The Top Ten Algorithms in Data Mining; Wu, X., Kumar, V., Eds.; CRC Press: Boca Raton, FL, USA, 2009; pp. 179–202. [Google Scholar]
- Nasir, V.; Fathi, H.; Kazemirad, S. Combined machine learning–wave propagation approach for monitoring timber mechanical properties under UV aging. Struct. Health Monit. 2021, 20, 2035–2053. [Google Scholar] [CrossRef]
- Modeler, S.P. Introducing TreeNet Gradient Boosting Machine; Minitab, LLC: State College, PA, USA, 2019. [Google Scholar]
- Mitsui, K.; Takada, H.; Sugiyama, M.; Hasegawa, R. Changes in the properties of light-irradiated wood with heat treatment. Part 1. Effect of treatment conditions on the change in color. Holzforschung 2001, 55, 601–605. [Google Scholar] [CrossRef]
- Nourian, S. Thermal Modification of Western Hemlock (Tsuga heterophylla); University of British Columbia: Vancouver, BC, Canada, 2018. [Google Scholar]
- Bourgois, J.; Janin, G.; Guyonnet, R. Measuring colour: A method of studying and optimizing the chemical transformations of thermally-treated wood. Holzforschung 1991, 45, 377–382. [Google Scholar] [CrossRef]
- Sehlstedt-Persson, M. Colour responses to heat-treatment of extractives and sap from pine and spruce. In Proceedings of the International IUFRO Wood Drying Conference, Firenze, Italy, 25–29 August 2003; pp. 459–464. [Google Scholar]
- Bekhta, P.; Niemz, P. Effect of high temperature on the change in color, dimensional stability and mechanical properties of spruce wood. Holzforschung 2010, 57, 539–546. [Google Scholar] [CrossRef]
- Sundqvist, B.; Karlsson, O.; Westermark, U. Determination of formic-acid and acetic acid concentrations formed during hydrothermal treatment of birch wood and its relation to colour, strength and hardness. Wood Sci. Technol. 2006, 40, 549–561. [Google Scholar] [CrossRef]
- Schwanninger, M.; Rodrigues, J.C.; Fackler, K. A review of band assignments in near infrared spectra of wood and wood components. J. Near Infrared Spectrosc. 2011, 19, 287–308. [Google Scholar] [CrossRef]
- Grinsztajn, L.; Oyallon, E.; Varoquaux, G. Why do tree-based models still outperform deep learning on typical tabular data? Adv. Neural Inf. Process. Syst. 2022, 35, 507–520. [Google Scholar]







| Statistics | Control vs. 170 °C | Control vs. 212 °C | Control vs. 230 °C | 170 °C vs. 212 °C | 170 °C vs. 230 °C | 212 °C vs. 230 °C | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Training | Test | Training | Test | Training | Test | Training | Test | Training | Test | Training | Test | |
| True positive rate (Sensitivity) % | 100.00 | 90.48 | 100.00 | 98.81 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 97.62 | 96.43 |
| False positive rate (type I error) % | 3.57 | 8.33 | 1.19 | 0.00 | 0.00 | 0.00 | 0.00 | 1.19 | 1.19 | 0.00 | 2.38 | 2.38 |
| False negative rate (type II error) % | 0.00 | 9.52 | 0.00 | 1.19 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 2.38 | 3.57 |
| True negative rate (specificity) % | 96.43 | 91.67 | 98.81 | 100.00 | 100.00 | 100.00 | 100.00 | 98.81 | 98.81 | 100.00 | 97.62 | 97.62 |
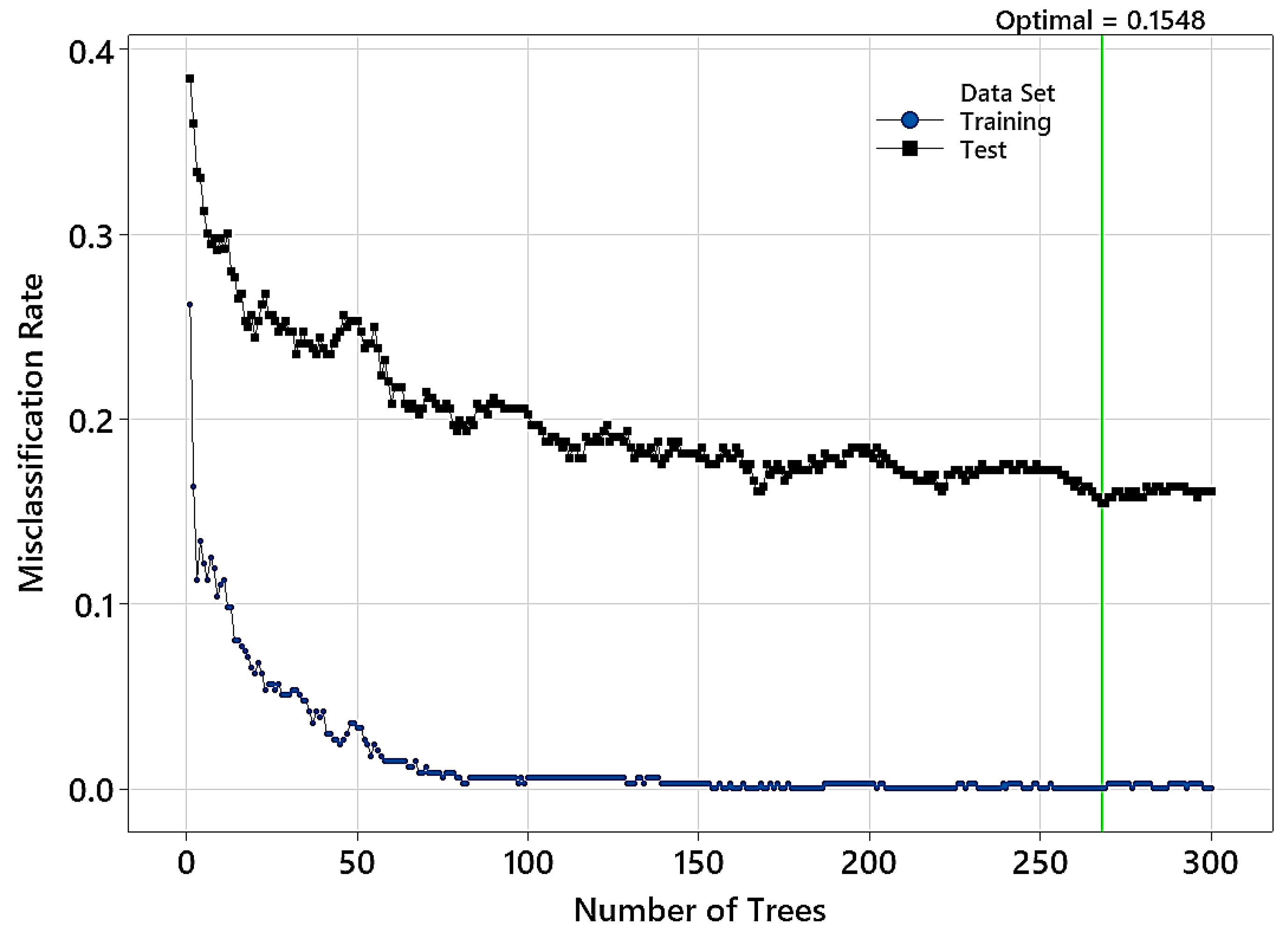
| Model | Optimal Number of Trees | Misclassification Rate | Learning Rate | Subsample Fraction | Maximum Terminal Nodes |
|---|---|---|---|---|---|
| 1 | 173 | 0.175 | 0.001 | 0.2 | 12 |
| 2 | 283 | 0.101 | 0.010 | 0.2 | 12 |
| 3 | 115 | 0.080 | 0.050 | 0.2 | 12 |
| 4 | 140 | 0.071 | 0.100 | 0.2 | 12 |
| 5 | 126 | 0.136 | 0.001 | 0.3 | 12 |
| 6 | 299 | 0.068 | 0.010 | 0.3 | 12 |
| 7 | 239 | 0.059 | 0.050 | 0.3 | 12 |
| 8 | 272 | 0.065 | 0.100 | 0.3 | 12 |
| 9 | 166 | 0.113 | 0.001 | 0.4 | 12 |
| 10 | 253 | 0.080 | 0.010 | 0.4 | 12 |
| 11 | 245 | 0.062 | 0.050 | 0.4 | 12 |
| 12 | 237 | 0.056 | 0.100 | 0.4 | 12 |
| 13 | 96 | 0.113 | 0.001 | 0.5 | 12 |
| 14 | 287 | 0.080 | 0.010 | 0.5 | 12 |
| 15 | 246 | 0.065 | 0.050 | 0.5 | 12 |
| 16 | 208 | 0.068 | 0.100 | 0.5 | 12 |
| Wood Class | Count | Predicted Class (Training) | Predicted Class (Test) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 230°C | 212 °C | 170 °C | Control | Correct % | 230 °C | 212 °C | 170 ° C | Control | Correct % | ||
| 230 °C | 84 | 84 | 0 | 0 | 0 | 100.00 | 81 | 3 | 0 | 0 | 96.43 |
| 212 °C | 84 | 0 | 84 | 0 | 0 | 100.00 | 3 | 81 | 0 | 0 | 96.43 |
| 170 °C | 84 | 0 | 0 | 84 | 0 | 100.00 | 0 | 0 | 81 | 3 | 96.43 |
| Control | 84 | 0 | 0 | 0 | 84 | 100.00 | 0 | 0 | 10 | 74 | 88.10 |
| All | 336 | 84 | 84 | 84 | 84 | 100.00 | 84 | 84 | 91 | 77 | 94.35 |
| Model | Optimal Number of Trees | Misclassification Rate | Learning Rate | Subsample Fraction | Maximum Terminal Nodes |
|---|---|---|---|---|---|
| 1 | 113 | 0.330 | 0.001 | 0.2 | 12 |
| 2 | 254 | 0.226 | 0.010 | 0.2 | 12 |
| 3 | 254 | 0.142 | 0.050 | 0.2 | 12 |
| 4 | 295 | 0.128 | 0.100 | 0.2 | 12 |
| 5 | 293 | 0.270 | 0.001 | 0.3 | 12 |
| 6 | 270 | 0.169 | 0.010 | 0.3 | 12 |
| 7 | 287 | 0.130 | 0.050 | 0.3 | 12 |
| 8 | 291 | 0.107 | 0.100 | 0.3 | 12 |
| 9 | 66 | 0.223 | 0.001 | 0.4 | 12 |
| 10 | 254 | 0.160 | 0.010 | 0.4 | 12 |
| 11 | 288 | 0.125 | 0.050 | 0.4 | 12 |
| 12 | 198 | 0.121 | 0.100 | 0.4 | 12 |
| 13 | 297 | 0.214 | 0.001 | 0.5 | 12 |
| 14 | 298 | 0.148 | 0.010 | 0.5 | 12 |
| 15 | 219 | 0.124 | 0.050 | 0.5 | 12 |
| 16 | 193 | 0.116 | 0.100 | 0.5 | 12 |
| Wood Class | Count | Predicted Class (Training) | Predicted Class (Test) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 230 °C | 212 °C | 170 °C | Control | Correct % | 230 °C | 212 °C | 170 °C | Control | Correct % | ||
| 230 °C | 84 | 84 | 0 | 0 | 0 | 100.00 | 77 | 4 | 3 | 0 | 91.67 |
| 212 °C | 84 | 1 | 83 | 0 | 0 | 98.81 | 6 | 76 | 2 | 0 | 90.48 |
| 170 °C | 84 | 0 | 0 | 84 | 0 | 100.00 | 0 | 5 | 73 | 6 | 86.90 |
| Control | 84 | 0 | 0 | 0 | 84 | 100.00 | 0 | 0 | 10 | 74 | 88.10 |
| All | 336 | 85 | 83 | 84 | 84 | 99.70 | 83 | 85 | 88 | 80 | 89.29 |
| Model | Optimal Number of Trees | Misclassification Rate | Learning Rate | Subsample Fraction | Maximum Terminal Nodes |
|---|---|---|---|---|---|
| 1 | 165 | 0.375 | 0.001 | 0.2 | 12 |
| 2 | 295 | 0.267 | 0.010 | 0.2 | 12 |
| 3 | 282 | 0.193 | 0.050 | 0.2 | 12 |
| 4 | 265 | 0.163 | 0.100 | 0.2 | 12 |
| 5 | 290 | 0.318 | 0.001 | 0.3 | 12 |
| 6 | 296 | 0.199 | 0.010 | 0.3 | 12 |
| 7 | 294 | 0.157 | 0.050 | 0.3 | 12 |
| 8 | 152 | 0.157 | 0.100 | 0.3 | 12 |
| 9 | 284 | 0.256 | 0.001 | 0.4 | 12 |
| 10 | 300 | 0.190 | 0.010 | 0.4 | 12 |
| 11 | 268 | 0.154 | 0.050 | 0.4 | 12 |
| 12 | 293 | 0.160 | 0.100 | 0.4 | 12 |
| 13 | 240 | 0.250 | 0.001 | 0.5 | 12 |
| 14 | 292 | 0.205 | 0.010 | 0.5 | 12 |
| 15 | 155 | 0.175 | 0.050 | 0.5 | 12 |
| 16 | 222 | 0.163 | 0.100 | 0.5 | 12 |
| Actual Class | Count | Predicted Class (Training) | Predicted Class (Test) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 230 °C | 212 °C | 170 °C | Control | Correct % | 230 °C | 212 °C | 170 °C | Control | Correct % | ||
| 230 °C | 84 | 84 | 0 | 0 | 0 | 100.00 | 75 | 7 | 2 | 0 | 89.29 |
| 212 °C | 84 | 0 | 84 | 0 | 0 | 100.00 | 9 | 70 | 5 | 0 | 83.33 |
| 170 °C | 84 | 0 | 0 | 84 | 0 | 100.00 | 2 | 9 | 67 | 6 | 79.76 |
| Control | 84 | 0 | 0 | 0 | 84 | 100.00 | 0 | 1 | 11 | 72 | 85.71 |
| All | 336 | 84 | 84 | 84 | 84 | 100.00 | 86 | 87 | 85 | 78 | 84.52 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nasir, V.; Schimleck, L.; Abdoli, F.; Rashidi, M.; Sassani, F.; Avramidis, S. Quality Control of Thermally Modified Western Hemlock Wood Using Near-Infrared Spectroscopy and Explainable Machine Learning. Polymers 2023, 15, 4147. https://doi.org/10.3390/polym15204147
Nasir V, Schimleck L, Abdoli F, Rashidi M, Sassani F, Avramidis S. Quality Control of Thermally Modified Western Hemlock Wood Using Near-Infrared Spectroscopy and Explainable Machine Learning. Polymers. 2023; 15(20):4147. https://doi.org/10.3390/polym15204147
Chicago/Turabian StyleNasir, Vahid, Laurence Schimleck, Farshid Abdoli, Maria Rashidi, Farrokh Sassani, and Stavros Avramidis. 2023. "Quality Control of Thermally Modified Western Hemlock Wood Using Near-Infrared Spectroscopy and Explainable Machine Learning" Polymers 15, no. 20: 4147. https://doi.org/10.3390/polym15204147
APA StyleNasir, V., Schimleck, L., Abdoli, F., Rashidi, M., Sassani, F., & Avramidis, S. (2023). Quality Control of Thermally Modified Western Hemlock Wood Using Near-Infrared Spectroscopy and Explainable Machine Learning. Polymers, 15(20), 4147. https://doi.org/10.3390/polym15204147











