Research on Resilient Modulus Prediction Model and Equivalence Analysis for Polymer Reinforced Subgrade Soil under Dry–Wet Cycle
Abstract
:1. Introduction
2. Resilient Modulus Prediction Model
2.1. Development of Resilient Modulus Model
2.2. Resilient Modulus with Dry–Wet Cycle
3. Materials and Experiments
3.1. Raw Materials and Specimen Preparation
3.1.1. Soil
3.1.2. Filter Paper Test
3.2. Triaxial Test of Dynamic Resilient Modulus with Dry–Wet Cycle
3.2.1. Dry–Wet Cycle
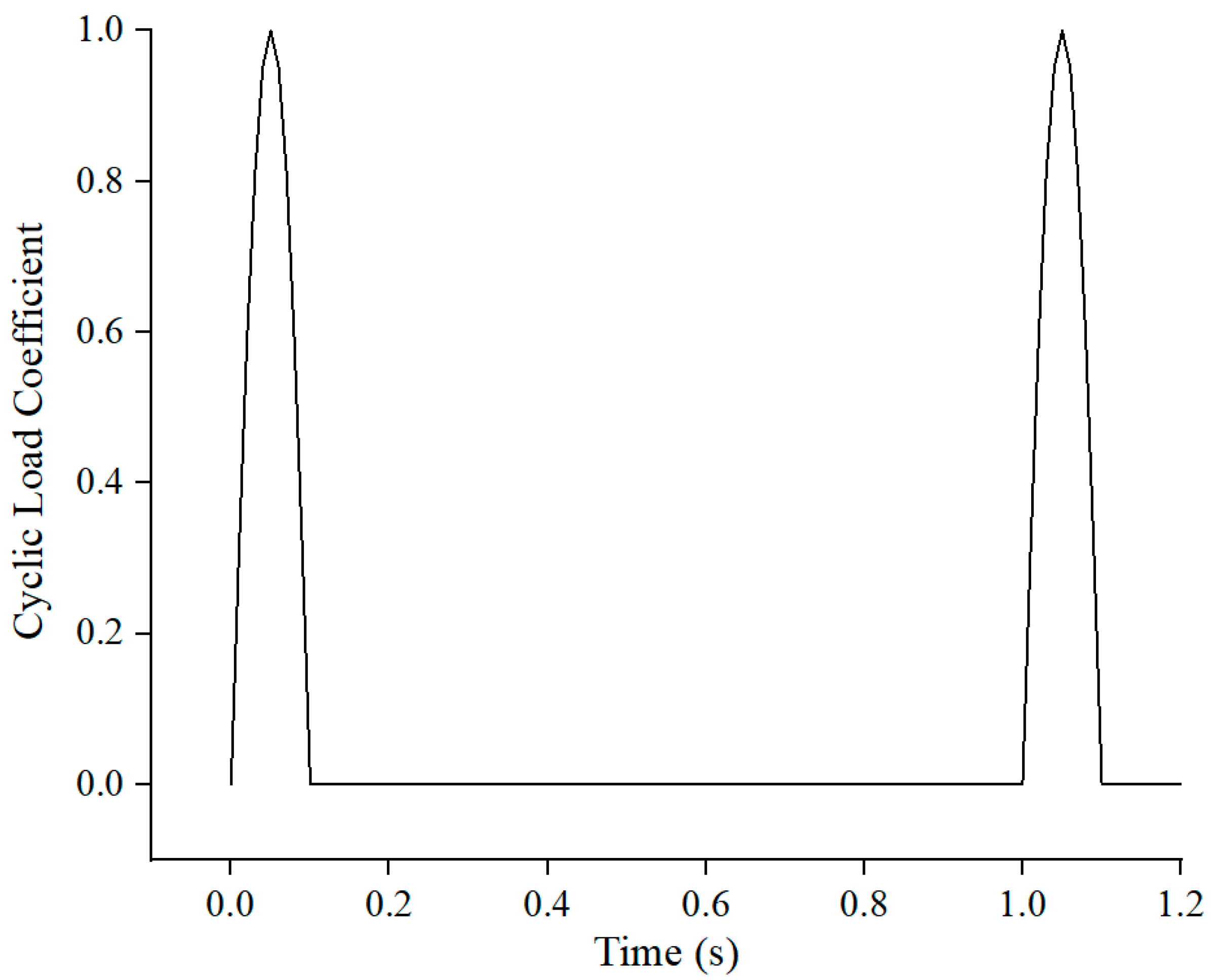
3.2.2. Dynamic Resilient Modulus
4. Analysis of Resilient Modulus Model
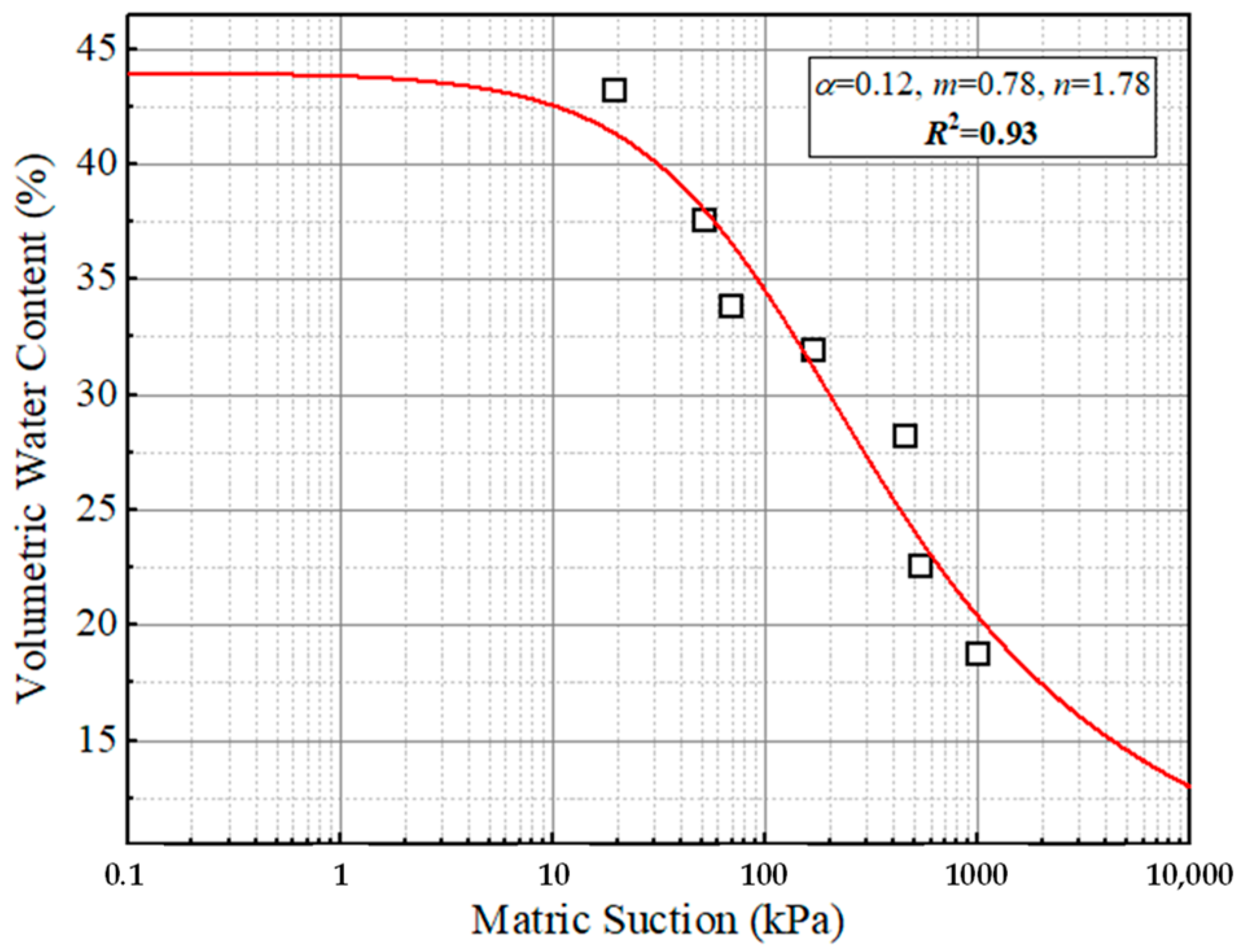
4.1. The Curve of SWCC
4.2. Results of Triaxial Test
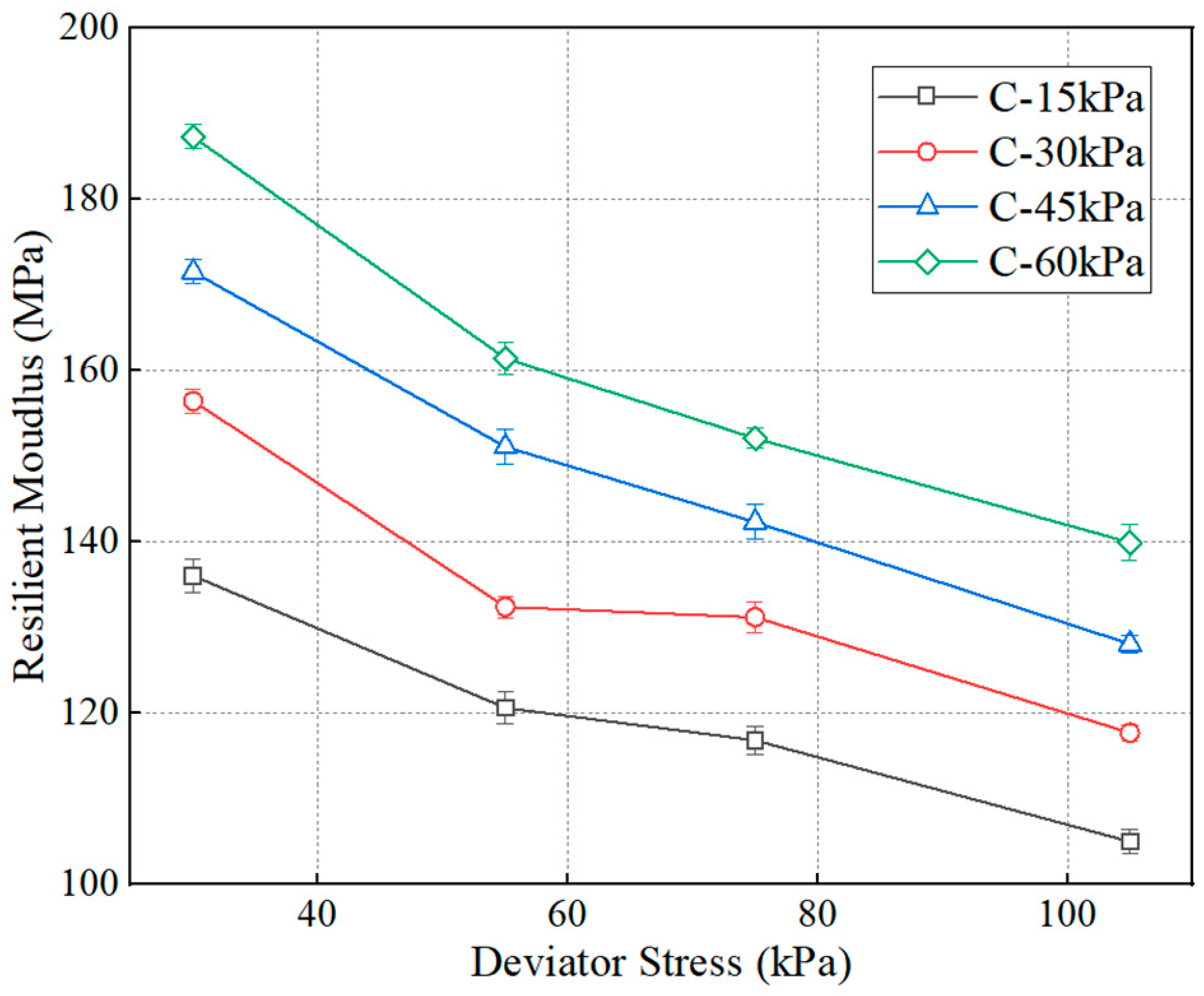
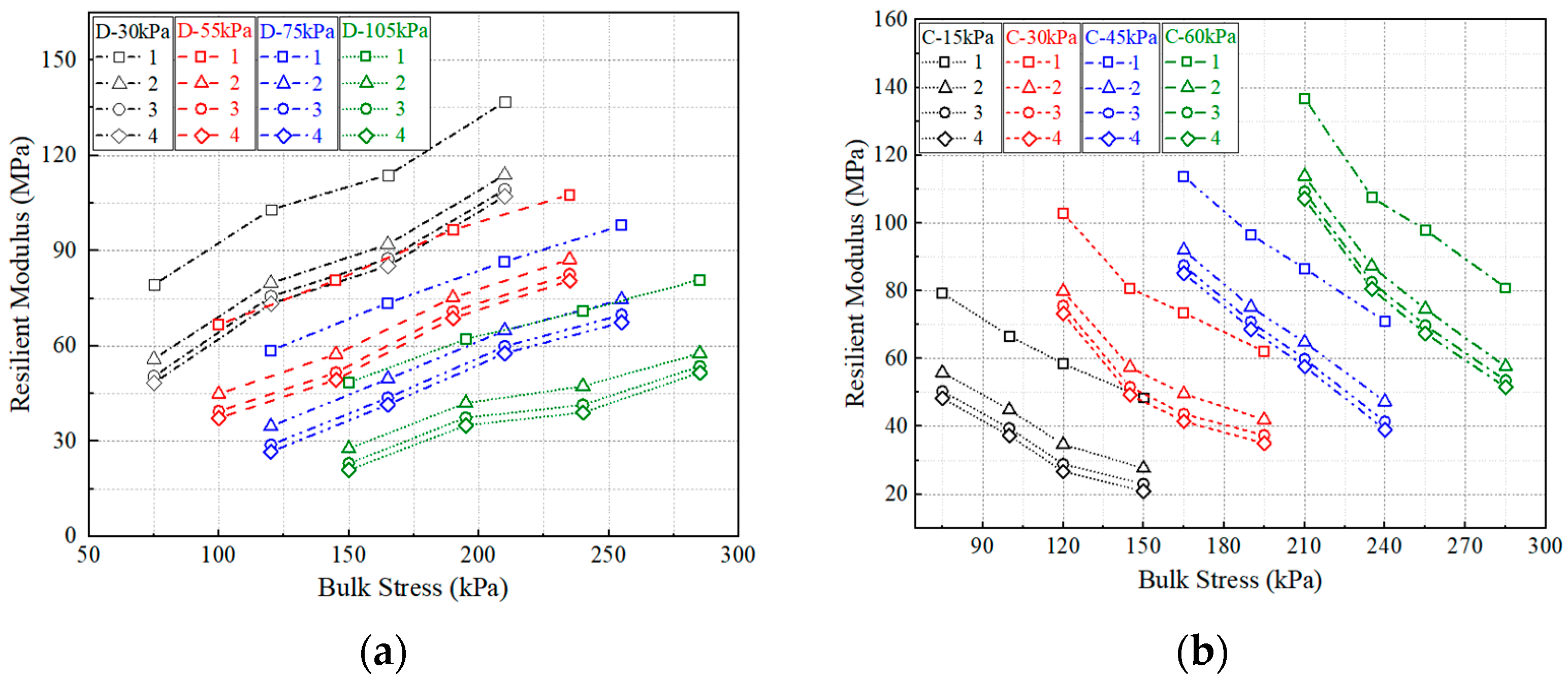
4.2.1. Effect of Deviator Stress
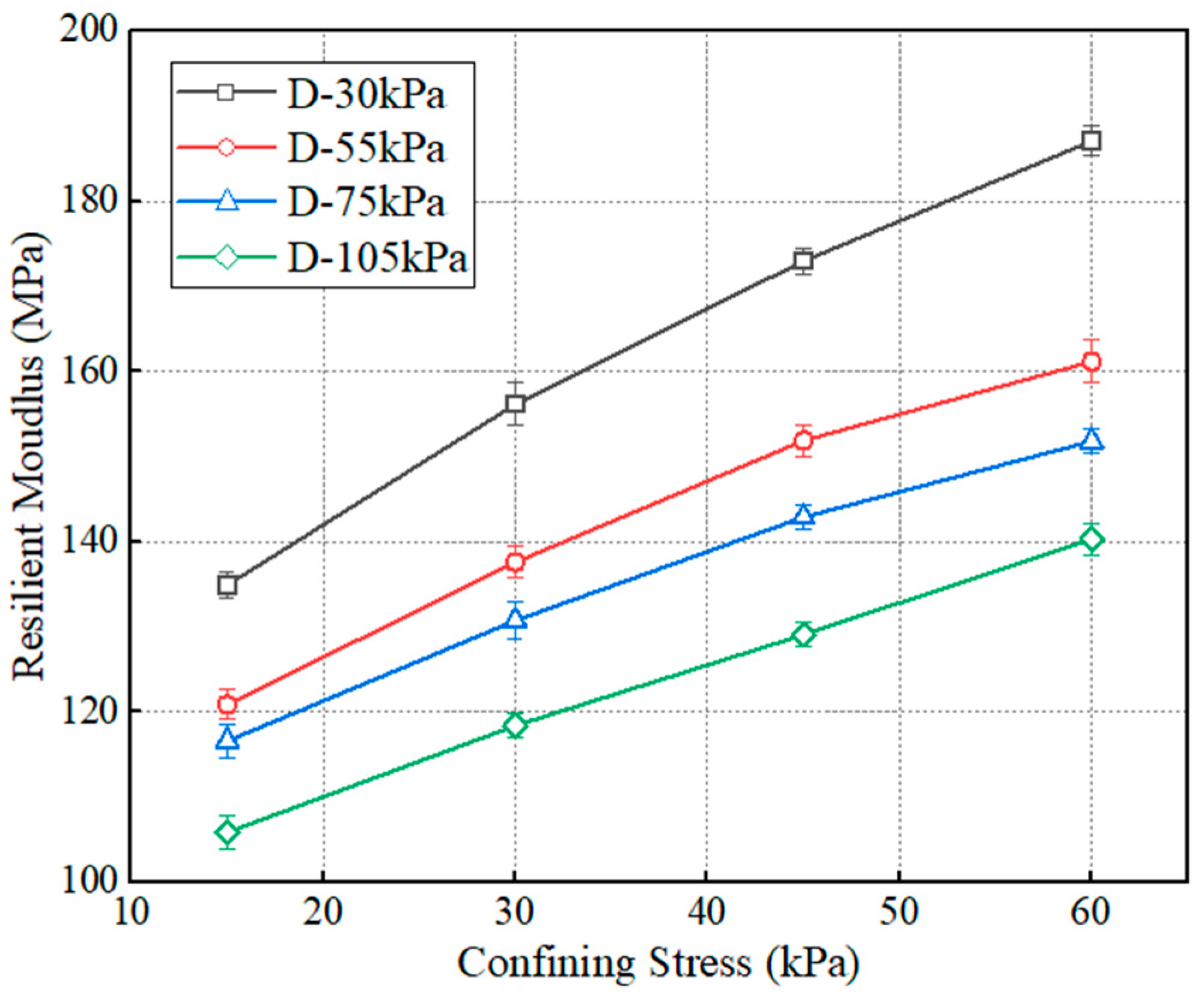
4.2.2. Effect of Confining Stress
4.2.3. Effect of Stress State
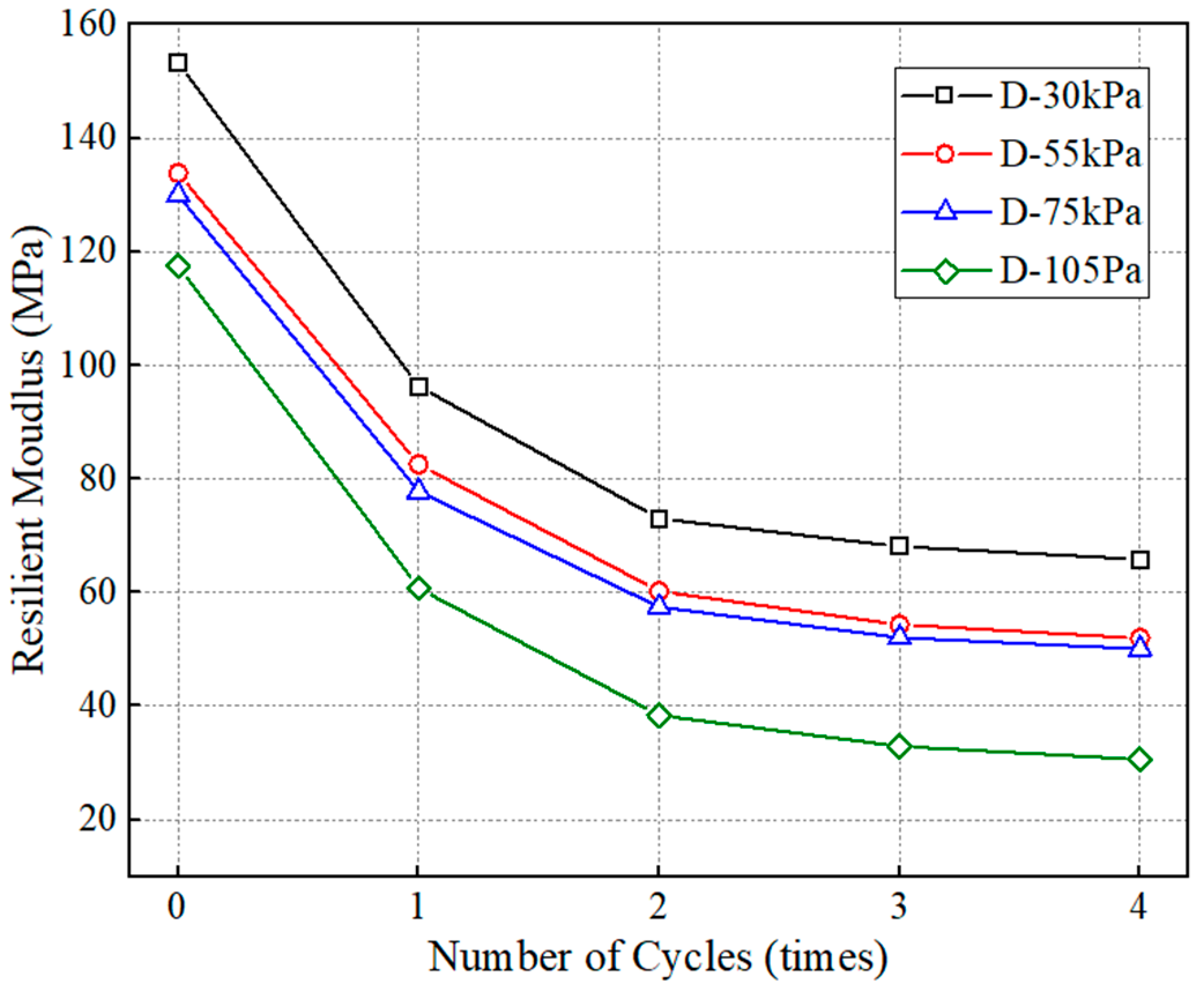
4.2.4. Effect of Dry–Wet Cycle Number
4.3. Determination of Resilient Modulus Prediction Model
5. FEM Analysis
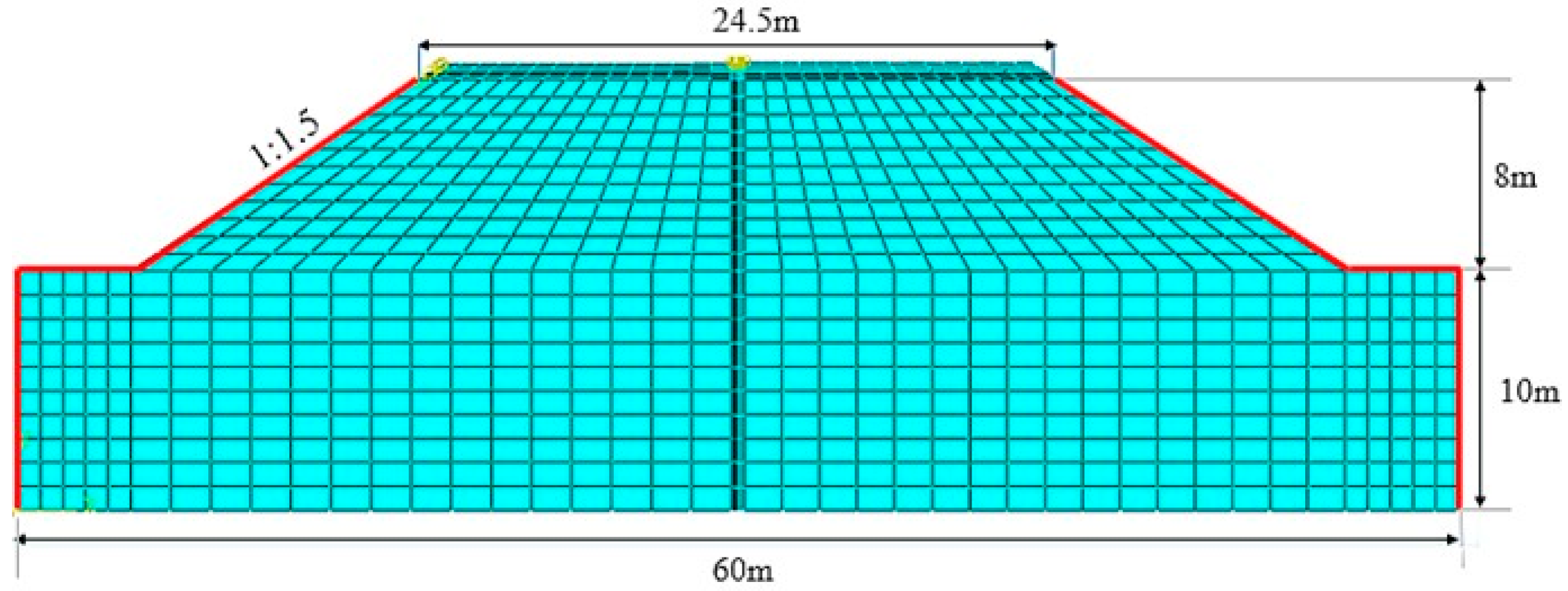
5.1. Establishment of FEM Model
5.1.1. FEM Model
5.1.2. Material Parameter
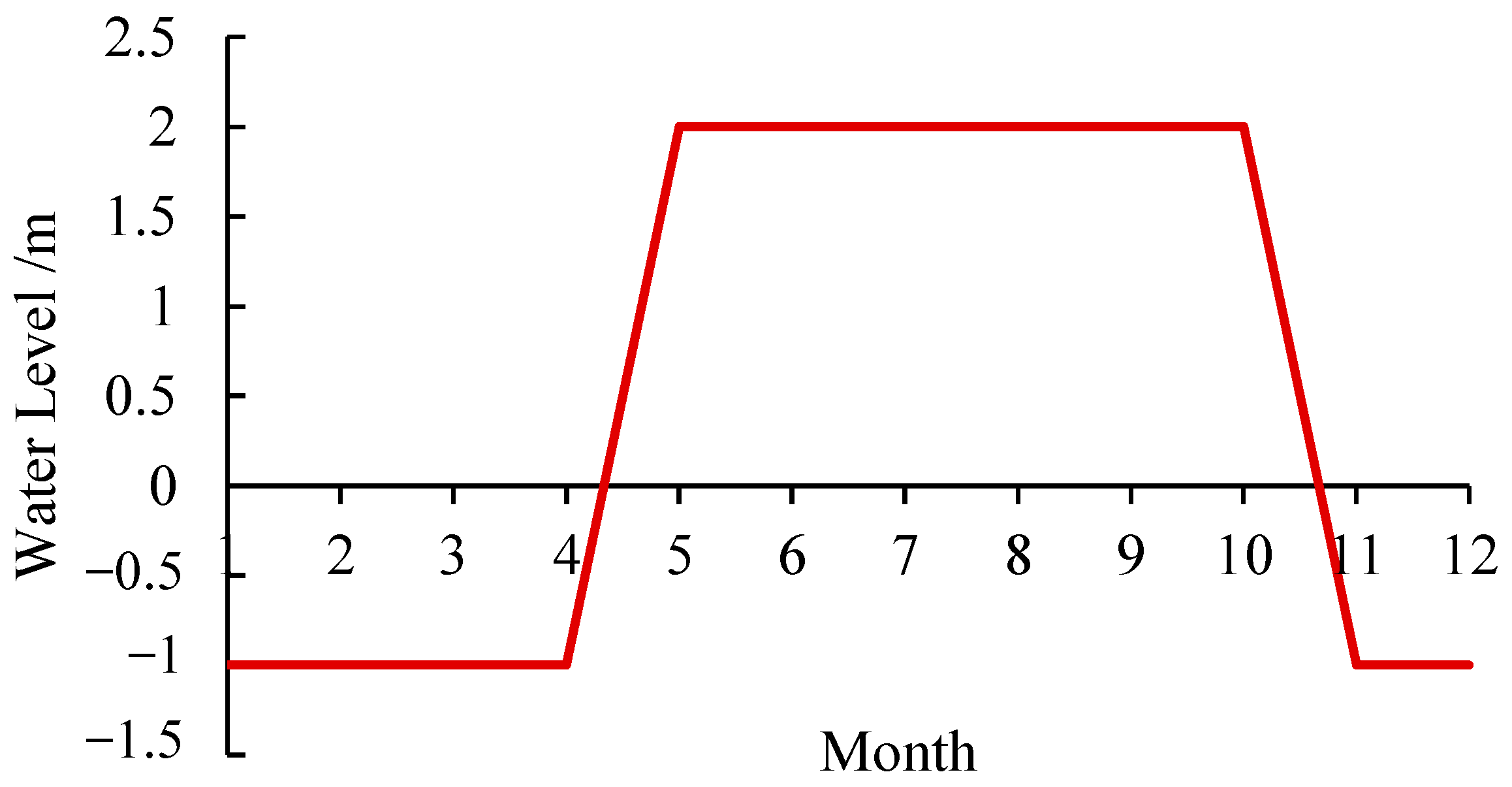
5.1.3. Periodic Change in Water Level
5.1.4. Load and Mesh
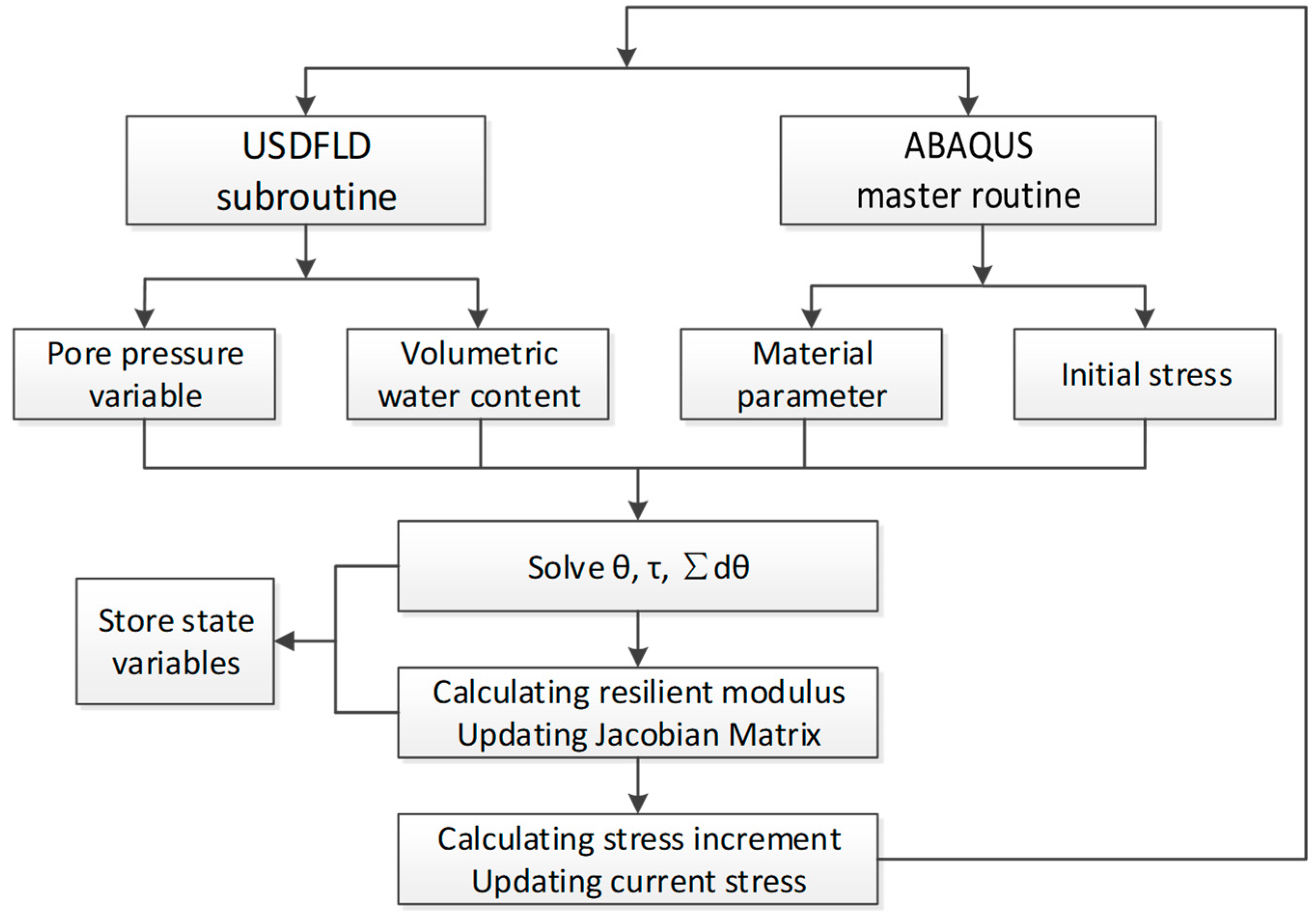
5.1.5. Calculation Logic
5.2. Result Analysis
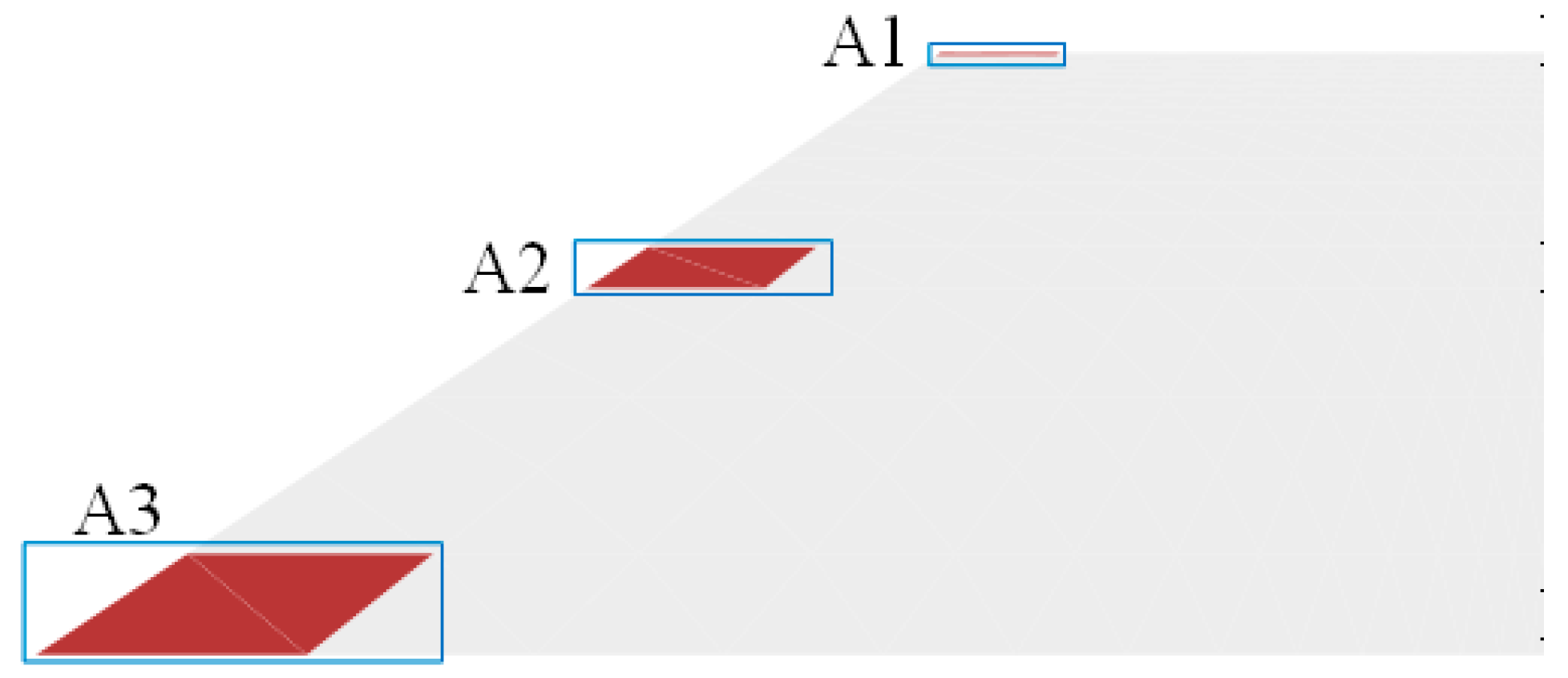
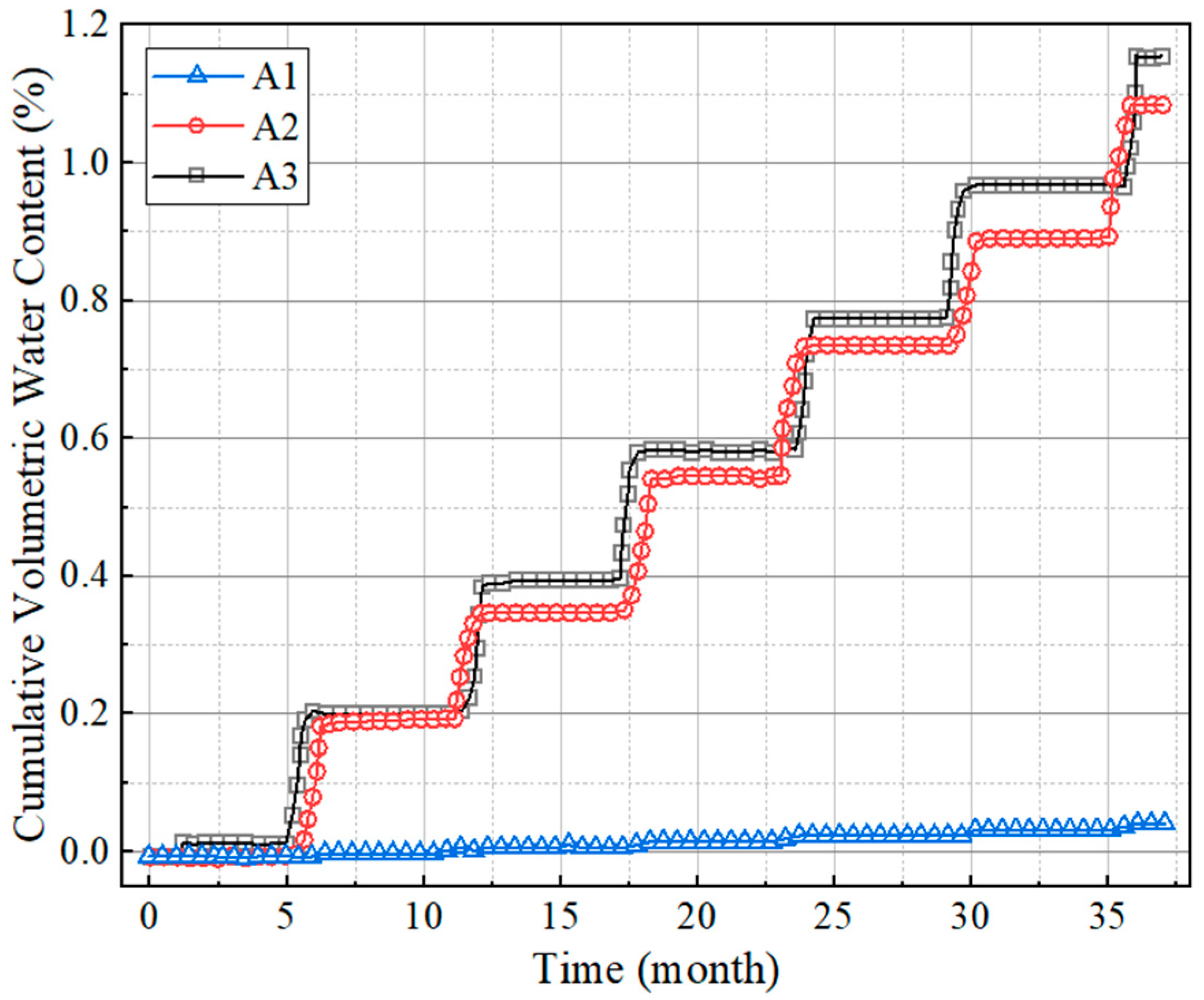
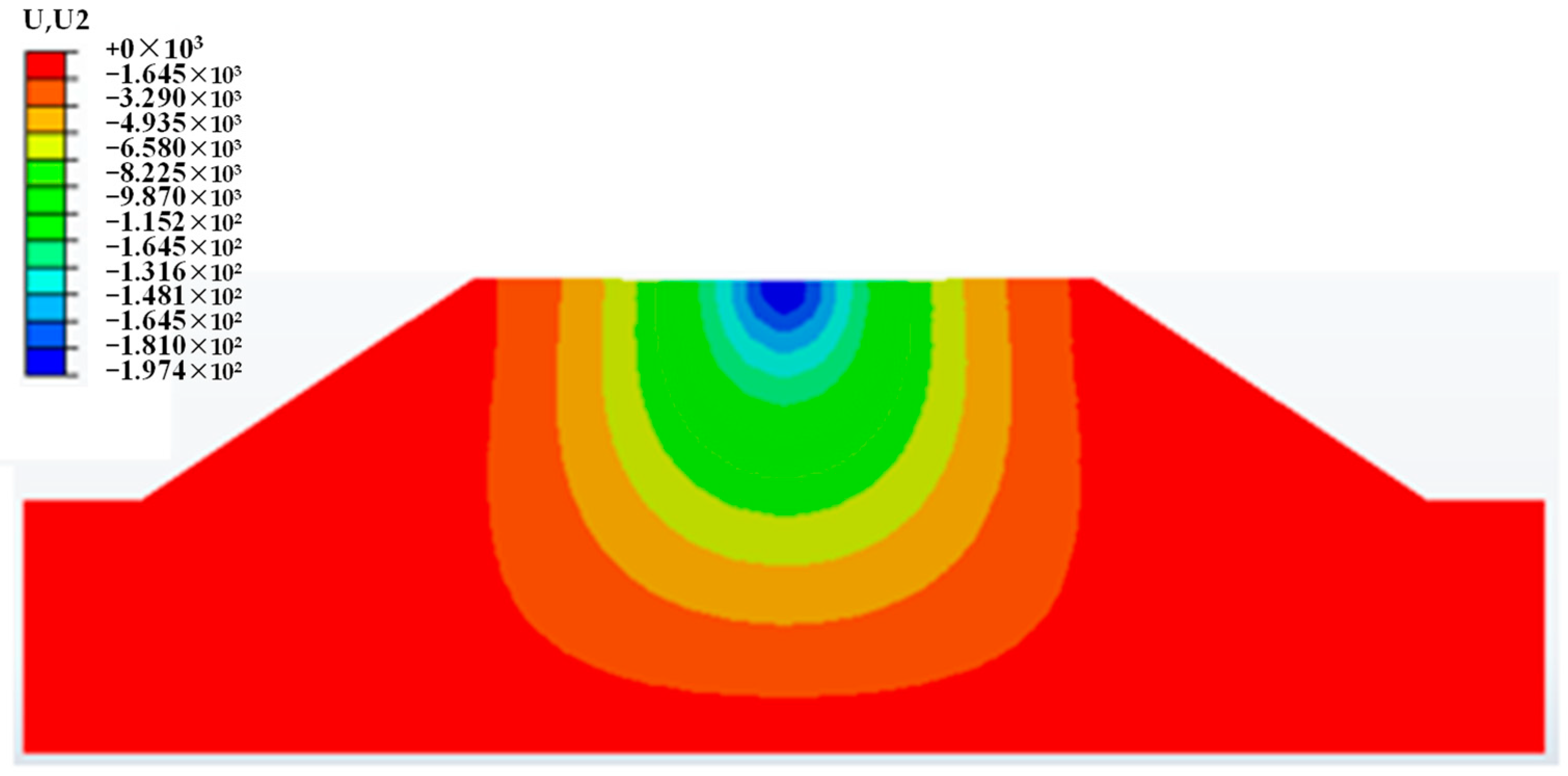
5.2.1. Analysis of Water Level Change
5.2.2. Analysis of Water Level Fluctuation
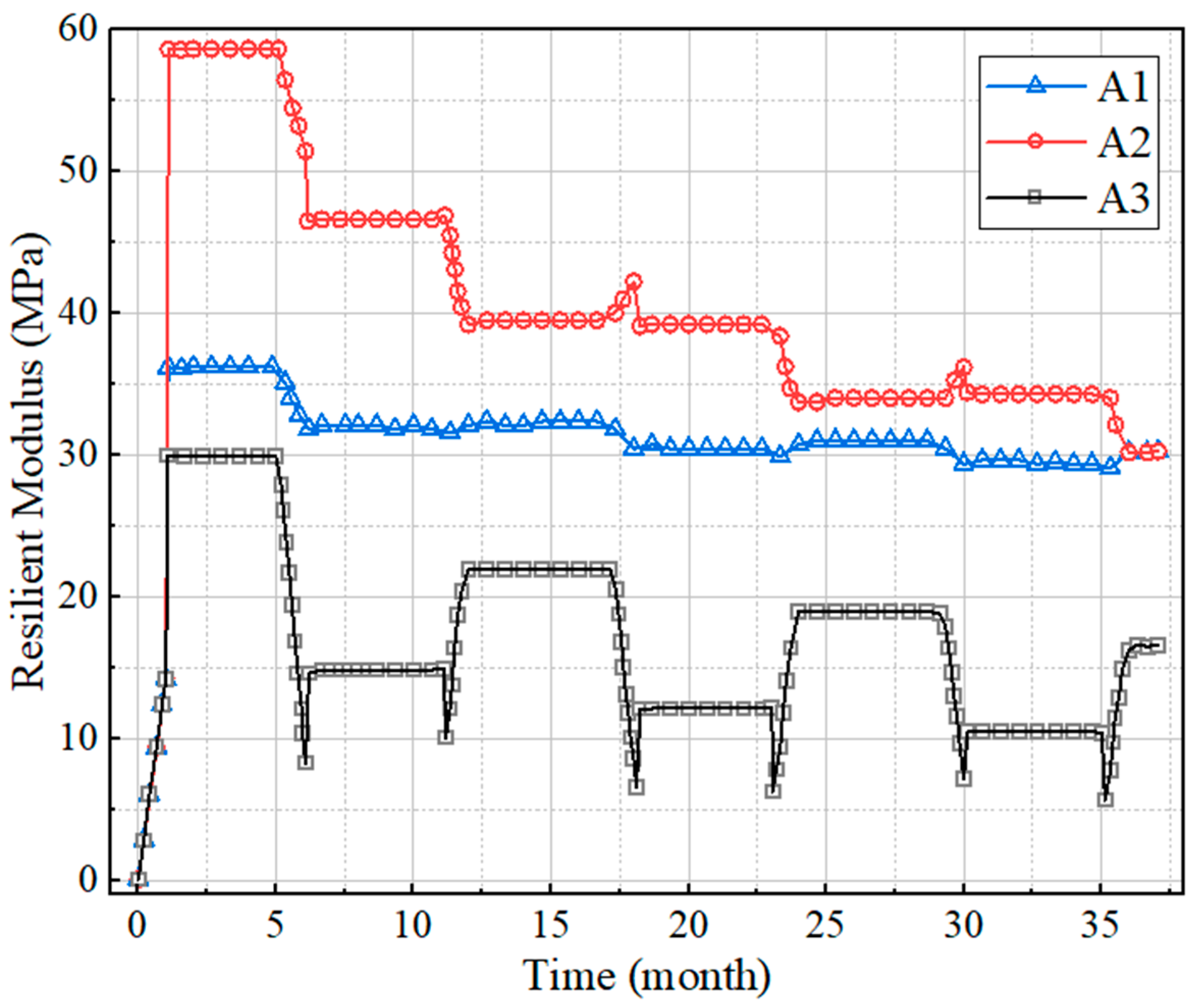
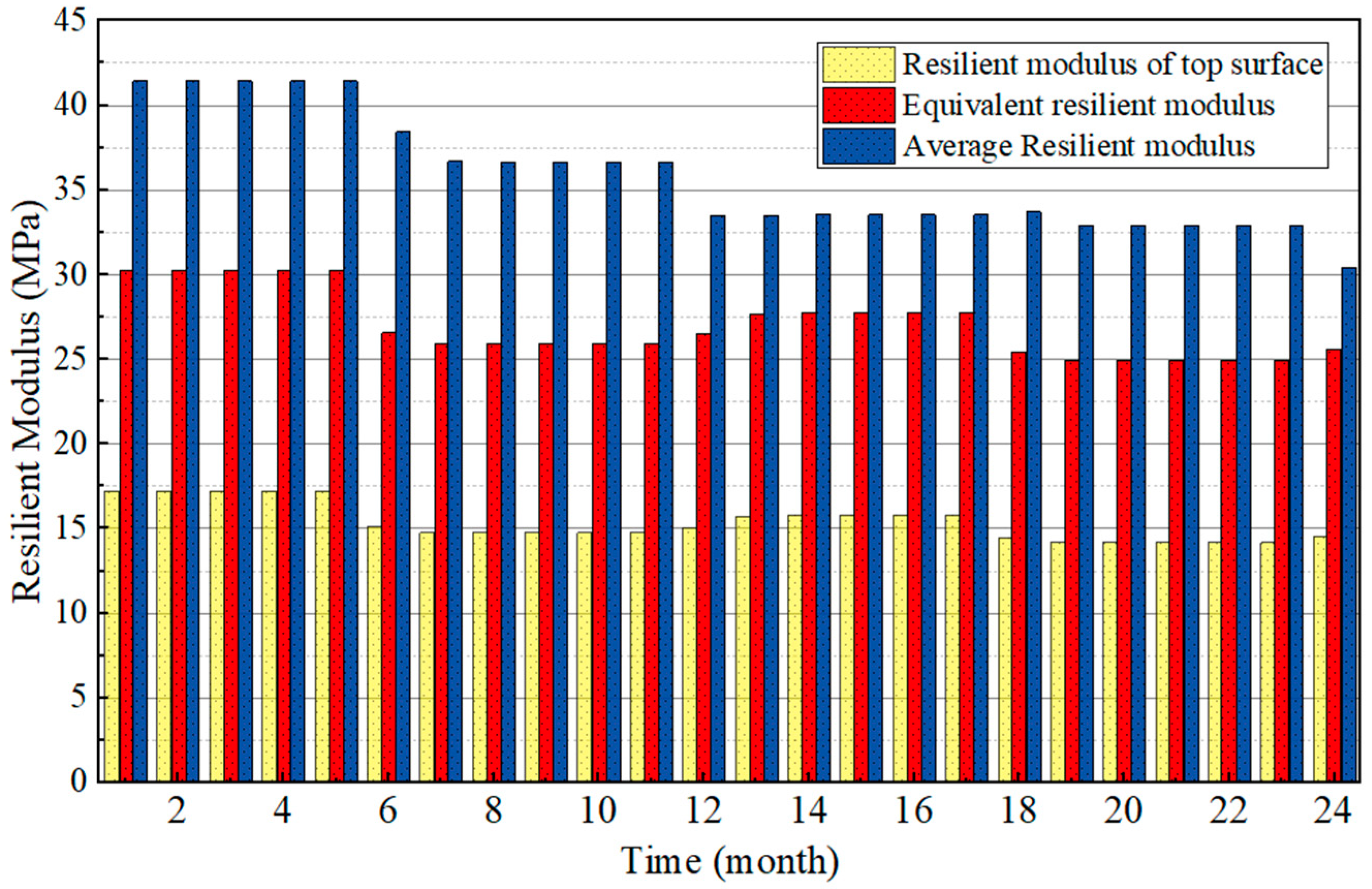
5.2.3. Analysis of Monthly Equivalent Resilient Modulus
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rahman, M.M.; Islam, K.M.; Gassman, S.L. Correlations of permanent strain and damping coefficients with resilient modulus for coarse-grained subgrade soils. Int. J. Geotech. Eng. 2021, 15, 714–723. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, X.; Wang, H.; Jiang, B. Laboratory testing and analysis of dynamic and static resilient modulus of subgrade soil under various influencing factors. Constr. Build. Mater. 2019, 195, 178–186. [Google Scholar] [CrossRef]
- Yan, R.Z.; Ke, G.J.; Zhao, S.L.; Xia, J.L. Experimental study on dynamic resilient modulus of subgrade with circulating fluidized bed combustion ash as filler. Constr. Build. Mater. 2023, 397, 132427. [Google Scholar] [CrossRef]
- Liu, F.R.; Zhou, Z.W.; Ma, W.; Zhang, S.J.; Sun, Z.Z. Dynamic Parameters and Hysteresis Loop Characteristics of Frozen Silt Clay under Different Cyclic Stress Paths. Adv. Mater. Sci. Eng. 2021, 2021, 3763181. [Google Scholar] [CrossRef]
- Coronado, O.; Caicedo, B.; Taibi, S.; Correia, A.G.; Fleureau, J. A macro geomechanical approach to rank non-standard unbound granular materials for pavements. Eng. Geol. 2021, 119, 64–73. [Google Scholar] [CrossRef]
- Han, Z.; Vanapalli, S.K. Relationship between resilient modulus and suction for compacted subgrade soils. Eng. Geol. 2016, 211, 85–97. [Google Scholar] [CrossRef]
- Hoyos, L.R.; Suescun-Florez, E.A.; Puppala, A.J. Stiffness of intermediate unsaturated soil from simultaneous suction-controlled resonant column and bender element testing. Eng. Geol. 2015, 188, 10–28. [Google Scholar] [CrossRef]
- Ekblad, J.; Isacsson, U. Influence of water on resilient properties of coarse granular materials. Road Mater. Pavement Des. 2006, 7, 369–404. [Google Scholar] [CrossRef]
- Cary, C.E.; Zapata, C.E. Pore Water Pressure Response of Soil Subjected to Dynamic Loading under Saturated and Unsaturated Conditions. Int. J. Geomech. 2016, 16, D4016004. [Google Scholar] [CrossRef]
- Salour, F.; Erlingsson, S. Resilient modulus modelling of unsaturated subgrade soils: Laboratory investigation of silty sand subgrade. Road Mater. Pavement Des. 2015, 16, 553–568. [Google Scholar] [CrossRef]
- Caicedo, B.; Coronado, O.; Fleureau, J.M.; Correia, A.G. Resilient Behaviour of non Standard Unbound Granular Materials. Road Mater. Pavement Des. 2009, 10, 287–312. [Google Scholar] [CrossRef]
- Ng, C.W.W.; Zhou, C.; Yuan, Q.; Xu, J. Resilient modulus of unsaturated subgrade soil: Experimental and theoretical investigations. Can. Geotech. J. 2013, 50, 223–232. [Google Scholar] [CrossRef]
- Gu, F.; Sahin, H.; Luo, X.; Luo, R.; Lytton, R.L. Estimation of Resilient Modulus of Unbound Aggregates Using Performance-Related Base Course Properties. J. Mater. Civ. Eng. 2015, 27, 04014188. [Google Scholar] [CrossRef]
- Nokkaew, K.; Tinjum, J.M.; Likos, W.J.; Edil, T.B. Effect of Matric Suction on Resilient Modulus for Compacted Recycled Base Course in Postcompaction State. Transp. Res. Record 2014, 2433, 68–78. [Google Scholar] [CrossRef]
- Yang, S.R.; Huang, W.H.; Tai, Y.T. Variation of resilient modulus with soil suction for compacted subgrade soils. In Proceedings of the 84th Annual Meeting of the Transportation-Research-Board, Washington, DC, USA, 9–13 January 2005; pp. 99–106. [Google Scholar]
- Rasul, J.M.; Ghataora, G.S.; Burrow, M. The effect of wetting and drying on the performance of stabilized subgrade soils. Transp. Geotech. 2018, 14, 1–7. [Google Scholar] [CrossRef]
- Lu, Z.; Fang, R.; Chen, L.H.; She, J.B.; Xian, S.H. Long-Term Deformation of Highway Subgrade under Coupling Effect of Traffic Load and Drying-Wetting Cycles. Int. J. Geomech. 2020, 20, 04019168. [Google Scholar] [CrossRef]
- Hu, C.M.; Yuan, Y.L.; Mei, Y.; Wang, X.Y.; Liu, Z. Comprehensive strength deterioration model of compacted loess exposed to drying-wetting cycles. Bull. Eng. Geol. Environ. 2020, 79, 383–398. [Google Scholar] [CrossRef]
- Chen, P.; Wei, C.F. Numerical Procedure for Simulating the Two-Phase Flow in Unsaturated Soils with Hydraulic Hysteresis. Int. J. Geomech. 2016, 16, 04015030. [Google Scholar] [CrossRef]
- Yaqi, W.Y.; Abdallah, I.; Nazarian, S.; Puppala, A.J. Moisture Content-Based Longitudinal Cracking Prediction and Evaluation Model for Low-Volume Roads over Expansive Soils. J. Mater. Civ. Eng. 2015, 27, 04014263. [Google Scholar] [CrossRef]
- El-Ashwah, A.S.; Mousa, E.; El-Badawy, S.M.; Abo-Hashema, M.A. Advanced characterization of unbound granular materials for pavement structural design in Egypt. Int. J. Pavement Eng. 2022, 23, 476–488. [Google Scholar] [CrossRef]
- Andrei, D.; Witczak, M.; Schwartz, C.; Uzan, J. Harmonized Resilient Modulus Test Method for Unbound Pavement Materials. Transp. Res. Rec. J. Transp. Res. Board 2004, 1874, 29–37. [Google Scholar] [CrossRef]
- Uzan, J. Characterization of granular material. Transp. Res. Record 1985, 1022, 52–59. [Google Scholar]
- NCHRP. Harmonized Test Methods for Laboratory Determination of Resilient Modulus for Flexible Pavement Design; National Cooperative Highway Research: Washington, DC, USA, 2003. [Google Scholar]
- AASHTO. Mechanistic-Empirical Pavement Design Guide: A Manual of Practice; AASHTO: Washington, DC, USA, 2008. [Google Scholar]
- Heath, A.C.; Pestana, J.M.; Harvey, J.T.; Bejerano, M.O. Normalizing behaviour of unsaturated granular pavement materials. J. Geotech. Geoenviron. Eng. 2004, 130, 896–904. [Google Scholar] [CrossRef]
- Fredlund, D.G.; Xing, A.Q. Equations for the soil-water characteristic curve. Can. Geotech. J. 1994, 31, 1026. [Google Scholar] [CrossRef]
- CJ/T 486-2015; Soil Solidification Admixture Urban Construction Industry Standard (CJ). China Standard Press: Beijing, China, 2015.
- Xin, G.; Zhang, A.; Wang, Z.; Shen, Q.; Mu, M. Influence of Humidity State on Dynamic Resilient Modulus of Subgrade Soils: Considering Repeated Wetting-Drying Cycles. Adv. Mater. Sci. Eng. 2021. [Google Scholar] [CrossRef]
- Yao, Y.; Luo, S.; Qian, J.; Li, J.; Xiao, H. Soil-Water Characteristics of the Low Liquid Limit Silt considering Compaction and Freeze-Thaw Action. Adv. Civ. Eng. 2020, 13. [Google Scholar] [CrossRef]
- Yao, Y.; Ni, J.; Li, J. Stress-dependent water retention of granite residual soil and its implications for ground settlement. Comput. Geotech. 2021, 129, 11. [Google Scholar] [CrossRef]
- Zhang, J.; Peng, J.; Zheng, J.; Yao, Y. Characterisation of stress and moisture-dependent resilient behaviour for compacted clays in South China. Road Mater. Pavement Des. 2020, 21, 262–275. [Google Scholar] [CrossRef]
- Han, Z.; Vanapalli, S.K.; Ren, J.; Zou, W. Characterizing cyclic and static moduli and strength of compacted pavement subgrade soils considering moisture variation. Soils Found. 2018, 58, 1187–1199. [Google Scholar] [CrossRef]
- Li, D.Q.; Selig, E.T. Resilient modulus for fine-grained subgrade soils. J. Geotech. Eng.-ASCE 1994, 120, 939–957. [Google Scholar] [CrossRef]
- Zaman, M.M.; Zhu, J.; Laguros, J.G. Durability effects on resilient moduli of stabilized aggregate base. Transp. Res. Record 1999, 1687, 29–38. [Google Scholar] [CrossRef]
- Ceratti, J.A.; Gehling, W.; Nunez, W.P. Seasonal variations of a subgrade soil resilient modulus in southern brazil. In Proceedings of the 83rd Annual Meeting of the Transportation-Research-Board, Washington, DC, USA, 11–15 January 2004; pp. 165–173. [Google Scholar]
- Allam, M.M.; Sridharan, A. Effect of Wetting and Drying on Shear-Strength. J. Geotech. Eng. Div. 1981, 107, 421–438. [Google Scholar] [CrossRef]
- Guney, Y.; Sari, D.; Cetin, M.; Tuncan, M. Impact of cyclic wetting-drying on swelling behavior of lime-stabilized soil. Build. Environ. 2007, 42, 681–688. [Google Scholar] [CrossRef]
- Chu, X. A Review on the Resilient Response of Unsaturated Subgrade Soils. Adv. Civ. Eng. 2020, 2020, 7367484. [Google Scholar] [CrossRef]
- JTG D30-2015; Specifications for Design of Highway Subgrades. M.O.T. China: Beijing, China, 2015.
- JTG D50-2017; Specifications for Design of Highway Asphalt Pavement. M.O.T. China: Beijing, China, 2017.
- JTG/T D33-2012; Specifications for Drainage Design of Highway. M.O.T. China: Beijing, China, 2012.




| Tested Item | Testing Standards | Reference Standards | Tested Results |
|---|---|---|---|
| Density (g/cm3) | Soil stabilizing admixtures CJ/T 486-2015 [28] | D ± 0.03 | 1.41 |
| pH | A ± 1.0 | 7.6 | |
| Soluble solids | S ± 2.0 | 96.5 | |
| Unconfined compression strength | ≥2.5 | 3.2 | |
| Unconfined compressive strength ratio | ≥120 | 148 | |
| Seven-day water stability coefficient ratio | ≥105 | 115 |
| Specific Gravity (g/cm3) | Maximum Dry Density (g/cm3) | Optimum Moisture Content (%) | Plastic Limit (%) | Liquid Limit (%) | Plasticity Index (%) |
|---|---|---|---|---|---|
| 2.701 | 1.78 | 17.0 | 23.63 | 35.29 | 11.66 |
| Sequence Number | Confining Stress σ3 (kPa) | Deviator Stress σd (kPa) | (kPa) | Load Times/s |
|---|---|---|---|---|
| Pre-loading | 30 | 55 | 85 | 1000 |
| 1 | 60 | 30 | 90 | 100 |
| 2 | 45 | 30 | 75 | 100 |
| 3 | 30 | 30 | 60 | 100 |
| 4 | 15 | 30 | 45 | 100 |
| 5 | 60 | 55 | 115 | 100 |
| 6 | 45 | 55 | 100 | 100 |
| 7 | 30 | 55 | 85 | 100 |
| 8 | 15 | 55 | 70 | 100 |
| 9 | 60 | 75 | 135 | 100 |
| 10 | 45 | 75 | 120 | 100 |
| 11 | 30 | 75 | 105 | 100 |
| 12 | 15 | 75 | 90 | 100 |
| 13 | 60 | 105 | 165 | 100 |
| 14 | 45 | 105 | 150 | 100 |
| 15 | 30 | 105 | 135 | 100 |
| 16 | 15 | 105 | 120 | 100 |
| Equation | q1 | q2 | q3 | q4 | q5 | R2 |
|---|---|---|---|---|---|---|
| (7) | 2340.93 | 0.40 | −2.43 | −0.61 | 0.28 | 0.93 |
| (8) | 1123.89 | 0.41 | −2.49 | 0.99 | −6.09 | 0.78 |
| Layer | Material Type | E (MPa) | μ | ρ (g/cm3) |
|---|---|---|---|---|
| Surface | AC13 | 11,000 | 0.25 | 2.42 |
| AC20 | 12,000 | 0.25 | 2.42 | |
| ATB25 | 9000 | 0.25 | 2.42 | |
| Base | Graded crush aggregate | 500 | 0.35 | 2.36 |
| Subbase | Cement stabilized gravel | 9000 | 0.25 | 2.35 |
| Subgrade Foundation | Soil | 60 | 0.4 | 1.83 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luan, Y.; Lu, W.; Fu, K. Research on Resilient Modulus Prediction Model and Equivalence Analysis for Polymer Reinforced Subgrade Soil under Dry–Wet Cycle. Polymers 2023, 15, 4187. https://doi.org/10.3390/polym15204187
Luan Y, Lu W, Fu K. Research on Resilient Modulus Prediction Model and Equivalence Analysis for Polymer Reinforced Subgrade Soil under Dry–Wet Cycle. Polymers. 2023; 15(20):4187. https://doi.org/10.3390/polym15204187
Chicago/Turabian StyleLuan, Yingcheng, Wei Lu, and Kun Fu. 2023. "Research on Resilient Modulus Prediction Model and Equivalence Analysis for Polymer Reinforced Subgrade Soil under Dry–Wet Cycle" Polymers 15, no. 20: 4187. https://doi.org/10.3390/polym15204187
APA StyleLuan, Y., Lu, W., & Fu, K. (2023). Research on Resilient Modulus Prediction Model and Equivalence Analysis for Polymer Reinforced Subgrade Soil under Dry–Wet Cycle. Polymers, 15(20), 4187. https://doi.org/10.3390/polym15204187





