Printing Parameter Optimization of Additive Manufactured PLA Using Taguchi Design of Experiment
Abstract
:1. Introduction
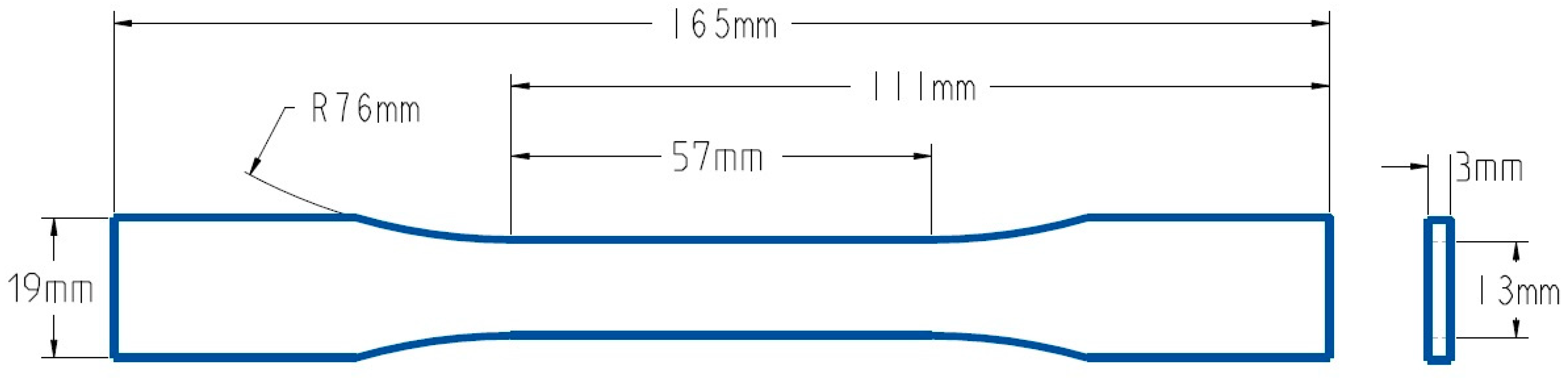
2. Experimental Procedure
3. Results and Discussion
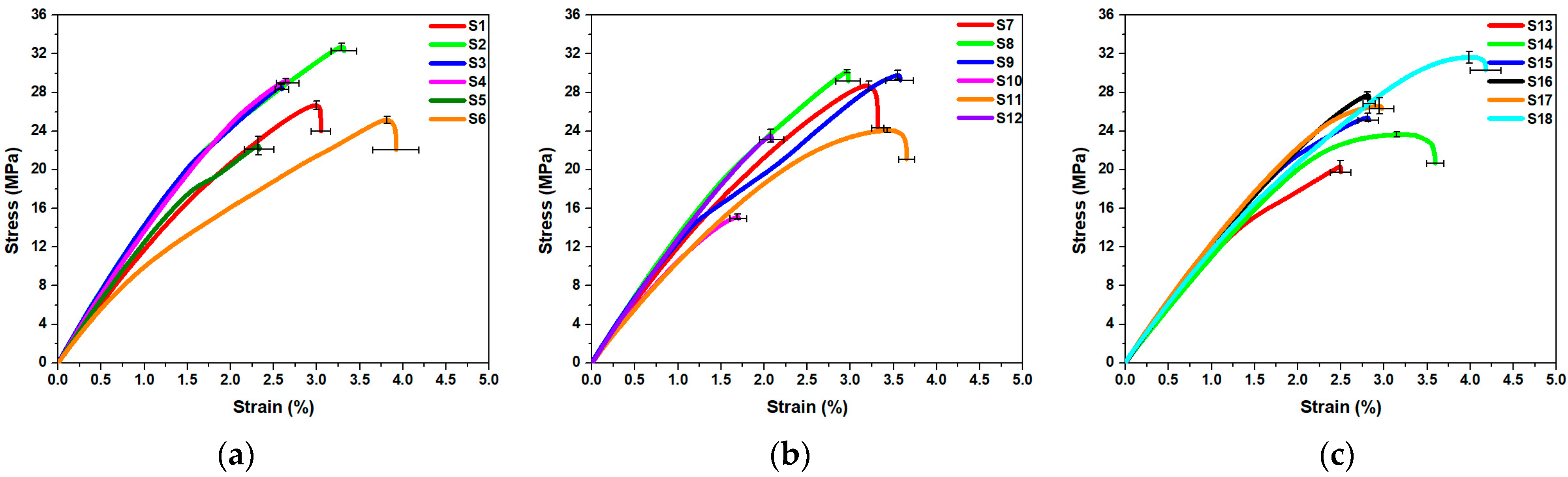
3.1. Tensile Test Results of Taguchi Matrix
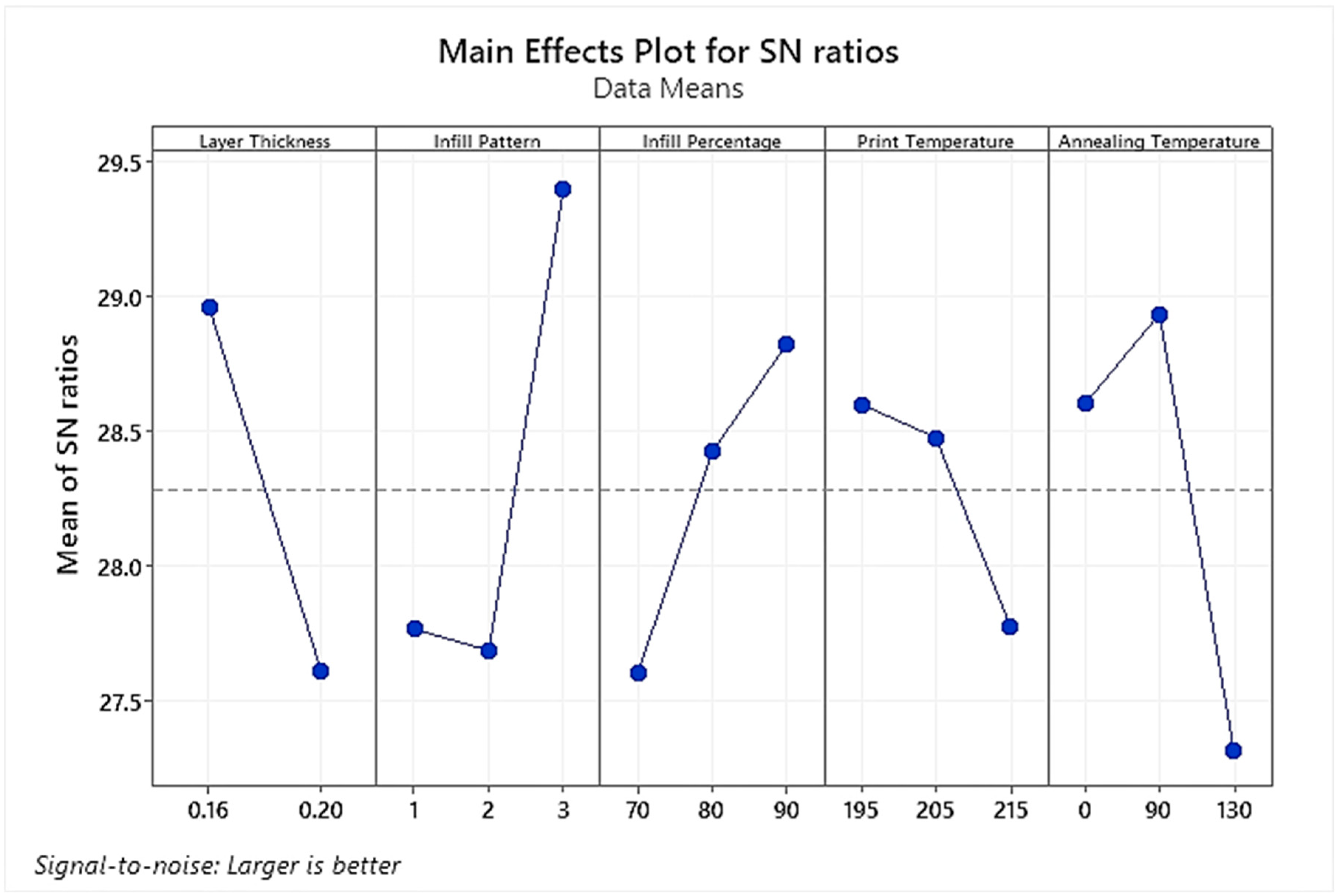
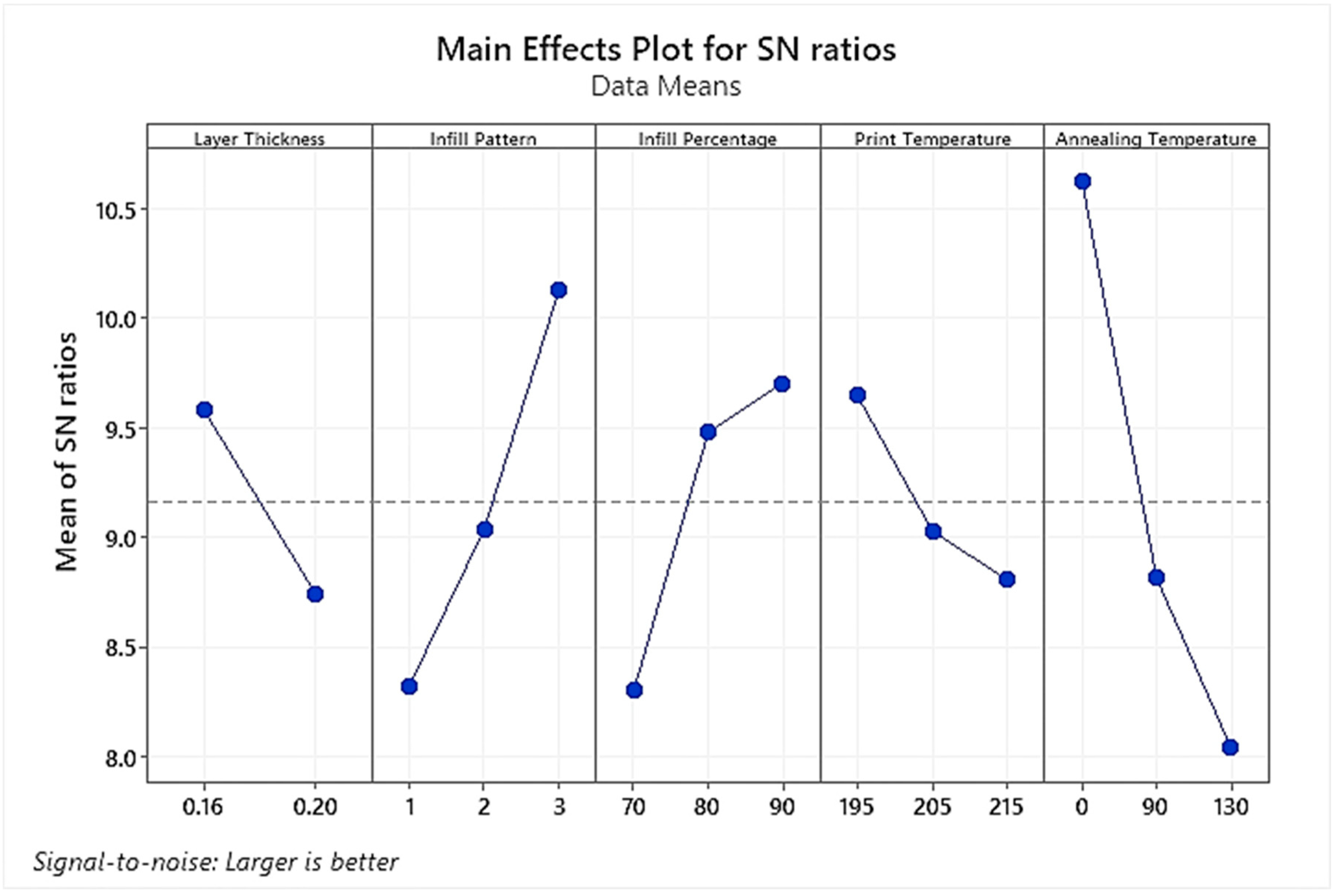
3.2. Signal/Noise Ratio Analysis
3.3. Regression Models
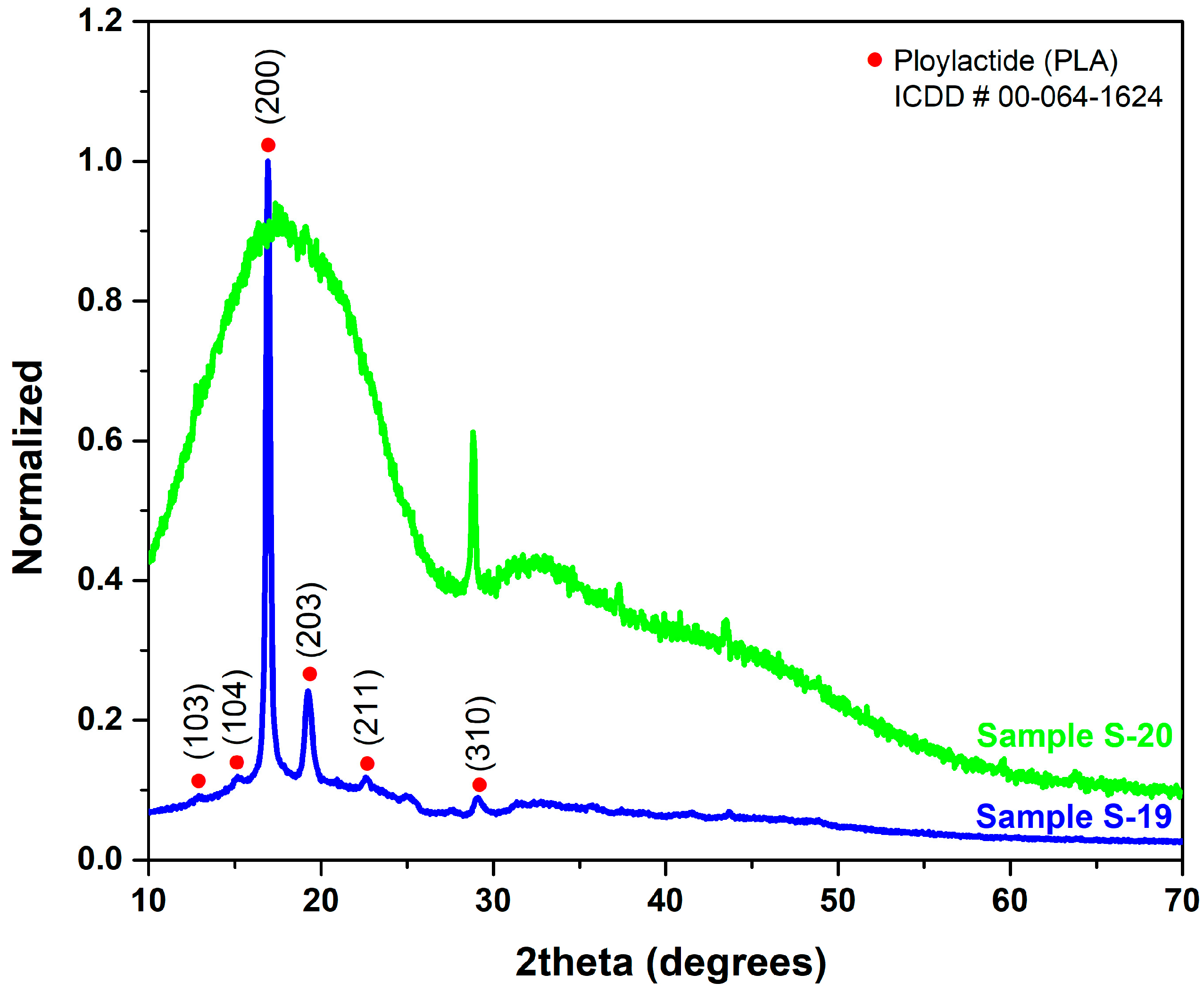
3.4. Structural Characterization
4. Conclusions
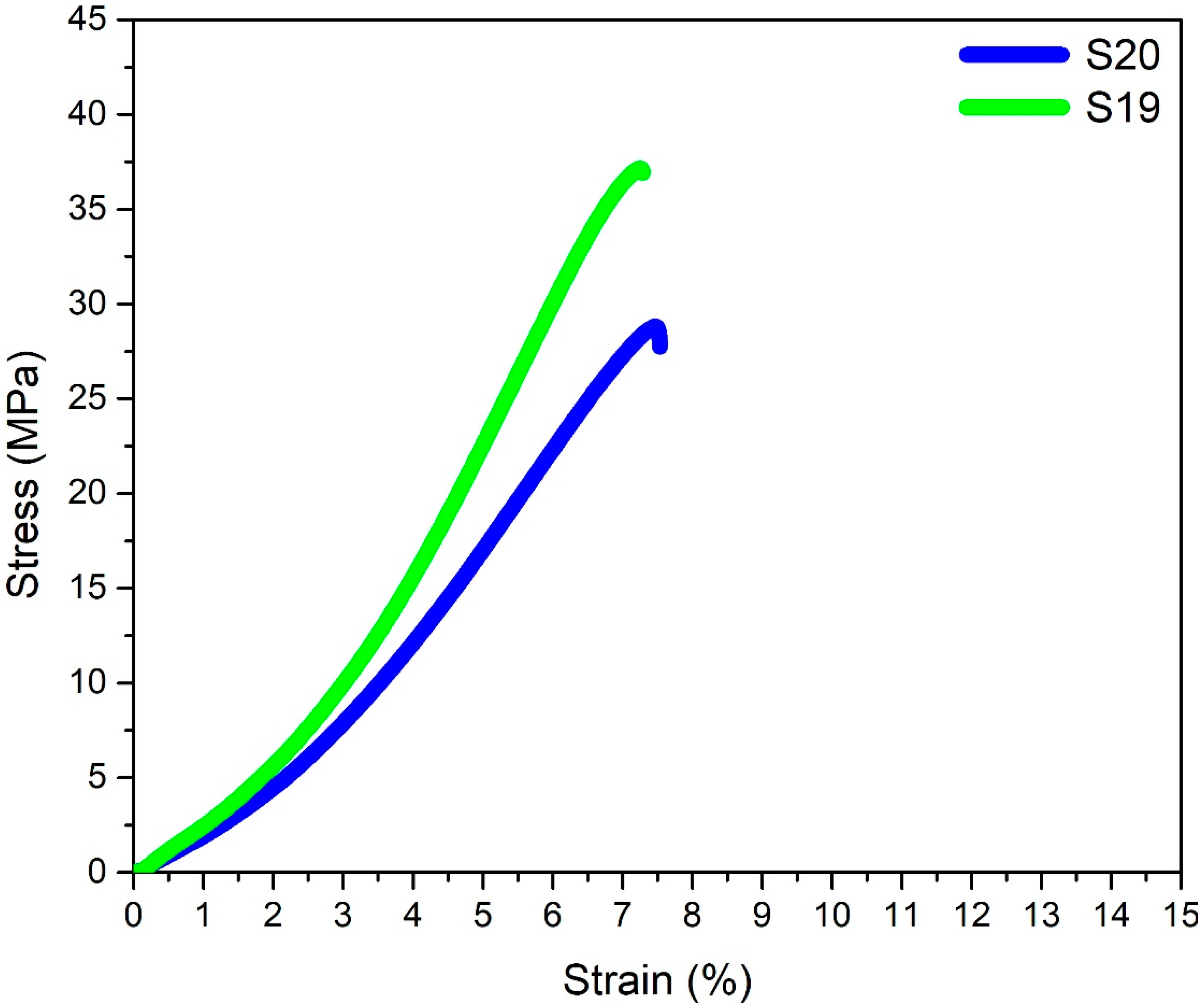
- Signal-to-noise ratio analysis showed that maximum tensile strength could be achieved with 0.16 mm layer height, 90% infill density, Gyroid-type infill pattern, 195 °C print temperature, and 90 °C annealing temperature. The maximum UTS value, as predicted by the regression model, was 35.79 MPa;
- Maximum tensile strength of 37.15 MPa was measured for the FDM sample developed using the optimized parameters. The developed regression model under-predicted the maximum UTS with a reasonably acceptable deviation of 3.6%;
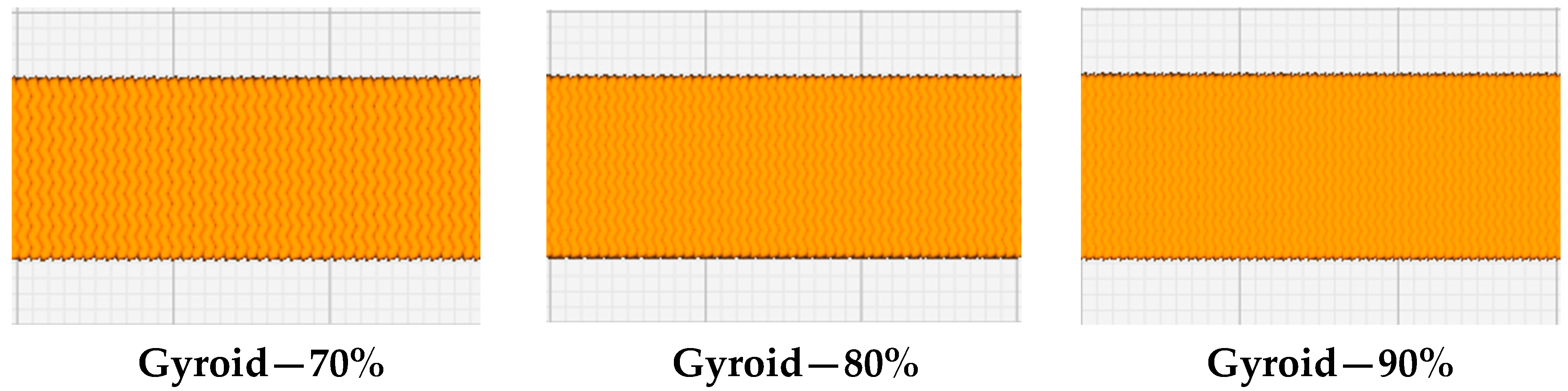
- Infill pattern and annealing temperature were identified as the most significant processing parameters. Octet infill pattern resulting in porous V-shaped wedges proved to be detrimental against tensile loading, whereas the Gyroid type having a wavy infill pattern resulted in much better inter and intra-layer adhesion, thereby imparting superior mechanical properties;
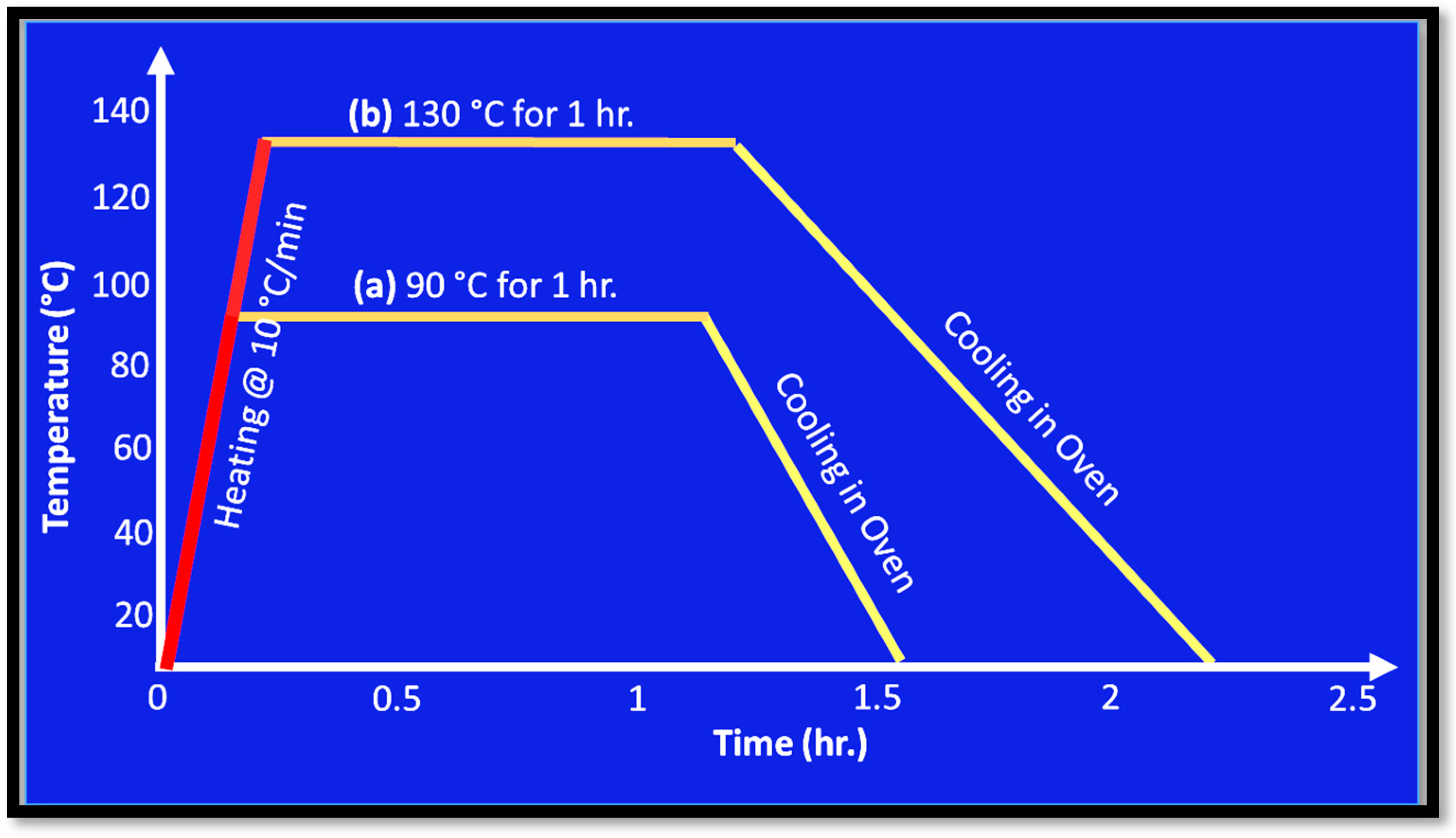
- Annealing at 90 °C for 1 h resulted in improved UTS compared to the as-printed (non-heat-treated) sample. Crystallographic analysis revealed the transformation of the amorphous structure of as-printed PLA samples to semi-crystalline orthorhombic α-form when subjected to annealing at 90 °C. The enhanced crystallinity is believed to have significantly contributed towards a higher UTS.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- 3D Printing Market Size, Growth, Share|Global Report. 2023. Available online: https://www.fortunebusinessinsights.com/industry-reports/3d-printing-market-101902 (accessed on 18 July 2023).
- Ngo, T.D.; Kashani, A.; Imbalzano, G.; Nguyen, K.T.Q.; Hui, D. Additive manufacturing (3D printing): A review of materials, methods, applications and challenges. Compos. B Eng. 2018, 143, 172–196. [Google Scholar] [CrossRef]
- Zegard, T.; Paulino, G.H. Bridging topology optimization and additive manufacturing. Struct. Multidiscip. Optim. 2016, 53, 175–192. [Google Scholar] [CrossRef]
- Atzeni, E.; Salmi, A. Economics of additive manufacturing for end-usable metal parts. Int. J. Adv. Manuf. Technol. 2012, 62, 1147–1155. [Google Scholar] [CrossRef]
- Mai, J.; Zhang, L.; Tao, F.; Ren, L. Customized production based on distributed 3D printing services in cloud manufacturing. Int. J. Adv. Manuf. Technol. 2016, 84, 71–83. [Google Scholar] [CrossRef]
- Thompson, M.K.; Moroni, G.; Vaneker, T.; Fadel, G.; Campbell, R.I.; Gibson, I.; Bernard, A.; Schulz, J.; Graf, P.; Ahuja, B.; et al. Design for additive manufacturing: Trends, opportunities, considerations, and constraints. CIRP Ann. Manuf. Technol. 2016, 65, 737–760. [Google Scholar] [CrossRef]
- Martinelli, A.; Mina, A.; Moggi, M. The enabling technologies of industry 4.0: Examining the seeds of the fourth industrial revolution. Ind. Corp. Chang. 2021, 30, 161–188. [Google Scholar] [CrossRef]
- Dilberoglu, U.M.; Gharehpapagh, B.; Yaman, U.; Dolen, M. The Role of Additive Manufacturing in the Era of Industry 4.0. Procedia Manuf. 2017, 11, 545–554. [Google Scholar] [CrossRef]
- Steenhuis, H.J.; Fang, X.; Ulusemre, T. Global Diffusion of Innovation during the Fourth Industrial Revolution: The Case of Additive Manufacturing or 3D Printing. Int. J. Innov. Technol. Manag. 2020, 17, 2050005. [Google Scholar] [CrossRef]
- Parandoush, P.; Lin, D. A review on additive manufacturing of polymer-fiber composites. Compos. Struct. 2017, 182, 36–53. [Google Scholar] [CrossRef]
- Wang, X.; Jiang, M.; Zhou, Z.; Gou, J.; Hui, D. 3D printing of polymer matrix composites: A review and prospective. Compos. B Eng. 2017, 110, 442–458. [Google Scholar] [CrossRef]
- Compton, B.G.; Lewis, J.A. 3D-printing of lightweight cellular composites. Adv. Mater. 2014, 26, 5930–5935. [Google Scholar] [CrossRef]
- Postiglione, G.; Natale, G.; Griffini, G.; Levi, M.; Turri, S. Conductive 3D microstructures by direct 3D printing of polymer/carbon nanotube nanocomposites via liquid deposition modeling. Compos. Part. A Appl. Sci. Manuf. 2015, 76, 110–114. [Google Scholar] [CrossRef]
- Wu, X.; Mu, F.; Lin, Z. Three-dimensional printing of graphene-based materials and the application in energy storage. Mater. Today Adv. 2021, 11, 100157. [Google Scholar] [CrossRef]
- Wu, T.; Gray, E.; Chen, B. A self-healing, adaptive and conductive polymer composite ink for 3D printing of gas sensors. J. Mater. Chem. C Mater. 2018, 6, 6200–6207. [Google Scholar] [CrossRef]
- Petersmann, S.; Spoerk, M.; Van De Steene, W.; Üçal, M.; Wiener, J.; Pinter, G.; Arbeiter, F. Mechanical properties of polymeric implant materials produced by extrusion-based additive manufacturing. J. Mech. Behav. Biomed. Mater. 2020, 104, 103611. [Google Scholar] [CrossRef] [PubMed]
- Bikas, H.; Stavropoulos, P.; Chryssolouris, G. Additive manufacturing methods and modeling approaches: A critical review. Int. J. Adv. Manuf. Technol. 2016, 83, 389–405. [Google Scholar] [CrossRef]
- Stansbury, J.W.; Idacavage, M.J. 3D printing with polymers: Challenges among expanding options and opportunities. Dent. Mater. 2016, 32, 54–64. [Google Scholar] [CrossRef] [PubMed]
- Romanova, N.; Shafigullin, L.; Gabdrakhmanov, A.; Buyatova, S. Thermal properties of products based on ABS/PC. MATEC Web Conf. 2019, 298, 00016. [Google Scholar] [CrossRef]
- Gebisa, A.W.; Lemu, H.G. Influence of 3D Printing FDM Process Parameters on Tensile Property of ULTEM 9085. Procedia Manuf. 2019, 30, 331–338. [Google Scholar] [CrossRef]
- Christiyan, K.G.J.; Chandrasekhar, U.; Venkateswarlu, K. A study on the influence of process parameters on the Mechanical Properties of 3D printed ABS composite. IOP Conf. Ser. Mater. Sci. Eng. 2016, 114, 012109. [Google Scholar] [CrossRef]
- Chacón, J.M.; Caminero, M.A.; García-Plaza, E.; Núñez, P.J. Additive manufacturing of PLA structures using fused deposition modelling: Effect of process parameters on mechanical properties and their optimal selection. Mater. Des. 2017, 124, 143–157. [Google Scholar] [CrossRef]
- Sandanamsamy, L.; Mogan, J.; Rajan, K.; Harun, W.S.W.; Ishak, I.; Romlay, F.R.M.; Samykano, M.; Kadirgama, K. Effect of process parameter on tensile properties of FDM printed PLA. Mater. Today Proc. 2023, in press. [Google Scholar] [CrossRef]
- Hikmat, M.; Rostam, S.; Ahmed, Y.M. Investigation of tensile property-based Taguchi method of PLA parts fabricated by FDM 3D printing technology. Results Eng. 2021, 11, 100264. [Google Scholar] [CrossRef]
- Zhao, Y.; Chen, Y.; Zhou, Y. Novel mechanical models of tensile strength and elastic property of FDM AM PLA materials: Experimental and theoretical analyses. Mater. Des. 2019, 181, 108089. [Google Scholar] [CrossRef]
- Rao, V.D.P.; Rajiv, P.; Geethika, V.N. Effect of fused deposition modelling (FDM) process parameters on tensile strength of carbon fibre PLA. Mater. Today Proc. 2019, 18, 2012–2018. [Google Scholar] [CrossRef]
- Szust, A.; Adamski, G. Using thermal annealing and salt remelting to increase tensile properties of 3D FDM prints. Eng. Fail. Anal. 2022, 132, 105932. [Google Scholar] [CrossRef]
- Lokesh, N.; Praveena, B.A.; Reddy, J.S.; Vasu, V.K.; Vijaykumar, S. Evaluation on effect of printing process parameter through Taguchi approach on mechanical properties of 3D printed PLA specimens using FDM at constant printing temperature. Mater. Today Proc. 2022, 52, 1288–1293. [Google Scholar] [CrossRef]
- Mani, M.; Karthikeyan, A.G.; Kalaiselvan, K.; Muthusamy, P.; Muruganandhan, P. Optimization of FDM 3-D printer process parameters for surface roughness and mechanical properties using PLA material. Mater. Today Proc. 2022, 66, 1926–1931. [Google Scholar] [CrossRef]
- Liu, Z.; Lei, Q.; Xing, S. Mechanical characteristics of wood, ceramic, metal and carbon fiber-based PLA composites fabricated by FDM. J. Mater. Res. Technol. 2019, 8, 3741–3751. [Google Scholar] [CrossRef]
- Sahoo, S.; Sutar, H.; Senapati, P.; Mohanto, B.S.; Dhal, P.R.; Baral, S.K. Experimental investigation and optimization of the FDM process using PLA. Mater. Today Proc. 2023, 74, 843–847. [Google Scholar] [CrossRef]
- Maurya, S.; Malik, B.; Sharma, P.; Singh, A.; Chalisgaonkar, R. Investigation of different parameters of cube printed using PLA by FDM 3D printer. Mater. Today Proc. 2022, 64, 1217–1222. [Google Scholar] [CrossRef]
- Rodríguez-Reyna, S.L.; Mata, C.; Díaz-Aguilera, J.H.; Acevedo-Parra, H.R.; Tapia, F. Mechanical properties optimization for PLA, ABS and Nylon + CF manufactured by 3D FDM printing. Mater. Today Commun. 2022, 33, 104774. [Google Scholar] [CrossRef]
- Hamat, S.; Ishak, M.R.; Sapuan, S.M.; Yidris, N.; Hussin, M.S.; Manan, M.S.A. Influence of filament fabrication parameter on tensile strength and filament size of 3D printing PLA-3D850. Mater. Today Proc. 2023, 74, 457–461. [Google Scholar] [CrossRef]
- Singh, J.; Goyal, K.K.; Kumar, R. Effect of filling percentage and raster style on tensile behavior of FDM produced PLA parts at different build orientation. Mater. Today Proc. 2022, 63, 433–439. [Google Scholar] [CrossRef]
- Zerankeshi, M.M.; Sayedain, S.S.; Tavangarifard, M.; Alizadeh, R. Developing a novel technique for the fabrication of PLA-graphite composite filaments using FDM 3D printing process. Ceram. Int. 2022, 48, 31850–31858. [Google Scholar] [CrossRef]
- Öteyaka, M.Ö.; Çakir, F.H.; Sofuoğlu, M.A. Effect of infill pattern and ratio on the flexural and vibration damping characteristics of FDM printed PLA specimens. Mater. Today Commun. 2022, 33, 104912. [Google Scholar] [CrossRef]
- Vidakis, N.; David, C.; Petousis, M.; Sagris, D.; Mountakis, N. Optimization of key quality indicators in material extrusion 3D printing of acrylonitrile butadiene styrene: The impact of critical process control parameters on the surface roughness, dimensional accuracy, and porosity. Mater. Today Commun. 2023, 34, 105171. [Google Scholar] [CrossRef]
- Alafaghani, A.; Qattawi, A. Investigating the effect of fused deposition modeling processing parameters using Taguchi design of experiment method. J. Manuf. Process 2018, 36, 164–174. [Google Scholar] [CrossRef]
- Sajjad, R.; Butt, S.U.; Saeed, H.A.; Anwar, M.T.; Rasheed, T. Impact of multiple infill strategy on the structural strength of single build FDM printed parts. J. Manuf. Process 2023, 89, 105–110. [Google Scholar] [CrossRef]
- Tandon, S.; Kacker, R.; Sudhakar, K.G. Experimental investigation on tensile properties of the polymer and composite specimens printed in a Triangular pattern. J. Manuf. Process 2021, 68, 706–715. [Google Scholar] [CrossRef]
- ASTM D638; Standard Test Method for Tensile Properties of Plastics. ASTM International: West Conshohocken, PA, USA, 2022.
- Barkhad, M.S.; Abu-Jdayil, B.; Mourad, A.H.I.; Iqbal, M.Z. Thermal Insulation and Mechanical Properties of Polylactic Acid (PLA) at Different Processing Conditions. Polymers 2020, 12, 2091. [Google Scholar] [CrossRef] [PubMed]
- Dillon, B.; Doran, P.; Fuenmayor, E.; Healy, A.V.; Gately, N.M.; Major, I.; Lyons, J.G. Influence of Annealing and Biaxial Expansion on the Properties of Poly(l-Lactic Acid) Medical Tubing. Polymers 2019, 11, 1172. [Google Scholar] [CrossRef] [PubMed]





| Process Parameters | Level I | Level II | Level III |
|---|---|---|---|
| Layer thickness (mm) | 0.16 | 0.20 | - |
| Infill Pattern * | 1 | 2 | 3 |
| Infill Percentage (%) | 70 | 80 | 90 |
| Printing Temperature (°C) | 195 | 205 | 215 |
| Annealing Temperature (°C) | 0 | 90 | 130 |
| Process Parameter | Parameter Value Set |
|---|---|
| Print Speed | 50 mm/s |
| Bed Temperature | 60 °C |
| Build Orientation | Flat/Horizontal |
| Raster Angle | 90° |
| Top and Bottom Layers thickness | 0.8 mm |
| Shell thickness | 0.8 mm |
| Line width | 0.4 mm |
| Sample No. | Layer Thickness (mm) | Infill Pattern 1 = Octet, 2 = Tri-hexagonal, 3 = Gyroid | Infill Percentage (%) | Print Temperature (°C) | Annealing Temperature (°C) |
|---|---|---|---|---|---|
| S1 | 0.16 | 1 | 70 | 195 | 0 |
| S2 | 0.16 | 1 | 80 | 205 | 90 |
| S3 | 0.16 | 1 | 90 | 215 | 130 |
| S4 | 0.16 | 2 | 70 | 195 | 90 |
| S5 | 0.16 | 2 | 80 | 205 | 130 |
| S6 | 0.16 | 2 | 90 | 215 | 0 |
| S7 | 0.16 | 3 | 70 | 205 | 0 |
| S8 | 0.16 | 3 | 80 | 215 | 90 |
| S9 | 0.16 | 3 | 90 | 195 | 130 |
| S10 | 0.20 | 1 | 70 | 215 | 130 |
| S11 | 0.20 | 1 | 80 | 195 | 0 |
| S12 | 0.20 | 1 | 90 | 205 | 90 |
| S13 | 0.20 | 2 | 70 | 205 | 130 |
| S14 | 0.20 | 2 | 80 | 215 | 0 |
| S15 | 0.20 | 2 | 90 | 195 | 90 |
| S16 | 0.20 | 3 | 70 | 215 | 90 |
| S17 | 0.20 | 3 | 80 | 195 | 130 |
| S18 | 0.20 | 3 | 90 | 205 | 0 |
| Sample No. | Ultimate Tensile Strength MPa | Percentage Elongation% | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | AV | SD | 1 | 2 | 3 | AV | SD | |
| S1 | 26.7 | 26.2 | 27.1 | 26.66 | (0.45) | 3.0 | 3.1 | 2.9 | 3.00 | (0.11) |
| S2 | 32.7 | 33.1 | 32.3 | 32.68 | (0.40) | 3.3 | 3.1 | 3.4 | 3.27 | (0.15) |
| S3 | 28.6 | 28.4 | 28.8 | 28.58 | (0.23) | 2.6 | 2.5 | 2.7 | 2.58 | (0.08) |
| S4 | 29.2 | 29.2 | 29.6 | 29.32 | (0.20) | 2.7 | 2.6 | 2.8 | 2.69 | (0.13) |
| S5 | 22.5 | 21.5 | 23.4 | 22.47 | (0.95) | 2.3 | 2.2 | 2.5 | 2.32 | (0.17) |
| S6 | 25.1 | 24.9 | 25.6 | 25.22 | (0.36) | 3.8 | 3.6 | 4.1 | 3.85 | (0.27) |
| S7 | 28.7 | 28.2 | 29.2 | 28.68 | (0.53) | 3.2 | 3.2 | 3.3 | 3.23 | (0.07) |
| S8 | 30.2 | 30.0 | 30.3 | 30.19 | (0.17) | 3.0 | 3.1 | 2.9 | 2.98 | (0.14) |
| S9 | 29.8 | 29.3 | 30.2 | 29.78 | (0.47) | 3.5 | 3.3 | 3.6 | 3.48 | (0.16) |
| S10 | 15.1 | 14.8 | 15.3 | 15.08 | (0.25) | 1.7 | 1.6 | 1.8 | 1.68 | (0.10) |
| S11 | 24.1 | 24.3 | 23.9 | 24.08 | (0.23) | 3.4 | 3.3 | 3.5 | 3.38 | (0.09) |
| S12 | 23.5 | 22.9 | 24.2 | 23.54 | (0.65) | 2.1 | 2.2 | 1.9 | 2.07 | (0.14) |
| S13 | 20.3 | 19.7 | 20.9 | 20.31 | (0.60) | 2.5 | 2.4 | 2.6 | 2.50 | (0.12) |
| S14 | 23.6 | 23.3 | 23.8 | 23.56 | (0.28) | 3.6 | 3.5 | 3.7 | 3.60 | (0.10) |
| S15 | 25.4 | 25.0 | 25.8 | 25.38 | (0.43) | 2.8 | 2.7 | 3.0 | 2.83 | (0.12) |
| S16 | 27.7 | 27.3 | 28.0 | 27.66 | (0.35) | 2.8 | 2.7 | 2.9 | 2.82 | (0.07) |
| S17 | 26.6 | 25.8 | 27.4 | 26.60 | (0.80) | 3.0 | 2.7 | 3.0 | 2.90 | (0.14) |
| S18 | 31.6 | 30.9 | 32.1 | 31.56 | (0.61) | 4.2 | 3.9 | 4.1 | 4.05 | (0.18) |
| Sample No. | UTS (MPa) | S/N Ratio | % Elongation | S/N Ratio |
|---|---|---|---|---|
| S1 | 26.7 | 28.53 | 3.0 | 9.54 |
| S2 | 32.7 | 30.29 | 3.3 | 10.37 |
| S3 | 28.6 | 29.13 | 2.6 | 8.30 |
| S4 | 29.2 | 29.34 | 2.7 | 8.63 |
| S5 | 22.5 | 27.04 | 2.3 | 7.23 |
| S6 | 25.1 | 28.03 | 3.8 | 11.60 |
| S7 | 28.7 | 29.16 | 3.2 | 10.10 |
| S8 | 30.2 | 29.60 | 3.0 | 9.54 |
| S9 | 29.8 | 29.48 | 3.5 | 10.88 |
| S10 | 15.1 | 23.58 | 1.7 | 4.61 |
| S11 | 24.1 | 27.64 | 3.4 | 10.63 |
| S12 | 23.5 | 27.42 | 2.1 | 6.44 |
| S13 | 20.3 | 26.15 | 2.5 | 7.96 |
| S14 | 23.6 | 27.46 | 3.6 | 9.83 |
| S15 | 25.4 | 28.10 | 2.8 | 8.94 |
| S16 | 27.7 | 28.85 | 2.8 | 8.94 |
| S17 | 26.6 | 28.50 | 3.0 | 9.25 |
| S18 | 31.6 | 30.78 | 4.2 | 12.04 |
| Process Parameters | S/N Ratio | Delta | Effectiveness Rank | ||
|---|---|---|---|---|---|
| Level 1 | Level 2 | Level 3 | |||
| Layer Thickness | 28.19 | 27.61 | - | 1.35 | 3 |
| Infill Pattern | 27.76 | 27.76 | 27.76 | 27.76 | 1 |
| Infill Percentage | 27.6 | 27.6 | 27.6 | 27.6 | 4 |
| Print Temperature | 28.6 | 28.6 | 28.6 | 28.6 | 5 |
| Annealing Temperature | 28.6 | 28.6 | 28.6 | 28.6 | 2 |
| Criterion: Larger is Better | |||||
| Process Parameters | S/N Ratio | Delta | Effectiveness Rank | ||
|---|---|---|---|---|---|
| Level 1 | Level 2 | Level 3 | |||
| Layer Thickness | 9.577 | 8.738 | - | 0.839 | 5 |
| Infill Pattern | 8.316 | 9.031 | 10.127 | 1.811 | 2 |
| Infill Percentage | 8.297 | 9.475 | 9.701 | 1.404 | 3 |
| Print Temperature | 9.645 | 9.025 | 8.803 | 0.842 | 4 |
| Annealing Temperature | 10.623 | 8.812 | 8.039 | 2.585 | 1 |
| Criterion: Larger is Better | |||||
| UTS Optimized Parameters | |||||
| Sample No. | Layer Thickness (mm) | Infill Pattern 3 = Gyroid | Infill Percentage (%) | Print Temperature (°C) | Annealing Temperature (°C) |
| S19 | 0.16 | 3 | 90 | 195 | 90 |
| % Elongation Optimized Parameters | |||||
| Sample No. | Layer Thickness (mm) | Infill Pattern 3 = Gyroid | Infill Percentage (%) | Print Temperature (°C) | Annealing Temperature (°C) |
| S20 | 0.16 | 3 | 90 | 195 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, B.A.; Nadeem, U.; Hakeem, A.S.; Ul-Hamid, A.; Khan, M.Y.; Younas, M.; Saeed, H.A. Printing Parameter Optimization of Additive Manufactured PLA Using Taguchi Design of Experiment. Polymers 2023, 15, 4370. https://doi.org/10.3390/polym15224370
Ahmed BA, Nadeem U, Hakeem AS, Ul-Hamid A, Khan MY, Younas M, Saeed HA. Printing Parameter Optimization of Additive Manufactured PLA Using Taguchi Design of Experiment. Polymers. 2023; 15(22):4370. https://doi.org/10.3390/polym15224370
Chicago/Turabian StyleAhmed, Bilal Anjum, Uzair Nadeem, Abbas Saeed Hakeem, Anwar Ul-Hamid, Mohd Yusuf Khan, Muhammad Younas, and Hasan Aftab Saeed. 2023. "Printing Parameter Optimization of Additive Manufactured PLA Using Taguchi Design of Experiment" Polymers 15, no. 22: 4370. https://doi.org/10.3390/polym15224370
APA StyleAhmed, B. A., Nadeem, U., Hakeem, A. S., Ul-Hamid, A., Khan, M. Y., Younas, M., & Saeed, H. A. (2023). Printing Parameter Optimization of Additive Manufactured PLA Using Taguchi Design of Experiment. Polymers, 15(22), 4370. https://doi.org/10.3390/polym15224370








