Wall Slip-Free Viscosity Determination of Filled Rubber Compounds Using Steady-State Shear Measurements
Abstract
:1. Introduction
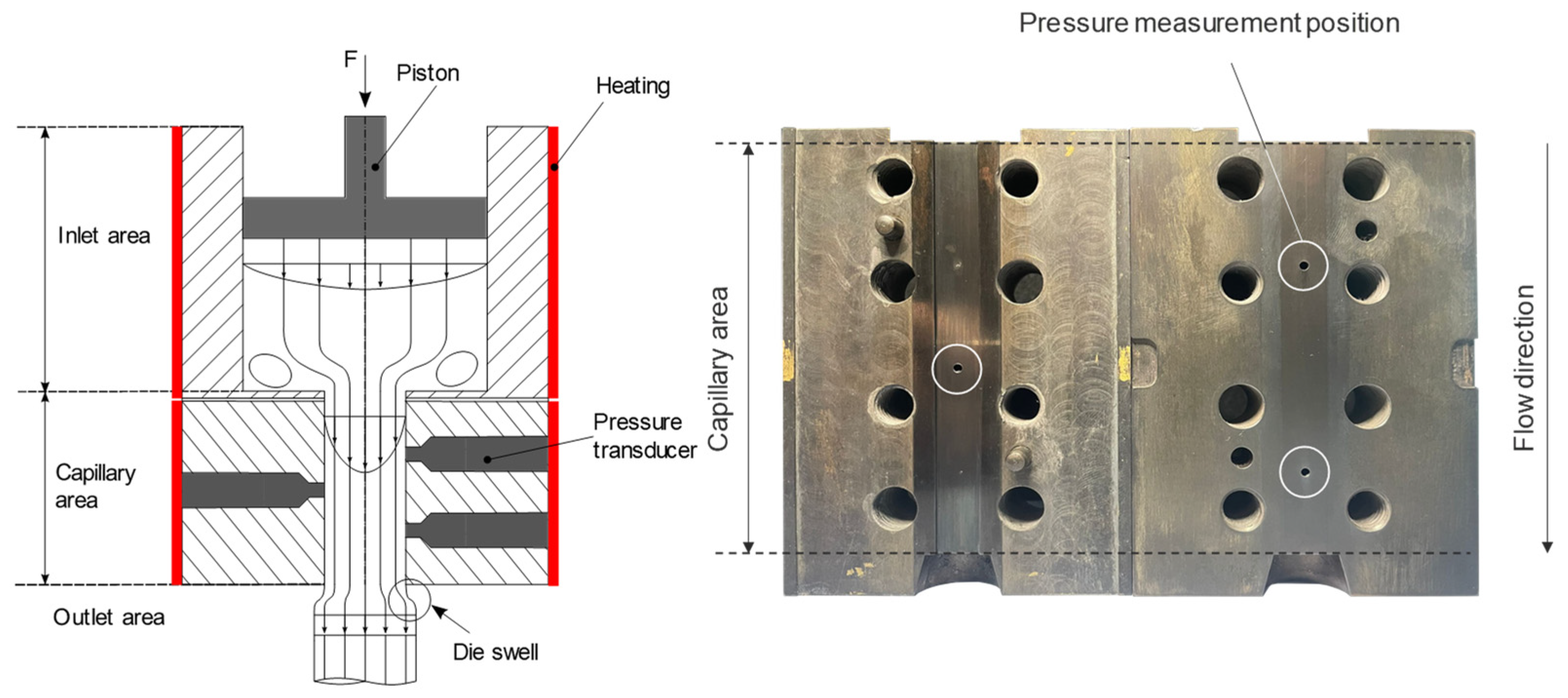
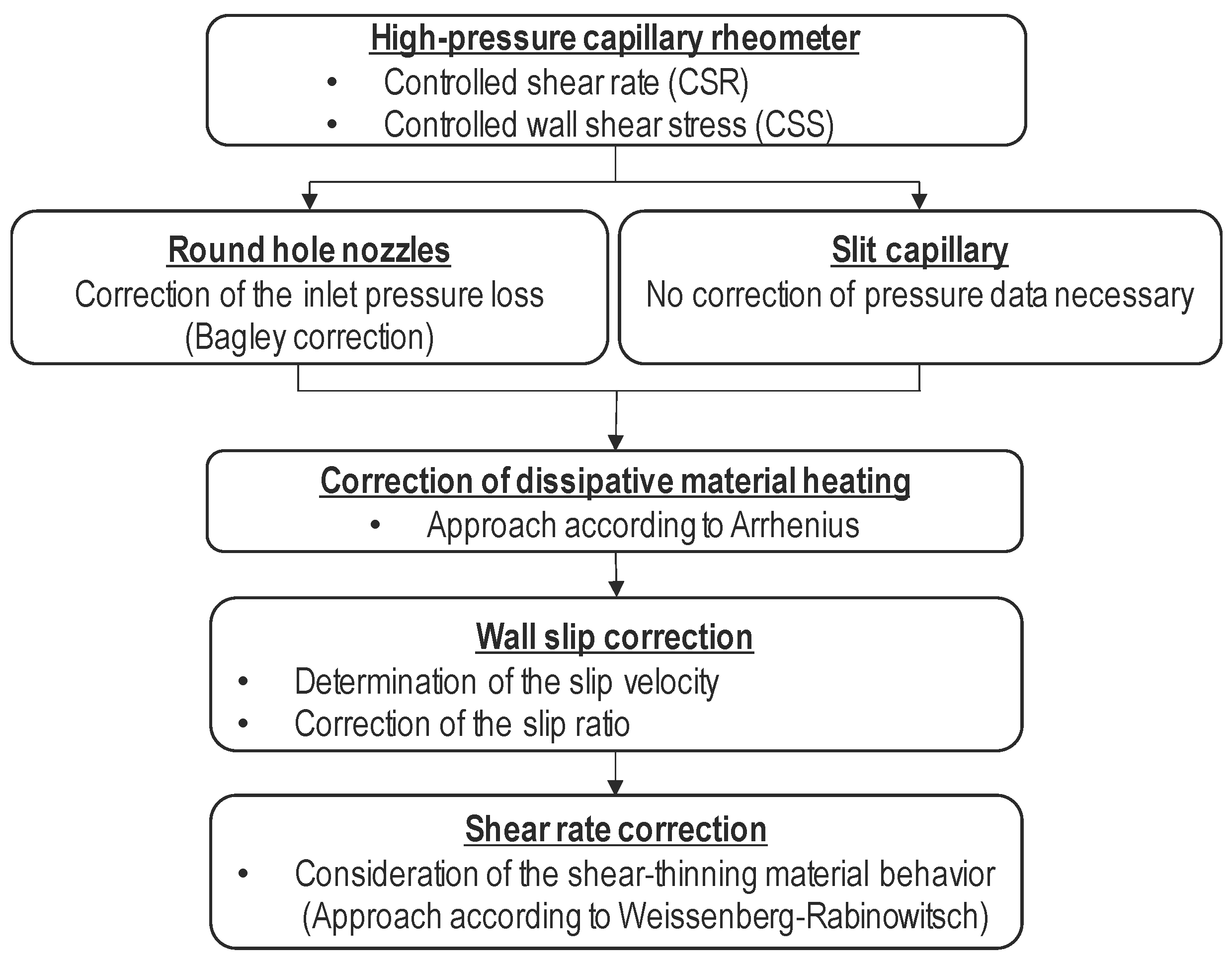
1.1. High-Pressure Capillary Rheometry
- Fully developed, steady, laminar flow (Newtonian flow behavior)
- No non-isothermal effects
- Incompressible fluid with no pressure dependence of viscosity
- Wall adhesion
- : Apparent shear rate
- : Total volume flow
- : Width of the slit capillary
- : Height of the slit capillary
- : Wall shear stress
- : Pressure drop in the slit capillary
- : Distance between pressure measuring points
- : Viscosity
- : Consistency factor
- : Shear rate
- : Flow exponent
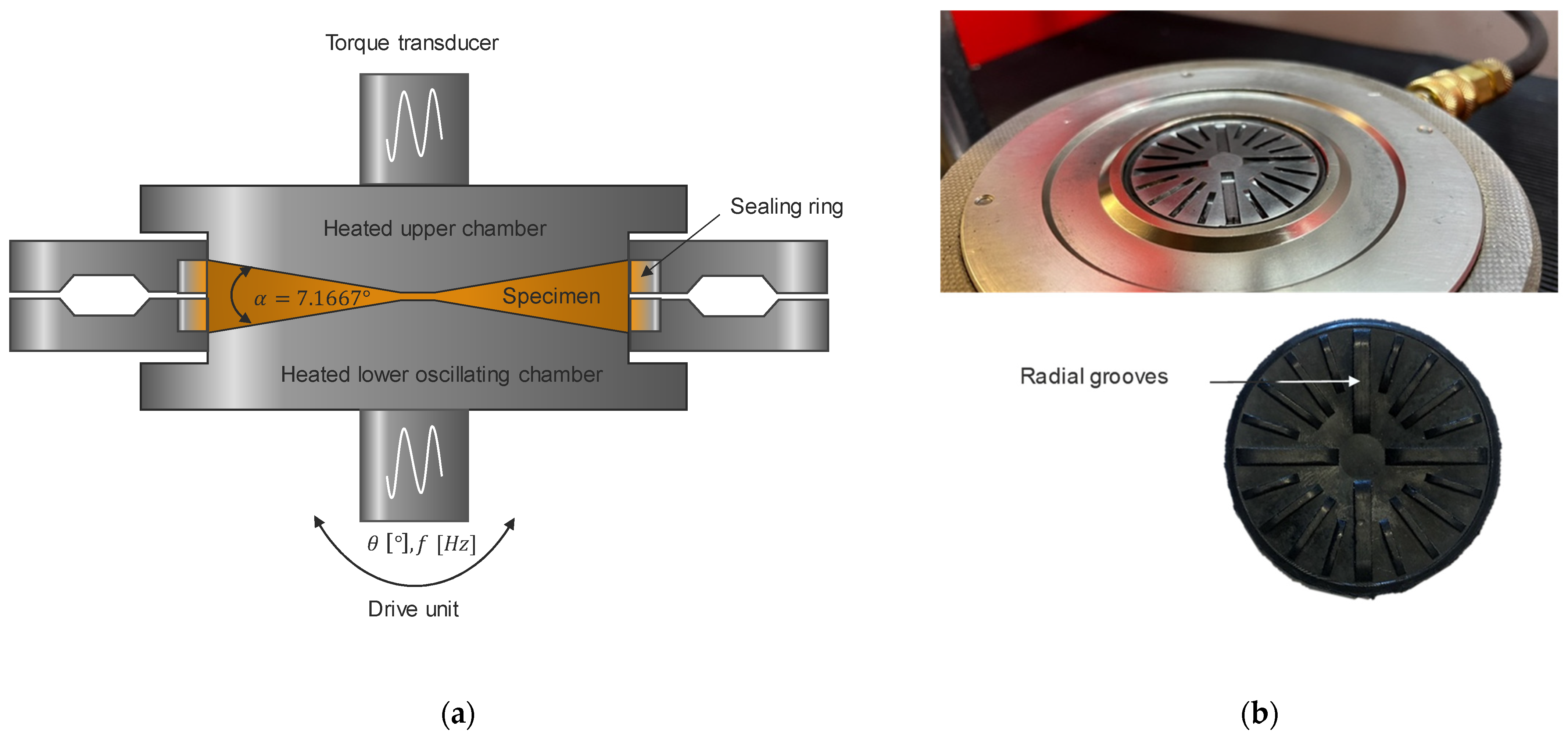
1.2. Rubber Process Analyzer
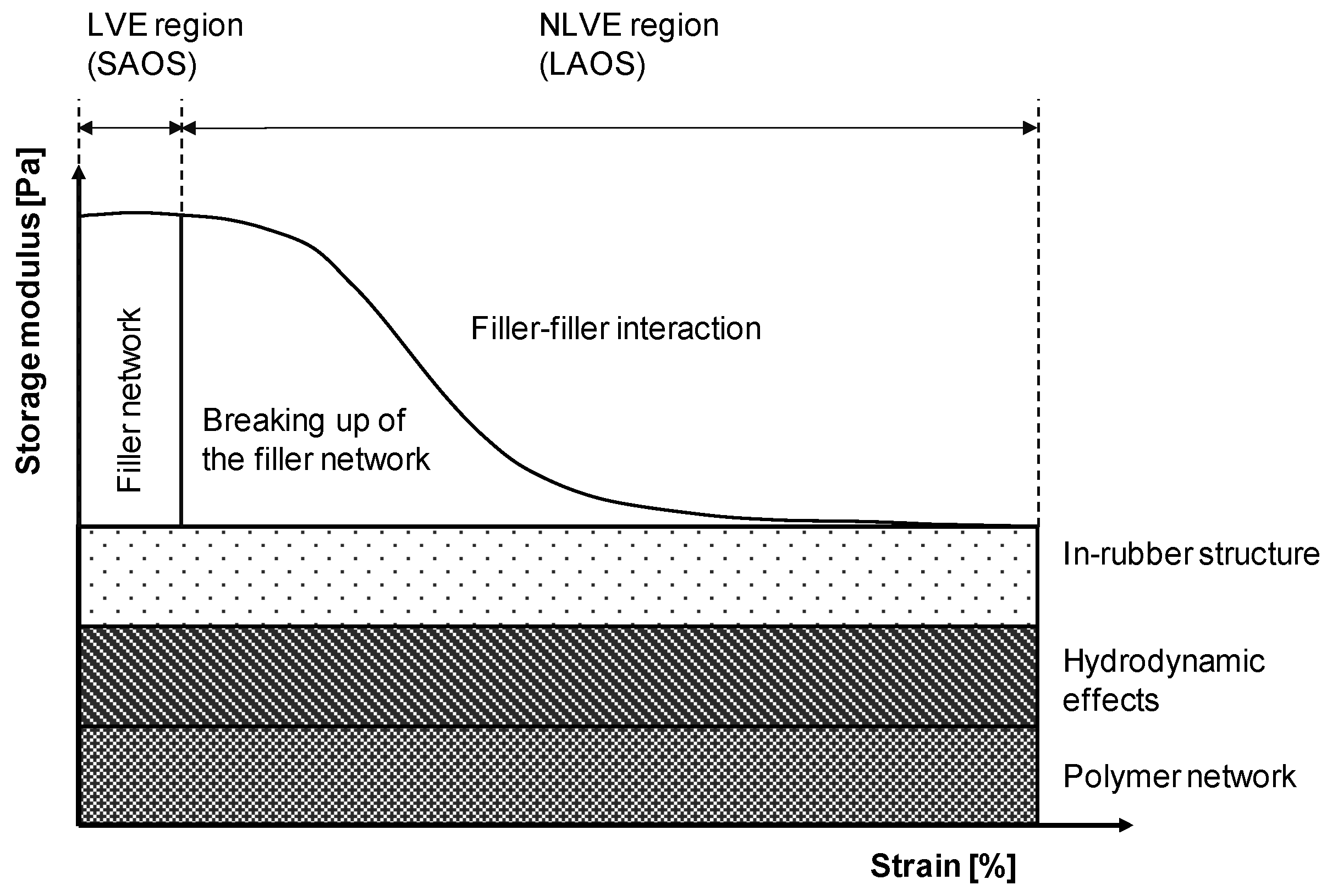
Characterization of Viscoelastic Material Behavior
- : Strain
- : Deflection angle
- : Double cone angle of the biconical test chamber
1.3. Empirical Rheological Transfer Functions
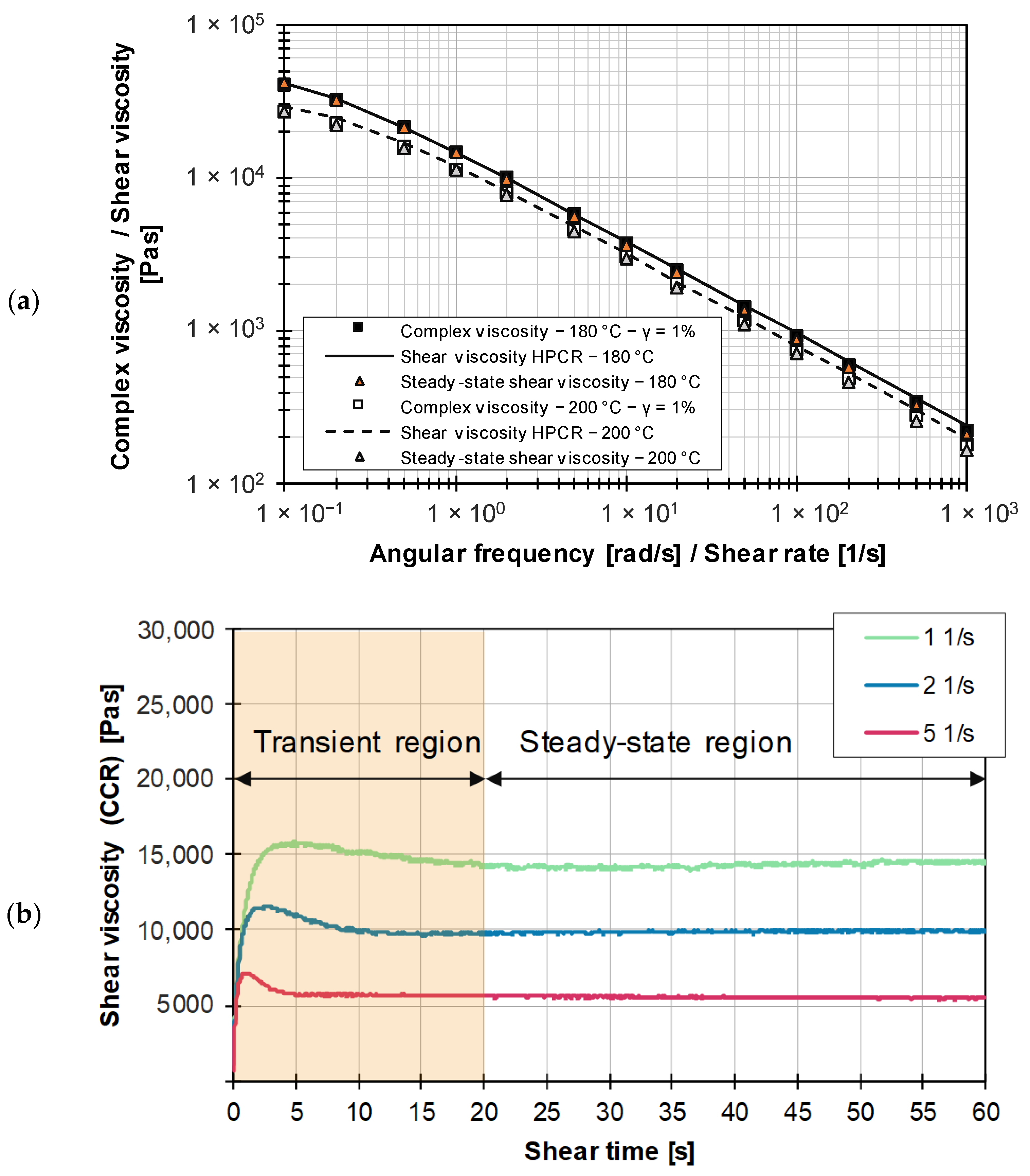
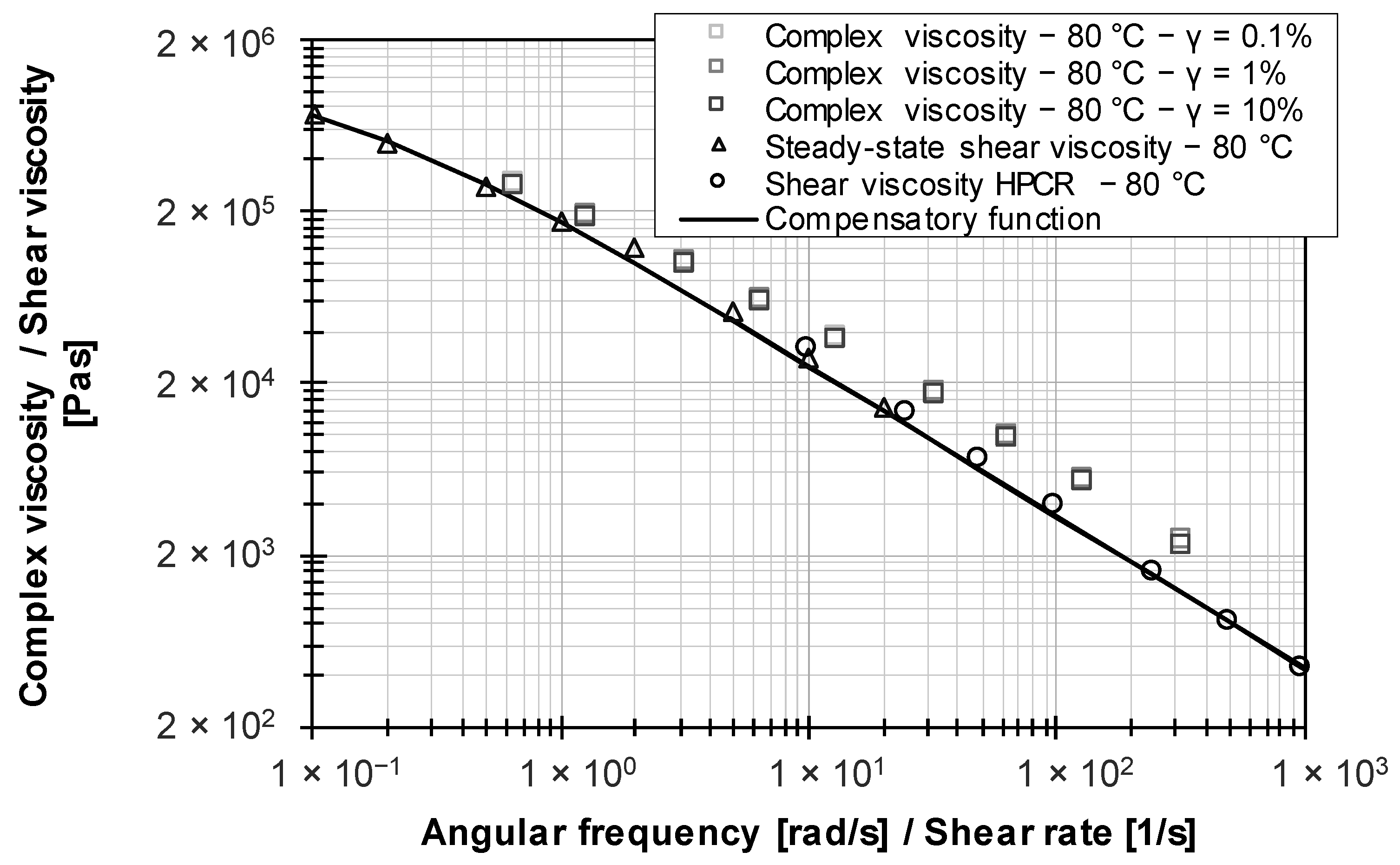
1.3.1. Cox–Merz Rule
- : Complex viscosity
- : Storage modulus
- : Loss modulus
- : Frequency
- Viscous material heating
- Pressure dependence of viscosity
- Wall slip effects
- : Shift factor
1.3.2. Ramp Test
- : Transient viscosity
- : Shear time
- : Edge shear stress
- : Linear viscoelastic stress viscosity
2. Materials and Methods
2.1. Investigated Materials
2.2. High-Pressure Capillary Rheometer
2.3. Closed Cavity Rheometer (Rubber Process Analyzer)
2.4. Investigation Plan and Evaluation Methods
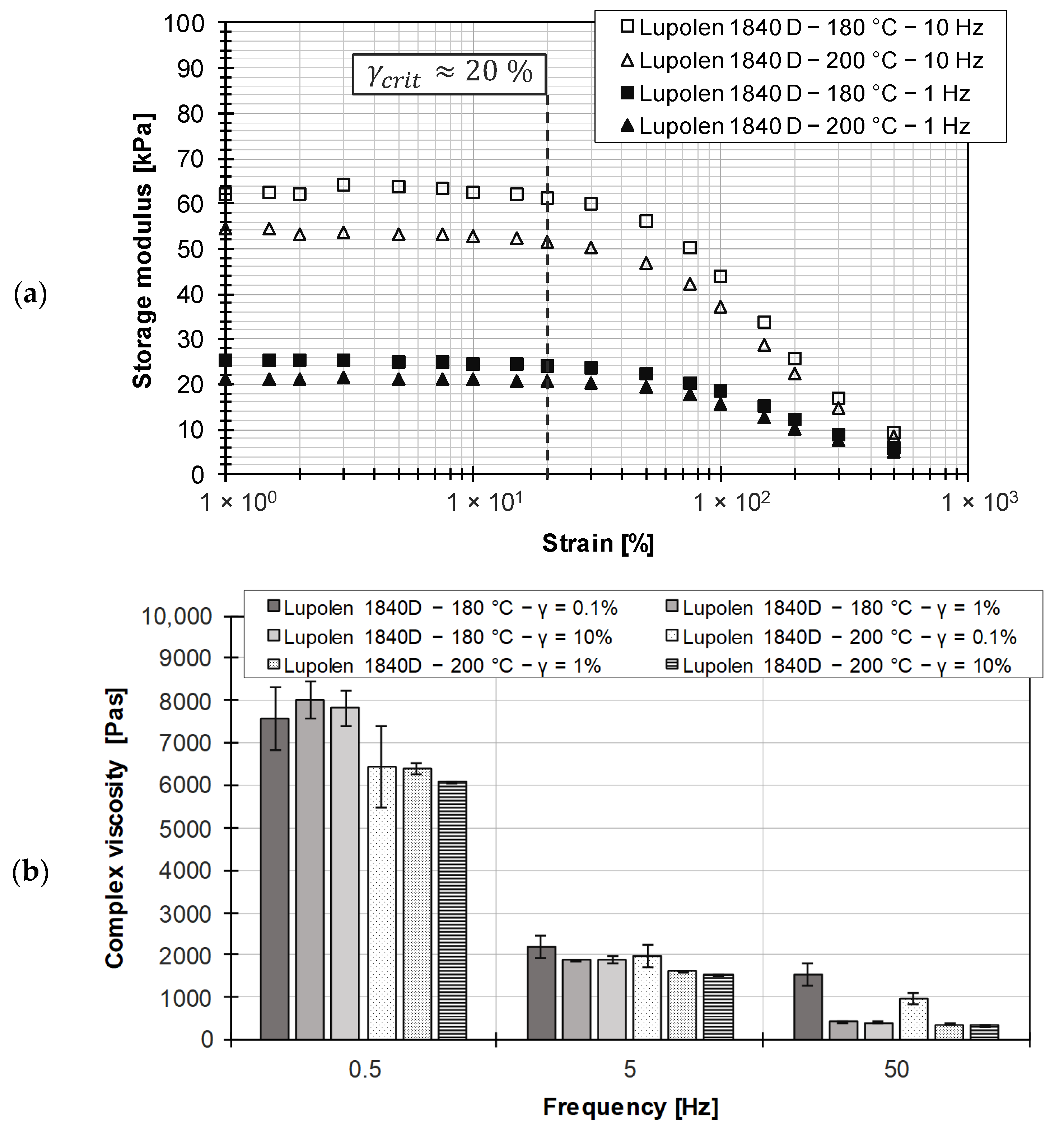
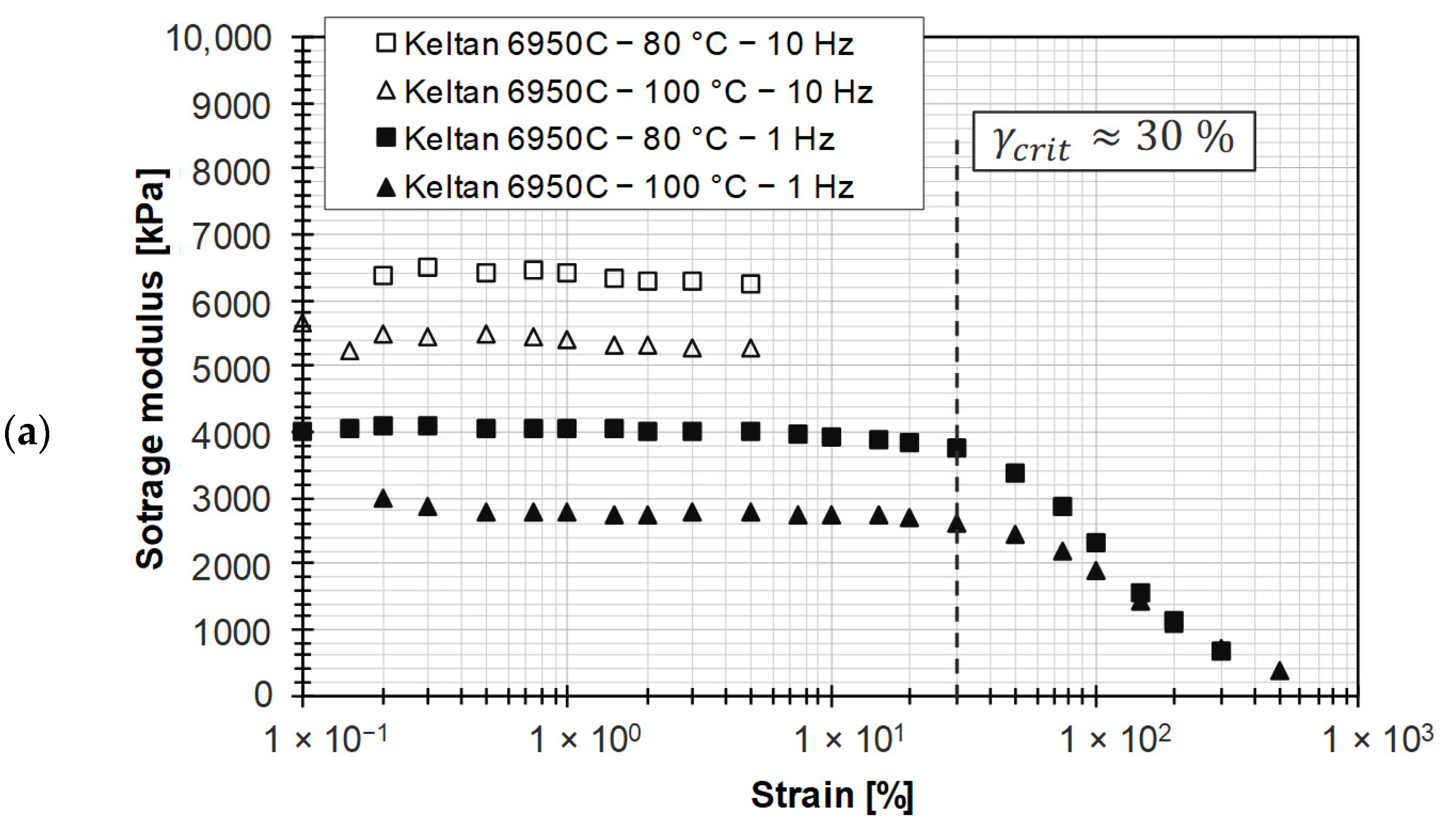
2.4.1. Amplitude Sweep
- : Zero modulus
- : Transition strain
- : Filler network fracture exponent
- : Diffraction coefficient
2.4.2. Frequency Sweep
2.4.3. Ramp Test
- : Peripheral speed
- : Die gap
- : Test-chamber perimeter
- : Rotational speed
- : Test-chamber radius
- : Torque
3. Results
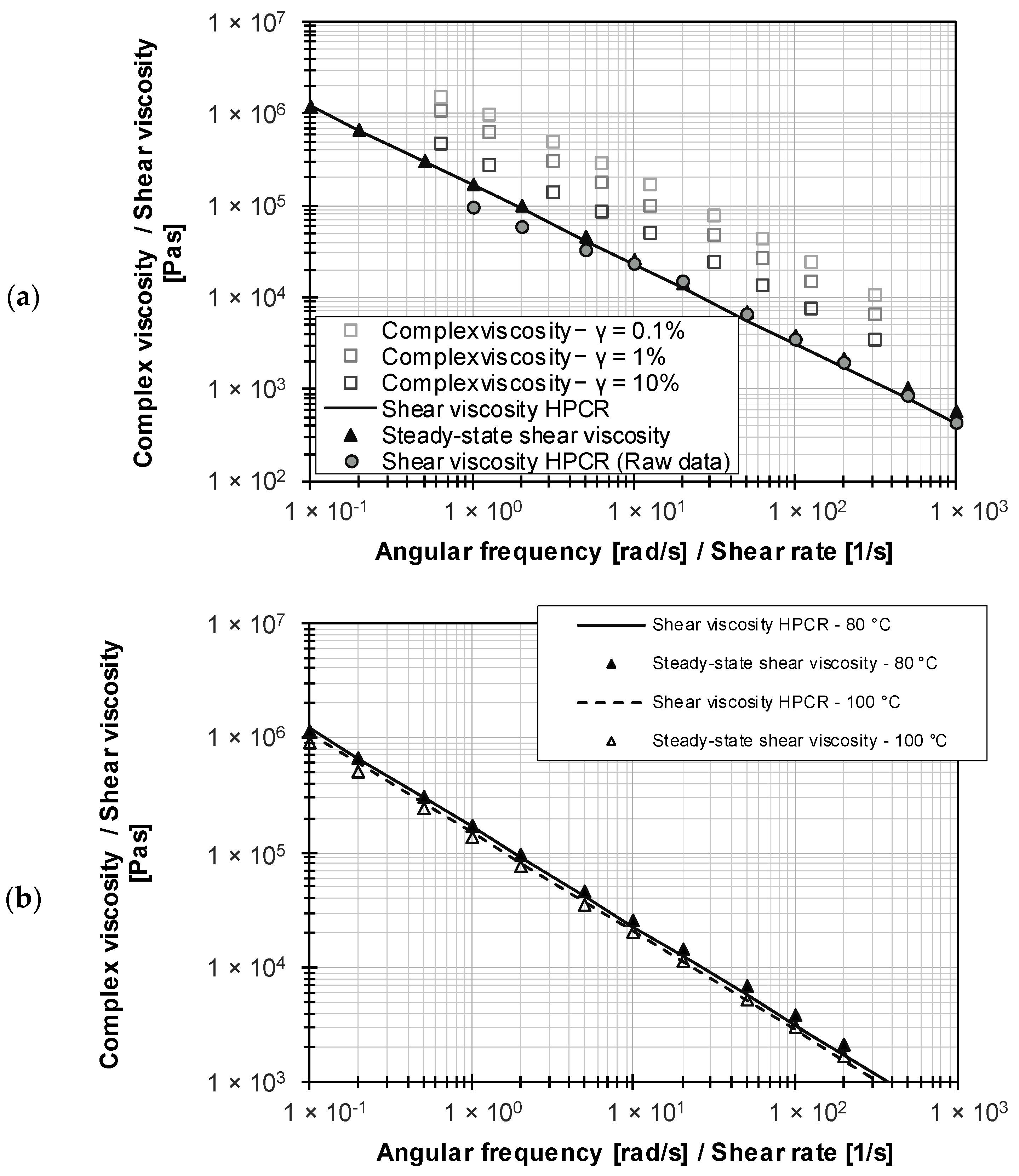
3.1. Lupolen 1840D
- : Zero shear viscosity
- : Temperature shift factor
- : Transition time
- : Flow exponent
3.2. Keltan 6950C
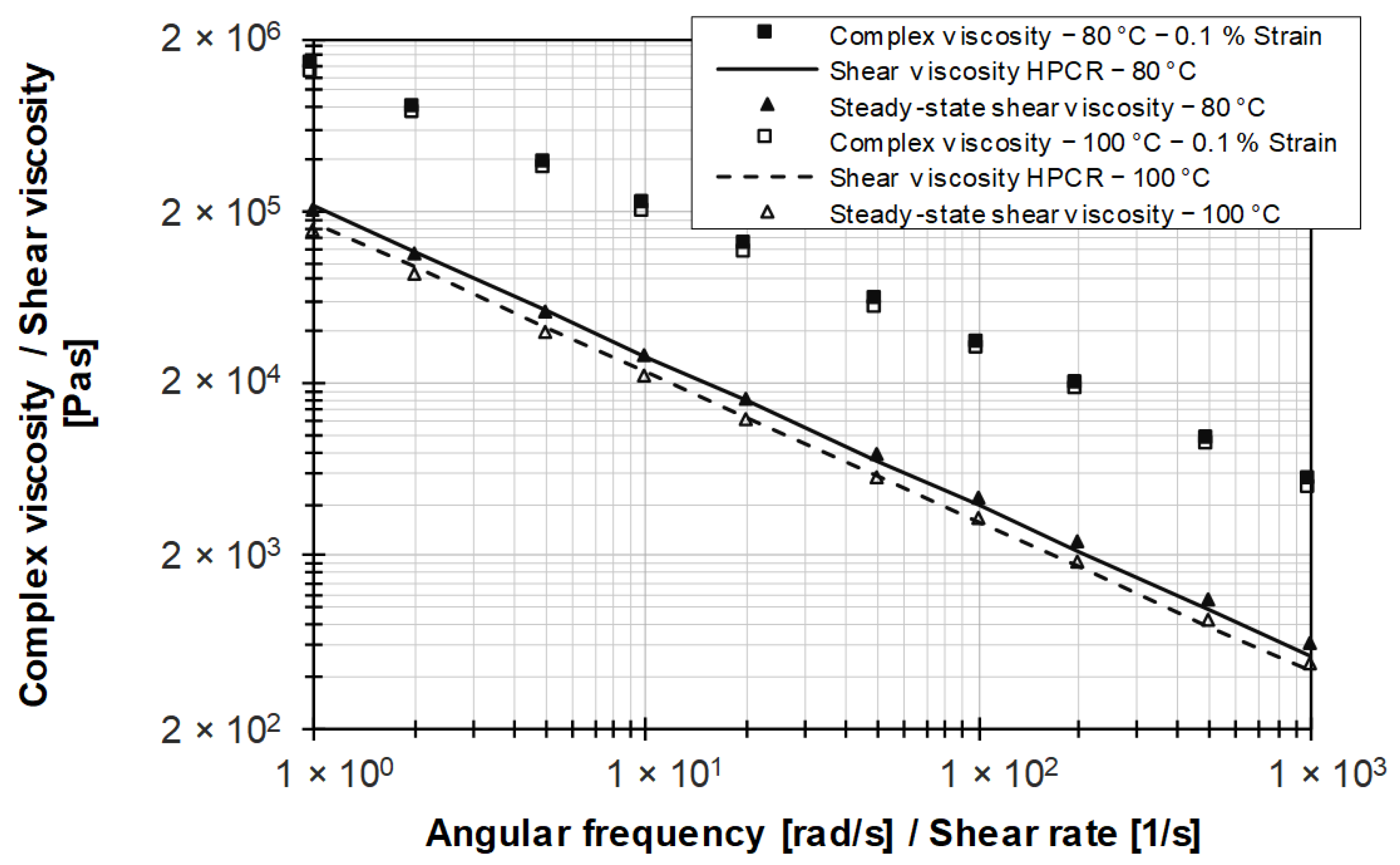
3.3. Rubber Compound with Wall-Adhering Properties (EPDM Pr. 5)
3.4. Rubber Compound with Wall-Slipping Properties (EPDM Pr. 3)
4. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Buhrin, H.G.; Rauschmann, T.; Graf, H.-J. Wall Slip in Processing Rubber Compound revisited. Kautsch. Gummi Kunstst. 2021, 3, 61–66. [Google Scholar]
- Kleinschmidt, D.; Schöppner, V. Improvement of a method for the correction of wall slip effects within the rheological measurements of filled rubber compounds. SPE Polym. 2023, 4, 63–79. [Google Scholar] [CrossRef]
- Pahl, M.; Gleißle, W.; Laun, H.-M. Practical Rheology of Plastics and Elastomers, 4th ed.; Gesellschaft Kunststofftechnik, VDI-Verlag: Düsseldorf, Germany, 1995. (In German) [Google Scholar]
- SIGMASOFT Engineering GmbH: Simulation in extrusion—Not as complicated as previously thought. Extrusion 2021, 4, 30–31. (In German)
- Brachwitz, K. RPA—Diverse testing options for rubbers and rubber compounds. In Proceedings of the 25th Technomer, Chemnitz, Germany, 9–10 November 2017. (In German). [Google Scholar]
- Mezger, T. The Rheology Handbook, 5th ed.; Vincentz Network: Hanover, Germany, 2016. (In German) [Google Scholar]
- Ansari, M.; Hatzikiriakos, S.G.; Sukhadia, A.M.; Rohlfing, D.C. Rheology of Ziegler-Natta and metallocene high-density polyethylenes: Broad molecular weight distribution effects. Rheol. Acta 2011, 50, 17–27. [Google Scholar] [CrossRef]
- Schwarzl, F.R. Polymer Mechanics. Structure and Mechanical Behavior of Polymers, 1st ed.; Springer: Berlin/Heidelberg, Germany, 1990. (In German) [Google Scholar]
- Yang, C.; Li, Z. A study of wall slip in the capillary flow of a filled rubber compound. Polym. Test. 2014, 37, 45–50. [Google Scholar] [CrossRef]
- Buhrin, H.G.; Rauschmann, T.; Graf, H.-J. A new and highly efficient method to measure steady shear viscosity and wall slip of rubber compounds. Closed boundary rheometer (RPA). Annu. Trans. Nord. Rheol. Soc. 2021, 29, 87–94. [Google Scholar]
- Ellwanger, F.; Georgantopoulos, C.K.; Karbstein, H.P.; Wilhelm, M.; Emin, M.A. Application of the ramp test from a closed cavity rheometer to obtain the steady-shear shear viscosity. Appl. Rheol. 2023, 33, 20220149. [Google Scholar] [CrossRef]
- Schröder, T. Rheology of Plastics. Theory and Practice, 1st ed.; Carl Hanser Verlag: München, Germany, 2018. (In German) [Google Scholar]
- Macosko, C.W. Rheology. Principles, Measurements, and Applications; Wiley-VCH: New York, NY, USA, 1994. [Google Scholar]
- Leblanc, J.L.; Barres, C. Recent developments in shear rheometry of uncured rubber compounds. I.: Design, construction and validation of a sliding cylinder rheometer. Polym. Test. 2000, 19, 177–191. [Google Scholar]
- Leblanc, J.L. Rubber—Filler interactions and rheological properties in filled compounds. Prog. Poly. Sci. 2002, 27, 624–687. [Google Scholar] [CrossRef]
- Hatzikiriakos, S.G. Slip mechanisms in complex fluid flows. Soft Matter 2015, 11, 7851–7856. [Google Scholar] [CrossRef]
- Hornig, R. Normal-stress-elasticity of FKM compounds basic observations on rheology and mixing process technology. GAK Gummi Fasern Kunststoffe 2011, 12, 732–743. [Google Scholar]
- Cloitre, M.; Bonnecaze, R.T. A review on wall slip in high solid dispersions. Rheol. Acta 2017, 17, 283–305. [Google Scholar] [CrossRef]
- Mooney, M. Explicit Formulas for Slip and Fluidity. J. Rheol. 1931, 2, 210–222. [Google Scholar] [CrossRef]
- Geiger, K. Rheological characterization of EPDM rubber compounds using capillary rheometer systems, Kautsch. Gummi Kunstst. 1989, 4, 273–283. (In German) [Google Scholar]
- Rabinowitsch, B. About the viscosity and elasticity of sols. Z. Phys. Chem. 1929, 1, 1–26. [Google Scholar] [CrossRef]
- Hornig, R.; Kielmann, J. Oscillation rheology vs. high-pressure capillary rheometry. GAK Gummi Fasern Kunststoffe 2014, 11, 708–719. [Google Scholar]
- Ryzko, P.J. Process Control and Optimization in the Elastomer Processing Based on Statistical Design of Experiments and Mathematical Process Models. Ph.D. Thesis, Rhenisch-Westphalian Technical University Aachen, Aachen, Germany, 13 November 2011. [Google Scholar]
- Payne, A.R. The Dynamic Properties of Carbon Black-Loaded Natural Rubber Vulcanizates. J. Appl. Polym. Sci. 1962, 6, 57–63. [Google Scholar] [CrossRef]
- Hojdis, N.W. Computer Simulations of Silica-Silane-Polymer Interfaces. Ph.D. Thesis, University of Wuppertal, Wuppertal, Germany, March 2013. (In German). [Google Scholar]
- Kahramann, H. Experimental Study and Characterization of the Deformation Induced Anisotropic Material Behavior of Reinforced Elastomers. Ph.D. Thesis, Rhenisch-Westphalian Technical University Aachen, Aachen, Germany, 7 December 2015. [Google Scholar]
- Roland, C.M. Reinforcement of Elastomers. Mater. Sci. Eng. 2016, 1, 2475–2480. [Google Scholar] [CrossRef]
- Tanner, R.I. Engineering Rheology; Oxford University Press: Oxford, UK, 2002; Volume 2. [Google Scholar]
- Cox, W.P.; Merz, E.H. Correlation of Dynamic and Steady Flow Viscosities. J. Poly. Sci. 1958, 28, 619–622. [Google Scholar] [CrossRef]
- Fuchs, R. Quantitative Description of the Non-Linear Viscoelastic Properties of Viscoelastic Surfactant Systems. Ph.D. Thesis, Technical University Dortmund, Dortmund, Germany, 2013. (In German). [Google Scholar]
- Snijkers, F.; Vlassopoulos, D. Appraisal of the Cox-Merz rule for well-characterized entangled linear and branched polymers. Rheol. Acta 2014, 53, 935–946. [Google Scholar] [CrossRef]
- Buhrin, H.G.; Rauschmann, T. Viscosity Measurement of filled Rubber Compounds—New insight for Error free Measurements. Kautsch. Gummi Kunstst. 2021, 2, 39–44. [Google Scholar]
- Rauschmann, T. Steady Shear Viscosity Measurements of Filled Rubber Compounds using New Enhanced RPA Technology. In Proceedings of the Deutsche Kautschuk Tagung, Nuremberg, Germany, 27–29 June 2022. [Google Scholar]
- Stieger, S.; Mitsoulis, E.; Walluch, M.; Ebner, C.; Kerschbaumer, R.C.; Haselmann, M.; Mostafaiyan, M.; Kämpfe, M.; Kühnert, I.; Wießner, S.; et al. On the Influence of Viscoelastic Modeling in Fluid Flow Simulations of Gum Acrylonitrile Butadiene Rubber. Polymers 2021, 13, 2323. [Google Scholar] [CrossRef] [PubMed]
- Phewthongin, N.; Saeoui, P.; Sirisinha, C. A study of rheological properties in sulfur-vulcanized CPE/NR blends. Polym. Test. 2005, 24, 227–233. [Google Scholar] [CrossRef]
- Yang, C.; Li, Z. Effects of wall slip on the rheological measurement and extrusion die design of a filled rubber compound. Plast. Rubber Compos. 2016, 7, 326–331. [Google Scholar] [CrossRef]
- Geisbüsch, P. Approaches to the Shrinkage Calculation of Unfilled and Mineral-Filled Thermoplastics. Ph.D. Thesis, Rhenish-Westphalian Technical University Aachen, Aachen, Germany, 5 December 1980. (In German). [Google Scholar]
- Musialek, M. Contribution to the Prediction of the Flow Behavior of Highly Filled Plastics. Ph.D. Thesis, University of Stuttgart, Stuttgart, Germany, 22 June 2016. (In German). [Google Scholar]
- Gleissle, W.; Hochstein, B. Validity of the Cox-Merz rule for concentrated suspension. J. Rheol. 2003, 47, 897–910. [Google Scholar] [CrossRef]
- Heyer, P.; Wurm, C.; Ehrentraut, H. Measurement and visualization of slip in rubber flow. In Proceedings of the Annual European Rheology Conference, Seville, Spain, 26–28 April 2022. [Google Scholar]
- White, J.L.; Han, M.H.; Nakajima, N.; Brzoskowski, R. The influence of materials of construction on biconical rotor and capillary measurements of shear viscosity of rubber and its compounds and considerations of slippage. J. Rheol. 1991, 1, 167–189. [Google Scholar] [CrossRef]
- ISO 4097:2020; Ethylene-Propylenediene (EPDM)—Evaluation Procedure. International Standard Organization: Vernier, Switzerland, 2020.
- Deutsches Institut für Normung, e.V. DIN 53019-4—Rheometry—Measurement of Flow Properties with Rotational Rheometers—Part 4: Oscillatory Rheology; Deutsches Institut für Normung e.V: Berlin, Germany, 2016. (In German) [Google Scholar]
- Norton, E.; Isayev, A.I. Steady State and Dynamic Oscillatory Shear Properties of Carbon Black Filled Elastomers. J. Elastomers Plast. 2023, 55, 719–767. [Google Scholar] [CrossRef]



| Component | EPDM Compound Pr. 3 | EPDM Compound Pr. 5 |
|---|---|---|
| Raw polymer (Keltan 6950 C) | 100 phr | 100 phr |
| Carbon black (N 550) | 100 phr | 65 phr |
| Silica | - | 25 phr |
| Other fillers | 20 phr | 90 phr |
| Oil | 50 phr | 55 phr |
| Other additives | 14.25 phr | 14.25 phr |
| Total amount | 284.25 phr | 349.25 phr |
| Mooney viscosity ML1+4 (100 °C) | 76 MU | 85 MU |
| Specification | Specification Value | |
|---|---|---|
| Die gap | 0.50 mm | |
| Frequency range | 0.001 Hz to 100 Hz | |
| Strain | Oscillation | ±0.001° to ±360° |
| Continuous rotation | No limitation | |
| Torque range | 0.0001 dNm to 235 dNm | |
| Temperature range | Ambient to 350 °C | |
| Parameter | Parameter Setting | ||
|---|---|---|---|
| Preconditioning | Frequency | 0 Hz | |
| Strain | 0% | ||
| Time | 5 min | ||
| Temperature | LDPE | 180 °C/200 °C | |
| EPDM | 80 °C/100 °C | ||
| Amplitude sweep | Frequency | 1 Hz/10 Hz | |
| Strain | ±0.1% to 500% in 23 steps | ||
| Number of cycles | 10 cycles per strain | ||
| Temperature | LDPE | 180 °C/200 °C | |
| EPDM | 80 °C/100 °C | ||
| Parameter | Parameter Setting | ||
|---|---|---|---|
| Preconditioning | Frequency | 0 Hz | |
| Strain | 0% | ||
| Time | 5 min | ||
| Temperature | LDPE | 180 °C/200 °C | |
| EPDM | 80 °C/100 °C | ||
| Frequency sweep | Frequency | 0.1 Hz to 50 Hz in 9 steps | |
| Strain | 0.1%/1%/10% | ||
| Number of cycles | 10 cycles per frequency | ||
| Temperature | LDPE | 180 °C/200 °C | |
| EPDM | 80 °C/100 °C | ||
| Parameter | Parameter Setting | ||
|---|---|---|---|
| Preconditioning | Frequency | 0 Hz | |
| Strain | 0% | ||
| Time | 5 min | ||
| Temperature | LDPE | 180 °C/200 °C | |
| EPDM | 80 °C/100 °C | ||
| Continuous rotation | Shear rate steps | 0.1 s−1 to 20 s−1 in 8 steps | |
| Shear time per shear rate | 1 min | ||
| Holding time between shear rate steps (No material deformation) | 1 min | ||
| Temperature | LDPE | 180 °C/200 °C | |
| EPDM | 80 °C/100 °C | ||
| Carreau Parameter | Shear Viscosity (HPCR) | Complex Viscosity (RPA) | Steady-State Shear Viscosity (RPA) | |||
|---|---|---|---|---|---|---|
| [°C] | 180 | 200 | 180 | 200 | 180 | 200 |
| [Pas] | 64,676.5 | 40,265.3 | 58,455.8 | 34,122.3 | 61,913.7 | 34,318.0 |
| [s] | 10.49 | 6.53 | 8.56 | 4.99 | 9.20 | 5.10 |
| [-] | 0.60 | 0.60 | 0.61 | 0.61 | 0.62 | 0.62 |
| Power Law Parameter | Shear Viscosity (HPCR) | Complex Viscosity (RPA, 0.1% Strain) | Steady-State Shear Viscosity (RPA) | |||
|---|---|---|---|---|---|---|
| [°C] | 80 | 100 | 80 | 100 | 80 | 100 |
| [Pas] | 214,404.54 | 170,912 | 1,437,150.1 | 1,286,695.6 | 205,404.29 | 155,354.83 |
| [-] | 0.13 | 0.13 | 0.19 | 0.19 | 0.16 | 0.16 |
| Power Law Parameter | Shear Viscosity (HPCR) | Complex Viscosity (RPA, 0.1% Strain) | Steady-State Shear Viscosity (RPA) | |||
|---|---|---|---|---|---|---|
| [°C] | 80 | 100 | 80 | 100 | 80 | 100 |
| [Pas] | 166,478.8 | 149,267.56 | 1,138,757.9 | 875,976.1 | 170,912.7 | 132,706.9 |
| [-] | 0.14 | 0.14 | 0.21 | 0.21 | 0.17 | 0.17 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kleinschmidt, D.; Brüning, F.; Petzke, J. Wall Slip-Free Viscosity Determination of Filled Rubber Compounds Using Steady-State Shear Measurements. Polymers 2023, 15, 4406. https://doi.org/10.3390/polym15224406
Kleinschmidt D, Brüning F, Petzke J. Wall Slip-Free Viscosity Determination of Filled Rubber Compounds Using Steady-State Shear Measurements. Polymers. 2023; 15(22):4406. https://doi.org/10.3390/polym15224406
Chicago/Turabian StyleKleinschmidt, Dennis, Florian Brüning, and Jonas Petzke. 2023. "Wall Slip-Free Viscosity Determination of Filled Rubber Compounds Using Steady-State Shear Measurements" Polymers 15, no. 22: 4406. https://doi.org/10.3390/polym15224406
APA StyleKleinschmidt, D., Brüning, F., & Petzke, J. (2023). Wall Slip-Free Viscosity Determination of Filled Rubber Compounds Using Steady-State Shear Measurements. Polymers, 15(22), 4406. https://doi.org/10.3390/polym15224406






