Continuous Phosphate Removal and Recovery Using a Calcium Silicate Hydrate Composite Monolithic Cryogel Column
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Preparation of the Cry–CSH Monolithic Column
2.3. Characterization of the Monolithic Cry–CSH Column
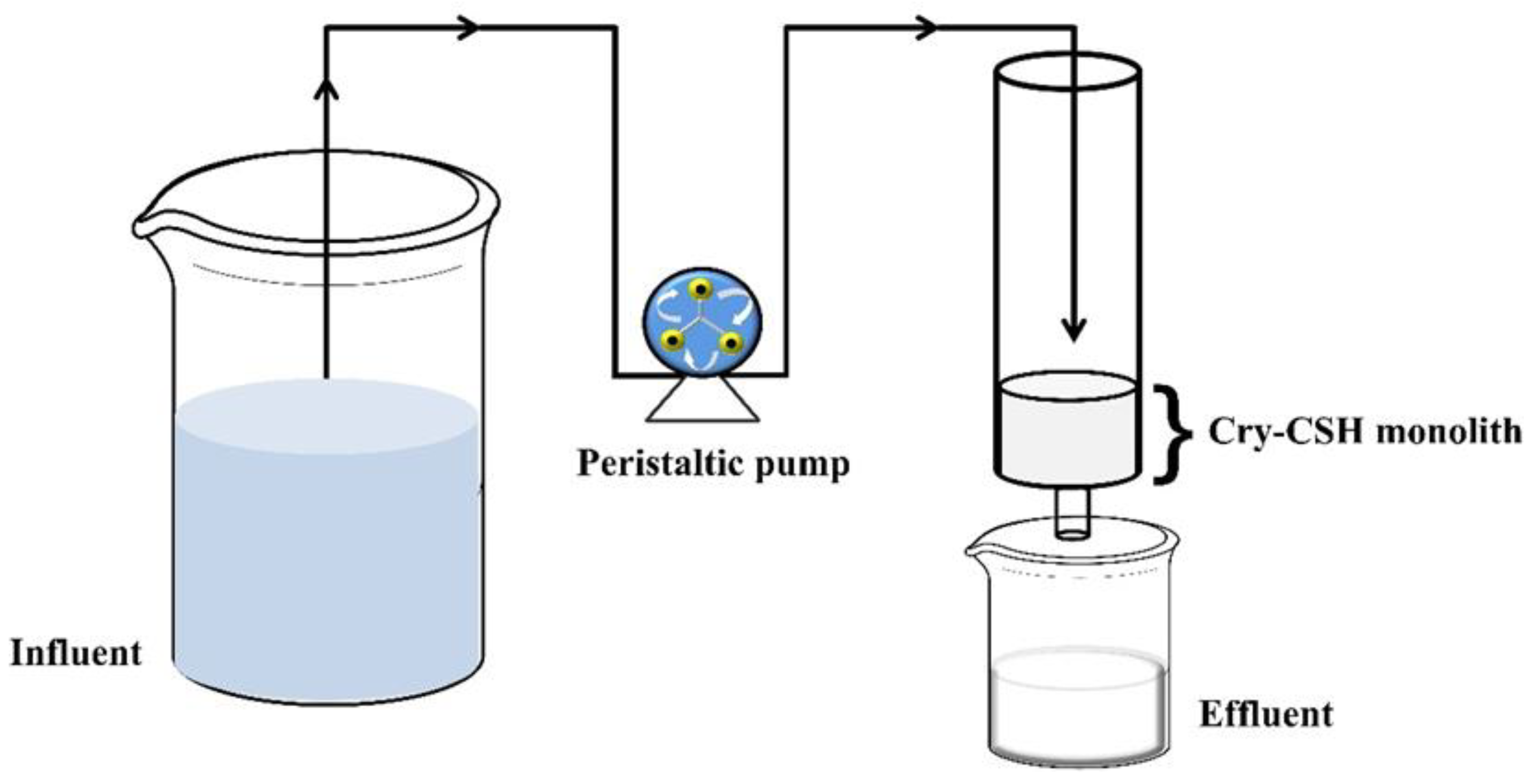
2.4. Experimental Setup for Continuous Flow Adsorption Study
2.5. Column Data Analysis
2.6. Real Sample Application
3. Results and Discussion
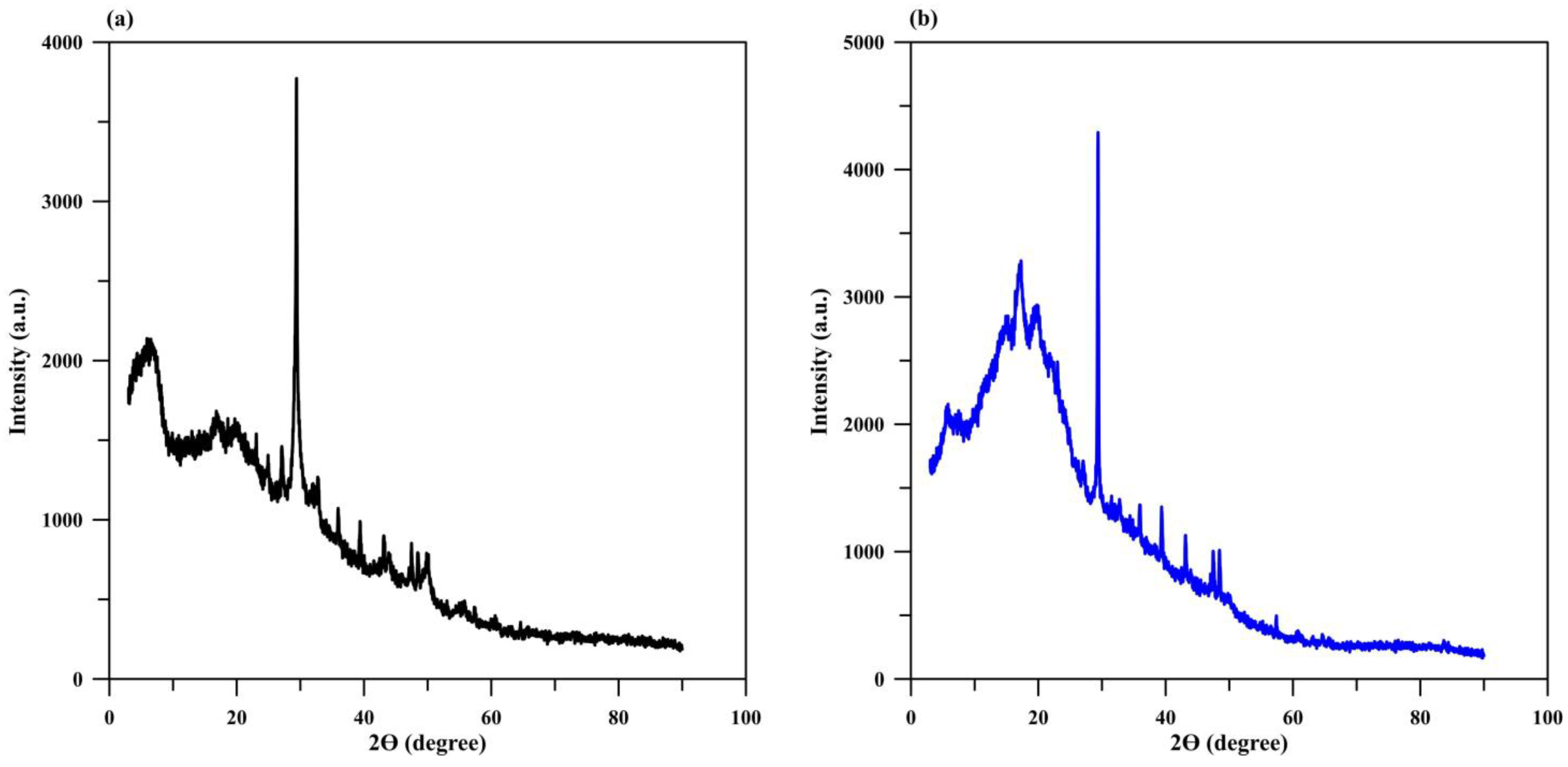
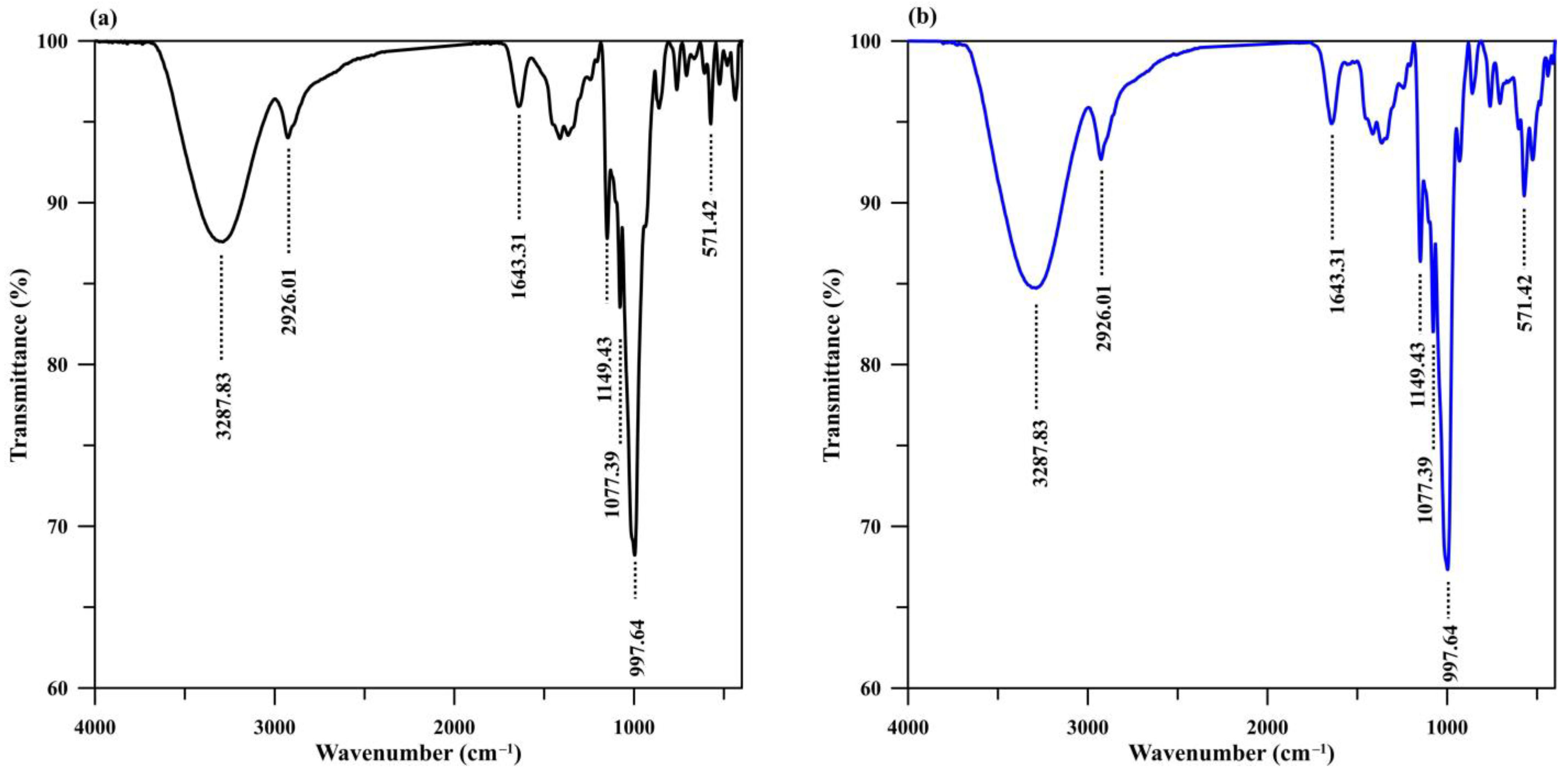
3.1. Characterization of the Adsorptive Material
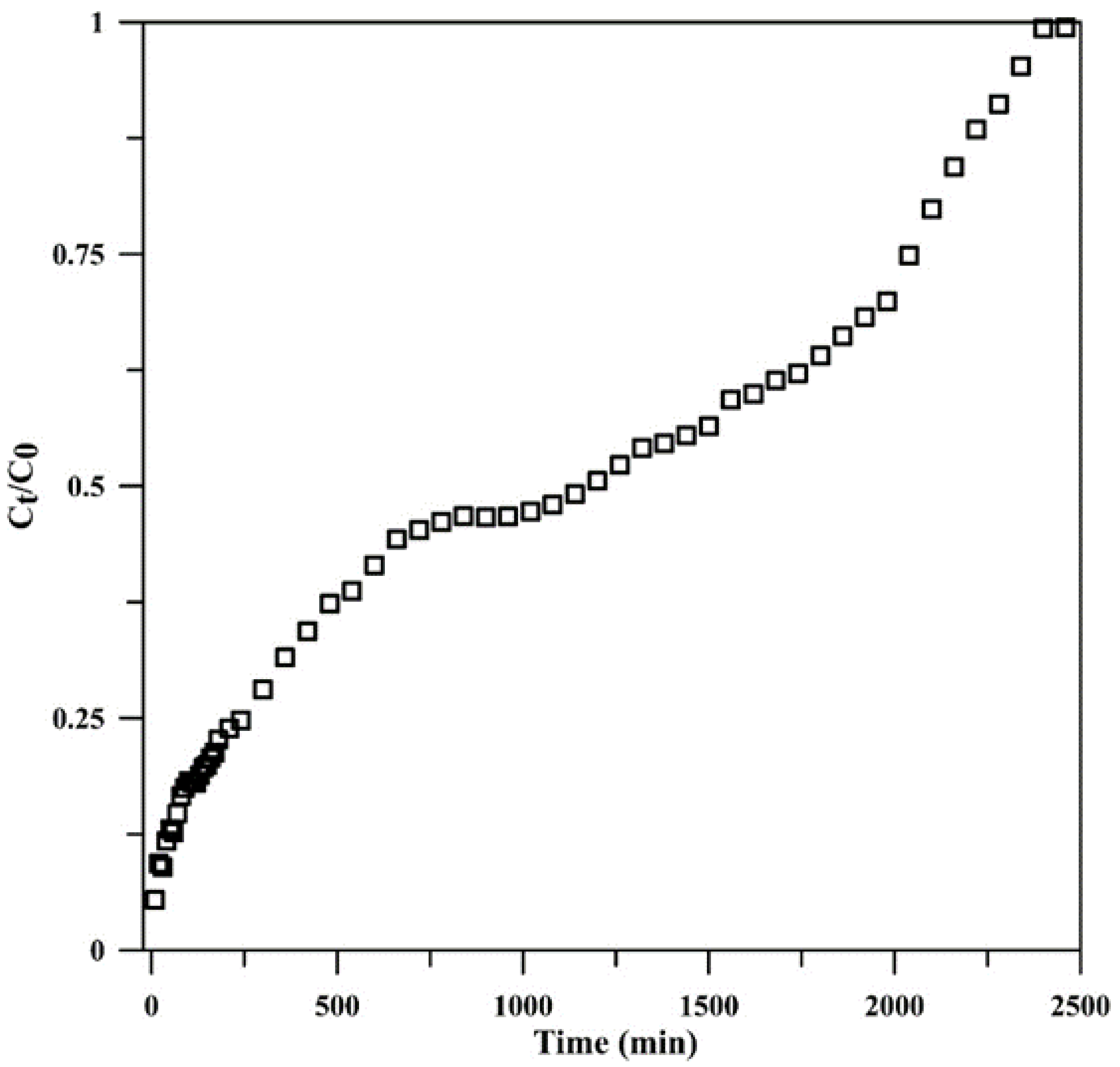
3.2. Continuous Flow Adsorption Studies
3.2.1. Effect of the Influent Flow Rate
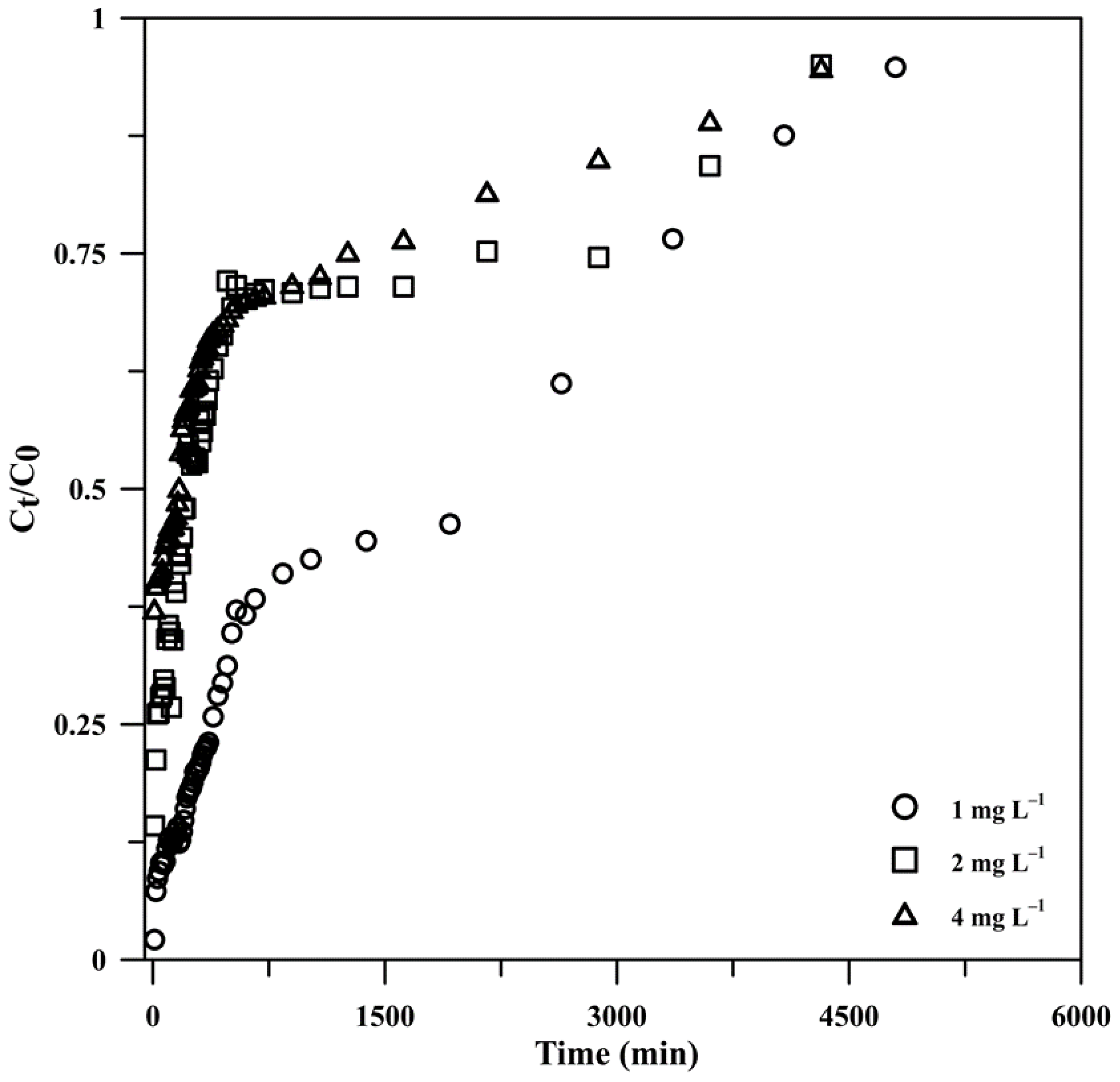
3.2.2. Effect of the Influent Phosphate Concentration
3.2.3. Effect of the Adsorbent Height
3.3. Adsorption Dynamics
3.3.1. Thomas Model
3.3.2. Adams–Bohart Model
3.3.3. Yoon–Nelson Model
3.4. Application of the Continuous Flow System for Real Sample Treatment
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kuwahara, Y.; Yamashita, H. Phosphate removal from aqueous solutions using calcium silicate hydrate prepared from blast furnace slag. ISIJ Int. 2017, 57, 1657–1664. [Google Scholar] [CrossRef] [Green Version]
- Maeda, H.; Yokota, S.; Kasuga, T. Structural changes in calcium silicate hydrate gel and resulting improvement in phosphate species removal properties after mechanochemical treatment. R. Soc. Open Sci. 2018, 5, 18143. [Google Scholar] [CrossRef] [PubMed]
- Ayoub, G.M.; Kalinian, H.; Zayyat, R. Efficient phosphate removal from contaminated water using functional raw dolomite powder. SN Appl. Sci. 2019, 1, 802. [Google Scholar] [CrossRef] [Green Version]
- Huo, J.; Min, X.; Wang, Y. Zirconium-modified natural clays for phosphate removal: Effect of clay minerals. Environ. Res. 2021, 194, 110685. [Google Scholar] [CrossRef] [PubMed]
- Mekonnen, D.T.; Alemayehu, E.; Lennartz, B. Fixed-bed column technique for the removal of phosphate from water using leftover coal. Materials 2021, 14, 5466. [Google Scholar] [CrossRef]
- Almanassra, I.W.; Kochkodan, V.; Subeh, M.; Mckay, G.; Atieh, M.; Al-Ansari, T. Phosphate removal from synthetic and treated sewage effluent by carbide derive carbon. J. Water Process. Eng. 2020, 36, 101323. [Google Scholar] [CrossRef]
- Seliem, M.K.; Komarneni, S.; Abu Khadra, M.R. Phosphate removal from solution by composite of MCM-41 silica with rice husk: Kinetic and equilibrium studies. Microporous Mesoporous Mater. 2016, 224, 51–57. [Google Scholar] [CrossRef]
- Wu, F.; Yu, Q.; Gauvin, F.; Brouwers, H.J.H.; Liu, C. Phosphorus removal from aqueous solutions by adsorptive concrete aggregates. J. Clean. Prod. 2021, 278, 123933. [Google Scholar] [CrossRef]
- Kumararaja, P.; Suvana, S.; Saraswathy, R.; Lalitha, N.; Muralidhar, M. Mitigation of eutrophication through phosphate removal by aluminium pillared bentonite from aquaculture discharge water. Ocean Coast. Manag. 2019, 182, 104951. [Google Scholar] [CrossRef]
- Taweekarn, T.; Wongniramaikul, W.; Choodum, A. Removal and recovery of phosphate using a novel calcium silicate hydrate composite starch cryogel. J. Environ. Manag. 2022, 301, 113923. [Google Scholar] [CrossRef]
- Chen, Y.; Long, J.; Chen, S.; Xie, Y.; Xu, Z.; Ning, Z.; Zhang, G.; Xiao, T.; Yu, M.; Ke, Y.; et al. Multi-step purification of electrolytic manganese residue leachate using hydroxide sedimentation, struvite precipitation, chlorination and coagulation: Advanced removal of manganese, ammonium, and phosphate. Sci. Total Environ. 2022, 805, 150237. [Google Scholar] [CrossRef]
- Lateef, A.; Chaudhry, M.N.; Ilyas, S. Biological treatment of dairy wastewater using activated sludge. Sci. Asia 2013, 39, 179–185. [Google Scholar] [CrossRef] [Green Version]
- Ihsanullah, I.; Khan, M.T.; Zubair, M.; Bilal, M.; Sajid, M. Removal of pharmaceuticals from water using sewage sludge-derived biochar: A review. Chemosphere 2022, 289, 133196. [Google Scholar] [CrossRef]
- Pohl, A. Removal of heavy metal ions from water and wastewaters by sulfur-containing precipitation agents. Wat. Air Soil Poll. 2020, 231, 503. [Google Scholar] [CrossRef]
- Peleka, E.; Deliyanni, E. Adsorptive removal of phosphates from aqueous solutions. Desalination 2009, 245, 357–371. [Google Scholar] [CrossRef]
- Loganathan, P.; Vigneswaran, S.; Kandasamy, J.; Bolan, N.S. Removal and recovery of phosphate from water using sorption. Crit. Rev. Environ. Sci. Technol. 2014, 44, 847–907. [Google Scholar] [CrossRef]
- Desmidt, E.; Ghyselbrecht, K.; Zhang, Y.; Pinoy, L.; Van der Bruggen, B.; Verstraete, W.; Rabaey, K.; Meesschaert, B. Global phosphorus scarcity and full-scale P-recovery techniques: A review. Crit. Rev. Environ. Sci. Technol. 2015, 45, 336–384. [Google Scholar] [CrossRef]
- Kong, L.; Tian, Y.; Li, N.; Liu, Y.; Zhang, J.; Zhang, J.; Zuo, W. Highly-effective phosphate removal from aqueous solutions by calcined nano-porous palygorskite matrix with embedded lanthanum hydroxide. Appl. Clay Sci. 2018, 162, 507–517. [Google Scholar] [CrossRef]
- Rajeswari, A.; Amalraj, A.; Pius, A. Removal of phosphate using chitosan-polymer composites. J. Environ. Chem. Eng. 2015, 3, 2331–2341. [Google Scholar] [CrossRef]
- Nazarian, R.; Desch, R.J.; Thiel, S.W. Kinetics and equilibrium adsorption of phosphate on lanthanum oxide supported on activated carbon. Colloids Surf. Physicochem. Eng. Asp. 2021, 624, 126813. [Google Scholar] [CrossRef]
- Khalil, A.K.A.; Dweiri, F.; Almanassra, I.W.; Chatla, A.; Atieh, M.A. Mg-Al layered double hydroxide doped activated carbon composites for phosphate removal from synthetic water: Adsorption and thermodynamics studies. Sustainability 2022, 14, 6991. [Google Scholar] [CrossRef]
- Zhang, B.; Xu, L.; Zhao, Z.; Peng, S.; Yu, C.; Zhang, X.; Zong, Y.; Wu, D. Enhanced phosphate removal by nano-lanthanum hydroxide embedded silica aerogel composites: Superior performance and insights into specific adsorption mechanism. Sep. Purif. Technol. 2021, 285, 120365. [Google Scholar] [CrossRef]
- Moharami, S.; Jalali, M. Use of modified clays for removal of phosphorus from aqueous solutions. Environ. Monit. Assess. 2015, 187, 639. [Google Scholar] [CrossRef] [PubMed]
- Wu, D.; Zhang, B.; Li, C.; Zhang, Z.; Kong, H. Simultaneous removal of ammonium and phosphate by zeolite synthesized from fly ash as influenced by salt treatment. J. Colloid Interface Sci. 2006, 304, 300–306. [Google Scholar] [CrossRef] [PubMed]
- Goscianska, J.; Ptaszkowska-Koniarz, M.; Frankowski, M.; Franus, M.; Panek, R.; Franus, W. Removal of phosphate from water by lanthanum-modified zeolites obtained from fly ash. J. Colloid Interface Sci. 2018, 513, 72–81. [Google Scholar] [CrossRef]
- Zheng, X.; Su, Y.; Chen, Y.; Wei, Y.; Li, M.; Huang, H. The effects of carbon nanotubes on nitrogen and phosphorus removal from real wastewater in the activated sludge system. RSC Adv. 2014, 4, 45953–45959. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, Q.; Huang, H. Effective adsorption of trace phosphate and aluminum in realistic water by carbon nanotubes and reduced graphene oxides. Sci. Total Environ. 2019, 662, 1003–1011. [Google Scholar] [CrossRef]
- Khan, S.; Ishaq, M.; Ahmad, I.; Hussain, S.; Ullah, H. Evaluation of coal as adsorbent for phosphate removal. Arab. J. Geosci. 2013, 6, 1113–1117. [Google Scholar] [CrossRef]
- Mekonnen, D.T.; Alemayehu, E.; Lennartz, B. Removal of phosphate ions from aqueous solutions by adsorption onto leftover coal. Water 2020, 12, 1381. [Google Scholar] [CrossRef]
- Chen, J.; Kong, H.; Wu, D.; Chen, X.; Zhang, D.; Sun, Z. Phosphate immobilization from aqueous solution by fly ashes in relation to their composition. J. Hazard. Mater. 2007, 139, 293–300. [Google Scholar] [CrossRef]
- Hakkar, M.; Arhouni, F.E.; Mahrou, A.; Bilal, E.; Bertau, M.; Roy, A.; Steiner, G.; Haneklaus, N.; Mazouz, H.; Boukhair, A.; et al. Enhancing rare earth element transfer from phosphate rock to phosphoric acid using an inexpensive fly ash additive. Miner. Eng. 2021, 172, 107166. [Google Scholar] [CrossRef]
- Guan, W.; Ji, F.Y.; Chen, Q.K.; Yan, P.; Zhou, W.W. Phosphorus recovery using porous calcium silicate hydrate as seed crystal in form of hydroxyapatite. Mater. Res. Innov. 2014, 18, 43–49. [Google Scholar] [CrossRef]
- Peng, L.; Dai, H.; Wu, Y.; Dai, Z.; Li, X.; Lu, X. Performance and adsorption mechanism of a magnetic calcium silicate hydrate composite for phosphate removal and recovery. Water Sci. Technol. 2017, 578–591. [Google Scholar] [CrossRef]
- Ding, S.; Fang, D.; Pang, Z.; Luo, B.; Kuang, L.; Wang, H.; Zhang, Q.; Shen, Q.; Ji, F. Immobilization of powdery calcium silicate hydrate via PVA covalent cross-linking process for phosphorus removal. Sci. Total Environ. 2018, 645, 937–945. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, X.; Zhao, J. Phosphate recovery from wastewater using calcium silicate hydrate (C-S-H): Sonochemical synthesis and properties. Environ. Sci. Water Res. Technol. 2019, 5, 131–139. [Google Scholar] [CrossRef]
- Okano, K.; Miyamaru, S.; Yamamoto, Y.; Kunisada, M.; Takano, H.; Toda, M.; Honda, K.; Ohtake, H. A mobile pilot-scale plant for in situ demonstration of phosphorus recovery from wastewater using amorphous calcium silicate hydrates. Separ. Purif. Technol. 2016, 170, 116–121. [Google Scholar] [CrossRef]
- Lee, C.-G.; Alvarez, P.J.J.; Kim, H.-G.; Jeong, S.; Lee, S.; Lee, K.B.; Lee, S.-H.; Choi, J.-W. Phosphorous recovery from sewage sludge using calcium silicate hydrates. Chemosphere 2018, 193, 1087–1093. [Google Scholar] [CrossRef]
- Okano, K.; Miyamaru, S.; Kitao, A.; Takano, H.; Aketo, T.; Toda, M.; Honda, K.; Ohtake, H. Amorphous calcium silicate hydrates and their possible mechanism for recovering phosphate from wastewater. Sep. Purif. Technol. 2015, 144, 63–69. [Google Scholar] [CrossRef]
- Takei, T.; Ikeda, K.; Ijima, H.; Kawakami, K. Fabrication of poly (vinyl alcohol) hydrogel beads crosslinked using sodium sulfate for microorganism immobilization. Process Biochem. 2011, 46, 566–571. [Google Scholar] [CrossRef]
- Zain, N.A.M.; Suhaimi, M.S.; Idris, A. Development and modification of PVA–alginate as a suitable immobilization matrix. Process Biochem. 2011, 46, 2122–2129. [Google Scholar] [CrossRef]
- United Nations. Transforming Our World: The 2030 Agenda for Sustainable Development [WWW Document]. Available online: https://sdgs.un.org/2030agenda (accessed on 29 May 2022).
- The American Public Health Association (APHA); the American Water Works Association (AWWA); the Water Environment Federation (WEF) (APHA-AWWA-WEF). Ascorbic acid method. In Standard Method for the Examination of Water and Wastewater, 24th ed.; Public Health Association: Washington, DC, USA, 1998; Available online: https://www.nemi.gov/methods/method_summary/7436/ (accessed on 29 May 2022).
- Aksu, Z.; Gönen, F. Biosorption of phenol by immobilized activated sludge in a continuous packed bed: Prediction of breakthrough curves. Process Biochem. 2004, 39, 599–613. [Google Scholar] [CrossRef]
- Mohammed, N.; Grishkewich, N.; Waeijen, H.A.; Berry, R.M.; Tam, K.C. Continuous flow adsorption of methylene blue by cellulose nanocrystal-alginate hydrogel beads in fixed bed columns. Carbohydr. Polym. 2016, 136, 1194–1202. [Google Scholar] [CrossRef] [PubMed]
- Ramírez-Rodríguez, A.E.; Morales-Barrera, L.; Cristiani-Urbina, E. Continuous biosorption of acid red 27 azo dye by Eichhornia crassipes leaves in a packed-bed column. Sci. Rep. 2021, 11, 18413. [Google Scholar] [CrossRef] [PubMed]
- Kapur, M.; Mondal, M.K. Design and model parameters estimation for fixed-bed column adsorption of Cu(II) and Ni(II) ions using magnetized saw dust. Desalin. Water Treat. 2016, 57, 12192–12203. [Google Scholar] [CrossRef]
- Yagub, M.T.; Sen, T.K.; Afroze, S.; Ang, H.M. Fixed-bed dynamic column adsorption study of methylene blue (MB) onto pine cone. Desalin. Water Treat. 2015, 55, 1026–1039. [Google Scholar] [CrossRef]
- Franceschini, A.; Abramson, S.; Mancini, V.; Bresson, B.; Chassenieux, C.; Lequeux, N. New covalent bonded polymer–calcium silicate hydrate composites. J. Mater. Chem. 2007, 17, 913–922. [Google Scholar] [CrossRef]
- Wongniramaikul, W.; Limsakul, W.; Choodum, A. A biodegradable colorimetric film for rapid low-cost field determination of formaldehyde contamination by digital image colorimetry. Food Chem. 2018, 249, 154–161. [Google Scholar] [CrossRef]
- Boonkanon, C.; Phatthanawiwat, K.; Wongniramaikul, W.; Choodum, A. Curcumin nanoparticle doped starch thin film as a green colorimetric sensor for detection of boron. Spectrochim. Acta A Mol. Biomol. Spectro. 2020, 224, 117351. [Google Scholar] [CrossRef]
- Boonkanon, C.; Phatthanawiwat, K.; Chuenchom, L.; Lamthornkit, N.; Taweekarn, T.; Wongniramaikul, W.; Choodum, A. Preparation and characterization of calcium cross-linked starch monolithic cryogel and its application as a cost-effective green filter. Polymers 2021, 13, 3975. [Google Scholar] [CrossRef]
- Chowdhury, Z.Z.; Abd Hamid, S.B.; Zain, S.M. Evaluating design parameters for breakthrough curve analysis and kinetics of fixed bed columns for Cu(II) cations using lignocellulosic wastes. BioResources 2015, 10, 732–749. [Google Scholar] [CrossRef]
- Nuryadin, A.; Imai, T. Application of amorphous zirconium (hydr)oxide/MgFe layered double hydroxides composite in fixed-bed column for phosphate removal from water. Glob. J. Environ. Sci. Manag. 2021, 7, 485–502. [Google Scholar] [CrossRef]
- Afroze, S.; Sen, T.K.; Ang, H.M. Adsorption performance of continuous fixed bed column for the removal of methylene blue (MB) dye using Eucalyptus sheathiana bark biomass. Res. Chem. Intermed. 2016, 42, 2343–2364. [Google Scholar] [CrossRef]
- Ramirez, A.; Giraldo, S.; García-Nunezb, J.; Flórez, E.; Acelas, N. Phosphate removal from water using a hybrid material in a fixed-bed column. J. Water Process. Eng. 2018, 26, 131–137. [Google Scholar] [CrossRef]
- Chen, N.; Zhang, Z.Y.; Feng, C.P.; Li, M.; Chen, R.Z.; Sugiura, N. Investigations on the batch and fixed-bed column performance of fluoride adsorption by Kanuma mud. Desalination 2011, 268, 76–82. [Google Scholar] [CrossRef] [Green Version]
- Baral, S.S.; Das, N.; Ramulu, T.S.; Sahoo, S.K.; Das, S.N.; Chaudhury, G.R. Removal of Cr (VI) by thermally activated weed Salvinia cucullata in a fixed-bed column. J. Hazard. Mater. 2009, 161, 1427–1435. [Google Scholar] [CrossRef]
- Auta, M.; Hameed, B.H. Chitosan–clay composite as highly effective and low-cost adsorbent for batch and fixed-bed adsorption of methylene blue. Chem. Eng. J. 2014, 237, 352–361. [Google Scholar] [CrossRef]
- Ahmad, A.A.; Hameed, B.H. Fixed-bed adsorption of reactive azo dye onto granular activated carbon prepared from waste. J. Hazard. Mater. 2010, 175, 298–303. [Google Scholar] [CrossRef]
- Song, J.Y.; Zou, W.H.; Bian, Y.Y.; Su, F.Y.; Han, R.P. Adsorption characteristics of methylene blue by peanut husk in batch and column mode. Desalination 2011, 265, 119–125. [Google Scholar] [CrossRef]
- Thomas, H.C. Heterogeneous ion exchange in a flowing system. J. Am. Chem. Soc. 1944, 66, 1664–1666. [Google Scholar] [CrossRef]
- Patel, H. Fixed-bed column adsorption study: A comprehensive review. Appl. Water Sci. 2019, 9, 45. [Google Scholar] [CrossRef]
- Rao, J.R.; Viraraghavan, T. Biosorption of phenol from an aqueous solution by Aspergillus niger biomass. Bioresour. Technol. 2002, 85, 165–171. [Google Scholar] [CrossRef] [PubMed]
- Bohart, G.S.; Adams, E.Q. Some aspects of the behavior of charcoal with respect to chlorine. J. Am. Chem. Soc. 1920, 42, 523–544. [Google Scholar] [CrossRef] [Green Version]
- Woumfo, E.D.; Siéwé, J.M.; Njopwouo, D. A fixed-bed column for phosphate removal from aqueous solutions using an andosol-bagasse mixture. J. Environ. Manag. 2015, 151, 450–460. [Google Scholar] [CrossRef] [PubMed]
- Lόpez-Cervantes, J.; Sánchez-Machado, D.I.; Sánchez-Duarte, R.G.; Correa-Murrieta, M.A. Study of a fixed-bed column in the adsorption of an azo dye from an aqueous medium using a chitosan-glutaraldehyde biosorbent. Adsorpt. Sci. Technol. 2018, 36, 215–232. [Google Scholar] [CrossRef]
- He, Y.; Zhang, L.; An, X.; Han, C.; Luo, Y. Microwave assistant rapid synthesis MCM-41-NH2 from fly ash and Cr(VI) removal performance. Environ. Sci. Pollut. Res. 2019, 26, 31463–31477. [Google Scholar] [CrossRef]
- Yoon, Y.H.; Nelson, J.H. Application of gas adsorption kinetics I. A theoretical model for respirator cartridge service life. Am. Ind. Hyg. Assoc. J. 1984, 45, 509–516. [Google Scholar] [CrossRef]
- Calero, M.; Hernáinz, F.; Blázquez, G.; Tenorio, G.; Martín-Lara, M.A. Study of Cr(III) biosorption in a fixed-bed column. J. Hazard. Mater. 2009, 171, 886–893. [Google Scholar] [CrossRef]



| Q (mL min−1) | C0 (mg L−1) | z (cm) | tb (min) | ttotal (min) | Veff (mL) | mtotal (mg) | qtotal (mg) | qe (mg g−1) | %Total Adsorption |
|---|---|---|---|---|---|---|---|---|---|
| 5.0 | 2 | 1 | 60 | 6240 | 31,200 | 62.40 | 61.00 | 15.93 | 97.75 |
| 7.5 | 2 | 1 | 20 | 5760 | 57,600 | 115.20 | 112.92 | 29.48 | 98.02 |
| 10 | 2 | 1 | <10 | 5040 | 50,400 | 100.80 | 86.48 | 22.58 | 85.79 |
| 15 | 2 | 1 | <10 | 2700 | 40,500 | 81.00 | 68.97 | 18.01 | 85.15 |
| Q (mL min−1) | C0 (mg L−1) | z (cm) | tb (min) | ttotal (min) | Veff (mL) | mtotal (mg) | qtotal (mg) | qe (mg g−1) | %Total Adsorption |
|---|---|---|---|---|---|---|---|---|---|
| 10 | 1 | 1 | 20 | 4800 | 48,000 | 48.00 | 46.97 | 12.26 | 97.85 |
| 10 | 2 | 1 | <10 | 4320 | 43,200 | 86.40 | 74.12 | 19.35 | 85.79 |
| 10 | 4 | 1 | <10 | 4320 | 43,200 | 172.80 | 108.42 | 28.31 | 62.74 |
| Q (mL min−1) | C0 (mg L−1) | z (cm) | tb (min) | ttotal (min) | Veff (mL) | mtotal (mg) | qtotal (mg) | qe (mg g−1) | %Total Adsorption |
|---|---|---|---|---|---|---|---|---|---|
| 10 | 2 | 1 | <10 | 4320 | 43,200 | 86.40 | 74.12 | 19.35 | 85.79 |
| 10 | 2 | 2 | <10 | 6120 | 61,200 | 122.40 | 104.23 | 13.61 | 85.15 |
| 10 | RW * (3.38) | 2 | 10 | 2460 | 24,600 | 83.15 | 78.67 | 10.27 | 94.61 |
| Thomas | Adams–Bohart | Yoon–Nelson | |||||||
|---|---|---|---|---|---|---|---|---|---|
| kTH (mL mg−1 min−1) | qe (mg g−1) | R2 | kAB (L−1 mg min) | Cs(mg L−1) | R2 | kYN (min−1) | τ (min) | R2 | |
| Q (mL min−1) | |||||||||
| 5.0 | 0.50 | 7.60 | 0.9026 | 0.0005 | 1428 | 0.8634 | 0.0009 | 2990 | 0.9043 |
| 7.5 | 0.65 | 7.82 | 0.9550 | 0.0011 | 1018 | 0.9566 | 0.0013 | 1998 | 0.9550 |
| 10 | 0.80 | 1.89 | 0.6227 | 0.0018 | 425 | 0.9551 | 0.0013 | 379 | 0.6227 |
| 15 | 0.90 | 3.96 | 0.8701 | 0.0020 | 625 | 0.9411 | 0.0014 | 453 | 0.8849 |
| C0 (mg L−1) | |||||||||
| 1 | 1.50 | 3.39 | 0.8267 | 0.0030 | 421 | 0.9562 | 0.001 | 1847 | 0.8267 |
| 2 | 0.80 | 1.89 | 0.6227 | 0.0018 | 425 | 0.9551 | 0.0013 | 379 | 0.5311 |
| 4 | 0.25 | 0.11 | 0.6593 | 0.0004 | 1225 | 0.9591 | 0.0015 | 92 | 0.7221 |
| z (cm) | |||||||||
| 1 | 0.80 | 1.89 | 0.6227 | 0.0018 | 425 | 0.9551 | 0.0013 | 379 | 0.5311 |
| 2 | 0.30 | 7.19 | 0.7668 | 0.0007 | 707 | 0.7172 | 0.0006 | 2754 | 0.7668 |
| RW 1 | 0.53 | 4.53 | 0.8259 | 0.0006 | 854 | 0.8701 | 0.018 | 103 | 0.8259 |
| Adsorbent | Adsorption System | Removal Capacity (mg PO43–/g) | Real Sample Application | Removal Efficiency in Real Sample | Problem | Reference |
|---|---|---|---|---|---|---|
| MCM-41 | Batch | 21.01 | No | - | Loss of material | [7] |
| C–S–H | Batch | 109.4 | No | - | Loss of material | [35] |
| Cry-CSH | Batch | 64.52 | Yes | 98.6% to 99.8% | No loss | [10] |
| PVA-CSH | Batch/fixed bed column | 28.15 | Yes | Not reported | Loss of material | [34] |
| Am-Zr/MgFe * | Fixed bed column | 25.15 | Yes | Not reported | Loss and clog | [53] |
| HFeO ** | Fixed bed column | 53.57 | No | - | Loss and clog | [55] |
| AdBg *** | Fixed bed column | 4.18 | Yes | 6.69 mg/g | Loss and clog | [65] |
| Cry-CSH | Monolithic column | 13.61 | Yes | 94.61% | No loss/no clog | This work |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Phawachalotorn, C.; Wongniramaikul, W.; Taweekarn, T.; Kleangklao, B.; Pisitaro, W.; Limsakul, W.; Sriprom, W.; Towanlong, W.; Choodum, A. Continuous Phosphate Removal and Recovery Using a Calcium Silicate Hydrate Composite Monolithic Cryogel Column. Polymers 2023, 15, 539. https://doi.org/10.3390/polym15030539
Phawachalotorn C, Wongniramaikul W, Taweekarn T, Kleangklao B, Pisitaro W, Limsakul W, Sriprom W, Towanlong W, Choodum A. Continuous Phosphate Removal and Recovery Using a Calcium Silicate Hydrate Composite Monolithic Cryogel Column. Polymers. 2023; 15(3):539. https://doi.org/10.3390/polym15030539
Chicago/Turabian StylePhawachalotorn, Chanadda, Worawit Wongniramaikul, Tarawee Taweekarn, Bussakorn Kleangklao, Wachiraporn Pisitaro, Wadcharawadee Limsakul, Wilasinee Sriprom, Wanchitra Towanlong, and Aree Choodum. 2023. "Continuous Phosphate Removal and Recovery Using a Calcium Silicate Hydrate Composite Monolithic Cryogel Column" Polymers 15, no. 3: 539. https://doi.org/10.3390/polym15030539
APA StylePhawachalotorn, C., Wongniramaikul, W., Taweekarn, T., Kleangklao, B., Pisitaro, W., Limsakul, W., Sriprom, W., Towanlong, W., & Choodum, A. (2023). Continuous Phosphate Removal and Recovery Using a Calcium Silicate Hydrate Composite Monolithic Cryogel Column. Polymers, 15(3), 539. https://doi.org/10.3390/polym15030539








