Performance of Reinforced Concrete Beams Strengthened by Bidirectional Carbon-Fiber-Reinforced Polymers Based on Numerical Models
Abstract
:1. Introduction
2. Experimental Program
2.1. Code Provisions (ACI 318, 440.2R)
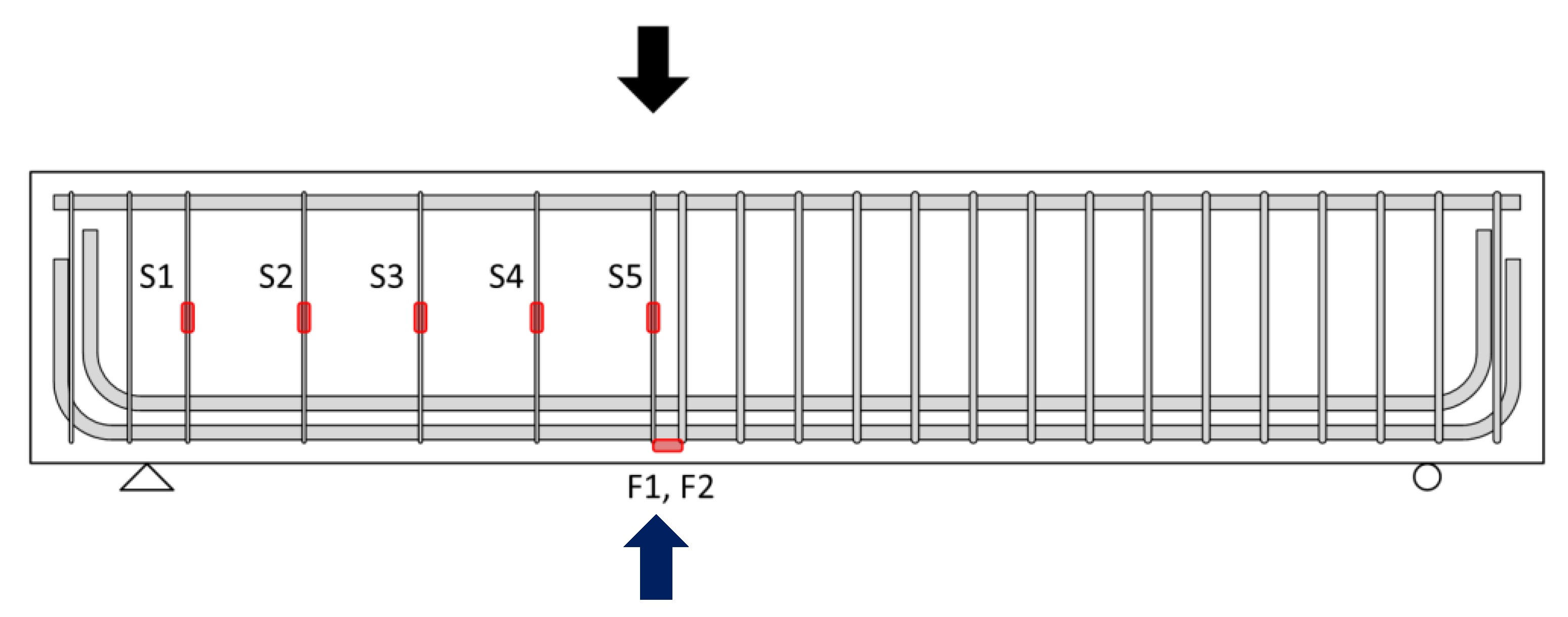
2.2. Specimen Detail
2.3. Test Equipment and Test Setup
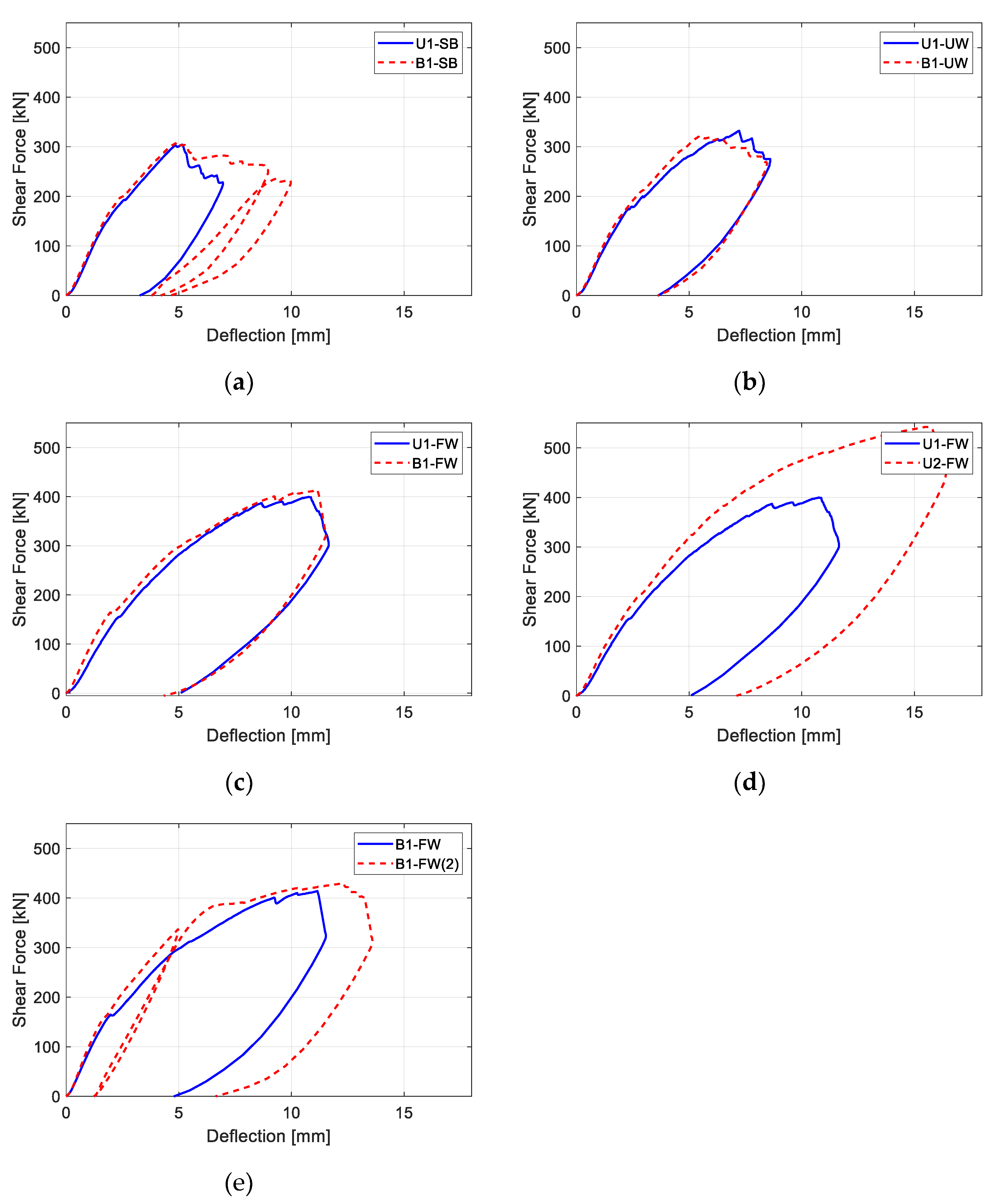
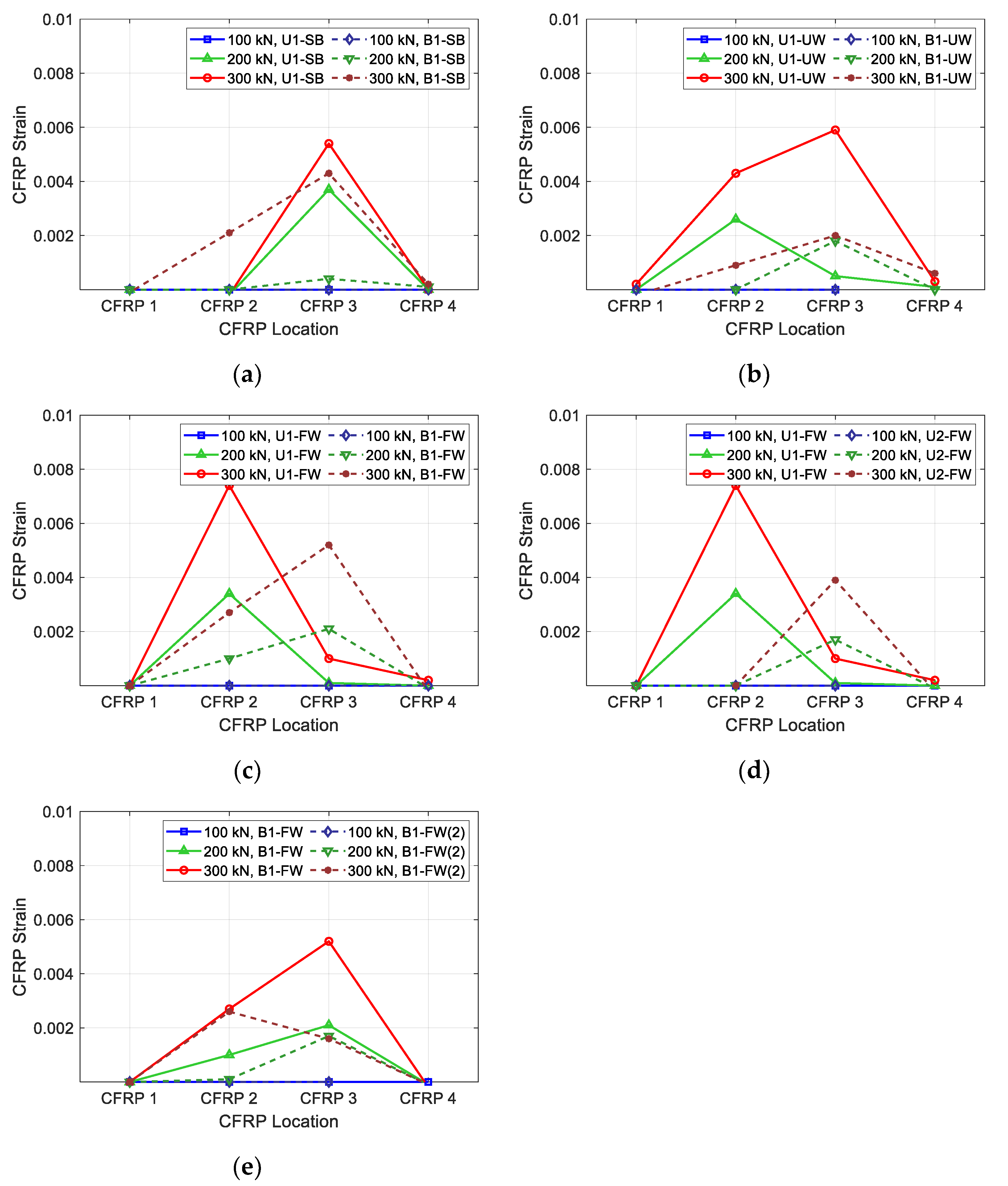
2.4. Test Results
3. Finite Element Analysis
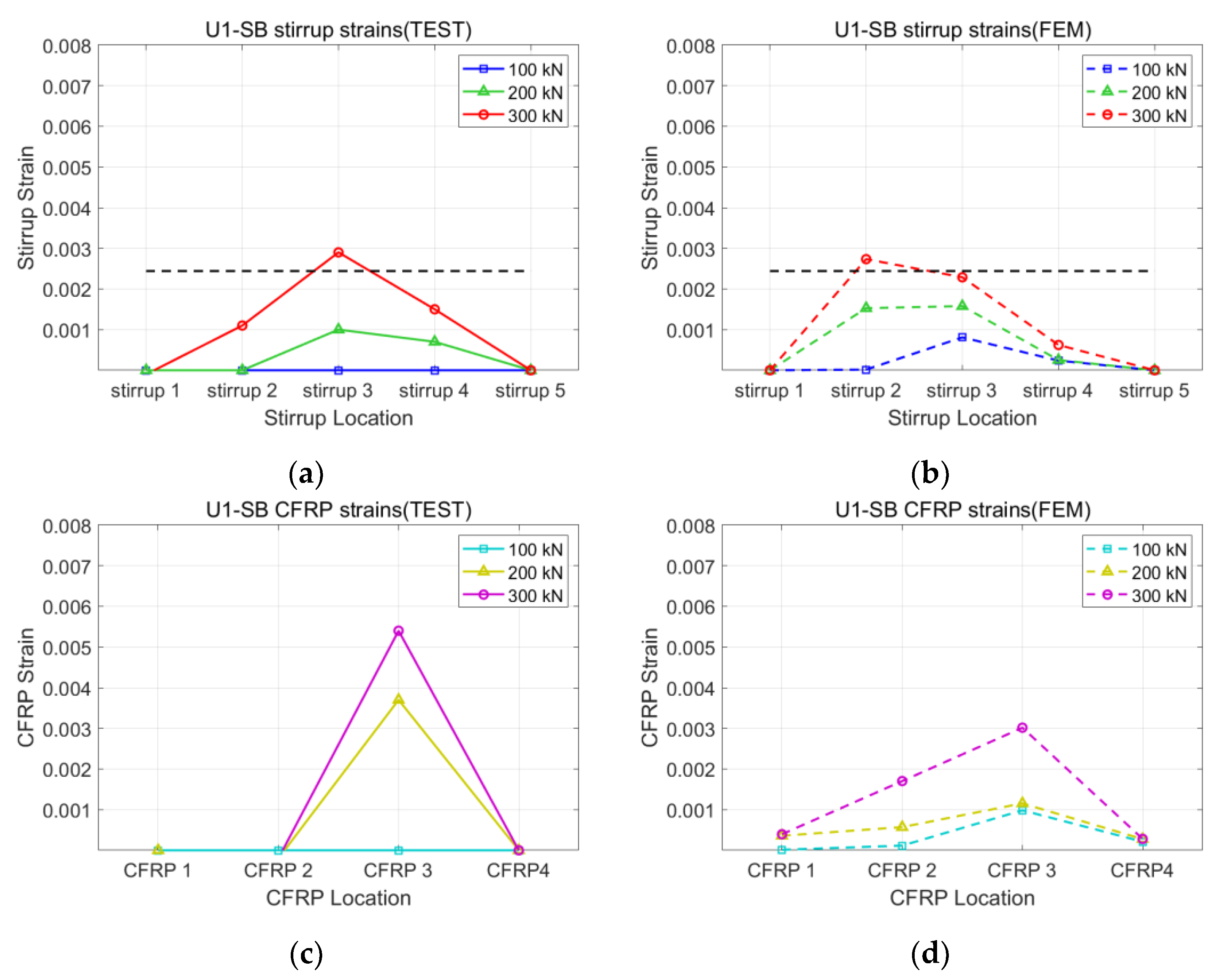
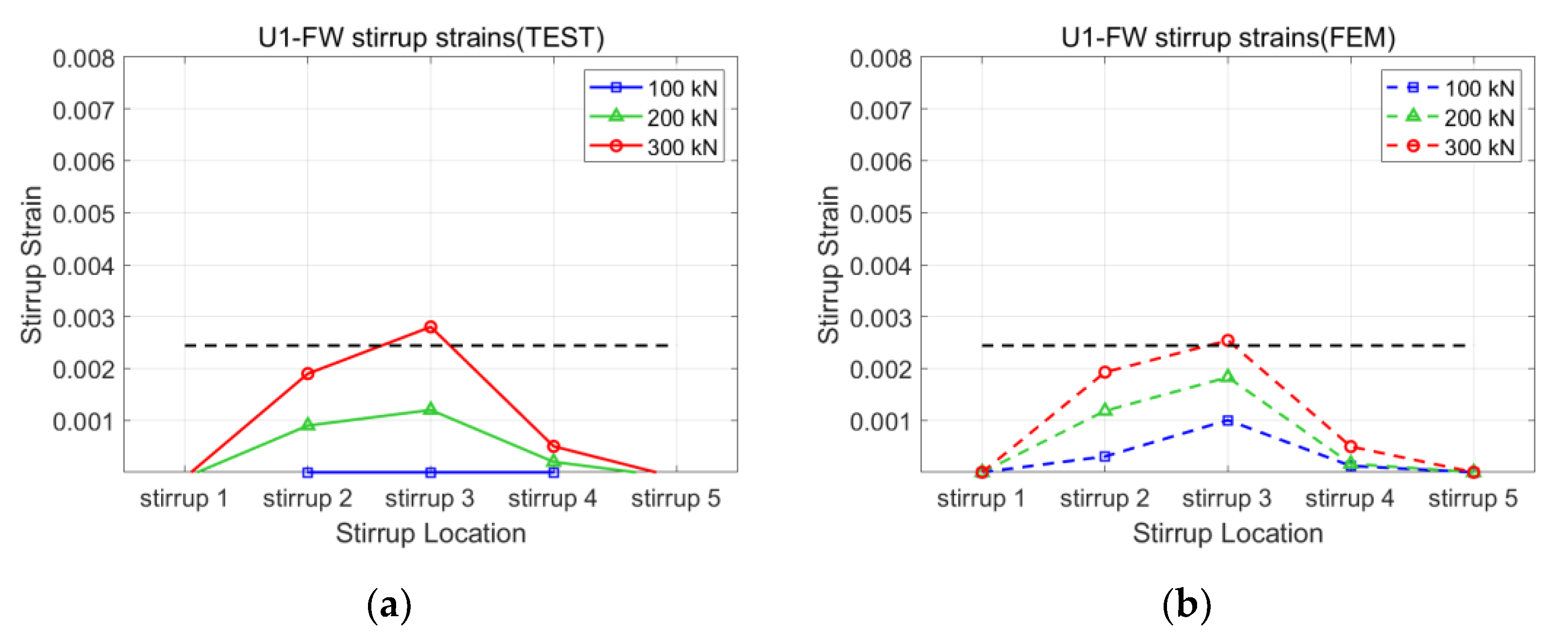
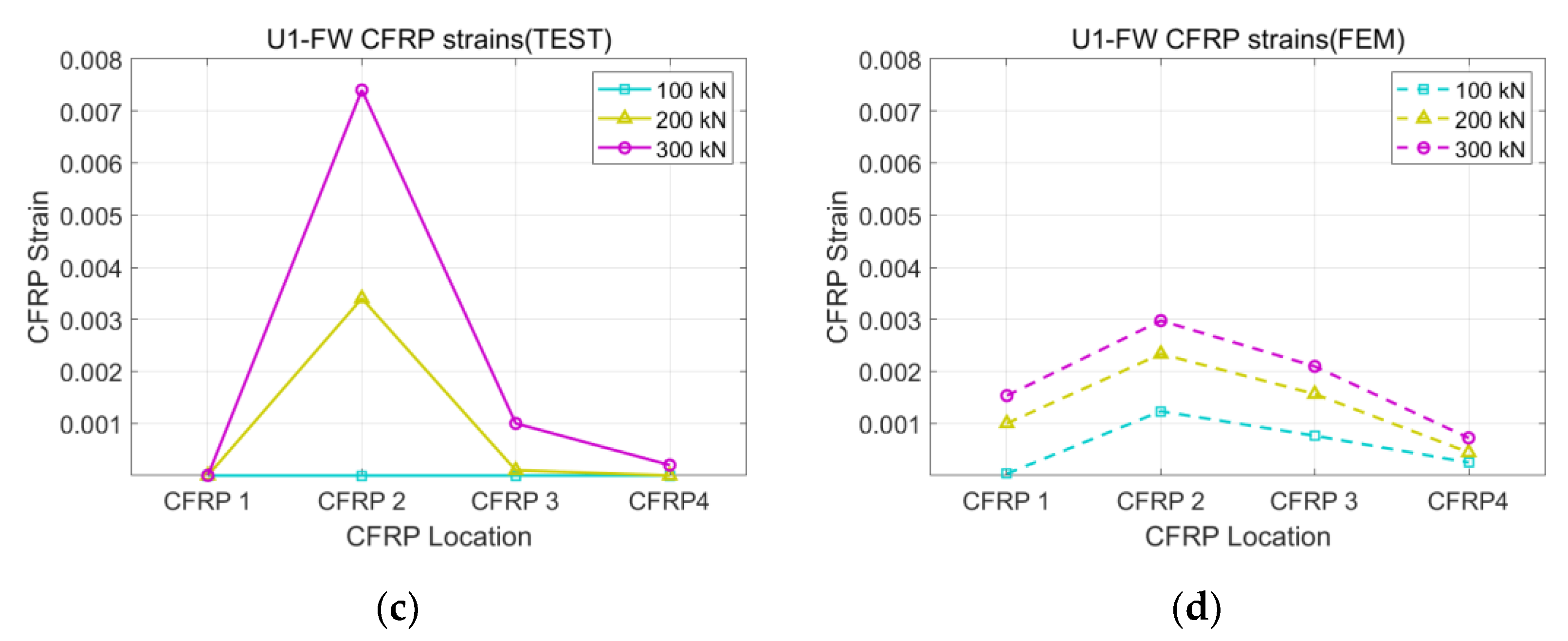
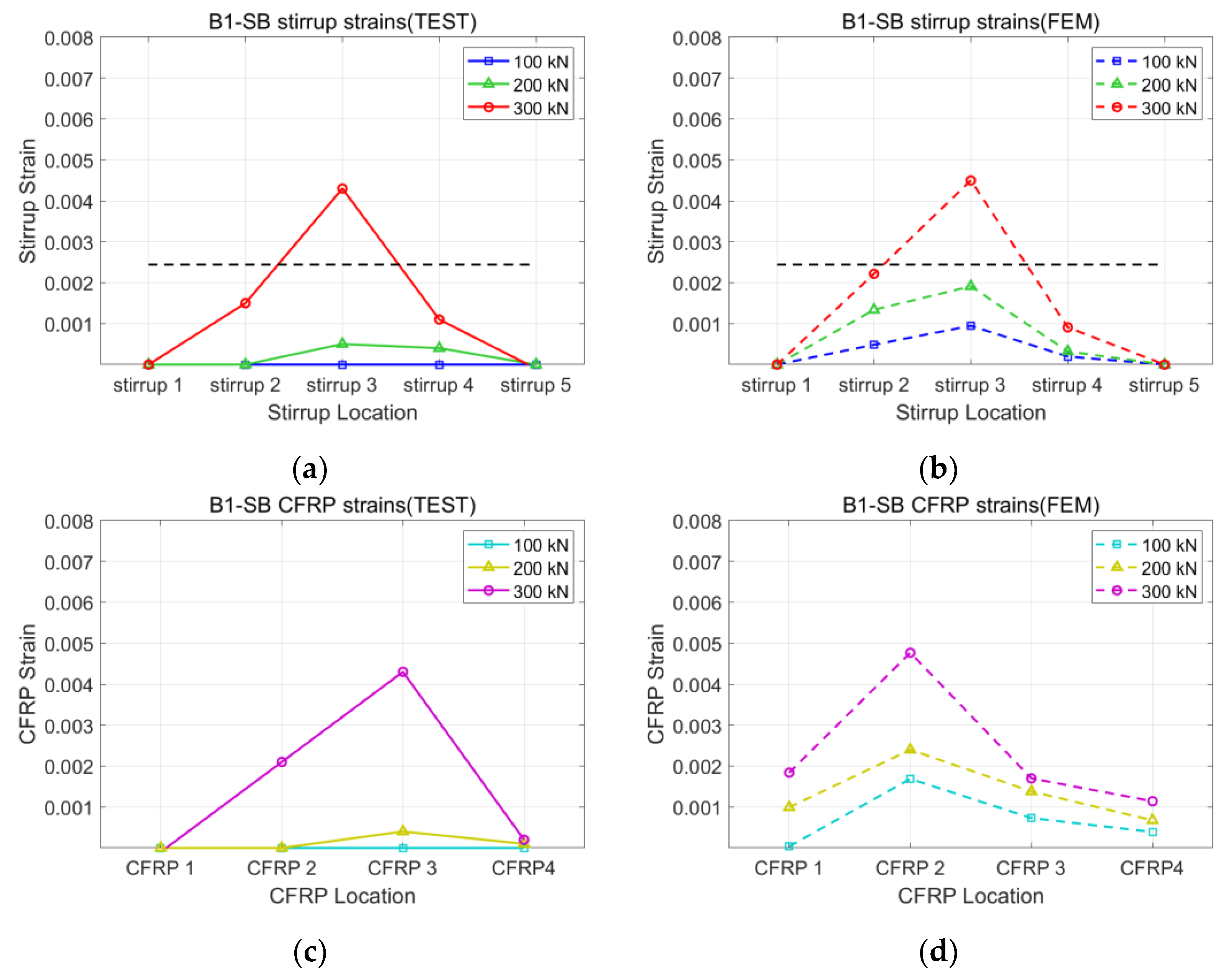
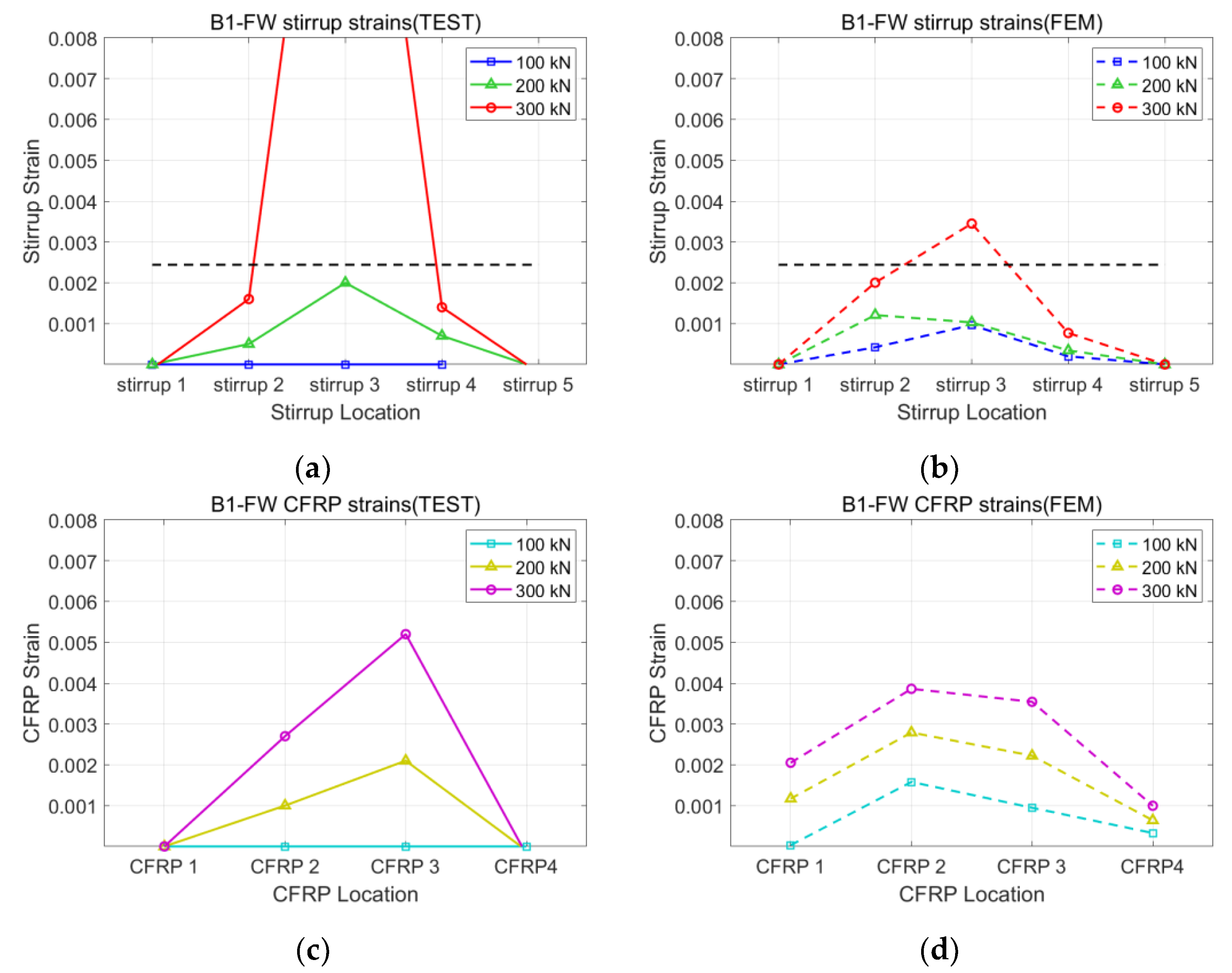
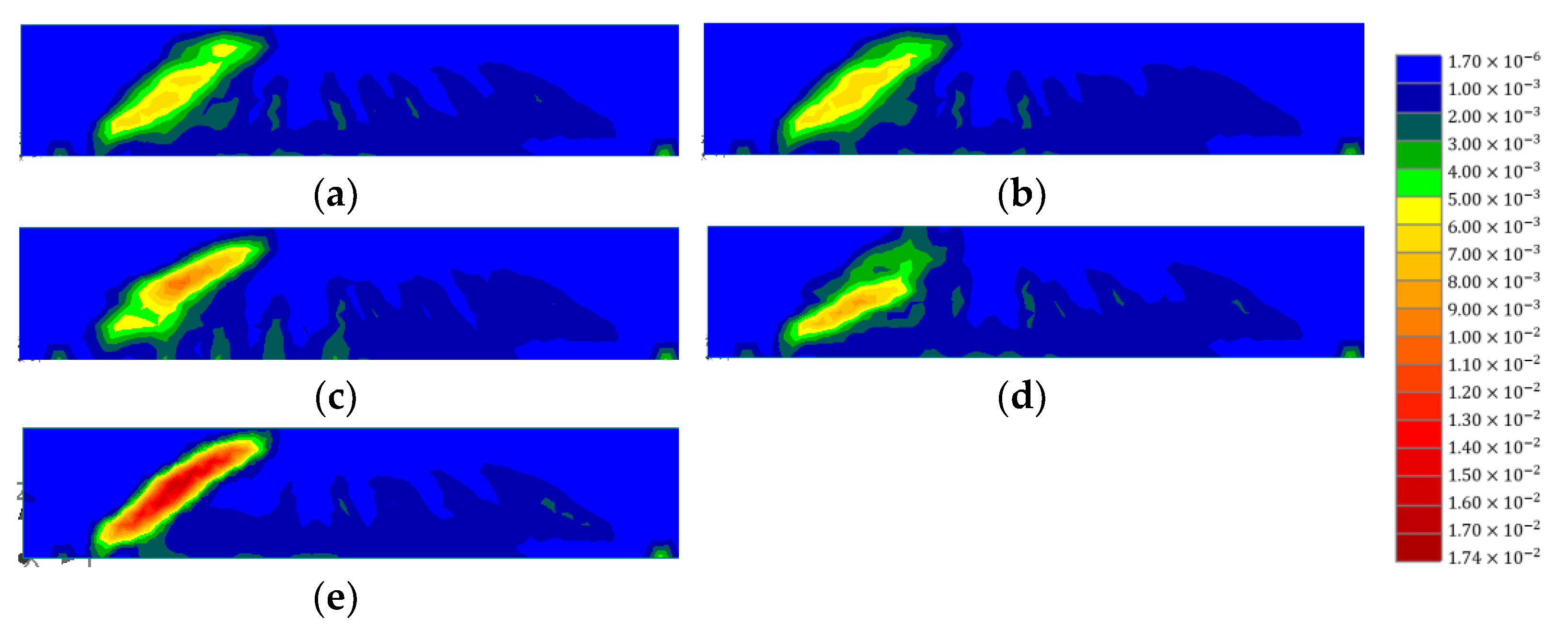
3.1. Validation of the Analysis Model
3.2. Parametric Study
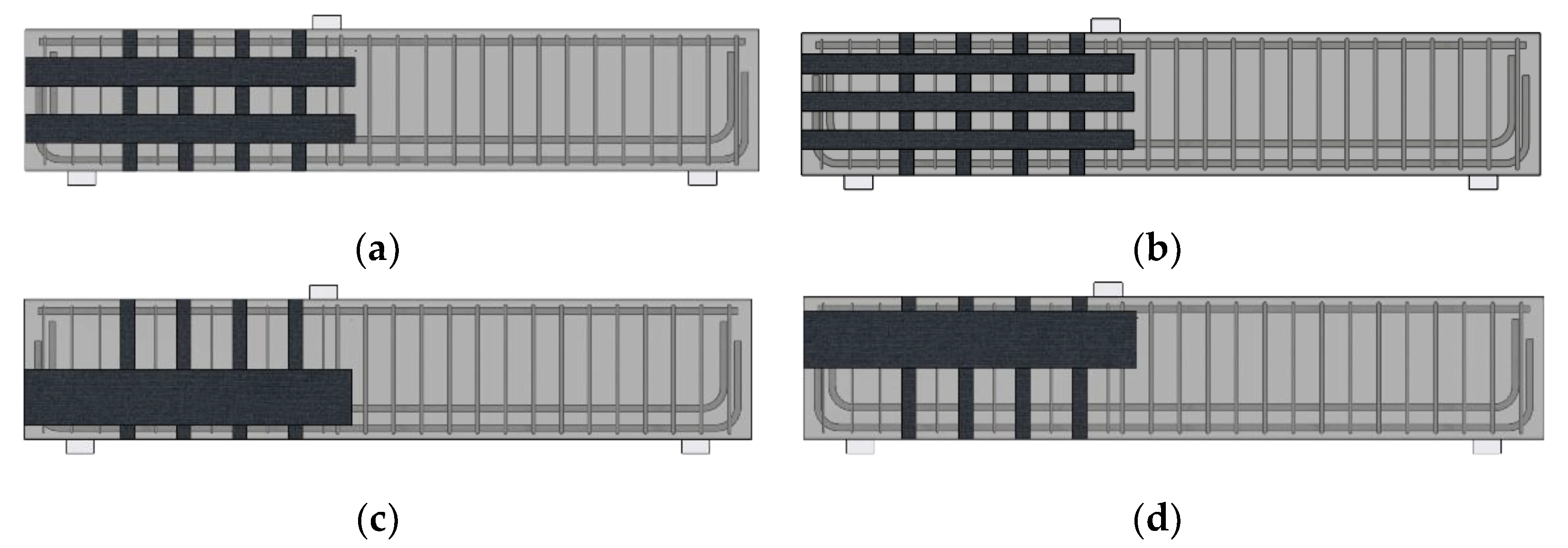
3.2.1. Horizontal CFRP Layout
3.2.2. Amount of Horizontal CFRP Layout
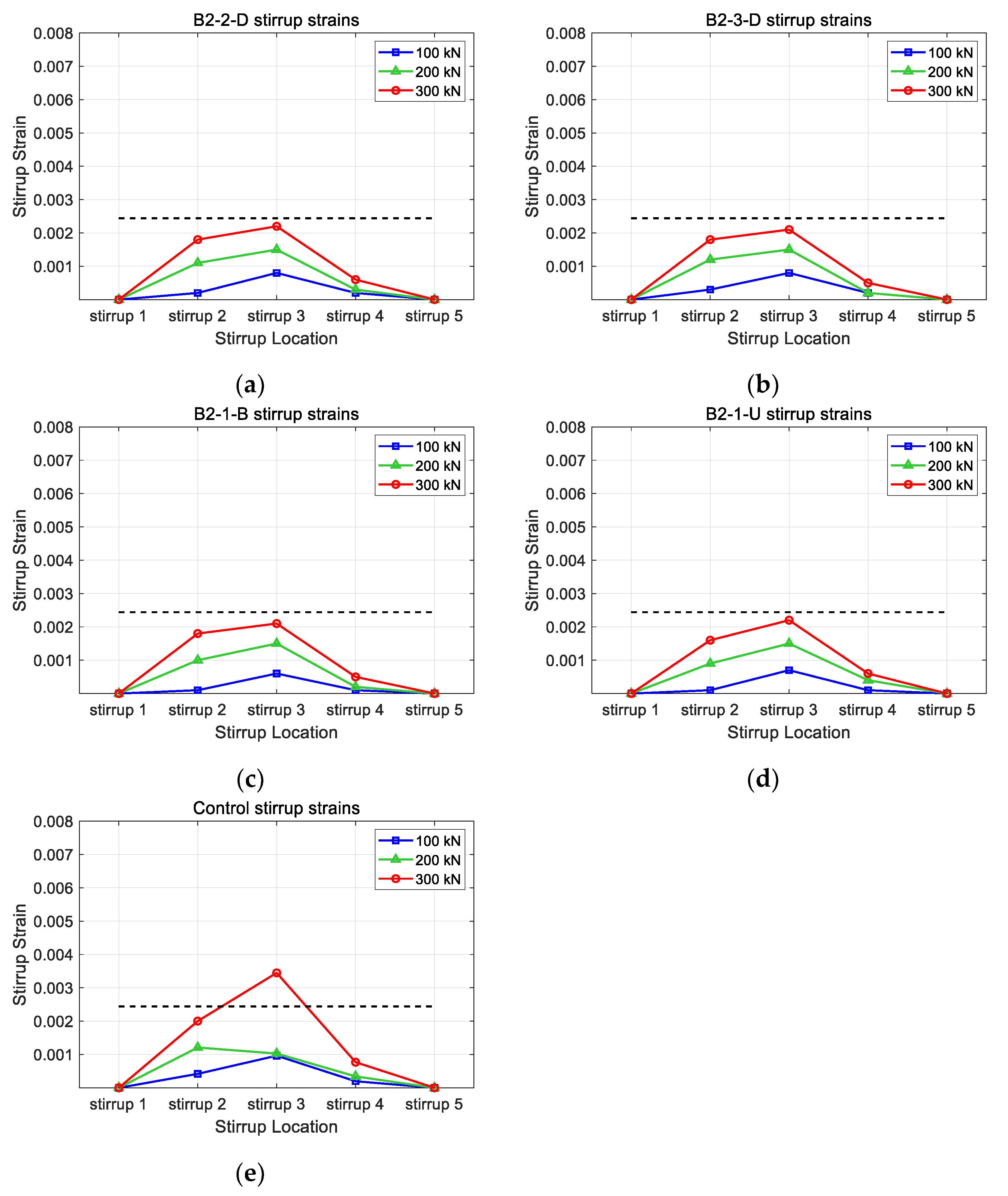
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Yang, K.-H. Axial Behavior of Reinforced Concrete Columns Strengthened with New Section Enlargement Approaches. ACI Struct. J. 2019, 116, 87–96. [Google Scholar] [CrossRef]
- Kaur, H.; Singh, J. A Review on External Prestressing in Concrete. Int. Res. J. Eng. Technol. 2017, 4, 1801–1805. [Google Scholar]
- Vilnay, O. The Analysis of Reinforced Concrete Beams Strengthened by Epoxy Bonded Steel Plates. Int. J. Cem. Compos. Lightweight Concr. 1988, 10, 73–78. [Google Scholar] [CrossRef]
- Adhikary, B.B.; Mutsuyoshi, H.; Sano, M. Shear Strengthening of Reinforced Concrete Beams Using Steel Plates Bonded on Beam Web: Experiments and Analysis. Constr. Build. Mater. 2000, 14, 237–244. [Google Scholar] [CrossRef]
- Zhang, S.; Raoof, M.; Wood, L.A. Prediction of Peeling Failure of Reinforced Concrete Beams with Externally Bonded Steel Plates. Proc. Inst. Civ. Eng.-Struct. Build. 1995, 110, 257–268. [Google Scholar] [CrossRef]
- Spoelstra, M.R.; Monti, G. FRP-Confined Concrete Model. J. Compos. Constr. 1999, 3, 143–150. [Google Scholar] [CrossRef]
- Rizkalla, S.; Hassan, T.; Hassan, N. Design Recommendations for the Use of FRP for Reinforcement and Strengthening of Concrete Structures. Prog. Struct. Eng. Mater. 2003, 5, 16–28. [Google Scholar]
- Bourget, S.; El-Saikaly, G.; Chaallal, O. Behavior of Reinforced Concrete T-Beams Strengthened in Shear Using Closed Carbon Fiber-Reinforced Polymer Stirrups Made of Laminates and Ropes. ACI Struct. J. 2017, 114, 1087. [Google Scholar] [CrossRef]
- Abbasi, A.; Benzeguir, Z.E.A.; Chaallal, O.; El-Saikaly, G. FE Modelling and Simulation of the Size Effect of RC T-Beams Strengthened in Shear with Externally Bonded FRP Fabrics. J. Compos. Sci. 2022, 6, 116. [Google Scholar] [CrossRef]
- Leung, C.K.Y.; Chen, Z.; Lee, S.; Ng, M.; Xu, M.; Tang, J. Effect of Size on the Failure of Geometrically Similar Concrete Beams Strengthened in Shear with FRP Strips. J. Compos. Constr. 2007, 11, 487–496. [Google Scholar] [CrossRef]
- Kim, Y.; Quinn, K.; Ghannoum, W.M.; Jirsa, J.O. Strengthening of Reinforced Concrete T-Beams Using Anchored CFRP Materials. ACI Struct. J. 2014, 111, 1027. [Google Scholar] [CrossRef]
- Dirar, S.; Lees Janet, M.; Morley, C. Phased Nonlinear Finite-Element Analysis of Precracked RC T-Beams Repaired in Shear with CFRP Sheets. J. Compos. Constr. 2013, 17, 476–487. [Google Scholar] [CrossRef] [Green Version]
- Mofidi, A.; Chaallal, O. Effect of Steel Stirrups on Shear Resistance Gain Due to Externally Bonded Fiber-Reinforced Polymer Strips and Sheets. Am. Concr. Inst. Struct. J. 2014, 111, 353–361. [Google Scholar]
- Chen, G.M.; Teng, J.G.; Chen, J.F.; Rosenboom, O.A. Interaction between Steel Stirrups and Shear-Strengthening FRP Strips in RC Beams. J. Compos. Constr. 2010, 14, 498–509. [Google Scholar] [CrossRef]
- de Freitas Arcine, M.; Villanova Menon, N.; Augusto Krahl, P. Numerical and Experimental Study of the Interaction between Stirrups and Shear Strengthening with CFRP in RC Beams. Eng. Struct. 2023, 278, 115514. [Google Scholar] [CrossRef]
- Jin, L.; Xia, H.; Jiang, X.; Du, X. Size Effect on Shear Failure of CFRP-Strengthened Concrete Beams without Web Reinforcement: Meso-Scale Simulation and Formulation. Compos. Struct. 2020, 236, 111895. [Google Scholar] [CrossRef]
- Ebadi-Jamkhaneh, M.; Homaioon-Ebrahimi, A.; Kontoni, D.-P.N. Numerical Finite Element Study of Strengthening of Damaged Reinforced Concrete Members with Carbon and Glass FRP Wraps. Comput. Concr. 2021, 28, 137–147. [Google Scholar]
- Bousselham, A.; Chaallal, O. Mechanisms of Shear Resistance of Concrete Beams Strengthened in Shear with Externally Bonded FRP. J. Compos. Constr. 2008, 12, 499–512. [Google Scholar] [CrossRef]
- Deniaud, C.; Roger Cheng, J.J. Reinforced Concrete T-Beams Strengthened in Shear with Fiber Reinforced Polymer Sheets. J. Compos. Constr. 2003, 7, 302–310. [Google Scholar] [CrossRef]
- Tanarslan, H.M.; Altin, S. Behavior of RC T-Section Beams Strengthened with CFRP Strips, Subjected to Cyclic Load. Mater. Struct. 2010, 43, 529–542. [Google Scholar] [CrossRef]
- Mofidi, A.; Chaallal, O. Shear Strengthening of RC Beams with Externally Bonded FRP Composites: Effect of Strip-Width-to-Strip-Spacing Ratio. J. Compos. Constr. 2011, 15, 732. [Google Scholar] [CrossRef]
- Khalifa, A.; Nanni, A. Improving Shear Capacity of Existing RC T-Section Beams Using CFRP Composites. Cem. Concr. Compos. 2000, 22, 165–174. [Google Scholar] [CrossRef]
- Norris, T.; Saadatmanesh, H.; Ehsani, M.R. Shear and Flexural Strengthening of R/C Beams with Carbon Fiber Sheets. J. Struct. Eng. 1997, 123, 903–911. [Google Scholar] [CrossRef]
- Chaallal, O.; Nollet, M.J.; Perraton, D. Shear Strengthening of RC Beams by Externally Bonded Side CFRP Strips. J. Compos. Constr. 1998, 2, 111–113. [Google Scholar] [CrossRef]
- Monti, G.; Liotta, M. Tests and Design Equations for FRP-Strengthening in Shear. Constr. Build. Mater. 2007, 21, 799–809. [Google Scholar] [CrossRef]
- Vrettos, I.; Kefala, E.; Triantaillou, T.C. Innovative Flexural Strengthening of Reinforced Concrete Columns Using Carbon-Fiber Anchors. ACI Struct. J. 2013, 110, 63–70. [Google Scholar]
- Sun, W.; Liu, S.; Zhang, C. An Effective Improvement for Enhancing the Strength and Feasibility of FRP Spike Anchors. Compos. Struct. 2020, 247, 112449. [Google Scholar] [CrossRef]
- Smith, S.T.; Hu, S.; Kim, S.J.; Seracino, R. FRP-Strengthened RC Slabs Anchored with FRP Anchors. Eng. Struct. 2011, 33, 1075–1087. [Google Scholar] [CrossRef]
- Li, G.; Zhang, A.; Jin, W.; Xiao, Y.; Li, H. A New Flexural Strength Model of CFRP-Strengthened RC Beams with Intermediate Crack Induced Debonding Failure. Compos. Struct. 2023, 308, 116681. [Google Scholar] [CrossRef]
- Zhou, C.; Liu, J.; Yu, Y. Experiment and Modeling of RC Beams Shear-Strengthened with Hybrid-Anchored CFRP U-Straps. Strain 2017, 1, S3. [Google Scholar]
- Zhang, H.W.; Smith, S.T. FRP-to-Concrete Joint Assemblages Anchored with Multiple FRP Anchors. Compos. Struct. 2012, 94, 403–414. [Google Scholar] [CrossRef]
- Sun, W.; Jirsa, J.O.; Ghannoum, W.M. Behavior of Anchored Carbon Fiber-Reinforced Polymer Strips Used for Strengthening Concrete Structures. ACI Mater. J. 2016, 113, 163–172. [Google Scholar] [CrossRef]
- Mostafa, A.; Razaqpur, A.G. CFRP Anchor for Preventing Premature Debonding of Externally Bonded FRP Laminates from Concrete. J. Compos. Constr. 2013, 17, 641–650. [Google Scholar] [CrossRef]
- Pudleiner, D.; Ghannoum, W.M.; Jirsa, J.O. Influence of Anchor Size on Anchored CFRP Systems. J. Compos. Constr. 2019, 23, 04019033. [Google Scholar] [CrossRef]
- Li, W.; Liu, W.; Yang, X.; Xing, F. Experimental Study on FRP-to-Concrete Bonded Joints with FRP Sheet Anchor System. Adv. Mater. Sci. Eng. 2020, 2020, 2514313. [Google Scholar] [CrossRef] [Green Version]
- Tatar, J.; Viniarski, C.; Ishfaq, M.; Harries, K.; Head, M. Effect of U-Wrap Anchors on Flexural Behavior of Reinforced Concrete Beams Flexurally Strengthened with Externally Bonded CFRP Sheets. J. Compos. Constr. 2023, 27, 04022099. [Google Scholar] [CrossRef]
- Zhang, J.; Li, H.; Liu, S.; Sun, L.; Yang, C.; Zhang, R. Effects of Sulfate and Freeze–Thaw Cycles on the Bond Behavior of CFRP-Concrete Interface. Constr. Build. Mater. 2023, 368, 130368. [Google Scholar] [CrossRef]
- Al-Lami, K.; Colombi, P.; D’Antino, T. Experimental and Numerical Analysis of CFRP-Concrete Joint Bond Behavior after Exposure to Wet-Dry Cycles. Compos. Struct. 2023, 303, 116273. [Google Scholar] [CrossRef]
- Yin, Y.; Zhang, J.; Zhang, G. Effect of Hygrothermal Acid Rain Environment on the Shear Bonding Performance of CFRP-Concrete Interface. Constr. Build. Mater. 2023, 364, 130002. [Google Scholar] [CrossRef]
- Kim, Y.; Quinn, K.; Satrom, N.; Garcia, J.; Sun, W.; Ghannoum, W.M.; Jirsa, J.O. Shear Strengthening of Reinforced and Prestressed Concrete Beams Using Carbon Fiber Reinforced Polymer (CFRP) Sheets and Anchors; Center for Transportation Research: Austin, TX, USA, 2012. [Google Scholar]
- Kim, C.; Ghannoum, W.M.; Jirsa, J.O. Behavior of Reinforced Concrete Panels Strengthened with Carbon Fiber-Reinforced Polymers. ACI Struct. J. 2016, 113, 1077. [Google Scholar] [CrossRef]
- Alotaibi, N.K. Shear Strengthening of Reinforced Concrete Beams with Bi-Directional Carbon Fiber Reinforced Polymer (CFRP) Strips and CFRP Anchors; The University of Texas at Austin: Austin, TX, USA, 2014. [Google Scholar]
- Kim, C.H. Performance of Concrete Panels Strengthened Using Carbon Fiber Reinforced Polymers (CFRP); The University of Texas at Austin: Austin, TX, USA, 2014. [Google Scholar]
- Kim, C.; Jirsa, J.O.; Ghannoum, W.M. Performance of Concrete Panels Reinforced with Carbon Fiber–Reinforced Polymer Materials. J. Compos. Constr. 2017, 21, 04016100. [Google Scholar] [CrossRef]
- Haroon, M.; Moon, J.S.; Kim, C. Performance of Reinforced Concrete Beams Strengthened with Carbon Fiber Reinforced Polymer Strips. Materials 2021, 14, 5866. [Google Scholar] [CrossRef]
- Rasheed, H.A.; Zaki, M.A.; Foerster, A.S. Efficient Bidirectional U-Wrap System to Anchor CFRP Sheets Bonded to Reinforced Concrete T-Girders. Structures 2022, 38, 226–236. [Google Scholar] [CrossRef]
- Kalfat, R.; Jumaah, R.; Al-Mahaidi, R.; Abdouka, K.; Hashemi, J. Post-Tensioned Concrete Beams Strengthened in Shear Using Fiber-Reinforced Polymer Laminates and Patch Anchors. J. Compos. Constr. 2020, 24, 04019065. [Google Scholar] [CrossRef]
- Yılmaz, T.; Kıraç, N.; Anil, Ö.; Erdem, R.T.; Sezer, C. Low-Velocity Impact Behaviour of Two Way RC Slab Strengthening with CFRP Strips. Constr. Build. Mater. 2018, 186, 1046–1063. [Google Scholar] [CrossRef]
- Al-Atta, B.; Kalfat, R.; Al-Mahaidi, R.; Al-Mosawe, A. Mitigation of IC Debonding in FRP-Plated Concrete Slabs Using Patch Anchors. Eng. Struct. 2020, 214, 110626. [Google Scholar] [CrossRef]
- Committee, A.C.I. Building Code Requirements for Structural Concrete and Commentary (ACI 318-19); American Concrete Institute: Farmington Hills, MI, USA, 2019; Volume 623. [Google Scholar]
- Committee, A.C.I. Building Code Requirements for Structural Concrete (ACI 318-14); American Concrete Institute: Farmington Hills, MI, USA, 2014. [Google Scholar]
- Committee, A.C.I. Guide for the Design and Construction of Externally Bonded FRP Systems for Strengthening Concrete Structures (ACI 440.2 R-17); American Concrete Institute: Farmington Hills, MI, USA, 2017. [Google Scholar]
- Cervenka, V.; Cervenka, J.; Pukl, R. ATENA—A Tool for Engineering Analysis of Fracture in Concrete. Sadhana 2002, 27, 485–492. [Google Scholar] [CrossRef]
- Alkurdi, Z. Evaluation of Pre-Tensioned Prestressed Concrete Beam Behavior by Finite Element Analysis Using ATENA 3D. In Proceedings of the 7th International Conference on Civil Structural and Transportation Engineering (ICCSTE’22), Niagara Falls, ON, Canada, 5–7 June 2022. [Google Scholar]
- Ayub, T.; Shafiq, N.; Nuruddin, M.F.; Khan, S.U. Flexural Behaviour of High Performance Basalt Fibre Reinforced Concrete Beams: 3D Nonlinear Finite Element Analysis. In Proceedings of the 2014 IEEE Colloquium on Humanities, Science and Engineering (CHUSER 2014), Penang, Malaysia, 7–9 April 2014. [Google Scholar]
- Le Hoang, A.; Fehling, E.; Ismail, M. Numerical Modelling of Circular Concrete Filled Steel Tube Stub Columns under Concentric Loading. In Proceedings of the 4th International Symposium on Ultra-High Performance Concrete and High Performance Construction Materials, Kassel, Germany, 9–11 March 2016. [Google Scholar]
- Abed, M.A.; Alkurdi, Z.; Fořt, J.; Černý, R.; Solyom, S. Bond Behavior of FRP Bars in Lightweight SCC under Direct Pull-Out Conditions: Experimental and Numerical Investigation. Materials 2022, 15, 3555. [Google Scholar] [CrossRef]
- Masne, N.; Suryawanshi, S. Analytical and Experimental Investigation of Recycled Aggregate Concrete Beams Subjected to Pure Torsion. Int. J. Eng. 2022, 35, 1959–1966. [Google Scholar] [CrossRef]
- Kalfat, R.; Al-Mahaidi, R. Numerical and Experimental Validation of FRP Patch Anchors Used to Improve the Performance of FRP Laminates Bonded to Concrete. J. Compos. Constr. 2014, 18, A4013008. [Google Scholar] [CrossRef]







| Specimen | Concrete | CFRP Strip | ||||||
|---|---|---|---|---|---|---|---|---|
(mm) | (mm) | (MPa) | (mm) | (mm) | (MPa) | |||
| U1-SB | 300 | 500 | 31.8 | 100 | 200 | N/A | N/A | 4600 |
| U1-UW | 300 | 500 | 31.8 | 100 | 200 | N/A | N/A | 4600 |
| U1-FW | 300 | 500 | 31.8 | 100 | 200 | N/A | N/A | 4600 |
| U2-FW | 300 | 500 | 31.8 | 100 | 200 | N/A | N/A | 4600 |
| B1-SB | 300 | 500 | 31.8 | 100 | 200 | 100 | 200 | 4600 |
| B1-UW | 300 | 500 | 31.8 | 100 | 200 | 100 | 200 | 4600 |
| B1-FW | 300 | 500 | 31.8 | 100 | 200 | 100 | 200 | 4600 |
| B1-FW(2) | 300 | 500 | 31.8 | 100 | 200 | 100 | 200 | 4600 |
| VACI (kN) | Vtest (kN) | Vtest/VACI | εs,max | εf,max | |
|---|---|---|---|---|---|
| U1-SB | 212 | 304 | 1.43 | 0.0046 | 0.0062 |
| U1-UW | 213 | 332 | 1.56 | 0.0033 | 0.0073 |
| U1-FW | 219 | 400 | 1.83 | 0.0040 | 0.0170 |
| U2-FW | 269 | 542 | 2.01 | 0.0031 | 0.0103 |
| B1-SB | 212 | 310 | 1.46 | 0.0075 | 0.0047 |
| B1-UW | 213 | 321 | 1.50 | 0.0094 | 0.0024 |
| B1-FW | 219 | 414 | 1.89 | 0.0142 | 0.0103 |
| B1-FW(2) | 219 | 429 | 1.96 | 0.0113 | 0.0095 |
| Model | B1-2-D | B1-3-D | B1-1-B | B1-1-U | B2-2-D | B2-3-D | B2-1-B | B2-1-U | |
|---|---|---|---|---|---|---|---|---|---|
| Horizontal CFRP | Total width (#×width) (mm) | 200 (2 × 100) | 210 (3 × 70) | 200 (1 × 200) | 200 (1 × 200) | 200 (2 × 100) | 210 (3 × 70) | 200 (1 × 200) | 200 (1 × 200) |
| Thickness (mm) | 0.3 | 0.3 | 0.3 | 0.3 | 0.6 | 0.6 | 0.6 | 0.6 | |
| Vertical CFRP | Total width (mm) | 70, fully wrapped | |||||||
| Thickness (mm) | 0.3 | ||||||||
| Model | VACI (kN) | Vtest (kN) | Vtest/VACI | εs,max | εf,max |
|---|---|---|---|---|---|
| Control | 219 | 307 | 1.40 | 0.0166 | |
| B1-2-D | 219 | 406 | 1.85 | 0.0093 | 0.0136(0.0124) |
| B1-3-D | 219 | 398 | 1.82 | 0.0078 | 0.0110(0.0098) |
| B1-1-B | 219 | 376 | 1.72 | 0.0150 | 0.0149(0.0121) |
| B1-1-U | 219 | 397 | 1.81 | 0.0190 | 0.0160(0.0100) |
| B2-2-D | 219 | 406 | 1.85 | 0.0089 | 0.0130(0.0129) |
| B2-3-D | 219 | 405 | 1.85 | 0.0101 | 0.0130(0.0117) |
| B2-1-B | 219 | 372 | 1.70 | 0.0129 | 0.0136(0.0133) |
| B2-1-U | 219 | 399 | 1.82 | 0.0185 | 0.0157(0.0101) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moon, J.S.; Kim, D.Y.; Ko, M.S.; Kim, C. Performance of Reinforced Concrete Beams Strengthened by Bidirectional Carbon-Fiber-Reinforced Polymers Based on Numerical Models. Polymers 2023, 15, 1012. https://doi.org/10.3390/polym15041012
Moon JS, Kim DY, Ko MS, Kim C. Performance of Reinforced Concrete Beams Strengthened by Bidirectional Carbon-Fiber-Reinforced Polymers Based on Numerical Models. Polymers. 2023; 15(4):1012. https://doi.org/10.3390/polym15041012
Chicago/Turabian StyleMoon, Jae Sang, Da Young Kim, Myeong Seop Ko, and Changhyuk Kim. 2023. "Performance of Reinforced Concrete Beams Strengthened by Bidirectional Carbon-Fiber-Reinforced Polymers Based on Numerical Models" Polymers 15, no. 4: 1012. https://doi.org/10.3390/polym15041012
APA StyleMoon, J. S., Kim, D. Y., Ko, M. S., & Kim, C. (2023). Performance of Reinforced Concrete Beams Strengthened by Bidirectional Carbon-Fiber-Reinforced Polymers Based on Numerical Models. Polymers, 15(4), 1012. https://doi.org/10.3390/polym15041012






