Damping Properties of Large-Scale Overlap Joints Bonded with Epoxy Hybrid Resin or Polyurethanes: Experimental Characterisation and Analytical Description
Abstract
:1. Introduction
1.1. Damping Properties of Adhesives and Adhesively Bonded Joints
1.2. Scope of This Paper
2. Materials and Methods
2.1. Materials and Samples
2.1.1. Adhesives and Their Experimental Characterisation
2.1.2. Overlap Joints Made of Steel Substrates
2.2. Experimental Investigations of Adhesively Bonded Overlap Joints
2.2.1. Experimental Series
- Test frequency (1 Hz, 3 Hz, 5 Hz);
- Overlap length L (20 mm, 60 mm);
- Adhesive layer thickness tadh (2.5 mm, 5.8 mm, 8.0 mm);
- Shear–strain level γ in the adhesive layer (2%, 8%).
2.2.2. Manufacturing of the Adhesively Bonded Overlap Joints
2.2.3. Quasi-Static Tensile Tests to Determine the Load–Deformation Behaviour of Adhesively Bonded Overlap Joints
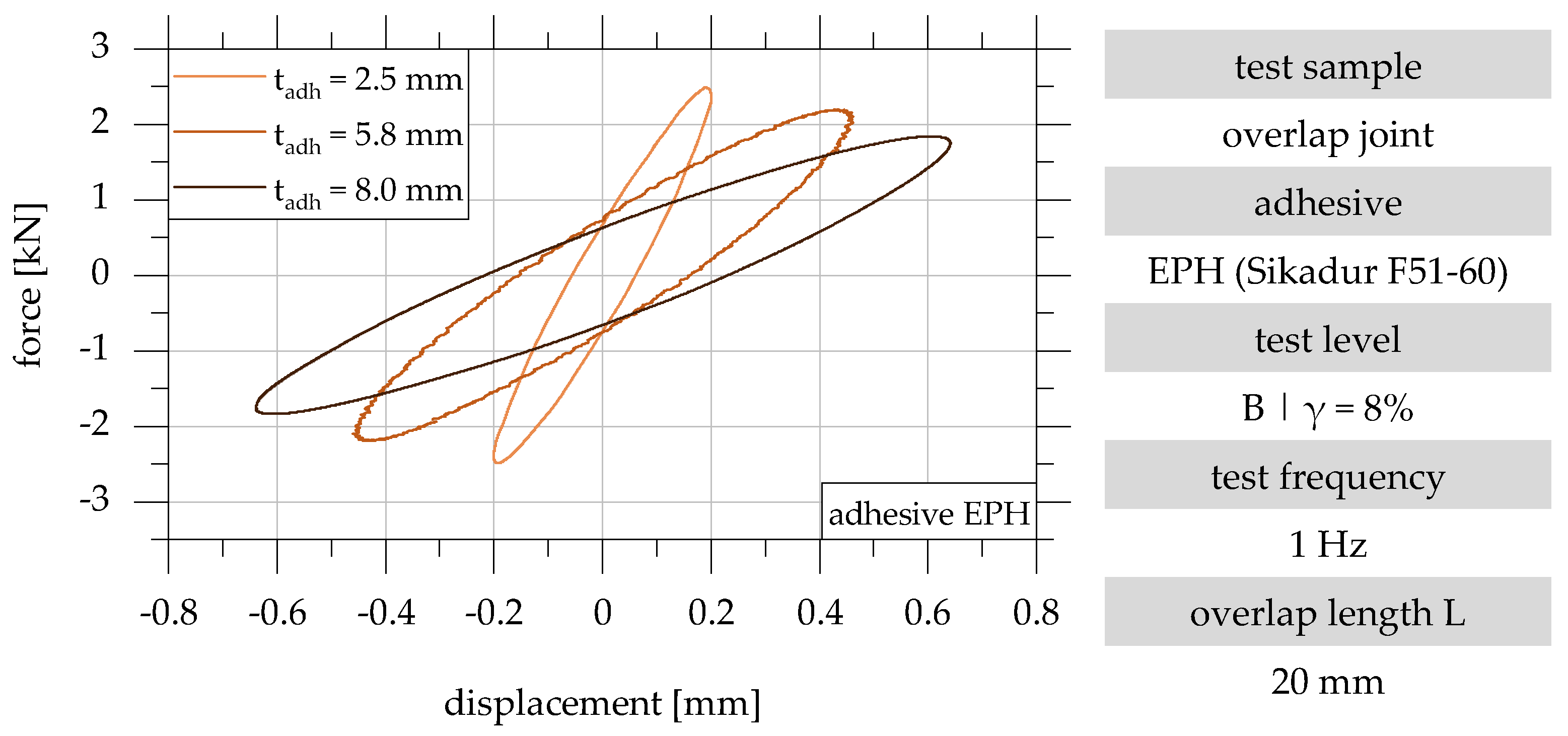
2.2.4. Dynamic Tests with Harmonic External Excitation to Determine the Damping Properties of Adhesively Bonded Overlap Joints
2.2.5. Analysis Routine
- η—loss factor
- Wd/We—quotient of dissipated and elastically stored energy
- Ψ—specific damping capacity
- Δ—logarithmic decrement
- tan δ—tangent of the phase angle δ
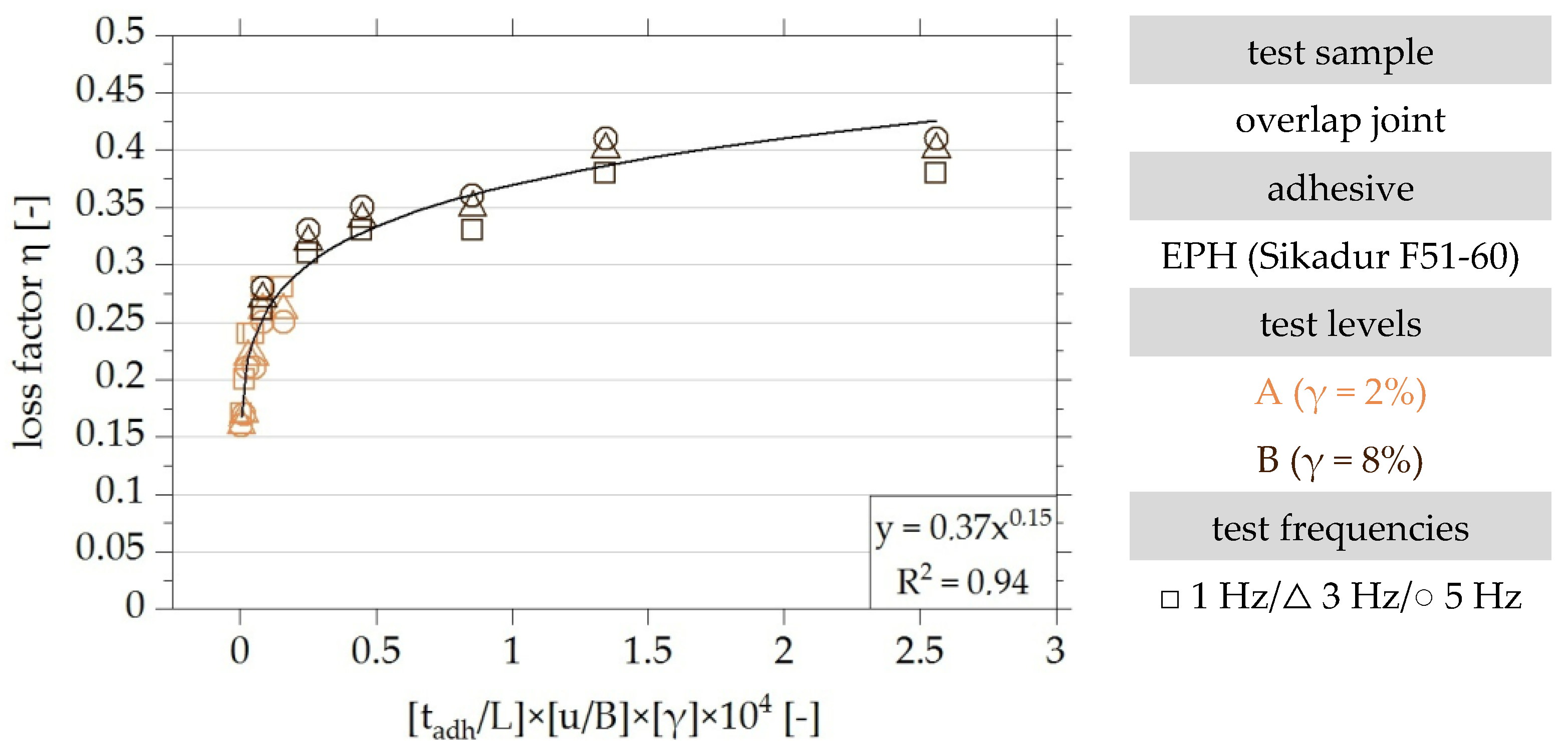
2.3. Dimensional Analysis of the Functional Relationship of the Results of the Experimental Investigation of the Damping Properties of Adhesively Bonded Overlap Joints
3. Results
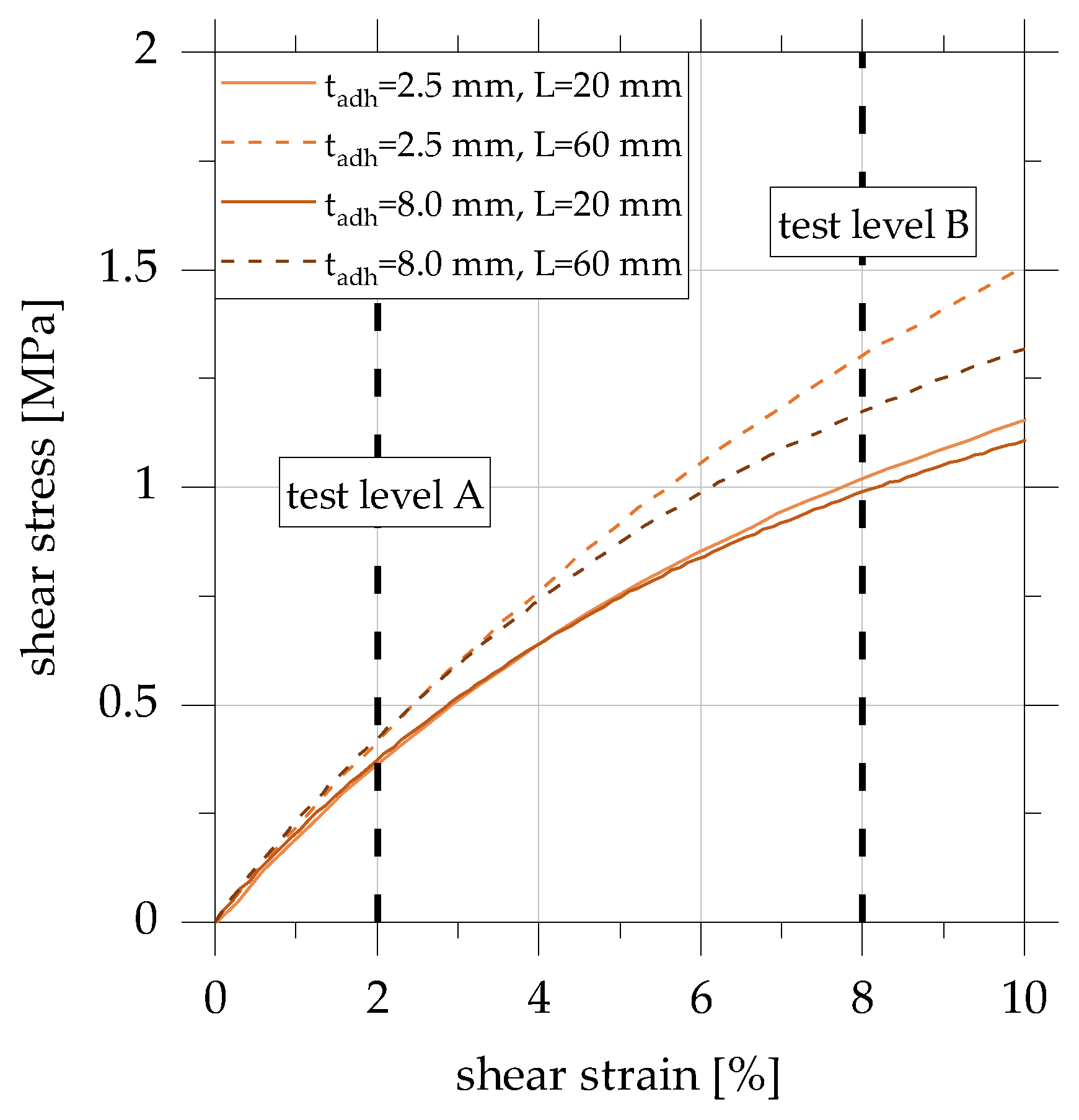
3.1. Load–Deformation Behaviour of Adhesively Bonded Overlap Joints under Quasi-Static Load
- Test level A: γ ± 2%, range of approx. linear initial stiffness and linear viscoelastic behaviour, low influence of non-linear material behavior,
- Test level B: γ ± 8%, end of the range of linear initial stiffness, decreasing joint stiffness depending on the adhesive layer geometry, the influence of non-linear material behavior.
3.2. Damping Properties of Overlap Joints Bonded with an Epoxy–Resin-Hybrid-Based 2-Component Adhesive
4. Discussion
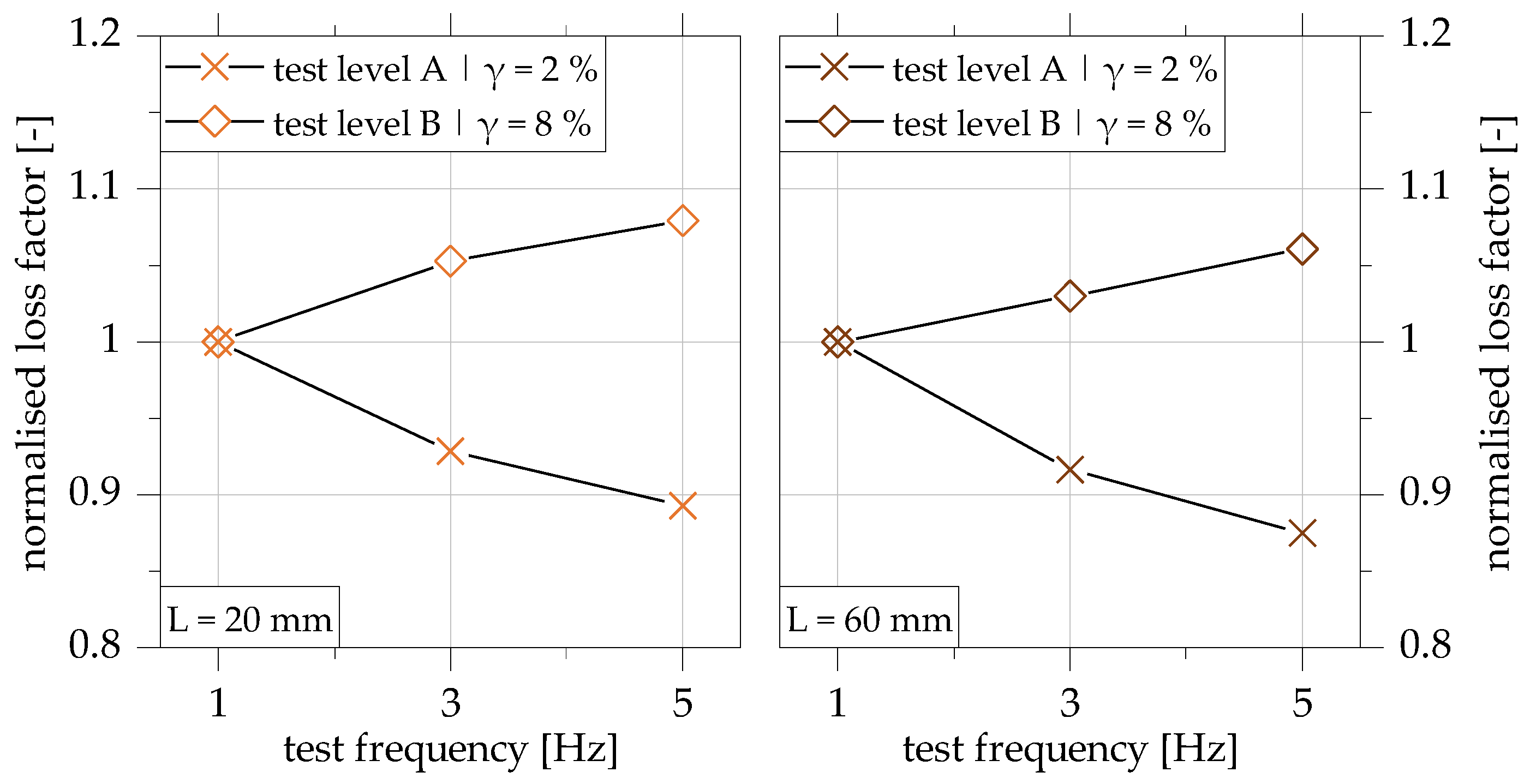
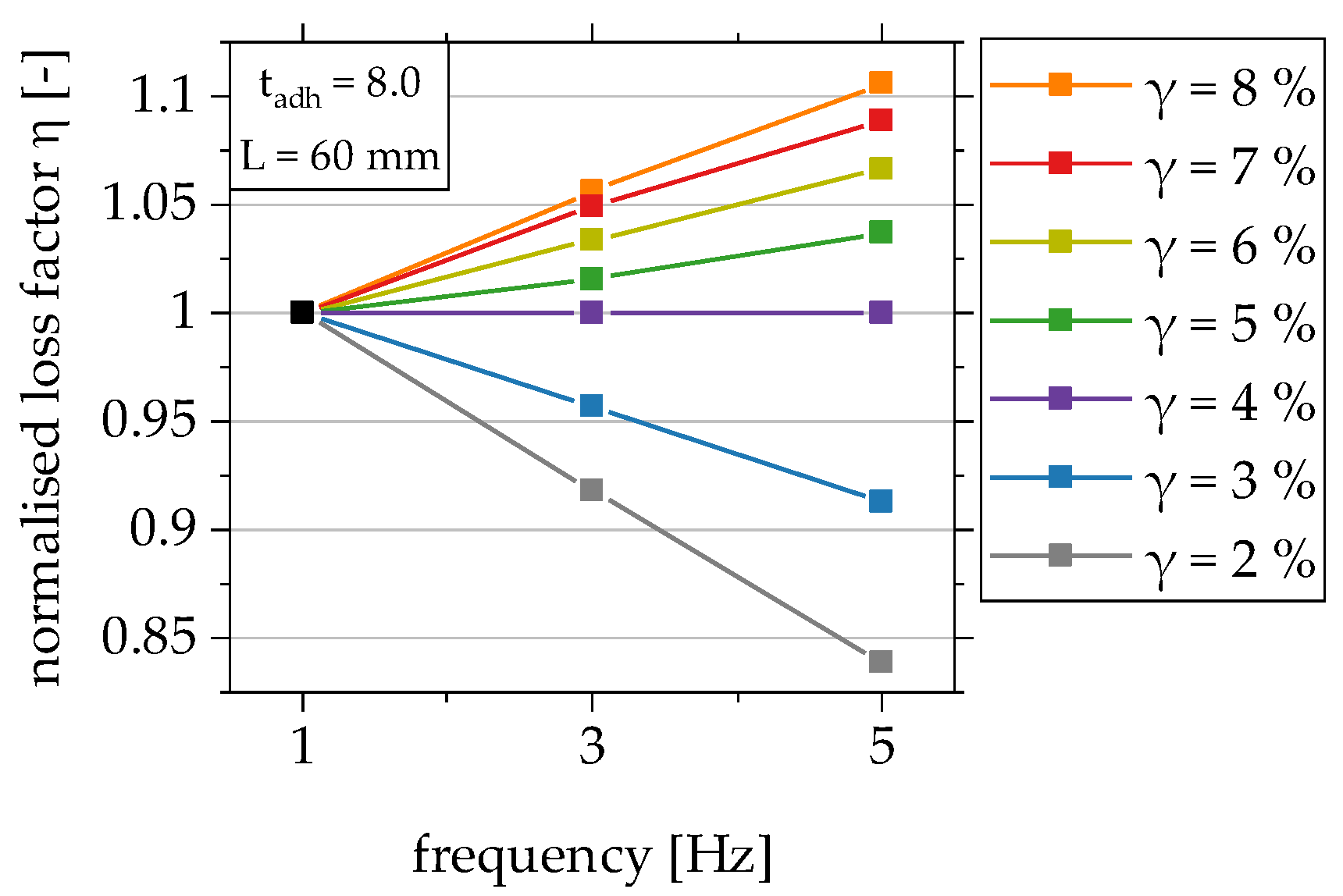
4.1. Influence of the Test Frequency
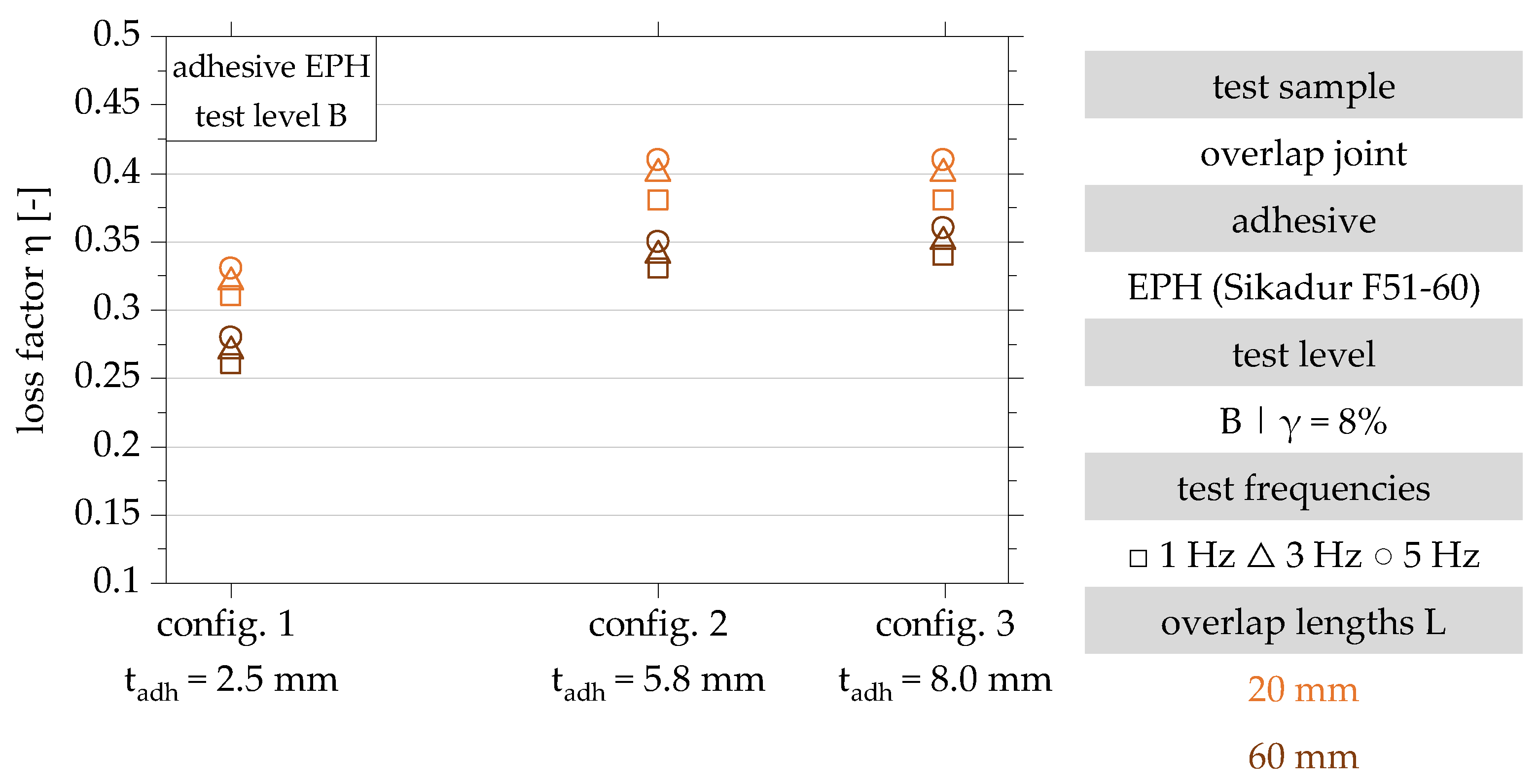
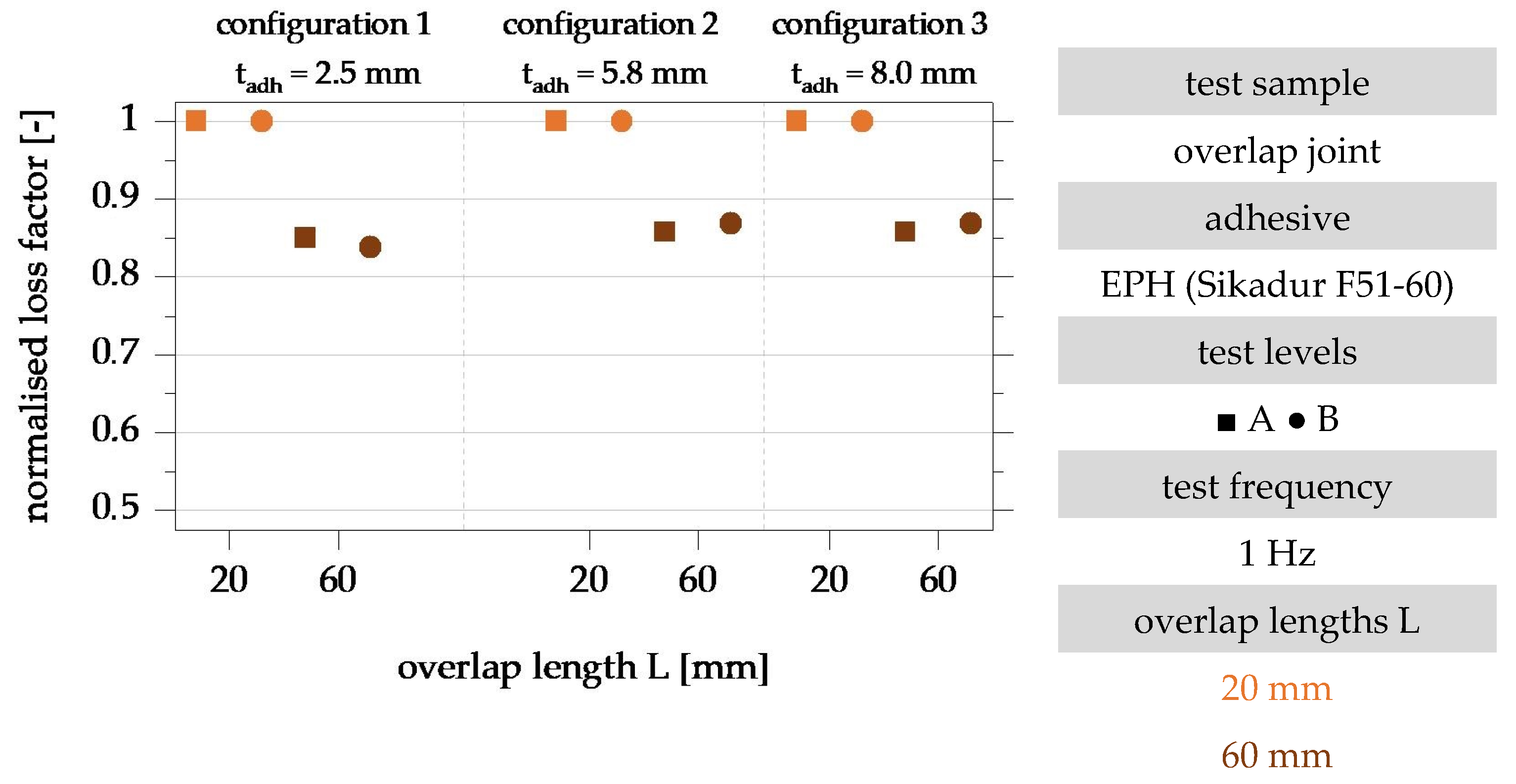
4.2. Influence of the Overlap Length
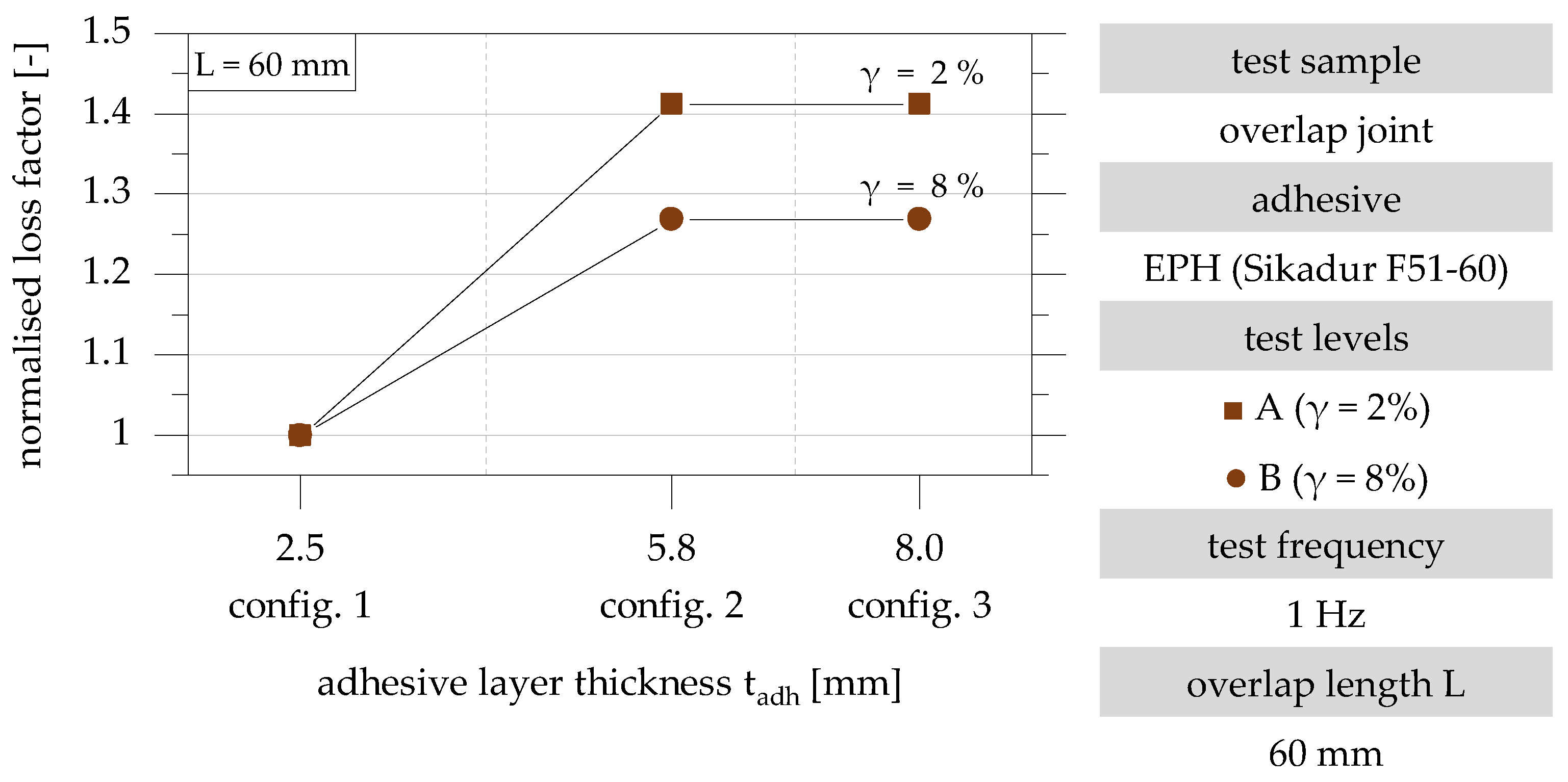
4.3. Influence of the Adhesive Layer Thickness
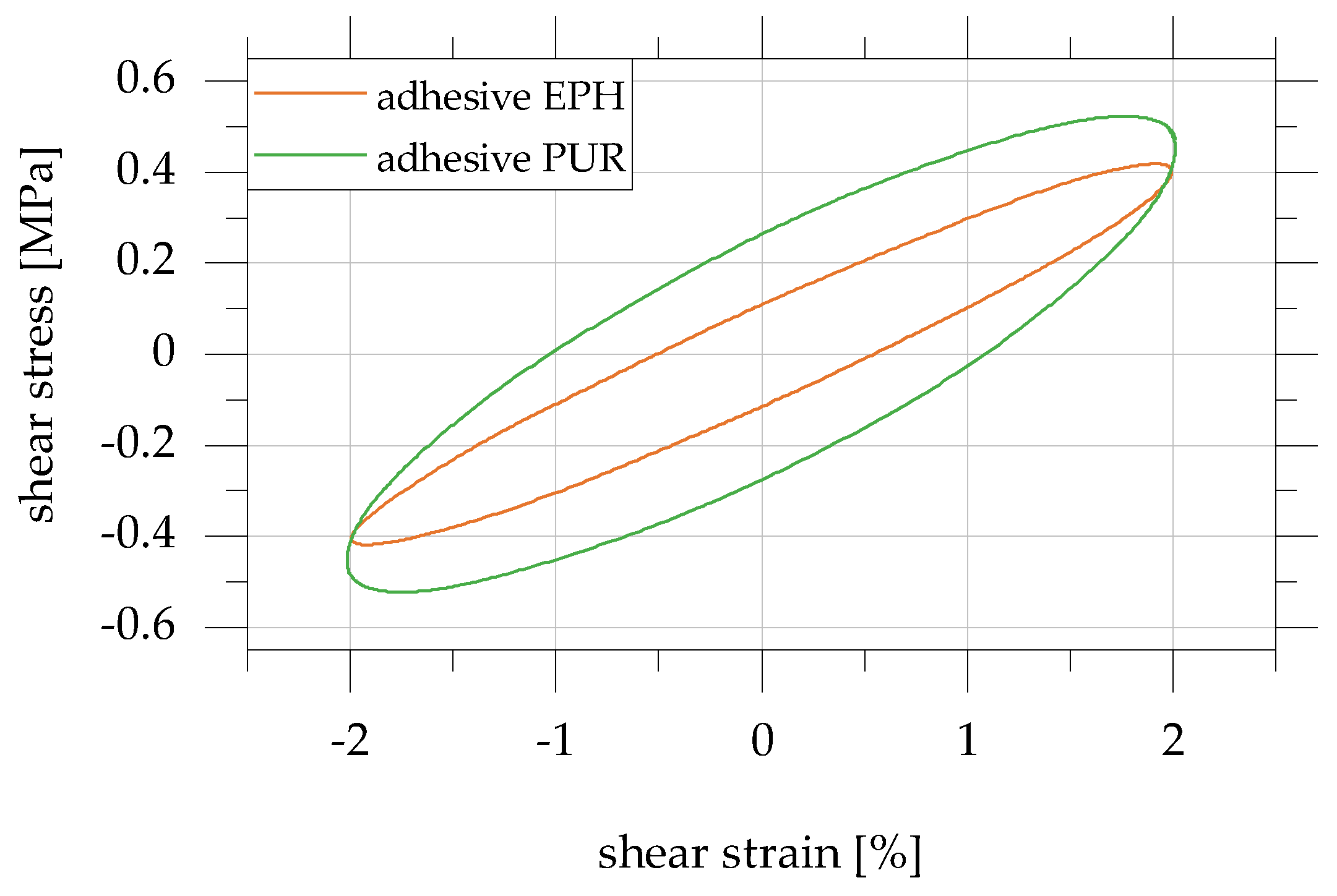
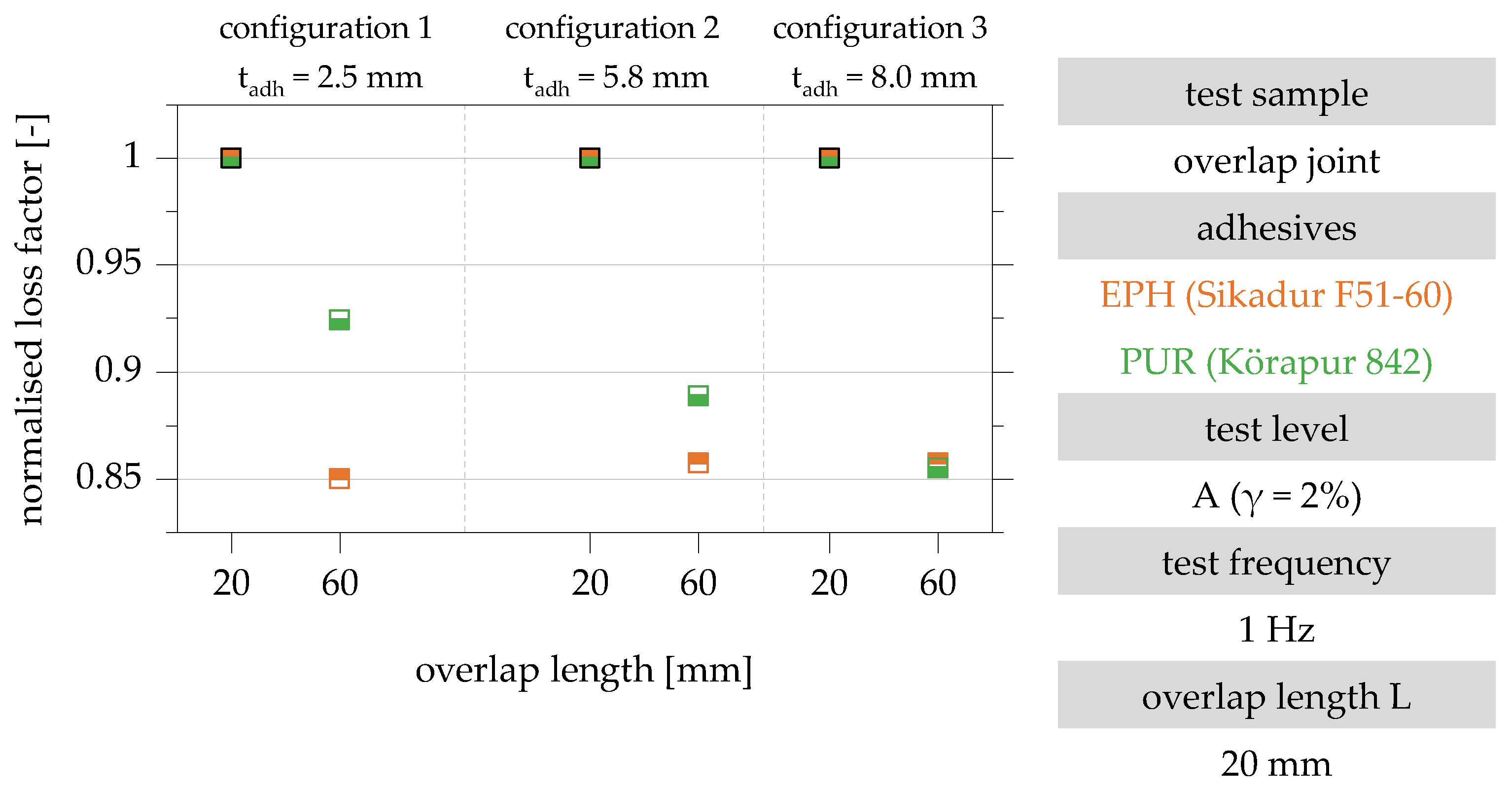
4.4. Influence of the Adhesive Used
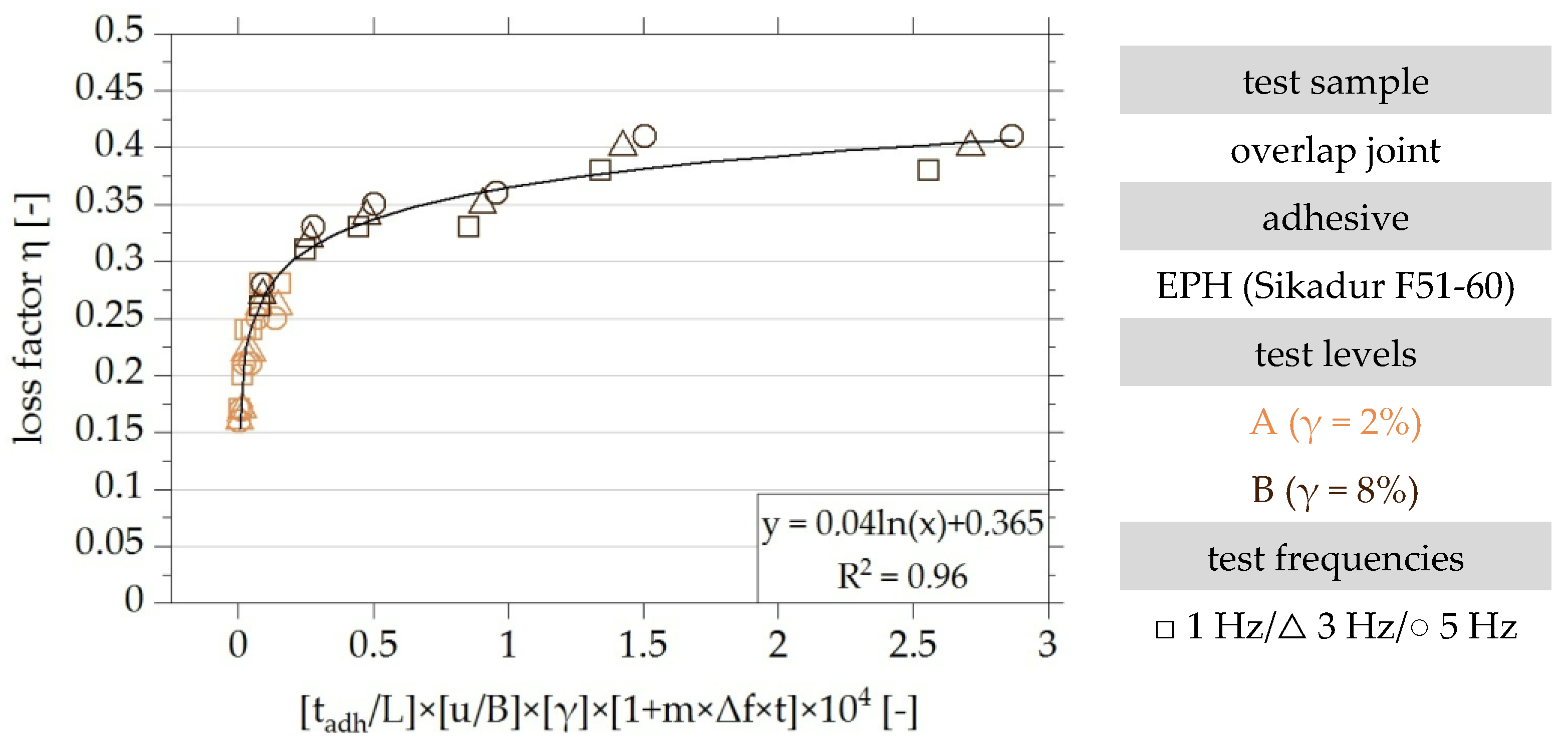
4.5. Analytical Description of the Damping Properties of Adhesively Bonded Overlap Joints
4.5.1. Definition of Dimensionally Dependent Influencing Factors
4.5.2. Identification of the Functional Relationship of the Dimensionless Parameters
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Strogatz, S.H.; Abrams, D.M.; McRobie, A.; Eckhardt, B.; Ott, E. Theoretical mechanics–Crowd synchrony on the Millennium Bridge. Nature 2005, 438, 43–44. [Google Scholar] [CrossRef]
- Vervaeke, R.; Debruyne, S.; Vandepitte, D. Numerical and experimental analysis of vibration damping performance of polyurethane adhesive in machine operations. Int. J. Adhes. Adhes. 2019, 90, 47–54. [Google Scholar] [CrossRef]
- Rao, M.D. Recent applications of viscoelastic damping for noise control in automobiles and commercial airplanes. J. Sound Vib. 2003, 262, 457–474. [Google Scholar] [CrossRef]
- Chen, S.; Wang, T.; Wang, Q.; Pei, X. Damping Properties of Polyurethane/Epoxy Graft Interpenetrating Polymer Network Composites Filled with Short Carbon Fiber and Nano-SiO2. J. Macromol. Sci. Part B 2011, 50, 931–941. [Google Scholar] [CrossRef]
- Wei, Y.; Li, H.; Yang, H.; Ma, Y.; Cheng, J.; Gao, P.; Shi, J.; Yu, B.; Lin, F. Damping and Mechanical Properties of Epoxy/316L Metallic Lattice Composites. Materials 2022, 16, 130. [Google Scholar] [CrossRef]
- Shchegolkov, A.V.; Nachtane, M.; Stanishevskiy, Y.M.; Dodina, E.P.; Rejepov, D.T.; Vetcher, A.A. The Effect of Multi-Walled Carbon Nanotubes on the Heat-Release Properties of Elastic Nanocomposites. J. Compos. Sci. 2022, 6, 333. [Google Scholar] [CrossRef]
- He, S.; Rao, M.D. Vibration analysis of adhesively bonded lap joint, part I–Theory. J. Sound Vib. 1992, 152, 405–416. [Google Scholar] [CrossRef]
- He, S.; Rao, M.D. Longitudinal Vibration and Damping Analysis of Adhesively Bonded Double-Strap Joints. J. Vib. Acoust. 1992, 114, 330–337. [Google Scholar] [CrossRef]
- He, S.; Rao, M.D. Vibration analysis of adhesively bonded lap joint, part II: Numerical solution. J. Sound Vib. 1992, 152, 417–425. [Google Scholar] [CrossRef]
- Kaya, A.; Tekelioğlu, M.S.; Findik, F. Effects of various parameters on dynamic characteristics in adhesively bonded joints. Mater. Lett. 2004, 58, 3451–3456. [Google Scholar] [CrossRef]
- Almitani, K.H.; Othman, R. Analytical solution of the harmonic response of visco-elastic adhesively bonded single-lap and double-lap joints. Int. J. Adhes. Adhes. 2016, 71, 55–65. [Google Scholar] [CrossRef]
- Yaman, M.; Şansveren, M.F. Numerical and experimental vibration analysis of different types of adhesively bonded joints. Structures 2021, 34, 368–380. [Google Scholar] [CrossRef]
- Albiez, M.; Vallée, T.; Fricke, H.; Ummenhofer, T. Adhesively bonded steel tubes—Part I: Experimental investigations. Int. J. Adhes. Adhes. 2019, 90, 199–210. [Google Scholar] [CrossRef]
- Albiez, M.; Vallée, T.; Ummenhofer, T. Adhesively bonded steel tubes—Part II: Numerical modelling and strength prediction. Int. J. Adhes. Adhes. 2019, 90, 211–224. [Google Scholar] [CrossRef]
- Kasper, Y.; Albiez, M.; Ummenhofer, T.; Mayer, C.; Meier, T.; Choffat, F.; Ciupack, Y.; Pasternak, H. Application of toughened epoxy-adhesives for strengthening of fatigue-damaged steel structures. Constr. Build. Mater. 2021, 275, 121579. [Google Scholar] [CrossRef]
- Ummenhofer, T.; Boretzki, J.; Albiez, M. Hybrid connection technologies for hollow sections in steel construction. Steel Constr. 2022, 15, 37–50. [Google Scholar] [CrossRef]
- Albiez, M.; Damm, J.; Ummenhofer, T.; Ehard, H.; Schuler, C.; Kaufmann, M.; Vallée, T.; Myslicki, S. Hybrid joining of jacket structures for offshore wind turbines–Validation under static and dynamic loading at medium and large scale. Eng. Struct. 2022, 252, 113595. [Google Scholar] [CrossRef]
- Albiez, M.; Damm, J.; Ummenhofer, T.; Kaufmann, M.; Vallée, T.; Myslicki, S. Hybrid joining of jacket structures for offshore wind turbines–Determination of requirements and adhesive characterisation. Eng. Struct. 2022, 259, 114186. [Google Scholar] [CrossRef]
- Boretzki, J.; Albiez, M. Static strength and load bearing behaviour of hybrid bonded bolted joints: Experimental and numerical investigations. J. Adhes. 2023, 99, 606–631. [Google Scholar] [CrossRef]
- Damm, J.; Ummenhofer, T.; Albiez, M.; Göddecke, J.; Meschut, G.; Kötz, F.; Matzenmiller, A. Experimental and numerical investigation of the damping properties of adhesively bonded tubular steel joints. J. Adhes. 2023. [Google Scholar] [CrossRef]
- Damm, J.; Ummenhofer, T.; Albiez, M. Influence of damping properties of adhesively bonded joints on the dynamic behaviour of steel structures: Numerical investigations. J. Adhes. 2022, 98, 934–962. [Google Scholar] [CrossRef]
- Damm, J. Zum Dämpfungsverhalten Viskoelastischer Klebverbindungen im Stahlbau. Ph.D. Thesis, Karlsruhe Institut of Technology (KIT), Karlsruhe, Germany, 2023. [Google Scholar]
- Damm, J.; Albiez, M.; Ummenhofer, T.; Göddecke, J.; Meschut, G.; Kötz, F.; Matzenmiller, A. Experimentelle und Numerische Untersuchung der Dämpfungseigenschaften Geklebter Strukturen unter Dynamischer Beanspruchung–Dämpfende Knoten (FOSTA P 1272, IGF Nr. 20080 N); Abschlussbericht; Forschungsvereinigung Stahlanwendung e. V. (FOSTA): Düsseldorf, Deutschland, 2022. [Google Scholar]
- Göddecke, J.; Meschut, G.; Kötz, F.; Matzenmiller, A.; Damm, J.; Albiez, M. Experimental investigation and numerical modelling of the damping properties of technological bonded joints. J. Adhes. 2023. submitted. [Google Scholar]
- DIN EN 10058; Hot Rolled Flat Steel Bars and Steel Wide Flats for General Purposes-Dimensions and Tolerances on Shape and Dimensions (German Version). Beuth Verlag GmbH: Berlin, Germany, February 2019.
- DIN EN 1993-1-1; Eurocode 3: Design of Steel Structures-Part 1-1: General Rules and Rules for Buildings (German Version). Beuth Verlag GmbH: Berlin, Germany, December 2010.
- DIN EN ISO 8501-1; Preparation of Steel Substrates Before Application of Paints And Related Products-Visual Assessment of Surface Cleanliness—Part 1: Rust Grades and Preparation Grades of Uncoated Steel Substrates and of Steel Substrates after Overall Removal of Previous Coatings (German Version). Beuth Verlag GmbH: Berlin, Germany, December 2007.
- da Silva, L.F.M.; Öchsner, A.; Adams, R.D. Handbook of Adhesion Technology, 2nd ed.; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Petersen, C.; Werkle, H. Dynamik der Baukonstruktionen; 2. Auflage; Springer Fachmedien Wiesbaden: Wiesbaden, Germany, 2017. [Google Scholar]
- Vaziri, A.; Nayeb-Hashemi, H. Dynamic response of tubular joints with an annular void subjected to a harmonic axial load. Int. J. Adhes. Adhes. 2002, 22, 367–373. [Google Scholar] [CrossRef]
- Vaziri, A.; Nayeb-Hashemi, H. Dynamic response of tubular joints with an annular void subjected to a harmonic torsional load. Proc. IMechE 2005, 216, 361–370. [Google Scholar] [CrossRef]
- Buckingham, E. On Physically Similar Systems; Illustrations of the Use of Dimensional Equations. Phys. Rev. 1914, 4, 345–376. [Google Scholar] [CrossRef]
- Herwig, H. Strömungsmechanik; 2. Auflage; Springer Fachmedien Wiesbaden: Wiesbaden, Germany, 2016. [Google Scholar]
- Khoshmanesh, S.; Watson, S.J.; Zarouchas, D. Characterisation of fatigue damage in a thick adhesive joint based on changes in material damping. J. Phys. Conf. Ser. 2020, 1618, 22058. [Google Scholar] [CrossRef]
- Khashaba, U.A. Potential energy as a new approach for detection and monitoring of fatigue damage in scarf adhesive joints modified with nanoparticles. J. Compos. Mater. 2022, 56, 2279–2298. [Google Scholar] [CrossRef]






| Configuration | Adhesive | Adhesive Layer Thickness tadh [mm] | Overlap Length L [mm] | Test Level | Frequency [Hz] |
|---|---|---|---|---|---|
| 1 | EPH/ PUR | 2.5 | 20 | A (γ ± 2%)/B (γ ± 8%) | 1/3/5 |
| 60 | |||||
| 2 | 5.8 | 20 | |||
| 60 | |||||
| 3 | 8.0 | 20 | |||
| 60 |
| Configuration | Adhesive, tadh [mm] | Overlap Length L [mm] | Test Level | Loss Factor at Frequency | |||||
|---|---|---|---|---|---|---|---|---|---|
| 1 Hz | CV | 3 Hz | CV | 5 Hz | CV | ||||
| 1 | EPH, 2.5 | 20 | A (γ ± 2%) | 0.20 | 0.04 | 0.17 | 0.10 | 0.17 | 0.13 |
| 60 | 0.17 | 0.03 | 0.16 | 0.09 | 0.16 | 0.09 | |||
| 2 | EPH, 5.8 | 20 | 0.28 | 0.02 | 0.26 | 0.04 | 0.25 | 0.09 | |
| 60 | 0.24 | 0.03 | 0.22 | 0.06 | 0.21 | 0.05 | |||
| 3 | EPH, 8.0 | 20 | 0.28 | 0.02 | 0.26 | 0.05 | 0.25 | 0.05 | |
| 60 | 0.24 | 0.08 | 0.22 | 0.10 | 0.21 | 0.06 | |||
| 1 | EPH, 2.5 | 20 | B (γ ± 8%) | 0.31 | 0.03 | 0.32 | 0.02 | 0.33 | 0.03 |
| 60 | 0.26 | 0.02 | 0.27 | 0.04 | 0.28 | 0.06 | |||
| 2 | EPH, 5.8 | 20 | 0.38 | 0.02 | 0.40 | 0.02 | 0.41 | 0.04 | |
| 60 | 0.33 | 0.03 | 0.34 | 0.03 | 0.35 | 0.03 | |||
| 3 | EPH, 8.0 | 20 | 0.38 | 0.02 | 0.40 | 0.03 | 0.41 | 0.03 | |
| 60 | 0.33 | 0.02 | 0.35 | 0.05 | 0.36 | 0.02 | |||
| Influencing Factors | Symbol | Dimension |
|---|---|---|
| loss factor | η | [1] |
| adhesive layer thickness | tadh | [L] |
| overlap length | L | [L] |
| adhesive layer width | B | [L] |
| maximum shear deformation of the adhesive layer | u | [L] |
| frequency | f | [T−1] |
| time | t | [T] |
| Dimensionless Parameter | Functional Form |
|---|---|
| Π1 | η |
| Π2 | tadh/L |
| Π3 | u/B |
| Π4 | u/tadh = γ |
| Π5 | f × t |
| Parameter | Interactional Relationships | Influence on η | |||
|---|---|---|---|---|---|
| frequency | f | ↑ | γ | low strain level | γ ≤ 2% | ↘ |
| increasing strain level | γ ≥ 8% | ↗ | ||||
| overlap length | L | ↑ | - | - | ↓ |
| adhesive layer thickness | tadh | ↑ | γ | increasing influence for higher strain level | ↑ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Damm, J.; Albiez, M. Damping Properties of Large-Scale Overlap Joints Bonded with Epoxy Hybrid Resin or Polyurethanes: Experimental Characterisation and Analytical Description. Polymers 2023, 15, 1102. https://doi.org/10.3390/polym15051102
Damm J, Albiez M. Damping Properties of Large-Scale Overlap Joints Bonded with Epoxy Hybrid Resin or Polyurethanes: Experimental Characterisation and Analytical Description. Polymers. 2023; 15(5):1102. https://doi.org/10.3390/polym15051102
Chicago/Turabian StyleDamm, Jannis, and Matthias Albiez. 2023. "Damping Properties of Large-Scale Overlap Joints Bonded with Epoxy Hybrid Resin or Polyurethanes: Experimental Characterisation and Analytical Description" Polymers 15, no. 5: 1102. https://doi.org/10.3390/polym15051102
APA StyleDamm, J., & Albiez, M. (2023). Damping Properties of Large-Scale Overlap Joints Bonded with Epoxy Hybrid Resin or Polyurethanes: Experimental Characterisation and Analytical Description. Polymers, 15(5), 1102. https://doi.org/10.3390/polym15051102







