Prediction Models of Mechanical Properties of Jute/PLA Composite Based on X-ray Computed Tomography
Abstract
:1. Introduction
2. Experiments
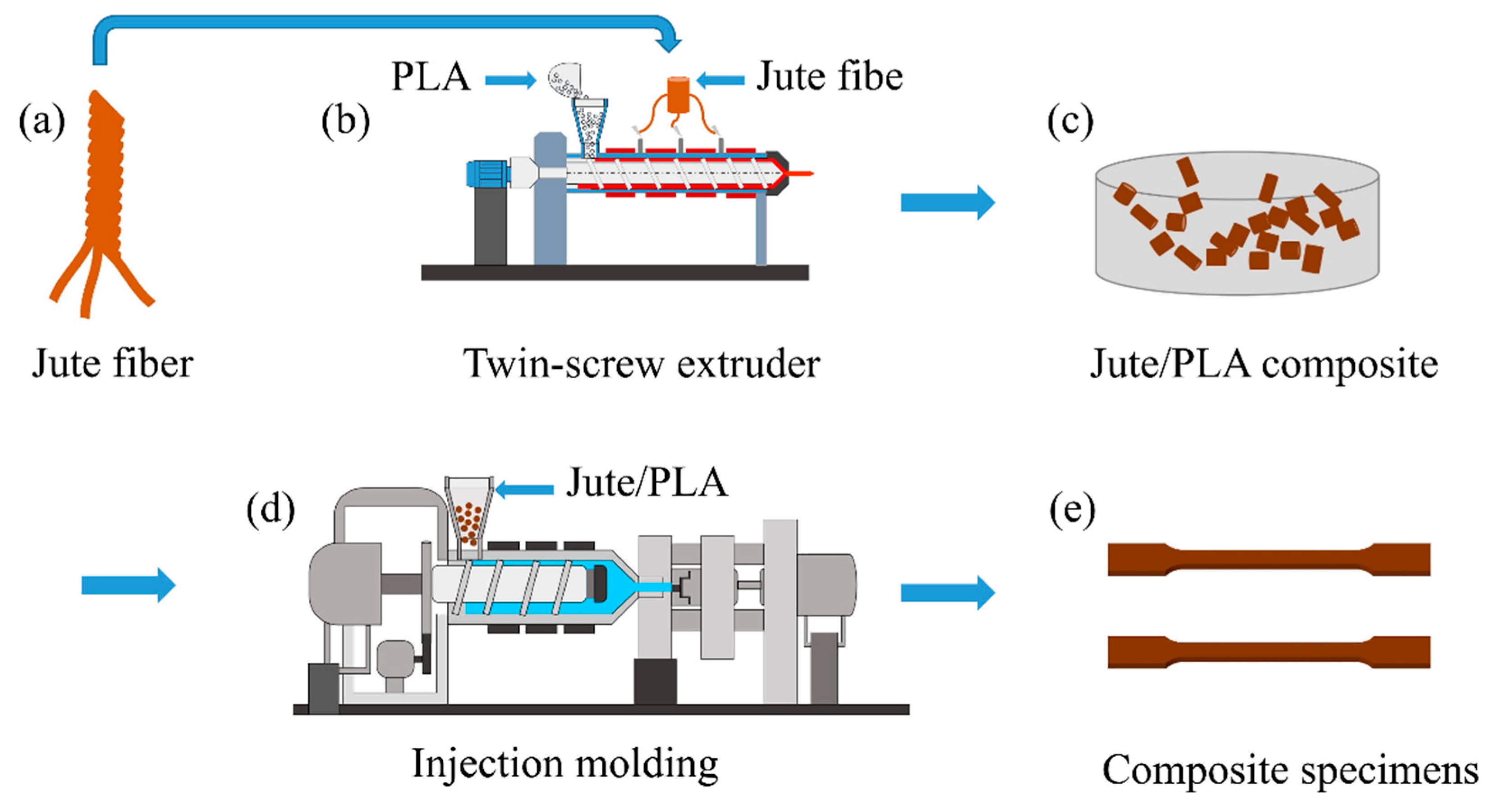
2.1. Experimental Materials
2.2. Experimental Methods
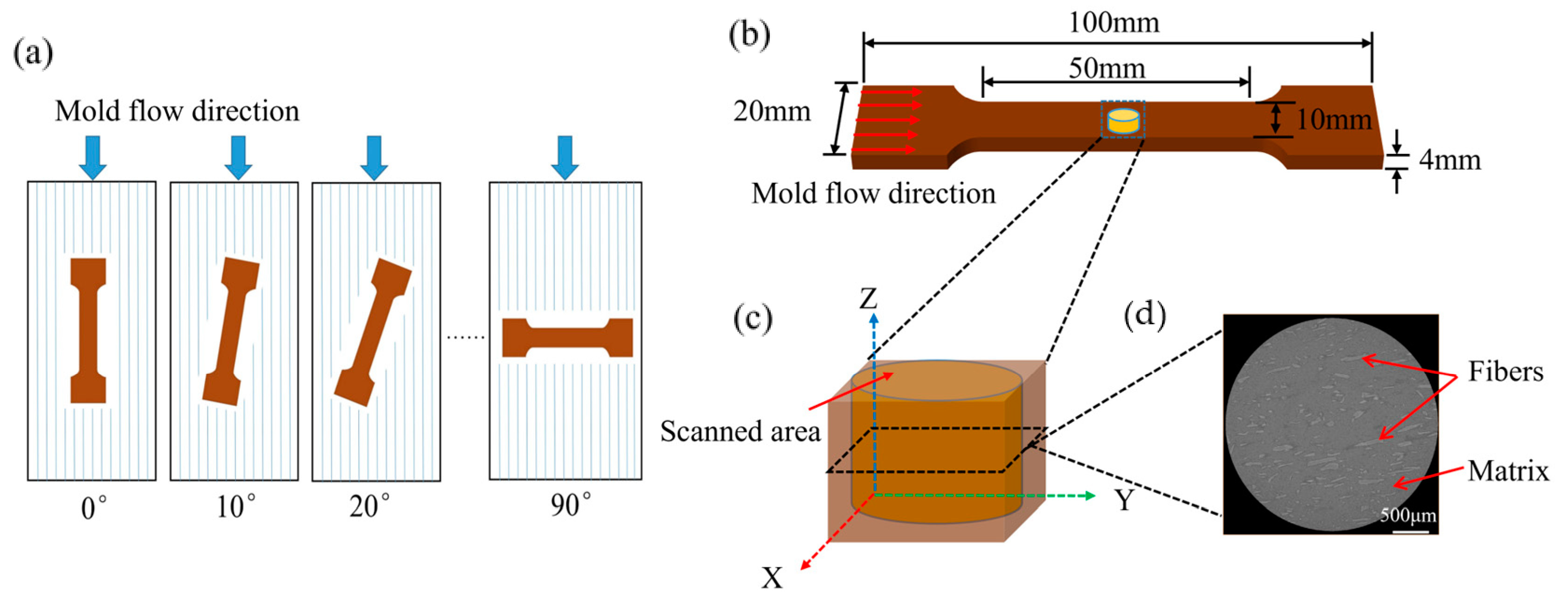
2.2.1. Tensile Test
2.2.2. X-ray Computed Tomography (XCT)
3. Results and Discussion
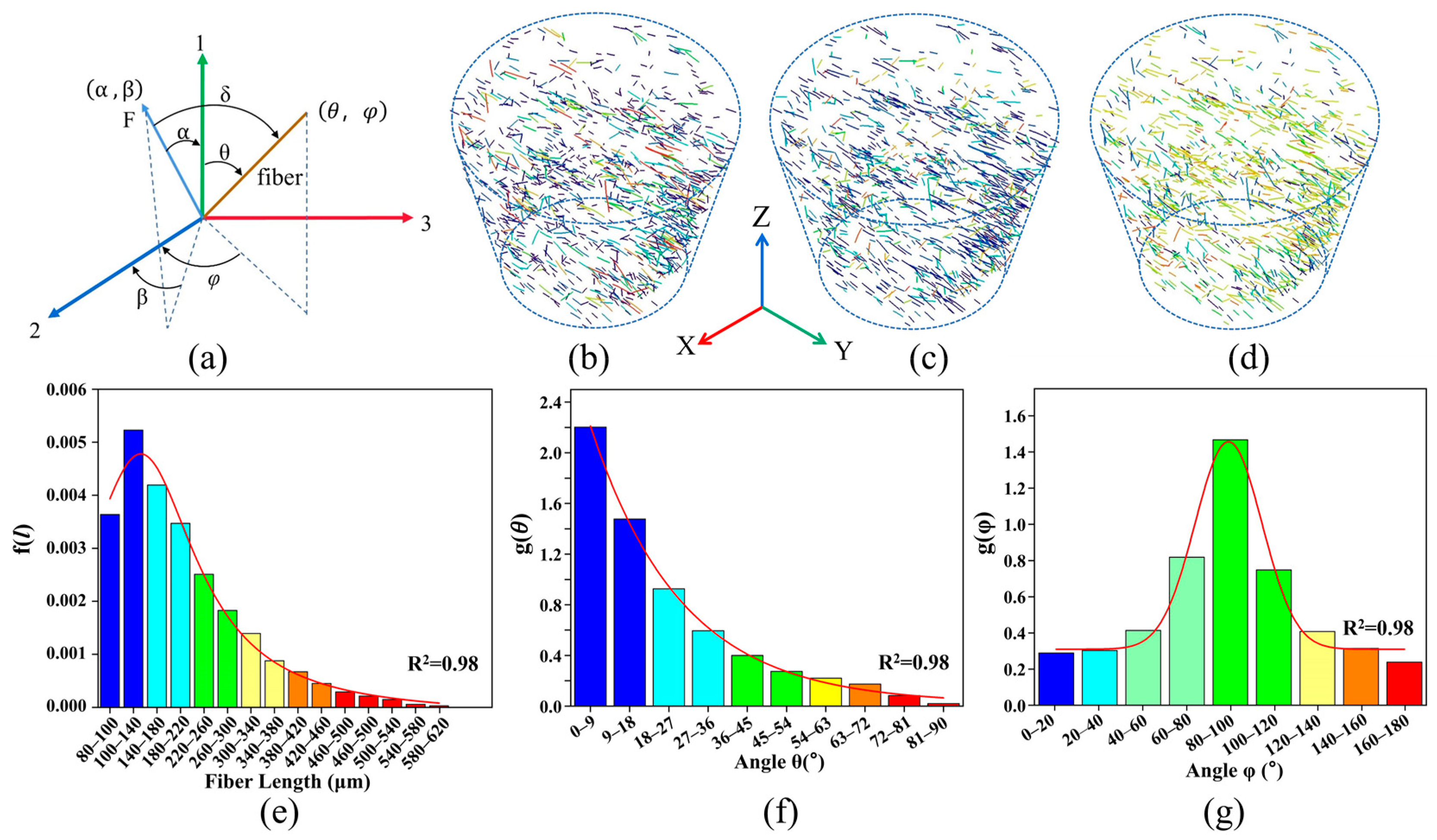
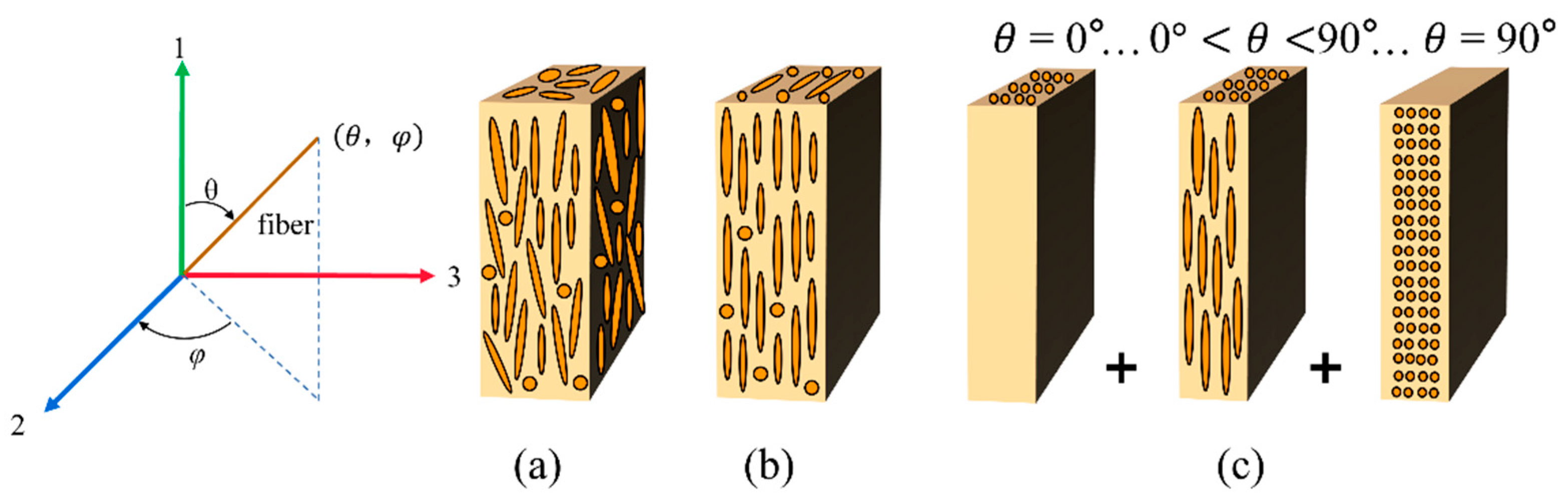
3.1. 3D Microanalysis
3.2. FLD and FOD Probability Density Functions
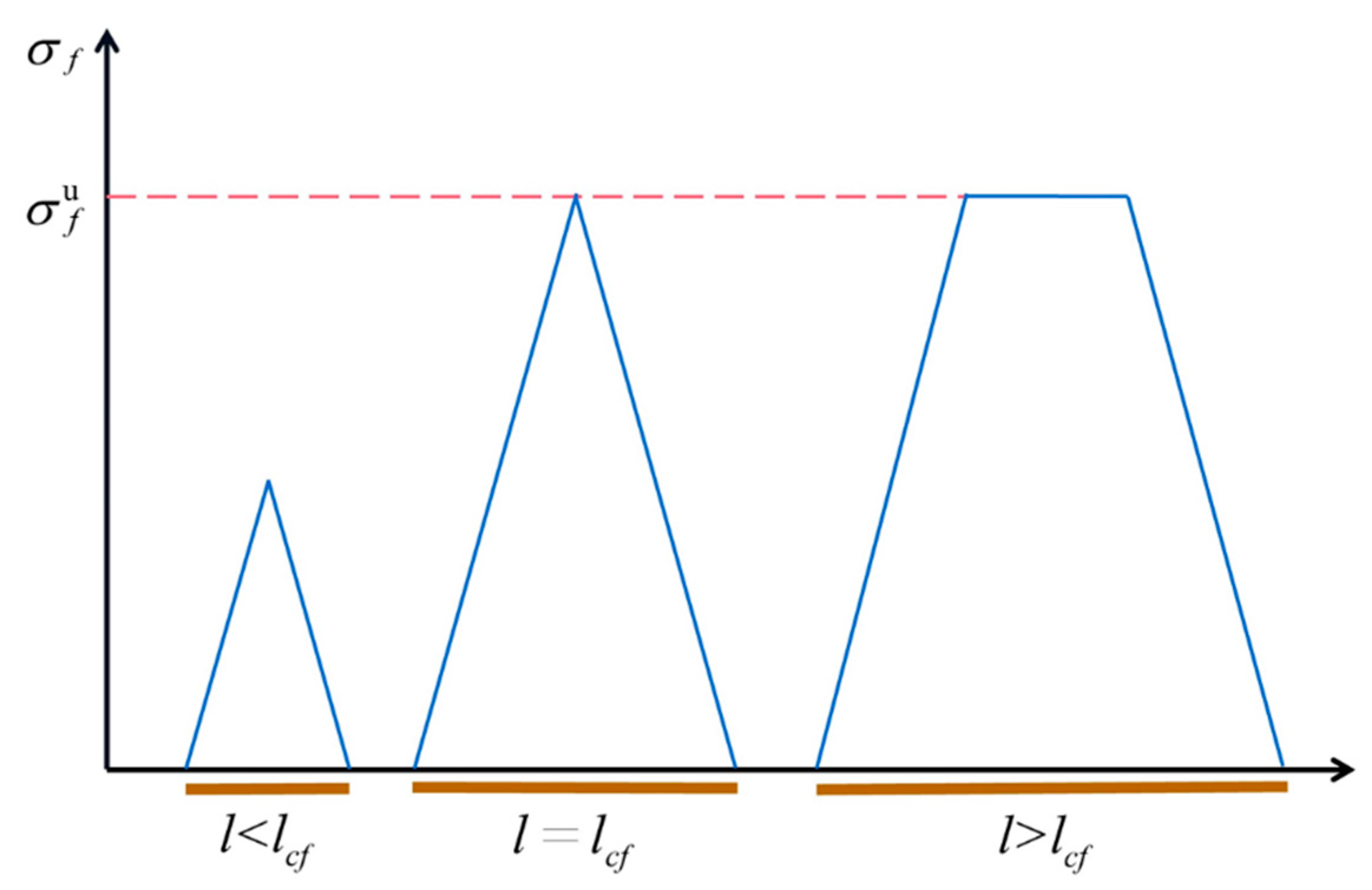
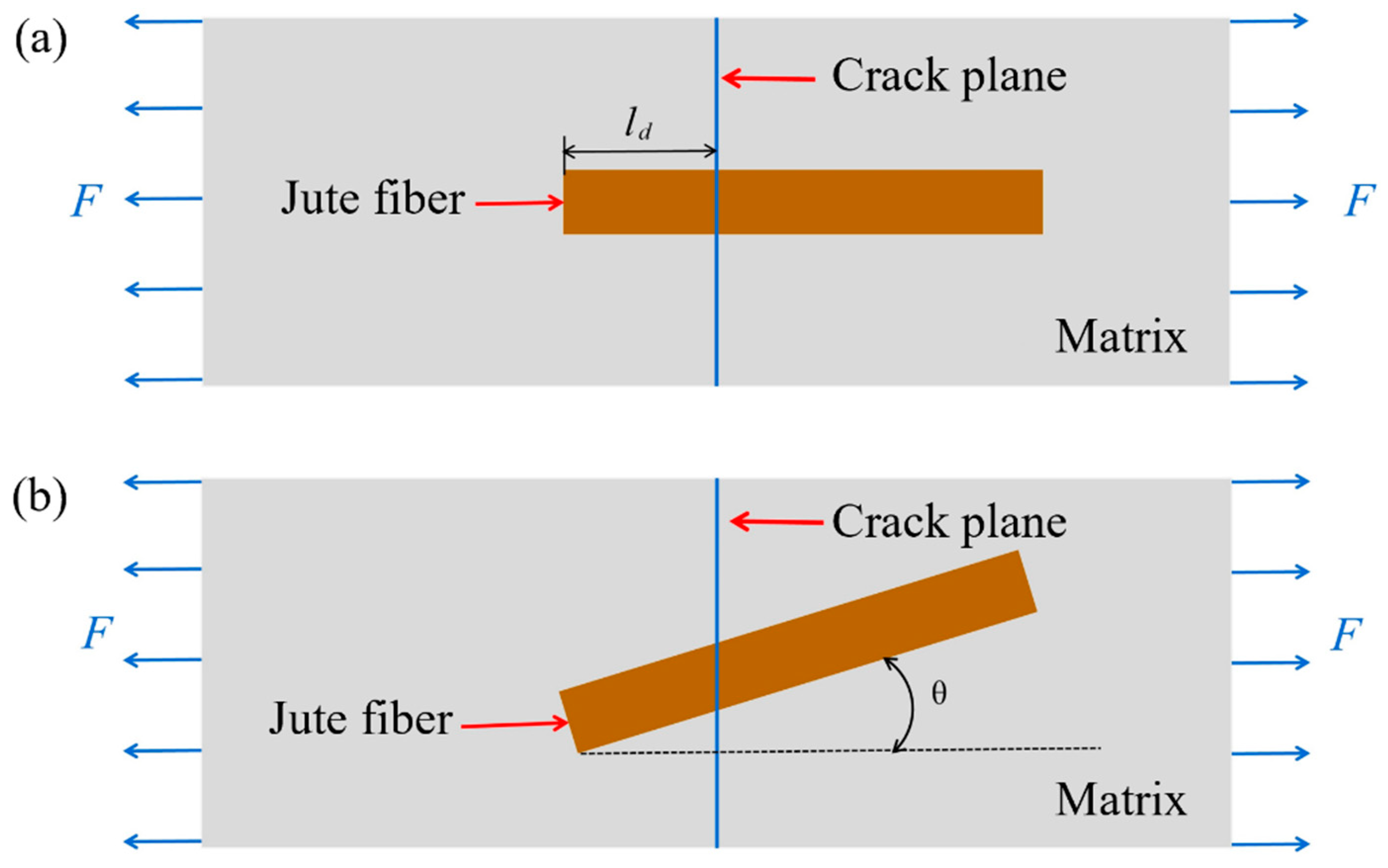
3.3. Critical Fiber Length
3.4. Predictions of Elastic Modulus and Tensile Strength
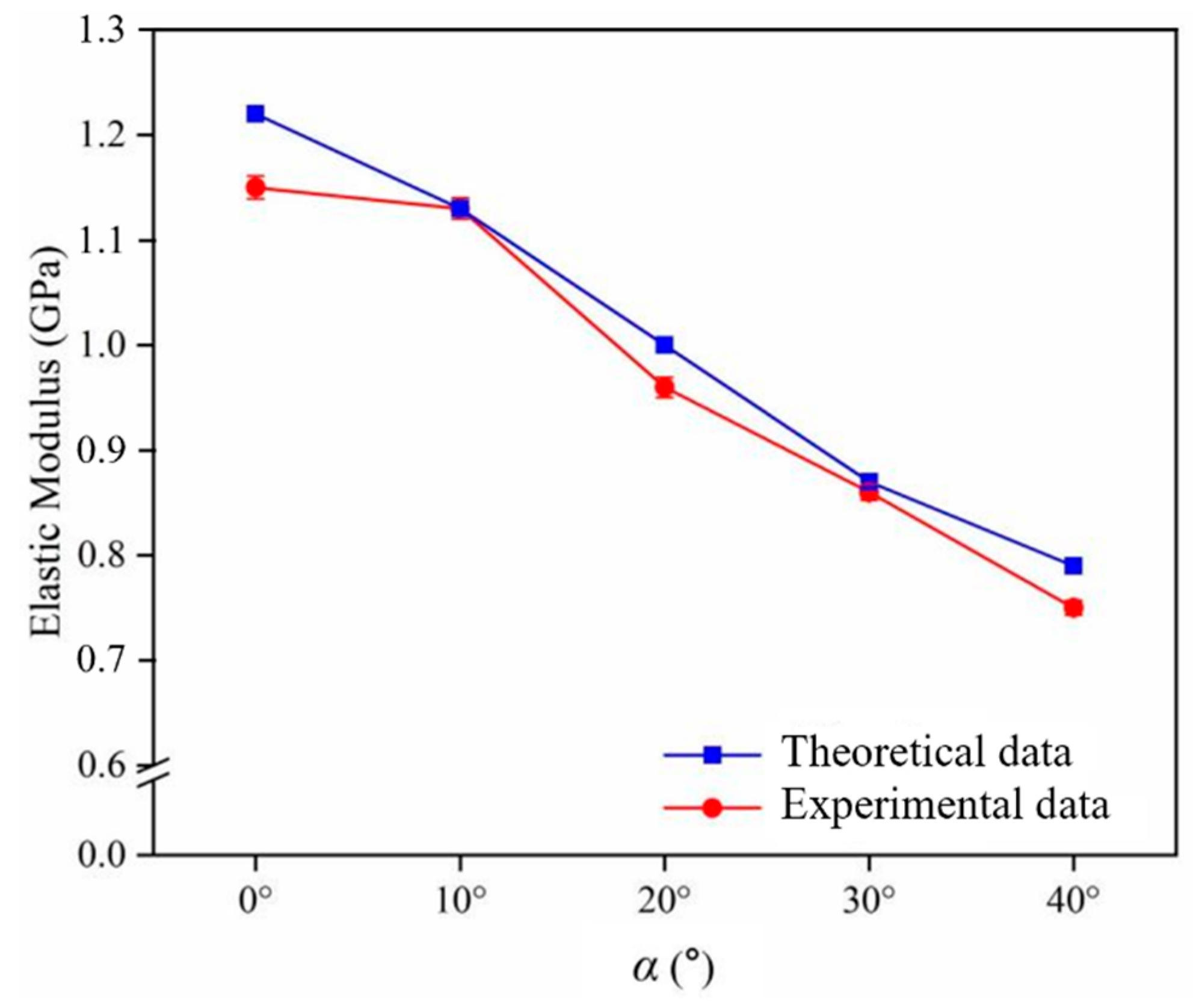
3.4.1. Prediction of Elastic Modulus
3.4.2. Prediction of Tensile Strength
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sanjay, M.R.; Arpitha, G.R.; Naik, L.L.; Gopalakrishna, K.; Yogesha, B. Applications of natural fibers and its composites: An overview. Nat. Resour. 2016, 7, 108–114. [Google Scholar] [CrossRef]
- Jiang, N.; Li, Y.; Li, Y.; Yu, T.; Li, Y.; Li, D.; Xu, J.; Wang, C.; Shi, Y. Effect of short jute fibers on the hydrolytic degradation behavior of poly (lactic acid). Polym. Degrad. Stab. 2020, 178, 109214. [Google Scholar] [CrossRef]
- Sanivada, U.K.; Mármol, G.; Brito, F.P.; Fangueiro, R. PLA Composites Reinforced with Flax and Jute Fibers–A Review of Recent Trends, Processing Parameters and Mechanical Properties. Polymers 2020, 12, 2373. [Google Scholar] [CrossRef] [PubMed]
- Bell, J.P. Flow orientation of short fiber composites. J. Compos. Mater. 1969, 3, 244–253. [Google Scholar] [CrossRef]
- Lusti, H.R.; Hine, P.J.; Gusev, A.A. Direct numerical predictions for the elastic and thermoelastic properties of short fiber composites. Compos. Sci. Technol. 2002, 62, 1927–1934. [Google Scholar] [CrossRef]
- Karamov, R.; Martulli, L.M.; Kerschbaum, M.; Sergeichev, I.; Swolfs, Y.; Lomov, S.V. Micro-CT based structure tensor analysis of fiber orientation in random fiber composites versus high-fidelity fiber identification methods. Compos. Struct. 2020, 235, 111818. [Google Scholar] [CrossRef]
- Bino, P.R.D.; Stanly, J.R.B. Effect of short fiber orientation on the mechanical characterization of a composite material-hybrid fiber reinforced polymer matrix. Bull. Mater. Sci. 2019, 42, 1–7. [Google Scholar]
- Huang, C.T.; Chen, X.W.; Fu, W.W. Investigation on the fiber orientation distributions and their influence on the mechanical property of the co-injection molding products. Polymers 2019, 12, 24. [Google Scholar] [CrossRef]
- Ramakrishnan, T.; Babu, M.S.; Balasubramani, S.; Manickaraj, K.; Jeyakumar, R. Effect of fiber orientation and mechanical properties of natural fiber reinforced polymer composites-A review. Paid. J. 2021, 14, 17–23. [Google Scholar]
- Ogierman, W.; Kokot, G. A study on fiber orientation influence on the mechanical response of a short fiber composite structure. Acta Mech. 2016, 227, 173–183. [Google Scholar] [CrossRef]
- Prade, F.; Schaff, F.; Senck, S.; Meyer, P.; Mohr, J.; Kastner, J.; Pfeiffer, F. Nondestructive characterization of fiber orientation in short fiber reinforced polymer composites with X-ray vector radiography. NDT E Int. 2017, 86, 65–72. [Google Scholar] [CrossRef]
- Zhou, Y.; Mallick, P.K. A non-linear damage model for the tensile behavior of an injection molded short E-glass fiber reinforced polyamide-6,6. Mater. Sci. Eng. A 2005, 393, 303–309. [Google Scholar] [CrossRef]
- Monte, M.D.; Moosbrugger, E.; Quaresimin, M. Influence of temperature and thickness on the off-axis behaviour of short glass fiber reinforced polyamide 6.6–cyclic loading. Compos. Part A 2010, 41, 1368–1379. [Google Scholar] [CrossRef]
- Hao, X.; Zhou, H.; Mu, B.; Chen, L.; Guo, Q.; Yi, X.; Sun, L.; Wang, Q.; Ou, R. Effects of fiber geometry and orientation distribution on the anisotropy of mechanical properties, creep behavior, and thermal expansion of natural fiber/HDPE composites. Compos. Part B 2020, 185, 107778. [Google Scholar] [CrossRef]
- Mortazavian, S.; Fatemi, A. Effects of fiber orientation and anisotropy on tensile strength and elastic modulus of short fiber reinforced polymer composites. Compos. Part B 2015, 72, 116–129. [Google Scholar] [CrossRef]
- Cordin, M.; Bechtold, T.; Pham, T. Effect of fiber orientation on the mechanical properties of polypropylene–lyocell composites. Cellulose 2018, 25, 7197–7210. [Google Scholar] [CrossRef]
- Bernasconi, A.; Davoli, P.; Basile, A.; Filippi, A. Effect of fiber orientation on the fatigue behaviour of a short glass fiber reinforced polyamide-6. Int. J. Fatigue 2007, 29, 199–208. [Google Scholar] [CrossRef]
- Mohd, N.N.; Khalina, A.; Chandrasekar, M.; Aisyah, H.; Rafiqah, S.A.; Ilyas, R.; Hanafee, Z. Effect of fiber orientation and fiber loading on the mechanical and thermal properties of sugar palm yarn fiber reinforced unsaturated polyester resin composites. Polimery 2020, 65, 1024–1037. [Google Scholar]
- Mentges, N.; Çelik, H.; Hopmann, C.; Fagerström, M.; Mirkhalaf, S. Micromechanical modelling of short fibre composites considering fibre length distributions. Compos. Part B 2023, 264, 110868. [Google Scholar] [CrossRef]
- Cox, H.L. The elasticity and strength of paper and other fibrous materials. Br. J. Appl. Phys. 1952, 3, 72. [Google Scholar] [CrossRef]
- Affdl, J.C.H.; Kardos, J.L. The Halpin-Tsai equations: A review. Polym. Eng. Sci. 1976, 16, 344–352. [Google Scholar] [CrossRef]
- Chou, T.W.; Nomura, S.; Taya, M. A self-consistent approach to the elastic stiffness of short-fiber composites. J. Compos. Mater. 1980, 14, 178–188. [Google Scholar] [CrossRef]
- Kelly, A.; Tyson, A.W. Tensile properties of fiber-reinforced metals: Copper/tungsten and copper/molybdenum. J. Mech. Phys. Solids 1965, 13, 329–350. [Google Scholar] [CrossRef]
- Liang, J.Z. Predictions of tensile strength of short inorganic fiber reinforced polymer composites. Polym. Test. 2011, 30, 749–752. [Google Scholar] [CrossRef]
- Halpin, J.C.; Pagano, N.J. The laminate approximation for randomly oriented fibrous composites. J. Compos. Mater. 1969, 3, 720–724. [Google Scholar] [CrossRef]
- Fu, S.Y.; Lauke, B. The elastic modulus of misaligned short-fiber-reinforced polymers. Compos. Sci. Technol. 1998, 58, 389–400. [Google Scholar] [CrossRef]
- Lusis, V.; Krasnikovs, A.; Kononova, O.; Lapsa, V.A.; Stonys, R.; Macanovskis, A.; Lukasenoks, A. Effect of short fibers orientation on mechanical properties of composite material–fiber reinforced concrete. J. Civ. Eng. Manag. 2017, 23, 1091–1099. [Google Scholar] [CrossRef]
- Fu, S.Y.; Mai, Y.W.; Ching, E.C.Y.; Li, R.K. Correction of the measurement of fiber length of short fiber reinforced thermoplastics. Compos. Part A 2002, 33, 1549–1555. [Google Scholar] [CrossRef]
- Fu, S.Y.; Lauke, B.; Mäder, E.; Hu, X.; Yue, C.Y. Fracture resistance of short-glass-fiber-reinforced and short-carbon-fiber-reinforced polypropylene under Charpy impact load and its dependence on processing. J. Mater. Process. Technol. 1999, 89, 501–507. [Google Scholar] [CrossRef]
- Gupta, V.B.; Mittal, R.K.; Sharma, P.K.; Mennig, G.; Wolters, J. Some studies on glass fiber-reinforced polypropylene. Part II: Mechanical properties and their dependence on fiber length, interfacial adhesion, and fiber dispersion. Polym. Compos. 1989, 10, 16–27. [Google Scholar] [CrossRef]
- Fakirov, S.; Fakirova, C. Direct determination of the orientation of short glass fibers in an injection-molded poly (ethylene terephthalate) system. Polym. Compos. 1985, 6, 41–46. [Google Scholar] [CrossRef]
- Hine, P.J.; Davidson, N.; Duckett, R.A.; Ward, I.M. Measuring the fiber orientation and modelling the elastic properties of injection-moulded long-glass-fiber-reinforced nylon. Compos. Sci. Technol. 1995, 53, 125–131. [Google Scholar] [CrossRef]
- Bay, R.S.; Tucker III, C.L. Stereological measurement and error estimates for three-dimensional fiber orientation. Polym. Eng. Sci. 1992, 32, 240–253. [Google Scholar] [CrossRef]
- Eberhardt, C.; Clarke, A.; Vincent, M.; Giroud, T.; Flouret, S. Fiber-orientation measurements in short-glass-fiber composites—II: A quantitative error estimate of the 2d image analysis technique. Compos. Sci. Technol. 2001, 61, 1961–1974. [Google Scholar] [CrossRef]
- Régnier, G.; Dray, D.; Jourdain, E.; Le Roux, S.; Schmidt, F.M. A simplified method to determine the 3D orientation of an injection molded fiber-filled polymer. Polym. Eng. Sci. 2008, 48, 2159–2168. [Google Scholar] [CrossRef]
- Mehdikhani, M.; Breite, C.; Swolfs, Y.; Wevers, M.; Lomov, S.V.; Gorbatikh, L. Combining digital image correlation with X-ray computed tomography for characterization of fiber orientation in unidirectional composites. Compos. Part A 2021, 142, 106234. [Google Scholar] [CrossRef]
- Sietins, J.M.; Sun, J.C.; Knorr, D.B., Jr. Fiber orientation quantification utilizing X-ray micro-computed tomography. J. Compos. Mater. 2021, 55, 1109–1118. [Google Scholar] [CrossRef]
- D3039/D3039M; Standard Test Method for Tensile Properties of Polymer Matrix Composite Material. ASTM (American Society for Testing and Materials): West Conshohocken, PA, USA, 2014.
- Jiang, N.; Li, Y.; Li, D.; Yu, T.; Li, Y.; Xu, J.; Li, N.; Marrow, T.J. 3D finite element modeling of water diffusion behavior of jute/PLA composite based on X-ray computed tomography. Compos. Sci. Technol. 2020, 199, 108313. [Google Scholar] [CrossRef]
- Fu, S.-Y.; Bernd, L. The fiber pull-out energy of misaligned short fiber composites. J. Mater. Sci. 1997, 32, 1985–1993. [Google Scholar] [CrossRef]
- Du, Y.; Wu, T.; Yan, N.; Kortschot, M.T.; Farnood, R. Fabrication and characterization of fully biodegradable natural fiber-reinforced poly (lactic acid) composites. Compos. Part B 2014, 56, 717–723. [Google Scholar] [CrossRef]
- Wang, C.; Uawongsuwan, P.; Yang, Y.; Hamada, H. Effect of molding condition and pellets material on the weld property of injection molded jute/polylactic acid. Polym. Eng. Sci. 2013, 53, 1657–1666. [Google Scholar] [CrossRef]
- Zafar, M.T.; Maiti, S.N.; Ghosh, A.K. Effect of surface treatment of jute fibers on the interfacial adhesion in poly (lactic acid)/jute fiber biocomposites. Fibers Polym. 2016, 17, 266–274. [Google Scholar] [CrossRef]
- Fu, S.Y.; Xu, G.; Mai, Y.W. On the elastic modulus of hybrid particle/short-fiber/polymer composites. Compos. Part B 2002, 33, 291–299. [Google Scholar] [CrossRef]
- Karthika, M.R.; Deb, A.; Venkatesh, G.S. An investigation into mechanical properties of jute–polyester laminates for numerical prediction of strength and failure. Polym. Compos. 2021, 42, 5975–5999. [Google Scholar] [CrossRef]
- Marcuello, C.; Chabbert, B.; Berzin, F.; Bercu, N.B.; Molinari, M.; Aguié-Béghin, V. Influence of Surface Chemistry of Fiber and Lignocellulosic Materials on Adhesion Properties with Polybutylene Succinate at Nanoscale. Materials 2023, 16, 2440. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, X.; Li, J.; Su, S.; Jiang, N. Prediction Models of Mechanical Properties of Jute/PLA Composite Based on X-ray Computed Tomography. Polymers 2024, 16, 160. https://doi.org/10.3390/polym16010160
Zhao X, Li J, Su S, Jiang N. Prediction Models of Mechanical Properties of Jute/PLA Composite Based on X-ray Computed Tomography. Polymers. 2024; 16(1):160. https://doi.org/10.3390/polym16010160
Chicago/Turabian StyleZhao, Xintao, Junteng Li, Shangbin Su, and Ning Jiang. 2024. "Prediction Models of Mechanical Properties of Jute/PLA Composite Based on X-ray Computed Tomography" Polymers 16, no. 1: 160. https://doi.org/10.3390/polym16010160
APA StyleZhao, X., Li, J., Su, S., & Jiang, N. (2024). Prediction Models of Mechanical Properties of Jute/PLA Composite Based on X-ray Computed Tomography. Polymers, 16(1), 160. https://doi.org/10.3390/polym16010160




