Mechanical Behavior of Closed-Cell Ethylene-Vinyl Acetate Foam under Compression
Abstract
:1. Introduction
2. Experimental Principles
2.1. Test Standards
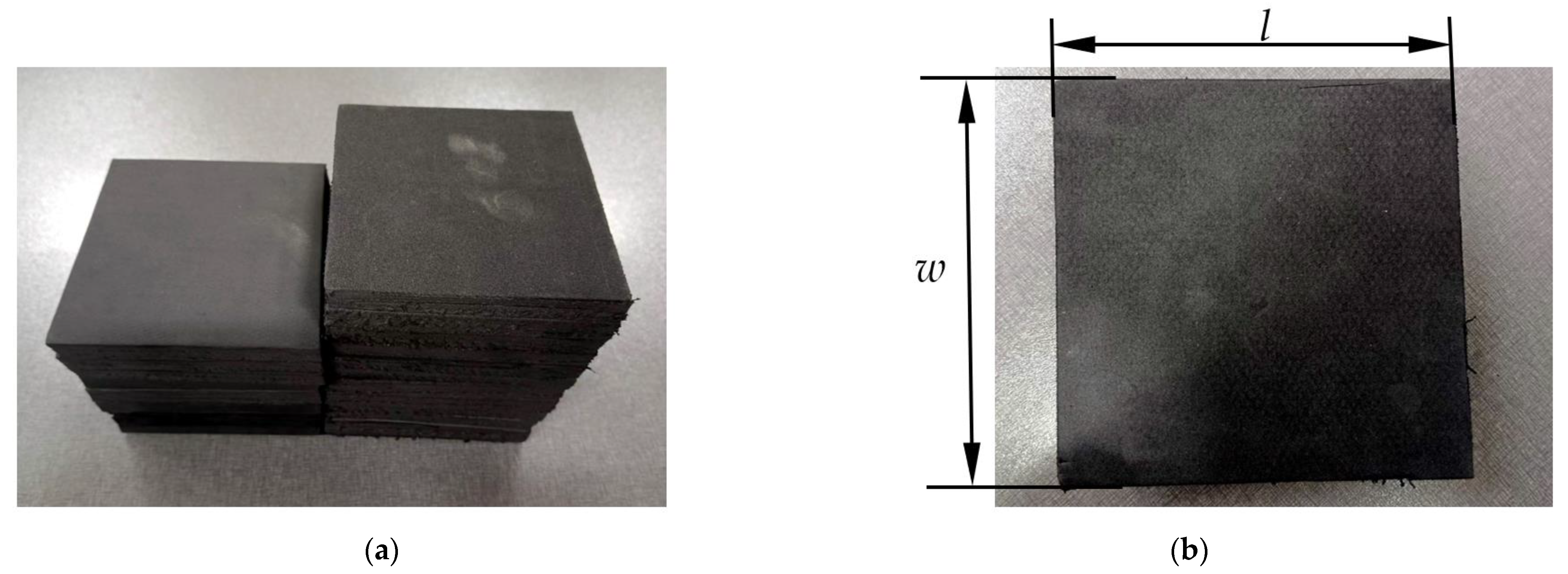
2.2. Specimens
2.3. Testing Devices
2.4. Experimental Schemes
3. Data analysis Methods
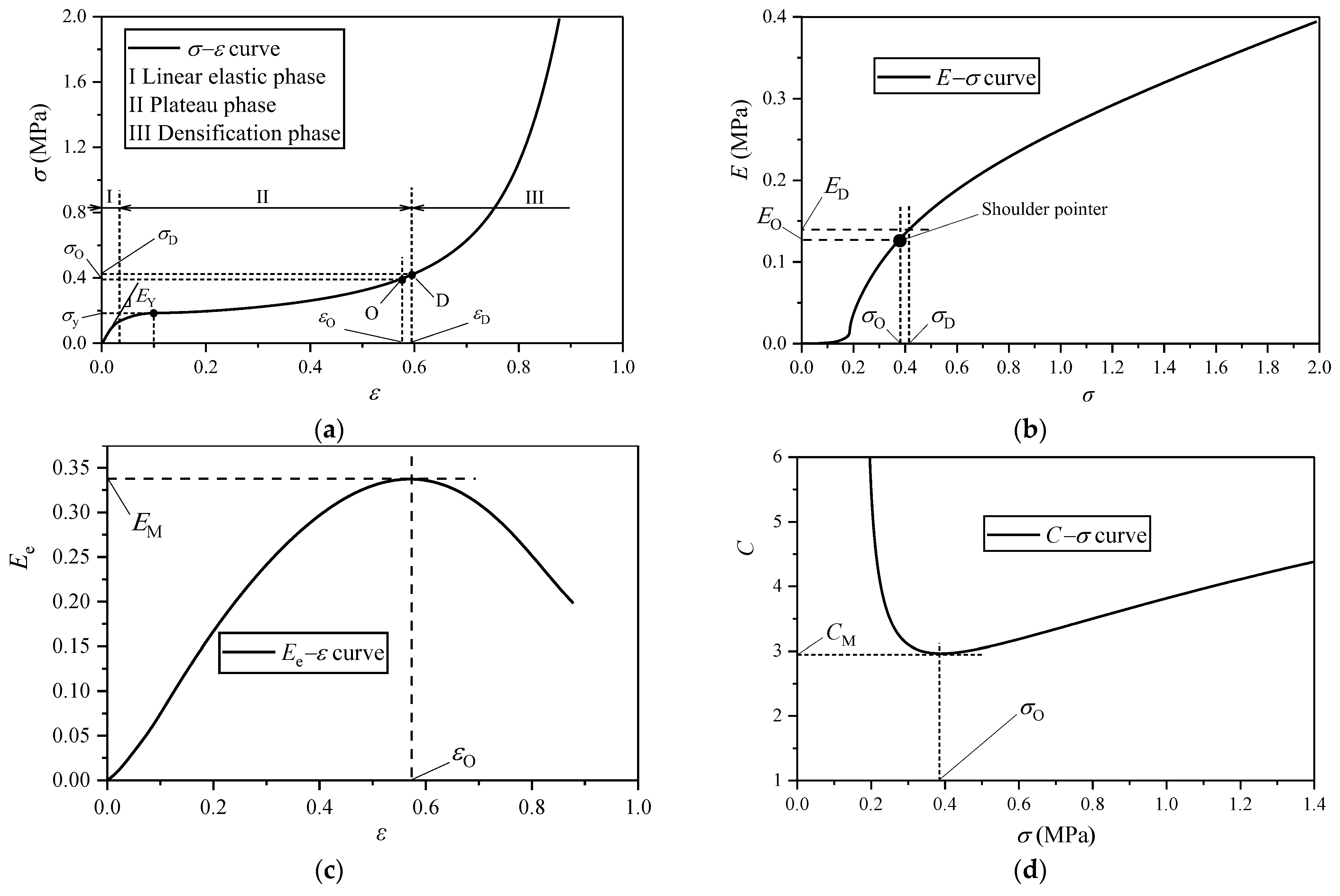
3.1. Generation of Response Curves
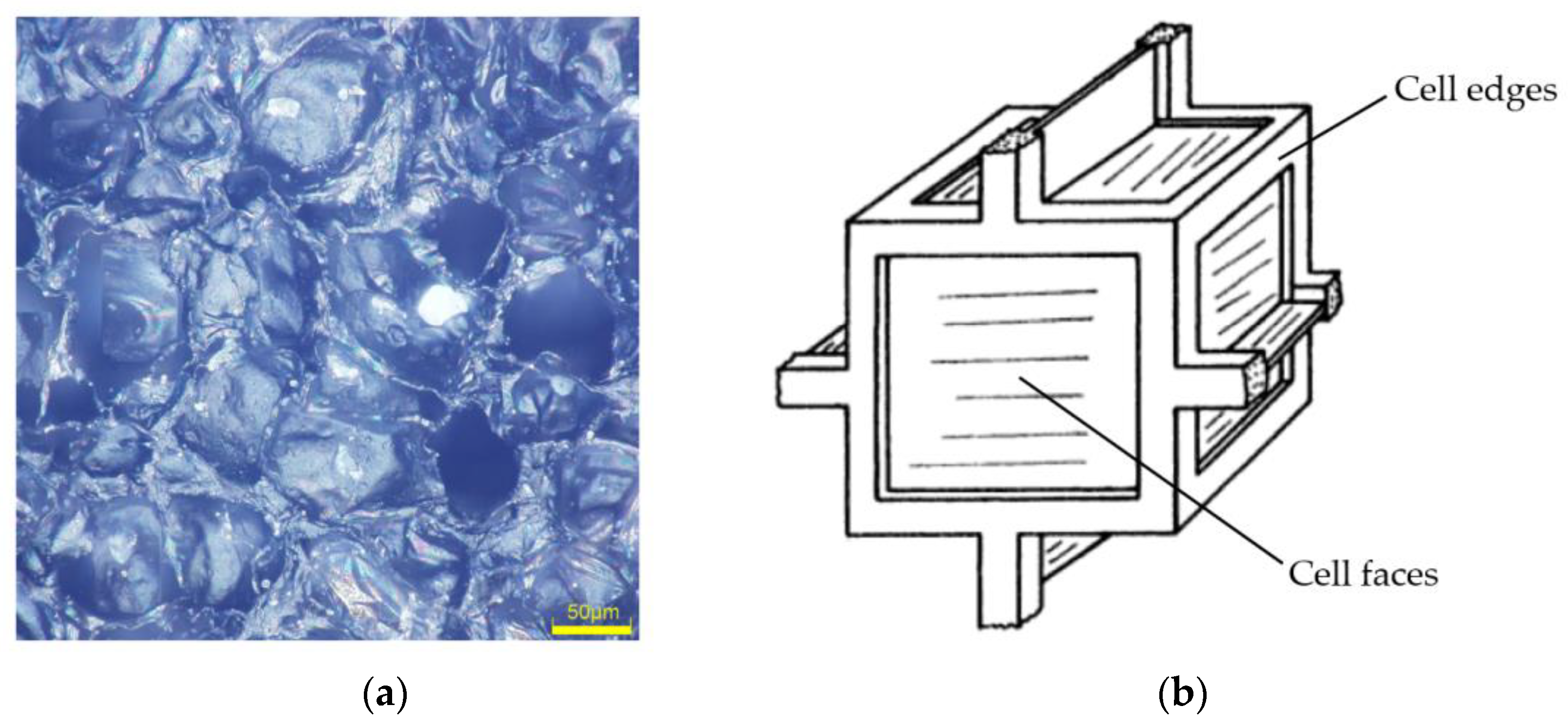
3.2. Equivalent Mechanical Model of Closed-Cell Foam
3.3. Evaluation Indicators
4. Results and Analysis
4.1. Stress−Strain Curves
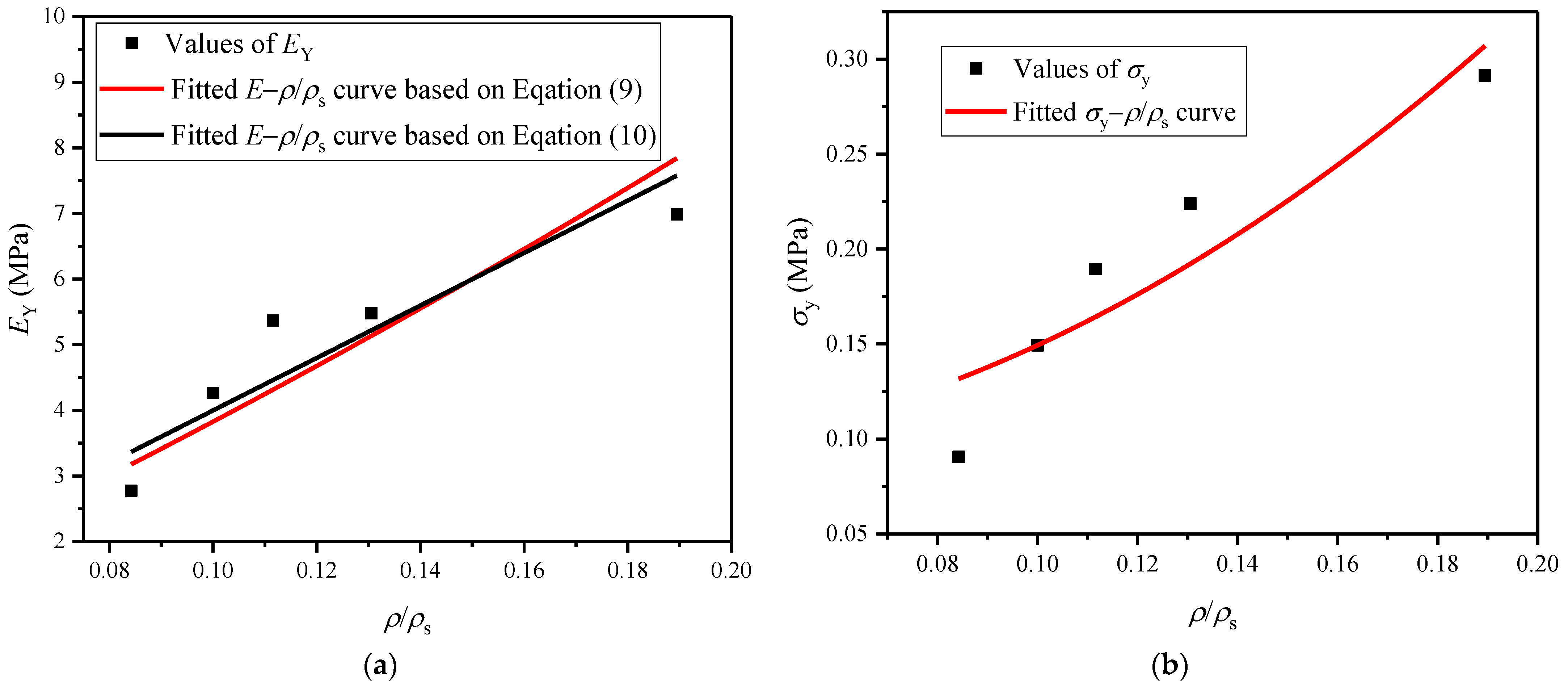
4.1.1. Influence of Density
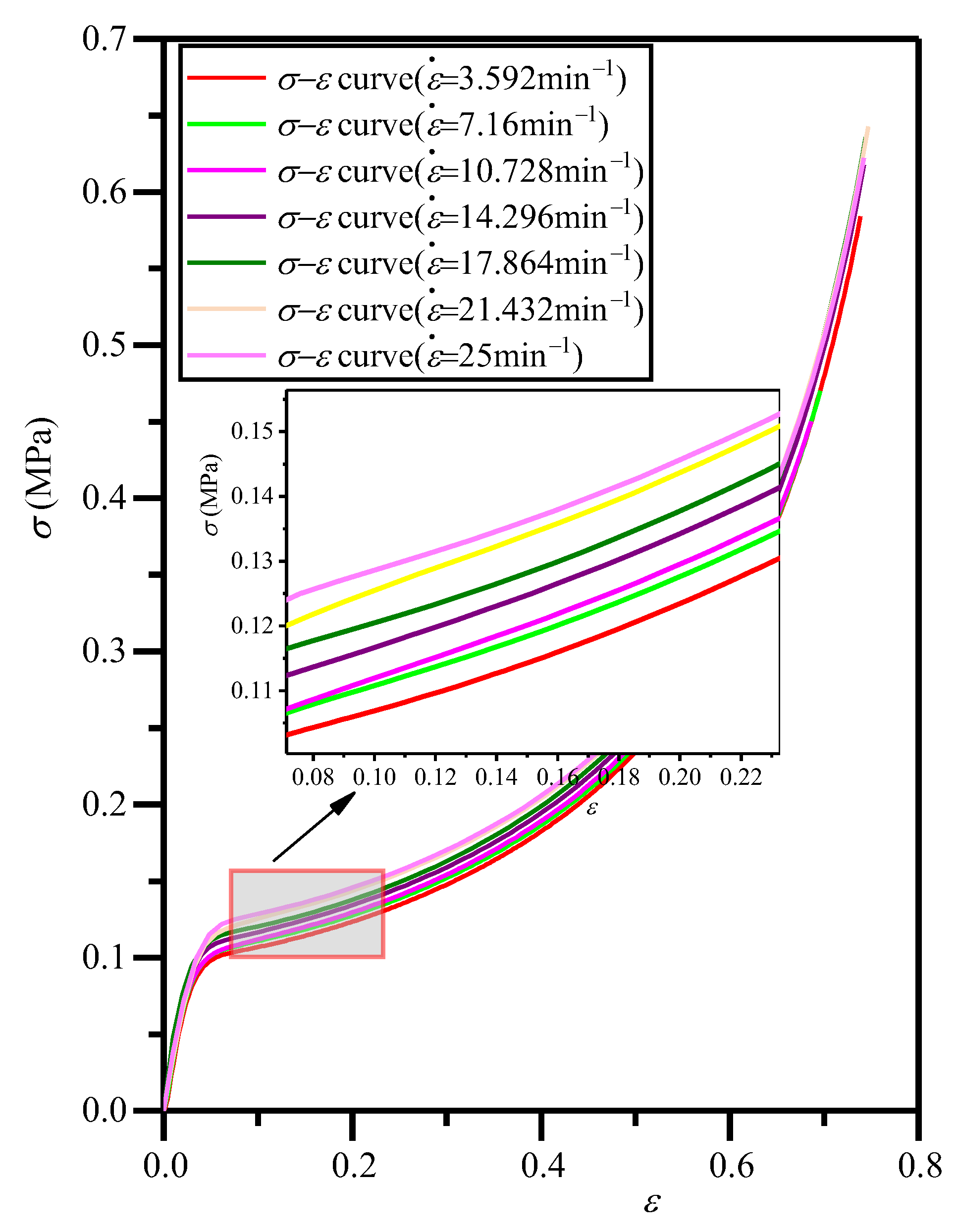
4.1.2. Influence of Strain Rate
4.2. Energy Absorption Efficiency
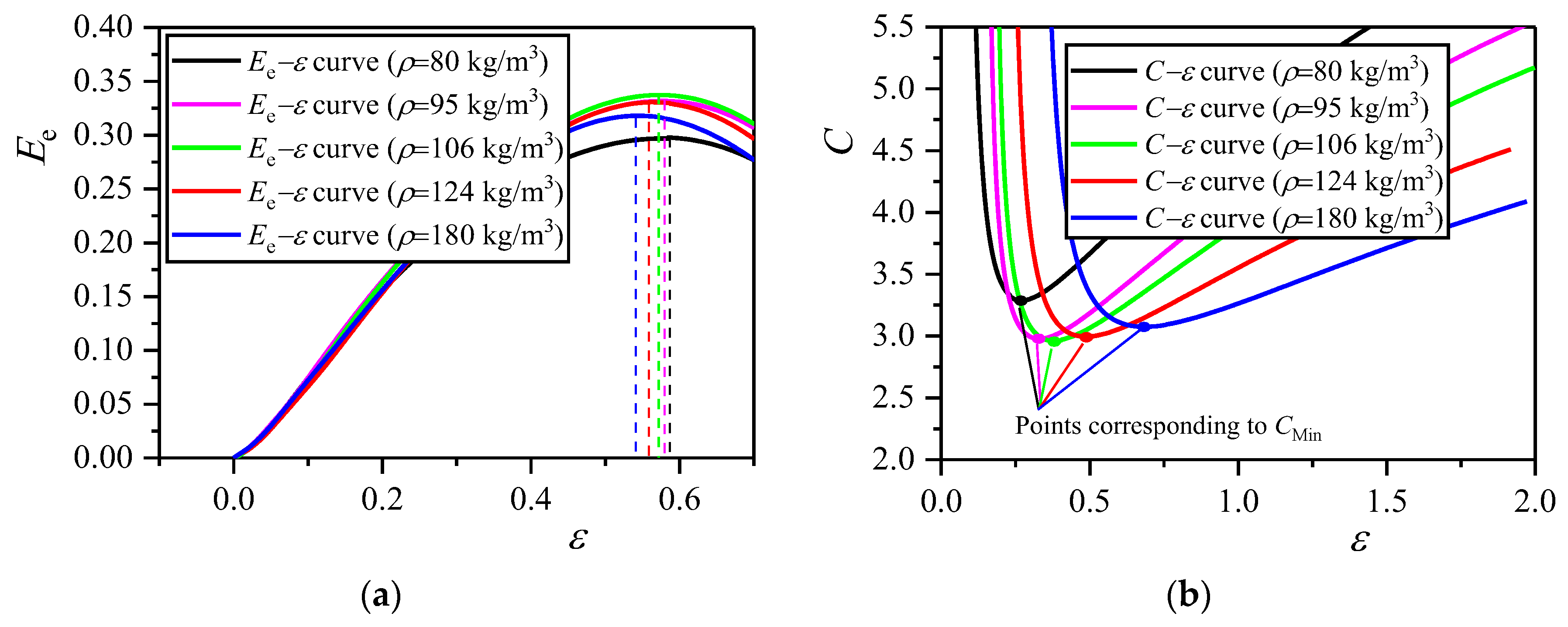
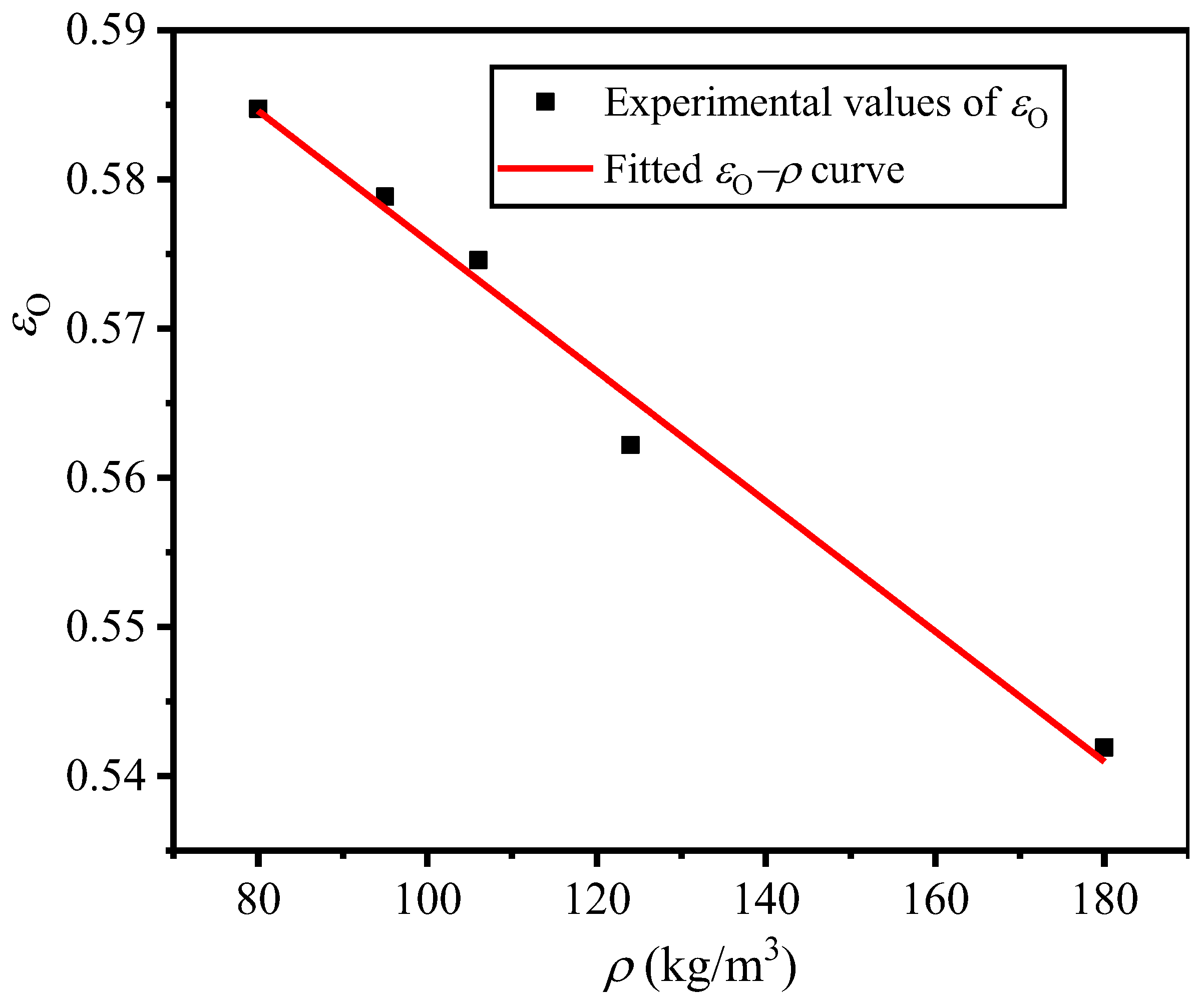
4.2.1. Influence of Density
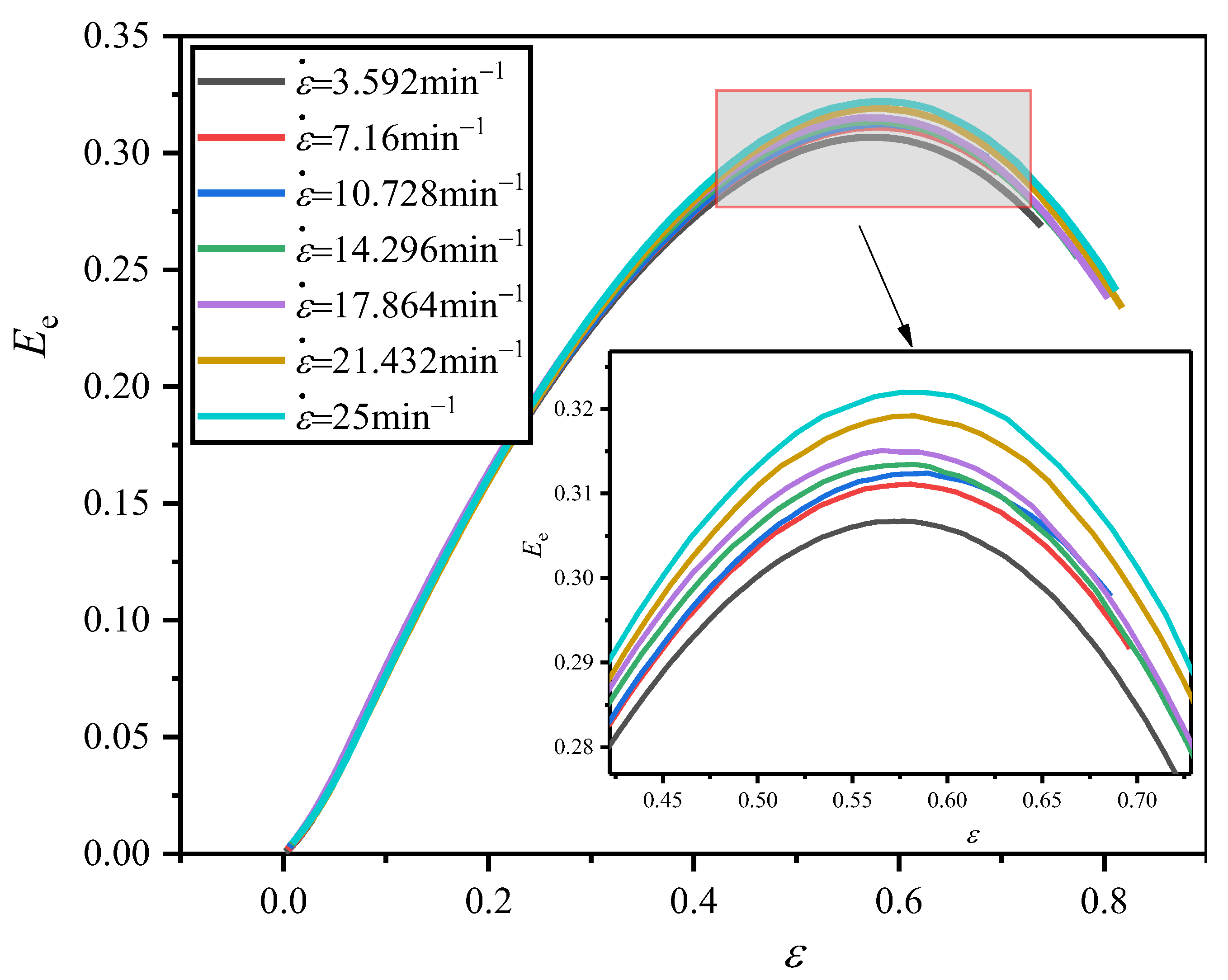
4.2.2. Influence of Strain Rate
4.3. Energy Absorption Diagram
4.3.1. Influence of Density
4.3.2. Influence of Strain Rate
5. Conclusions
- (1)
- The influences of density and strain rate on the σ−ε curve, elastic modulus, and yield stress of EVA foam are disclosed. Under a certain compressive strain rate, the EVA foam with a higher density has a larger stress and energy absorption, elastic modulus, and yield strength, and the whole σ−ε curve can be fitted with the Rusch formula. The strain rate does not change the shape of σ−ε curve and the elastic modulus is not sensitive to strain rate. For the EVA foam with a constant density, the higher the strain rate, the higher the yield strength and energy absorption.
- (2)
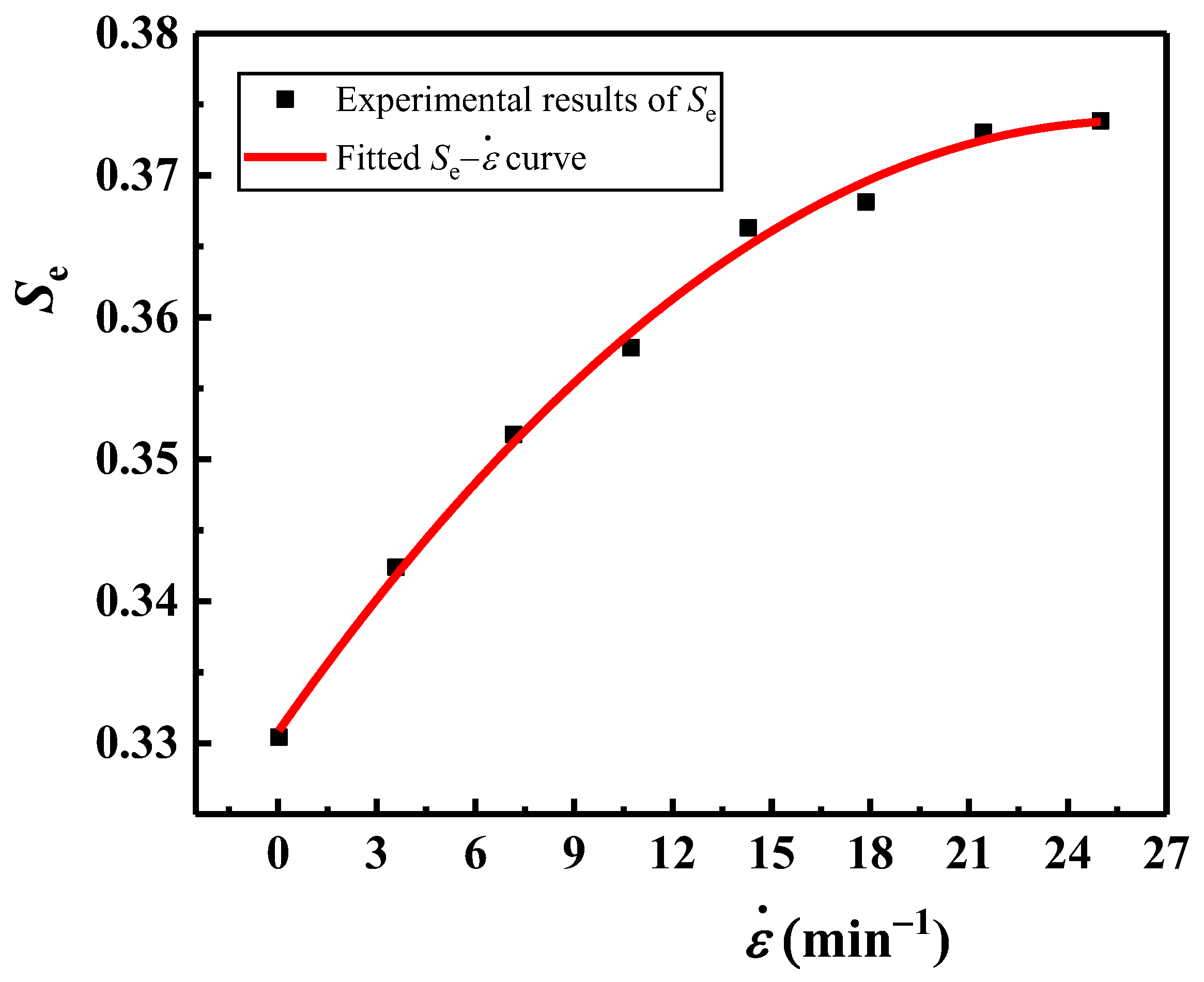
- The dependence relationship of maximum energy absorption efficiency and optical strain on density and strain rate were discovered. Under a certain strain rate, with the density increase in EVA foam, the EM value first increases and then decreases. Meanwhile, the CM value first decreases and then increases, the εO and εD values decrease, but εO becomes closer to εD. There is an optimal density corresponding to the maximum value of EM and the minimum value of CM. With the increase in strain rate, for the EVA foam with a given density, the stress in the plateau stage increases. Meanwhile, the εO value also increases, which leads to the increase in EM and the decrease in CM.
- (3)
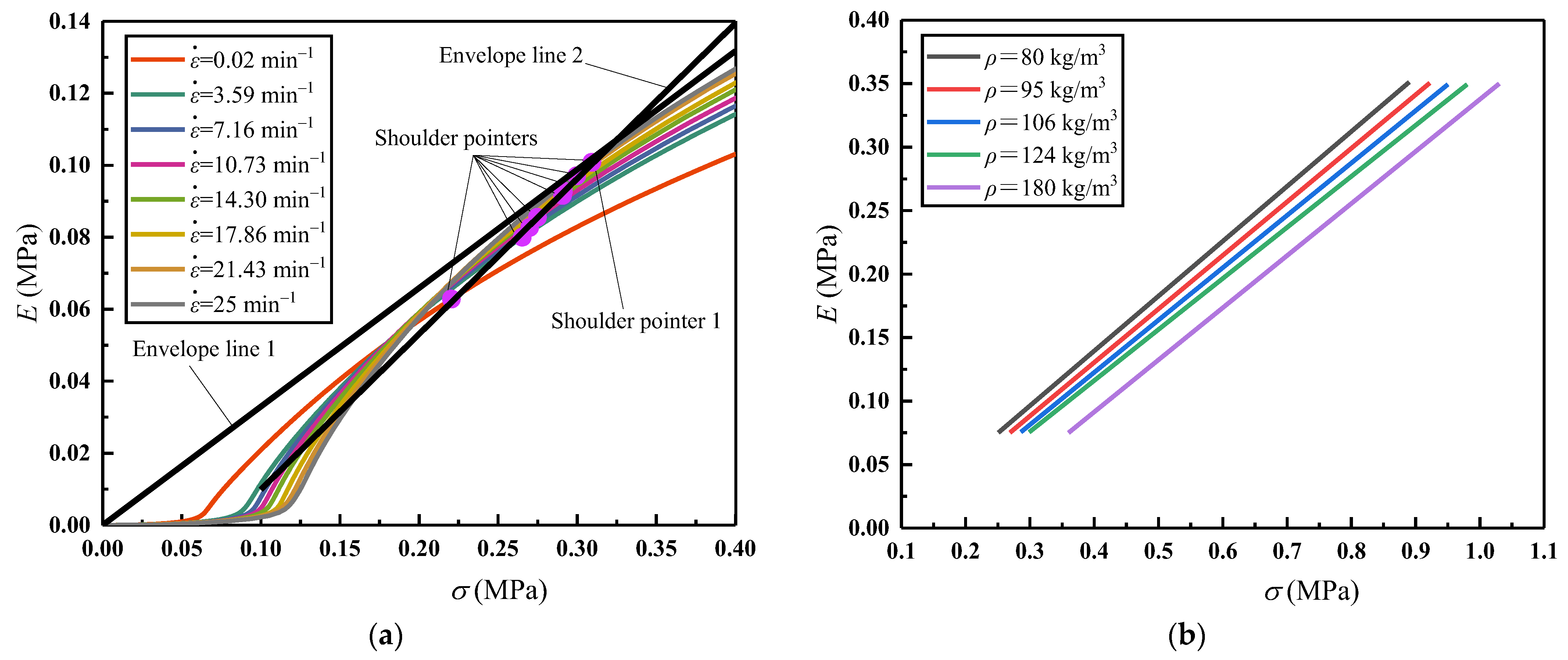
- Concrete energy absorption diagrams of EVA foams with different densities under various strain rates are depicted. Under a certain strain rate, the optical energy absorption per unit volume on the envelope line of E−σ curves of EVA foams with different densities is proportional to the optical stress. The change in strain rate leads to the larger slope and negative intercept of the envelope line of the E−σ curves for the EVA foam specimens with a constant density. But, the optical energy absorption per unit volume on the envelope line still linearly depends on the optical stress.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rosa, V.B.; Zattera, A.J.; Poletto, M. Evaluation of different mechanical recycling methods of EVA foam waste. J. Elastom. Plast. 2021, 53, 841–860. [Google Scholar] [CrossRef]
- Rumianek, P.; Dobosz, T.; Nowak, R.; Dziewit, P.; Aromiński, A. Static mechanical properties of expanded polypropylene crushable foam. Materials 2021, 14, 249. [Google Scholar] [CrossRef] [PubMed]
- Lutfi, S.N.N.; Razak, N.A.A.; Ali, S.; Gholizadeh, H. Compression and tension behavior of the prosthetic foam materials polyurethane, EVA, Pelite™ and a combination of polyurethane and EVA: A preliminary study. Biomed. Eng. Biomed. Tech. 2020, 66, 317–322. [Google Scholar] [CrossRef] [PubMed]
- Xin, Z.D. The reciprocating compression properties and life prediction of the elastomer foaming materials. Master’s Thesis, Qingdao University of Science and Technology, Qingdao, China, 2021. [Google Scholar]
- Wen, S.; Xin, Z.; Phule, A.D.; Zhang, Z.X. Microcellular ethylene-vinyl acetate copolymer foam: Life prediction under reciprocating compression. Adv. Eng. Mater. 2022, 24, 2101089. [Google Scholar] [CrossRef]
- Duncan, O.; Bailly, N.; Allen, T.; Petit, Y.; Wagnac, E.; Alderson, A. Effect of Compressive Strain Rate on Auxetic Foam. Appl. Sci. 2021, 11, 1207. [Google Scholar] [CrossRef]
- Liu, D.S.; Chen, Z.H.; Tsai, C.Y.; Ye, R.J.; Yu, K.T. Compressive mechanical property analysis of EVA foam: Its buffering effects at different impact velocities. J. Mech. 2017, 33, 435–441. [Google Scholar] [CrossRef]
- Ye, C.X.; Wang, Z.W. Characterization of energy absorption characteristics of foam buffer materials of EPE and EVA. Packag. Eng. 2012, 33, 40–45. [Google Scholar]
- Verdejo, R.; Mills, N.J. Heel-shoe interactions and the durability of EVA foam running-shoe midsoles. J. Biomech. 2004, 37, 1379–1386. [Google Scholar] [CrossRef] [PubMed]
- Lam, C.; Kwan, J.S.H.; Su, Y.; Choi, C.E.; Ng, C.W.W. Performance of ethylene-vinyl acetate foam as cushioning material for rigid debris-resisting barriers. Landslides 2018, 15, 1779–1786. [Google Scholar] [CrossRef]
- ASTM International. Standard Test Method for Compressive Properties of Rigid Cellular Plastics. Available online: https://www.astm.org/d1621-16r23.html (accessed on 24 May 2023).
- International Organization for Standardization. Rigid Cellular Plastics-Determination of Compression Properties. Available online: https://www.iso.org/standard/73560.html (accessed on 28 May 2023).
- National Standard of the People’s Republic of China. Rigid Cellular Plastics-Determination of Compression Properties (Text of Document is in Chinese). Available online: https://webstore.ansi.org/standards/spc/gb88132020 (accessed on 28 June 2023).
- National Standard of the People’s Republic of China. Testing Methods of Static Compression for Package Cushioning Materials. Available online: https://webstore.ansi.org/standards/spc/gb81682008 (accessed on 14 March 2023).
- Duarte, A.P.C.; Mazzuca, P.; Lopo de Carvalho, J.M.; Tiago, C.; Firmo, J.P.; Correia, J.R. Determination of the temperature-dependent thermophysical properties of polymeric foams using numerical inverse analysis. Constr. Build. Mater. 2023, 349, 131980. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, R.; Li, X.; Lu, C.; Wang, Z.; Wang, W. Energy absorption performance of open-cell aluminum foam and its application in landing buffer system. J. Mater. Eng. Perform. 2021, 30, 6132–6145. [Google Scholar] [CrossRef]
- National Standard of the People’s Republic of China. Packaging-Basic Tests for Transport Packages-Part 2: Temperature and Humidity Conditioning. Available online: https://webstore.ansi.org/standards/spc/gb48572005 (accessed on 16 March 2023).
- Miltz, J.; Gruenbaum, G. Evaluation of cushioning properties of plastic foams from compressive measurements. Polym. Eng. Sci. 1981, 21, 1010–1014. [Google Scholar] [CrossRef]
- Peng, G.; Guo, Y.; Shi, Z.; Li, X.; Zhou, D.; Zhang, B.; Gong, G.; Hu, G.; Han, X.; Chen, Z. Logistics Transportation Packaging Design, 2nd ed.; Printing industry Press: Beijing, China, 2012; pp. 106–139. [Google Scholar]
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure and Properties, 2nd ed.; Cambridge University Press: Cambridge, UK, 1997; pp. 175–343. [Google Scholar]
- Simone, A.E.; Gibson, L.J. Effects of solid distribution on the stiffness and strength of metallic foams. Acta Mater. 1998, 46, 2139–2150. [Google Scholar] [CrossRef]
- Li, X.; Li, Z.; Zhang, D. Compression performance of closed-cell aluminium foam under different temperatures and strain rates. J. Vib. Shock. 2020, 39, 17–21, 29. [Google Scholar]
- Miralbes, R.; Higuera, S.; Ranz, D.; Gomez, J.A. Comparative analysis of mechanical properties and energy absorption capabilities of functionally graded and non-graded thermoplastic sheet gyroid structures. Mech. Adv. Mater. Struct. 2022, 29, 5142–5155. [Google Scholar] [CrossRef]




| ρ (kg/m3) | EY (MPa) | σy (MPa) |
|---|---|---|
| 80 | 2.7734 | 0.0905 |
| 95 | 4.2659 | 0.1493 |
| 106 | 5.3702 | 0.1894 |
| 124 | 5.4784 | 0.2239 |
| 180 | 6.9843 | 0.2914 |
| (min−1) | E* (MPa) | σ*y (MPa) |
|---|---|---|
| 3.592 | 3.0046 | 0.107 |
| 7.16 | 3.0929 | 0.1113 |
| 10.728 | 3.3872 | 0.1123 |
| 14.296 | 3.1872 | 0.1172 |
| 17.864 | 3.512 | 0.1217 |
| 21.432 | 3.0608 | 0.1259 |
| 25 | 3.092 | 0.1291 |
| ρ (kg/m3) | EM | εO | CM | εD |
|---|---|---|---|---|
| 80 | 0.298 | 0.5847 | 3.3559 | 0.8821 |
| 95 | 0.3319 | 0.5789 | 3.0131 | 0.86 |
| 106 | 0.3374 | 0.5746 | 2.9637 | 0.8438 |
| 124 | 0.3306 | 0.5622 | 3.0244 | 0.8173 |
| 180 | 0.3181 | 0.5419 | 3.1438 | 0.7347 |
| (min−1) | EM | εO |
|---|---|---|
| 3.592 | 0.3067 | 0.5758 |
| 7.16 | 0.3111 | 0.5808 |
| 10.728 | 0.3124 | 0.5838 |
| 14.296 | 0.3134 | 0.5841 |
| 17.864 | 0.3149 | 0.5851 |
| 21.432 | 0.3192 | 0.5829 |
| 25 | 0.3219 | 0.5895 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, H.; Sun, D.; Gao, L.; Liu, X.; Zhang, M. Mechanical Behavior of Closed-Cell Ethylene-Vinyl Acetate Foam under Compression. Polymers 2024, 16, 34. https://doi.org/10.3390/polym16010034
Chen H, Sun D, Gao L, Liu X, Zhang M. Mechanical Behavior of Closed-Cell Ethylene-Vinyl Acetate Foam under Compression. Polymers. 2024; 16(1):34. https://doi.org/10.3390/polym16010034
Chicago/Turabian StyleChen, Hongjuan, Deqiang Sun, Lulu Gao, Xiaochen Liu, and Meilin Zhang. 2024. "Mechanical Behavior of Closed-Cell Ethylene-Vinyl Acetate Foam under Compression" Polymers 16, no. 1: 34. https://doi.org/10.3390/polym16010034
APA StyleChen, H., Sun, D., Gao, L., Liu, X., & Zhang, M. (2024). Mechanical Behavior of Closed-Cell Ethylene-Vinyl Acetate Foam under Compression. Polymers, 16(1), 34. https://doi.org/10.3390/polym16010034





