Liquid Crystal Orientation and Shape Optimization for the Active Response of Liquid Crystal Elastomers
Abstract
:1. Introduction
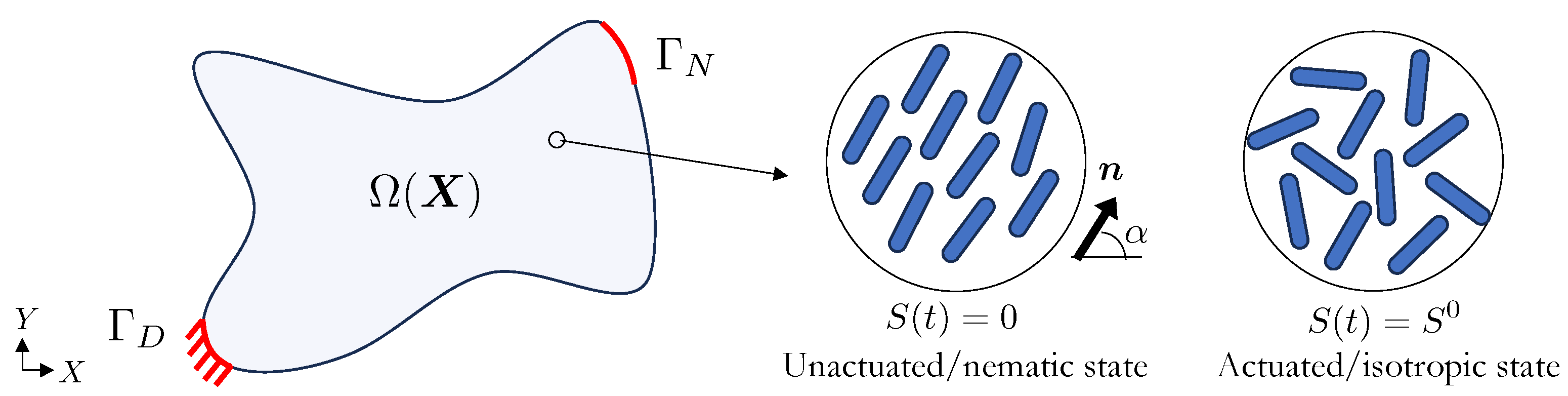
2. Problem Description
2.1. Design Parameterization
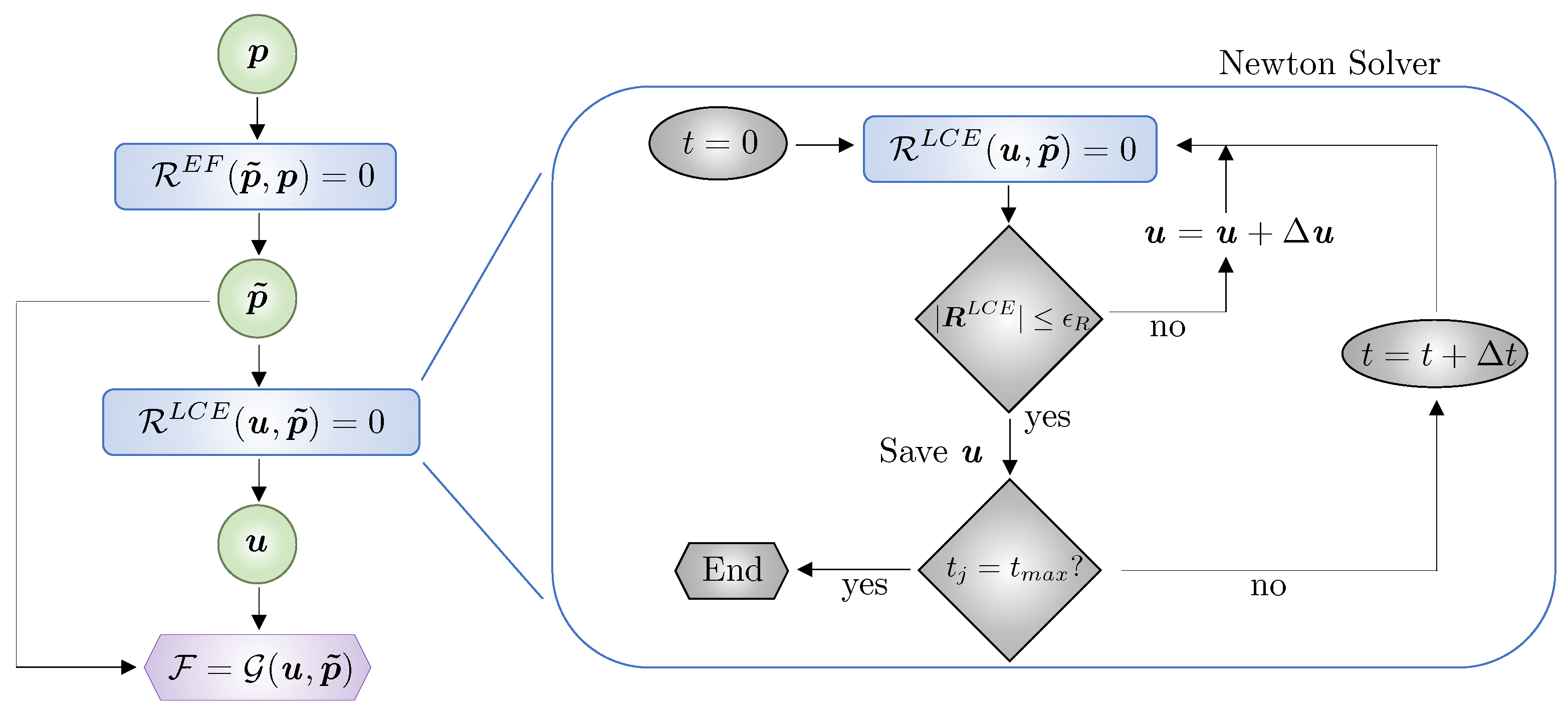
2.2. Filter Analysis
2.3. LCE Forward Analysis
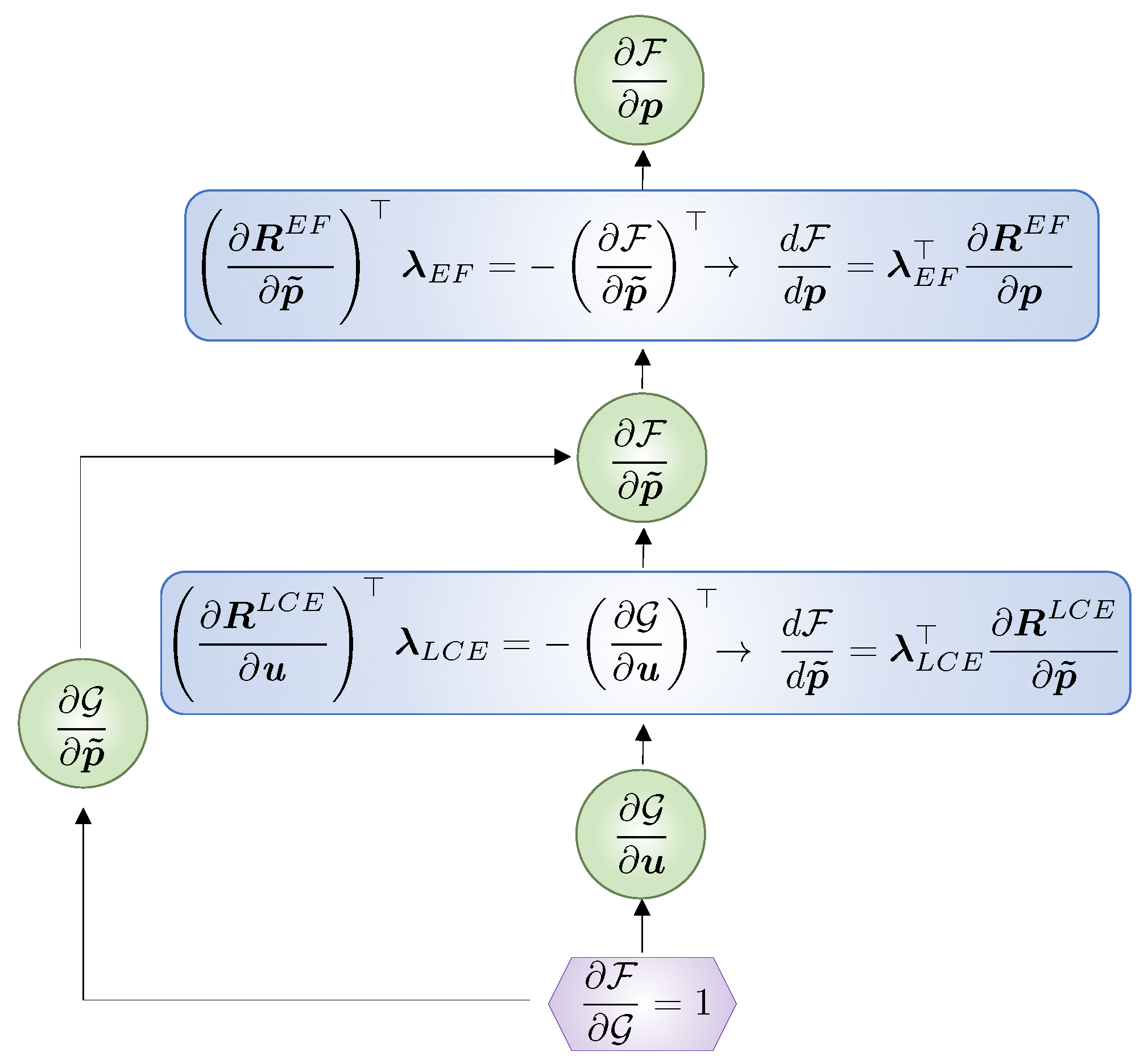
3. Optimization Framework
4. Case Studies
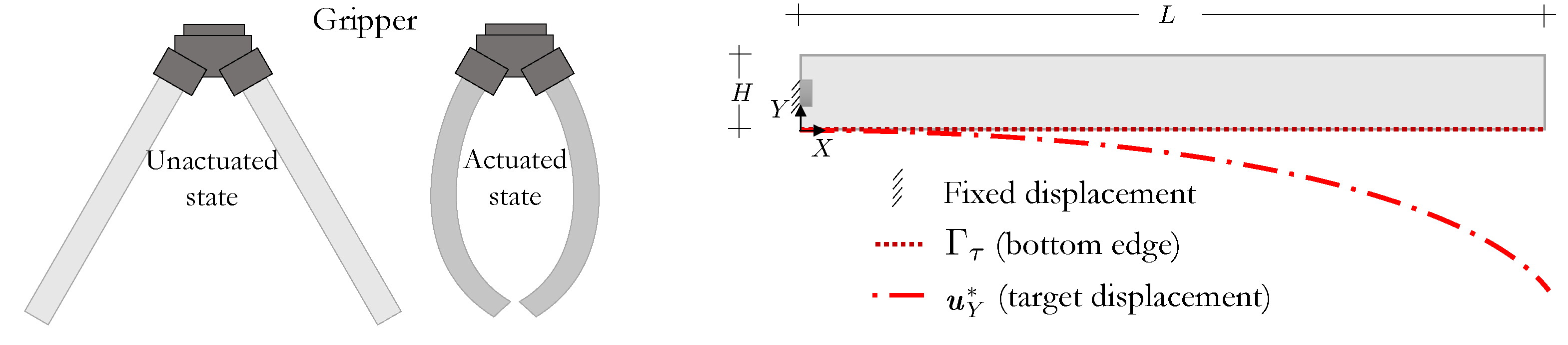
4.1. Lc Orientation Optimization of Soft Gripper
4.2. Shape Optimization of a Leaping LCE Strip
4.3. LC Orientation and Shape Optimization for Energy Absorbing Lattice Structures
4.4. Actuation-Driven Compliant Mechanism Design Optimization
5. Discussion and Future Work
- The constitutive model selection can be a difficult task for the simulation of LCEs, and responsive materials in general. Advanced applications such as controlled locomotion [1,3] require intricate material models (e.g., mutiscale modeling [52,62,63]) to accurately predict the LCE motion. These may require heat transfer simulations to design thermally actuated LCEs, for example. Furthermore, given the diverse stimuli that LCEs respond to, the constitutive model employed must accurately capture their multi-stimuli response in optimization scenarios where designs are influenced by more than one stimulus. Other physical phenomena such as rate effects may also need to be considered, e.g., high strain rate compression/impact. Fortunately, emerging AI-based trends can ease some of this burden. For example, machine learning can help characterize LCE materials and provide more accurate constitutive models [64]. Progress has been made in physics-informed neural networks (PINNs) for hyperelastic materials [65,66], and strategies to generate models that obey the laws of physics are being explored under the umbrella of constitutive artificial neural networks (CANNs, [67,68]). Once open questions regarding data quality and diversity for multi-physics responses are resolved, future developments could integrate classical physics-based methods with the mentioned emerging machine learning methods to more accurately simulate these complex materials.
- Simulation challenges associated with the robust numerical analysis of complex geometries, nontrivial time-dependent boundary and interface conditions, including contact, and parameterized material properties and shapes, need to be addressed. Appropriate linear and nonlinear solvers, and preconditioning strategies must be selected as well as stabilization terms added to avoid undesirable pathologies, e.g., spurious oscillations, and locking [69,70]. Existing literature directed towards this issue for LCEs or similar responsive structures is lacking, except in the context of simplified benchmarks [52].
- Implementing adjoint sensitivity analysis that can accommodate the dynamic nature of advanced systems (e.g., controlled actuation in time of an LCE structure) introduces another challenge, notably efficient check-pointing schemes [71]. Three-dimensional design applications characterized by extensive arrays of design parameters call for approaches that transcend rudimentary high-level programming or reliance on commercial software [72]. Implementations must use alternative HPC simulation and design libraries and AD tools to solve more complex engineering problems.
- Alternative shape optimization methodologies using the level set method (LSM, [73,74,75]) allow for topological changes and thus, potentially generate better performing designs. The increased design freedom of LSMs is also favorable for designing systems for which a suitable initial design is unknown, or organic geometries are expected (e.g., biomimicry engineering). For LCE structures, the more flexible parameterization offered by LSMs can accommodate additional manufacturing constraints such as aligning the LC fibers with the printing direction. However, considerable additional effort both in the analysis and optimization is needed to guarantee a robust framework [76,77,78].
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ford, M.J.; Porcincula, D.H.; Telles, R.; Mancini, J.A.; Wang, Y.; Rizvi, M.H.; Loeb, C.K.; Moran, B.D.; Tracy, J.B.; Lewis, J.A.; et al. Movement with light: Photoresponsive shape morphing of printed liquid crystal elastomers. Matter 2024, 7, 1207–1229. [Google Scholar] [CrossRef]
- Yuan, C.; Roach, D.J.; Dunn, C.K.; Mu, Q.; Kuang, X.; Yakacki, C.M.; Wang, T.; Yu, K.; Qi, H.J. 3D printed reversible shape changing soft actuators assisted by liquid crystal elastomers. Soft Matter 2017, 13, 5558–5568. [Google Scholar] [CrossRef]
- Hebner, T.S.; Korner, K.; Bowman, C.N.; Bhattacharya, K.; White, T.J. Leaping liquid crystal elastomers. Sci. Adv. 2023, 9, eade1320. [Google Scholar] [CrossRef] [PubMed]
- Konya, A.; Gimenez-Pinto, V.; Selinger, R.L. Modeling defects, shape evolution, and programmed auto-origami in liquid crystal elastomers. Front. Mater. 2016, 3, 24. [Google Scholar] [CrossRef]
- Sydney Gladman, A.; Matsumoto, E.A.; Nuzzo, R.G.; Mahadevan, L.; Lewis, J.A. Biomimetic 4D printing. Nat. Mater. 2016, 15, 413–418. [Google Scholar] [CrossRef] [PubMed]
- George, D.; Madou, M.J.; Hernandez, E.A.P. Programmable self-foldable films for origami-based manufacturing. Smart Mater. Struct. 2020, 30, 025012. [Google Scholar] [CrossRef]
- Kotikian, A.; Morales, J.M.; Lu, A.; Mueller, J.; Davidson, Z.S.; Boley, J.W.; Lewis, J.A. Innervated, self-sensing liquid crystal elastomer actuators with closed loop control. Adv. Mater. 2021, 33, 2101814. [Google Scholar] [CrossRef]
- Doi, H.; Takahashi, K.Z.; Tagashira, K.; Fukuda, J.i.; Aoyagi, T. Machine learning-aided analysis for complex local structure of liquid crystal polymers. Sci. Rep. 2019, 9, 16370. [Google Scholar] [CrossRef] [PubMed]
- Hu, Q.; Chen, K.; Liu, F.; Zhao, M.; Liang, F.; Xue, D. Smart Materials Prediction: Applying Machine Learning to Lithium Solid-State Electrolyte. Materials 2022, 15, 1157. [Google Scholar] [CrossRef] [PubMed]
- Ortigosa, R.; Martínez-Frutos, J.; Gil, A.J. Programming shape-morphing electroactive polymers through multi-material topology optimisation. Appl. Math. Model. 2023, 118, 346–369. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Kim, J.; Alacoque, L.R.; James, K.A. Design Synthesis of a 4D-Printed Self-Tying Knot with Programmable Morphology. J. Mech. Des. 2024, 146. [Google Scholar] [CrossRef]
- Kirchdoerfer, T.; Ortiz, M. Data-driven computational mechanics. Comput. Methods Appl. Mech. Eng. 2016, 304, 81–101. [Google Scholar] [CrossRef]
- Kumar, S.; Kochmann, D.M. What machine learning can do for computational solid mechanics. In Current Trends and Open Problems in Computational Mechanics; Springer: Berlin/Heidelberg, Germany, 2022; pp. 275–285. [Google Scholar]
- Brodnik, N.; Muir, C.; Tulshibagwale, N.; Rossin, J.; Echlin, M.; Hamel, C.; Kramer, S.; Pollock, T.; Kiser, J.; Smith, C.; et al. Perspective: Machine learning in experimental solid mechanics. J. Mech. Phys. Solids 2023, 173, 105231. [Google Scholar] [CrossRef]
- Kang, Z.; James, K.A. Multiphysics design of programmable shape-memory alloy-based smart structures via topology optimization. Struct. Multidiscip. Optim. 2022, 65, 24. [Google Scholar] [CrossRef]
- Geiss, M.J.; Boddeti, N.; Weeger, O.; Maute, K.; Dunn, M.L. Combined Level-Set-XFEM-Density Topology Optimization of Four-Dimensional Printed Structures Undergoing Large Deformation. J. Mech. Des. 2019, 141, 051405. [Google Scholar] [CrossRef]
- Ortigosa, R.; Martínez-Frutos, J. Topology optimisation of stiffeners layout for shape-morphing of dielectric elastomers. Struct. Multidiscip. Optim. 2021, 64, 3681–3703. [Google Scholar] [CrossRef]
- Fuchi, K.; Ware, T.H.; Buskohl, P.R.; Reich, G.W.; Vaia, R.A.; White, T.J.; Joo, J.J. Topology optimization for the design of folding liquid crystal elastomer actuators. Soft Matter 2015, 11, 7288–7295. [Google Scholar] [CrossRef] [PubMed]
- Yan, J.; Xiang, R.; Kamensky, D.; Tolley, M.T.; Hwang, J.T. Topology optimization with automated derivative computation for multidisciplinary design problems. Struct. Multidiscip. Optim. 2022, 65, 151. [Google Scholar] [CrossRef]
- Koda, M.; Dogru, A.H.; Seinfeld, J.H. Sensitivity analysis of partial differential equations with application to reaction and diffusion processes. J. Comput. Phys. 1979, 30, 259–282. [Google Scholar] [CrossRef]
- Tortorelli, D.A.; Michaleris, P. Design sensitivity analysis: Overview and review. Inverse Probl. Eng. 1994, 1, 71–105. [Google Scholar] [CrossRef]
- Van Keulen, F.; Haftka, R.; Kim, N.H. Review of options for structural design sensitivity analysis. Part 1: Linear systems. Comput. Methods Appl. Mech. Eng. 2005, 194, 3213–3243. [Google Scholar] [CrossRef]
- Allaire, G. A review of adjoint methods for sensitivity analysis, uncertainty quantification and optimization in numerical codes. Ing. L’Automob. 2015, 836, 33–36. [Google Scholar]
- Sienz, J.; Hinton, E. Reliable structural optimization with error estimation, adaptivity and robust sensitivity analysis. Comput. Struct. 1997, 64, 31–63. [Google Scholar] [CrossRef]
- vom Lehn, F.; Cai, L.; Pitsch, H. Sensitivity analysis, uncertainty quantification, and optimization for thermochemical properties in chemical kinetic combustion models. Proc. Combust. Inst. 2019, 37, 771–779. [Google Scholar] [CrossRef]
- Borgonovo, E.; Plischke, E. Sensitivity analysis: A review of recent advances. Eur. J. Oper. Res. 2016, 248, 869–887. [Google Scholar] [CrossRef]
- Barrera Cruz, J.L.; Maute, K.K. Immersed Boundary Analysis of Models with Internal State Variables: Applications to Hydrogels. In Proceedings of the ECCOMAS Congress 2022—8th European Congress on Computational Methods in Applied Sciences and Engineering, Oslo, Norway, 5–9 June 2022. [Google Scholar]
- Chung, S.H.; Fourment, L.; Chenot, J.L.; Hwang, S. Adjoint state method for shape sensitivity analysis in non-steady forming applications. Int. J. Numer. Methods Eng. 2003, 57, 1431–1444. [Google Scholar] [CrossRef]
- Wang, W.; Clausen, P.M.; Bletzinger, K.U. Efficient adjoint sensitivity analysis of isotropic hardening elastoplasticity via load steps reduction approximation. Comput. Methods Appl. Mech. Eng. 2017, 325, 612–644. [Google Scholar] [CrossRef]
- Ozaki, I.; Kimura, F.; Berz, M. Higher-order sensitivity analysis of finite element method by automatic differentiation. Comput. Mech. 1995, 16, 223–234. [Google Scholar] [CrossRef]
- Hou, G.; Satyanarayana, A.; Tiwari, S. First-and second-order sensitivity analysis of finite element equations via automatic differentiation. In Proceedings of the 7th AIAA/USAF/NASA/ISSMO Symposium on Multidisciplinary Analysis and Optimization, St. Louis, MO, USA, 2–4 September 1998; p. 4764. [Google Scholar]
- Rathgeber, F.; Ham, D.A.; Mitchell, L.; Lange, M.; Luporini, F.; McRae, A.T.; Bercea, G.T.; Markall, G.R.; Kelly, P.H. Firedrake: Automating the finite element method by composing abstractions. ACM Trans. Math. Softw. (Toms) 2016, 43, 1–27. [Google Scholar] [CrossRef]
- Arndt, D.; Bangerth, W.; Davydov, D.; Heister, T.; Heltai, L.; Kronbichler, M.; Maier, M.; Pelteret, J.P.; Turcksin, B.; Wells, D. The deal. II finite element library: Design, features, and insights. Comput. Math. Appl. 2021, 81, 407–422. [Google Scholar] [CrossRef]
- Anderson, R.; Andrej, J.; Barker, A.; Bramwell, J.; Camier, J.S.; Cerveny, J.; Dobrev, V.; Dudouit, Y.; Fisher, A.; Kolev, T.; et al. MFEM: A modular finite element methods library. Comput. Math. Appl. 2021, 81, 42–74. [Google Scholar] [CrossRef]
- Bramwell, J.; White, C.; Essman, J.; Mish, S.; Chapman, A.; Talamini, B.; Wong, J.; Chin, E.; Tupek, M. Serac. 2023. Available online: https://github.com/LLNL/serac/ (accessed on 15 March 2024).
- Brighenti, R.; McMahan, C.G.; Cosma, M.P.; Kotikian, A.; Lewis, J.A.; Daraio, C. A micromechanical-based model of stimulus responsive liquid crystal elastomers. Int. J. Solids Struct. 2021, 219, 92–105. [Google Scholar] [CrossRef]
- Mihai, L.A.; Goriely, A. Instabilities in liquid crystal elastomers. Mrs Bull. 2021, 46, 784–794. [Google Scholar] [CrossRef]
- Bartels, S.; Griehl, M.; Keck, J.; Neukamm, S. Modeling and simulation of nematic LCE rods. arXiv 2022, arXiv:2205.15174. [Google Scholar]
- Lee, V.; Wihardja, A.; Bhattacharya, K. A macroscopic constitutive relation for isotropic-genesis, polydomain liquid crystal elastomers. J. Mech. Phys. Solids 2023, 179, 105369. [Google Scholar] [CrossRef]
- Finkelmann, H.; Greve, A.; Warner, M. The elastic anisotropy of nematic elastomers. Eur. Phys. J. 2001, 5, 281–293. [Google Scholar] [CrossRef]
- Mbanga, B.L.; Ye, F.; Selinger, J.V.; Selinger, R.L. Modeling elastic instabilities in nematic elastomers. Phys. Rev. 2010, 82, 051701. [Google Scholar] [CrossRef]
- Wang, Z.; Chehade, A.E.H.; Govindjee, S.; Nguyen, T.D. A nonlinear viscoelasticity theory for nematic liquid crystal elastomers. J. Mech. Phys. Solids 2022, 163, 104829. [Google Scholar] [CrossRef]
- Duffy, D.; McCracken, J.M.; Hebner, T.S.; White, T.J.; Biggins, J.S. Lifting, loading, and buckling in conical shells. Phys. Rev. Lett. 2023, 131, 148202. [Google Scholar] [CrossRef] [PubMed]
- Cosma, M.P.; Brighenti, R. Controlled morphing of architected liquid crystal elastomer elements: Modeling and simulations. Mech. Res. Commun. 2022, 121, 103858. [Google Scholar] [CrossRef]
- Mihai, L.A. Liquid Crystal Elastomers. In Stochastic Elasticity: A Nondeterministic Approach to the Nonlinear Field Theory; Springer: Berlin/Heidelberg, Germany, 2022; pp. 183–215. [Google Scholar]
- Bartels, S.; Griehl, M.; Neukamm, S.; Padilla-Garza, D.; Palus, C. A nonlinear bending theory for nematic LCE plates. Math. Model. Methods Appl. Sci. 2023, 33, 1437–1516. [Google Scholar] [CrossRef]
- Li, W.; Zhang, X.S. Arbitrary curvature programming of thermo-active liquid crystal elastomer via topology optimization. Comput. Methods Appl. Mech. Eng. 2023, 417, 116393. [Google Scholar] [CrossRef]
- Li, S.; Librandi, G.; Yao, Y.; Richard, A.J.; Schneider-Yamamura, A.; Aizenberg, J.; Bertoldi, K. Controlling liquid crystal orientations for programmable anisotropic transformations in cellular microstructures. Adv. Mater. 2021, 33, 2105024. [Google Scholar] [CrossRef]
- Zhu, W.; Shelley, M.; Palffy-Muhoray, P. Modeling and simulation of liquid-crystal elastomers. Phys. Rev. 2011, 83, 051703. [Google Scholar] [CrossRef] [PubMed]
- Luo, C.; Calderer, M.C. Numerical Study of Liquid Crystal Elastomer Using Mixed Finite Element Method. arXiv 2009, arXiv:0911.5415. [Google Scholar]
- Nochetto, R.H.; Walker, S.W.; Zhang, W. A finite element method for nematic liquid crystals with variable degree of orientation. Siam J. Numer. Anal. 2017, 55, 1357–1386. [Google Scholar] [CrossRef]
- Soltani, M.; Raahemifar, K.; Nokhosteen, A.; Kashkooli, F.M.; Zoudani, E.L. Numerical methods in studies of liquid crystal elastomers. Polymers 2021, 13, 1650. [Google Scholar] [CrossRef] [PubMed]
- Park, S.; Oh, Y.; Moon, J.; Chung, H. Recent Trends in Continuum Modeling of Liquid Crystal Networks: A Mini-Review. Polymers 2023, 15, 1904. [Google Scholar] [CrossRef] [PubMed]
- Holzapfel, G.A. Nonlinear Solid Mechanics: A Continuum Approach for Engineering Science; John Wiley & Sons: Chichester, UK, 2002. [Google Scholar]
- Swartz, K.E.; Mittal, K.; Schmidt, M.; Barrera, J.L.; Watts, S.; Tortorelli, D.A. Yet another parameter-free shape optimization method. Struct. Multidiscip. Optim. 2023, 66, 245. [Google Scholar] [CrossRef]
- Sigmund, O.; Maute, K. Topology optimization approaches. Struct. Multidiscip. Optim. 2013, 48, 1031–1055. [Google Scholar]
- Lazarov, B.S.; Sigmund, O. Filters in topology optimization based on Helmholtz-type differential equations. Int. J. Numer. Methods Eng. 2011, 86, 765–781. [Google Scholar] [CrossRef]
- Smith, D.E.; Tortorelli, D.A.; Tucker III, C.L. Optimal design for polymer extrusion. Part I: Sensitivity analysis for nonlinear steady-state systems. Comput. Methods Appl. Mech. Eng. 1998, 167, 283–302. [Google Scholar] [CrossRef]
- Ghysels, P.; Synk, R. High performance sparse multifrontal solvers on modern GPUs. Parallel Comput. 2022, 110, 102897. [Google Scholar] [CrossRef]
- Svanberg, K. The method of moving asymptotes—a new method for structural optimization. Int. J. Numer. Methods Eng. 1987, 24, 359–373. [Google Scholar] [CrossRef]
- LLNL. The Livermore Design Optimization (LiDO) Code. 2023. Available online: https://str.llnl.gov/2018-03 (accessed on 15 March 2024).
- Moon, J.; Shin, H.; Baek, K.; Choi, J.; Cho, M. Multiscale modeling of photomechanical behavior of photo-responsive nanocomposite with carbon nanotubes. Compos. Sci. Technol. 2018, 166, 27–35. [Google Scholar] [CrossRef]
- Kalina, K.A.; Ra<i>β</i>loff, A.; Wollner, M.; Metsch, P.; Brummund, J.; Kästner, M. Multiscale modeling and simulation of magneto-active elastomers based on experimental data. Phys. Sci. Rev. 2023, 8, 1–31. [Google Scholar] [CrossRef]
- Kovachki, N.; Liu, B.; Sun, X.; Zhou, H.; Bhattacharya, K.; Ortiz, M.; Stuart, A. Multiscale modeling of materials: Computing, data science, uncertainty and goal-oriented optimization. Mech. Mater. 2022, 165, 104156. [Google Scholar] [CrossRef]
- Abueidda, D.W.; Koric, S.; Guleryuz, E.; Sobh, N.A. Enhanced physics-informed neural networks for hyperelasticity. Int. J. Numer. Methods Eng. 2023, 124, 1585–1601. [Google Scholar] [CrossRef]
- Linden, L.; Klein, D.K.; Kalina, K.A.; Brummund, J.; Weeger, O.; Kästner, M. Neural networks meet hyperelasticity: A guide to enforcing physics. J. Mech. Phys. Solids 2023, 179, 105363. [Google Scholar] [CrossRef]
- Linka, K.; Kuhl, E. A new family of Constitutive Artificial Neural Networks towards automated model discovery. Comput. Methods Appl. Mech. Eng. 2023, 403, 115731. [Google Scholar] [CrossRef]
- Tac, V.; Linka, K.; Sahli-Costabal, F.; Kuhl, E.; Tepole, A.B. Benchmarks for physics-informed data-driven hyperelasticity. arXiv 2023, arXiv:2301.10714. [Google Scholar]
- Hughes, T.J.; Mallet, M.; Akira, M. A new finite element formulation for computational fluid dynamics: II. Beyond SUPG. Comput. Methods Appl. Mech. Eng. 1986, 54, 341–355. [Google Scholar] [CrossRef]
- Franca, L.P.; Do Carmo, E.G.D. The Galerkin gradient least-squares method. Comput. Methods Appl. Mech. Eng. 1989, 74, 41–54. [Google Scholar] [CrossRef]
- Griewank, A.; Walther, A. Algorithm 799: Revolve: An implementation of checkpointing for the reverse or adjoint mode of computational differentiation. ACM Trans. Math. Softw. (Toms) 2000, 26, 19–45. [Google Scholar] [CrossRef]
- Pyzer-Knapp, E.O.; Pitera, J.W.; Staar, P.W.; Takeda, S.; Laino, T.; Sanders, D.P.; Sexton, J.; Smith, J.R.; Curioni, A. Accelerating materials discovery using artificial intelligence, high performance computing and robotics. NPJ Comput. Mater. 2022, 8, 84. [Google Scholar] [CrossRef]
- Duysinx, P.; Van Miegroet, L.; Jacobs, T.; Fleury, C. Generalized shape optimization using X-FEM and level set methods. In Proceedings of the IUTAM Symposium on Topological Design Optimization of Structures, Machines and Materials: Status and Perspectives; Springer: Berlin/Heidelberg, Germany, 2006; pp. 23–32. [Google Scholar]
- Barrera, J.L.; Geiss, M.J.; Maute, K. Hole seeding in level set topology optimization via density fields. Struct. Multidiscip. Optim. 2020, 61, 1319–1343. [Google Scholar] [CrossRef]
- Schmidt, M.; Barrera, J.L.; Swartz, K.; Mittal, K.; Tortorelli, D. Level-set topology optimization with PDE-generated conformal meshes. Struct. Multidiscip. Optim. 2024. submitted. [Google Scholar]
- Geiss, M.J.; Barrera, J.L.; Boddeti, N.; Maute, K. A regularization scheme for explicit level-set XFEM topology optimization. Front. Mech. Eng. 2019, 14, 153–170. [Google Scholar] [CrossRef]
- Soghrati, S.; Barrera, J.L. On the application of higher-order elements in the hierarchical interface-enriched finite element method. Int. J. Numer. Methods Eng. 2016, 105, 403–415. [Google Scholar] [CrossRef]
- Barrera, J.L.; Maute, K. Ambiguous phase assignment of discretized 3D geometries in topology optimization. Comput. Methods Appl. Mech. Eng. 2020, 369, 113201. [Google Scholar] [CrossRef]


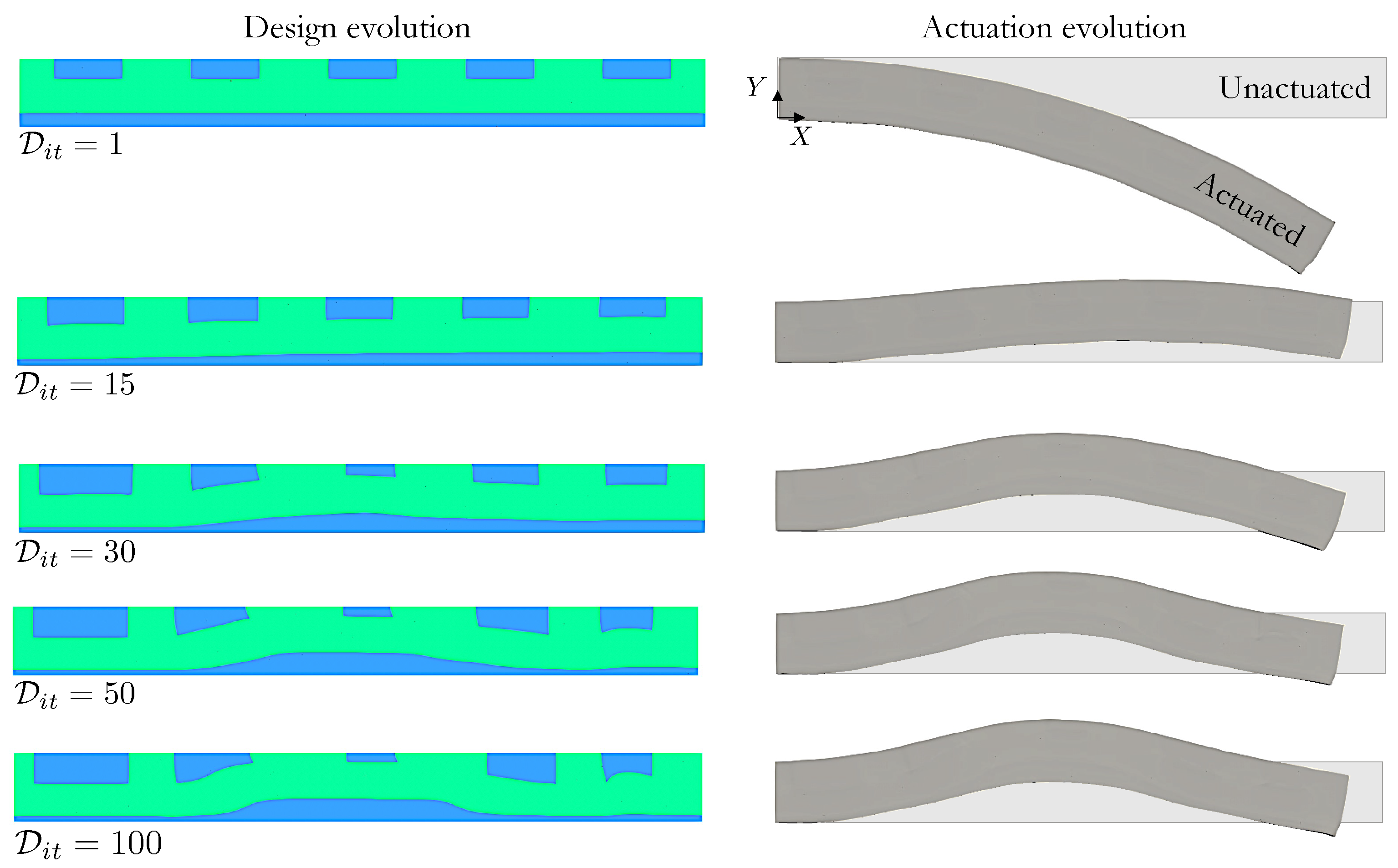
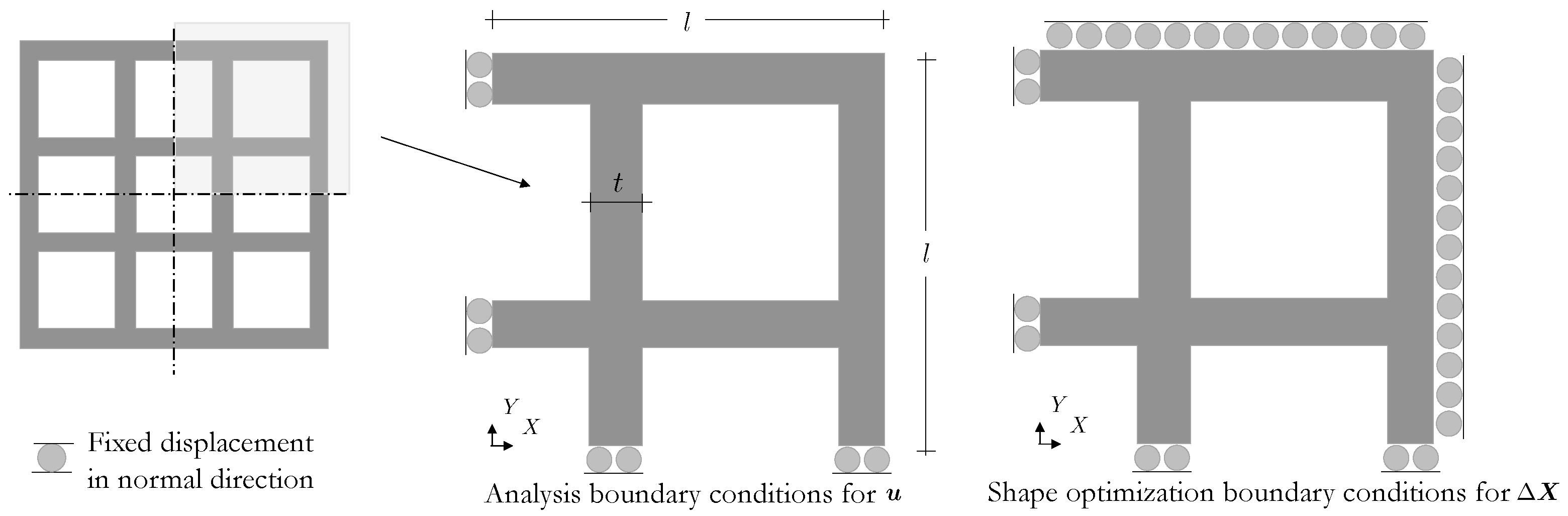
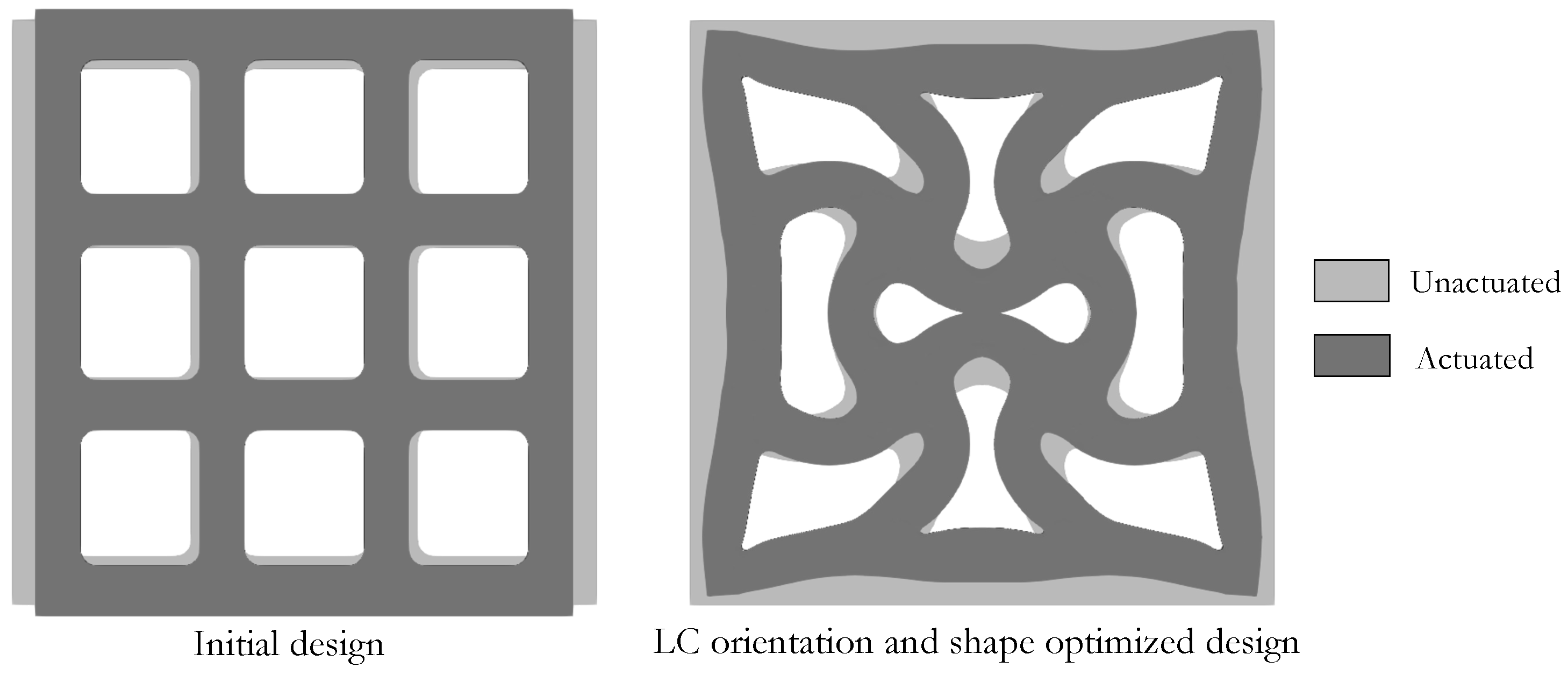
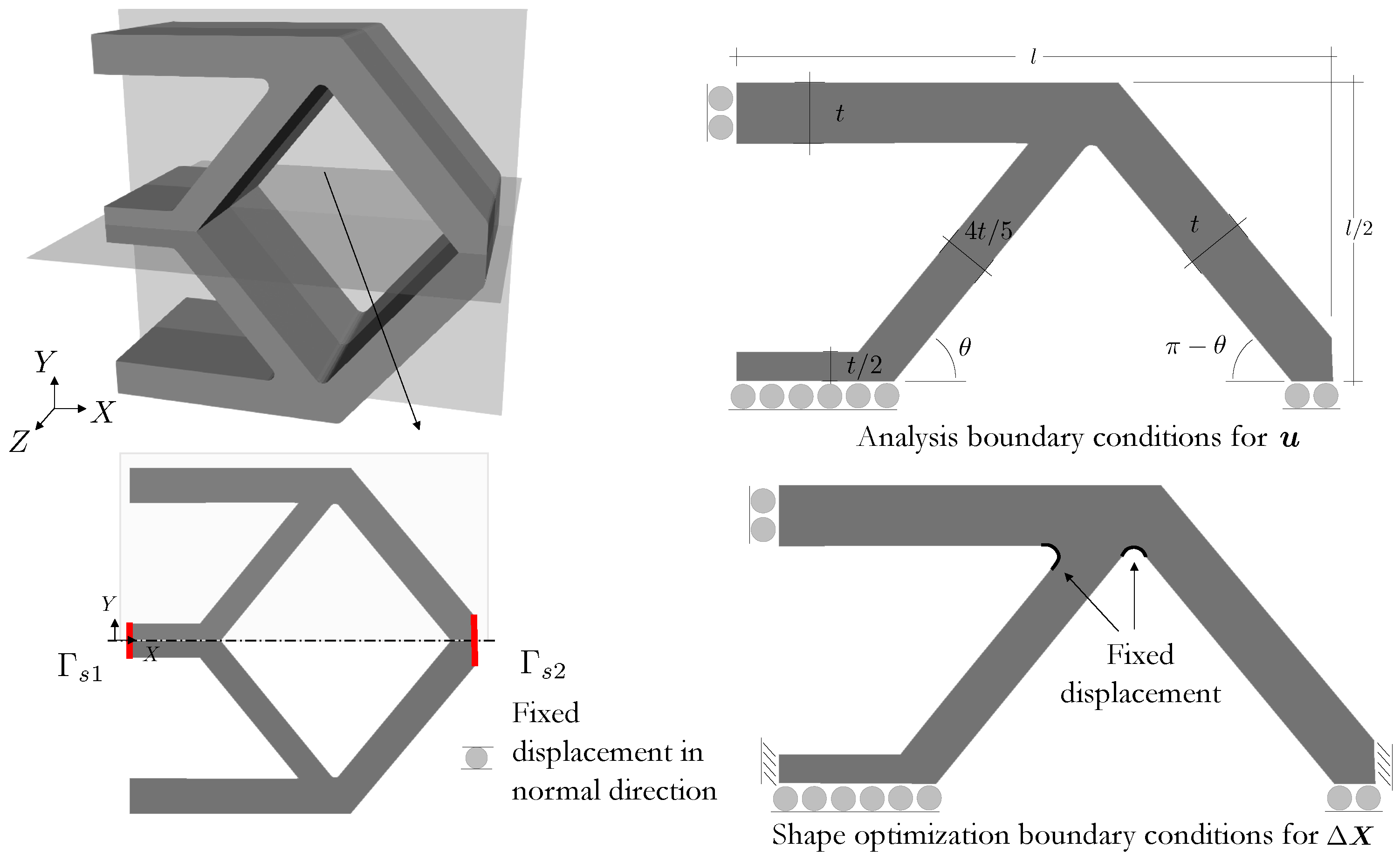
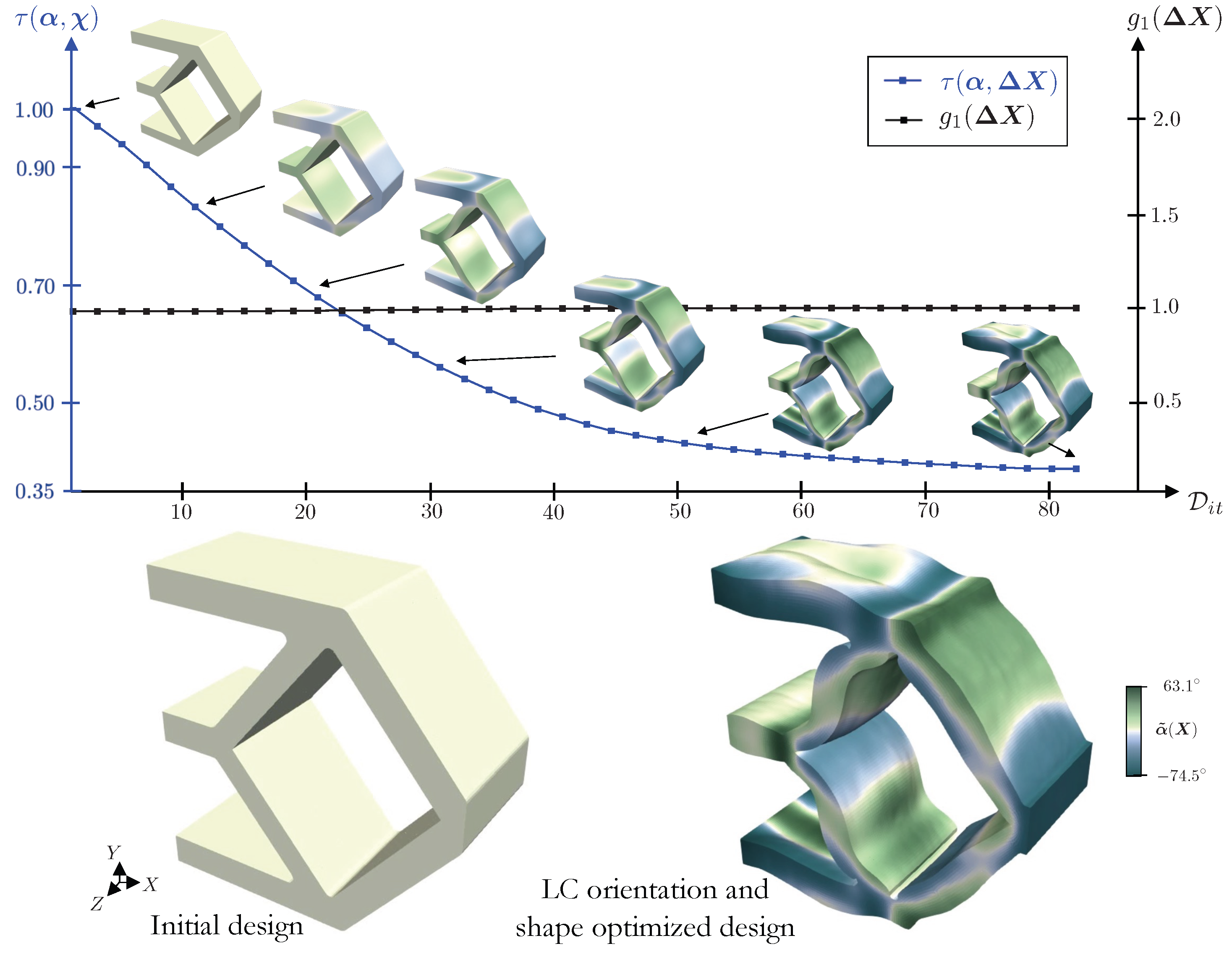
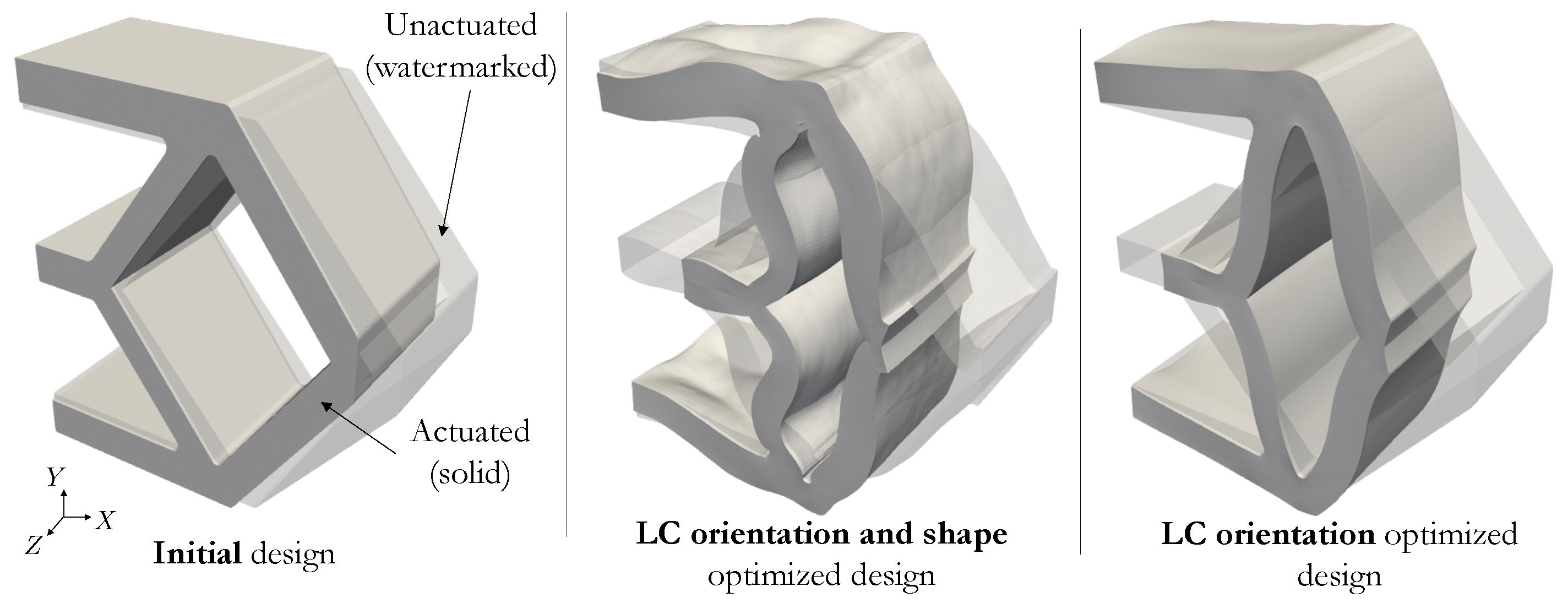
| Parameter | Value |
|---|---|
| Nematic–isotropic coupling parameter, | [N/m2] |
| Elastic modulus, | [N/m2] |
| Poisson’s ratio, | |
| Initial order parameter, | |
| Total actuation time, | |
| Newton tolerance, |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barrera, J.L.; Cook, C.; Lee, E.; Swartz, K.; Tortorelli, D. Liquid Crystal Orientation and Shape Optimization for the Active Response of Liquid Crystal Elastomers. Polymers 2024, 16, 1425. https://doi.org/10.3390/polym16101425
Barrera JL, Cook C, Lee E, Swartz K, Tortorelli D. Liquid Crystal Orientation and Shape Optimization for the Active Response of Liquid Crystal Elastomers. Polymers. 2024; 16(10):1425. https://doi.org/10.3390/polym16101425
Chicago/Turabian StyleBarrera, Jorge Luis, Caitlyn Cook, Elaine Lee, Kenneth Swartz, and Daniel Tortorelli. 2024. "Liquid Crystal Orientation and Shape Optimization for the Active Response of Liquid Crystal Elastomers" Polymers 16, no. 10: 1425. https://doi.org/10.3390/polym16101425
APA StyleBarrera, J. L., Cook, C., Lee, E., Swartz, K., & Tortorelli, D. (2024). Liquid Crystal Orientation and Shape Optimization for the Active Response of Liquid Crystal Elastomers. Polymers, 16(10), 1425. https://doi.org/10.3390/polym16101425






