A Numerical Model to Predict the Relaxation Phenomena in Thermoset Polymers and Their Effects on Residual Stress during Curing—Part I: A Theoretical Formulation and Numerical Evaluation of Relaxation Phenomena
Abstract
1. Introduction
2. Materials and Methods
2.1. Mathematical Formulation
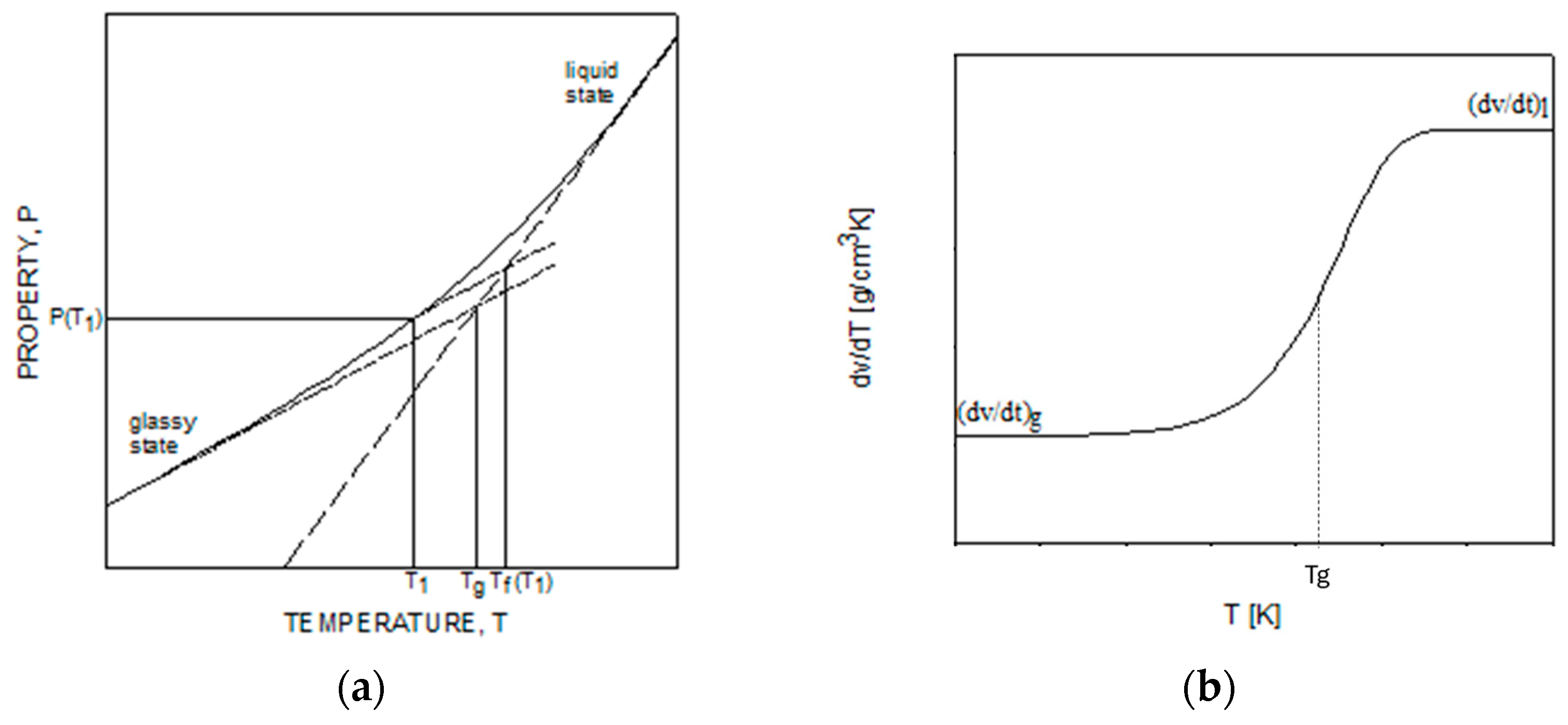
- (a)
- Thermo-rheological simplicity: At a given degree of curing, the mechanical response at short times and high temperatures is the same as the response at low temperatures and long times. It is a well-validated hypothesis for a large class of amorphous polymers, including epoxy, for a wide temperature range;
- (b)
- Chemo-rheological simplicity: The shape of the viscoelastic curve is the same at different degrees of conversion. The only effect of the degree of conversion is to translate the curves on the timescale. The hypothesis of time–degree of the cure superposition was introduced by Adolf and Martin [30], and its validity has been a debated issue among many researchers. In particular, Simon et al. [31] proposed a mathematical formulation based on TCS to describe the cure-dependent viscoelasticity of epoxy after gelation, showing that TCS is probably not strictly valid but represents a good approximation for engineering purposes. Similarly, Saseendran et al. [33] reported that the epoxy’s viscoelastic behavior, at any degree of conversion, can be obtained from a single master curve by scaling it along the timescale using an appropriate shift factor.
2.2. Model Parameters
3. Results and Discussion
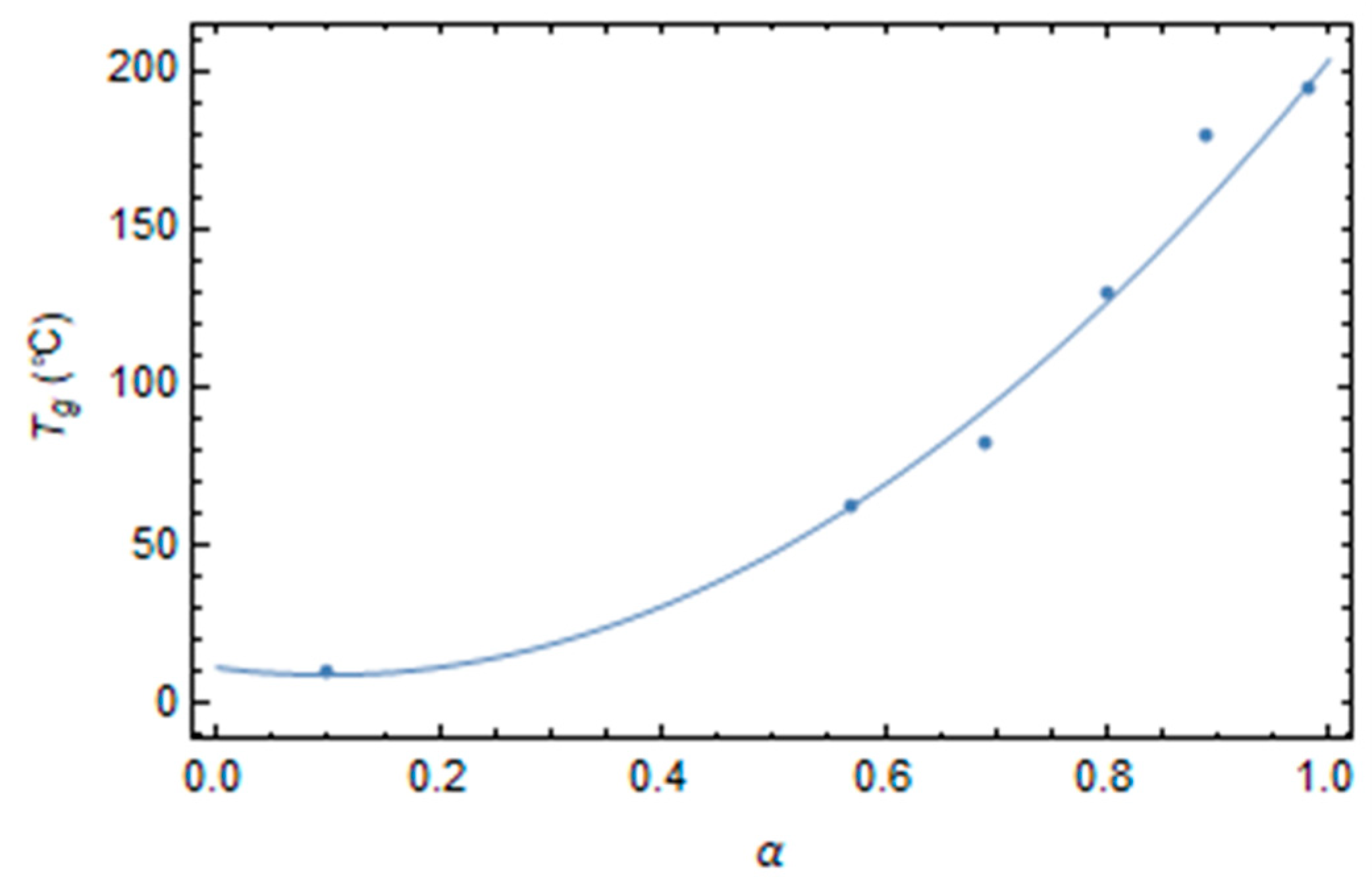
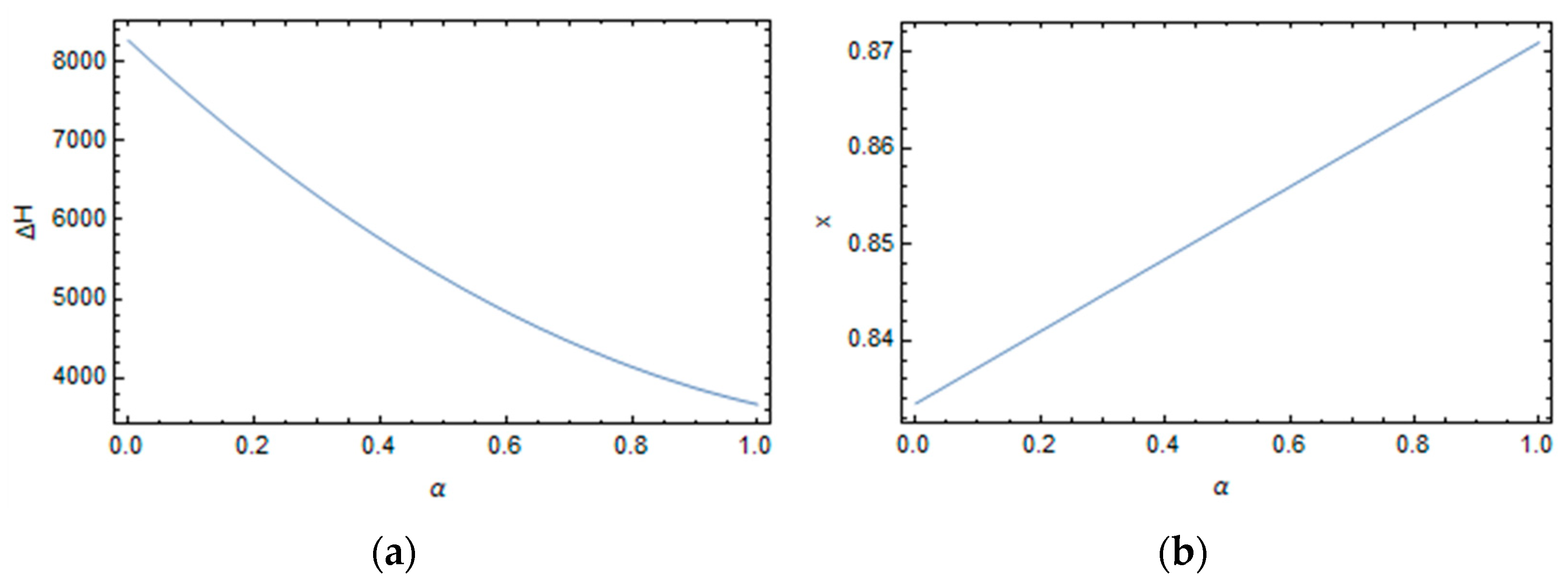
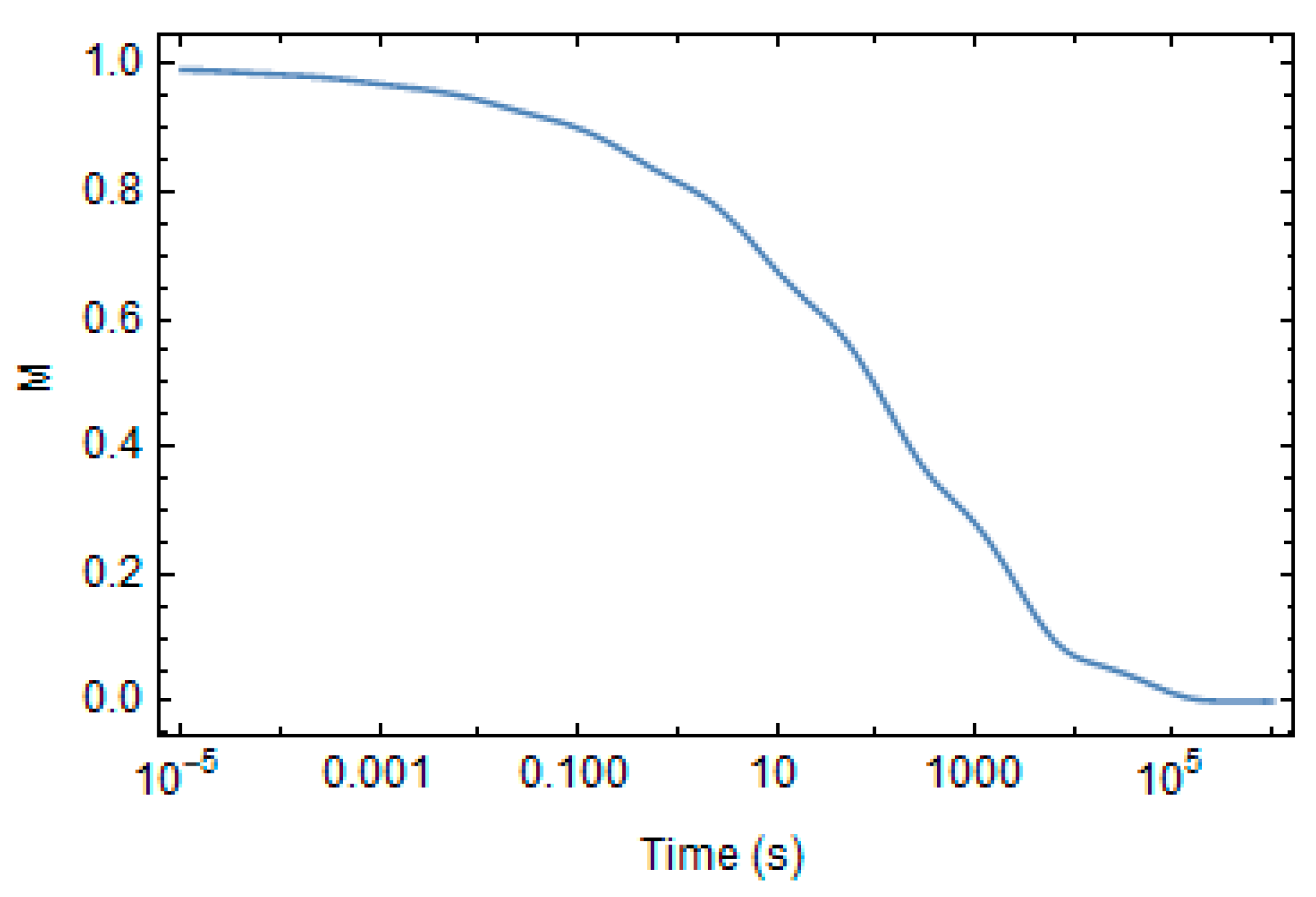
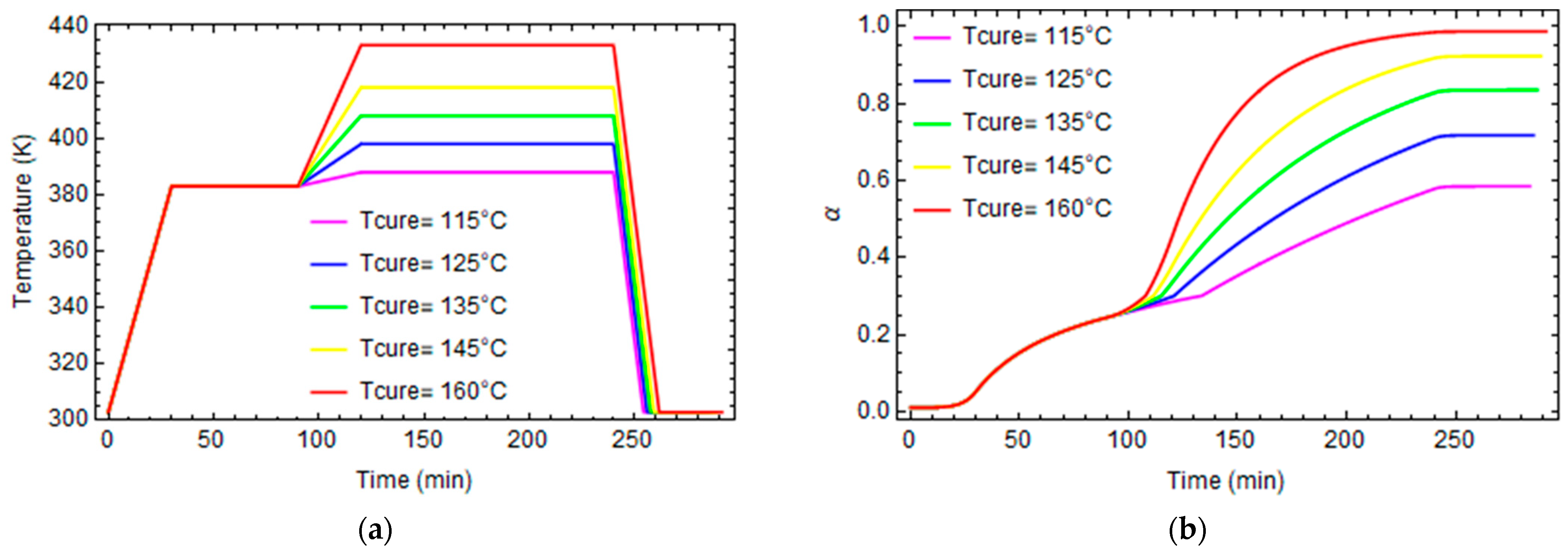
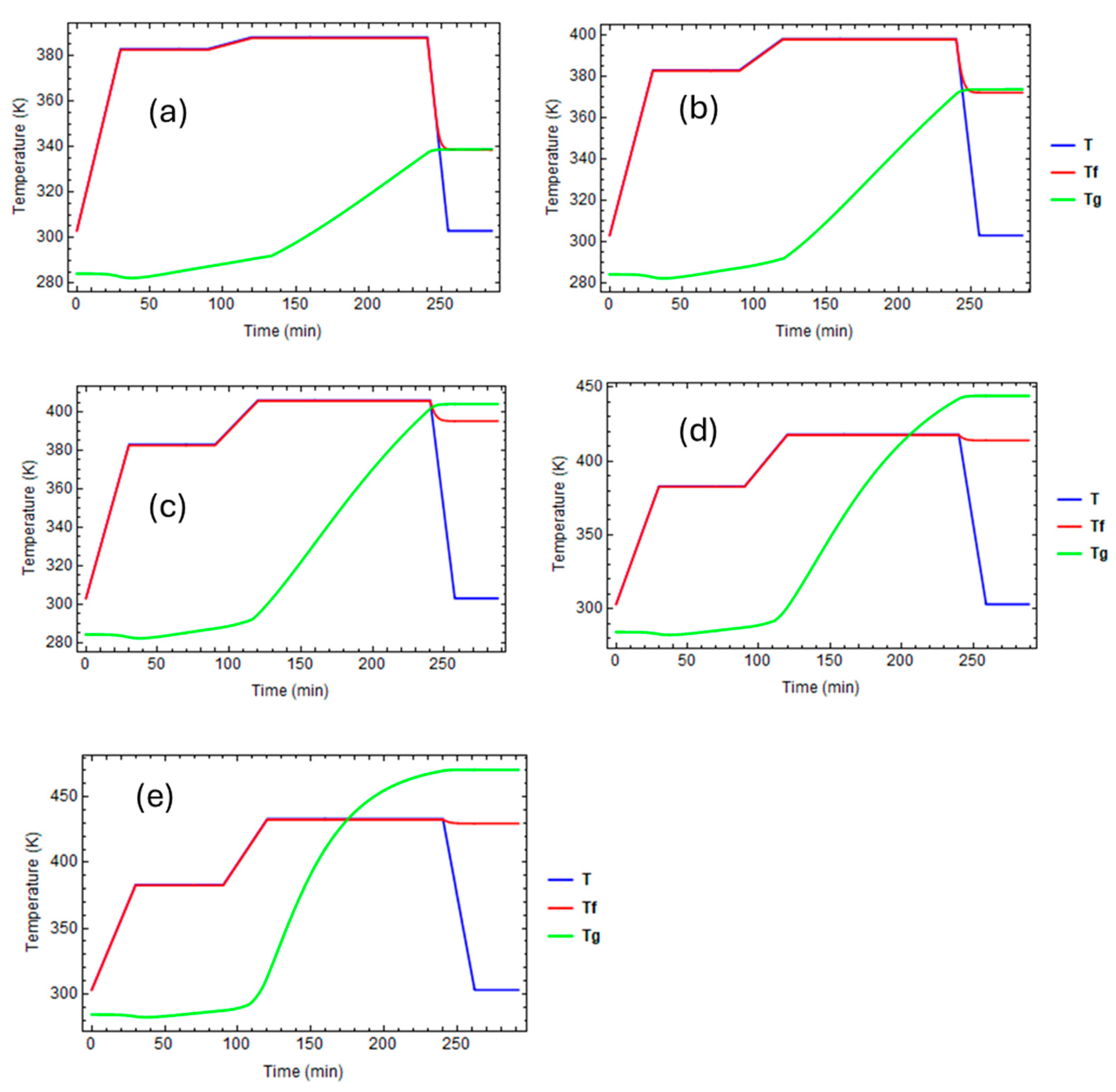
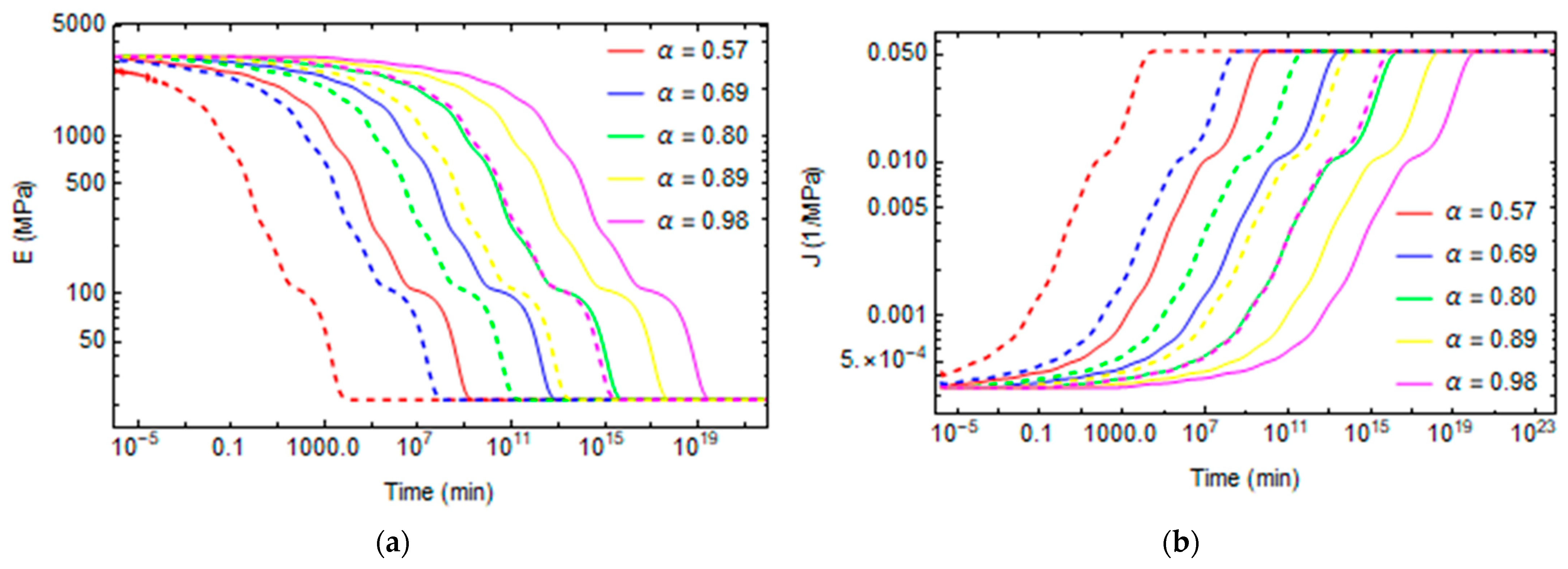
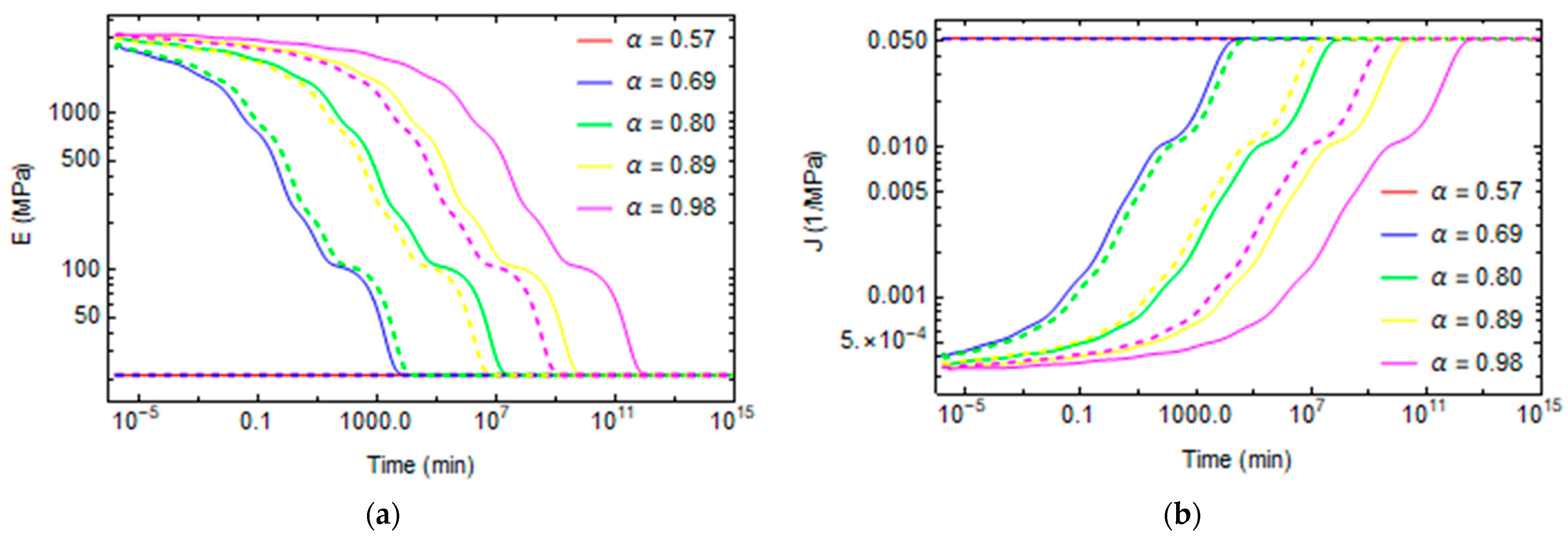
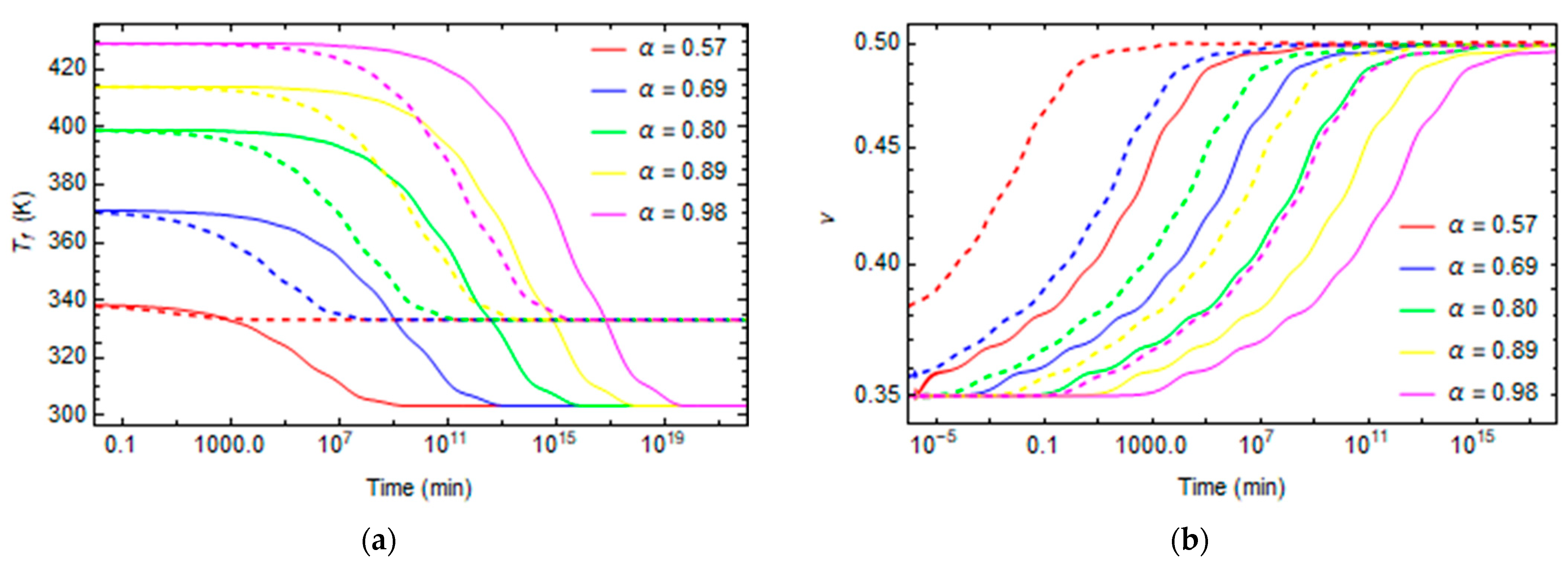
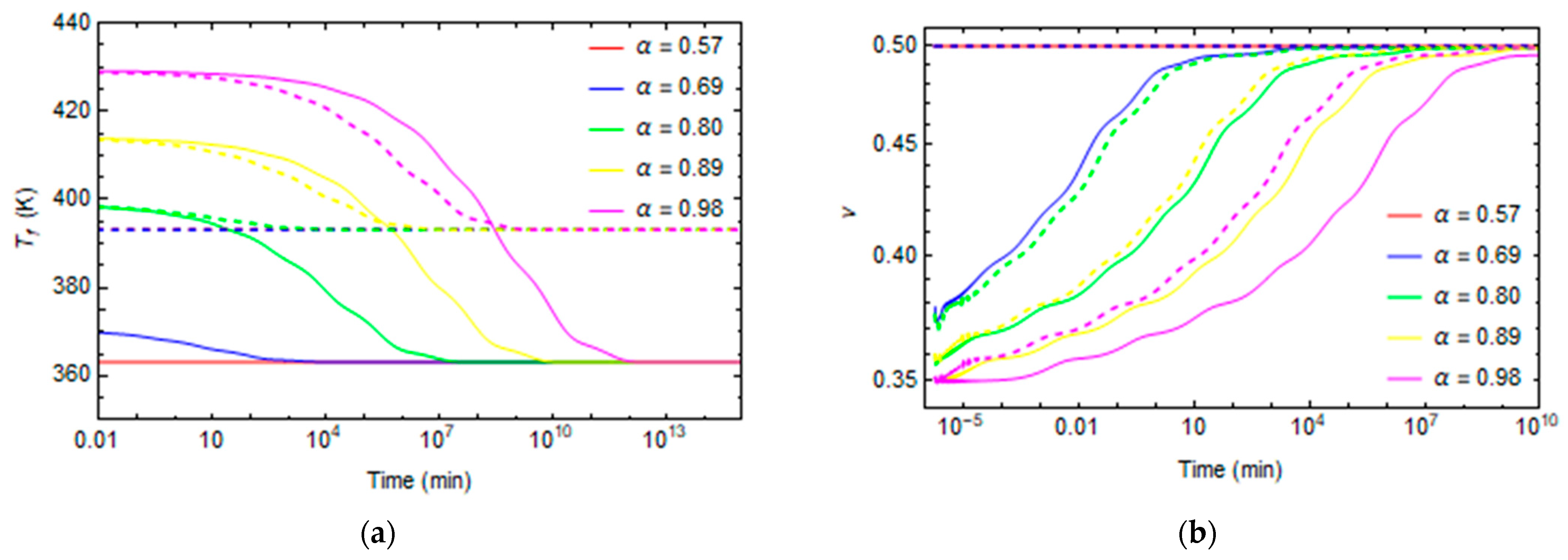
3.1. Effect of Curing on Structural Relaxation
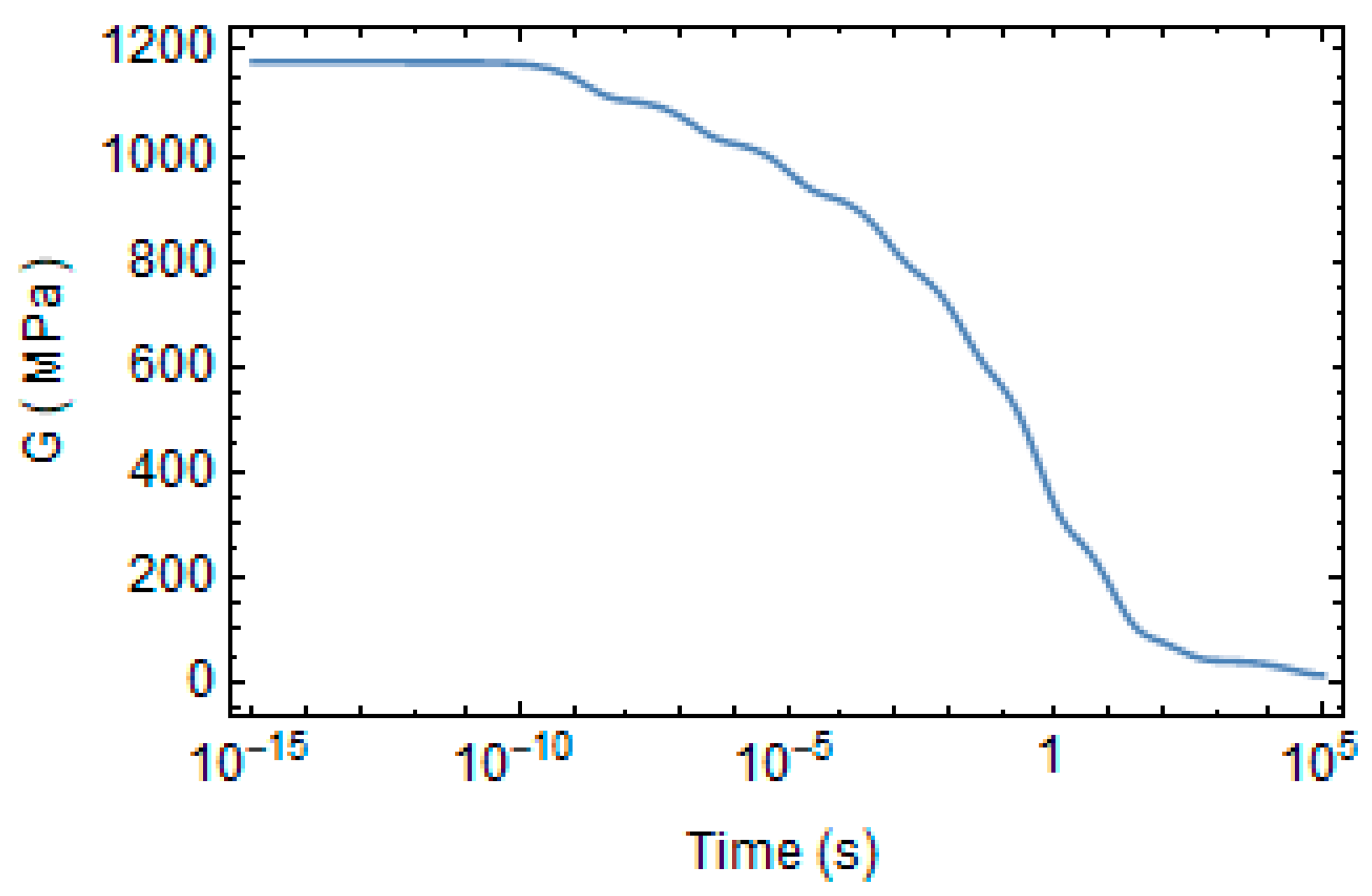
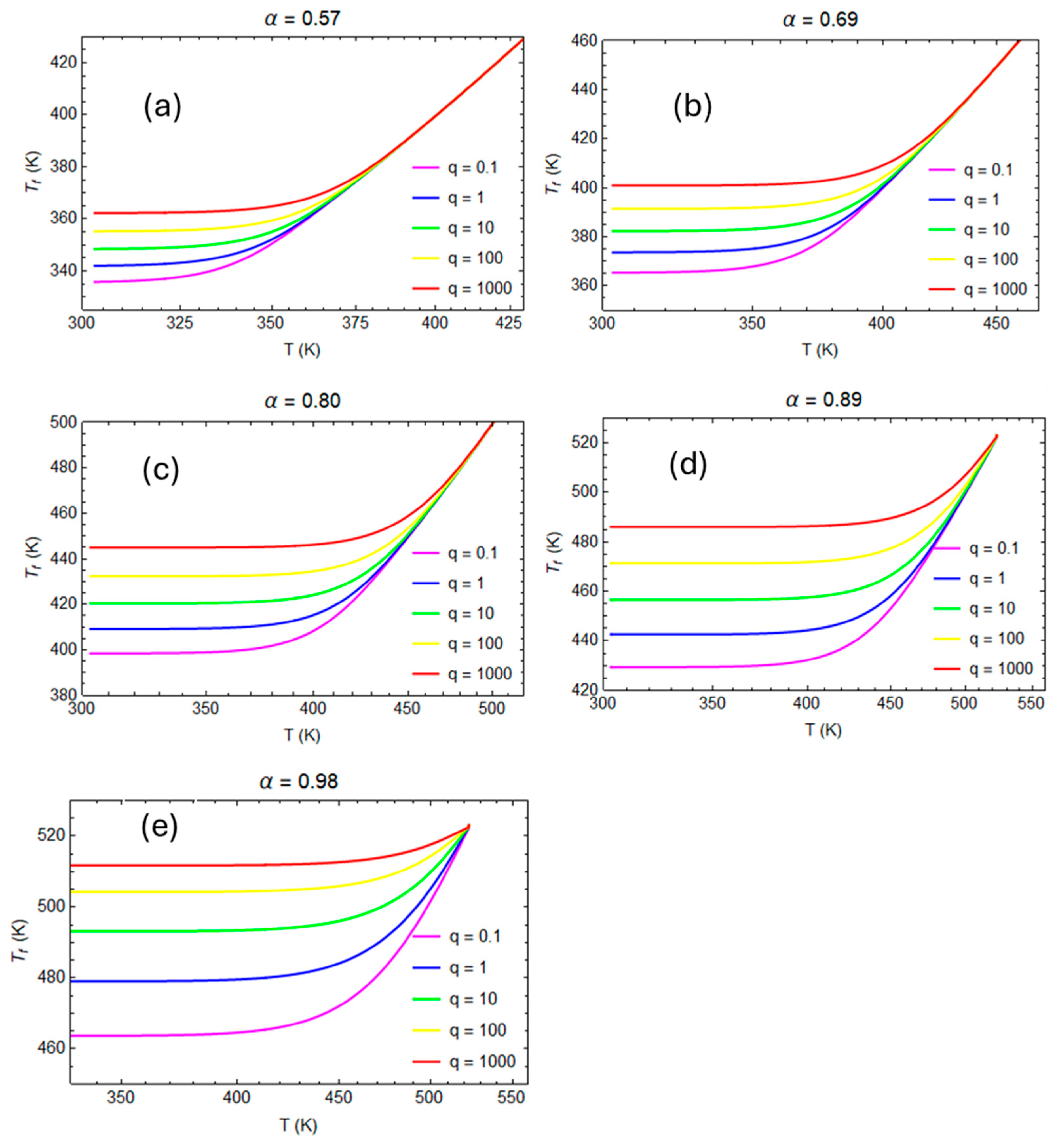
3.2. Numerical Evaluation of Creep and Stress Relaxation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Vidil, T.; Tournilhac, F.; Musso, S.; Robisson, A.; Leibler, L. Control of reactions and network structures of epoxy thermosets. Prog. Polym. Sci. 2016, 62, 126–179. [Google Scholar] [CrossRef]
- Plazek, D.J.; Frund, Z.N. Epoxy Resins (DGEBA): The Curing and Physical Aging Process. J. Polym. Sci. B Polym. Phys. 1990, 28, 431–448. [Google Scholar] [CrossRef]
- McKenna, G.B. Looking at the Glass Transition: Challenges of Extreme Time Scales and Other Interesting Problems. Rubber Chem. Technol. 2020, 93, 79–120. [Google Scholar] [CrossRef]
- Kovacs, A.; Aklonis, J.J.; Hutchinson, J.; Ramos, A.R. Isobaric Volume and Enthalpy Recovery of Glasses. II. A Transparent Multiparameter Theory. J. Polym. Sci. Polym. Phys. Ed. 1996, 34, 2467–2532. [Google Scholar] [CrossRef]
- Narayanaswamy, S. A Model of Structural Relaxation in Glass. J. Am. Ceram. Soc. 1971, 54, 491–498. [Google Scholar] [CrossRef]
- Koh, Y.P.; Grassia, L.; Simon, S.L. Structural recovery of a single polystyrene thin film using nanocalorimetry to extend the aging time and temperature range. Thermochim. Acta 2015, 603, 135–141. [Google Scholar] [CrossRef]
- Grassia, L.; Koh, Y.P.; Rosa, M.; Simon, S.L. Complete Set of Enthalpy Recovery Data Using Flash DSC: Experiment and Modeling. Macromolecules 2018, 51, 1549–1558. [Google Scholar] [CrossRef]
- Simon, S.L.; Sobieski, J.W.; Plazek, D.J. Volume and enthalpy recovery of polystyrene. Polymer 2001, 6, 2555–2567. [Google Scholar] [CrossRef]
- Monnier, X.; Marina, S.; Lopez de Pariza, X.; Sardon, H.; Martin, J.; Cangialosi, D. Physical Aging Behavior of a Glassy Polyether. Polymers 2021, 13, 954. [Google Scholar] [CrossRef]
- Morvan, A.; Delpouve, N.; Vella, A.; Saiter-Fourcin, A. Physical aging of selenium glass: Assessing the double mechanism of equilibration and the crystallization process. J. Non Cryst. Solids 2021, 570, 121013. [Google Scholar] [CrossRef]
- Drozdov, A.D.; Hoj Jermiin, R.; de Claville Christiansen, J. Lifetime Predictions for High-Density Polyethylene under Creep: Experiments and Modeling. Polymers 2023, 15, 334. [Google Scholar] [CrossRef] [PubMed]
- Korolev, A.; Mishnev, M.; Vatin, N.I.; Ignatova, A. Prolonged Thermal Relaxation of the Thermosetting Polymers. Polymers 2021, 13, 4104. [Google Scholar] [CrossRef] [PubMed]
- Johnsen, J.; Clausen, A.H.; Grytten, F.; Benallal, A.; Hopperstad, O.S. A thermo-elasto-viscoplastic constitutive model for polymers. J. Mech. Phys. Solids 2019, 124, 681–701. [Google Scholar] [CrossRef]
- Courtois, A.; Hirsekorn, M.; Benavente, M.; Jaillon, A.; Marcin, L.; Ruiz, E.; Lévesque, M. Viscoelastic behavior of an epoxy resin during cure below the glass transition temperature: Characterization and modeling. J. Compos. Mater. 2018, 53, 155–171. [Google Scholar] [CrossRef]
- Eom, Y.; Hirsekorn, M.; Benavente, M.; Jaillon, A.; Marcin, L.; Ruiz, E.; Lévesque, M. Time-cure-temperature superposition for the prediction of instantaneous viscoelastic properties during cure. Polym. Eng. Sci. 2004, 40, 1281–1292. [Google Scholar] [CrossRef]
- Grassia, L.; D’Amore, A. The relative placement of linear viscoelastic functions in amorphous glassy polymers. J. Rheol. 2009, 53, 339–356. [Google Scholar] [CrossRef]
- Müller-Pabel, M.; Rodríguez Agudo, J.A.; Gude, M. Measuring and understanding cure-dependent viscoelastic properties of epoxy resin: A review. Polym. Test. 2022, 114, 107701. [Google Scholar] [CrossRef]
- Rahul, R.; Kitey, R. Effect of cross-linking on dynamic mechanical and fracture behavior of epoxy variants. Compos. B Eng. 2016, 85, 336–342. [Google Scholar] [CrossRef]
- Grassia, L.; D’Amore, A. On the interplay between viscoelasticity and structural relaxation in glassy amorphous polymers. J. Polym. Sci. B Polym. Phys. 2009, 47, 724–739. [Google Scholar] [CrossRef]
- D’Amore, A.; Caputo, F.; Grassia, L.; Zarelli, M. Numerical evaluation of structural relaxation-induced stresses in amorphous polymers. Compos. Part A Appl. Sci. Manuf. 2006, 37, 556–564. [Google Scholar] [CrossRef]
- Kim, Y.K.; White, S.R. Stress relaxation behavior of 3501-6 epoxy resin during cure. Polym. Eng. Sci. 1996, 36, 2852–2862. [Google Scholar] [CrossRef]
- Geissberger, R.; Maldonado, J.; Bahamonde, N.; Keller, A.; Dransfeld, C.; Masania, K. Rheological modelling of thermoset composite processing. Compos. B Eng. 2017, 124, 182–189. [Google Scholar] [CrossRef]
- O’Brien, D.J.; Sottos, N.R.; White, S.R. Cure-dependent Viscoelastic Poisson’s Ratio of Epoxy. Exp. Mech. 2007, 47, 237–249. [Google Scholar] [CrossRef]
- Maiarù, M.; D’Mello, R.J.; Waas, A.M. Characterization of intralaminar strengths of virtually cured polymer matrix composites. Compos. B Eng. 2018, 149, 285–295. [Google Scholar] [CrossRef]
- Johnston, A.; Vaziri, R.; Poursartip, A. A Plane Strain Model for Process-Induced Deformation of Laminated Composite Structures. J. Compos. Mater. 2001, 35, 1435–1469. [Google Scholar] [CrossRef]
- Zhang, F.; Ye, Y.; Li, M.; Wang, H.; Cheng, L.; Wang, Q.; Ke, Y. Computational modeling of micro curing residual stress evolution and out-of-plane tensile damage behavior in fiber-reinforced composites. Compos. Struct. 2023, 322, 117370. [Google Scholar] [CrossRef]
- Liu, X.; Guan, Z.; Wang, X.; Jiang, T.; Geng, K.; Li, Z. Study on cure-induced residual stresses and spring-in deformation of L-shaped composite laminates using a simplified constitutive model considering stress relaxation. Compos. Struct. 2021, 272, 114203. [Google Scholar] [CrossRef]
- Bogetti, T.A.; Gillespie, J.W. Two-Dimensional Cure Simulation of Thick Thermosetting Composites. J. Compos. Mater. 1991, 25, 239–273. [Google Scholar] [CrossRef]
- Vieira de Mattos, D.F.; Huang, R.; Liechti, K.M. The effect of moisture on the nonlinearly viscoelastic behavior of an epoxy. Mech. Time-Depend. Mater. 2020, 24, 435–461. [Google Scholar] [CrossRef]
- Adolr, D.; Martin, J.E. Time-Cure Superposition during Cross-Linking. Macromulecules 1990, 23, 3700–3704. [Google Scholar] [CrossRef]
- Simon, S.L.; McKenna, G.B.; Sindt, O. Modeling the evolution of the dynamic mechanical properties of a commercial epoxy during cure after gelation. J. Appl. Polym. Sci. 2000, 76, 495–508. [Google Scholar]
- D’Elia, R.; Sanches, L.; Des, J.M.; Michon, G. Experimental characterization and numerical modeling of a viscoelastic expandable epoxy foam: Time–temperature transformation and time–temperature equivalence diagrams. J. Appl. Polym. Sci. 2023, 140, e53929. [Google Scholar] [CrossRef]
- Saseendran, S.; Wysocki, M.; Varna, J. Volution of viscoelastic behavior of a curing LY5052 epoxy resin in the glassy state. Adv. Manuf. Polym. Compos. Sci. 2016, 2, 74–82. [Google Scholar] [CrossRef]
- Tool, A. Relation between inelastic deformability and thermal expansion of glass in its annealing range. J. Am. Ceram. Soc. 1946, 29, 240–253. [Google Scholar] [CrossRef]
- Markovsky, A.; Soules, T.F. An Efficient and Stable Algorithm for Calculating Fictive Temperatures. J. Am. Ceram. Soc. 1984, 67, c56–c57. [Google Scholar] [CrossRef]
- Zarrelli, M.; Skordos, A.A.; Partridge, I.K. Investigation of cure induced shrinkage in unreinforced epoxy resin. Plast. Rubber Compos. 2013, 31, 377–384. [Google Scholar] [CrossRef]
- Moynihan, C.T.; Easteal, A.J.; Debolt, M.A. Dependence of the Fictive Temperature of Glass on Cooling Rate. J. Am. Ceram. Soc. 1976, 59, 12–16. [Google Scholar] [CrossRef]


| A1 | 2.102 × 109 | min−1 |
| A2 | −2.014 × 109 | min−1 |
| A3 | 1.960 × 105 | min−1 |
| ΔE1 | 8.07 × 104 | J/mol |
| ΔE2 | 7.78 × 104 | J/mol |
| ΔE3 | 5.66 × 104 | J/mol |
| Hr | 473.16 | kJ/Kg |
| R | 8.314 | J/Kg mol |
| ρ | 1200 | Kg/m3 |
| cp | 1260 | J/Kg K |
| k | 0.167 | W/m K |
| Viscoelasticity | G0, K0, τiG, wiG i = 1,… |
| Structural Relaxation | τiM, αiM, Tf i, ΔH, x i = 1,… |
| Curing | , Hr, Ai i = 1,…3 |
| Glass Transition Temperature | b1, b2, b3 |
| N | τG (s) | αiG |
|---|---|---|
| 1 | 1.75 × 10−9 | 0.059 |
| 2 | 1.75 × 10−7 | 0.066 |
| 3 | 1.09 × 10−5 | 0.083 |
| 4 | 6.60 × 10−4 | 0.112 |
| 5 | 1.70 × 10−2 | 0.154 |
| 6 | 4.76 × 10−1 | 0.262 |
| 7 | 1.17 × 101 | 0.184 |
| 8 | 2.00 × 102 | 0.049 |
| 9 | 2.95 × 104 | 0.025 |
| N | τM (s) | αiM |
|---|---|---|
| 1 | 1.21 × 10−6 | 0.0062 |
| 2 | 2.60 × 10−5 | 0.0072 |
| 3 | 5.60 × 10−4 | 0.0175 |
| 4 | 1.21 × 10−2 | 0.0390 |
| 5 | 2.60 × 10−1 | 0.0856 |
| 6 | 5.60 | 0.1730 |
| 7 | 1.21 × 102 | 0.2950 |
| 8 | 2.60 × 103 | 0.298 |
| 9 | 5.60 × 104 | 0.0785 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Verde, R.; D’Amore, A.; Grassia, L. A Numerical Model to Predict the Relaxation Phenomena in Thermoset Polymers and Their Effects on Residual Stress during Curing—Part I: A Theoretical Formulation and Numerical Evaluation of Relaxation Phenomena. Polymers 2024, 16, 1433. https://doi.org/10.3390/polym16101433
Verde R, D’Amore A, Grassia L. A Numerical Model to Predict the Relaxation Phenomena in Thermoset Polymers and Their Effects on Residual Stress during Curing—Part I: A Theoretical Formulation and Numerical Evaluation of Relaxation Phenomena. Polymers. 2024; 16(10):1433. https://doi.org/10.3390/polym16101433
Chicago/Turabian StyleVerde, Raffaele, Alberto D’Amore, and Luigi Grassia. 2024. "A Numerical Model to Predict the Relaxation Phenomena in Thermoset Polymers and Their Effects on Residual Stress during Curing—Part I: A Theoretical Formulation and Numerical Evaluation of Relaxation Phenomena" Polymers 16, no. 10: 1433. https://doi.org/10.3390/polym16101433
APA StyleVerde, R., D’Amore, A., & Grassia, L. (2024). A Numerical Model to Predict the Relaxation Phenomena in Thermoset Polymers and Their Effects on Residual Stress during Curing—Part I: A Theoretical Formulation and Numerical Evaluation of Relaxation Phenomena. Polymers, 16(10), 1433. https://doi.org/10.3390/polym16101433






