Modeling Analysis of Complex Deformation of Woven Coating Film during the Cyclic Tensile Process
Abstract
1. Introduction
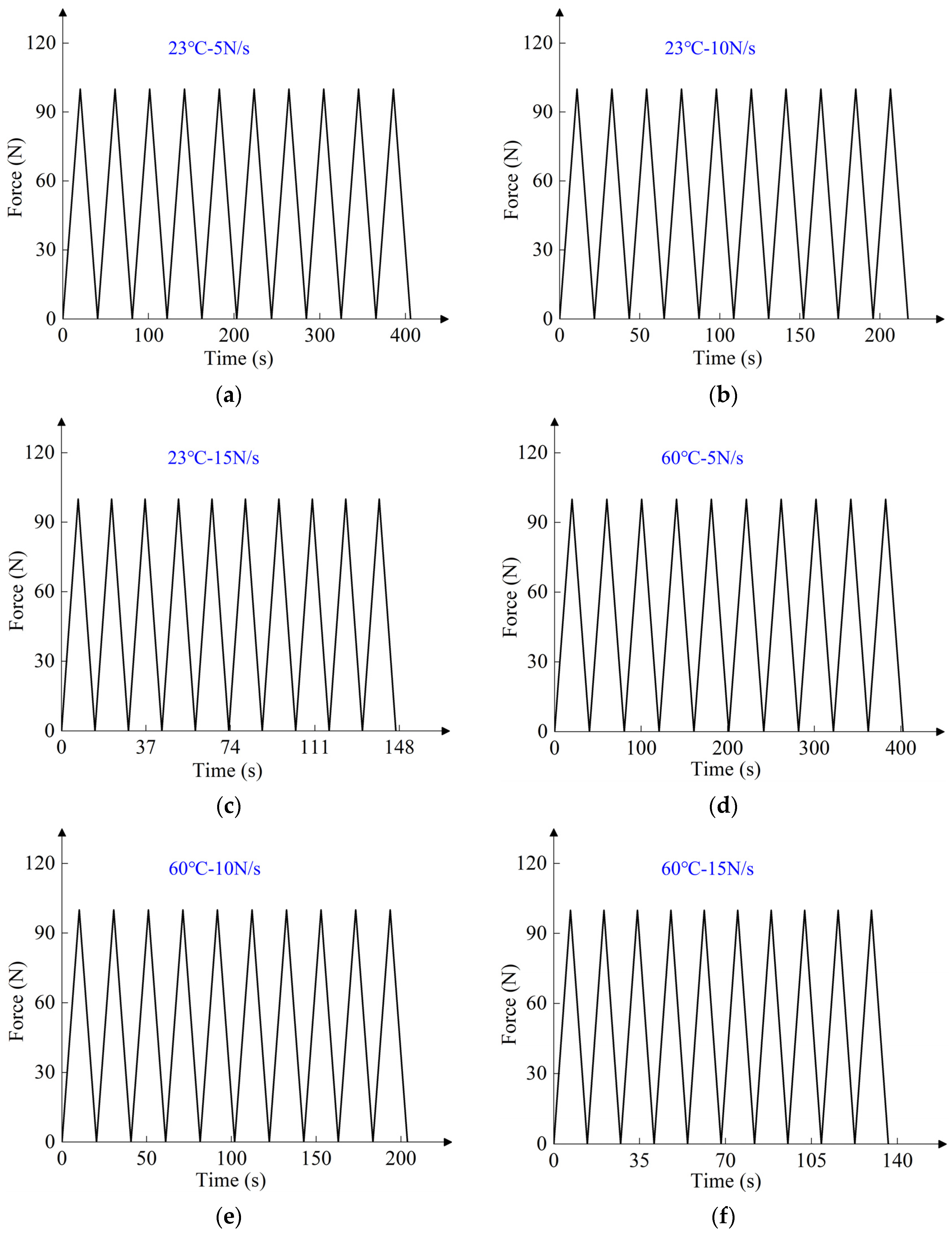
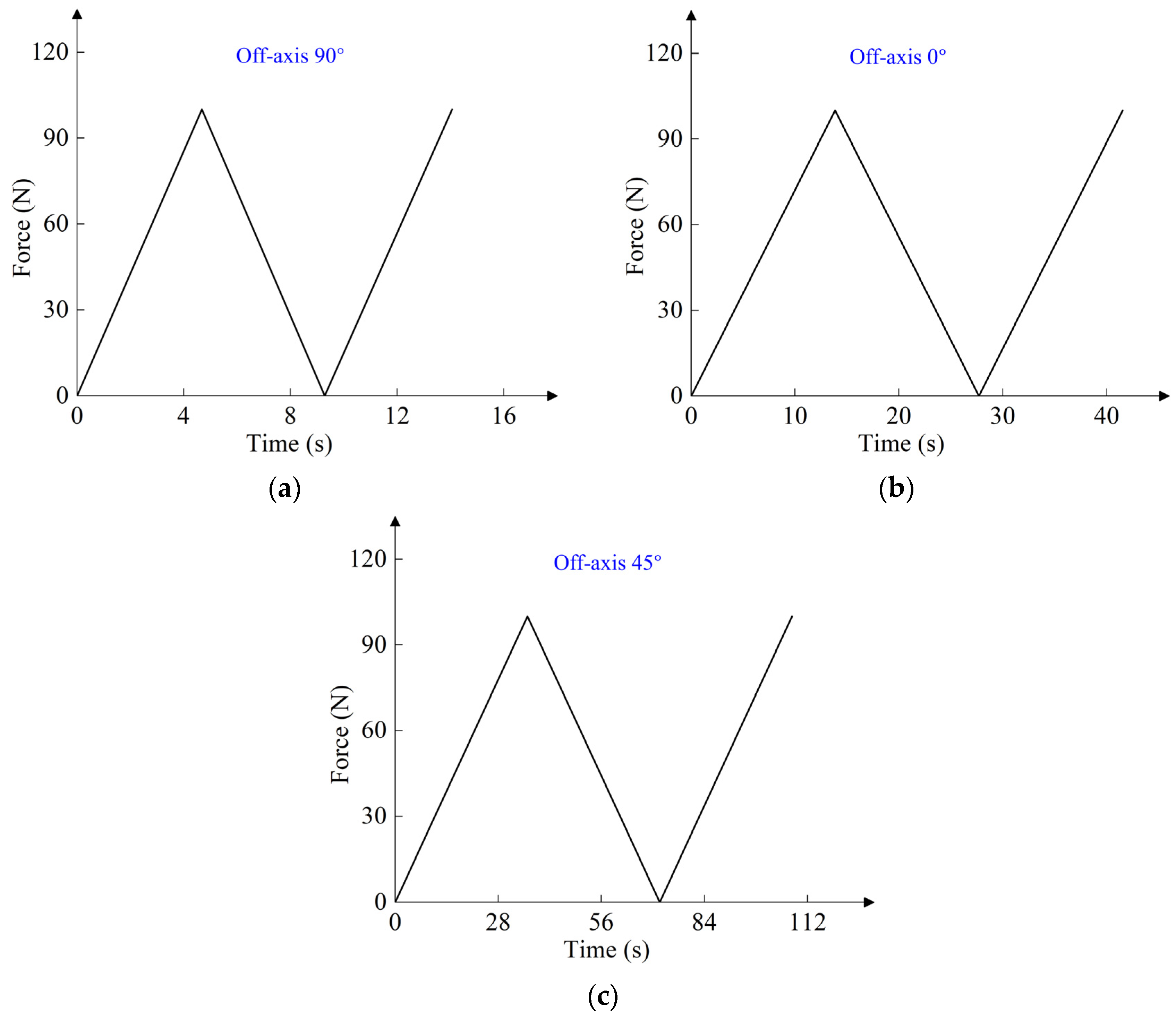
2. Cyclic Tensile Test
2.1. Samples
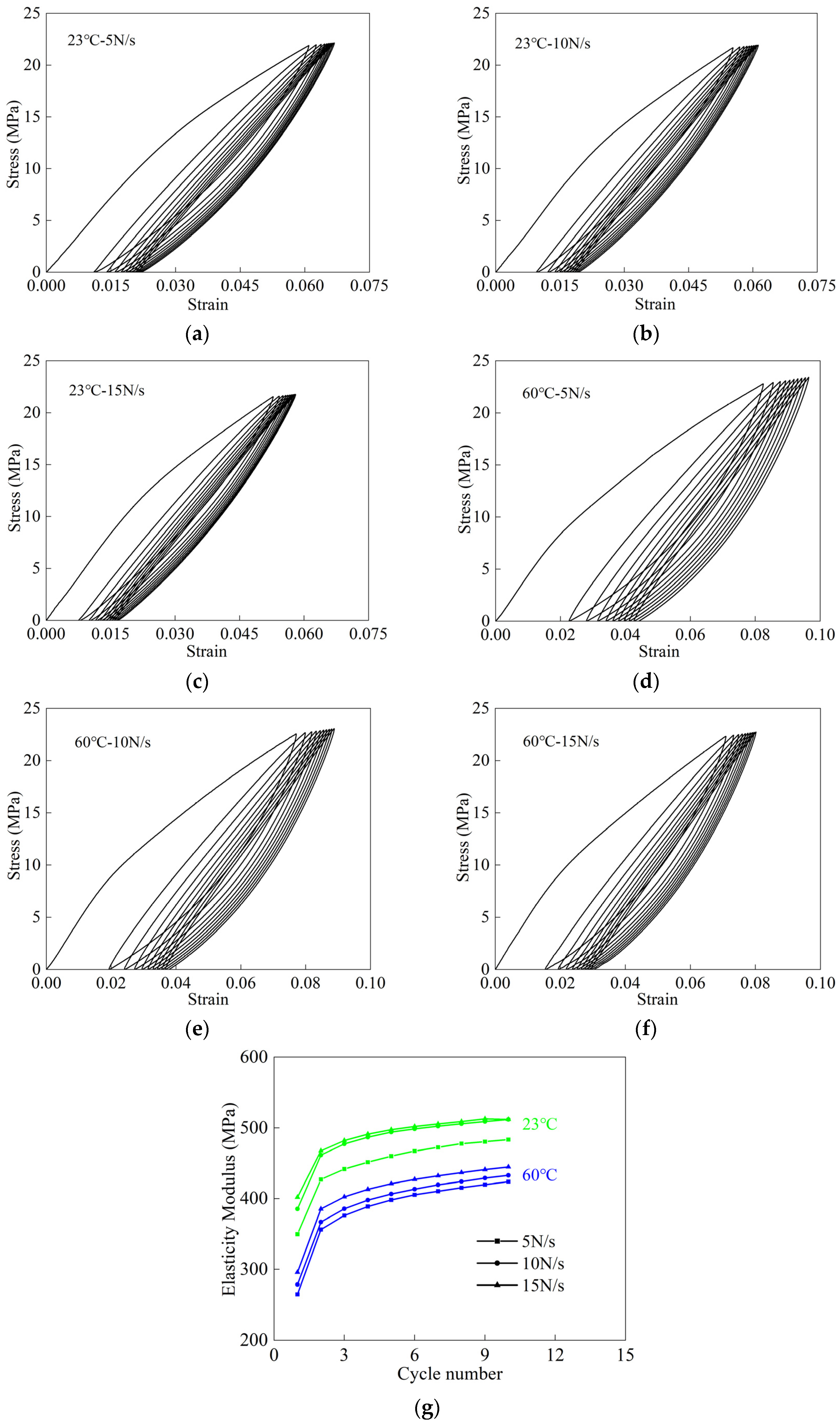
2.2. Experimental Results and Discussion
3. One-Dimensional Model of Woven Coating Films
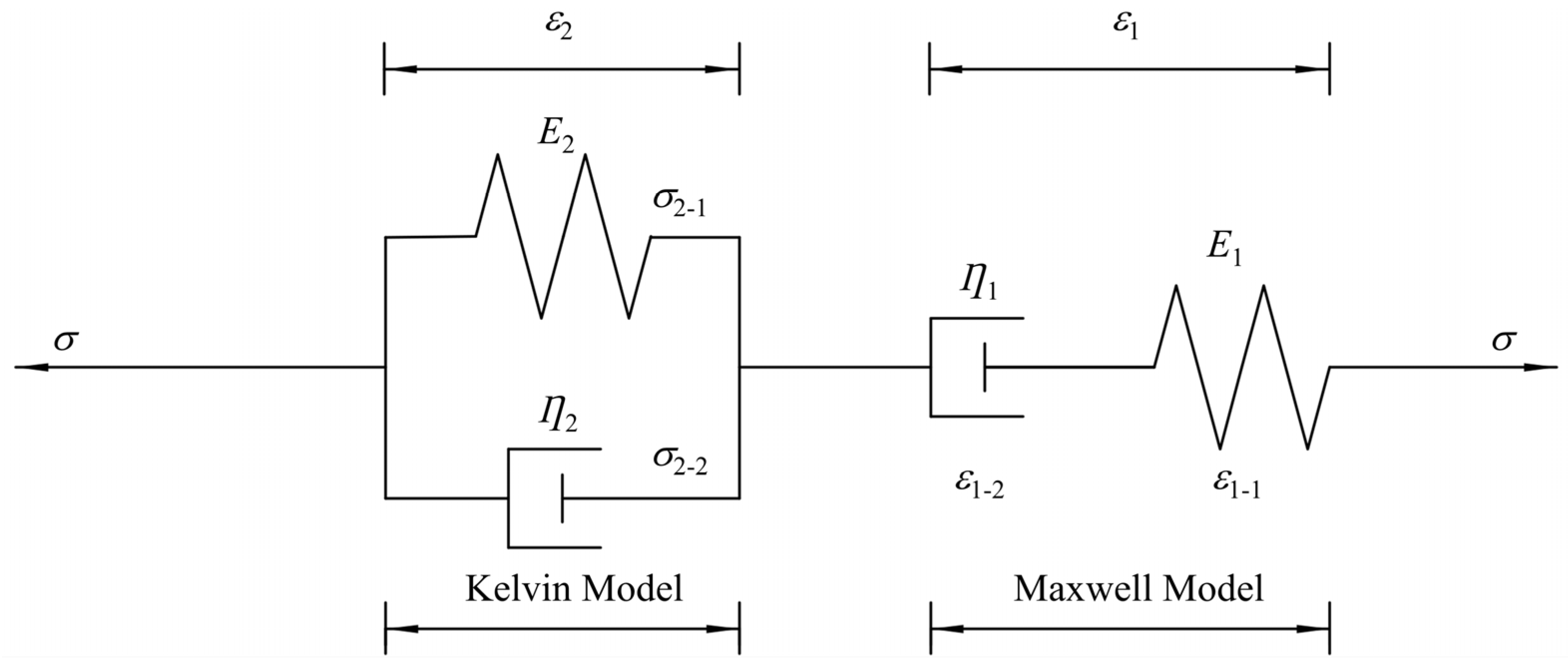
3.1. Burgers Constitutive Model
3.1.1. Loading Phase
3.1.2. Unloading Phase
3.2. Improved Burgers Constitutive Model
4. Two-Dimensional Model of Woven Coating Films
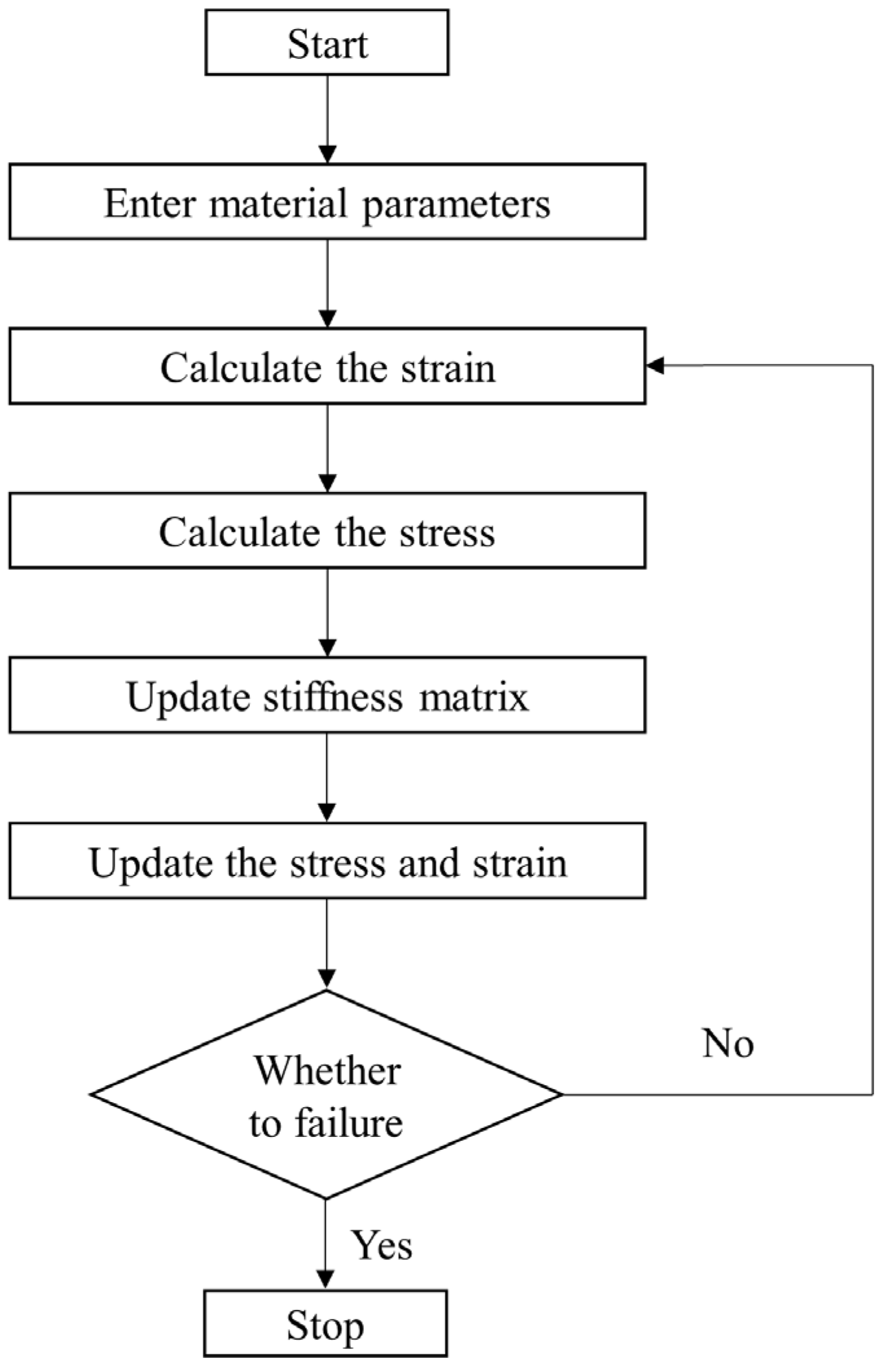
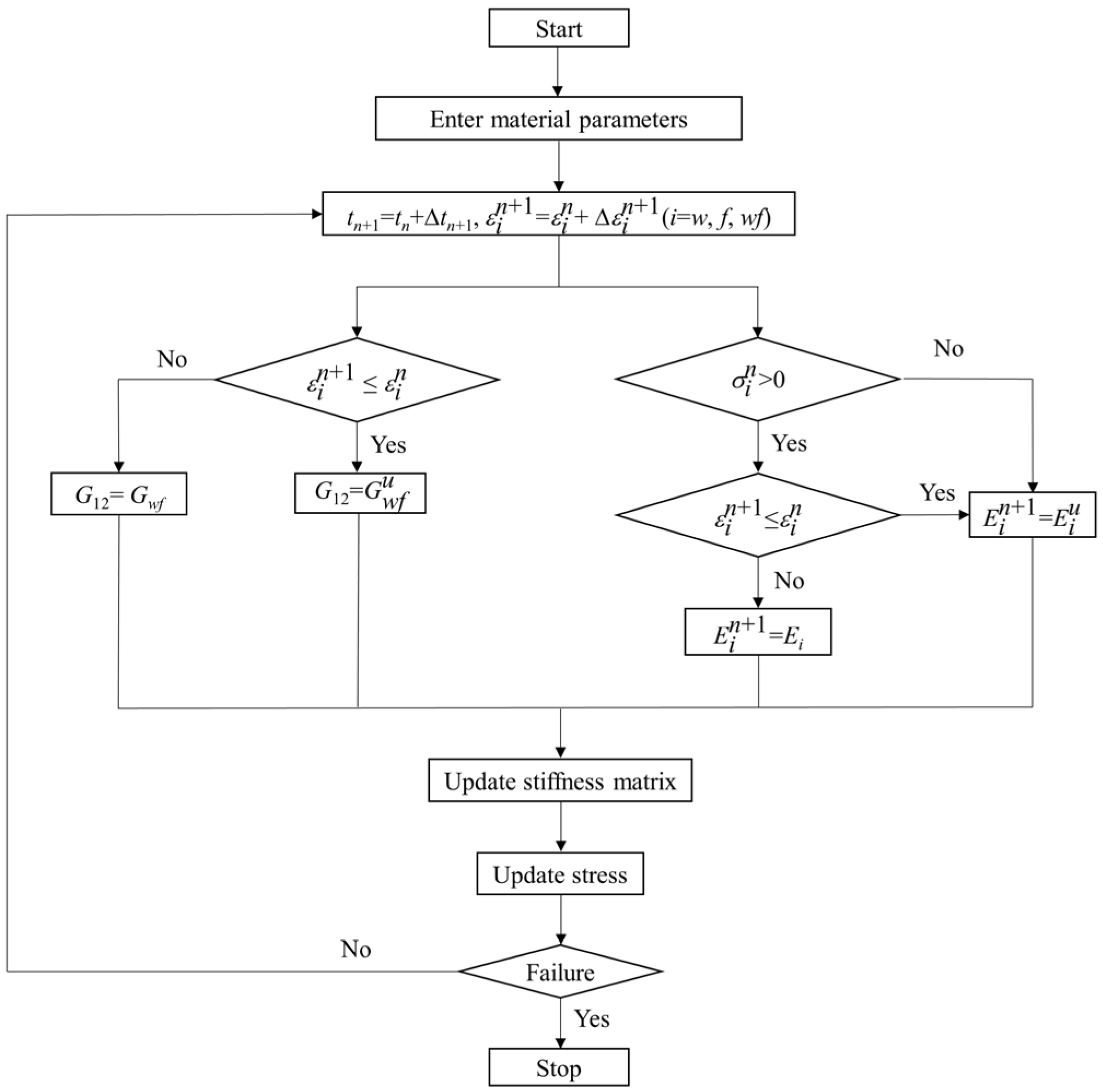
4.1. Constitutive Model
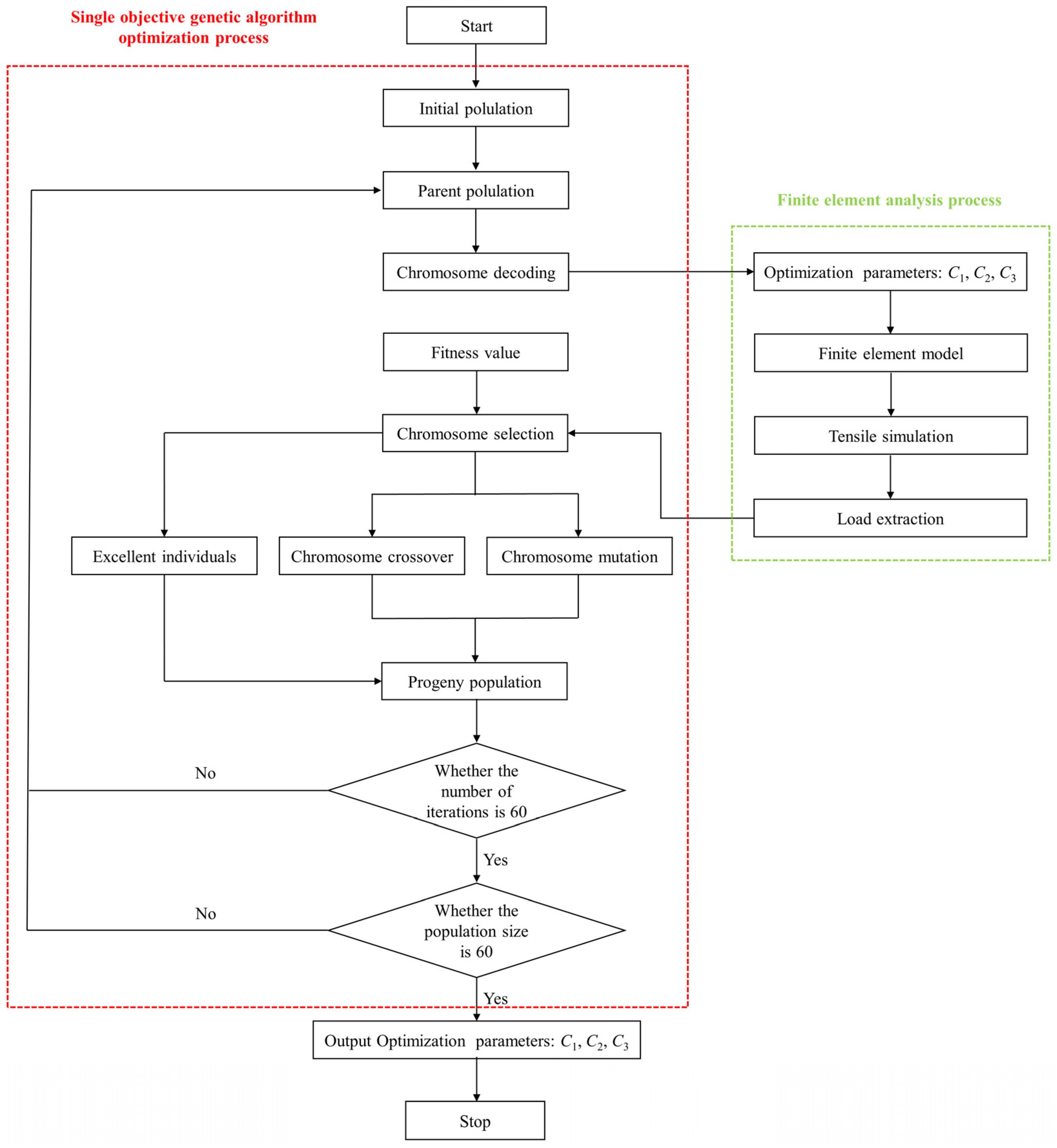
4.2. Coefficient Acquisition
- (1)
- Chromosome encoding
- (2)
- Fitness function
- (3)
- Chromosome decoding
- (4)
- Chromosome selection
- (5)
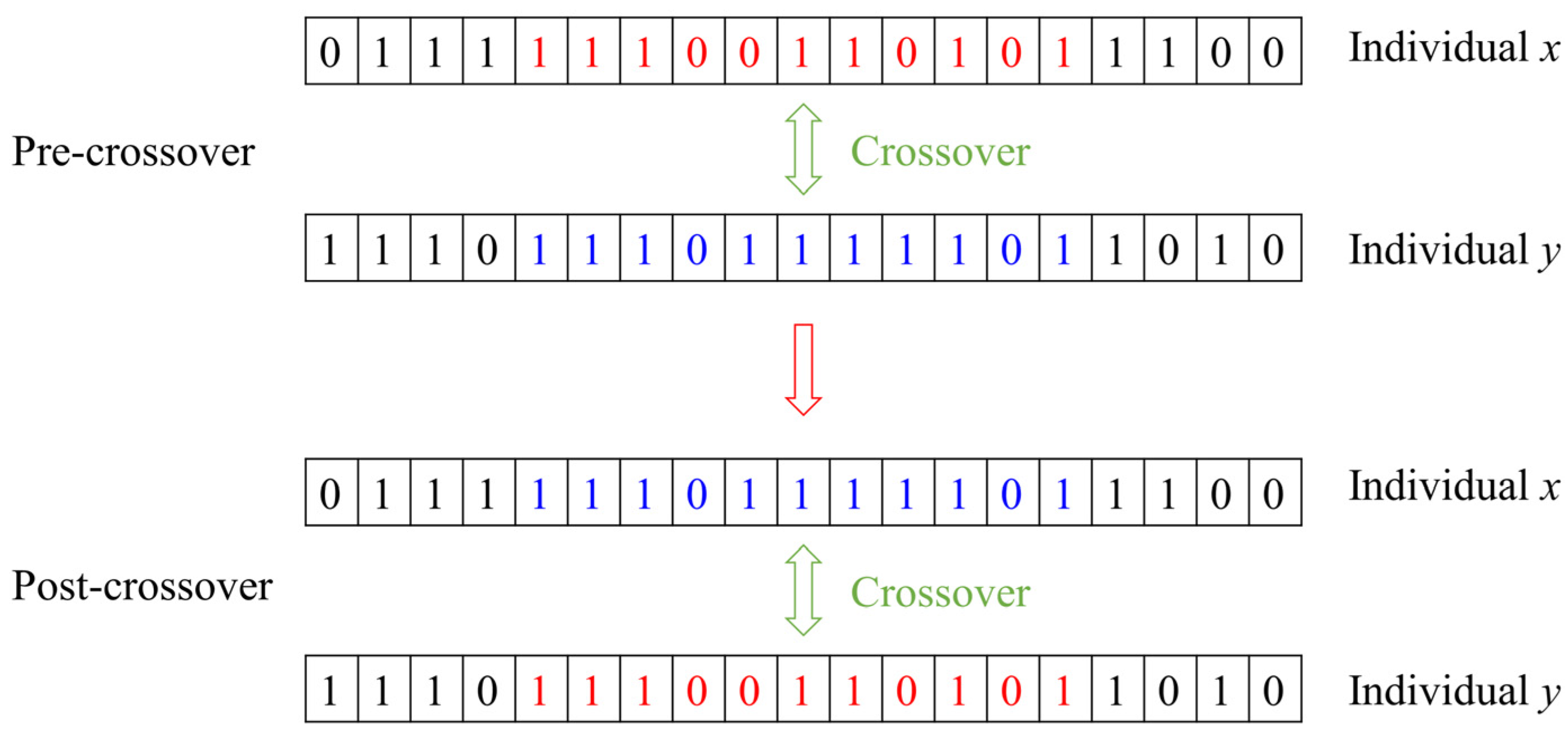
- Chromosome crossover
- (6)
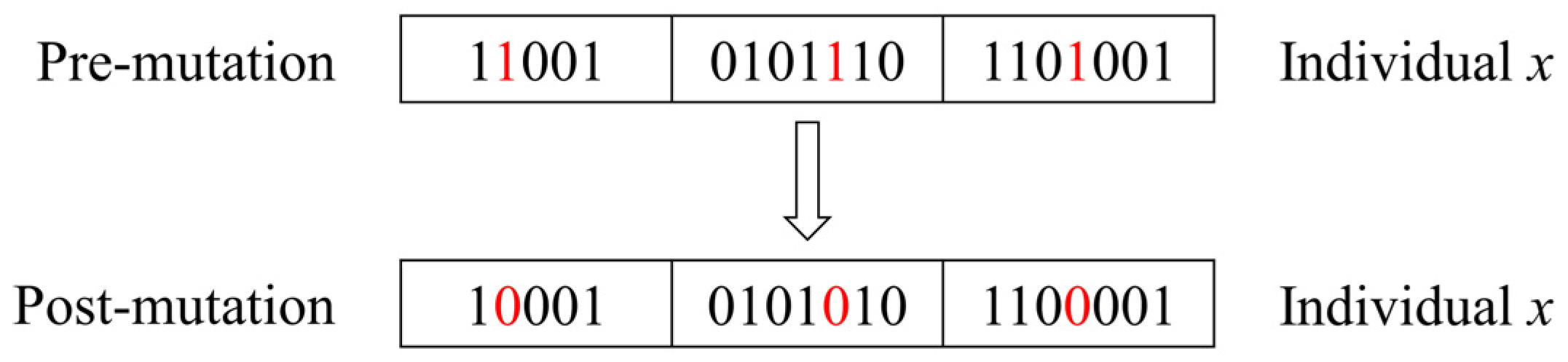
- Chromosome mutation
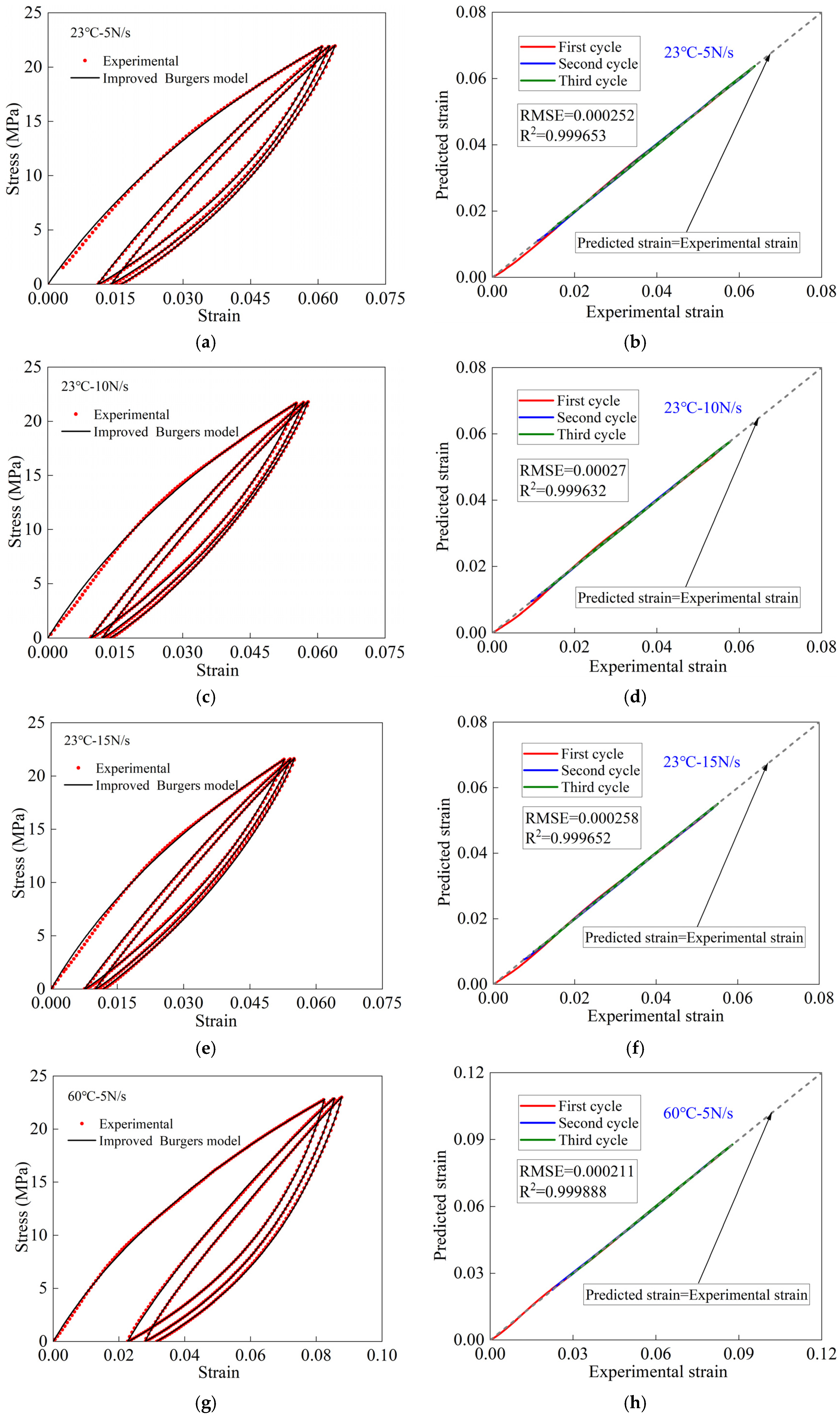
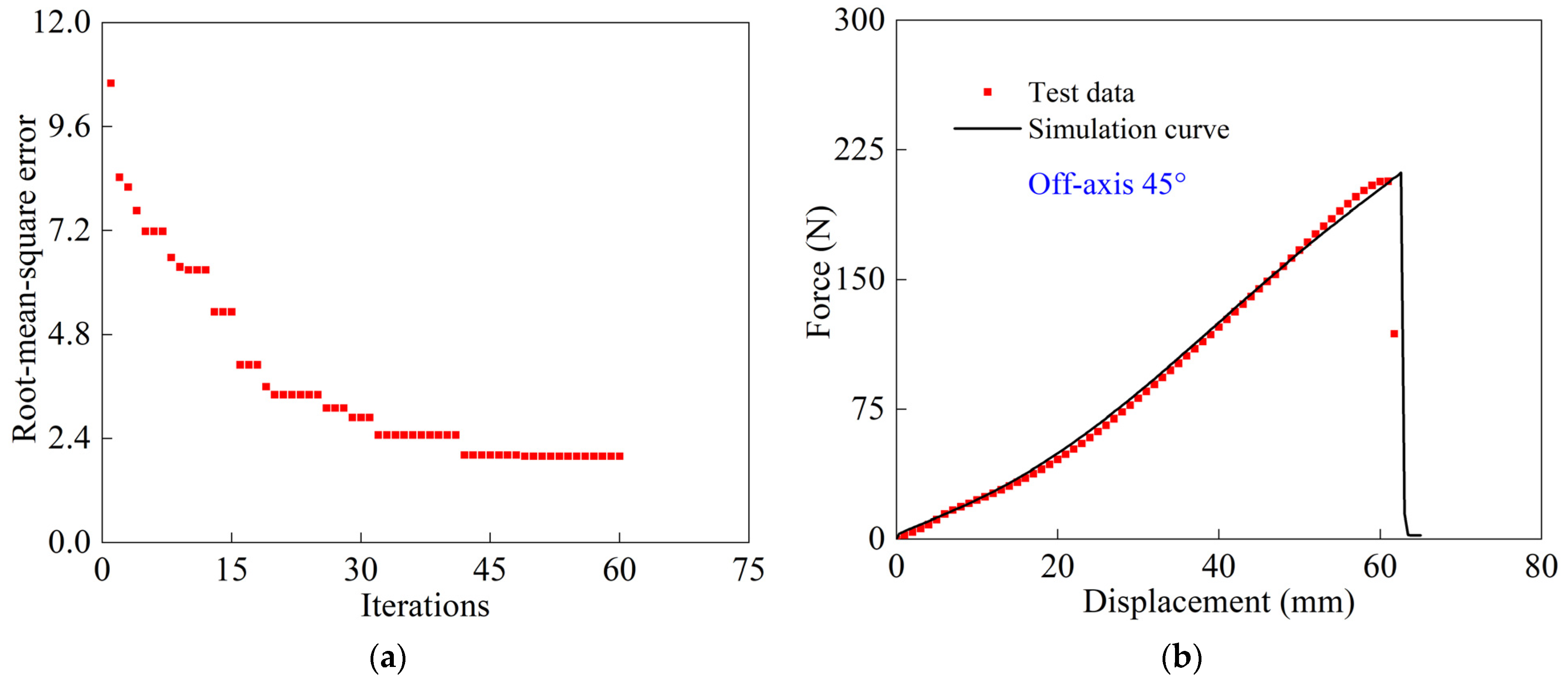
4.3. Constitutive Model Validation
4.4. Uniaxial Cyclic Test Simulation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Jabbar, M.; Adnan, M.; Shaker, K.; Abdullah, T.; Nawab, Y.; Hussain, R.; Malik, A. Strength and durability that last Mechanical propertiesof polyurea and polyurethane coated composites. Polym. Compos. 2023, 44, 4324–4335. [Google Scholar] [CrossRef]
- Xu, X.; Wang, G.; Yan, H.; Yao, X. Constitutive relationship of fabric rubber composites and its application. Compo. Struct. 2023, 304, 116302. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, J.; Zhang, Q. Advances in mechanical properties of coated fabrics in civil engineering. J. Ind. Text. 2016, 48, 255–271. [Google Scholar]
- Zhang, C.; Shao, H.; Liang, S.; Geng, Y.; Chen, N.; Gu, Z.; Jiang, J. Single edge crack effect on mechanical property of polyimide flexible composite envelope. Compos. Struct. 2021, 274, 114340. [Google Scholar] [CrossRef]
- Li, Z.; Li, W. Study on tensile strain of carbon fiber triaxial woven fabric/thermoplastic polyurethane flexible textile composites. Polym. Compos. 2024, 45, 2337–2351. [Google Scholar] [CrossRef]
- Roy, R.; Laha, A.; Awasthi, N.; Majumdar, A.; Butola, B. Multi Layered Natural Rubber Coated WovenP-aramidand UHMWPE Fabric Composites for Soft Body ArmorApplication. Polym. Compos. 2018, 39, 3636–3644. [Google Scholar] [CrossRef]
- Ambroziak, A.; Kłosowski, P. Mechanical properties for preliminary design of structures made from PVC coated fabric. Constr. Build. Mater. 2014, 50, 74–81. [Google Scholar] [CrossRef]
- Faal, R.; Sourki, R.; Crawford, B.; Vaziri, R.; Milani, A. Using fractional derivatives for improved viscoelastic modeling of textile composites. Part II: Fabric under different temperatures. Compos. Struct. 2020, 248, 112494. [Google Scholar] [CrossRef]
- Kabasi, S.; Marbaniang, A.; Ghosh, S. Physics-informed neural networks for the form-finding of tensile membranes by solving the Euler–Lagrange equation of minimal surfaces. Thin-Walled Struct. 2023, 182, 110309. [Google Scholar] [CrossRef]
- Marbaniang, A.; Kabasi, S.; Ghosh, S.; Dutta, S. Analysis and prestress optimisation of membrane structures with optimal fabric alignment using modified energy minimisation. Compos. Struct. 2023, 322, 117404. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, Y.; Zhao, Q.; Zhang, L. Experiment and simulation analysis on dynamic response of plane cable-membrane structure under impact load. Thin-Walled Struct. 2022, 171, 108814. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, Y.; Wu, M.; Li, X.; Zhang, L. Damping characteristics of the architectural coated fabric and its influence on the vibration response of membrane structures. Compos. Struct. 2022, 285, 115207. [Google Scholar] [CrossRef]
- Li, D.; Zheng, Z.; Tian, Y.; Sun, J.; He, X.; Lu, Y. Stochastic nonlinear vibration and reliability of orthotropic membrane structure under impact load. Thin-Walled Struct. 2017, 119, 247–255. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, J.; Zhou, Y.; Zhang, Q.; Wu, F. Central tearing behaviors of PVC coated fabrics with initial notch. Compos. Struct. 2019, 208, 618–633. [Google Scholar] [CrossRef]
- Sun, X.; He, R.; Wu, Y. A novel tearing residual strength model for architectural coated fabrics with central crack. Constr. Build. Mater. 2020, 263, 120133. [Google Scholar] [CrossRef]
- He, R.; Sun, X.; Wu, Y. Central crack tearing test and fracture parameter determination of PTFE coated fabric. Constr. Build. Mater. 2019, 208, 472–481. [Google Scholar] [CrossRef]
- Li, C.; Gao, J.; Chen, H.; Huang, Y.; Wang, P.; Li, X. Mechanical property degradation and structural failure of flexible laminated composite envelope upon exposure to high-altitude atmosphere. Compos. Sci. Technol. 2023, 241, 110100. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, S.; Xue, J.; Zhang, Q. Anisotropic mechanical properties and constitutive relations of PTFE coated glass fibers. Compos. Struct. 2017, 179, 601–616. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, Y.; Wu, M.; Zhao, Y. A phenomenological material model for PTFE coated fabrics. Constr. Build. Mater. 2020, 237, 117667. [Google Scholar] [CrossRef]
- Dib, W.; Bles, G.; Blaise, A.; Tourabi, A. Modelling of cyclic visco-elasto-plastic behaviour of coated woven fabrics under biaxial loading and finite strain. Int. J. Solids Struct. 2018, 154, 147–167. [Google Scholar] [CrossRef]
- Xu, G.; Qing, Q.; Yang, Y.; Gong, J. A practical biaxial time-dependent material model of PVDF-coated polyester fabrics for structural applications. Thin-Walled Struct. 2023, 186, 110666. [Google Scholar] [CrossRef]
- Dinh, T.; Rezaei, A.; De-Laet, L.; Mollaert, M.; Van-Hemelrijck, D.; Van-Paepegem, W. A new elasto-plastic material model for coated fabric. Eng. Struct. 2014, 71, 222–233. [Google Scholar] [CrossRef]
- Meng, J.; Hu, J.; Xiao, H.; Lv, M. Hierarchical optimization of the composite blade of a stratospheric airship propeller based on genetic algorithm. Struct. Multidisc. Optim. 2017, 56, 1341–1352. [Google Scholar] [CrossRef]
- Yang, X.; Wu, Z.; Yang, Y.; Pan, Y.; Wang, S.; Lei, H. Optimization Design of Cruciform Specimens for Biaxial Testing Based on Genetic Algorithm. J. Mater. Eng. Perform. 2022, 32, 2330–2343. [Google Scholar] [CrossRef]
- Bai, J.; Liu, T.; Wang, Z.; Lin, Q.; Cong, Q.; Wang, Y.; Ran, J.; Li, D.; Bu, G. Determining the best practice– Optimal designs of composite helical structures using Genetic Algorithms. Compos. Struct. 2021, 268, 113982. [Google Scholar] [CrossRef]
- Pourrajabian, A.; Dehghan, M.; Rahgozar, S. Genetic algorithms for the design and optimization of horizontal axis wind turbine (HAWT) blades: A continuous approach or a binary one? Sustain. Energy Technol. Assess. 2021, 44, 101022. [Google Scholar] [CrossRef]
- ISO 527-2; Plastics: Determination of Tensile Properties. Zwick/Roell: Ulm, Germany, 2012; p. 27.
- Xu, J.; Zhang, Y.; Wu, M.; Zhao, Y. Experimental analysis of off-axis mechanical behaviors of PVC coated fabrics subjected to cyclic loading. Polym. Test. 2019, 80, 106090. [Google Scholar] [CrossRef]
- Korus, K.; Salamak, M.; Jasinski, M. Optimization of geometric parameters of arch bridges using visual programming FEM components and genetic algorithm. Eng. Struct. 2021, 241, 112465. [Google Scholar] [CrossRef]










| Weight (g/m2) | Thickness (mm) | Tensile Strength (N/5 cm) | Weave Density (yarns/cm) | ||
|---|---|---|---|---|---|
| Warp | Weft | Warp | Weft | ||
| 750 | 0.73 | 2400 | 2100 | 8.5 | 8.5 |
| Warp | Weft | ||
|---|---|---|---|
| Variable | Value (Mpa) | Variable | Value (Mpa) |
| A1 | 1654.15 | B1 | 245.22 |
| A2 | −53,272.88 | B2 | 4172.43 |
| A3 | 975,249.21 | B3 | −89,829.62 |
| A4 | −9,123,857.73 | B4 | 746,159.5 |
| A5 | 42,965,800.57 | B5 | −2,649,681.06 |
| A6 | −79,551,644.73 | B6 | 3,517,207.21 |
| Variable | Value (Mpa) |
|---|---|
| C1 | 9.11 |
| C2 | 1.03 |
| C3 | 55.28 |
| Variable | Value (Mpa) |
|---|---|
| 998.72 | |
| 575.95 | |
| 69.87 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, L.; Zhang, Z.; Cai, D.; Zhou, G.; Wang, X. Modeling Analysis of Complex Deformation of Woven Coating Film during the Cyclic Tensile Process. Polymers 2024, 16, 1623. https://doi.org/10.3390/polym16121623
Cai L, Zhang Z, Cai D, Zhou G, Wang X. Modeling Analysis of Complex Deformation of Woven Coating Film during the Cyclic Tensile Process. Polymers. 2024; 16(12):1623. https://doi.org/10.3390/polym16121623
Chicago/Turabian StyleCai, Li, Zhengyan Zhang, Deng’an Cai, Guangming Zhou, and Xinwei Wang. 2024. "Modeling Analysis of Complex Deformation of Woven Coating Film during the Cyclic Tensile Process" Polymers 16, no. 12: 1623. https://doi.org/10.3390/polym16121623
APA StyleCai, L., Zhang, Z., Cai, D., Zhou, G., & Wang, X. (2024). Modeling Analysis of Complex Deformation of Woven Coating Film during the Cyclic Tensile Process. Polymers, 16(12), 1623. https://doi.org/10.3390/polym16121623








