A Multi-Objective Optimization of Neural Networks for Predicting the Physical Properties of Textile Polymer Composite Materials
Abstract
:1. Introduction
2. Materials and Methods
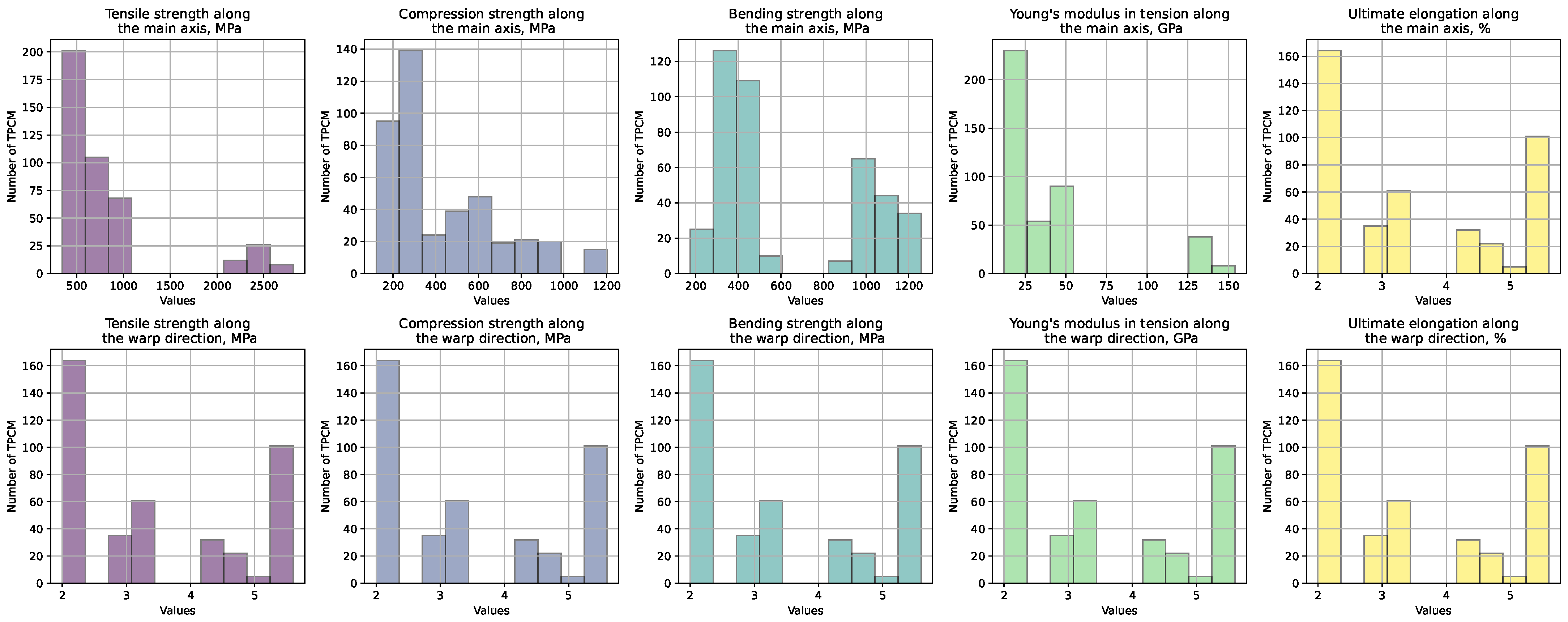
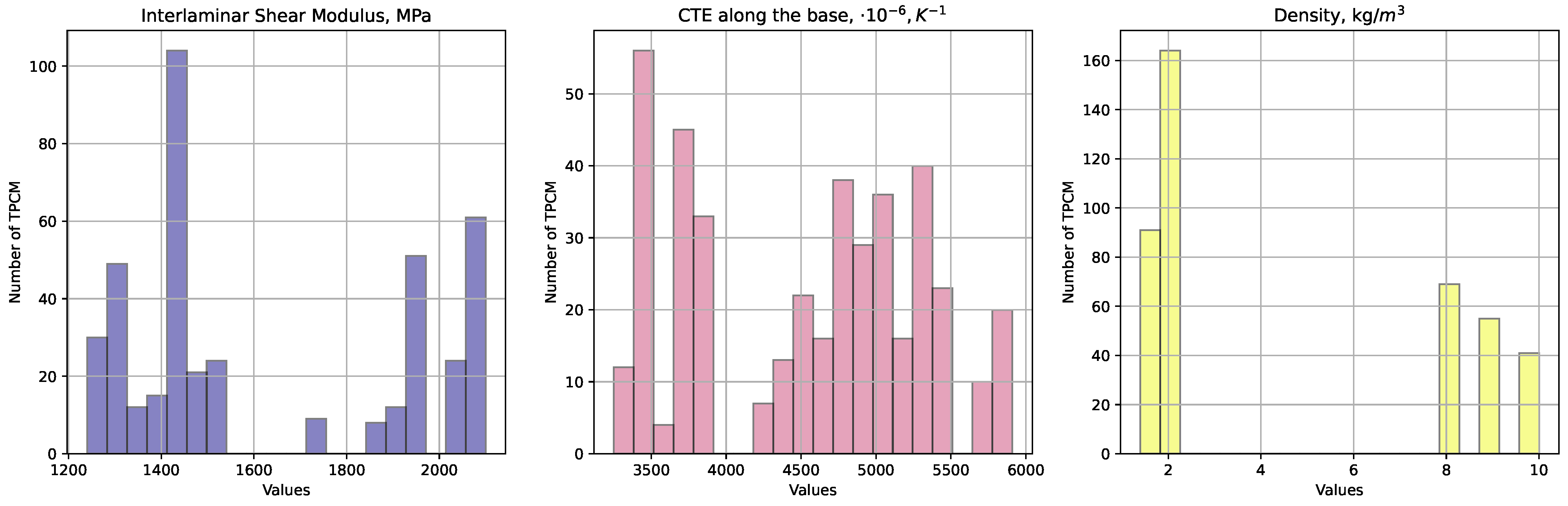
2.1. Dataset Description
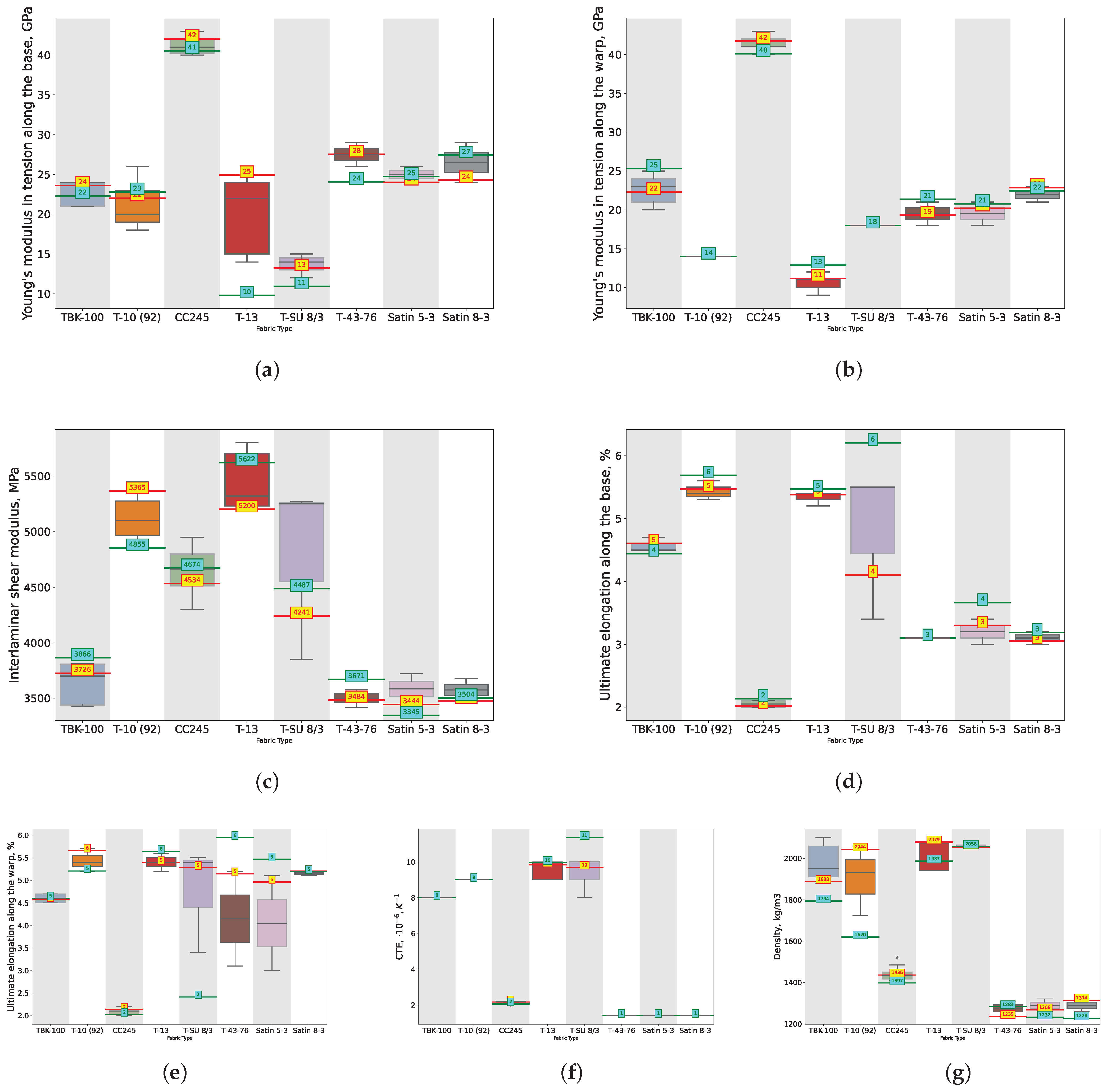
- Basalt plastic, designated as TBK-100 [70,71], is a composite material comprising basalt fibers [72] as the reinforcement phase embedded in a polymer matrix. Basalt fibers are derived from natural volcanic rock [73] and have high tensile strength and resistance to temperature variations. TBK-100 finds application in construction [74]. The weave pattern of these samples is canvas.
- Fiberglass-reinforced plastic, commonly known as fiberglass [75], is a composite material composed of fine glass fibers embedded in a polymer matrix, typically epoxy or polyester resin [76]. This material exhibits a high strength-to-weight ratio [77], excellent corrosion resistance [78,79], and dimensional stability [80], making it suitable for applications requiring durability and structural integrity [81]. We considered types such as T-10 [82], T-13 [83], T-11 [84], T-SU 8/3(VMP)-78 [85], and T-25 [86]. The fabric construction of these samples predominantly consisted of canvas [87] and satin weaves [88].
- Carbon fiber-reinforced plastic, also known as carbon fiber composite or carbon composite [89], consists of carbon fibers infused in a polymer matrix, often epoxy resin. This material offers exceptional strength, stiffness, and lightweight properties, making it ideal for aerospace [90], automotive [91], and sporting goods [92] applications where weight reduction and high performance are critical. We considered CC245 [93], CC206 [94], T700SC [95], UMT49 [96], UT-900-3 [97], HTS45 [98], and IMS65 [99]. The weave pattern observed in these samples primarily included twill [100] and unidirectional [101] weaves.
- Aramid fiber-reinforced plastic, or aramid composite [102], incorporates aramid fibers, such as Kevlar® [103], as the reinforcing component in a polymer matrix. Aramid fibers are known for their exceptional strength, stiffness, and resistance to impact and abrasion [104]. Aramid composites offer high tensile strength, heat resistance, and low weight, making them suitable for ballistic protection [105]. We considered varieties like T-43-76 [106], Satin 5/3 [107], Satin 8/3 [108], T-42-78 [109], and T-42/1-76 [110]. For this type of TPCM, the weave patterns also included canvas and satin.
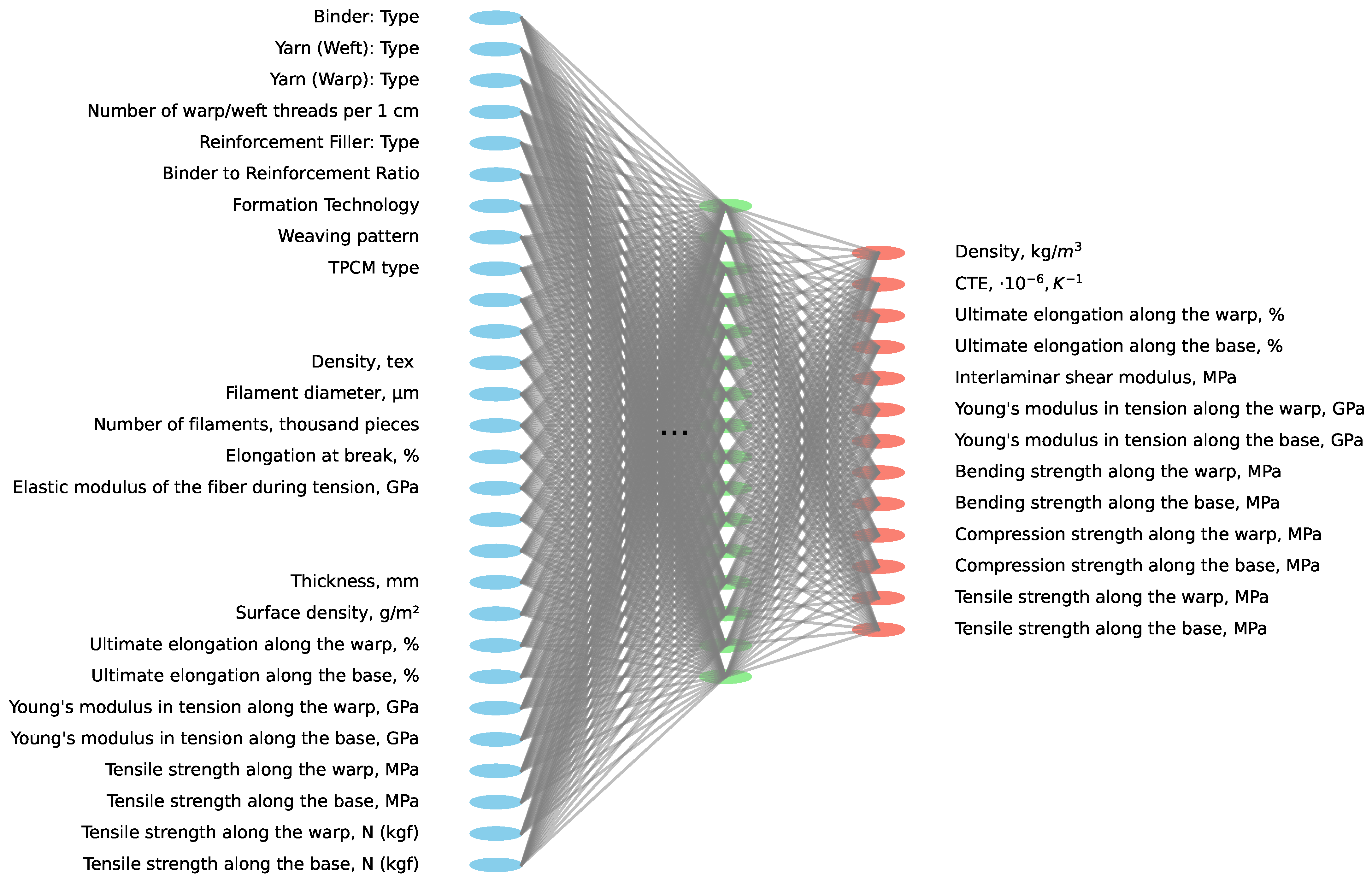
2.2. Model Development
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Hsissou, R.; Seghiri, R.; Benzekri, Z.; Hilali, M.; Rafik, M.; Elharfi, A. Polymer composite materials: A comprehensive review. Compos. Struct. 2021, 262, 113640. [Google Scholar] [CrossRef]
- Fan, J.; Njuguna, J. An introduction to lightweight composite materials and their use in transport structures. In Lightweight Composite Structures in Transport; Elsevier: Amsterdam, The Netherlands, 2016; pp. 3–34. [Google Scholar]
- Qian, D.; Bao, L.; Takatera, M.; Kemmochi, K.; Yamanaka, A. Fiber-reinforced polymer composite materials with high specific strength and excellent solid particle erosion resistance. Wear 2010, 268, 637–642. [Google Scholar] [CrossRef]
- Bazli, L.; Yusuf, M.; Farahani, A.; Kiamarzi, M.; Seyedhosseini, Z.; Nezhadmansari, M.; Aliasghari, M.; Iranpoor, M. Application of composite conducting polymers for improving the corrosion behavior of various substrates: A Review. J. Compos. Compd. 2020, 2, 228–240. [Google Scholar] [CrossRef]
- Dobrzański, L.; Drak, M.; Trzaska, J. Corrosion resistance of the polymer matrix hard magnetic composite materials Nd–Fe–B. J. Mater. Process. Technol. 2005, 164, 795–804. [Google Scholar] [CrossRef]
- Kangishwar, S.; Radhika, N.; Sheik, A.A.; Chavali, A.; Hariharan, S. A comprehensive review on polymer matrix composites: Material selection, fabrication, and application. Polym. Bull. 2023, 80, 47–87. [Google Scholar] [CrossRef]
- Ali, B.A.; Sapuan, S.; Zainudin, E.; Othman, M. Implementation of the expert decision system for environmental assessment in composite materials selection for automotive components. J. Clean. Prod. 2015, 107, 557–567. [Google Scholar]
- Sapuan, S.; Kho, J.; Zainudin, E.; Leman, Z.; Ali, B.; Hambali, A. Materials selection for natural fiber reinforced polymer composites using analytical hierarchy process. Indian J. Eng. Mater. Sci. 2011, 18, 255–267. [Google Scholar]
- DeArmitt, C.; Rothon, R. Particulate fillers, selection and use in polymer composites. In Encyclopedia of Polymers and Composites; Springer: Berlin/Heidelberg, Germany, 2017; pp. 1–19. [Google Scholar]
- Rajak, D.K.; Pagar, D.D.; Kumar, R.; Pruncu, C.I. Recent progress of reinforcement materials: A comprehensive overview of composite materials. J. Mater. Res. Technol. 2019, 8, 6354–6374. [Google Scholar] [CrossRef]
- Kamath, S.S.; Chandrappa, R.K. Additives used in natural fibre reinforced polymer composites—A review. Mater. Today Proc. 2022, 50, 1417–1424. [Google Scholar] [CrossRef]
- Lhamo, P.; Mahanty, B. Tuning material properties of microbially synthesized poly (3-hydroxybutyrate-co-hydroxyvalerate) and their composites for various applications. J. Polym. Environ. 2023, 31, 4641–4661. [Google Scholar] [CrossRef]
- Xue, T.; He, T.; Peng, L.; Syzgantseva, O.A.; Li, R.; Liu, C.; Sun, D.T.; Xu, G.; Qiu, R.; Wang, Y.; et al. A customized MOF-polymer composite for rapid gold extraction from water matrices. Sci. Adv. 2023, 9, eadg4923. [Google Scholar] [CrossRef]
- Krishnan, M.R.; Omar, H.; Almohsin, A.; Alsharaeh, E.H. An overview on nanosilica–polymer composites as high-performance functional materials in oil fields. Polym. Bull. 2024, 81, 3883–3933. [Google Scholar] [CrossRef]
- Yadav, R.; Singh, M.; Shekhawat, D.; Lee, S.Y.; Park, S.J. The role of fillers to enhance the mechanical, thermal, and wear characteristics of polymer composite materials: A review. Compos. Part A Appl. Sci. Manuf. 2023, 175, 107775. [Google Scholar] [CrossRef]
- Hasan, K.F.; Al Hasan, K.N.; Ahmed, T.; György, S.T.; Pervez, M.N.; Bejó, L.; Sándor, B.; Alpár, T. Sustainable bamboo fiber reinforced polymeric composites for structural applications: A mini review of recent advances and future prospects. Case Stud. Chem. Environ. Eng. 2023, 8, 100362. [Google Scholar] [CrossRef]
- Fu, X.; Lin, J.; Liang, Z.; Yao, R.; Wu, W.; Fang, Z.; Zou, W.; Wu, Z.; Ning, H.; Peng, J. Graphene oxide as a promising nanofiller for polymer composite. Surfaces Interfaces 2023, 37, 102747. [Google Scholar] [CrossRef]
- Xu, J.; Sun, J.; Zhao, J.; Zhang, W.; Zhou, J.; Xu, L.; Guo, H.; Liu, Y.; Zhang, D. Eco-friendly wood plastic composites with biomass-activated carbon-based form-stable phase change material for building energy conversion. Ind. Crop. Prod. 2023, 197, 116573. [Google Scholar] [CrossRef]
- Huseynov, O.; Hasanov, S.; Fidan, I. Influence of the matrix material on the thermal properties of the short carbon fiber reinforced polymer composites manufactured by material extrusion. J. Manuf. Process. 2023, 92, 521–533. [Google Scholar] [CrossRef]
- Al-Tamimi, A.A.; Tlija, M.; Abidi, M.H.; Anis, A.; Abd Elgawad, A.E.E. Material Extrusion of Multi-Polymer Structures Utilizing Design and Shrinkage Behaviors: A Design of Experiment Study. Polymers 2023, 15, 2683. [Google Scholar] [CrossRef] [PubMed]
- Zou, W.; Zheng, X.; Hu, X.; Huang, J.; Wang, G.; Guo, Z. Recent advances in injection molding of carbon fiber reinforced thermoplastic polymer composites: A review. ES Gen. 2023, 1, 938. [Google Scholar] [CrossRef]
- Barthod-Malat, B.; Hauguel, M.; Behlouli, K.; Grisel, M.; Savary, G. Influence of the Compression Molding Temperature on VOCs and Odors Produced from Natural Fiber Composite Materials. Coatings 2023, 13, 371. [Google Scholar] [CrossRef]
- Błachut, A.; Wollmann, T.; Panek, M.; Vater, M.; Kaleta, J.; Detyna, J.; Hoschützky, S.; Gude, M. Influence of fiber tension during filament winding on the mechanical properties of composite pressure vessels. Compos. Struct. 2023, 304, 116337. [Google Scholar] [CrossRef]
- Mayakannan, S.; Raj, J.B.; Raja, V.; Nagaraj, M. Effectiveness of silicon nanoparticles on the mechanical, wear, and physical characteristics of PALF/sisal fiber–based polymer hybrid nanocomposites. Biomass Convers. Biorefinery 2023, 13, 13291–13305. [Google Scholar] [CrossRef]
- Ali, A.; Koloor, S.S.R.; Alshehri, A.H.; Arockiarajan, A. Carbon nanotube characteristics and enhancement effects on the mechanical features of polymer-based materials and structures—A review. J. Mater. Res. Technol. 2023, 24, 6495–6521. [Google Scholar] [CrossRef]
- dos Anjos, E.G.; Moura, N.K.; Antonelli, E.; Baldan, M.R.; Gomes, N.A.; Braga, N.F.; Santos, A.P.; Rezende, M.C.; Pessan, L.A.; Passador, F.R. Role of adding carbon nanotubes in the electric and electromagnetic shielding behaviors of three different types of graphene in hybrid nanocomposites. J. Thermoplast. Compos. Mater. 2023, 36, 3209–3235. [Google Scholar] [CrossRef]
- Low, K.O.; Wong, K.J. Influence of ball burnishing on surface quality and tribological characteristics of polymers under dry sliding conditions. Tribol. Int. 2011, 44, 144–153. [Google Scholar] [CrossRef]
- Feih, S.; Mouritz, A.; Mathys, Z.; Gibson, A. Tensile strength modeling of glass fiber—polymer composites in fire. J. Compos. Mater. 2007, 41, 2387–2410. [Google Scholar] [CrossRef]
- Chang, S.M.; Hur, S.; Park, J.; Lee, D.G.; Shin, J.; Kim, H.S.; Song, S.E.; Baik, J.M.; Kim, M.; Song, H.C.; et al. Optimization of piezoelectric polymer composites and 3D printing parameters for flexible tactile sensors. Addit. Manuf. 2023, 67, 103470. [Google Scholar] [CrossRef]
- Wen, S.M.; Chen, S.M.; Gao, W.; Zheng, Z.; Bao, J.Z.; Cui, C.; Liu, S.; Gao, H.L.; Yu, S.H. Biomimetic Gradient Bouligand Structure Enhances Impact Resistance of Ceramic-Polymer Composites. Adv. Mater. 2023, 35, 2211175. [Google Scholar] [CrossRef] [PubMed]
- He, L.; Zhang, W.; Liu, X.; Tong, L. Substantial improvement of thermal conductivity and mechanical properties of polymer composites by incorporation of boron nitride nanosheets and modulation of thermal curing reaction. Polym. Compos. 2024, 45, 2215–2231. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, Z.; Weng, L.; Ge, S.; Jiang, D.; Huang, M.; Mulvihill, D.M.; Chen, Q.; Guo, Z.; Jazzar, A.; et al. A roadmap review of thermally conductive polymer composites: Critical factors, progress, and prospects. Adv. Funct. Mater. 2023, 33, 2301549. [Google Scholar] [CrossRef]
- Taye, M.M. Theoretical understanding of convolutional neural network: Concepts, architectures, applications, future directions. Computation 2023, 11, 52. [Google Scholar] [CrossRef]
- Roy, A.; Chakraborty, S. Support vector machine in structural reliability analysis: A review. Reliab. Eng. Syst. Saf. 2023, 233, 109126. [Google Scholar] [CrossRef]
- Hu, J.; Szymczak, S. A review on longitudinal data analysis with random forest. Briefings Bioinform. 2023, 24, bbad002. [Google Scholar] [CrossRef]
- Gao, Y.; Shigidi, I.M.; Ali, M.A.; Homod, R.Z.; Safaei, M.R. Thermophysical properties prediction of carbon-based nano-enhanced phase change material’s using various machine learning methods. J. Taiwan Inst. Chem. Eng. 2023, 148, 104662. [Google Scholar] [CrossRef]
- Fontes, A.; Shadmehri, F. Data-driven failure prediction of Fiber-Reinforced Polymer composite materials. Eng. Appl. Artif. Intell. 2023, 120, 105834. [Google Scholar] [CrossRef]
- Groenwold, A.A.; Haftka, R.T. Optimization with non-homogeneous failure criteria like Tsai–Wu for composite laminates. Struct. Multidiscip. Optim. 2006, 32, 183–190. [Google Scholar] [CrossRef]
- Rezasefat, M.; Gonzalez-Jimenez, A.; Giglio, M.; Manes, A. An evaluation of Cuntze and Puck inter fibre failure criteria in simulation of thin CFRP plates subjected to low velocity impact. Compos. Struct. 2021, 278, 114654. [Google Scholar] [CrossRef]
- Pimenta, S.; Pinho, S.T. Recycling carbon fibre reinforced polymers for structural applications: Technology review and market outlook. Waste Manag. 2011, 31, 378–392. [Google Scholar] [CrossRef]
- Fahem, N.; Belaidi, I.; Brahim, A.O.; Noori, M.; Khatir, S.; Wahab, M.A. Prediction of resisting force and tensile load reduction in GFRP composite materials using Artificial Neural Network-Enhanced Jaya Algorithm. Compos. Struct. 2023, 304, 116326. [Google Scholar] [CrossRef]
- Sathishkumar, T.; Satheeshkumar, S.; Naveen, J. Glass fiber-reinforced polymer composites—A review. J. Reinf. Plast. Compos. 2014, 33, 1258–1275. [Google Scholar] [CrossRef]
- Rajak, D.K.; Pagar, D.D.; Menezes, P.L.; Linul, E. Fiber-Reinforced Polymer Composites: Manufacturing, Properties, and Applications. Polymers 2019, 11, 1667. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Chi, A.; Mirjalili, S. Enhanced Jaya algorithm: A simple but efficient optimization method for constrained engineering design problems. Knowl.-Based Syst. 2021, 233, 107555. [Google Scholar] [CrossRef]
- Cervera, M.; Barbat, G.; Chiumenti, M.; Wu, J.Y. A comparative review of XFEM, mixed FEM and phase-field models for quasi-brittle cracking. Arch. Comput. Methods Eng. 2022, 29, 1009–1083. [Google Scholar] [CrossRef]
- Houssein, E.H.; Gad, A.G.; Wazery, Y.M. Jaya algorithm and applications: A comprehensive review. In Metaheuristics and Optimization in Computer and Electrical Engineering; Springer: Cham, Switzerland, 2021; pp. 3–24. [Google Scholar]
- Nayak, J.; Swapnarekha, H.; Naik, B.; Dhiman, G.; Vimal, S. 25 years of particle swarm optimization: Flourishing voyage of two decades. Arch. Comput. Methods Eng. 2023, 30, 1663–1725. [Google Scholar] [CrossRef]
- Nguyen, M.H.; D’Mello, R.J.; Waas, A.M. Use of a neural network constitutive model for the size-dependent effects of curing on the deformation response and failure of fiber-reinforced polymer matrix composites. Arch. Appl. Mech. 2023, 93, 369–387. [Google Scholar] [CrossRef]
- Gupta, S.; Mukhopadhyay, T.; Kushvaha, V. Microstructural image based convolutional neural networks for efficient prediction of full-field stress maps in short fiber polymer composites. Def. Technol. 2023, 24, 58–82. [Google Scholar] [CrossRef]
- Sharma, A.; Munde, Y.; Kushvaha, V. Representative volume element based micromechanical modelling of rod shaped glass filled epoxy composites. SN Appl. Sci. 2021, 3, 1–10. [Google Scholar] [CrossRef]
- Kim, S.; Lee, J.; Jeong, K.; Lee, J.; Hong, T.; An, J. Automated door placement in architectural plans through combined deep-learning networks of ResNet-50 and Pix2Pix-GAN. Expert Syst. Appl. 2024, 244, 122932. [Google Scholar] [CrossRef]
- El Said, B. Predicting the non-linear response of composite materials using deep recurrent convolutional neural networks. Int. J. Solids Struct. 2023, 276, 112334. [Google Scholar] [CrossRef]
- Koller, O.; Zargaran, S.; Ney, H. Re-sign: Re-aligned end-to-end sequence modelling with deep recurrent CNN-HMMs. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4297–4305. [Google Scholar]
- Reinaldo, A.A.; Javier, L.M.; Pablo, J.S. Multiscale formulation for saturated porous media preserving the representative volume element size objectivity. Int. J. Numer. Methods Eng. 2024, 125, e7381. [Google Scholar] [CrossRef]
- Zhang, H.; Li, B. Improvement of thermal protection performance of polymer composites based on optimized piecewise porosity distribution using a neural network method. Therm. Sci. Eng. Prog. 2023, 43, 102010. [Google Scholar] [CrossRef]
- Song, Y.; Qu, Z.; Liao, H.; Ai, S. Material twins generation of woven polymer composites based on ResL-U-Net convolutional neural networks. Compos. Struct. 2023, 307, 116672. [Google Scholar] [CrossRef]
- Xu, J.; Li, Z.; Du, B.; Zhang, M.; Liu, J. Reluplex made more practical: Leaky ReLU. In Proceedings of the 2020 IEEE Symposium on Computers and Communications (ISCC), Rennes, France, 7–10 July 2020; pp. 1–7. [Google Scholar]
- Li, M.; Li, S.; Tian, Y.; Fu, Y.; Pei, Y.; Zhu, W.; Ke, Y. A deep learning convolutional neural network and multi-layer perceptron hybrid fusion model for predicting the mechanical properties of carbon fiber. Mater. Des. 2023, 227, 111760. [Google Scholar] [CrossRef]
- Chen, L.; Hao, L.; Liu, S.; Ding, G.; Sun, X.; Zhang, W.; Li, F.; Jiao, W.; Yang, F.; Xu, Z.; et al. Modulus distribution in polyacrylonitrile-based carbon fiber monofilaments. Carbon 2020, 157, 47–54. [Google Scholar] [CrossRef]
- Li, M.; Zhang, H.; Ma, J.; Li, S.; Zhu, W.; Ke, Y. Greedy-based approach for generating anisotropic random fiber distributions of unidirectional composites and transverse mechanical properties prediction. Comput. Mater. Sci. 2023, 218, 111966. [Google Scholar] [CrossRef]
- Doddashamachar, M.; Sen, S.; Nama Vasudeva Setty, R. A novel Artificial Neural Network-based model for predicting dielectric properties of banana fiber filled with polypropylene composites. J. Thermoplast. Compos. Mater. 2023, 36, 4106–4123. [Google Scholar] [CrossRef]
- Arpitha, G.; Jain, N.; Verma, A. Banana biofiber and glass fiber reinforced hybrid composite for lightweight structural applications: Mechanical, thermal, and microstructural characterization. Biomass Convers. Biorefinery 2023, 1–10. [Google Scholar] [CrossRef]
- Amor, N.; Noman, M.T.; Petru, M.; Sebastian, N.; Balram, D. A review on computational intelligence methods for modelling of light weight composite materials. Appl. Soft Comput. 2023, 147, 110812. [Google Scholar] [CrossRef]
- Mukhopadhyay, S. Artificial Neural Network Applications in Textile Composites; Soft Computing in Textile Engineering; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Amor, N.; Noman, M.T.; Petru, M. Classification of textile polymer composites: Recent trends and challenges. Polymers 2021, 13, 2592. [Google Scholar] [CrossRef]
- Borhanazad, H.; Mekhilef, S.; Ganapathy, V.G.; Modiri-Delshad, M.; Mirtaheri, A. Optimization of micro-grid system using MOPSO. Renew. Energy 2014, 71, 295–306. [Google Scholar] [CrossRef]
- Verma, S.; Pant, M.; Snasel, V. A comprehensive review on NSGA-II for multi-objective combinatorial optimization problems. IEEE Access 2021, 9, 57757–57791. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, D. An improved SPEA2 algorithm with local search for multi-objective investment decision-making. Appl. Sci. 2019, 9, 1675. [Google Scholar] [CrossRef]
- Cervantes, J.; Garcia-Lamont, F.; Rodríguez-Mazahua, L.; Lopez, A. A comprehensive survey on support vector machine classification: Applications, challenges and trends. Neurocomputing 2020, 408, 189–215. [Google Scholar] [CrossRef]
- Sapozhnikov, S.; Kudryavtsev, O. Modeling of thermoplastic composites used in protective structures. Mech. Compos. Mater. 2015, 51, 419–426. [Google Scholar] [CrossRef]
- Kreutzer-Schmid, C.; Schmid, H.P. The prosomal protein of 27 kDa and a nuclear 38 kDa protein are immunologically related. FEBS Lett. 1990, 267, 142–146. [Google Scholar] [CrossRef] [PubMed]
- Hashim, U.R.; Jumahat, A.; Jawaid, M.; Dungani, R.; Alamery, S. Effects of accelerated weathering on degradation behavior of basalt fiber reinforced polymer nanocomposites. Polymers 2020, 12, 2621. [Google Scholar] [CrossRef] [PubMed]
- Jamshaid, H.; Mishra, R. A green material from rock: Basalt fiber—A review. J. Text. Inst. 2016, 107, 923–937. [Google Scholar] [CrossRef]
- Kozinets, G.L.; Chernov, P.V.; Kolotvina, N.S.; Zotov, D.K.; Kärki, T.; Lahtela, V. Optimization of wooden constructions with basalt-based materials. In Proceedings of the International Seminar, Saint Petersburg, Germany, 25 May 2021; pp. 7–20. [Google Scholar]
- Wallenberger, F.T.; Bingham, P.A. Fiberglass and Glass Technology. Energy-Friendly Compositions And Applications; Springer: New York, NY, USA, 2010. [Google Scholar]
- Patel, A.; Kravchenko, O.; Manas-Zloczower, I. Effect of curing rate on the microstructure and macroscopic properties of epoxy fiberglass composites. Polymers 2018, 10, 125. [Google Scholar] [CrossRef] [PubMed]
- Poopakdee, N.; Thammawichai, W. Improvement on cost-performance ratio of fiberglass/carbon fiber hybrid composite. J. Met. Mater. Miner. 2021, 31. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, X.; Qin, Z.; Wu, Y.; Zhang, W.; Yang, R. High-transparency polysilsesquioxane/glycidyl-azide-polymer resin and its fiberglass-reinforced composites with excellent fire resistance, mechanical properties, and water resistance. Compos. Part B Eng. 2021, 219, 108913. [Google Scholar] [CrossRef]
- Trentin, A.; Pakseresht, A.; Duran, A.; Castro, Y.; Galusek, D. Electrochemical characterization of polymeric coatings for corrosion protection: A review of advances and perspectives. Polymers 2022, 14, 2306. [Google Scholar] [CrossRef] [PubMed]
- Thomason, J.; Ali, J. The dimensional stability of glass–fibre reinforced polyamide 66 during hydrolysis conditioning. Compos. Part A Appl. Sci. Manuf. 2009, 40, 625–634. [Google Scholar] [CrossRef]
- Stickel, J.M.; Nagarajan, M. Glass fiber-reinforced composites: From formulation to application. Int. J. Appl. Glass Sci. 2012, 3, 122–136. [Google Scholar] [CrossRef]
- Kalinin, Y.E.; Kudrin, A.; Ovdak, O.; Popov, I. Internal friction in an epoxy polymer and a fiberglass reinforced plastic based on it. Polym. Sci. Ser. A 2022, 64, 1–9. [Google Scholar] [CrossRef]
- Tusnin, A.; Nikolay, L.; Aleksandr, K. The Load-Bearing Capacity and Deformability of Connections of Wooden Elements with Composite Materials Based on Fiberglass. Buildings 2023, 13, 3063. [Google Scholar] [CrossRef]
- Bashkov, O.; Bryansky, A. Cluster analysis of the acoustic emission signals registered during bending deformation of FGRP. AIP Conf. Proc. 2023, 2899, 020013. [Google Scholar]
- Gorev, Y.A.; Rivkind, V. Polyester composites for shipbuilding. Russ. J. Gen. Chem. 2010, 80, 2098–2114. [Google Scholar] [CrossRef]
- Chermoshentseva, A.; Pokrovskiy, A.; Bokhoeva, L. The behavior of delaminations in composite materials-experimental results. IOP Conf. Ser. Mater. Sci. Eng. 2016, 116, 012005. [Google Scholar] [CrossRef]
- Shmoilov, E.; Fedotov, M.; Sharutin, I.; Ilyukhin, R.; Stepanov, S.; Panina, N.; Gurenchuk, L.; Kapyrin, P.; Kabantsev, O.; Kornev, O. Polymer Composites for External Reinforcement of Building Structures. Int. J. Comput. Civ. Struct. Eng. 2024, 20, 21–34. [Google Scholar]
- Liang, B.; Zhao, Z.; Cheng, H.; Boisse, P.; Zhang, K.; Luo, B. A combined method for analyzing the effective thermal conductivity evolution of satin weave thermoset prepregs during preforming process. Int. J. Therm. Sci. 2022, 177, 107574. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Q.; Chen, G. Carbon and carbon composites for thermoelectric applications. Carbon Energy 2020, 2, 408–436. [Google Scholar] [CrossRef]
- Srinivasan, V.; Kunjiappan, S.; Palanisamy, P. A brief review of carbon nanotube reinforced metal matrix composites for aerospace and defense applications. Int. Nano Lett. 2021, 11, 321–345. [Google Scholar] [CrossRef]
- Ahmad, H.; Markina, A.; Porotnikov, M.; Ahmad, F. A review of carbon fiber materials in automotive industry. IOP Conf. Ser. Mater. Sci. Eng. 2020, 971, 032011. [Google Scholar] [CrossRef]
- Sharma, S.; Sudhakara, P.; Misra, S.; Singh, J. A comprehensive review of current developments on the waste-reinforced polymer-matrix composites for automotive, sports goods and construction applications: Materials, processes and properties. Mater. Today Proc. 2020, 33, 1671–1679. [Google Scholar] [CrossRef]
- Garifullin, A.; Krasina, I.; Skidchenko, E.; Shaekhov, M.; Tikhonova, N. Modification of carbon fabrics by radio-frequency capacitive discharge at low pressure to regulate mechanical properties of carbon fiber reinforced plastics based on it. J. Phys. Conf. Ser. 2017, 789, 012014. [Google Scholar] [CrossRef]
- Ghiringhelli, G.; Terraneo, M.; Vigoni, E. Improvement of structures vibroacoustics by widespread embodiment of viscoelastic materials. Aerosp. Sci. Technol. 2013, 28, 227–241. [Google Scholar] [CrossRef]
- Wang, Z.; Dong, S.; Ding, Y.; Zhang, X.; Zhou, H.; Yang, J.; Lu, B. Mechanical properties and microstructures of Cf/SiC–ZrC composites using T700SC carbon fibers as reinforcements. Ceram. Int. 2011, 37, 695–700. [Google Scholar] [CrossRef]
- Slovikov, S.; Babushkin, A.; Gusina, M. Nonlinearity of compression behavior of 3D-epoxy reinforced with carbon fibers composites. Frat. Integrità Strutt. 2023, 17, 311–321. [Google Scholar] [CrossRef]
- Gordeev, Y.I.; Binchurov, A.; Yasinskii, V.; Pikalov, Y.Y.; Vakulin, M.; Kazakov, I. Influence of Cutting Conditions and End Mill Geometry on the Surface Quality in High-Speed Machining of Carbon Composites. Russ. Eng. Res. 2023, 43, 592–597. [Google Scholar] [CrossRef]
- Käppler, I.; Hund, R.D.; Cherif, C. Surface modification of carbon fibres using plasma technique. Autex Res. J. 2014, 14, 34–38. [Google Scholar] [CrossRef]
- Kravchuk, L.; Buiskikh, K.; Derevyanko, I.; Potapov, O. Load-bearing capacity of elements of composite shell structures in rocket and space engineering made of composite materials. Strength Mater. 2022, 54, 613–621. [Google Scholar] [CrossRef]
- Chairman, C.A.; Jayasathyakawin, S.; Babu, S.K.; Ravichandran, M. Mechanical properties of basalt fabric plain and twill weave reinforced epoxy composites. Mater. Today Proc. 2021, 46, 9480–9483. [Google Scholar] [CrossRef]
- Ahmed, U.; Tariq, A.; Nawab, Y.; Shaker, K.; Khaliq, Z.; Umair, M. Comparison of mechanical behavior of biaxial, unidirectional and standard woven fabric reinforced composites. Fibers Polym. 2020, 21, 1308–1315. [Google Scholar] [CrossRef]
- Fan, Y.; Li, Z.; Wei, J. Application of aramid nanofibers in nanocomposites: A brief review. Polymers 2021, 13, 3071. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Li, X.; Shen, J.; Gao, C.; Van der Bruggen, B. The potential of Kevlar aramid nanofiber composite membranes. J. Mater. Chem. A 2020, 8, 7548–7568. [Google Scholar] [CrossRef]
- Bijwe, J.; Awtade, S.; Ghosh, A. Influence of orientation and volume fraction of Aramid fabric on abrasive wear performance of polyethersulfone composites. Wear 2006, 260, 401–411. [Google Scholar] [CrossRef]
- Farias-Aguilar, J.; Ramírez-Moreno, M.; Gonzalez-García, D.; Téllez-Jurado, L.; Balmori-Ramirez, H. Evaluation of the ballistic protection level of (glass-fiber reinforced polyamide 6)-aramid fabric sandwich composite panels. J. Mater. Res. Technol. 2021, 12, 1606–1614. [Google Scholar] [CrossRef]
- Dos Santos, D.; Carbas, R.; Marques, E.; Da Silva, L. Reinforcement of CFRP joints with fibre metal laminates and additional adhesive layers. Compos. Part B Eng. 2019, 165, 386–396. [Google Scholar] [CrossRef]
- Xiaobo, Y.; Binjie, X.; Baciu, G.; Jinlian, H. Fourier-analysis based satin fabric density and weaving pattern extraction. Res. J. Text. Appar. 2007, 11, 71. [Google Scholar]
- Saiman, M.; Wahab, M.; Wahit, M. The effect of fabric weave on the tensile strength of woven kenaf reinforced unsaturated polyester composite. In Proceedings of the International Colloquium in Textile Engineering, Fashion, Apparel and Design 2014 (ICTEFAD 2014); Springer: Singapore, 2014; pp. 25–29. [Google Scholar]
- Lobkovskiy, S.; Shaydurova, G.; Zubarev, S. Study of waste utilization technology generated during the production of rocket engine casings from polymer composite materials. Ecol. Ind. Russ. 2016, 20, 10–15. [Google Scholar]
- Barannikov, A.A.; Veshkin, E.A.; Postnov, V.I.; Strelnikov, S.V. On the issue of producing PCM floor panels for aircraft (review article). Proc. Samara Sci. Cent. Russ. Acad. Sci. 2017, 19, 198–213. [Google Scholar]
- Karamzadeh, N.S.; Aliha, M.; Karimi, H.R. Investigation of the effect of components on tensile strength and mode-I fracture toughness of polymer concrete. Arab. J. Geosci. 2022, 15, 1213. [Google Scholar] [CrossRef]
- Mohammed, A.; Mahmood, W.; Ghafor, K. TGA, rheological properties with maximum shear stress and compressive strength of cement-based grout modified with polycarboxylate polymers. Constr. Build. Mater. 2020, 235, 117534. [Google Scholar] [CrossRef]
- Iqbal, M.; Aminanda, Y.; Firsa, T.; Nazaruddin, N.; Nasution, I.S.; Erawan, D.F.; Saputra, D.A.; Nasution, A.R. The effect of fiber content and fiber orientation on bending strength of abaca fiber reinforce polymer composite fabricated by press method. AIP Conf. Proc. 2023, 2643, 050055. [Google Scholar]
- Kim, S.; Lee, Y.; Lee, M.; An, S.; Cho, S.J. Quantitative visualization of the nanomechanical Young’s modulus of soft materials by atomic force microscopy. Nanomaterials 2021, 11, 1593. [Google Scholar] [CrossRef] [PubMed]
- Akagi, Y.; Katashima, T.; Sakurai, H.; Chung, U.i.; Sakai, T. Ultimate elongation of polymer gels with controlled network structure. RSC Adv. 2013, 3, 13251–13258. [Google Scholar] [CrossRef]
- Yavas, D.; Zhang, Z.; Liu, Q.; Wu, D. Interlaminar shear behavior of continuous and short carbon fiber reinforced polymer composites fabricated by additive manufacturing. Compos. Part B Eng. 2021, 204, 108460. [Google Scholar] [CrossRef]
- Kamarian, S.; Bodaghi, M.; Isfahani, R.B.; Shakeri, M.; Yas, M. Influence of carbon nanotubes on thermal expansion coefficient and thermal buckling of polymer composite plates: Experimental and numerical investigations. Mech. Based Des. Struct. Mach. 2021, 49, 217–232. [Google Scholar] [CrossRef]
- Wei, J.; Zhu, L. Intrinsic polymer dielectrics for high energy density and low loss electric energy storage. Prog. Polym. Sci. 2020, 106, 101254. [Google Scholar] [CrossRef]
- Zouambi, M.; Dhaenens, C.; Jacques, J. An Alternative Pareto-based Approach to Multi-objective Neural Architecture Search. In Proceedings of the 2023 IEEE Congress on Evolutionary Computation (CEC), Chicago, IL, USA, 1– 5 July 2023; pp. 1–8. [Google Scholar]
- Ngo, S.T.; Jaafar, J.; Aziz, I.A.; Tong, G.T.; Nguyen, G.H.; Bui, A.N. Different Approaches of Evolutionary Algorithms to Multiple Objective RCPSP. In Proceedings of the 7th International Conference on Big Data and Computing, Yogyakarta, Indonesia, 7–11 November 2022; pp. 58–66. [Google Scholar]
- Wan, L.; Deng, K.; Li, X.; Zhao, L.; Long, J. Multi-objective optimization strategy for industrial catalytic cracking units: Kinetic model and enhanced SPEA-2 algorithm with economic, CO2, and SO2 emission considerations. Chem. Eng. Sci. 2023, 282, 119331. [Google Scholar] [CrossRef]
- Mohanty, R.; Das, S.K.; Mohanty, M. Shear Wave Velocity-Based Liquefaction Susceptibility of Soil Using Extreme Learning Machine (ELM) with Strength Pareto Evolutionary Algorithm (SPEA 2). In Earthquake Geotechnics: Select Proceedings of 7th ICRAGEE 2021; Springer: Singapore, 2022; pp. 33–44. [Google Scholar]
- Zhang, X.; Wang, J.; Zhou, Y.; Wang, H.; Xie, N. A multi-objective optimization method for enclosed-space lighting design based on MOPSO. Build. Environ. 2024, 250, 111185. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, Z.; Liu, X.; Dan, H.; Xiong, W.; Ling, T.; Su, M. Weighting factor design based on SVR–MOPSO for finite set MPC operated power electronic converters. J. Power Electron. 2022, 22, 1085–1099. [Google Scholar] [CrossRef]
- Guo, X.; Zhu, C.; Hao, J.; Zhang, S. Multi-step wind speed prediction based on an improved multi-objective seagull optimization algorithm and a multi-kernel extreme learning machine. Appl. Intell. 2023, 53, 16445–16472. [Google Scholar] [CrossRef]
- Vapnik, V.; Izmailov, R. Reinforced SVM method and memorization mechanisms. Pattern Recognit. 2021, 119, 108018. [Google Scholar] [CrossRef]
- Tettelaar, K. Towards Multi-Objective Bayesian Global Optimization for Space Missions. Master’s Thesis, Leiden Institute of Advanced Computer Science, Leiden, The Netherlands, 2020. [Google Scholar]
- Hassanat, A.; Almohammadi, K.; Alkafaween, E.; Abunawas, E.; Hammouri, A.; Prasath, V.S. Choosing mutation and crossover ratios for genetic algorithms—A review with a new dynamic approach. Information 2019, 10, 390. [Google Scholar] [CrossRef]
- Nti, I.K.; Nyarko-Boateng, O.; Aning, J. Performance of machine learning algorithms with different K values in K-fold cross-validation. Int. J. Inf. Technol. Comput. Sci. 2021, 13, 61–71. [Google Scholar]
- Hodson, T.O. Root mean square error (RMSE) or mean absolute error (MAE): When to use them or not. Geosci. Model Dev. Discuss. 2022, 15, 5481–5487. [Google Scholar] [CrossRef]
- Abdul-Muneer, P. Application of microsatellite markers in conservation genetics and fisheries management: Recent advances in population structure analysis and conservation strategies. Genet. Res. Int. 2014, 2014, 691759. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X. Differential Evolution without the Scale Factor and the Crossover Probability. J. Math. 2023, 2023, 8973912. [Google Scholar] [CrossRef]
- Li, Q.; Ma, Z. A hybrid dynamic probability mutation particle swarm optimization for engineering structure design. Mob. Inf. Syst. 2021, 2021, 1–32. [Google Scholar] [CrossRef]
- Angelova, M.; Pencheva, T. Tuning genetic algorithm parameters to improve convergence time. Int. J. Chem. Eng. 2011, 2011. [Google Scholar] [CrossRef]
- Manjula Devi, R.; Kuppuswami, S.; Suganthe, R. Fast linear adaptive skipping training algorithm for training artificial neural network. Math. Probl. Eng. 2013, 2013. [Google Scholar] [CrossRef]
- Johny, A.; Madhusoodanan, K. Dynamic learning rate in deep CNN model for metastasis detection and classification of histopathology images. Comput. Math. Methods Med. 2021, 2021, 5557168. [Google Scholar] [CrossRef] [PubMed]
- Lalwani, S.; Singhal, S.; Kumar, R.; Gupta, N. A comprehensive survey: Applications of multi-objective particle swarm optimization (MOPSO) algorithm. Trans. Comb. 2013, 2, 39–101. [Google Scholar]
- Klincewicz, J.G. Avoiding local optima in the p-hub location problem using tabu search and GRASP. Ann. Oper. Res. 1992, 40, 283–302. [Google Scholar] [CrossRef]
- Lin, Q.; Li, J.; Du, Z.; Chen, J.; Ming, Z. A novel multi-objective particle swarm optimization with multiple search strategies. Eur. J. Oper. Res. 2015, 247, 732–744. [Google Scholar] [CrossRef]
- Qasem, S.; Shamsuddin, S. Generalization improvement of radial basis function network based on multi-objective particle swarm optimization. J. Artif. Intell 2010, 3, 1–16. [Google Scholar] [CrossRef]
- Mannodi-Kanakkithodi, A.; Pilania, G.; Ramprasad, R.; Lookman, T.; Gubernatis, J.E. Multi-objective optimization techniques to design the Pareto front of organic dielectric polymers. Comput. Mater. Sci. 2016, 125, 92–99. [Google Scholar] [CrossRef]
- García-Carrillo, M.; Espinoza-Martínez, A.B.; Ramos-de Valle, L.F.; Sánchez-Valdés, S. Simultaneous optimization of thermal and electrical conductivity of high density polyethylene-carbon particle composites by artificial neural networks and multi-objective genetic algorithm. Comput. Mater. Sci. 2022, 201, 110956. [Google Scholar] [CrossRef]
- Kong, Y.; Mei, Y.; Wang, X.; Ben, Y. Solution selection from a pareto optimal set of multi-objective reservoir operation via clustering operation processes and objective values. Water 2021, 13, 1046. [Google Scholar] [CrossRef]
- Montavon, G.; Binder, A.; Lapuschkin, S.; Samek, W.; Müller, K.R. Layer-wise relevance propagation: An overview. In Explainable AI: Interpreting, Explaining and Visualizing Deep Learning; Springer: Cham, Switzerland, 2019; pp. 193–209. [Google Scholar]
- Pickering, B.; Choudhary, R. Quantifying resilience in energy systems with out-of-sample testing. Appl. Energy 2021, 285, 116465. [Google Scholar] [CrossRef]
- Talebi, H.; Silani, M.; Bordas, S.P.; Kerfriden, P.; Rabczuk, T. A computational library for multiscale modeling of material failure. Comput. Mech. 2014, 53, 1047–1071. [Google Scholar] [CrossRef]
- Liu, B.; Vu-Bac, N.; Rabczuk, T. A stochastic multiscale method for the prediction of the thermal conductivity of Polymer nanocomposites through hybrid machine learning algorithms. Compos. Struct. 2021, 273, 114269. [Google Scholar] [CrossRef]
- Vu-Bac, N.; Lahmer, T.; Zhang, Y.; Zhuang, X.; Rabczuk, T. Stochastic predictions of interfacial characteristic of polymeric nanocomposites (PNCs). Compos. Part B Eng. 2014, 59, 80–95. [Google Scholar] [CrossRef]
- Bakar, I.A.A.; Kramer, O.; Bordas, S.; Rabczuk, T. Optimization of elastic properties and weaving patterns of woven composites. Compos. Struct. 2013, 100, 575–591. [Google Scholar] [CrossRef]
- Nguyen-Thanh, V.M.; Anitescu, C.; Alajlan, N.; Rabczuk, T.; Zhuang, X. Parametric deep energy approach for elasticity accounting for strain gradient effects. Comput. Methods Appl. Mech. Eng. 2021, 386, 114096. [Google Scholar] [CrossRef]
- Cuomo, S.; Di Cola, V.S.; Giampaolo, F.; Rozza, G.; Raissi, M.; Piccialli, F. Scientific machine learning through physics–informed neural networks: Where we are and what’s next. J. Sci. Comput. 2022, 92, 88. [Google Scholar] [CrossRef]
- Dimas, E.; Briassoulis, D. 3D geometric modelling based on NURBS: A review. Adv. Eng. Softw. 1999, 30, 741–751. [Google Scholar] [CrossRef]



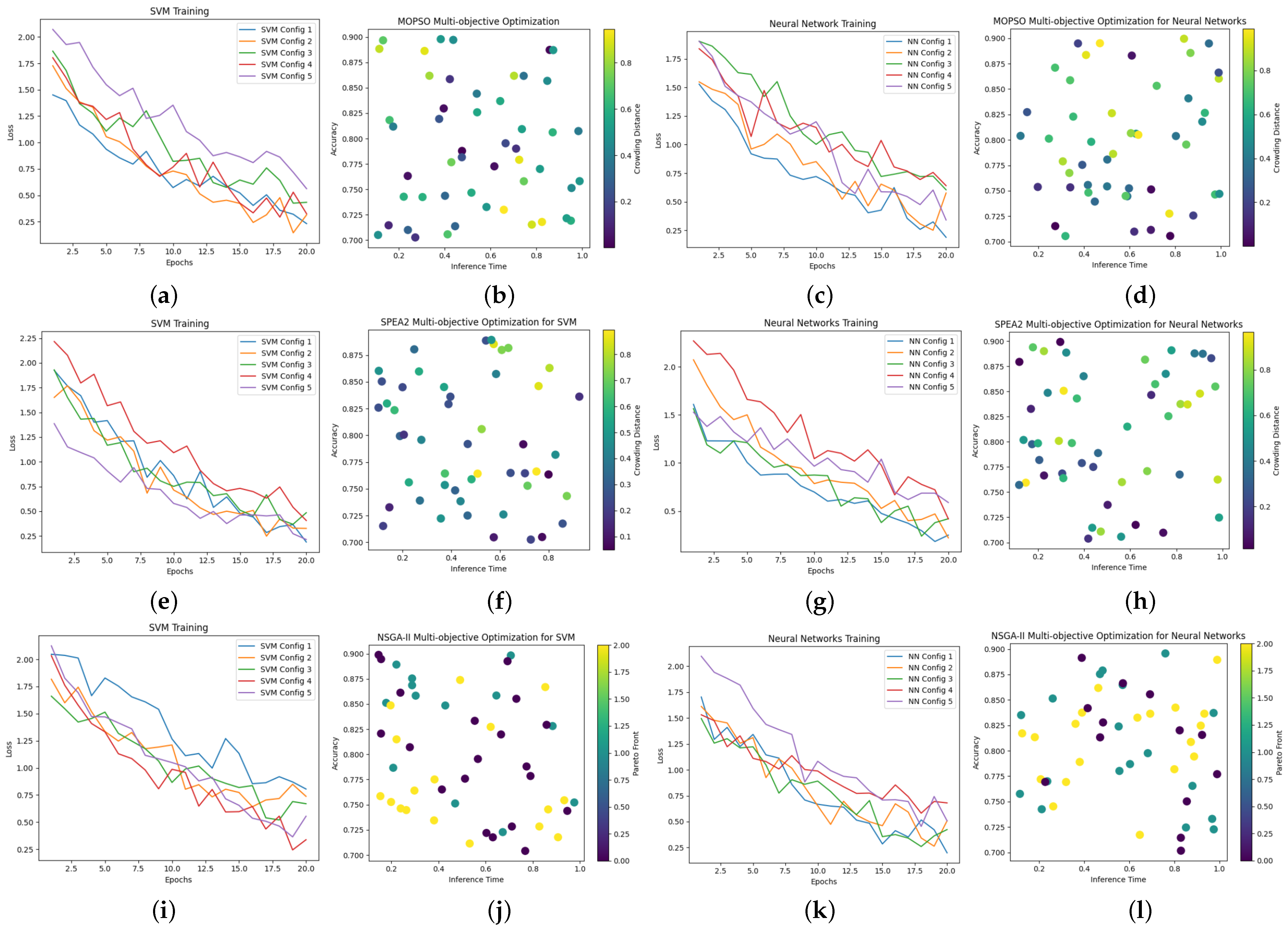

| ML Model | Optimized Value | MOPSO | SPEA2 | NSGA-II |
|---|---|---|---|---|
| SVM | accuracy | 0.878 | 0.876 | 0.899 |
| inference time, ms | 0.88 | 0.85 | 0.78 | |
| Parameters (C, ) | (1.0, 0.1) | (1.2, 0.08) | (0.9, 0.15) | |
| ANN | accuracy | 0.902 | 0.901 | 0.898 |
| inference time, ms | 0.42 | 0.36 | 0.43 | |
| Architecture (layers, neurons, activation) | (4, [4, 28, 20, 12], ReLU) | (4, [2, 16, 8, 16], sigmoid) | (3, [6, 4, 8], tanh) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malashin, I.; Tynchenko, V.; Gantimurov, A.; Nelyub, V.; Borodulin, A. A Multi-Objective Optimization of Neural Networks for Predicting the Physical Properties of Textile Polymer Composite Materials. Polymers 2024, 16, 1752. https://doi.org/10.3390/polym16121752
Malashin I, Tynchenko V, Gantimurov A, Nelyub V, Borodulin A. A Multi-Objective Optimization of Neural Networks for Predicting the Physical Properties of Textile Polymer Composite Materials. Polymers. 2024; 16(12):1752. https://doi.org/10.3390/polym16121752
Chicago/Turabian StyleMalashin, Ivan, Vadim Tynchenko, Andrei Gantimurov, Vladimir Nelyub, and Aleksei Borodulin. 2024. "A Multi-Objective Optimization of Neural Networks for Predicting the Physical Properties of Textile Polymer Composite Materials" Polymers 16, no. 12: 1752. https://doi.org/10.3390/polym16121752
APA StyleMalashin, I., Tynchenko, V., Gantimurov, A., Nelyub, V., & Borodulin, A. (2024). A Multi-Objective Optimization of Neural Networks for Predicting the Physical Properties of Textile Polymer Composite Materials. Polymers, 16(12), 1752. https://doi.org/10.3390/polym16121752








