A Multiscale Modeling and Experimental Study on the Tensile Strength of Plain-Woven Composites with Hybrid Bonded–Bolted Joints
Abstract
:1. Introduction
2. Experimental Section
2.1. Material Parameters
2.2. Specimen Fabrication
2.3. Experimental Methodology
2.4. Experimental Results Analysis
2.4.1. Effect of Overlap Length (L1) on Joint Mechanical Performance
2.4.2. Effect of Bolt-Hole Spacing (L2) on Joint Mechanical Performance
2.4.3. Effect of Fit Clearance on Joint Mechanical Performance
3. Finite Element Analysis
3.1. Model Establishment
3.2. Simulation Results Validation
3.2.1. The Impact of Overlap Length (L1) on the Mechanical Performance of Joints
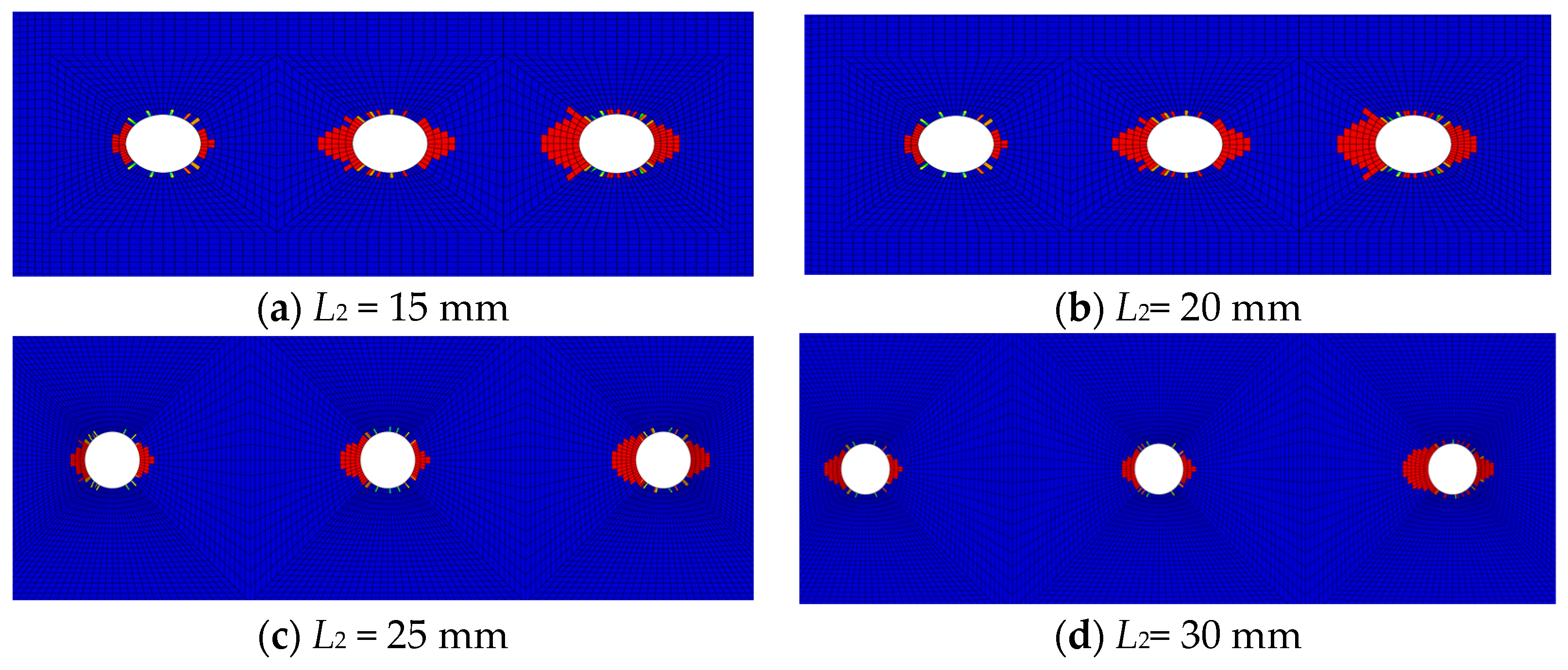
3.2.2. The Influence of Bolt-Hole Spacing on the Mechanical Performance of Joints
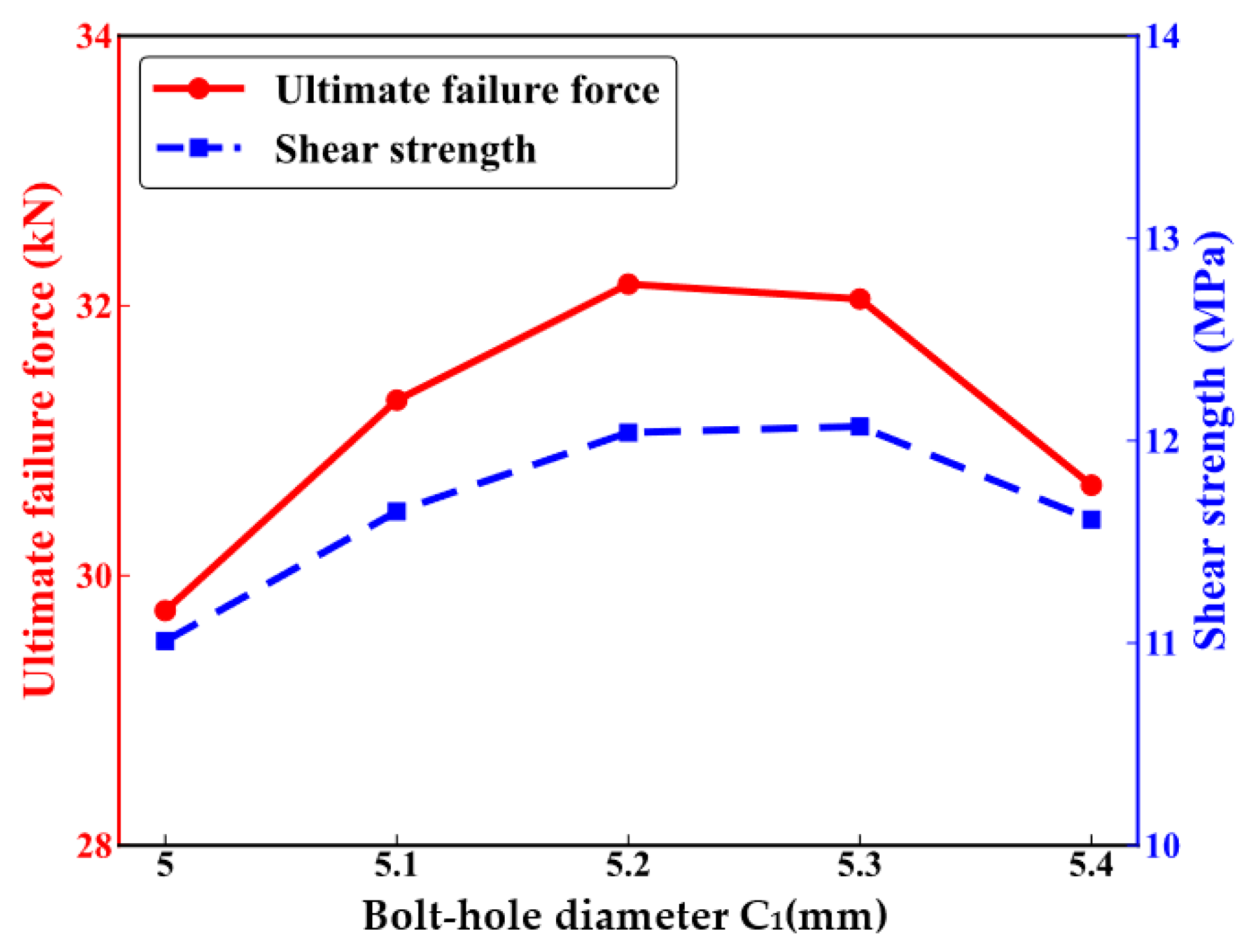
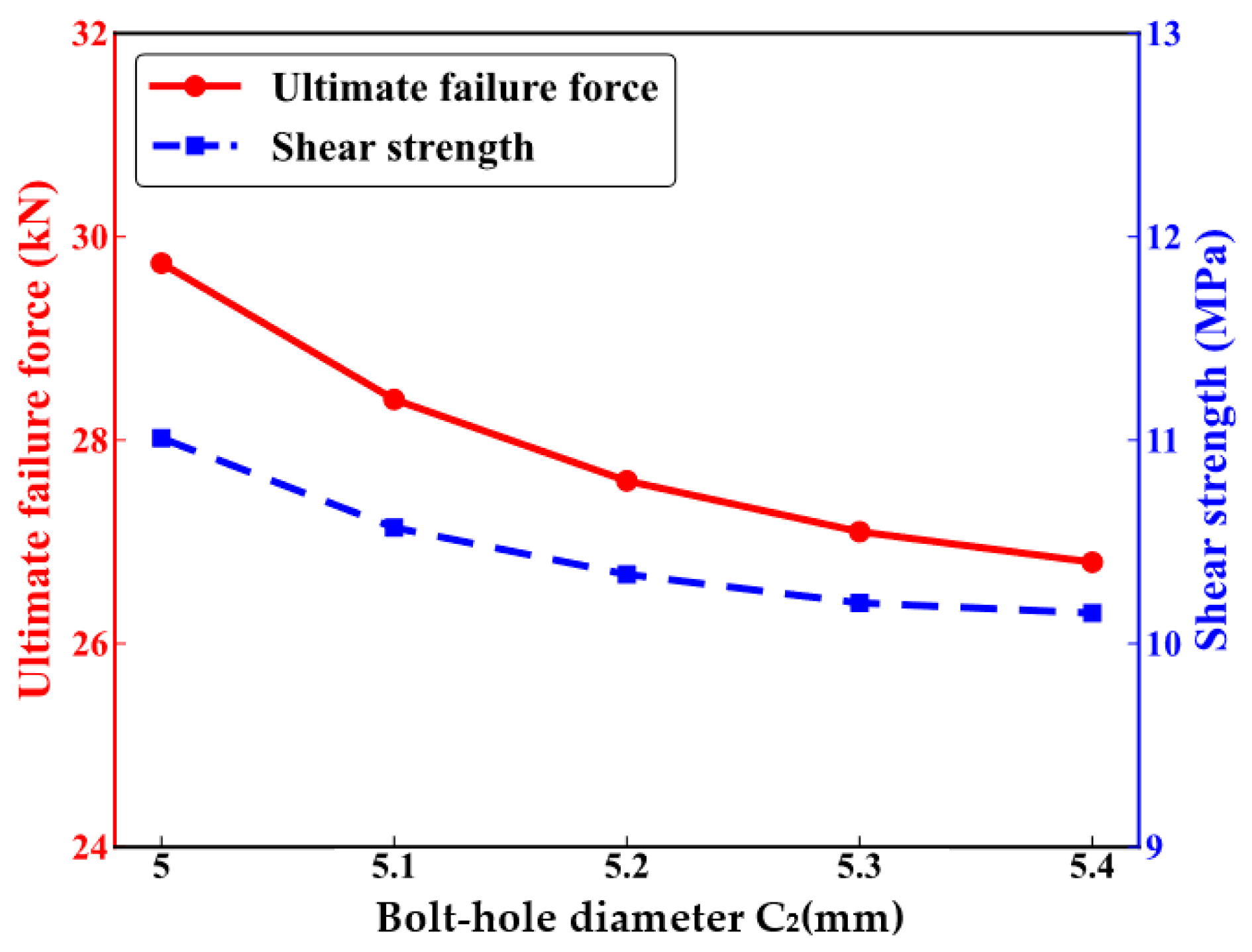
3.2.3. The Impact of the Fit Clearance Relationship on the Mechanical Performance of Joints
4. Analysis of Mechanical Properties of HBB Joints Based on Artificial Intelligence
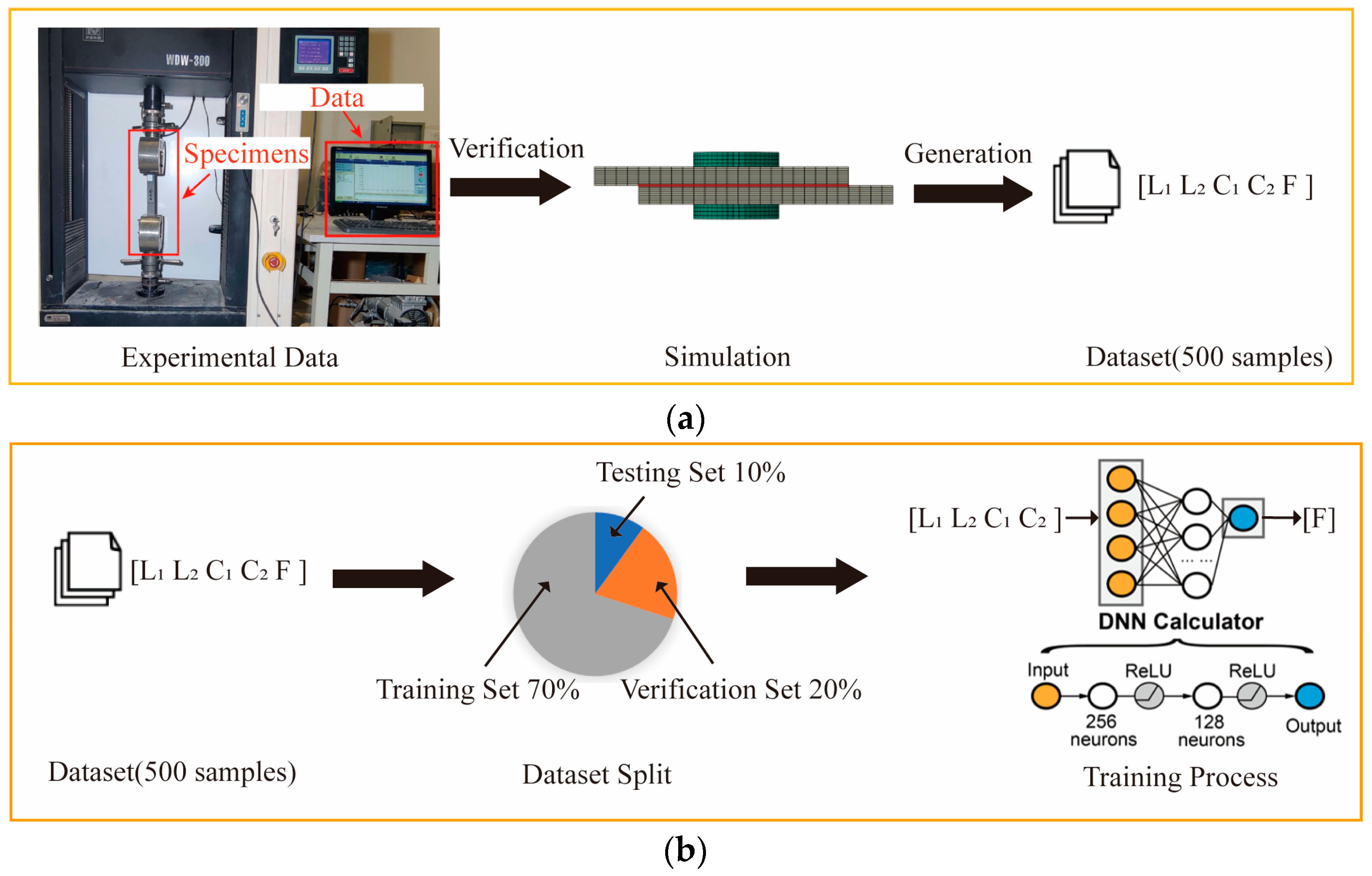
4.1. Design of Deep Neural Network (DNN) Calculator
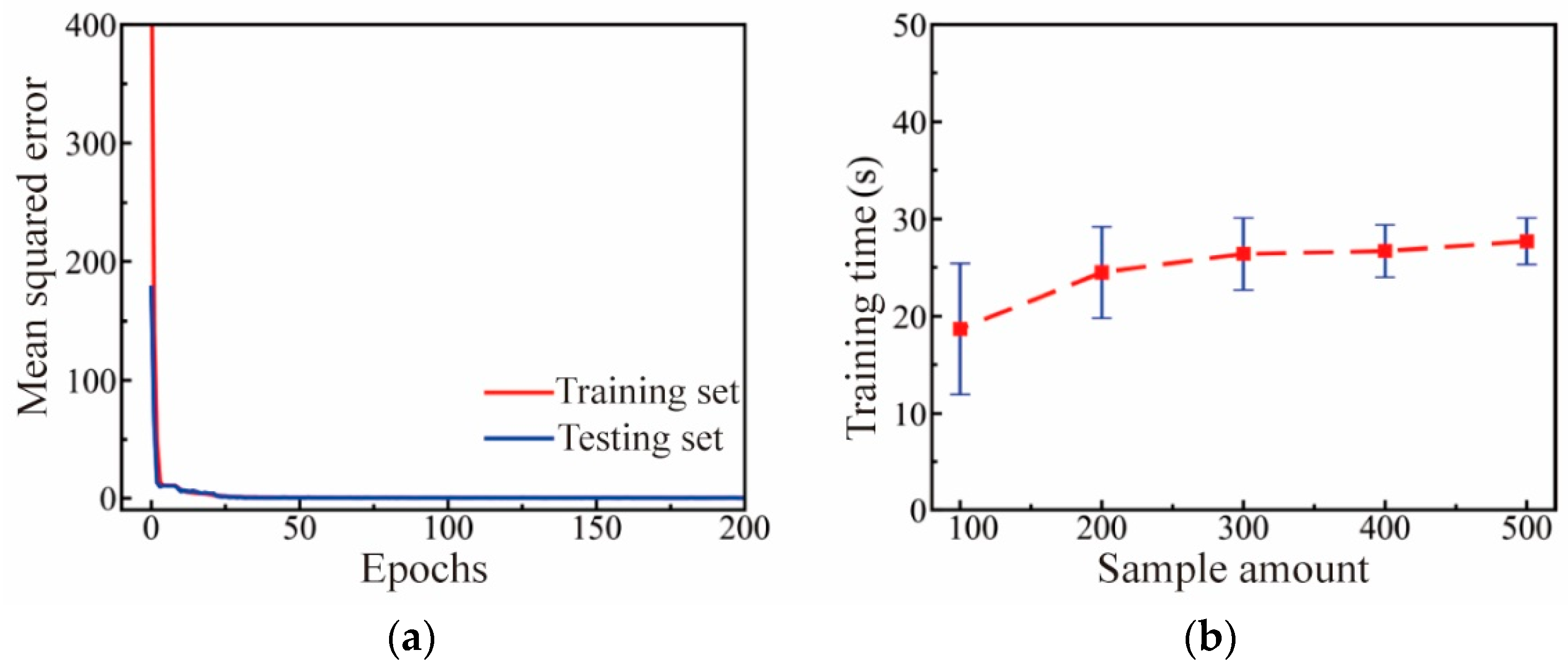
4.2. Performance Evaluation of DNN Calculator
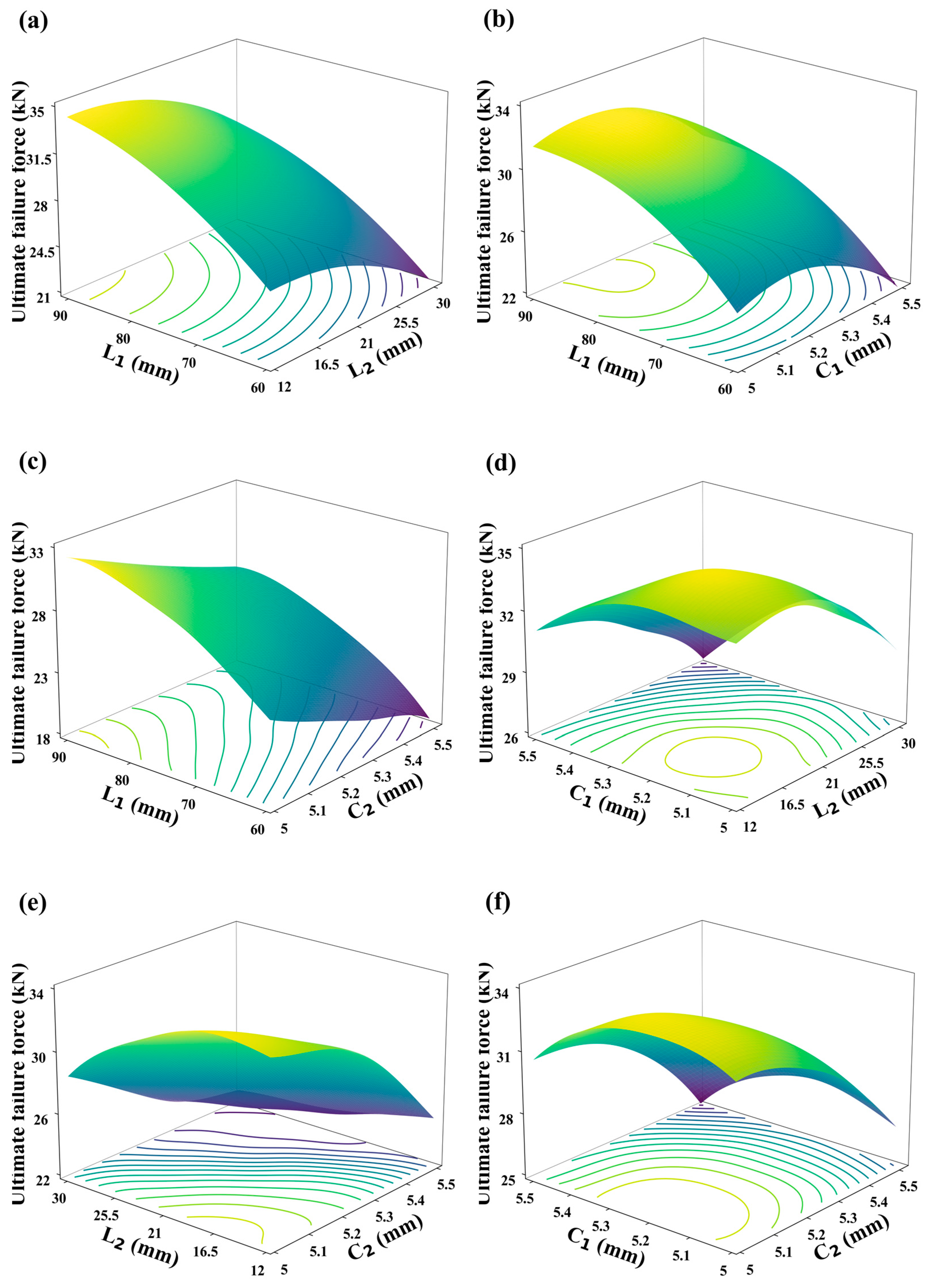
4.3. Utilization of DNN Calculator for Analyzing Influence Relations in CFRP HBB Joints
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rajak, D.; Pagar, D.; Menezes, P.; Linul, E. Fiber-Reinforced Polymer Composites: Manufacturing, Properties, and Applications. Polymers 2019, 11, 1667. [Google Scholar] [CrossRef] [PubMed]
- Yao, S.-S.; Jin, F.-L.; Rhee, K.Y.; Hui, D.; Park, S.-J. Recent Advances in Carbon-Fiber-Reinforced Thermoplastic Composites: A Review. Compos. Part B Eng. 2018, 142, 241–250. [Google Scholar] [CrossRef]
- Swolfs, Y.; Gorbatikh, L.; Verpoest, I. Fibre Hybridisation in Polymer Composites: A Review. Compos. Part A Appl. Sci. Manuf. 2014, 67, 181–200. [Google Scholar] [CrossRef]
- Amor, N.; Noman, M.T.; Petru, M. Classification of Textile Polymer Composites: Recent Trends and Challenges. Polymers 2021, 13, 2592. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Zwingmann, B.; Schlaich, M. Carbon Fiber Reinforced Polymer for Cable Structures—A Review. Polymers 2015, 7, 2078–2099. [Google Scholar] [CrossRef]
- Pawlak, A.M.; Górny, T.; Dopierała, Ł.; Paczos, P. The Use of CFRP for Structural Supervised—Literature Review. Metals 2022, 12, 1470. [Google Scholar] [CrossRef]
- Lima, R.A.A.; Tao, R.; Bernasconi, A.; Carboni, M.; Carrere, N.; Teixeira De Freitas, S. Uncovering the Toughening Mechanisms of Bonded Joints through Tailored CFRP Layup. Compos. Part B Eng. 2023, 263, 110853. [Google Scholar] [CrossRef]
- Zhang, J.; Lin, G.; Vaidya, U.; Wang, H. Past, Present and Future Prospective of Global Carbon Fibre Composite Developments and Applications. Compos. Part B Eng. 2023, 250, 110463. [Google Scholar] [CrossRef]
- Sun, G.; Yu, H.; Wang, Z.; Xiao, Z.; Li, Q. Energy Absorption Mechanics and Design Optimization of CFRP/Aluminium Hybrid Structures for Transverse Loading. Int. J. Mech. Sci. 2019, 150, 767–783. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, T.; He, Y.; Ye, J.; Zhang, H.; Fan, X. Analysis of Damage of Typical Composite/Metal Connecting Structure in Aircraft under the Influences of High-Velocity Fragments. Appl. Sci. 2022, 12, 9268. [Google Scholar] [CrossRef]
- Liu, K.; Liu, Y.; Sabbrojjaman, M.; Tafsirojjaman, T. Effect of Bolt Size on the Bearing Strength of Bolt-Connected Orthotropic CFRP Laminate. Polym. Test. 2023, 118, 107894. [Google Scholar] [CrossRef]
- Xu, C.; Wang, W.; Liu, Z.; Fu, C. Prediction Model and Parametric Study on CFRP Flat-Joggle-Flat Hybrid (Bonded/Bolted) Joints. J. Compos. Mater. 2020, 54, 4025–4034. [Google Scholar] [CrossRef]
- Gamdani, F.; Boukhili, R.; Vadean, A. Tensile Behavior of Hybrid Multi-Bolted/Bonded Joints in Composite Laminates. Int. J. Adhes. Adhes. 2019, 95, 102426. [Google Scholar] [CrossRef]
- Gamdani, F.; Boukhili, R.; Vadean, A. Fatigue Behavior of Hybrid Multi-Bolted-Bonded Single-Lap Joints in Woven Composite Plates. Int. J. Fatigue 2022, 158, 106738. [Google Scholar] [CrossRef]
- Ulus, H. An Experimental Assessment of Hybrid Bolted/Bonded Basalt Fiber Reinforced Polymer Composite Joints’ Temperature-Dependent Mechanical Performances by Static and Dynamic Mechanical Analyses. Int. J. Adhes. Adhes. 2022, 114, 103120. [Google Scholar] [CrossRef]
- Jiang, L.; Dong, D.; Xiao, S.; Chen, D.; Yang, B.; Yang, G.; Zhu, T. Experiment and Simulation Study on Bonded, Bolted and Hybrid Bolted/Bonded Joints of Textile CFRP Using Bimodulus Constitutive Model. Int. J. Adhes. Adhes. 2022, 116, 103154. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhang, C.; Tie, Y.; Wang, X.; Li, M. Tensile Properties Analysis of CFRP-Titanium Plate Multi-Bolt Hybrid Joints. Chin. J. Aeronaut. 2022, 35, 464–474. [Google Scholar] [CrossRef]
- He, B. Experimental and Semianalytical Investigation of X850 ± IM190 CFRP Bolted Joints. Adv. Compos. Lett. 2020, 29, 096369351989500. [Google Scholar] [CrossRef]
- Li, X.; Xu, B.; Hong, Y.; Luo, H. A Detailed Experimental Parametric Analysis of Bolted and Hybrid Bolted/Bonded Composite Joints. J Appl. Polym. Sci 2023, 140, e53394. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, Y. Analysis of Effects of Polyhedral Oligomeric Silsesquioxane on Thermal Properties of Epoxy Resin. Eng. Plast. Appl. 2021, 49, 140–144. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, Y. Study on Atomic Oxygen Resistance of EP Resin Modified by POSS. New Chem. Mater. 2022, 50, 176–179. [Google Scholar] [CrossRef]
- Delzendehrooy, F.; Akhavan-Safar, A.; Barbosa, A.Q.; Carbas, R.J.C.; Marques, E.A.S.; Da Silva, L.F.M. Investigation of the Mechanical Performance of Hybrid Bolted-Bonded Joints Subjected to Different Ageing Conditions: Effect of Geometrical Parameters and Bolt Size. J. Adv. Join. Process. 2022, 5, 100098. [Google Scholar] [CrossRef]
- Li, X.; Cheng, X.; Guo, X.; Liu, S.; Wang, Z. Tensile Properties of a Hybrid Bonded/Bolted Joint: Parameter Study. Compos. Struct. 2020, 245, 112329. [Google Scholar] [CrossRef]
- Xu, Z.X. FE Modeling for Load Distribution Analysis of Multi-Bolt Composite Joints. AMM 2014, 551, 104–107. [Google Scholar] [CrossRef]
- Liu, F.; Zhang, J.; Zhao, L.; Xin, A.; Zhou, L. An Analytical Joint Stiffness Model for Load Transfer Analysis in Highly Torqued Multi-Bolt Composite Joints with Clearances. Compos. Struct. 2015, 131, 625–636. [Google Scholar] [CrossRef]
- Liu, F.; Lu, X.; Zhao, L.; Zhang, J.; Hu, N.; Xu, J. An Interpretation of the Load Distributions in Highly Torqued Single-Lap Composite Bolted Joints with Bolt-Hole Clearances. Compos. Part B Eng. 2018, 138, 194–205. [Google Scholar] [CrossRef]
- Qiu, C.; Han, Y.; Shanmugam, L.; Jiang, F.; Guan, Z.; Du, S.; Yang, J. An Even-Load-Distribution Design for Composite Bolted Joints Using a Novel Circuit Model and Neural Network. Compos. Struct. 2022, 279, 114709. [Google Scholar] [CrossRef]
- McCarthy, M.A.; McCarthy, C.T.; Padhi, G.S. A Simple Method for Determining the Effects of Bolt–Hole Clearance on Load Distribution in Single-Column Multi-Bolt Composite Joints. Compos. Struct. 2006, 73, 78–87. [Google Scholar] [CrossRef]
- Gu, Z.; Liu, Y.; Hughes, D.J.; Ye, J.; Hou, X. A Parametric Study of Adhesive Bonded Joints with Composite Material Using Black-Box and Grey-Box Machine Learning Methods: Deep Neuron Networks and Genetic Programming. Compos. Part B Eng. 2021, 217, 108894. [Google Scholar] [CrossRef]
- Shan Libin Zhao, M.; Huang, W.; Liu, F.; Zhang, J. Effect Mechanisms of Hygrothermal Environments on Failure of Single-Lap and Double-Lap CFRP-Aluminum Bolted Joints. Comput. Model. Eng. Sci. 2020, 123, 101–127. [Google Scholar] [CrossRef]
- Guo, K.; Yang, Z.; Yu, C.-H.; Buehler, M.J. Artificial Intelligence and Machine Learning in Design of Mechanical Materials. Mater. Horiz. 2021, 8, 1153–1172. [Google Scholar] [CrossRef]
- Wang, H.; Duan, Y.; Abulizi, D.; Zhang, X. Design Optimization of CFRP Stacking Sequence Using a Multi-Island Genetic Algorithms under Low-Velocity Impact Loads. J. Wuhan Univ. Technol. Mat. Sci. Edit. 2017, 32, 720–725. [Google Scholar] [CrossRef]
- ASTM 5961; Test Method for Bearing Response of Polymer Matrix Composite Laminates. ASTM Committee D30; ASTM International: West Conshohocken, PA, USA, June 2013. [CrossRef]
- Hou, Y.; Wang, W.; Meng, L.; Sapanathan, T.; Li, J.; Xu, Y. An Insight into the Mechanical Behavior of Adhesively Bonded Plain-Woven-Composite Joints Using Multiscale Modeling. Int. J. Mech. Sci. 2022, 219, 107063. [Google Scholar] [CrossRef]
- Shi, J.; Yang, X.; Chen, X.; Du, K.; Li, C.; Yang, Y. Numerical and Experimental Investigation on the Load-bearing Performance of Plain-woven Composites Hybrid Bonded-bolted Joints. Polym. Compos. 2024, 45, 1195–1207. [Google Scholar] [CrossRef]
- Tedjopurnomo, D.A.; Bao, Z.; Zheng, B.; Choudhury, F.; Qin, A.K. A Survey on Modern Deep Neural Network for Traffic Prediction: Trends, Methods and Challenges. IEEE Trans. Knowl. Data Eng. 2020, 34, 1544–1561. [Google Scholar] [CrossRef]
- Nafees, A.; Amin, M.N.; Khan, K.; Nazir, K.; Ali, M.; Javed, M.F.; Aslam, F.; Musarat, M.A.; Vatin, N.I. Modeling of Mechanical Properties of Silica Fume-Based Green Concrete Using Machine Learning Techniques. Polymers 2021, 14, 30. [Google Scholar] [CrossRef] [PubMed]
- Xue, X.; Makota, C.; Khalaf, O.I.; Jayabalan, J.; Samui, P.; Abdulsahib, G.M. Machine Learning Approach for Prediction of Lateral Confinement Coefficient of CFRP-Wrapped RC Columns. Symmetry 2023, 15, 545. [Google Scholar] [CrossRef]
- Singhal, S.; Jatana, N.; Subahi, A.F.; Gupta, C.; Ibrahim Khalaf, O.; Alotaibi, Y. Fault Coverage-Based Test Case Prioritization and Selection Using African Buffalo Optimization. Comput. Mater. Contin. 2023, 74, 6755–6774. [Google Scholar] [CrossRef]
- Rahman, H.; Tariq, J.; Ali Masood, M.; Subahi, A.F.; Ibrahim Khalaf, O.; Alotaibi, Y. Multi-Tier Sentiment Analysis of Social Media Text Using Supervised Machine Learning. Comput. Mater. Contin. 2023, 74, 5527–5543. [Google Scholar] [CrossRef]
- Banumathy, D.; Ibrahim Khalaf, O.; Andr閟 Tavera Romero, C.; Vishnu Raja, P.; Kumar Sharma, D. Breast Calcifications and Histopathological Analysis on Tumour Detection by CNN. Comput. Syst. Sci. Eng. 2023, 44, 595–612. [Google Scholar] [CrossRef]
- Chang, Z.; Zhang, Y.; Chen, W. Electricity Price Prediction Based on Hybrid Model of Adam Optimized LSTM Neural Network and Wavelet Transform. Energy 2019, 187, 115804. [Google Scholar] [CrossRef]
- Smith, L.N. Cyclical Learning Rates for Training Neural Networks. In Proceedings of the 2017 IEEE Winter Conference on Applications of Computer Vision (WACV), Santa Rosa, CA, USA, 24–31 March 2017; IEEE: Santa Rosa, CA, USA, 2017; pp. 464–472. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Liu, X.; Qin, J.; Zhao, K.; Featherston, C.A.; Kennedy, D.; Jing, Y.; Yang, G. Design Optimization of Laminated Composite Structures Using Artificial Neural Network and Genetic Algorithm. Compos. Struct. 2023, 305, 116500. [Google Scholar] [CrossRef]









| Elastic Properties | Value | Damage Properties | Value |
|---|---|---|---|
| Longitudinal Elasticity Modulus, | 138 | 2 | |
| Transverse Elasticity Modulus, | 11 | 1.15 | |
| Normal Modulus of Elasticity, | 11 | 0.06 | |
| 0.28 | 0.152 | ||
| 0.28 | 0.075 | ||
| 0.4 | 0.075 | ||
| 6 | 1.69 | ||
| 6 | |||
| 3.7 |
| Properties | Value |
|---|---|
| 2 | |
| 0.9 | |
| 30 | |
| 0.014 | |
| 0.014 |
| Reference Experiment | L1 | L2 | C1 | C2 |
|---|---|---|---|---|
| a | 90 | 30 | 5 | 5 |
| b | 90 | 30 | 5.3 | 5 |
| c | 90 | 15 | 5 | 5 |
| d | 60 | 15 | 5 | 5 |
| Sample Amount | 100 | 200 | 300 | 400 | 500 |
|---|---|---|---|---|---|
| Training set accuracy | 97.5% | 97.9% | 99.2% | 99.5% | 99.6% |
| Testing set accuracy | 91.5% | 92.6% | 97.5% | 98.9% | 99.2% |
| Error | 0–0.5% | 0.5–1% | 1–1.5% | 1.5–2% | 2–2.5% |
|---|---|---|---|---|---|
| Training set | 66% | 23% | 3% | 3% | 2% |
| Testing set | 56% | 26% | 4% | 4% | 2% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, J.; Zhang, J.; Du, K.; Guo, Q.; Hou, Y.; Dong, C. A Multiscale Modeling and Experimental Study on the Tensile Strength of Plain-Woven Composites with Hybrid Bonded–Bolted Joints. Polymers 2024, 16, 2074. https://doi.org/10.3390/polym16142074
Shi J, Zhang J, Du K, Guo Q, Hou Y, Dong C. A Multiscale Modeling and Experimental Study on the Tensile Strength of Plain-Woven Composites with Hybrid Bonded–Bolted Joints. Polymers. 2024; 16(14):2074. https://doi.org/10.3390/polym16142074
Chicago/Turabian StyleShi, Jianwei, Junwei Zhang, Kou Du, Qiming Guo, Yuliang Hou, and Cheng Dong. 2024. "A Multiscale Modeling and Experimental Study on the Tensile Strength of Plain-Woven Composites with Hybrid Bonded–Bolted Joints" Polymers 16, no. 14: 2074. https://doi.org/10.3390/polym16142074
APA StyleShi, J., Zhang, J., Du, K., Guo, Q., Hou, Y., & Dong, C. (2024). A Multiscale Modeling and Experimental Study on the Tensile Strength of Plain-Woven Composites with Hybrid Bonded–Bolted Joints. Polymers, 16(14), 2074. https://doi.org/10.3390/polym16142074





