Triaxiality and Plastic-Strain-Dependent Proposed PEAK Parameter for Predicting Crack Formation in Polypropylene Polymer Reservoir Subjected to Pressure Load
Abstract
:1. Introduction
2. Material Definition
3. Experiment Definition
3.1. Laboratory Pressure Test
3.2. Simulation Analysis
4. PEAK Calibration
4.1. Data Comparison
4.2. Mathematical Formulation of PEAK
- —non-linear dependence on the basic parameter PEEQ;
- —asymptotic drop of isoline to the limit value for higher TRIAX;
- —lack of sensitivity for points with negative TRIAX values, which automatically receive negative values of PEAK.
4.3. PEAK’s Prediction of Crack Initiation Pressure
- The place of rupture was selected correctly in 66.7% of cases;
- The average utilization value reached 91.7% for all results and 90.8% excluding tank 8.3 from the analysis (due to a false positive result in this test);
- For 93.3% of tanks, the estimated result was obtained in the form of a lower result in the simulation than in laboratory tests with the highest possible utilization (close to 100% as possible).
- The obtained utilization results fit well into the normal distribution with parameters mean = 0.9174 and standard deviation = 0.06225, as indicated by the Anderson–Darling parameter = 0.218 and p-value = 0.803;
- The probability of a false positive simulation result compared to the laboratory result, forecast in accordance with the above parameters, is 9.2%;
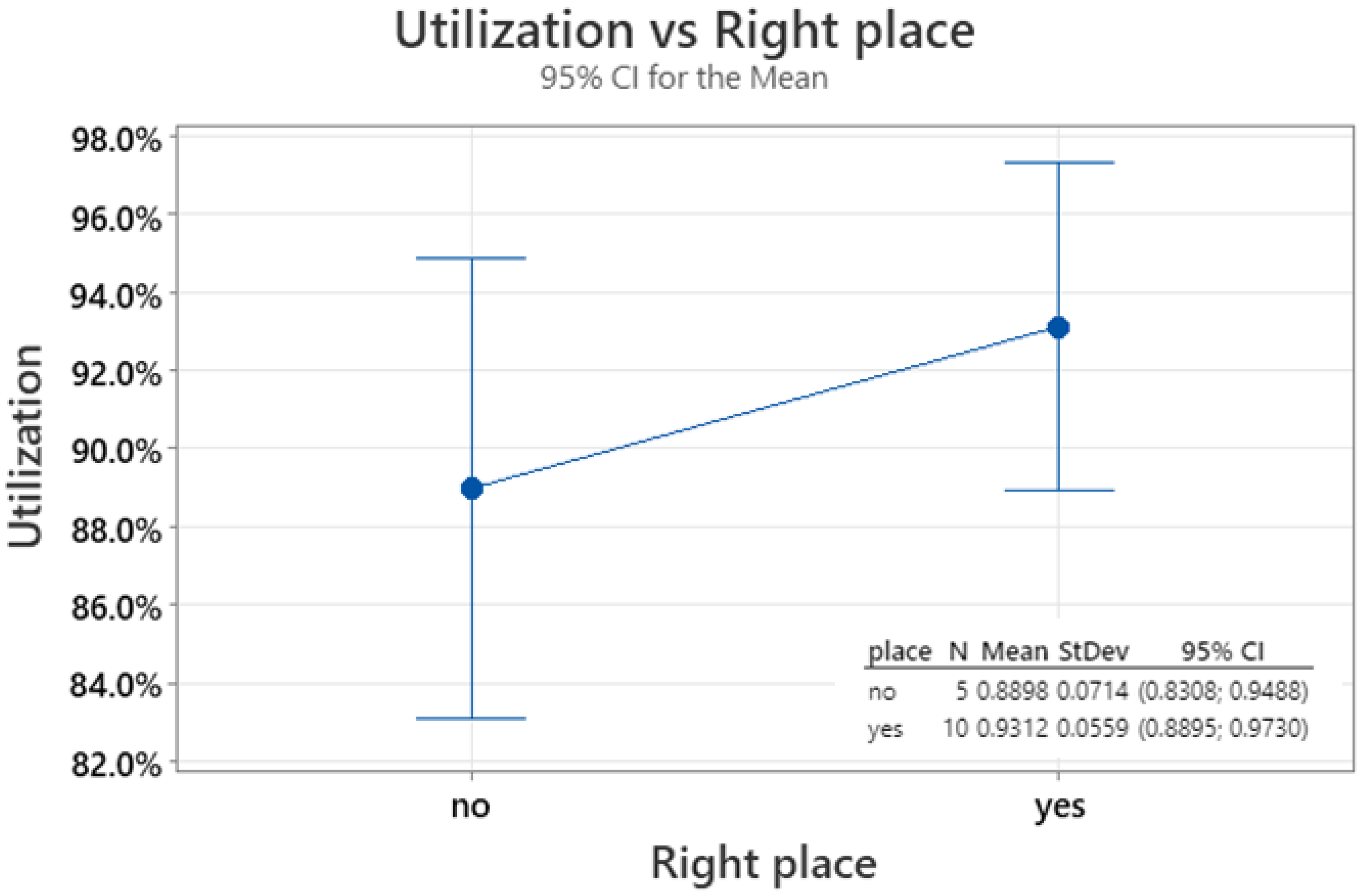
- The analysis of variance for different utilization indications depending on the correct (or not) place of crack initiation showed statistically significantly different results, with a probability of approximately 76% (p-value = 0.237) (utilization for “yes”: mean = 93%, standard deviation = 5.6%, utilization for “no”: mean = 89%, standard deviation = 7.1%).
5. Conclusions
6. Discussion and Areas for Further Research
- Dependence of Young’s modulus, yield strength and hardening curve on the strain rate;
- Taking into account the phenomena of material creep and relaxation and their impact on the formation of plastic deformations;
- Material anisotropy and its influence on the yield strength and Young’s modulus.
- Material Variability and the PEAK Parameter: Investigating how variations in polypropylene formulations (including different molecular weights, copolymers, and composite materials) affect the PEAK parameter. This could help in refining the parameter for broader applicability across various polypropylene types.
- Comparison with Other Polymeric Materials: Extending the application of the PEAK parameter to other polymeric materials used in the automotive industry, such as polyethylene (PE), polyamide (PA) and other polypropylene (PP) blends from different suppliers.
- Economic Analysis: Performing a comprehensive economic analysis to quantify the cost savings achieved by optimizing component design using the PEAK parameter. This could also include assessing the impact on the manufacturing process, such as reduced material waste and improved production efficiency.
- Integration with Advanced Simulation Tools: Further integrating the PEAK parameter with advanced simulation tools and methodologies, such as machine learning algorithms, to enhance the predictive accuracy and efficiency of component design and optimization processes.
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Stinson, S. Discoverers of Polypropylene Share Prize. Chem. Eng. News 1987, 65, 30. [Google Scholar] [CrossRef]
- INEOS. Polypropylene Processing Guide. Available online: https://www.ineos.com (accessed on 23 April 2024).
- Maddah, H.A. Polypropylene as a Promising Plastic: A Review. Am. J. Polym. Sci. 2016, 6, 1–11. [Google Scholar] [CrossRef]
- Hossain, M.T.; Shahid, M.A.; Mahmud, N.; Habib, A.; Rana, M.M.; Khan, S.A.; Hossain, M.D. Research and application of polypropylene: A review. Nano 2024, 19, 2. [Google Scholar] [CrossRef]
- Karger-Kocsis, J.; Bárány, T. Polypropylene Handbook: Morphology, Blends and Composites; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar] [CrossRef]
- Maier, C.; Calafut, T. Applications. In Polypropylene; Maier, C., Calafut, T., Eds.; William Andrew Publishing: Norwich, NY, USA, 1998; pp. 87–107. ISBN 9781884207587. [Google Scholar]
- Zienkiewicz, O.C.; Taylor, R.L.; Zhu, J.Z. The Finite Element Method: Its Basis and Fundamentals, 6th ed.; Elsevier: Amsterdam, The Netherlands, 2005; ISBN 9780750663205. [Google Scholar]
- Xie, M.; Gerstle, W.H.; Rahulkumar, P. Energy-based automatic mixed-mode crack-propagation modeling. J. Eng. Mech. 1995, 121, 914–923. [Google Scholar] [CrossRef]
- Bittencourt, T.N.; Wawrzynek, P.A.; Ingraffea, A.R.; Sousa, J.L. Quasi-automatic simulation of crack propagation for 2D LEFM problems. Eng. Fract. Mech. 1996, 55, 321–334. [Google Scholar] [CrossRef]
- Bouchard, P.O.; Bay, F.; Chastel, Y. Numerical modelling of crack propagation: Automatic remeshing and comparison of different criteria. Comput. Methods Appl. Mech. Eng. 2003, 192, 3887–3908. [Google Scholar] [CrossRef]
- Khoei, A.R.; Azadi, H.; Moslemi, H. Modeling of crack propagation via an automatic adaptive mesh refinement based on modified superconvergent patch recovery technique. Eng. Fract. Mech. 2008, 75, 2921–2945. [Google Scholar] [CrossRef]
- Khoei, A.R.; Yasbolaghi, R.; Biabanak, S.O.R. A polygonal finite element method for modeling crack propagation with minimum remeshing. Int. J. Fract. 2015, 194, 123–148. [Google Scholar] [CrossRef]
- Liao, M.; Deng, X.; Guo, Z. Crack propagation modelling using the weak form quadrature element method with minimal remeshing. Theor. Appl. Fract. Mech. 2018, 93, 293–301. [Google Scholar] [CrossRef]
- Kabir, H.; Mohammadi Aghdam, M. A generalized 2D Bézier-based solution for stress analysis of notched epoxy resin plates reinforced with graphene nanoplatelets. Thin-Walled Struct. 2021, 169, 108484. [Google Scholar] [CrossRef]
- Șerban, D.-A.; Coșa, A.V.; Belgiu, G.; Negru, R. Failure Locus of an ABS-Based Compound Manufactured through Photopolymerization. Polymers 2022, 14, 3822. [Google Scholar] [CrossRef] [PubMed]
- Choi, J.; Lee, H.; Lee, H.; Kim, N. A Methodology to Predict the Fatigue Life under Multi-Axial Loading of Carbon Fiber-Reinforced Polymer Composites Considering Anisotropic Mechanical Behavior. Materials 2023, 16, 1952. [Google Scholar] [CrossRef] [PubMed]
- Lv, B.; Zhao, Y.; Li, N.; Yu, Y.; Wu, Y.; Gu, M. Triaxial Mechanical Properties and Mechanism of Waterborne Polyurethane-Reinforced Road Demolition Waste as Road Bases. Polymers 2022, 14, 2725. [Google Scholar] [CrossRef] [PubMed]
- Ovalle, C.; Boisot, G.; Laiarinandrasana, L. Effects of Stress Triaxiality Ratio on the Heat Build-Up of Polyamide 11 under Loading. Mech. Mater. 2020, 145, 103375. [Google Scholar] [CrossRef]
- Tiejun, W.; Kishimoto, K.; Notomi, M. Effect of triaxial stress constraint on the deformation and fracture of polymers. Acta Mech. Sin. 2002, 18, 480–493. [Google Scholar] [CrossRef]
- Sha, J.; Sun, J.; Deng, Z.; Zhou, H. The Finite Analysis of Deformation and Stress Triaxiality of a Mixed I + II Mode Elastic-Plastic Crack Tip. Int. J. Fract. 1997, 87, 47–58. [Google Scholar] [CrossRef]
- Kuang, J.H.; Chen, Y.C. The tip plastic strain energy applied to ductile fracture initiation under mixed-mode loading. Eng. Fract. Mech. 1997, 58, 61–70. [Google Scholar] [CrossRef]
- Kuang, J.H.; Chen, Y.C. Crack initiation load characterization using the critical plastic energy. Eng. Fract. Mech. 1996, 53, 571–580. [Google Scholar] [CrossRef]
- Sharanaprabhu, C.M.; Kudari, S.K. Mixed-mode (I/II) crack initiation direction for elastic-plastic materials based on crack-tip plastic zone. Int. J. Eng. Sci. Technol. 2010, 2, 113–122. [Google Scholar] [CrossRef]
- Benzerga, A.A.; Besson, J.; Pineau, A. Anisotropic ductile fracture: Part I: Experiments. Acta Mater. 2004, 52, 4623–4638. [Google Scholar] [CrossRef]
- Schowtjak, A.; Gerlach, J.; Muhammad, W.; Brahme, A.P.; Clausmeyer, T.; Inal, K.; Tekkaya, A.E. Prediction of ductile damage evolution based on experimental data using artificial neural networks. Int. J. Solids Struct. 2022, 257, 111950. [Google Scholar] [CrossRef]
- Available online: https://www.sabic.com/en/products/polymers/polypropylene-pp/sabic-pp (accessed on 23 June 2024).







| Parameter | Value |
|---|---|
| Density | 905 [kg/m3] |
| Tensile modulus | 1200 [MPa] |
| Poisson ratio | 0.4 [−] |
| Yield stress in RT | 25 [MPa] |
| RSV no | Result * | PEEQ [−] | TRIAX [−] |
|---|---|---|---|
| 1.1 | nok | 0.613 | 0.348 |
| ok | 0.452 | 0.316 | |
| ok | 0.385 | 0.527 | |
| 1.2 | nok | 0.634 | 0.289 |
| ok | 0.418 | 0.428 | |
| ok | 0.342 | 0.486 | |
| 1.3 | nok | 0.566 | 0.325 |
| ok | 0.327 | 0.470 | |
| ok | 0.326 | 0.327 | |
| 2.1 | nok | 0.553 | 0.583 |
| ok | 0.519 | 0.375 | |
| ok | 0.385 | 0.527 | |
| 2.2 | nok | 0.445 | 0.523 |
| ok | 0.478 | 0.401 | |
| ok | 0.386 | 0.485 | |
| 2.3 | nok | 0.624 | 0.300 |
| ok | 0.403 | 0.492 | |
| ok | 0.312 | 0.540 | |
| 3.1 | nok | 0.487 | 0.432 |
| ok | 0.364 | 0.695 | |
| ok | 0.325 | 0.647 | |
| 3.2 | nok | 0.398 | 0.713 |
| ok | 0.385 | 0.689 | |
| ok | 0.325 | 0.836 | |
| 3.3 | nok | 0.419 | 0.705 |
| ok | 0.289 | 0.946 | |
| ok | 0.304 | 0.774 | |
| 4.1 | nok | 0.695 | 0.202 |
| ok | 0.528 | 0.225 | |
| ok | 0.517 | 0.195 | |
| 4.2 | nok | 0.645 | 0.253 |
| ok | 0.579 | 0.217 | |
| ok | 0.474 | 0.284 | |
| 4.3 | nok | 0.822 | 0.178 |
| ok | 0.406 | 0.341 | |
| ok | 0.384 | 0.398 | |
| 5.1 | nok | 0.349 | 1.079 |
| ok | 0.281 | 0.936 | |
| ok | 0.295 | 0.973 | |
| 5.2 | nok | 0.343 | 0.983 |
| ok | 0.306 | 0.839 | |
| ok | 0.285 | 1.022 | |
| 5.3 | nok | 0.381 | 0.879 |
| ok | 0.327 | 0.794 | |
| ok | 0.388 | 0.802 |
| RSV No | Right Place * | Lab Result [bar] | Sim Result [bar] | Utilization |
|---|---|---|---|---|
| 6.1 | yes | 17.8 | 17.4 | 97.8% |
| 6.2 | yes | 18.9 | 92.1% | |
| 6.3 | no | 18.0 | 96.7% | |
| 7.1 | yes | 13.5 | 12.3 | 91.1% |
| 7.2 | yes | 14.0 | 87.9% | |
| 7.3 | yes | 14.1 | 87.2% | |
| 8.1 | yes | 16.9 | 16.5 | 97.6% |
| 8.2 | no | 17.2 | 95.9% | |
| 8.3 | yes | 15.8 | 104.4% | |
| 9.1 | yes | 10.5 | 9.7 | 92.4% |
| 9.2 | yes | 10.3 | 94.2% | |
| 9.3 | yes | 11.2 | 86.6% | |
| 10.1 | no | 21.4 | 18.2 | 85.0% |
| 10.2 | no | 22.7 | 80.2% | |
| 10.3 | no | 20.9 | 87.1% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kasprzak, A. Triaxiality and Plastic-Strain-Dependent Proposed PEAK Parameter for Predicting Crack Formation in Polypropylene Polymer Reservoir Subjected to Pressure Load. Polymers 2024, 16, 2128. https://doi.org/10.3390/polym16152128
Kasprzak A. Triaxiality and Plastic-Strain-Dependent Proposed PEAK Parameter for Predicting Crack Formation in Polypropylene Polymer Reservoir Subjected to Pressure Load. Polymers. 2024; 16(15):2128. https://doi.org/10.3390/polym16152128
Chicago/Turabian StyleKasprzak, Adam. 2024. "Triaxiality and Plastic-Strain-Dependent Proposed PEAK Parameter for Predicting Crack Formation in Polypropylene Polymer Reservoir Subjected to Pressure Load" Polymers 16, no. 15: 2128. https://doi.org/10.3390/polym16152128
APA StyleKasprzak, A. (2024). Triaxiality and Plastic-Strain-Dependent Proposed PEAK Parameter for Predicting Crack Formation in Polypropylene Polymer Reservoir Subjected to Pressure Load. Polymers, 16(15), 2128. https://doi.org/10.3390/polym16152128







