Stress Wave Propagation and Decay Based on Micro-Scale Modelling in the Topology of Polymer Composite with Circular Particles
Abstract
1. Introduction
- the method of determining the stress wave damping of the composite material based on the use of explicit FEA analysis of the composite microstructure;
- the quantification of individual parameters affecting the stress wave decay and internal damping of a particulate composite with circular particles;
- the visualisation of the internal damping process using the visualisation of the stress wave in the composite microstructure;
- contribution to the understanding of the physical nature of internal damping.
2. Methodology of Simulation of Stress Wave Propagation Generated by Impulsive Load
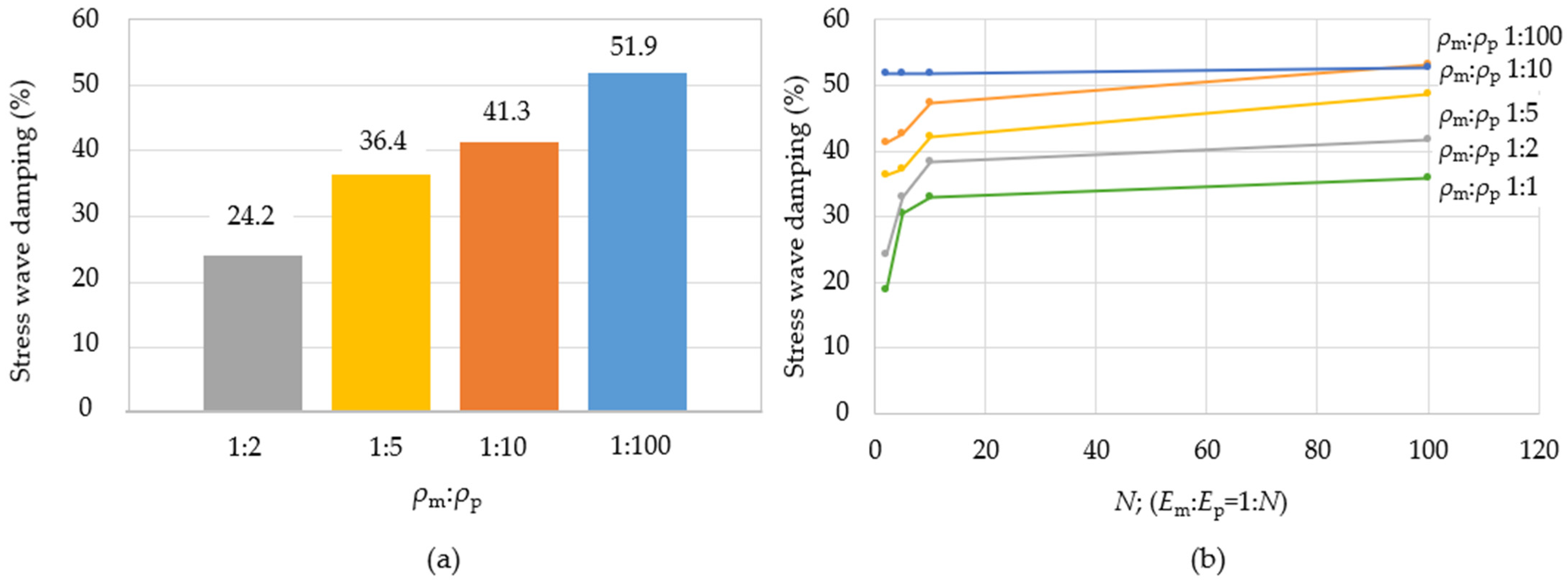
- The effect of stiffness and density of particles and the base material (matrix) Em:Ep and ρm:ρp (Em and Ep is Young’s modulus of matrix and particle, respectively; ρm and ρp is the density of matrix and particle material, respectively);
- The effect of the percentage proportion of particles;
- The effect of the size of particles at their same volume (area) percentage;
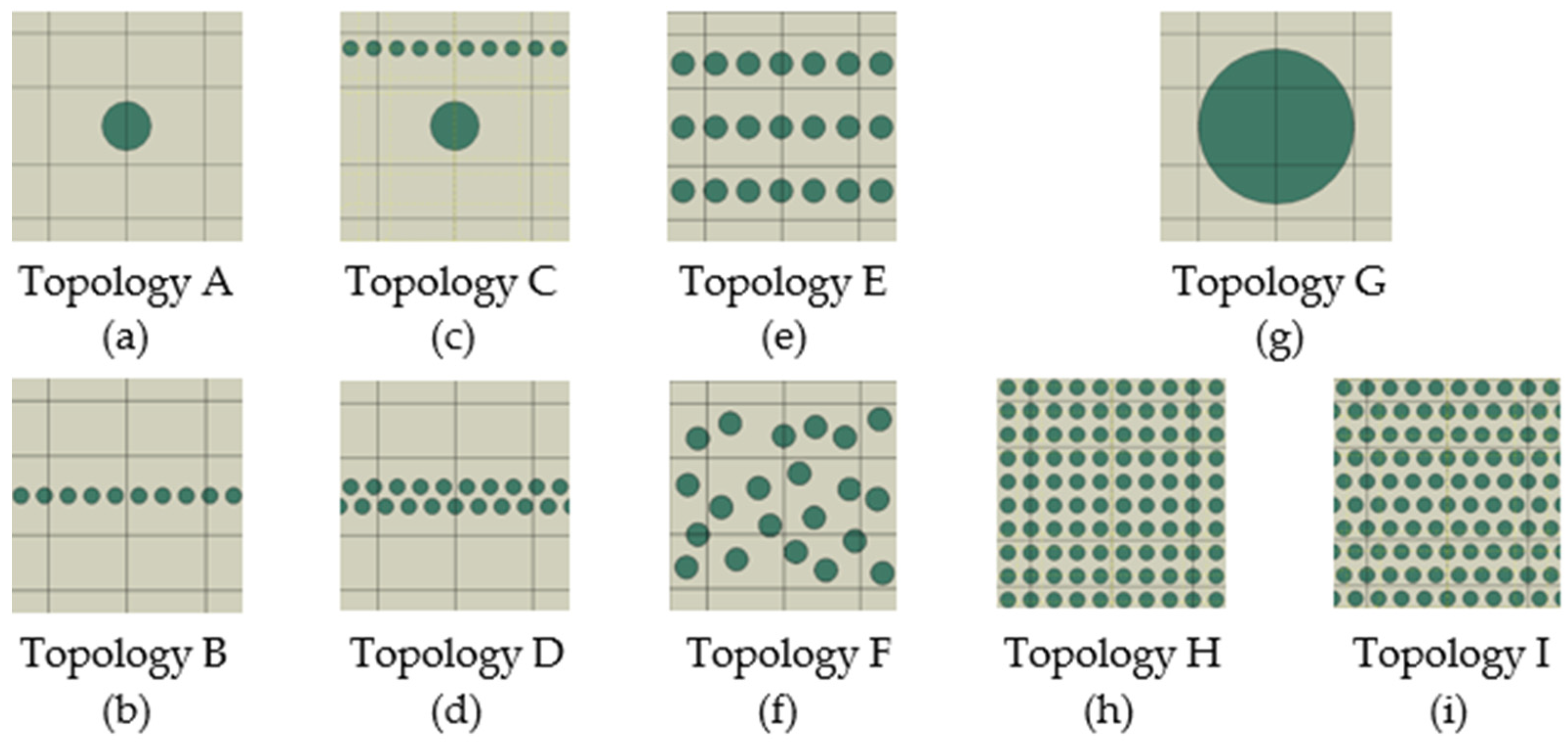
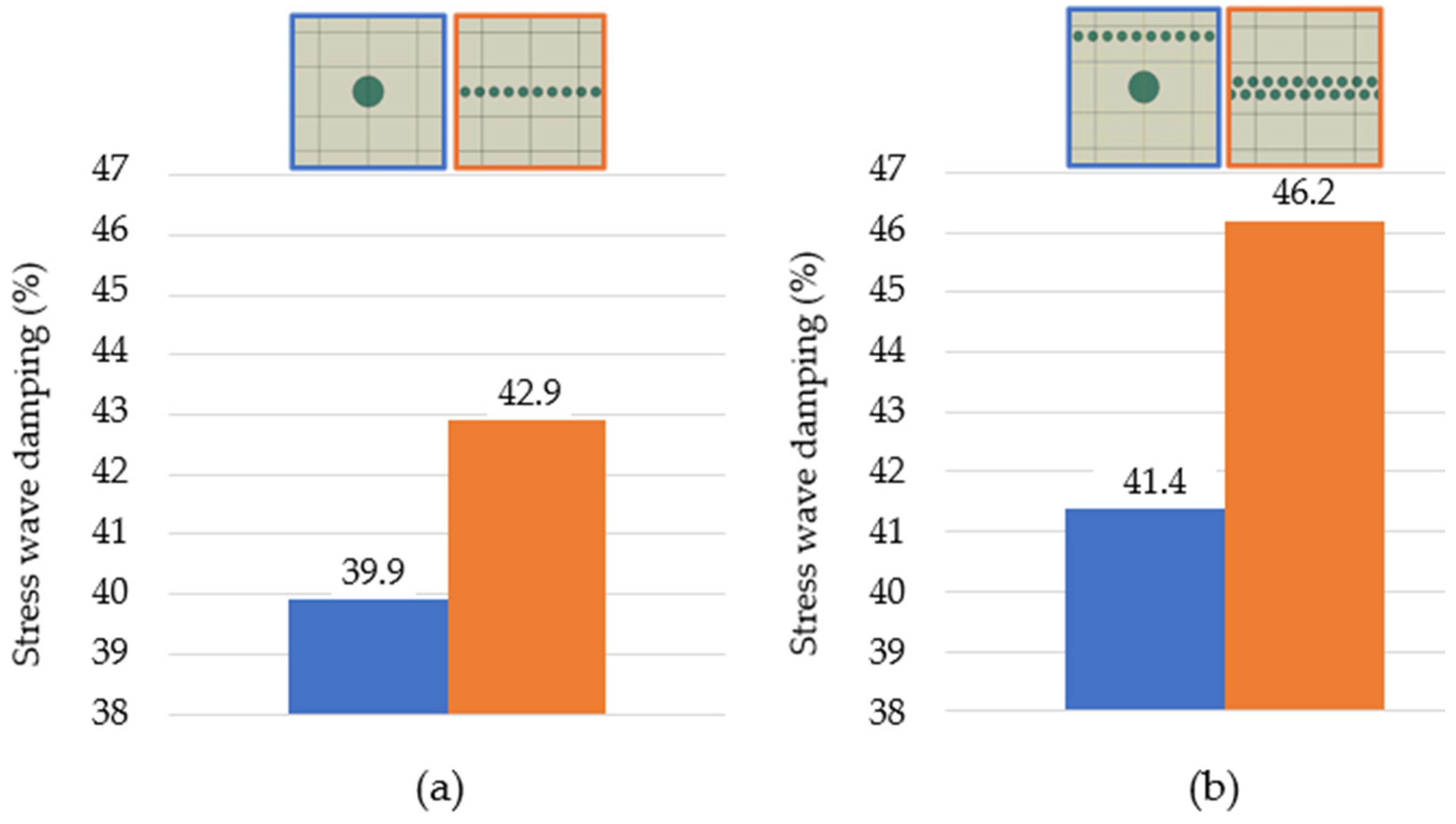
- The effect of the topology with circular particles of the composite microstructure.
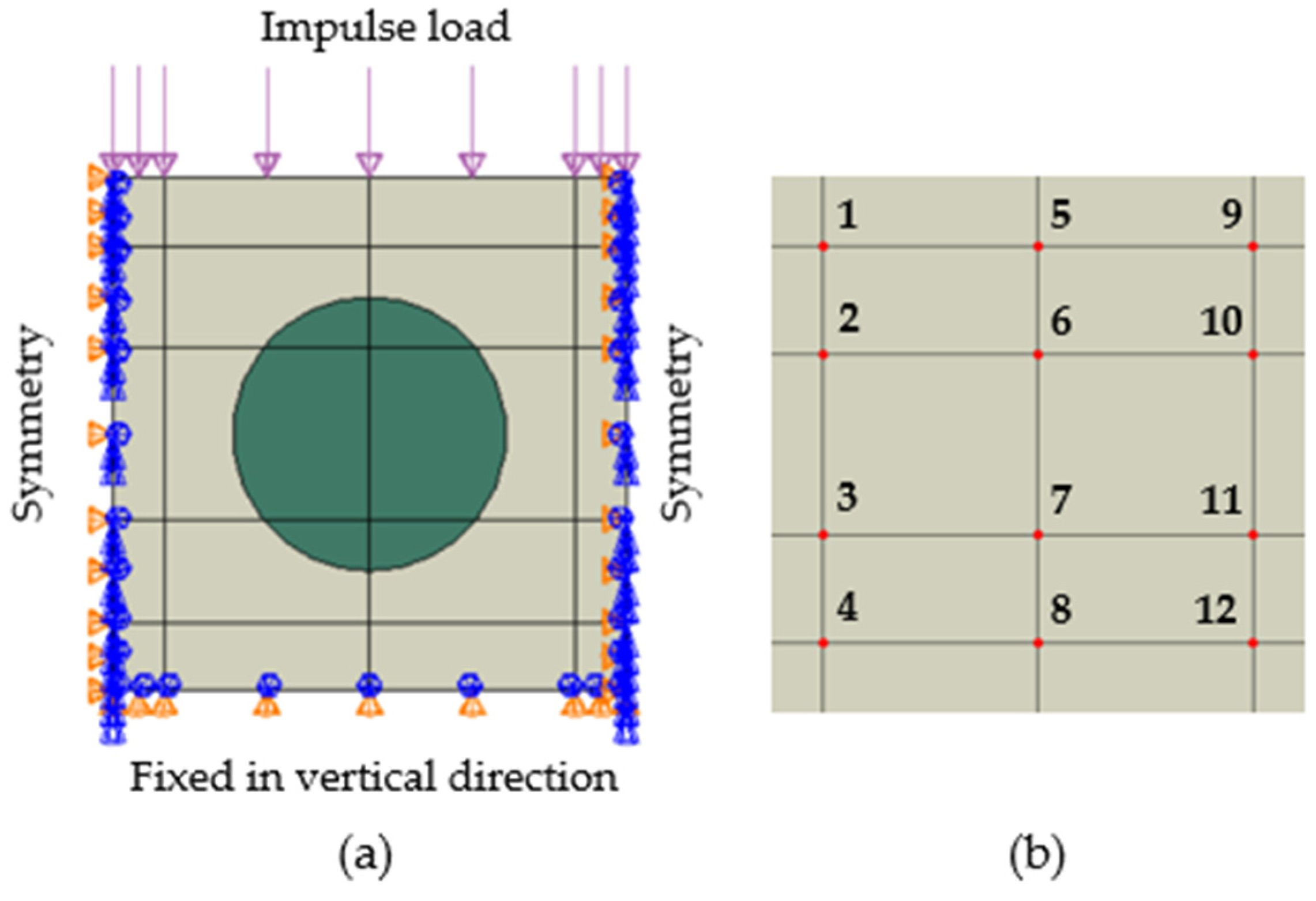
2.1. Computational Model and Numerical Simulation Conditions
2.2. Evaluation of Numerical Results
3. Results
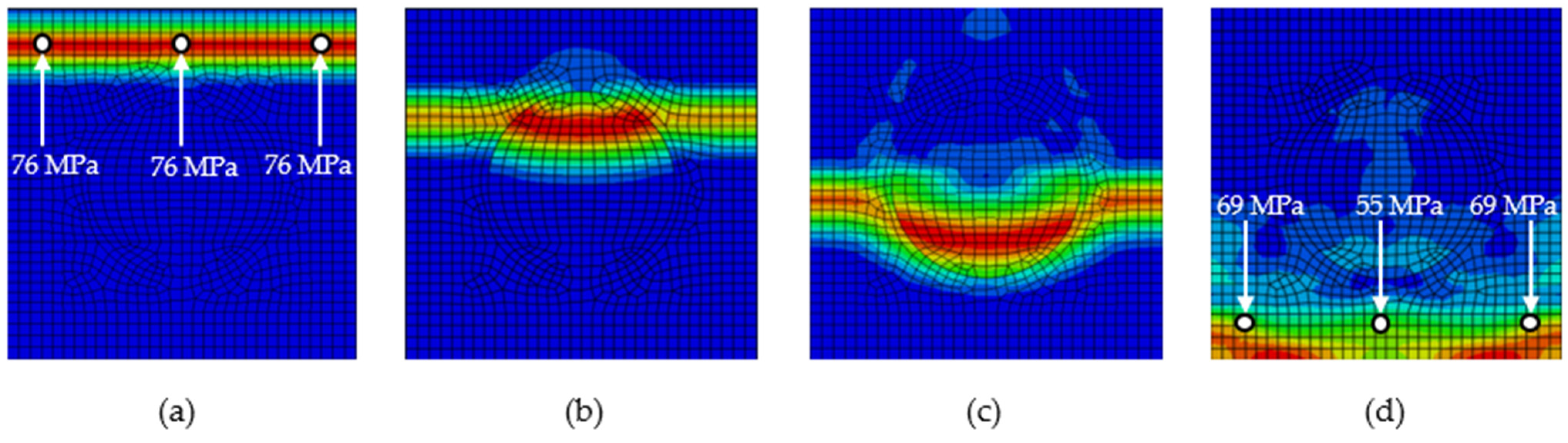
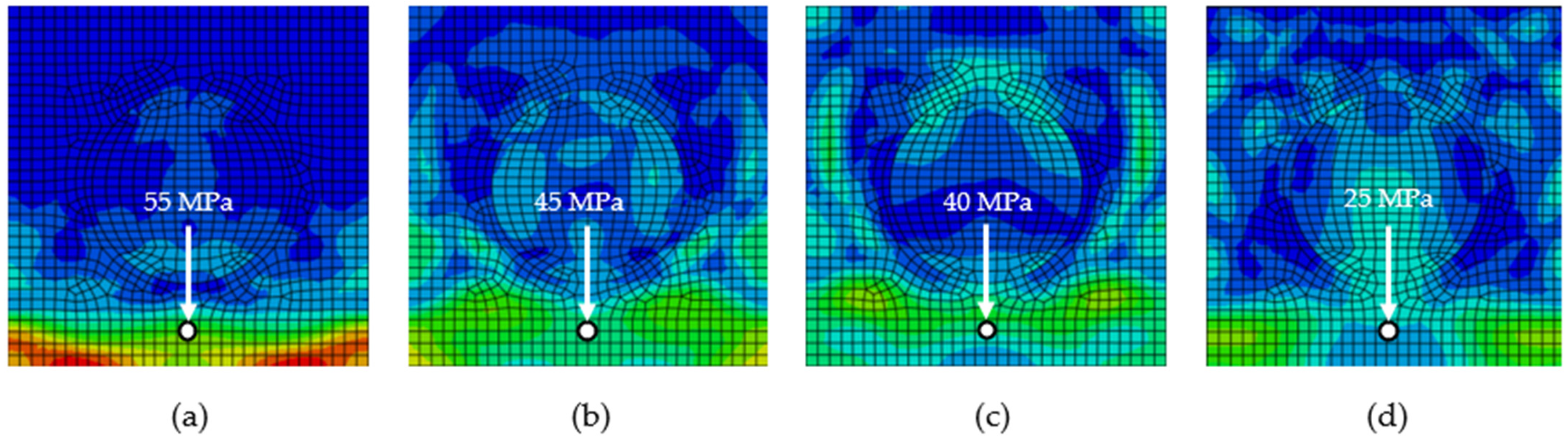
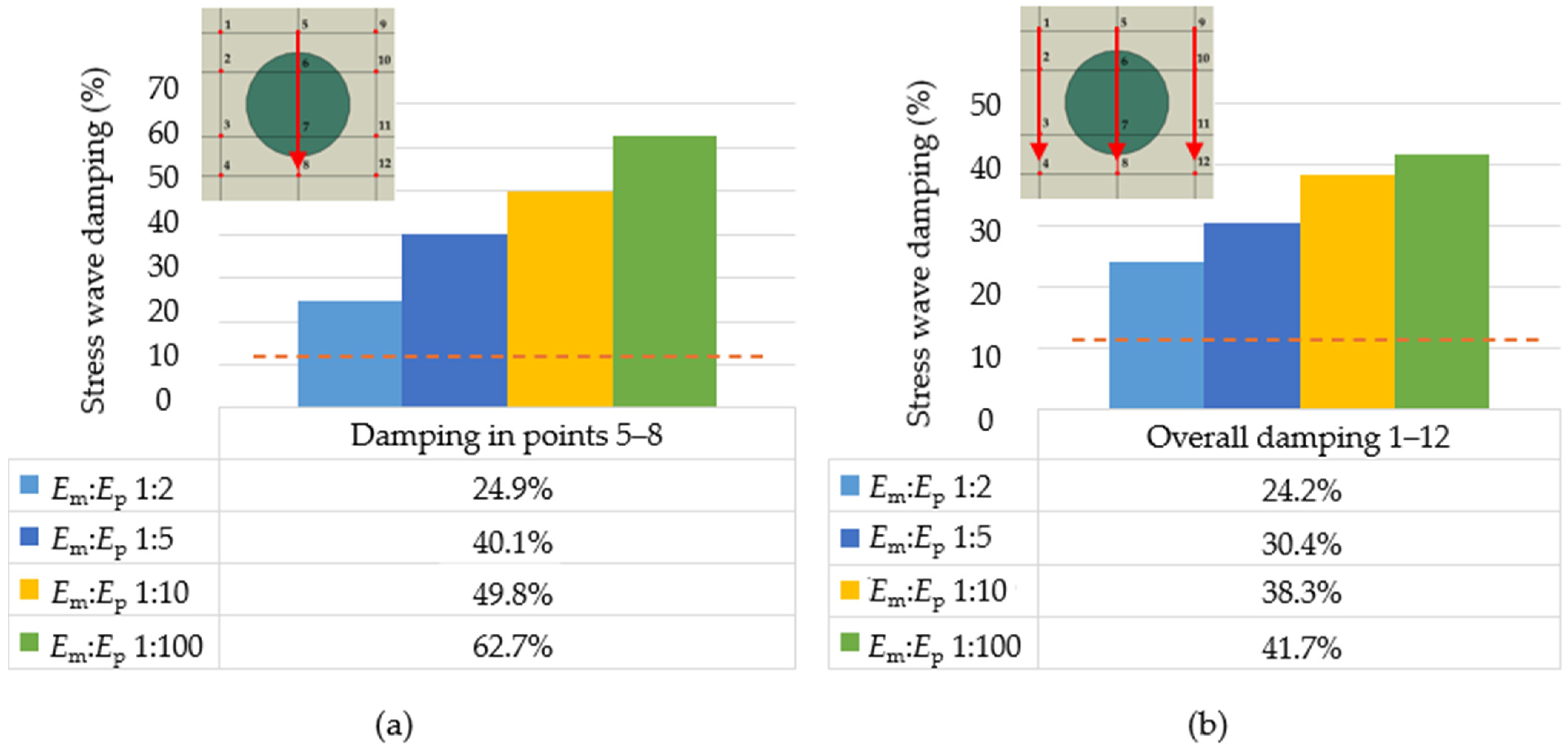
3.1. Numerical Simulation of Different Stiffness and Density Ratios of Matrix and Particle
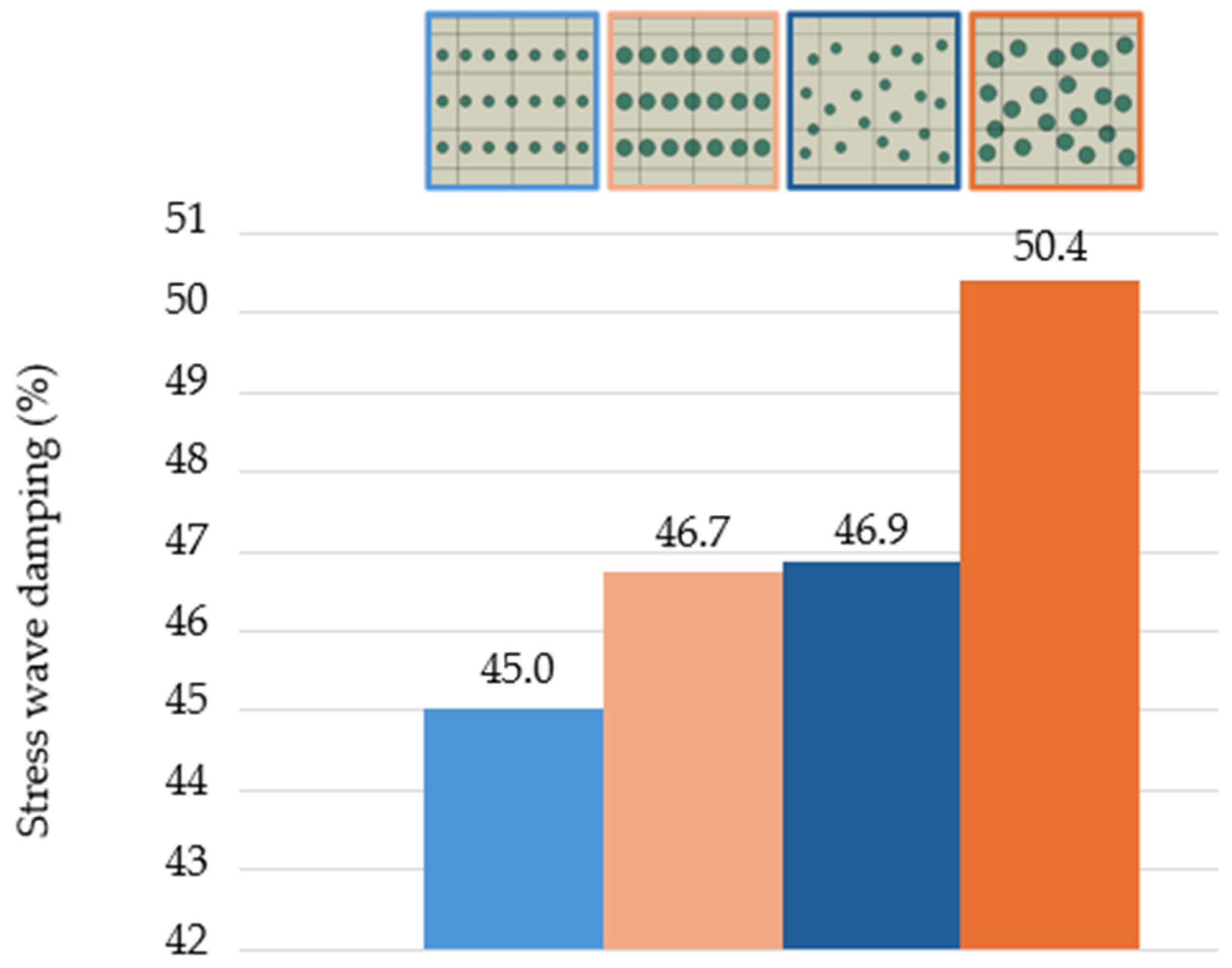
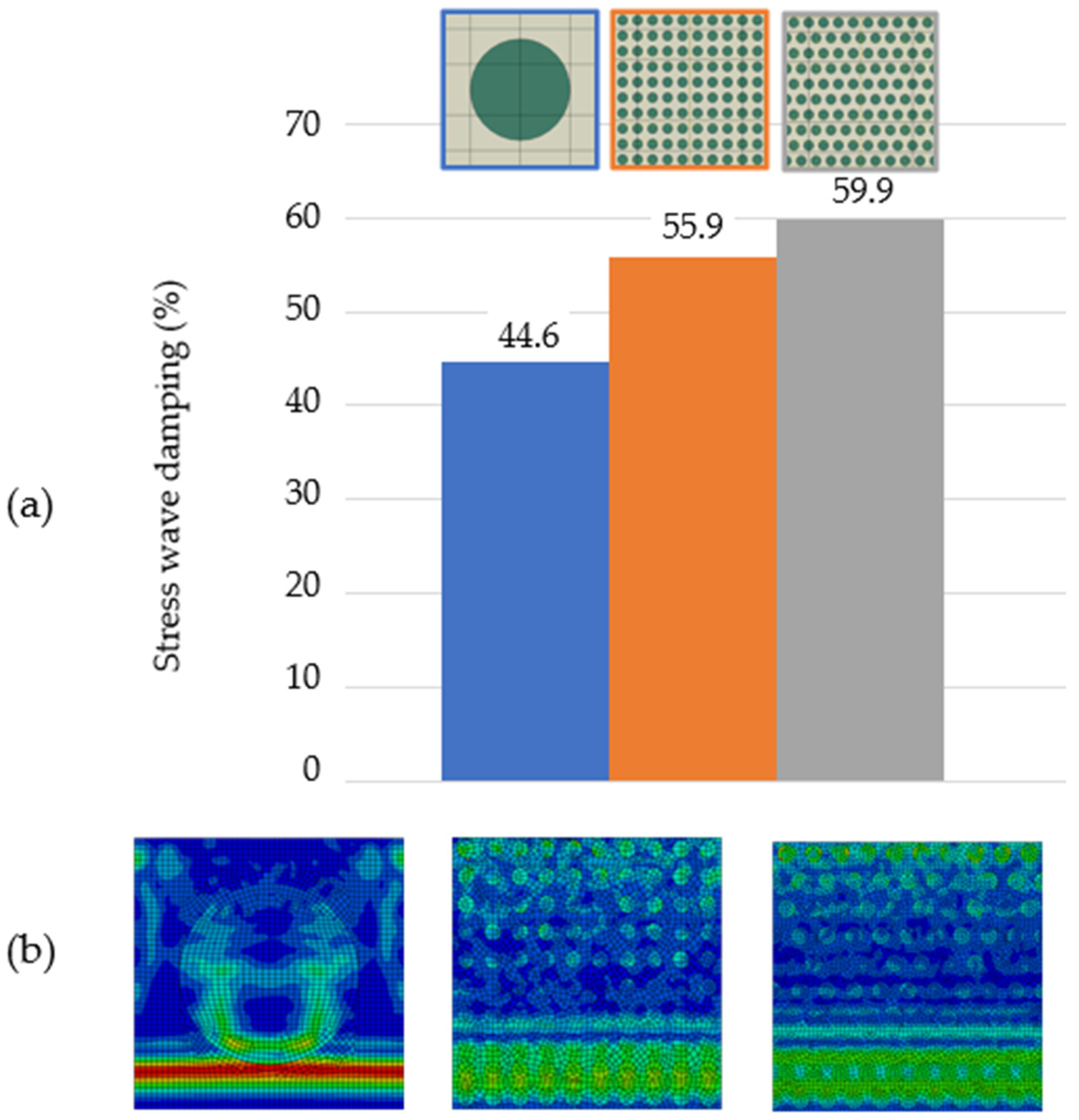
3.2. Numerical Simulation of Different RUC Topologies
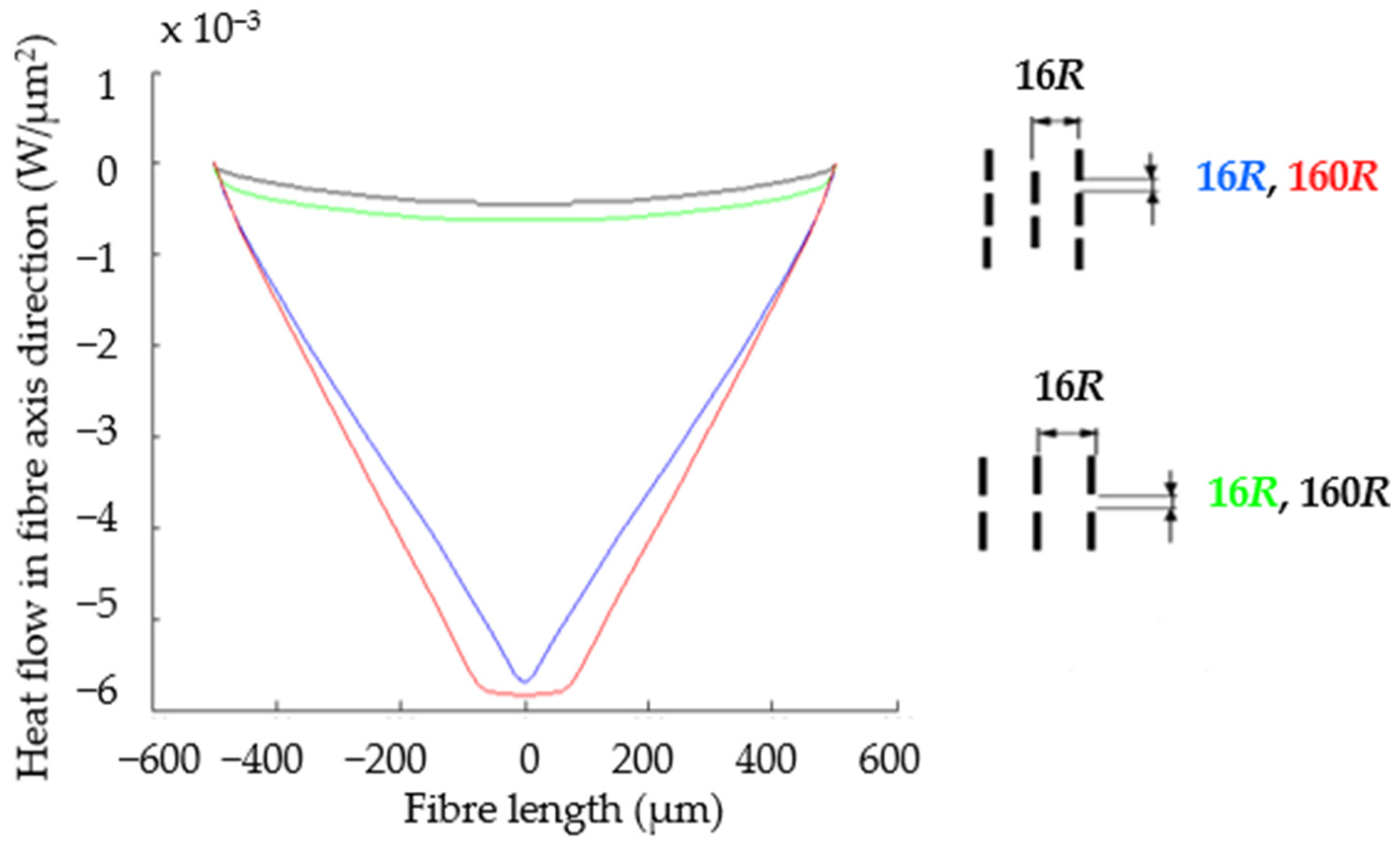
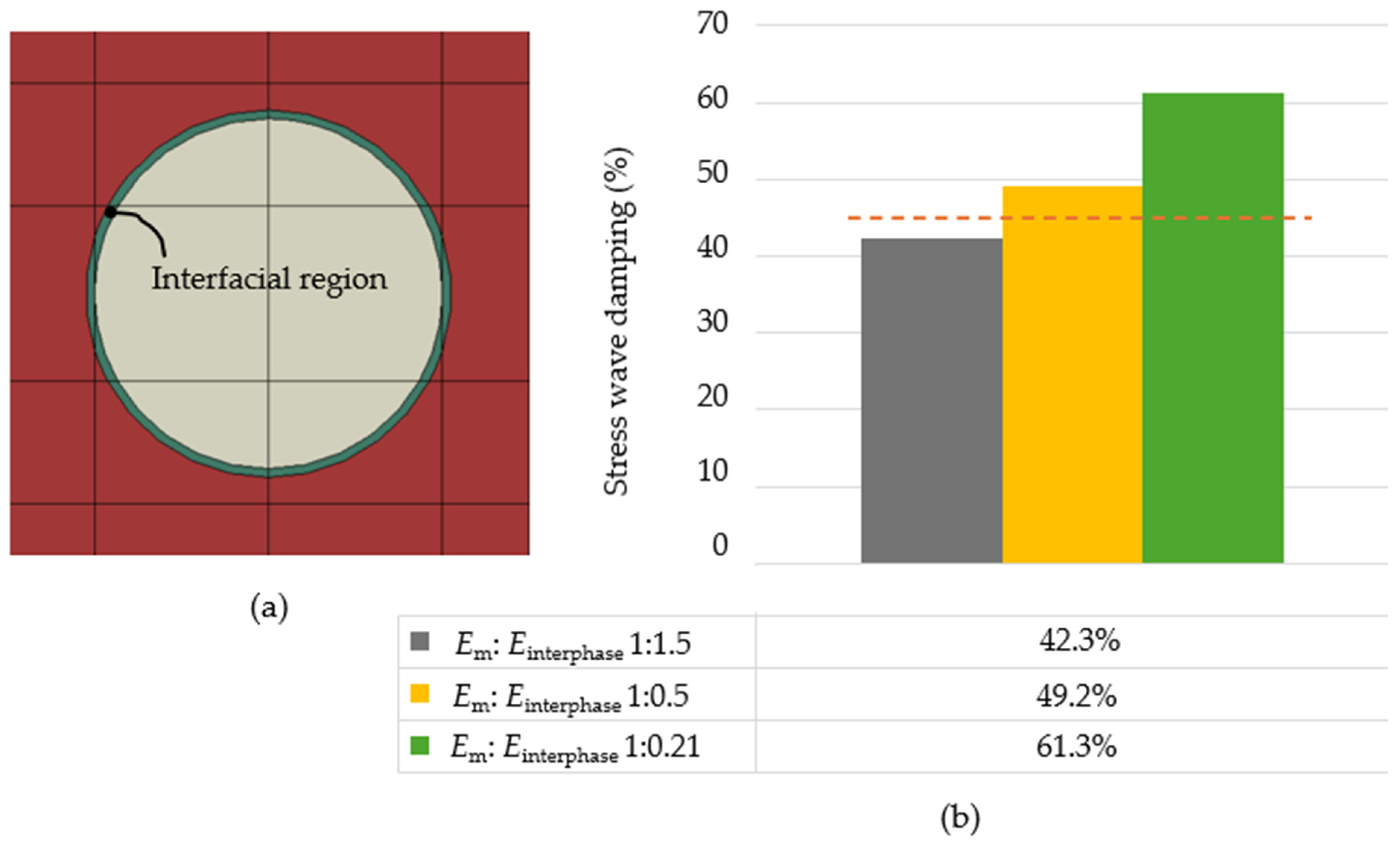
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Li, J.C.M. Microstructure and Properties of Materials (Vol. 2); World Scientific: Singapore, 1996. [Google Scholar]
- Harničárová, M.; Valíček, J.; Kušnerová, M.; Kmec, J.; Palková, Z.; Kopal, I.; Krmela, J.; Panda, A. Study of the influence of the structural grain size on the mechanical properties of technical materials. Mater. Und Werkst. 2019, 50, 635–645. [Google Scholar] [CrossRef]
- Thornton, P.A. The influence of nonmetallic inclusions on the mechanical properties of steel: A review. J. Mater. Sci. 1971, 6, 347–356. [Google Scholar] [CrossRef]
- Tang, X.; Yan, X. A review on the damping properties of fiber reinforced polymer composites. J. Ind. Text. 2020, 49, 693–721. [Google Scholar] [CrossRef]
- Goldsmith, W. Impact: The Theory and Physical Behaviour of Colliding; Courier Dover Publications: Mineola, NY, USA, 2001. [Google Scholar]
- Fleck, N.A.; Deshpande, V.S.; Ashby, M.F. Micro-architectured materials: Past, present and future. Proc. R. Soc. A Math. Phys. Eng. Sci. 2010, 466, 2495–2516. [Google Scholar] [CrossRef]
- Abtew, M.A.; Boussu, F.; Bruniaux, P.; Loghin, C.; Cristian, I. Ballistic impact mechanisms—A review on textiles and fibre-reinforced composites impact responses. Compos. Struct. 2019, 223, 110966. [Google Scholar] [CrossRef]
- Estrin, Y.; Bréchet, Y.; Dunlop, J.; Fratzl, P. Architectured Materials in Nature and Engineering; Springer Nature: Cham, Switzerland, 2019. [Google Scholar]
- Aggogeri, F.; Borboni, A.; Merlo, A.; Pellegrini, N.; Ricatto, R. Vibration damping analysis of lightweight structures in machine tools. Materials 2017, 10, 297. [Google Scholar] [CrossRef] [PubMed]
- Vivek, A.; Holla, V.; Krupashankara, M.S.; Vignesh, A.; Kulkarni, P. Effect of improving damping ratio on surface finish by filling particulate reinforced polymer composites in machine tool structures. Mater. Today Proc. 2018, 5, 13664–13673. [Google Scholar] [CrossRef]
- Murčinková, Z.; Adamčík, P.; Živčák, J. Re-design of machine tool joint components based on polymer fillings for high-speed performance. Materials 2021, 14, 6913. [Google Scholar] [CrossRef] [PubMed]
- Möhring, H.C.; Brecher, C.; Abele, E.; Fleischer, J.; Bleicher, F. Materials in machine tool structures. CIRP Ann. 2015, 64, 725–748. [Google Scholar] [CrossRef]
- Ramana, M.V.; Thyla, P.R.; Mahendrakumar, N.; Praveena, K. Selection of resin and aggregates for particulate polymer concrete machine tool structures—A review. Mater. Today Proc. 2021, 46, 8621–8628. [Google Scholar] [CrossRef]
- Mula, V.R.; Ramachandran, A.; Pudukarai Ramasamy, T. A review on epoxy granite reinforced polymer composites in machine tool structures–Static, dynamic and thermal characteristics. Polym. Compos. 2023, 44, 2022–2070. [Google Scholar] [CrossRef]
- Poklemba, R.; Duplakova, D.; Zajac, J.; Duplak, J.; Simkulet, V.; Goldyniak, D. Design and investigation of machine tool bed based on polymer concrete mixture. Int. J. Simul. Model. 2020, 19, 291–302. [Google Scholar] [CrossRef]
- Bhudolia, S.; Perrotey, P.; Joshi, C. Enhanced vibration damping and dynamic mechanical characteristics of composites with novel pseudo-thermoset matrix system. Compos. Struct. 2017, 179, 502–513. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, J.; Li, Z.; Zhang, H.; Chen, J.; Yang, W.; Yu, T.; Liu, W.; Li, Y. Intelligent methods for optimization design of lightweight fibre-reinforced composite structures: A review and the-state-of-the-art. Sec. Polym. Compos. Mater. 2023, 10, 1125328. [Google Scholar]
- Jia, Z.; Yu, Y.; Hou, S.; Wang, L. Biomimetic architected materials with improved dynamic performance. J. Mech. Phys. Solids 2019, 125, 178–197. [Google Scholar] [CrossRef]
- Zhang, P.; Heyne, M.A.; To, A.C. Biomimetic staggered composites with highly enhanced energy dissipation: Modeling, 3D printing, and testing. J. Mech. Phys. Solids. 2015, 83, 285–300. [Google Scholar] [CrossRef]
- Wakasawa, Y.; Hashimoto, M.; Marui, E. The damping capacity improvement of machine tool structures by balls packing. Int. J. Mach. Tools Manuf. 2004, 44, 1527–1536. [Google Scholar] [CrossRef]
- Ahmad, M.J.; Zhu, X.; Zhu, Z.; Kang, R.; Dong, Z.; Saboor, H.A. Structural behavior of the deep hole internal grinding machine structure with artificial granite material. Int. J. Adv. Manuf. Technol. 2023, 128, 3077–3091. [Google Scholar] [CrossRef]
- Kormanikova, E.; Kotrasova, K. Multiscale modeling of a composite cylindrical tank. Data Brief 2018, 18, 1777–1783. [Google Scholar] [CrossRef]
- Müzel, S.D.; Bonhin, E.P.; Guirmaräes, N.M.; Guidi, E.S. Application of the Finite Element Method in the Analysis of Composite Materials: A Review. Polymers 2020, 12, 818. [Google Scholar] [CrossRef]
- Volkova, E.I.; Jones, A.; Brooks, R.; Zhu, Y.; Besley, E. Meso-scale modelling of shock wave propagation in a SiC/Al nanocomposite reinforced with WS2-inorganic fullerene nanoparticles. Compos. Struct. 2013, 96, 601–605. [Google Scholar] [CrossRef]
- Brown, K.A.; Brooks, R.; Awoyemi, O. Meso-scale modelling of shock wave propagation in a cellular glass particle reinforced thermoplastic composite. In Proceedings of the 18th International Conference on Composite Materials, Jeju, Republic of Korea, 21–26 August 2011. [Google Scholar]
- Zhang, C.; Zhu, Q.; Wang, Y.; Ma, P. Finite element simulation of tensile preload effects on high-velocity impact behavior of fibre metal laminates. Appl. Compos. Mater. 2020, 27, 251–268. [Google Scholar] [CrossRef]
- Dewapriya, M.A.N.; Miller, R.E. Energy absorption mechanisms of nanoscopic multilayer structures under ballistic impact loading. Comput. Mater. Sci. 2021, 195, 110504. [Google Scholar] [CrossRef]
- Yang, H.; Gao, D.; Chen, P.; Lu, G. Numerical Investigation on the Ballistic Performance of Semi-Cylindrical Nacre-like Composite Shells under High-Velocity Impact. Materials 2023, 16, 3699. [Google Scholar] [CrossRef] [PubMed]
- Žmindák, M.; Pelagić, Z. Modeling of shock wave resistance in composite solids. Procedia Eng. 2014, 96, 517–526. [Google Scholar] [CrossRef]
- Walley, S.M.; Field, J.E. Elastic wave propagation in materials. Ref. Modul. Mater. Sci. Mater. Eng. 2016, 1, 1–7. [Google Scholar]
- Sato, C.; Marzi, S. High-rate loading and impact in adhesively bonding joints. In Adhesive Bonding; Woodhead Publishing: Sawston, UK, 2021; pp. 257–293. [Google Scholar]
- Chung, D.D.L. Structural composite materials tailored for damping. J. Alloys Compd. 2003, 355, 216–223. [Google Scholar] [CrossRef]
- Agrawal, N.; Thakur, O.P.; Singh, A.K. Role of shape, size and concentration of filler particles on filler matrix interface: A mathematical analysis. Mater. Today Proc. 2021, 44, 890–894. [Google Scholar] [CrossRef]
- Bokobza, L. Elastomer nanocomposites: Effect of filler–matrix and filler–filler interactions. Polymers 2023, 15, 2900. [Google Scholar] [CrossRef] [PubMed]
- Finegan, I.C.; Gibson, R.F. Recent research on enhancement of damping in polymer composites. Compos. Struct. 1999, 44, 89–98. [Google Scholar] [CrossRef]
- Murčinková, Z.; Novák, P.; Kompiš, V.; Žmindák, M. Homogenization of the finite-length fibre composite materials by boundary meshless type method. Arch. Appl. Mech. 2018, 88, 789–804. [Google Scholar] [CrossRef]
- Bednarcyk, B.A.; Aboudi, J.; Arnold, S.M. Enhanced composite damping through engineered interfaces. Int. J. Solids Struct. 2016, 92, 91–104. [Google Scholar] [CrossRef]
| Young’s Modulus E (GPa) | Ratio Em:Ep | Poisson’s Ratio ν | Density ρ (g/cm3) | Ratio ρm:ρp | |
|---|---|---|---|---|---|
| Matrix | Em = 2.4 GPa | - | 0.35 | ρm = 1.2 g/cm3 | - |
| Particle | 2.4 × 1 | 1:1 | 0.35 | 1.2 × 1 | 1:1 |
| 2.4 × 2 | 1:2 | 1.2 × 2 | 1:2 | ||
| 2.4 × 5 | 1:5 | 1.2 × 5 | 1:5 | ||
| 2.4 × 10 | 1:10 | 1.2 × 10 | 1:10 | ||
| 2.4 × 100 | 1:100 | 1.2 × 100 | 1:100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sabol, D.; Murčinková, Z. Stress Wave Propagation and Decay Based on Micro-Scale Modelling in the Topology of Polymer Composite with Circular Particles. Polymers 2024, 16, 2189. https://doi.org/10.3390/polym16152189
Sabol D, Murčinková Z. Stress Wave Propagation and Decay Based on Micro-Scale Modelling in the Topology of Polymer Composite with Circular Particles. Polymers. 2024; 16(15):2189. https://doi.org/10.3390/polym16152189
Chicago/Turabian StyleSabol, Dominik, and Zuzana Murčinková. 2024. "Stress Wave Propagation and Decay Based on Micro-Scale Modelling in the Topology of Polymer Composite with Circular Particles" Polymers 16, no. 15: 2189. https://doi.org/10.3390/polym16152189
APA StyleSabol, D., & Murčinková, Z. (2024). Stress Wave Propagation and Decay Based on Micro-Scale Modelling in the Topology of Polymer Composite with Circular Particles. Polymers, 16(15), 2189. https://doi.org/10.3390/polym16152189








