Investigation of Partial Discharge Transformation Characteristics in Polyimide (PI) Insulations under High-Frequency Electric Stress
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Arrangements
2.2. Plasma Simulation Model
2.3. Plasma Chemical Reactions
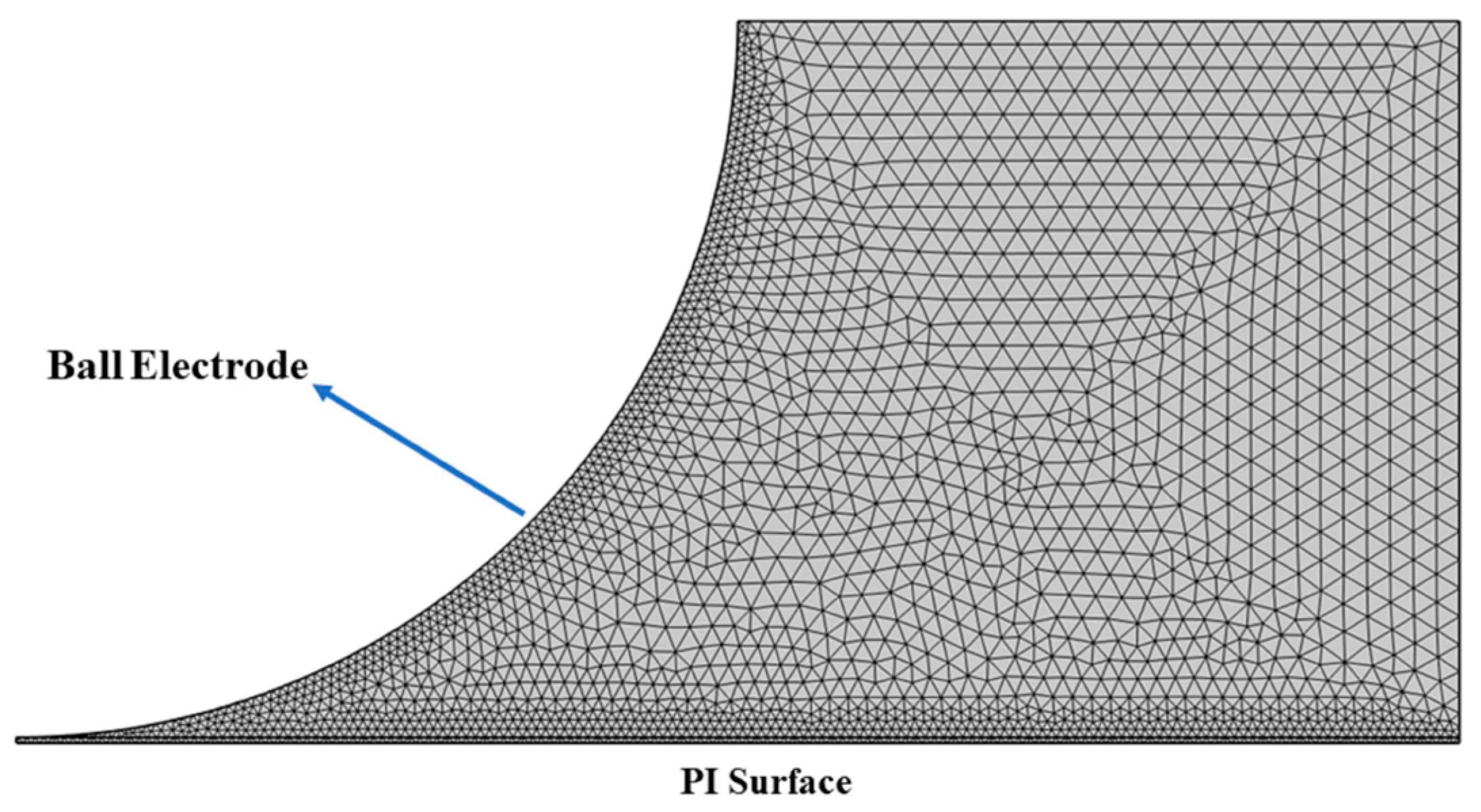
2.4. Mesh for Model Solution
3. Results and Discussion
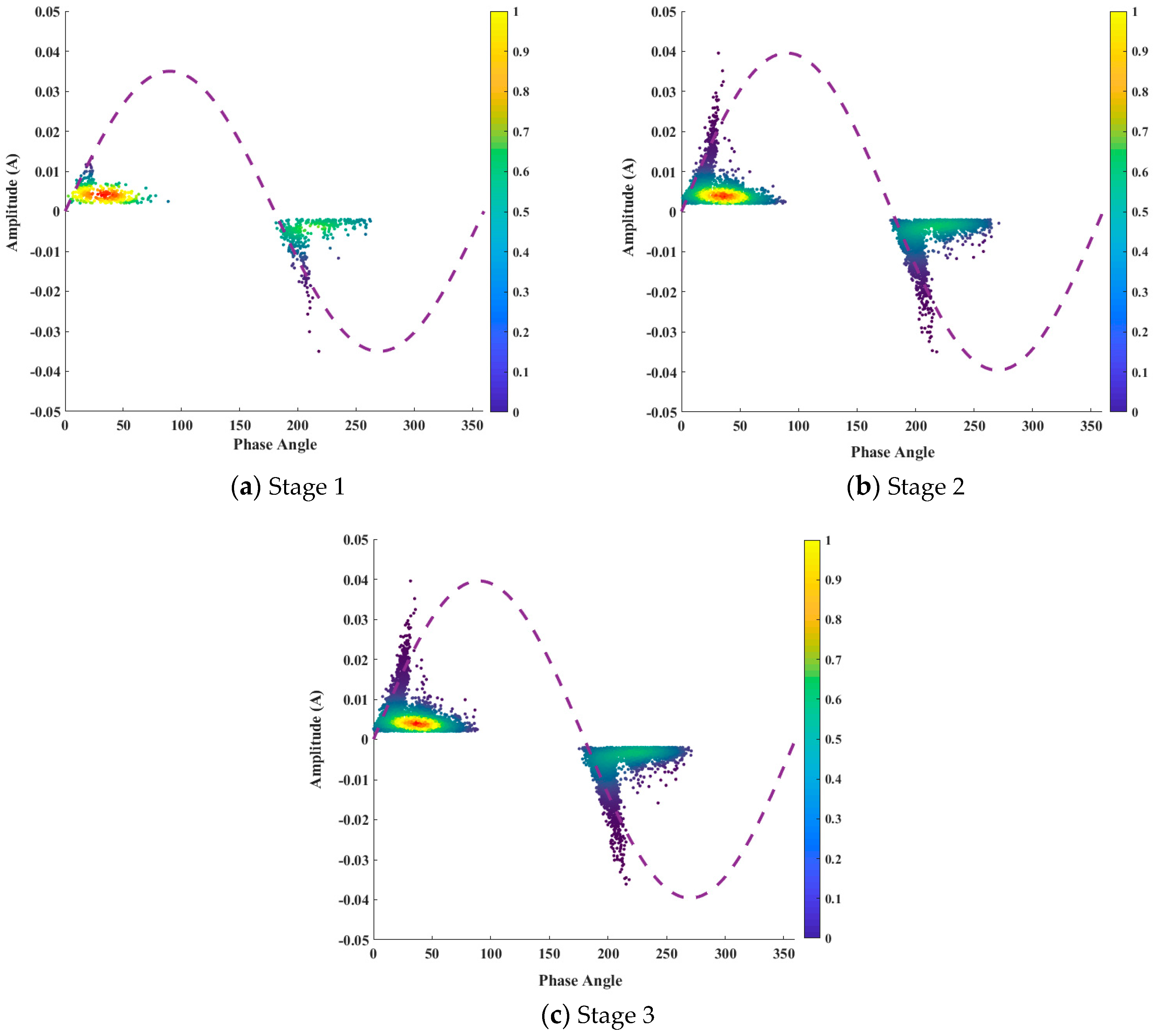
3.1. Partial Discharge Evolution Characteristics Analysis
- Stage 1. Partial Discharge Initiation
- Stage 2. PD Propagation
- Stage 3. Breakdown
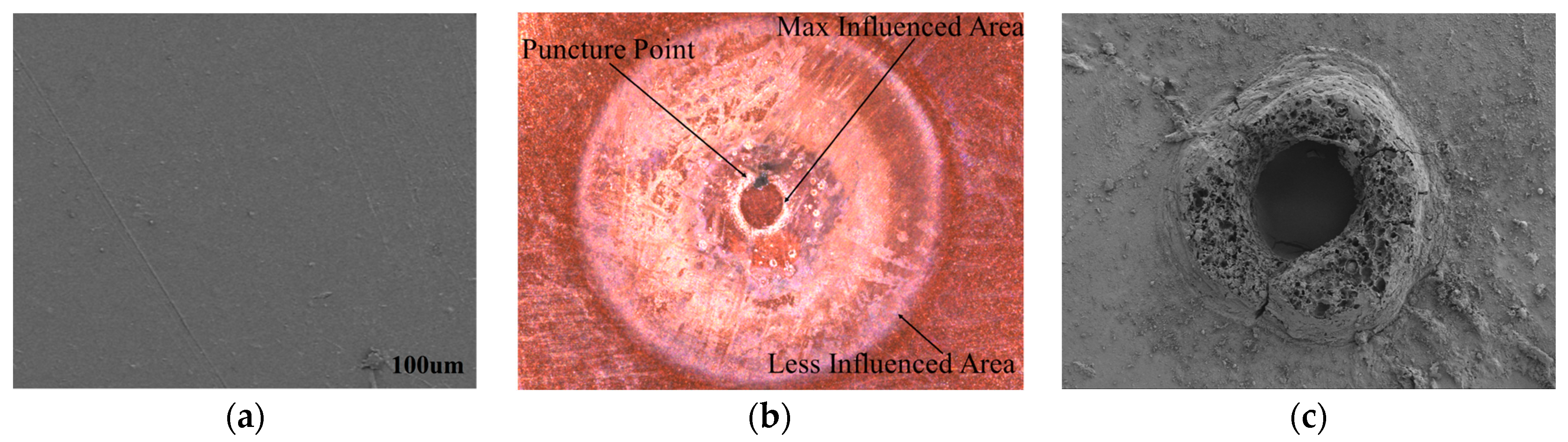
3.2. PD Damage Analysis
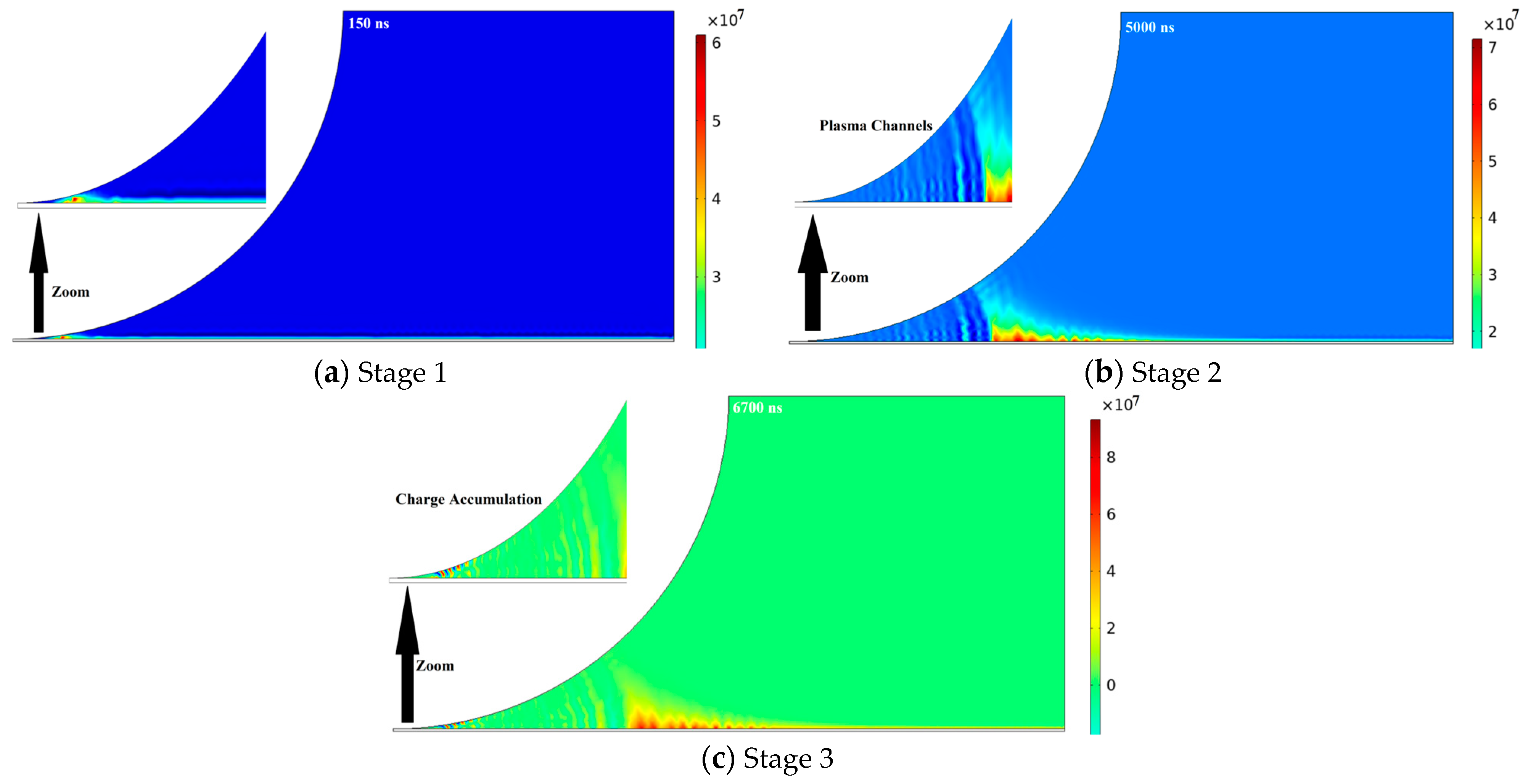
3.3. Evolution of Microscopic Parameters Distribution during Partial Discharge
- Stage 1. Plasma Initiation
- Stage 2. Plasma Propagation
- Stage 3. Partial Discharge activity
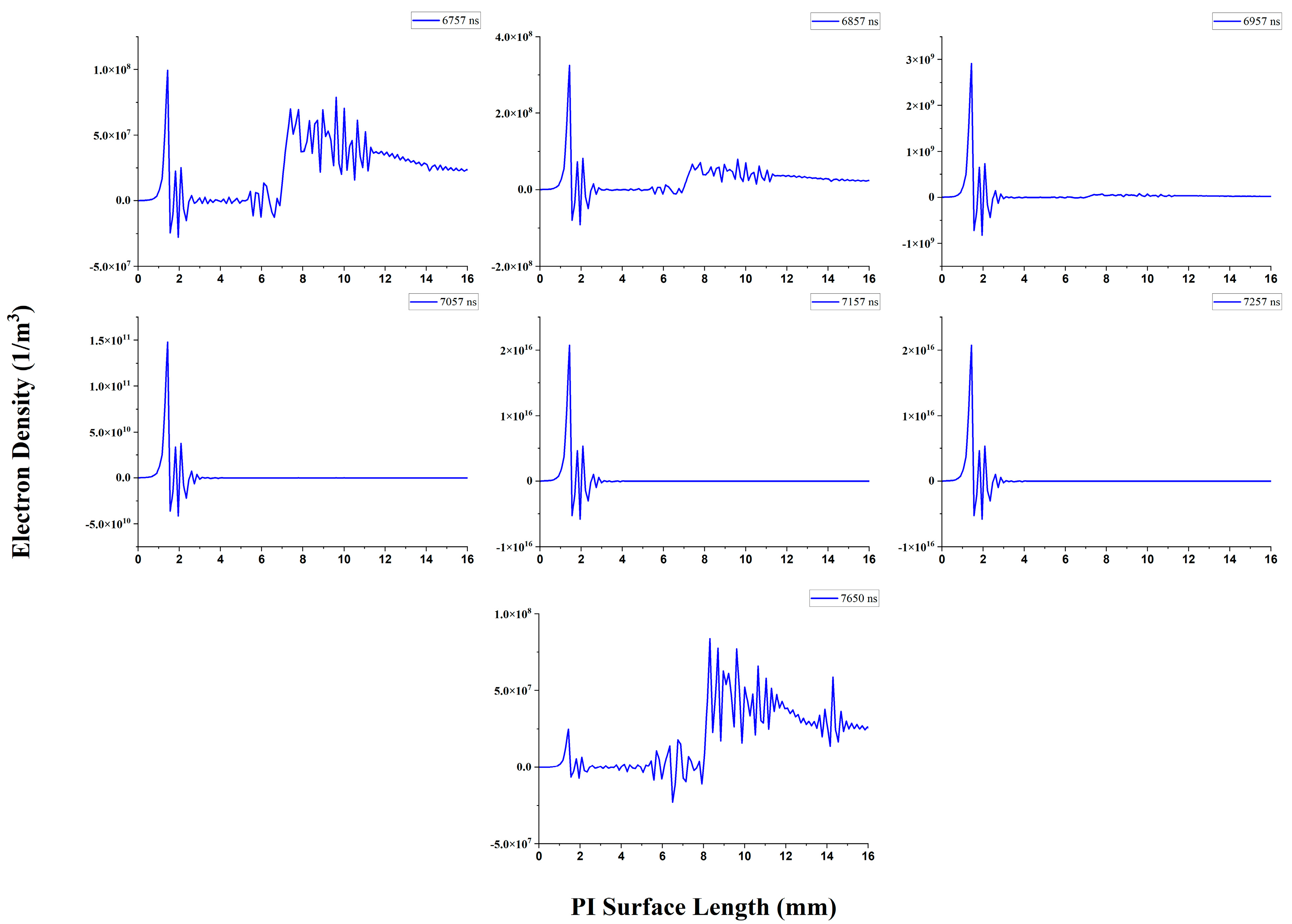
3.4. Electron Density and Electric Field Distribution
3.5. Surface Charge and Space Charge Distribution
3.6. Validation of Model
3.7. Distribution Parameters during PD Activities
3.8. Effect of Voltage Polarity
3.9. Electrical Energy Effect on PD
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, D.; Tian, J.; Mao, C.; Lu, J.; Duan, Y.; Qiu, J.; Cai, H. A 10-kV/400-V 500-kVA Electronic Power Transformer. IEEE Trans. Ind. Electron. 2016, 63, 6653–6663. [Google Scholar] [CrossRef]
- Saleh, S.A.M.; Richard, C.; Onge, X.F.S.; McDonald, K.M.; Ozkop, E.; Chang, L.; Alsayid, B. Solid-State Transformers for Distribution Systems–Part I: Technology and Construction. IEEE Trans. Ind. Appl. 2019, 55, 4524–4535. [Google Scholar] [CrossRef]
- Ayubi, B.I.; Li, Z.; Zhou, S.; Wang, Y.; Liang, Z. A Four Factor Lifetime Estimation Model of Polyimide (PI.) Insulations Using Full Factorial Design of Experiment Method (DOE). IEEE Trans. Dielectr. Electr. Insul. 2023, 31, 844–851. [Google Scholar] [CrossRef]
- Wu, M.; Cao, H.; Cao, J.; Nguyen, H.L.; Gomes, J.B.; Krishnaswamy, S.P. An overview of state-of-the-art partial discharge analysis techniques for condition monitoring. IEEE Electr. Insul. Mag. 2015, 31, 22–35. [Google Scholar] [CrossRef]
- Kim, G.Y.; Choi, M.C.; Lee, D.; Ha, C.S. 2D-Aligned Graphene Sheets in Transparent Polyimide/Graphene Nanocomposite Films Based on Noncovalent Interactions Between Poly(amic acid) and Graphene Carboxylic Acid. Macromol. Mater. Eng. 2012, 297, 303–311. [Google Scholar] [CrossRef]
- Lee, J.; Ko, Y.; Kim, J. Effect of poly(amic acid)-treated BaTiO3 on the dielectric and mechanical properties of BaTiO3/polyimide composites. Macromol. Res. 2010, 18, 200–203. [Google Scholar] [CrossRef]
- Sili, E.; Cambronne, J.; Naude, N.; Khazaka, R. Polyimide lifetime under partial discharge aging: Effects of temperature, pressure and humidity. IEEE Trans. Dielectr. Electr. Insul. 2013, 20, 435–442. [Google Scholar] [CrossRef]
- Li, Z.; Han, Y.; Xie, Z.; Ren, H.; Li, Q.; Wang, Z. High-Frequency Partial Discharge Characteristics of Solid-State Transformer Interturn Multilayer Insulation Under Repetitive Electrical Stress. IEEE Trans. Ind. Electron. 2024, 71, 13331–13340. [Google Scholar] [CrossRef]
- Wang, P.; Cavallini, A.; Montanari, G.C.; Wu, G. Effect of rise time on PD pulse features under repetitive square wave voltages. IEEE Trans. Dielectr. Electr. Insul. 2013, 20, 245–254. [Google Scholar] [CrossRef]
- Meyer, D.R.; Cavallini, A.; Lusuardi, L.; Barater, D.; Pietrini, G.; Soldati, A. Influence of impulse voltage repetition frequency on RPDIV in partial vacuum. IEEE Trans. Dielectr. Electr. Insul. 2018, 25, 873–882. [Google Scholar] [CrossRef]
- Okamoto, T.; Uehara, H. Partial Discharge Current Measurements With Small Discharge Gaps Over Polyimide Film. IEEE Trans. Dielectr. Electr. Insul. 2023, 30, 158–164. [Google Scholar] [CrossRef]
- Emersic, C.; Lowndes, R.; Cotton, I.; Rowland, S.; Freer, R. The effects of pressure and temperature on partial discharge degradation of silicone conformai coatings. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 2986–2994. [Google Scholar] [CrossRef]
- Mi, Y.; Chen, Y.; Liu, C.; Zhu, Y.; Liao, R. Partial Discharge Characteristics of Biaxially Oriented Polypropylene Film under Nanosecond Pulse Voltage with High Rise Rate. IEEE Trans. Plasma Sci. 2023, 51, 498–506. [Google Scholar] [CrossRef]
- Liu, T.; Li, Q.; Huang, X.; Lu, Y.; Asif, M.; Wang, Z. Partial discharge behavior and ground insulation life expectancy under different voltage frequencies. IEEE Trans. Dielectr. Electr. Insul. 2018, 25, 603–613. [Google Scholar] [CrossRef]
- Guo, Z.; Huang, A.Q.; Hebner, R.E.; Montanari, G.C.; Feng, X. Characterization of Partial Discharges in High-Frequency Transformer Under PWM Pulses. IEEE Trans. Power Electron. 2022, 37, 11199–11208. [Google Scholar] [CrossRef]
- Borghei, M.; Ghassemi, M. A Finite Element Analysis Model for Partial Discharges in Silicone Gel under a High Slew Rate, High-Frequency Square Wave Voltage in Low-Pressure Conditions. Energies 2020, 13, 2152. [Google Scholar] [CrossRef]
- Jiang, J.; Zhang, B.; Li, Z.; Ranjan, P.; Chen, J.; Zhang, C. Partial Discharge Features for Power Electronic Transformers Under High-Frequency Pulse Voltage. IEEE Trans. Plasma Sci. 2021, 49, 845–853. [Google Scholar] [CrossRef]
- Zheng, C.; Wang, Q.; Shen, Z.; Bak, C.L.; Da Silva, F.F.; Wang, H. Influence of Pressure on the PD and Induced Aging Behavior of Polyimide Insulation Under Repetitive Pulse Voltage. IEEE Trans. Dielectr. Electr. Insul. 2023, 30, 1283–1293. [Google Scholar] [CrossRef]
- Chen, C.; Wang, J.; Wang, J.; Li, Z.; Guo, R.; Jin, H.; Li, B. Numerical Simulation Research on Partial Discharge of Particle Defects at Epoxy Interface Excited by High-Frequency Sinusoidal Voltage. Polymers 2023, 15, 2320. [Google Scholar] [CrossRef]
- Rodríguez-Serna, J.M.; Albarracín-Sánchez, R. A Study on the Life Estimation and Cavity Surface Degradation Due to Partial Discharges in Spherical Cavities within Solid Polymeric Dielectrics Using a Simulation Based Approach. Polymers 2021, 13, 324. [Google Scholar] [CrossRef]
- Electric Strength of Insulating Materials—Test Methods—Part 1. IEC 60243–1, 2013. Available online: https://webstore.iec.ch/en/publication/1101 (accessed on 5 July 2024).
- Tochikubo, F.; Komuro, A. Review of numerical simulation of atmospheric-pressure non-equilibrium plasmas: Streamer discharges and glow discharges. Jpn. J. Appl. Phys. 2021, 60, 040501. [Google Scholar] [CrossRef]
- Mahadevan, S.; Raja, L.L. Simulations of direct-current air glow discharge at pressures ∼1 Torr: Discharge model validation. J. Appl. Phys. 2010, 107, 093304. [Google Scholar] [CrossRef]
- Sima, W.; Liu, C.; Yang, M.; Shao, Q.; Xu, H.; Liu, S. Plasma model of discharge along a dielectric surface in N2/O2 mixtures. Phys. Plasmas 2016, 23, 063508. [Google Scholar] [CrossRef]
- Liang, Q. Numerical simulation on the surface charge accumulation process of epoxy insulator under needle-plane corona discharge in air. IET Sci. Meas. Technol. 2018, 12, 9–16. [Google Scholar] [CrossRef]
- Liu, K.; Liao, R.; Zhao, X. Numerical Simulation of the Characteristics of Electrons in Bar-plate DC Negative Corona Discharge Based on a Plasma Chemical Model. J. Electr. Eng. Technol. 2015, 10, 1804–1814. [Google Scholar] [CrossRef]
- Hagelaar, G.J.M.; Pitchford, L.C. Solving the Boltzmann equation to obtain electron transport coefficients and rate coefficients for fluid models. Plasma Sources Sci. Technol. 2005, 14, 722–733. [Google Scholar] [CrossRef]
- Duy, C.T.; Bonifaci, N.; Denat, A.; Lesaint, O.; Caliap, L.; Girodet, A.; Gelloz, B.; Ponchon, P. Partial discharges at a triple junction metal/solid insulator/gas and simulation of inception voltage. J. Electrost. 2008, 66, 319–327. [Google Scholar]
- Primc, G. Surface Modification of Polyamides by Gaseous Plasma—Review and Scientific Challenges. Polymers 2020, 12, 3020. [Google Scholar] [CrossRef] [PubMed]
- Meng, X.; Lin, L.; Li, H.; Chen, Y.; Mei, H. Characteristics of streamer discharge along the insulation surface with embedded electrode. IEEE Trans. Dielectr. Electr. Insul. 2024, 31, 2038–2044. [Google Scholar] [CrossRef]
- Othman, N.; Piah, M.; Adzis, Z. Charge distribution measurement of solid insulator materials: A review and new approach. Renew. Sustain. Energy Rev. 2017, 70, 413–426. [Google Scholar] [CrossRef]
- Ju, T.; Chen, X.; Langhe, D.; Ponting, M.; Baer, E.; Zhu, L. Enhancing breakdown strength and lifetime of multilayer dielectric films by using high temperature polycarbonate skin layers. Energy Storage Mater. 2022, 45, 494–503. [Google Scholar] [CrossRef]
- Deshpande, A.S.; Mangalvedekar, H.A.; Cheeran, A.N. Partial discharge analysis using energy patterns. Int. J. Electr. Power Energy Syst. 2013, 53, 184–195. [Google Scholar] [CrossRef]










| No. | Formula | Type | Reaction Rate k | Energy Loss Δε |
|---|---|---|---|---|
| R1 | N2 + e => N2+ + 2e | Ionization | f (e) | 15.6 eV |
| R2 | O2 + e => O2+ + 2e | Ionization | f (e) | 12.06 eV |
| R3 | 2O2 + e => O2 + O2− | Attachment | 2 × 10−45 × (300/plas.Te) | |
| R4 | O4+ + e => 2O2 | Attachment | 1.42 × 10−14 × (300/plas.Te)−0.5 | |
| R5 | O2+ + e => 2O | Attachment | 2 × 10−15 × (300/plas.Te) | |
| R6 | N2+ + N2 + e => 2N2 | Attachment | 6.07 × 10−36 × (plas.Te−2.5) | |
| R7 | N2+ + 2e => N2 + e | Attachment | 5.651 × 10−48 × (plas.Te−0.8) | |
| R8 | N2+ + N2 + O2 => N4+ + O2 | Reaction | 5 × 10−45 | |
| R9 | N2+ + N2 + N2 => N4+ + N2 | Reaction | 5 × 10−45 | |
| R10 | N4+ + O2 => O2+ + 2N2 | Reaction | 2.5 × 10−20 | |
| R11 | N2+ + O2 => O2+ + N2 | Reaction | 6 × 10−31 | |
| R12 | O2+ + O2 + O2 => O4+ + O2 | Reaction | 2.4 × 10−46 | |
| R13 | O2+ + O2 + N2 => O4+ + N2 | Reaction | 2.4 × 10−46 | |
| R14 | O4+ + O2− => 3O2 | Reaction | 1.0 × 10−17 | |
| R15` | O4+ + O2- + O2 => 3O2 + O2 | Reaction | 2.0 × 10−41 | |
| R16 | O4+ + O2- + N2 => 3O2 + N2 | Reaction | 2.0 × 10−41 | |
| R17 | O2+ + O2-+O2 => 2O2 + O2 | Reaction | 2.0 × 10−41 | |
| R18 | O2+ + O2- + N2 => 2O2 + N2 | Reaction | 2.0 × 10−41 | |
| R19 | O + O2 + O2 => O3 + O2 | Reaction | 5.651 × 10−34 | |
| R20 | O + O2 + N2 => O3 + N2 | Reaction | 5.651 × 10−34 |
| No. | Total No. of PDs | No. of PDs Positive Cycle | No. of PDs Negative Cycle | Positive Cycle PD Amp | Negative Cycle PD Amp |
|---|---|---|---|---|---|
| Stage.1 | 706 | 349 | 357 | 0.002−0.013 | 0.002−0.034 |
| Stage.2 | 4836 | 2514 | 2322 | 0.002−0.039 | 0.002−0.034 |
| Stage.3 | 8910 | 4709 | 4201 | 0.002−0.039 | 0.002−0.036 |
| No. | Time (ns) | PD Amp (V) | Electric Field Strength (V/m) | Electron Density (1/m3) | Electron Temp (V) | Surface Charge (C/m2) | Space Charge (C/m3) |
|---|---|---|---|---|---|---|---|
| PD1 | 6700–7650 | 0.002 | 7.68 × 107 | 3.77 × 1016 | 5.25 | −3.2 × 10−5 | −4.1 × 10−3 |
| PD2 | 22,110–22,560 | 0.0022 | 6.5 × 107 | 9.14 × 1016 | 5.25 | −13.5 × 10−5 | −1.8 × 10−4 |
| PD3 | 22,900–23,450 | 0.001 | 7.68 × 107 | 3.17 × 1016 | 5.25 | −2.2 × 10−4 | −3.6 × 10−3 |
| PD4 | 23,700–24,490 | 0.0005 | 7.38 × 107 | 1.52 × 1016 | 5.25 | −1.9 × 10−4 | −1.5 × 10−3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ayubi, B.I.; Zhang, L.; Zhou, S.; Wang, Y.; Zou, L. Investigation of Partial Discharge Transformation Characteristics in Polyimide (PI) Insulations under High-Frequency Electric Stress. Polymers 2024, 16, 2450. https://doi.org/10.3390/polym16172450
Ayubi BI, Zhang L, Zhou S, Wang Y, Zou L. Investigation of Partial Discharge Transformation Characteristics in Polyimide (PI) Insulations under High-Frequency Electric Stress. Polymers. 2024; 16(17):2450. https://doi.org/10.3390/polym16172450
Chicago/Turabian StyleAyubi, Bilal Iqbal, Li Zhang, Shengrui Zhou, Yiwei Wang, and Liang Zou. 2024. "Investigation of Partial Discharge Transformation Characteristics in Polyimide (PI) Insulations under High-Frequency Electric Stress" Polymers 16, no. 17: 2450. https://doi.org/10.3390/polym16172450
APA StyleAyubi, B. I., Zhang, L., Zhou, S., Wang, Y., & Zou, L. (2024). Investigation of Partial Discharge Transformation Characteristics in Polyimide (PI) Insulations under High-Frequency Electric Stress. Polymers, 16(17), 2450. https://doi.org/10.3390/polym16172450









