Analysis of Mechanical Properties and Parameter Dependency of Novel, Doubly Re-Entrant Auxetic Honeycomb Structures
Abstract
:1. Introduction
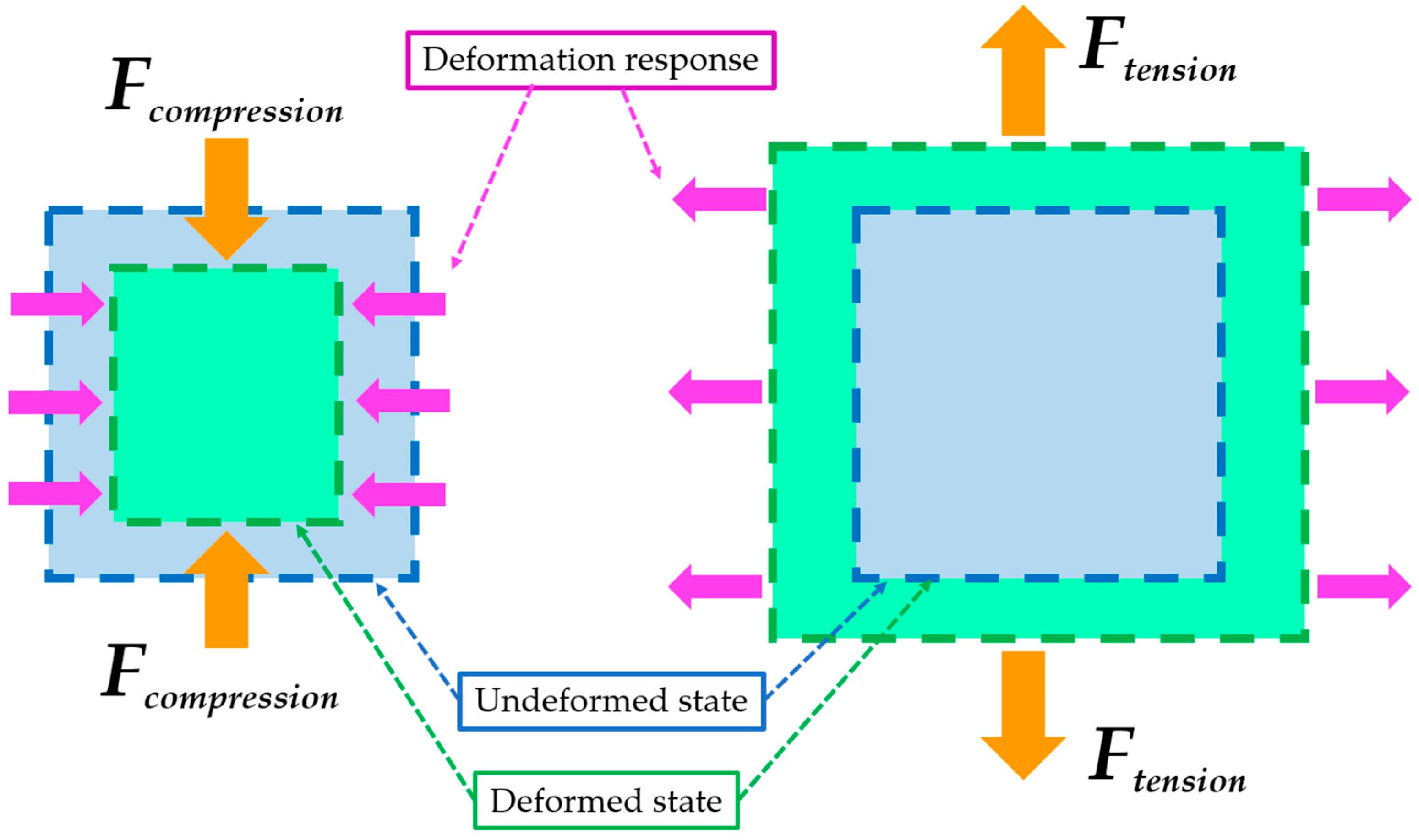
2. Materials and Methods
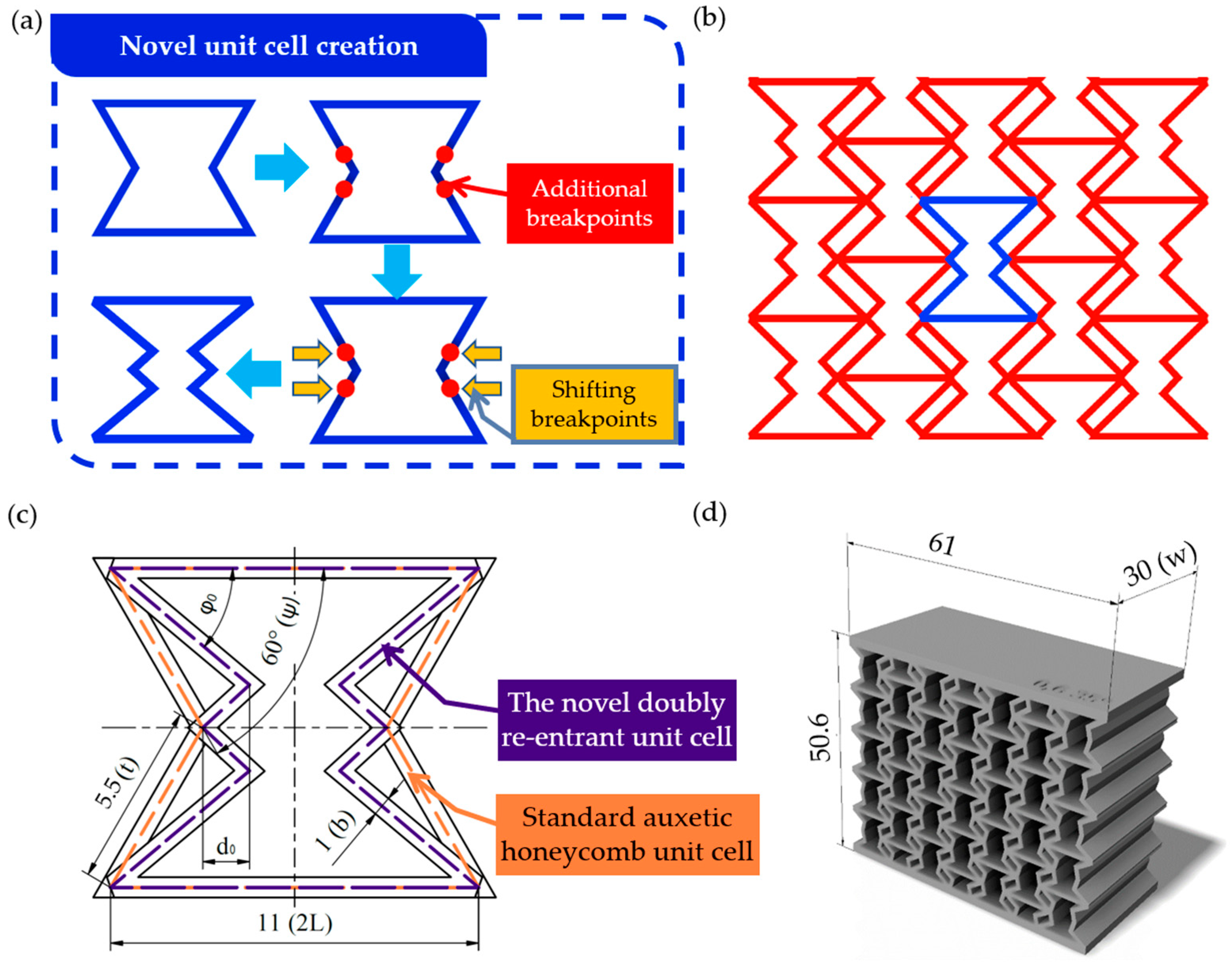
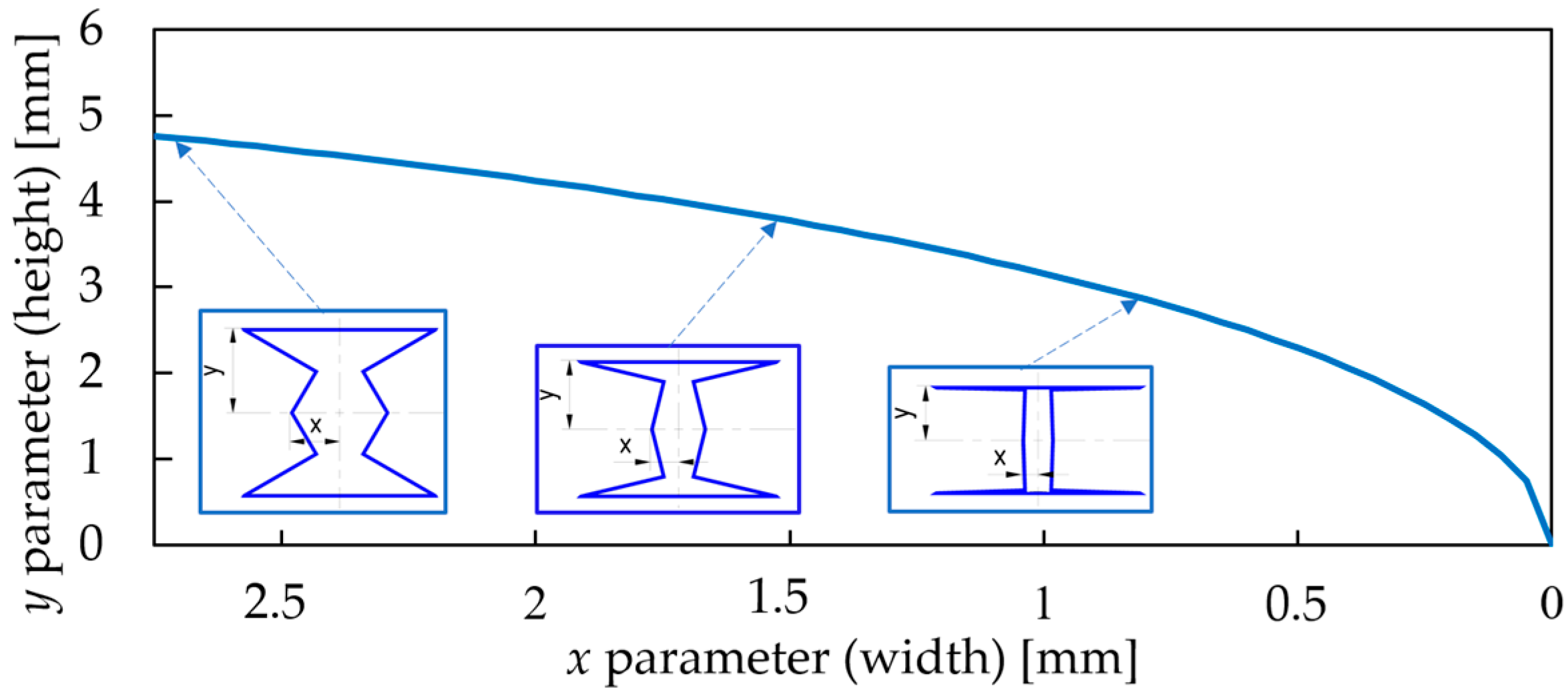
2.1. Introducing the Novel Geometry
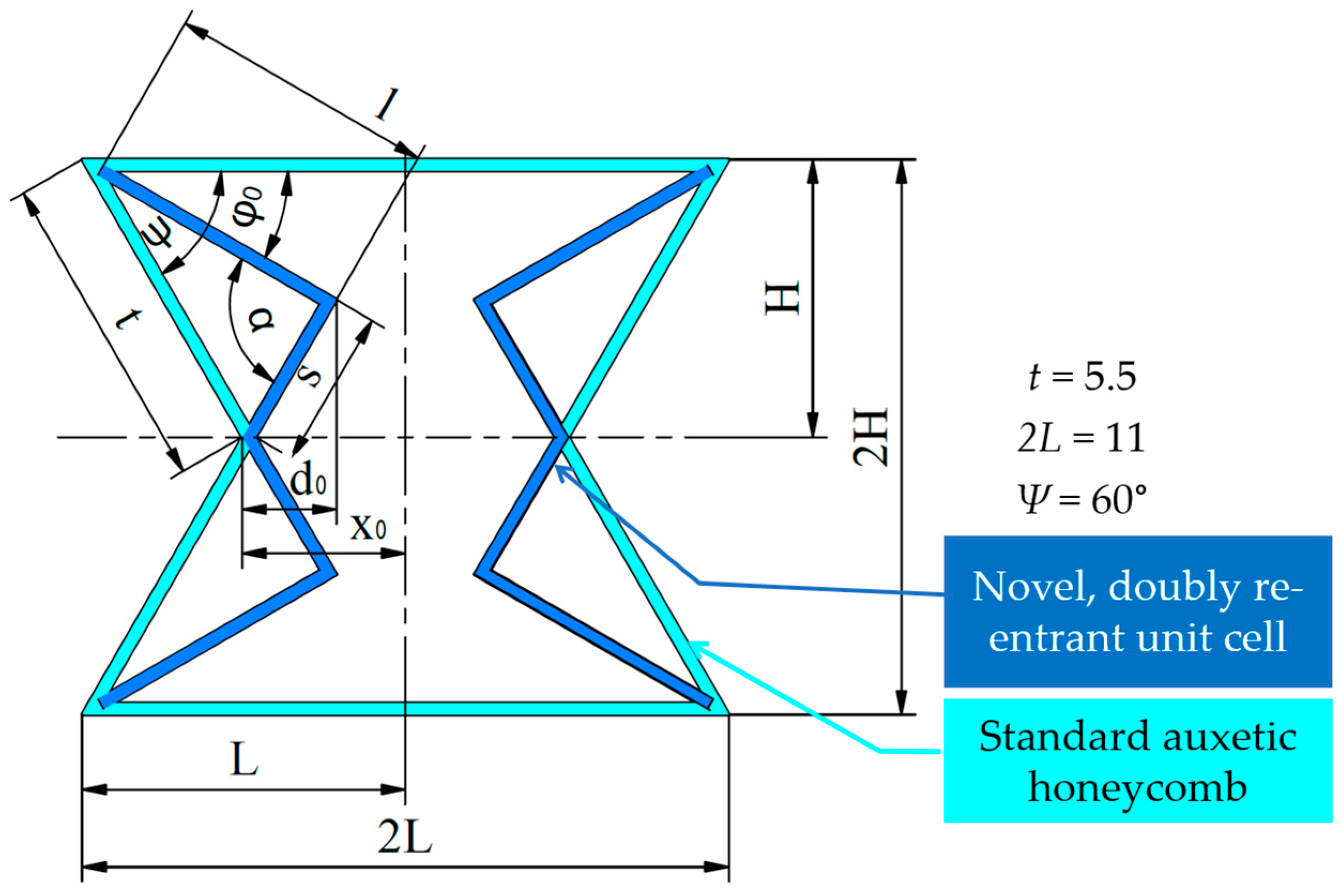
2.2. Geometrical Description of the Tested Specimens
2.3. Preparation of Specimens
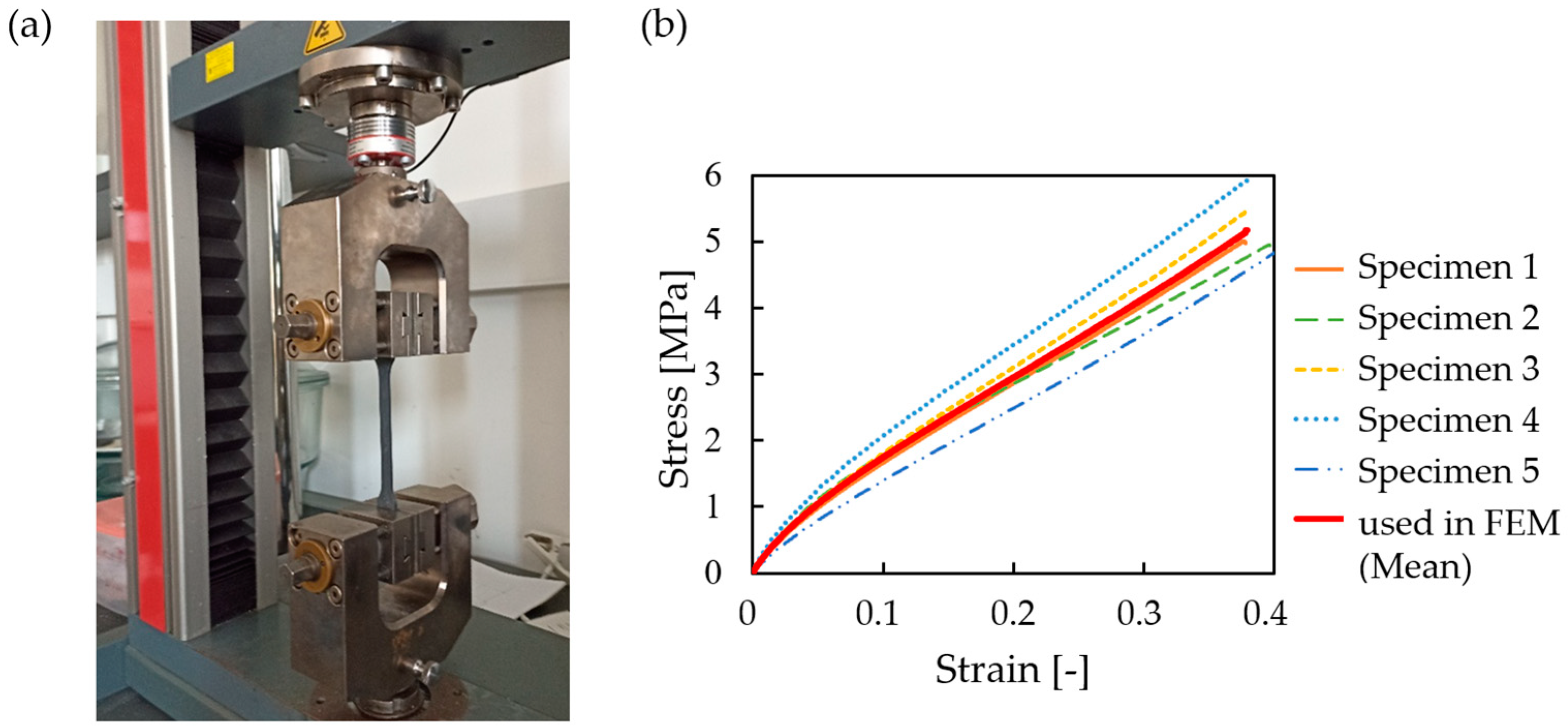
2.4. Mechanical Properties of the Resin Mixture
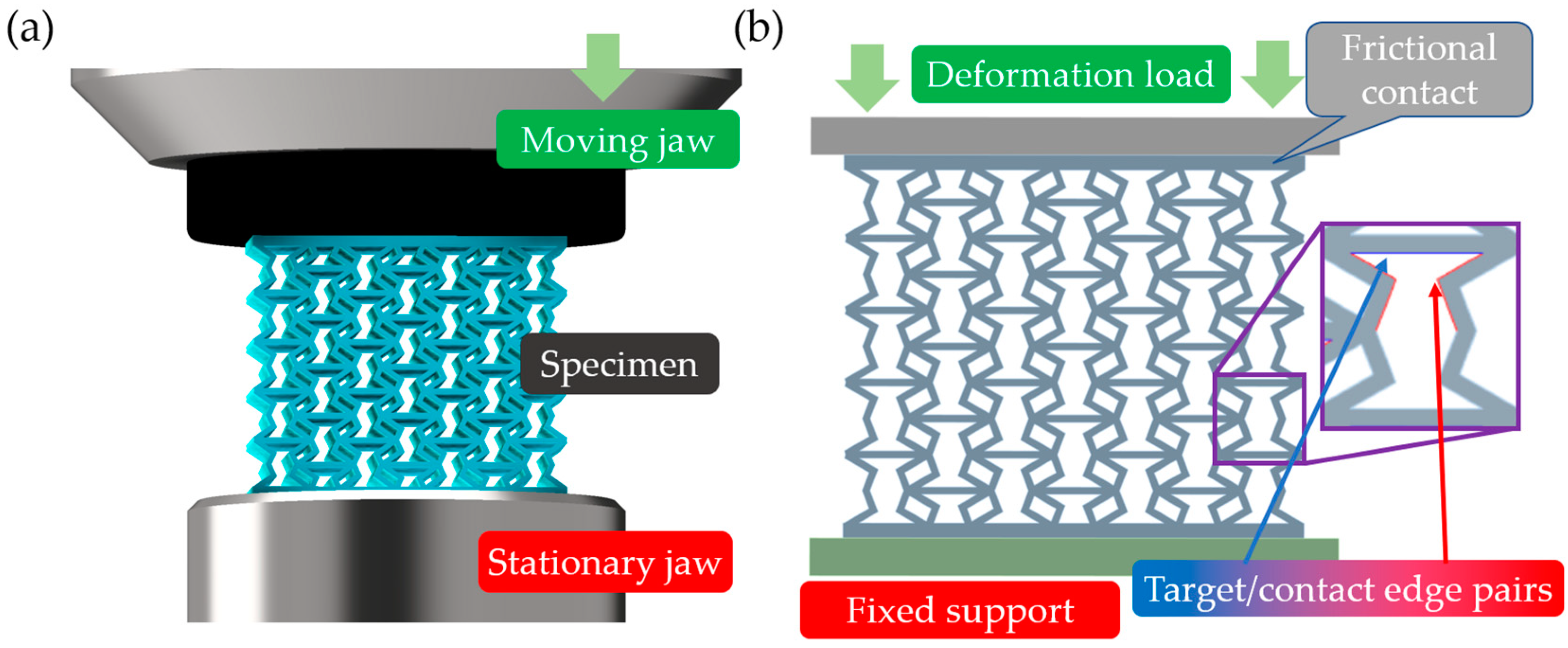
2.5. Compression Test Parameters
2.6. Finite Element Method Test Environment
2.7. Analytical Approach
2.7.1. Description of the Continuous Auxetic Deformation Behaviour
2.7.2. Deformation of the Unit Cell and Characterization of Poisson’s Ratio
2.7.3. Buckling of the Novel Unit Cell
2.7.4. Results of the Analytical Approach
3. Results
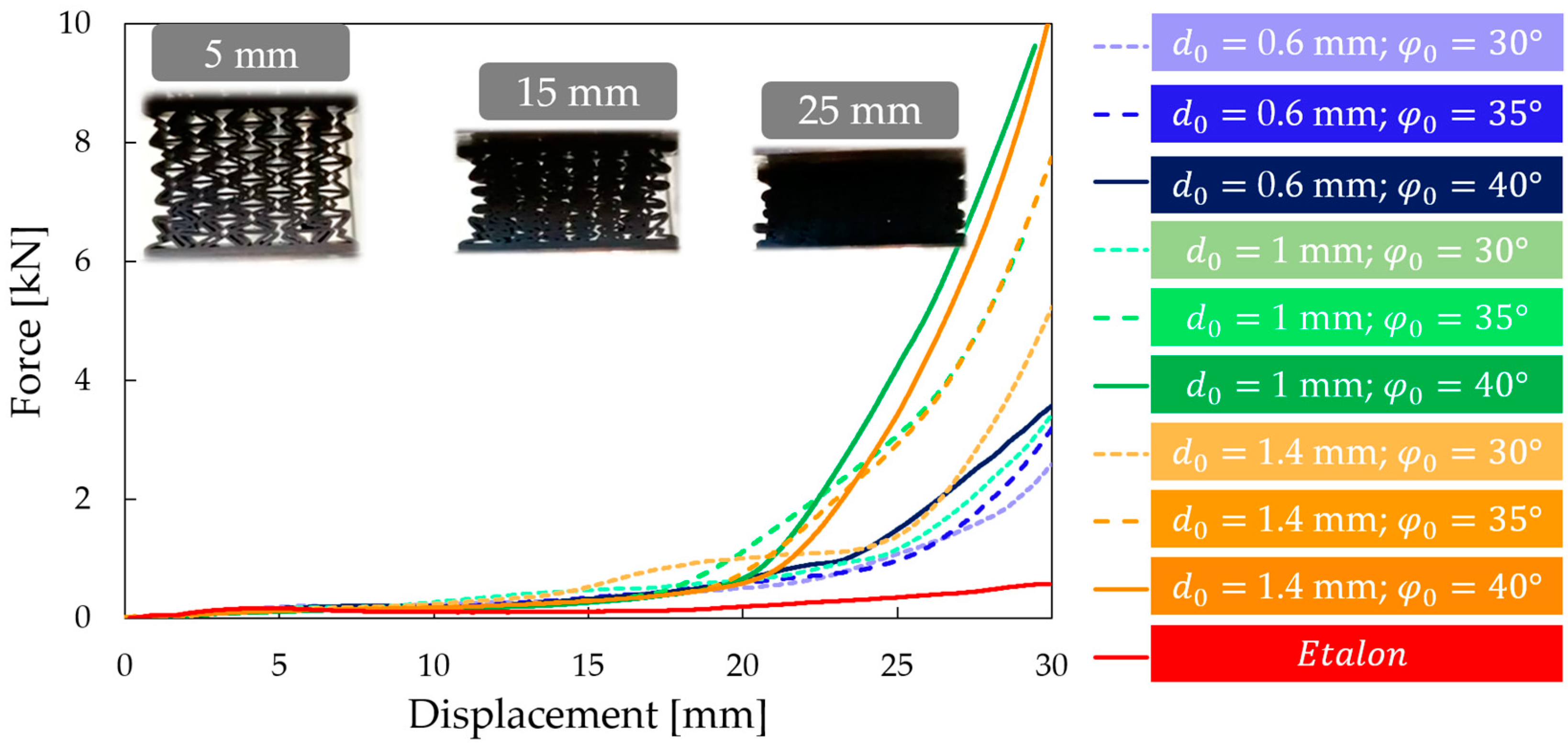
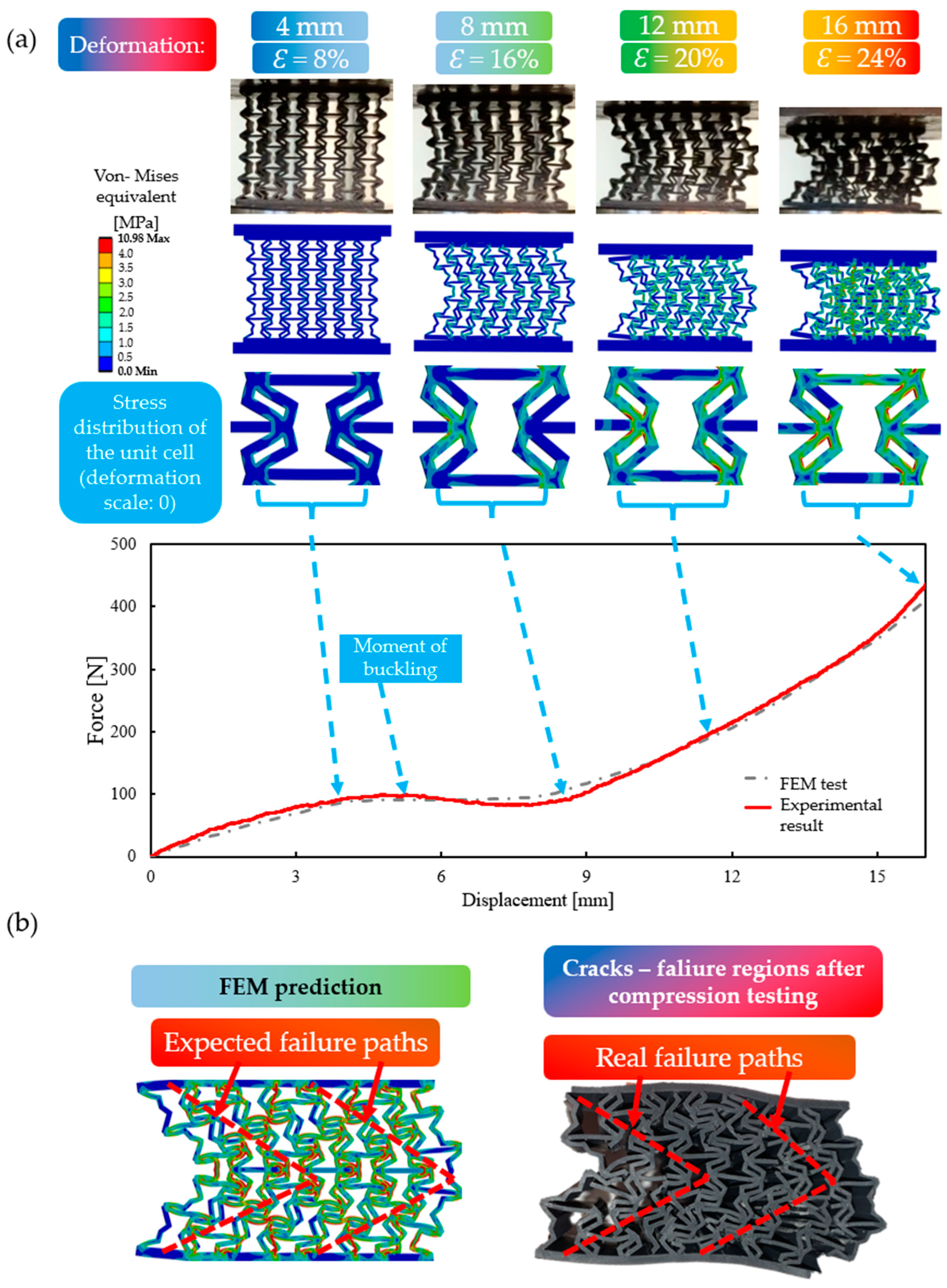
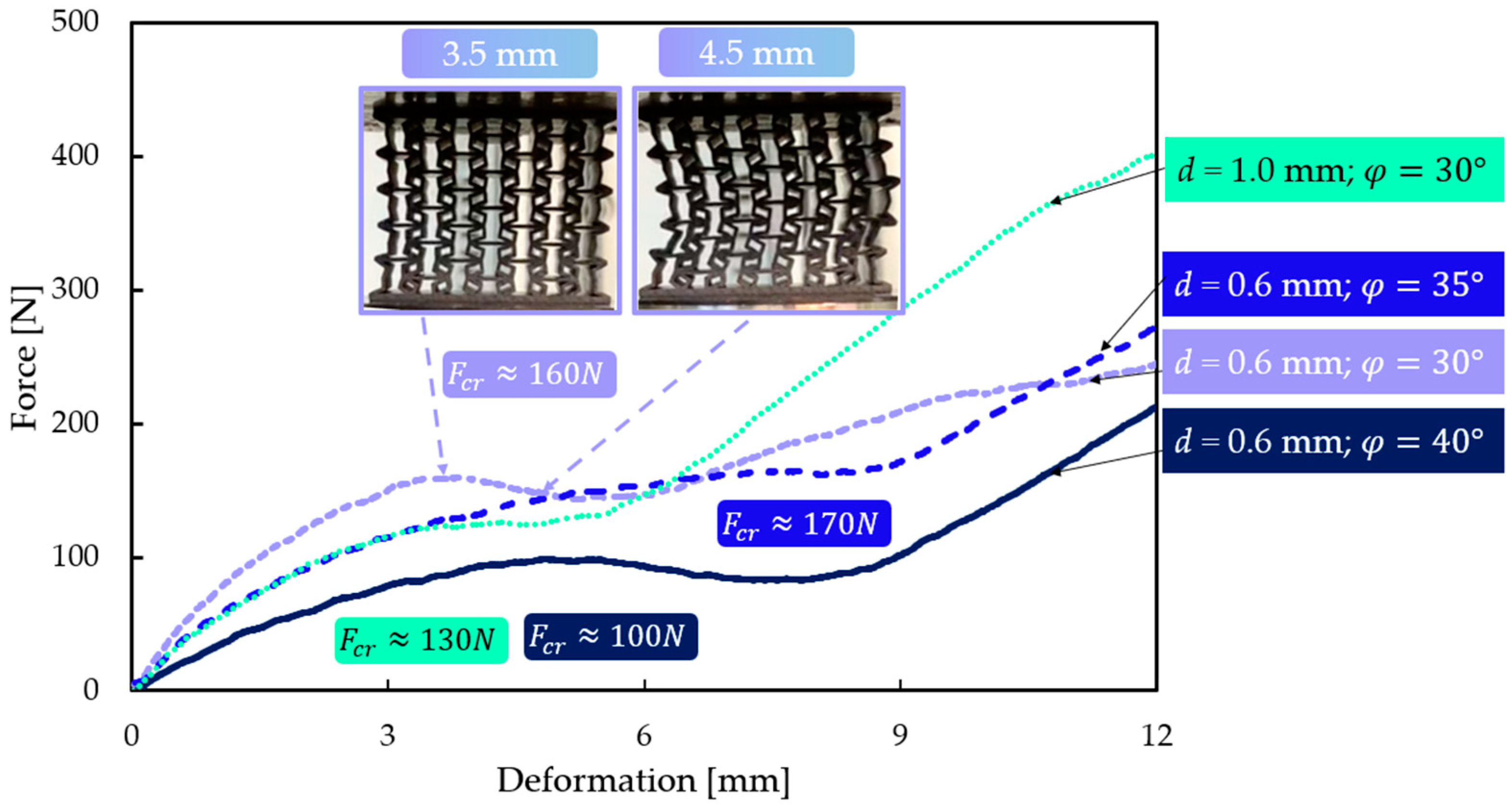
3.1. Compression Test
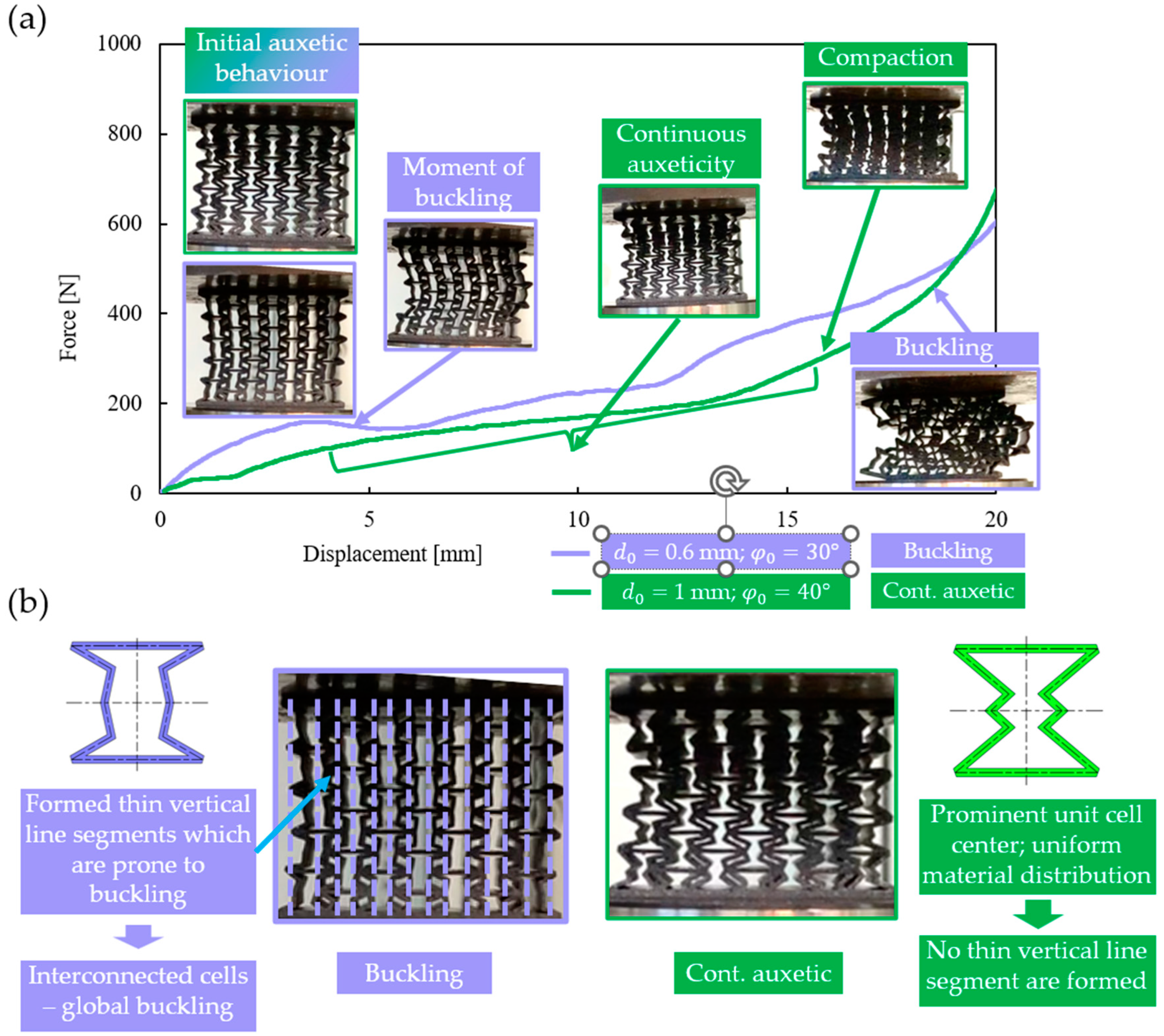
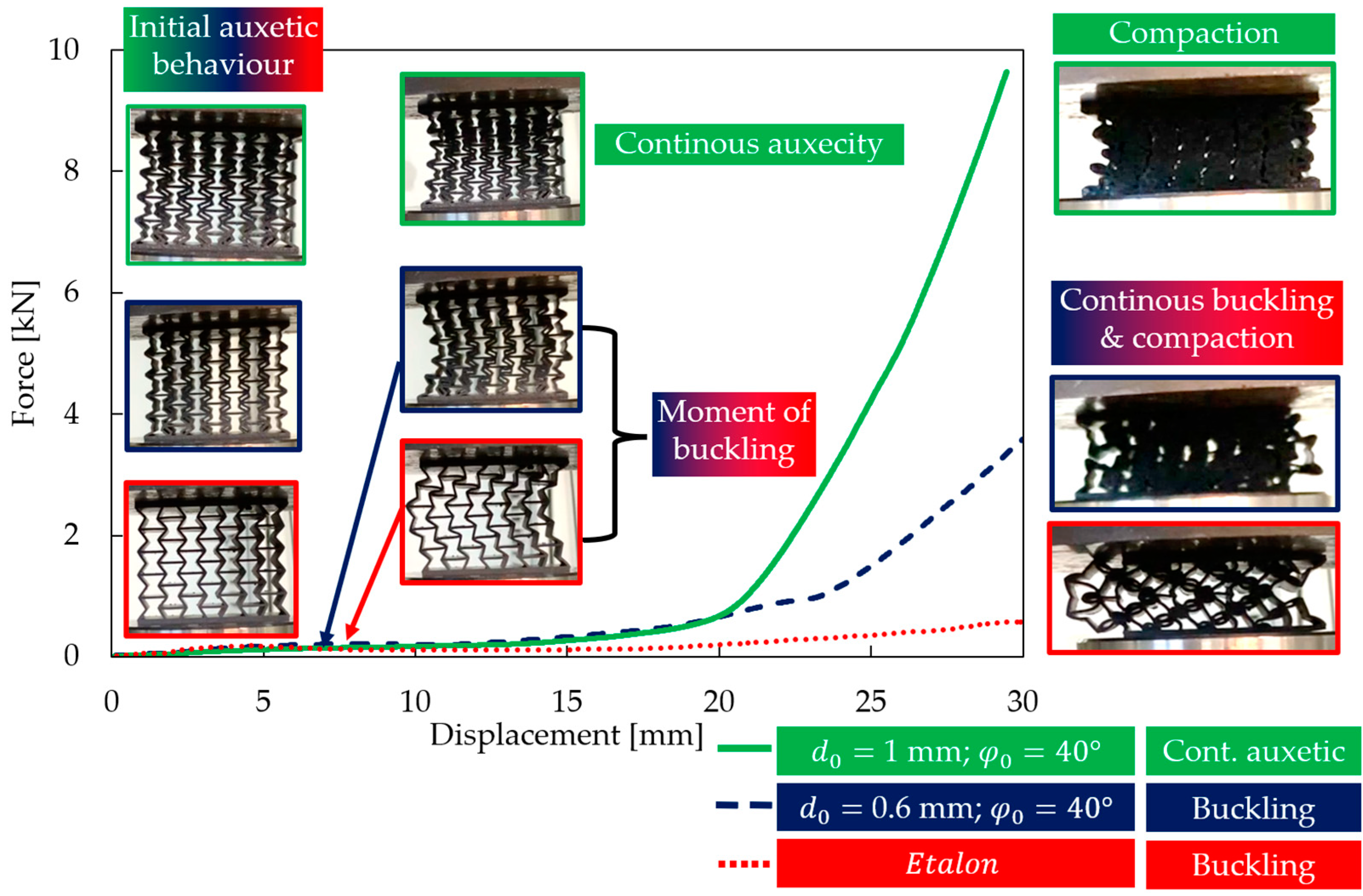
3.2. Description of the Two Typical Behavioural Mechanisms
3.3. FEM Simulation Results
3.3.1. Specimens with Continuous Auxetic Behaviour
3.3.2. Specimens with Buckling Behaviour
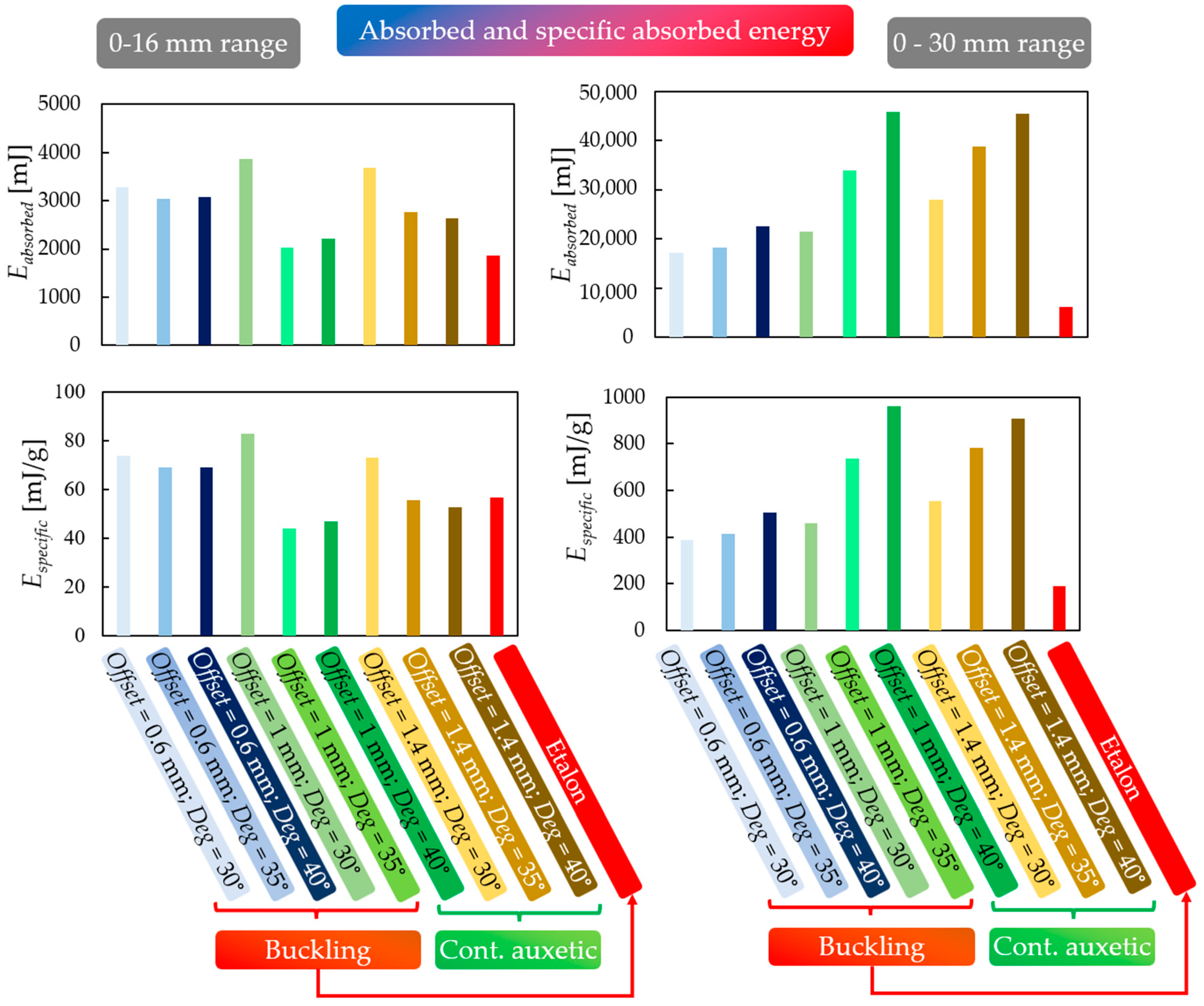
3.4. Result Evaluation
- Lattice-like behaviour boundary point: the point where compaction is not yet significant and unit-cell deformations are still present. The results suggest that this point is, on average, at 16 mm of deformation.
- The limit of our measurement range is 30 mm of deformation.
3.5. Poisson’s Ratio of Specimens with Continuous Auxetic Behaviour
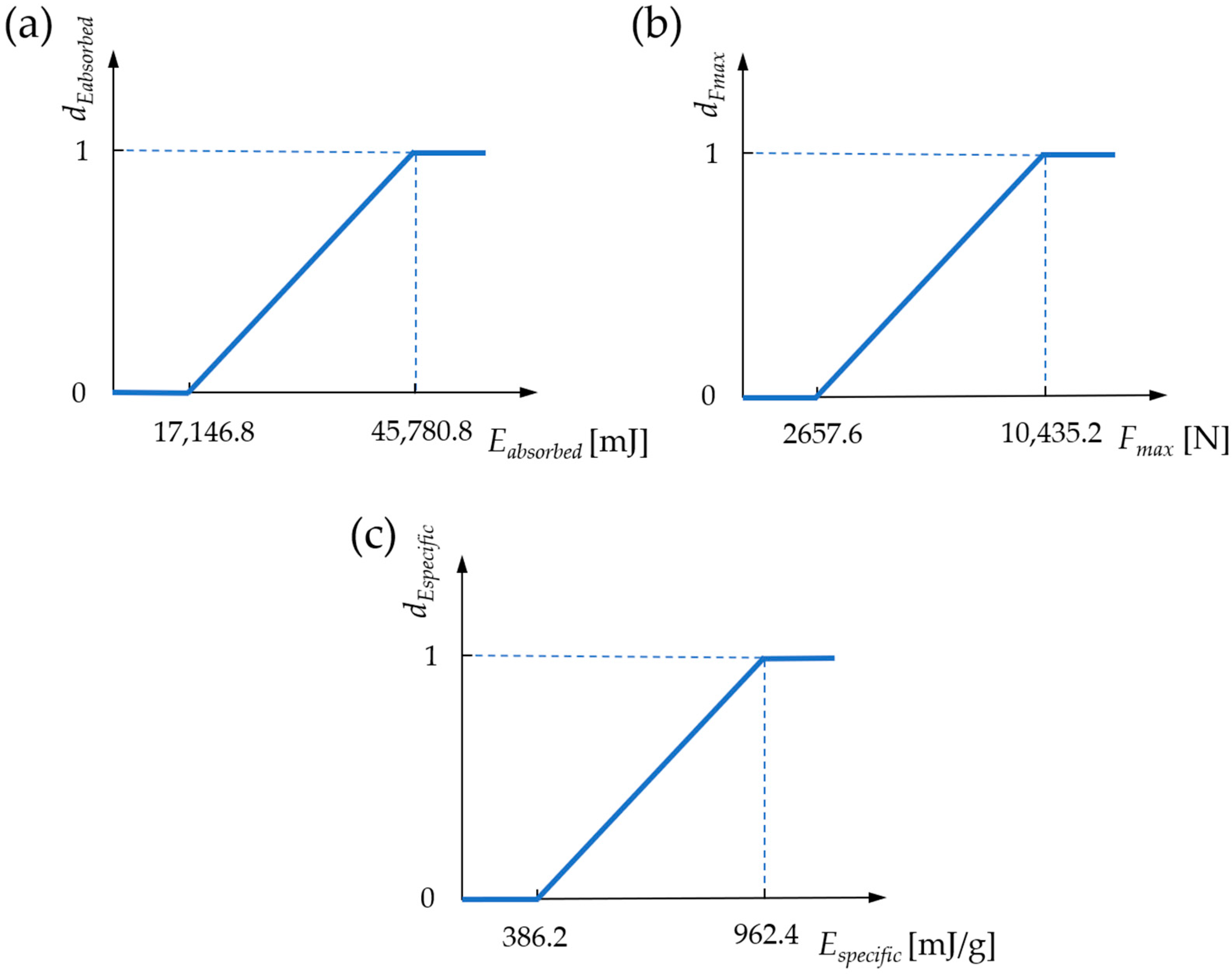
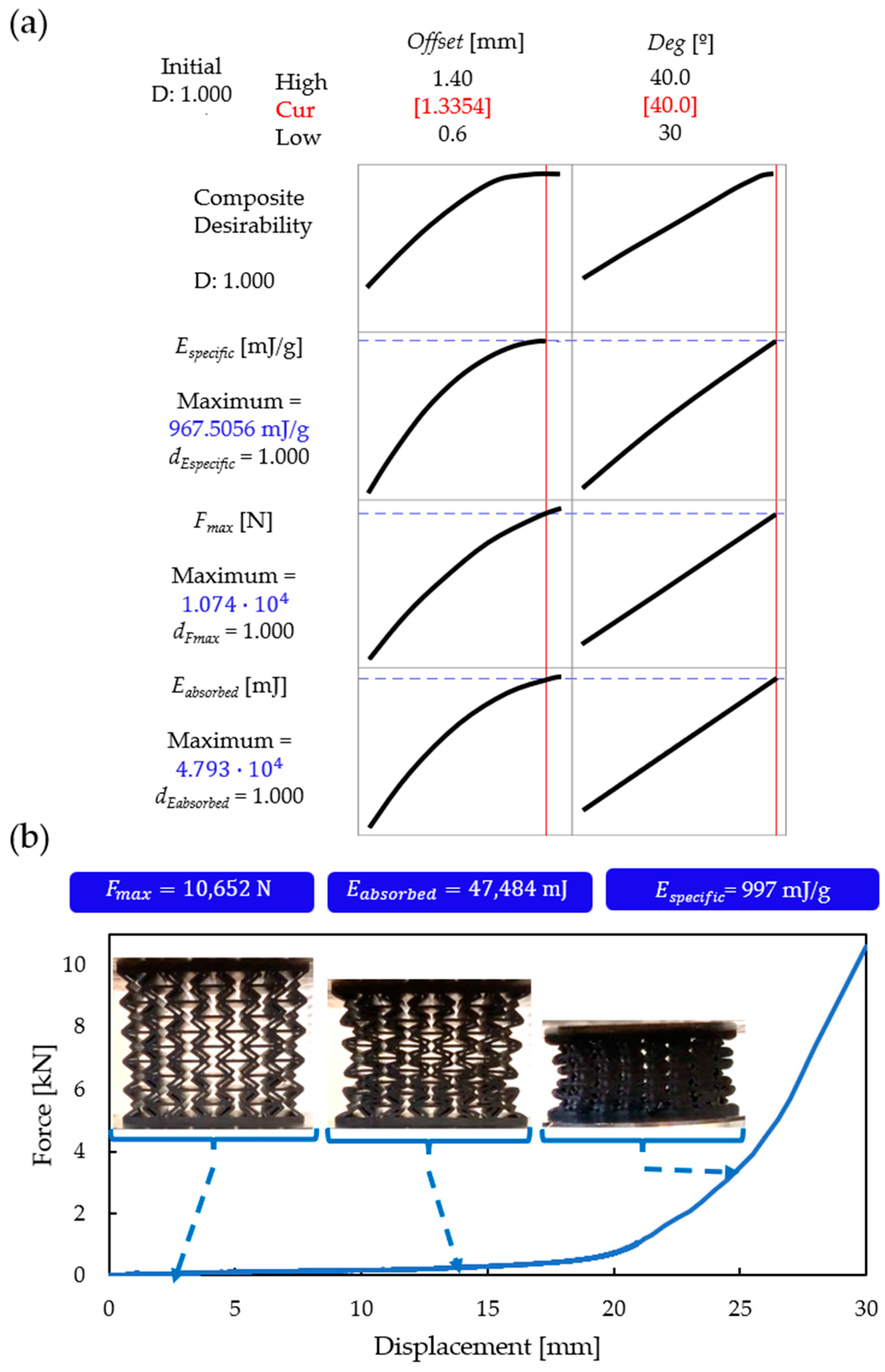
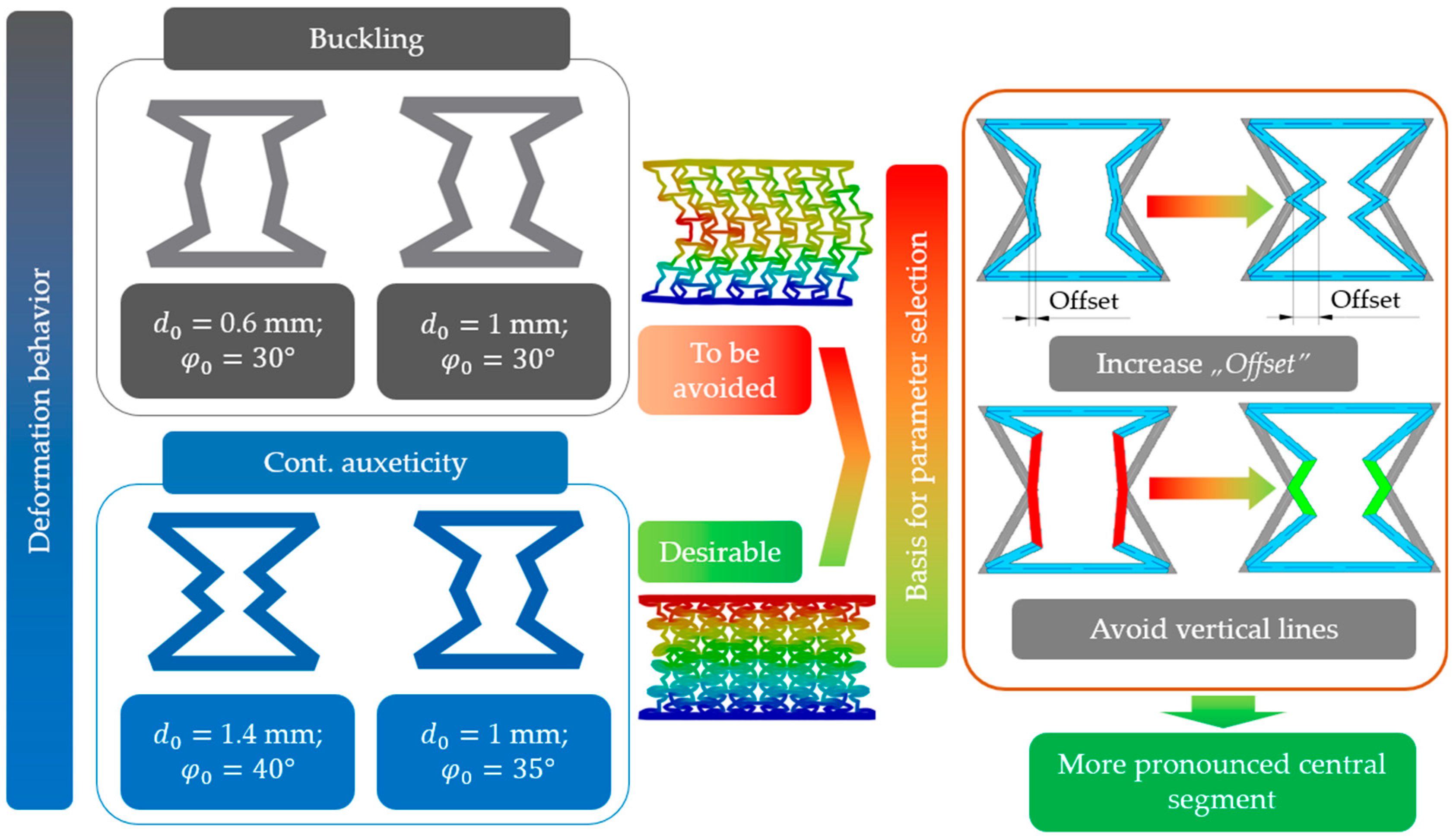
3.6. Effect of Geometric Parameters on the Examined Properties and Optimization
Optimization
3.7. Behavioural Mechanisms and Parameter Effects—Comparing the Results with the Analytical Prediction
Specimen Stiffness
4. Discussion
5. Conclusions
- Owing to the wide spectrum of the two parameters (offset: 0.6 … 1.4 mm; deg: 30° … 40°), their effects can be tested extensively.
- The proposed novel geometry shows improved mechanical properties compared to the auxetic honeycomb structure, regardless of the parameter values.
- Increasing the offset and deg parameters results in an increased energy absorption capability and maximum compressive force.
- The specific energy absorption capability of the novel specimens increases with increasing geometrical parameters (offset and deg).
- Based on an optimisation method using desirability functions, the optimal geometric parameters in the considered parameter range are deg, 40° and offset, 1.33 mm. The expected properties and auxeticity of the optimal specimens were also verified with experimental compression tests.
- The specimens exhibited two distinctly different behavioural mechanisms, namely, buckling and continuous auxetic behaviours.
- At low deformations, specimens with buckling behaviour showed better mechanical properties; however, buckling is an unpredictable behaviour mechanism.
- At high deformation loads, specimens with continuous auxetic behaviour showed more favourable mechanical properties.
- Following the proposed stabilization design guidelines, the expected operating mechanism can be designed while achieving more favourable mechanical properties as well.
- The established finite element environment is a sufficiently accurate representation of the real measurement results and the expected behaviour mechanism.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| [mm] | Initial offset value of the novel specimen | |
| [] | Initial deg value of the novel specimen | |
| [mm] | Re-entrant edge length of the auxetic honeycomb unit cell | |
| [mm] | Half width of the unit cell | |
| [mm] | Half height of the unit cell | |
| ψ | [] | Re-entrant angle |
| [mm] | Upper re-entrant edge length of the novel unit cell | |
| [mm] | Lower re-entrant edge length of the novel unit cell | |
| [mm] | Initial half central width of the unit cell | |
| [mm] | Depth of the specimen | |
| [mm] | Unit-cell cross-section characteristic thickness | |
| [°] | The angle enclosed by the edges of length and | |
| [mm] | Height of the unit cell (its value changes with deformation) | |
| [mm] | Width of the unit cell (its value changes with deformation) | |
| [mm] | Offset of the novel unit cell (its value changes with deformation) | |
| [°] | Deg of the novel unit cell (its value changes with deformation) | |
| [%] | Axial strain | |
| [%] | Transverse strain | |
| [-] | Poisson’s ratio | |
| [mm] | Critical displacement value in direction (width) | |
| [mm] | Critical displacement value in direction (height) | |
| [°] | Value of at the critical moment | |
| [-] | Slenderness ratio | |
| [-] | Number of unit cells forming the vertical beam | |
| [] | Cross-section | |
| [] | Minimal moment of inertia | |
| [-] | Critical slenderness ratio | |
| [MPa] | Elastic modulus of the material | |
| [MPa] | Elastic stress value of the material | |
| [N] | Critical buckling force | |
| [mJ] | Energy absorbed by specimens | |
| [mJ/g] | Specific absorbed energy of specimens | |
| [N] | Maximum compression force | |
| [-] | Input parameter for the phenomenological model | |
| [-] | Predicted output for the phenomenological model | |
| [-] | Desirability function of absorbed energy | |
| [-] | Desirability function of maximal compressive force | |
| [-] | Desirability function of specific energy | |
| [-] | Composite desirability function | |
| [mm] | Dimension change in the x direction | |
| [mm] | Dimension change in the y direction | |
| [mm] | Initial unit-cell width | |
| [mm] | Initial unit-cell height | |
| a0, a1, a2, a3, a4, a5 | [-] | Constant coefficients of predicted models |
| ε | [-] | Error of the predicted models |
Appendix A
CAD Models of Specimens

Appendix B
Unit-Cell-Geometry Equations
| Specimen No. (from Figure A1) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| (°) (mm) | 30 1.4 | 35 1.4 | 40 1.4 | 30 1 | 35 1 | 40 1 | 30 0.6 | 35 0.6 | 40 0.6 |
| l (mm) | 4.792 | 5.066 | 5.417 | 4.330 | 4.578 | 4.895 | 3.868 | 4.089 | 4.373 |
| s (mm) | 2.750 | 2.326 | 1.898 | 2.784 | 2.360 | 1.901 | 2.892 | 2.491 | 2.042 |
Appendix C
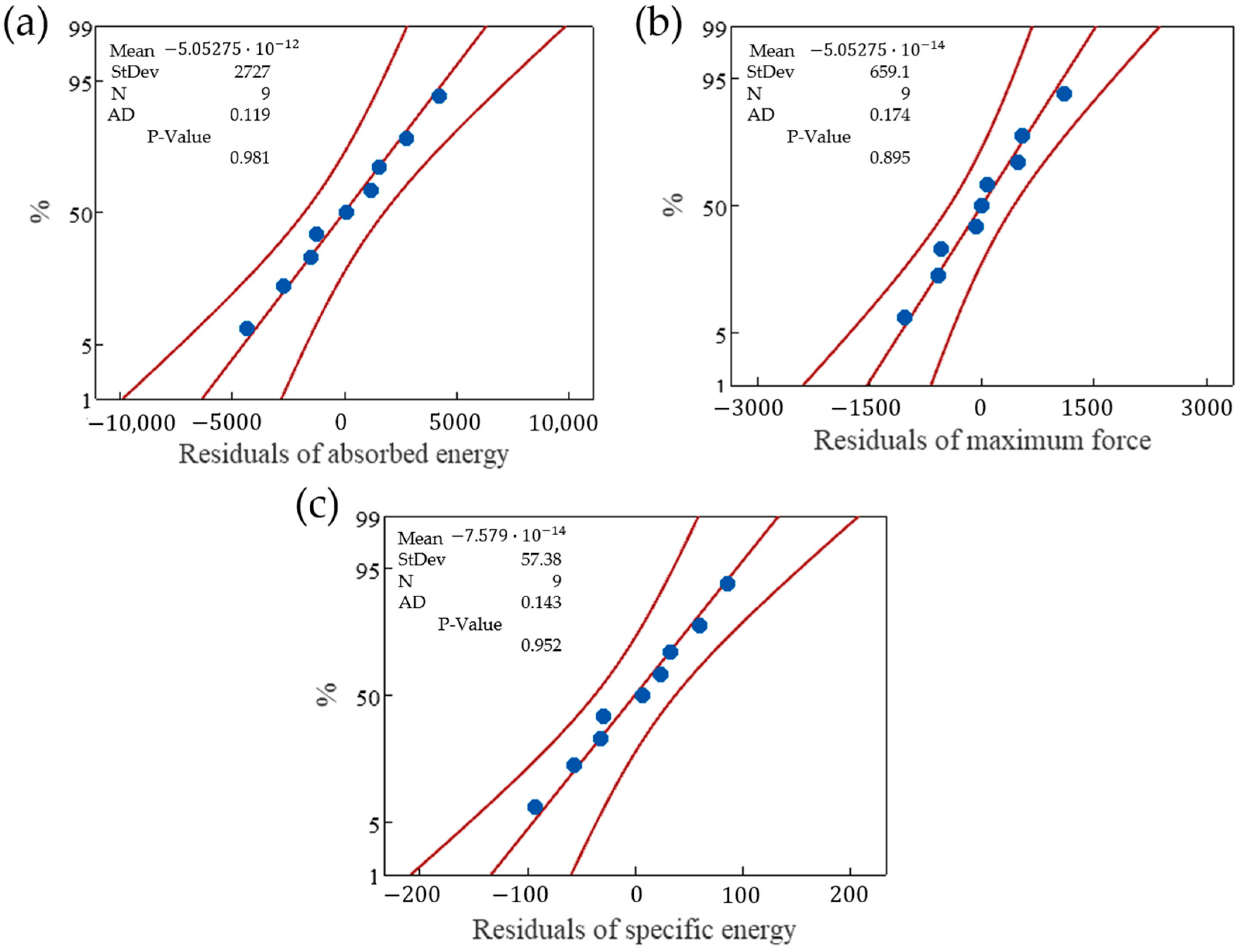
Appendix D
References
- Aggen, S. Metals Handbook: Properties and Selection: Irons, Steels and High Performance Alloys; ASM International: Detroit, MI, USA, 2005. [Google Scholar]
- Sas, W.; Gabryś, K.; Szymański, A. Determination of Poisson’s ratio by means of resonant column tests. Electron. J. Pol. Agric. Univ. 2013, 16, 1–11. [Google Scholar]
- Evans, K.E. Auxetic polymers: A new range of materials. Endeavour 1991, 15, 170–174. [Google Scholar] [CrossRef]
- Bhullar, S.K. Three decades of auxetic polymers: A review. E-Polymers 2015, 15, 205–215. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F.; Schajer, G.S.; Robertson, C.I. The mechanics of two-dimensional cellular materials. Proc. R. Soc. Lond. A Math. Phys. Sci. 1982, 382, 25–42. [Google Scholar] [CrossRef]
- Rad, M.S.; Hatami, H.; Alipouri, R.; Nejad, A.F.; Omidinasab, F. Omidinasab, Determination of energy absorption in different cellular auxetic structures. Mech. Ind. 2019, 20, 302. [Google Scholar] [CrossRef]
- Cho, H.; Seo, D.; Kim, D.N. Mechanics of auxetic materials. In Handbook of Mechanics of Materials; Springer: Singapore, 2019; pp. 733–757. [Google Scholar] [CrossRef]
- Alderson, K.; Pickles, A.; Neale, P.; Evans, K. Evans, Auxetic polyethylene: The effect of a negative poisson’s ratio on hardness. Acta Metall. Et Mater. 1994, 42, 2261–2266. [Google Scholar] [CrossRef]
- Bohara, R.P.; Linforth, S.; Nguyen, T.; Ghazlan, A.; Ngo, T. Anti-blast and -impact performances of auxetic structures: A review of structures, materials, methods, and fabrications. Eng. Struct. 2023, 276, 115377. [Google Scholar] [CrossRef]
- Li, J.; Wei, Y.; Wu, H.; Shen, X.; Yuan, M. Experimental crushing behavior and energy absorption of angular gradient honeycomb structures under quasi-static and dynamic compression. Def. Technol. 2024, 36, 47–63. [Google Scholar] [CrossRef]
- Lakes, R. Foam Structures with a Negative Poisson’s Ratio. Science (1979) 1987, 235, 1038–1040. [Google Scholar] [CrossRef]
- Choi, J.B.; Lakes, R.S. Fracture toughness of re-entrant foam materials with a negative Poisson’s ratio: Experiment and analysis. Int. J. Fract. 1996, 80, 73–83. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, W.; Zhou, G.; Gao, Q.; Wang, C. Optimization of an auxetic jounce bumper based on Gaussian process metamodel and series hybrid GA-SQP algorithm. Struct. Multidiscip. Optim. 2018, 57, 2515–2525. [Google Scholar] [CrossRef]
- Biswas, A.N.; Mahesh, N.; Peri, S.R.; Krishnan, B.R.; Sreekanth, P.R. Hybrid auxetic materials implemented in crates & non-pneumatic wheels for shock absorption. Mater. Today Proc. 2022, 56, 1327–1334. [Google Scholar] [CrossRef]
- Foster, L.; Peketi, P.; Allen, T.; Senior, T.; Duncan, O.; Alderson, A. Application of Auxetic Foam in Sports Helmets. Appl. Sci. 2018, 8, 354. [Google Scholar] [CrossRef]
- Khaghani, O.; Mostofinejad, D.; Abtahi, S.M. Auxetic structures in civil engineering applications: Experimental (by 3D printing) and numerical investigation of mechanical behavior. Results Mater. 2024, 21, 100528. [Google Scholar] [CrossRef]
- Wu, S.; Sikdar, P.; Bhat, G.S. Recent progress in developing ballistic and anti-impact materials: Nanotechnology and main approaches. Def. Technol. 2023, 21, 33–61. [Google Scholar] [CrossRef]
- Gao, Y.; Chen, X. A Study of Woven Fabrics Made of Helical Auxetic Yarns. Appl. Compos. Mater. 2022, 29, 109–119. [Google Scholar] [CrossRef]
- Asad, M.; Dhanasekar, M.; Zahra, T.; Thambiratnam, D. Impact mitigation of masonry walls with carbon fibre and Auxetic fibre composite renders—A numerical study. Structures 2020, 28, 2733–2751. [Google Scholar] [CrossRef]
- Zhong, R.; Ren, X.; Zhang, X.Y.; Luo, C.; Zhang, Y.; Xie, Y.M. Mechanical properties of concrete composites with auxetic single and layered honeycomb structures. Constr. Build. Mater. 2022, 322, 126453. [Google Scholar] [CrossRef]
- Wojciechowski, K. Two-dimensional isotropic system with a negative poisson ratio. Phys. Lett. A 1989, 137, 60–64. [Google Scholar] [CrossRef]
- Evans, K.E.; Caddock, B.D. Microporous materials with negative Poisson’s ratios. II. Mechanisms and interpretation. J. Phys. D Appl. Phys. 1989, 22, 1883–1887. [Google Scholar] [CrossRef]
- Wojciechowski, K. Constant thermodynamic tension Monte Carlo studies of elastic properties of a two-dimensional system of hard cyclic hexamers. Mol. Phys. 1987, 61, 1247–1258. [Google Scholar] [CrossRef]
- Wang, Z.; Hu, H. Auxetic materials and their potential applications in textiles. Text. Res. J. 2014, 84, 1600–1611. [Google Scholar] [CrossRef]
- Choi, J.B.; Lakes, R.S. Non-linear properties of polymer cellular materials with a negative Poisson’s ratio. J. Mater. Sci. 1992, 27, 4678–4684. [Google Scholar] [CrossRef]
- Lees, C.; Vincent, J.F.; Hillerton, J.E. Poisson’s Ratio in Skin. Biomed. Mater. Eng. 1991, 1, 19–23. [Google Scholar] [CrossRef]
- Veronda, D.R.; Westmann, R.A. Mechanical characterization of skin—Finite deformations. J. Biomech. 1970, 3, 111–124. [Google Scholar] [CrossRef]
- Frolich, L.M.; LaBarbera, M.; Stevens, W.P. Poisson’s ratio of a crossed fibre sheath: The skin of aquatic salamanders. J. Zool. 1994, 232, 231–252. [Google Scholar] [CrossRef]
- Baughman, R.H.; Shacklette, J.M.; Zakhidov, A.A.; Stafström, S. Negative Poisson’s ratios as a common feature of cubic metals. Nature 1998, 392, 362–365. [Google Scholar] [CrossRef]
- Yeganeh-Haeri, A.; Weidner, D.J.; Parise, J.B. Elasticity of α-Cristobalite: A Silicon Dioxide with a Negative Poisson’s Ratio. Science 1992, 257, 650–652. [Google Scholar] [CrossRef]
- Gunton, D.J.; Saunders, G.A. The Young’s modulus and Poisson’s ratio of arsenic, antimony and bismuth. J. Mater. Sci. 1972, 7, 1061–1068. [Google Scholar] [CrossRef]
- Li, Y. The anisotropic behavior of Poisson’s ratio, Young’s modulus, and shear modulus in hexagonal materials. Phys. Status Solidi (a) 1976, 38, 171–175. [Google Scholar] [CrossRef]
- Montazeri, A.; Saeedi, A.; Bahmanpour, E.; Safarabadi, M. Enhancing the compressive properties of re-entrant honeycombs by line defects with insight from nature. Mater. Today Commun. 2024, 38, 107700. [Google Scholar] [CrossRef]
- He, C.; Liu, P.; Griffin, A.C. Toward Negative Poisson Ratio Polymers through Molecular Design. Macromolecules 1998, 31, 3145–3147. [Google Scholar] [CrossRef]
- Kang, D.; Mahajan, M.P.; Zhang, S.; Petschek, R.G.; Rosenblatt, C.; He, C.; Liu, P.; Griffin, A.C. Pretransitional behavior above the nematic-isotropic phase transition of an auxetic trimer liquid crystal. Phys. Rev. E 1999, 60, 4980–4982. [Google Scholar] [CrossRef] [PubMed]
- Sahariah, B.J.; Namdeo, A.; Khanikar, P. Composite-inspired multilattice metamaterial structure: An auxetic lattice design with improved strength and energy absorption. Mater. Today Commun. 2022, 30, 103159. [Google Scholar] [CrossRef]
- Alderson, A. A triumph of lateral thought. Chem. Ind. 1999, 17, 384–391. [Google Scholar]
- Lantada, A.D.; Muslija, A.; García-Ruíz, J.P. Auxetic tissue engineering scaffolds with nanometric features and resonances in the megahertz range. Smart Mater. Struct. 2015, 24, 055013. [Google Scholar] [CrossRef]
- Smith, C.; Grima, J.; Evans, K. A novel mechanism for generating auxetic behaviour in reticulated foams: Missing rib foam model. Acta Mater. 2000, 48, 4349–4356. [Google Scholar] [CrossRef]
- Huang, X.; Blackburn, S. Developing a New Processing Route to Manufacture Honeycomb Ceramics with Negative Poisson’s Ratio. Key Eng. Mater. 2001, 206–213, 201–204. [Google Scholar] [CrossRef]
- Chen, G.; Cheng, Y.; Zhang, P.; Cai, S.; Liu, J. Blast resistance of metallic double arrowhead honeycomb sandwich panels with different core configurations under the paper tube-guided air blast loading. Int. J. Mech. Sci. 2021, 201, 106457. [Google Scholar] [CrossRef]
- Arifurrahman, F.; Critchley, R.; Horsfall, I. Experimental and numerical study of auxetic sandwich panels on 160 grams of PE4 blast loading. J. Sandw. Struct. Mater. 2021, 23, 3902–3931. [Google Scholar] [CrossRef]
- Zhu, Y.; Gao, D.; Shao, Y.; Chen, H.; Yu, C.; Wang, Q. A novel prefabricated auxetic honeycomb meta-structure based on mortise and tenon principle. Compos. Struct. 2024, 329, 117782. [Google Scholar] [CrossRef]
- Shao, L.; Xue, N.; Li, W.; Liu, S.; Tu, Z.; Chen, Y.; Zhang, J.; Dai, S.; Liu, Q.; Shi, X.; et al. Effect of Cold-Spray Parameters on Surface Roughness, Thickness and Adhesion of Copper-Based Composite Coating on Aluminum Alloy 6061 T6 Substrate. Processes 2023, 11, 959. [Google Scholar] [CrossRef]
- Verma, S.; Yang, C.-K.; Lin, C.-H.; Jeng, J.Y. Additive manufacturing of lattice structures for high strength mechanical interlocking of metal and resin during injection molding. Addit. Manuf. 2022, 49, 102463. [Google Scholar] [CrossRef]
- Lu, Z.-X.; Li, X.; Yang, Z.-Y.; Xie, F. Novel structure with negative Poisson’s ratio and enhanced Young’s modulus. Compos. Struct. 2016, 138, 243–252. [Google Scholar] [CrossRef]
- Fu, M.-H.; Chen, Y.; Hu, L.-L. A novel auxetic honeycomb with enhanced in-plane stiffness and buckling strength. Compos. Struct. 2017, 160, 574–585. [Google Scholar] [CrossRef]
- Fu, M.-H.; Chen, Y.; Hu, L.-L. Bilinear elastic characteristic of enhanced auxetic honeycombs. Compos. Struct. 2017, 175, 101–110. [Google Scholar] [CrossRef]
- Chen, Y.; Fu, M.-H. Design and modeling of a combined embedded enhanced honeycomb with tunable mechanical properties. Appl. Compos. Mater. 2018, 25, 1041–1055. [Google Scholar] [CrossRef]
- Baran, T.; Öztürk, M. In-plane elasticity of a strengthened re-entrant honeycomb cell. Eur. J. Mech. A/Solids 2020, 83, 104037. [Google Scholar] [CrossRef]
- Jiang, H.; Ren, Y.; Jin, Q.; Zhu, G.; Hu, Y.; Cheng, F. Crashworthiness of novel concentric auxetic reentrant honeycomb with negative Poisson’s ratio biologically inspired by coconut palm. Thin-Walled Struct. 2020, 154, 106911. [Google Scholar] [CrossRef]
- Tatlıer, M.S.; Öztürk, M.; Baran, T. Linear and non-linear in-plane behaviour of a modified re-entrant core cell. Eng. Struct. 2021, 234, 111984. [Google Scholar] [CrossRef]
- Chen, Z.; Li, J.; Wu, B.; Chen, X.; Xie, Y.M. Enhanced mechanical properties of re-entrant auxetic honeycomb with self-similar inclusion. Compos. Struct. 2024, 331, 117921. [Google Scholar] [CrossRef]
- Zhu, Y.; Luo, Y.; Gao, D.; Yu, C.; Ren, X.; Zhang, C. In-plane elastic properties of a novel re-entrant auxetic honeycomb with zigzag inclined ligaments. Eng. Struct. 2022, 268, 114788. [Google Scholar] [CrossRef]
- Bora, K.M.; Varshney, S.K.; Kumar, C.S. Rounded corner thicken strut re-entrant auxetic honeycomb: Analytical and numerical modeling. Mech. Res. Commun. 2024, 136, 104246. [Google Scholar] [CrossRef]
- Zhu, S.; Hu, J.; Tan, X.; Wang, B.; Chen, S.; Ma, L. Mechanics of sandwich panels with a buckling-dominated lattice core: The effects of the initial rod curvatures. Compos. Struct. 2020, 251, 112669. [Google Scholar] [CrossRef]
- Etemadi, E.; Zamani, A.M.; Scarpa, F.; Zeeshan, M.; Hosseinabadi, M.; Hu, H. Modified re-entrant auxetic metamaterials with energy absorption enhancement. Mater. Today Commun. 2024, 38, 108079. [Google Scholar] [CrossRef]
- Guo, M.-F.; Yang, H.; Ma, L. Design and analysis of 2D double-U auxetic honeycombs. Thin-Walled Struct. 2020, 155, 106915. [Google Scholar] [CrossRef]
- Meena, K.; Singamneni, S. A new auxetic structure with significantly reduced stress concentration effects. Mater. Des. 2019, 173, 107779. [Google Scholar] [CrossRef]
- Chen, Y.; Fu, M.-H.; Hu, H.; Xiong, J. Curved inserts in auxetic honeycomb for property enhancement and design flexibility. Compos. Struct. 2022, 280, 114892. [Google Scholar] [CrossRef]
- Bhat, C.; Kumar, A.; Lin, S.-C.; Jeng, J.-Y. Design, fabrication, and properties evaluation of novel nested lattice structures. Addit. Manuf. 2023, 68, 103510. [Google Scholar] [CrossRef]
- Nedoushan, R.J.; An, Y.; Yu, W.-R.; Abghary, M.J. Novel triangular auxetic honeycombs with enhanced stiffness. Compos. Struct. 2021, 277, 114605. [Google Scholar] [CrossRef]
- Zhang, W.; Yan, Z.; Zhang, J.; Wang, H.; Han, F.; Jiang, P.; Wu, T.; Qin, Q. On in-plane crushing behavior of an improved double-arrow auxetic metamaterial with two-step deformation mode. Eng. Struct. 2024, 303, 117482. [Google Scholar] [CrossRef]
- Zolfagharian, A.; Bodaghi, M.; Hamzehei, R.; Parr, L.; Fard, M.; Rolfe, B.F. 3D-Printed Programmable Mechanical Metamaterials for Vibration Isolation and Buckling Control. Sustainability 2022, 14, 6831. [Google Scholar] [CrossRef]
- Hamzehei, R.; Zolfagharian, A.; Dariushi, S.; Bodaghi, M. 3D-printed bio-inspired zero Poisson’s ratio graded metamaterials with high energy absorption performance. Smart Mater. Struct. 2022, 31, 035001. [Google Scholar] [CrossRef]
- Lu, F.; Chen, X.; Zhu, Y.; Zhang, C.; Hou, Y. A Novel Re-Entrant-Type Metamaterial with Tunable Negative Poisson’s Ratios and Coefficients of Thermal Expansion. Int. J. Appl. Mech. 2022, 14, 2250040. [Google Scholar] [CrossRef]
- Han, D.; Ren, X.; Luo, C.; Zhang, Y.; Zhang, X.Y.; Zhang, X.G.; Jiang, W.; Hao, J.; Xie, Y.M. Experimental and computational investigations of novel 3D printed square tubular lattice metamaterials with negative Poisson’s ratio. Addit. Manuf. 2022, 55, 102789. [Google Scholar] [CrossRef]
- Wang, W.; Jin, Y.; Mu, Y.; Zhang, M.; Du, J. A novel tubular structure with negative Poisson’s ratio based on gyroid-type triply periodic minimal surfaces. Virtual Phys. Prototyp. 2023, 18, e2203701. [Google Scholar] [CrossRef]
- Hu, Q.; Lu, G.; Tse, K.M. Compressive and tensile behaviours of 3D hybrid auxetic-honeycomb lattice structures. Int. J. Mech. Sci. 2024, 263, 108767. [Google Scholar] [CrossRef]
- Albertini, F.; Dirrenberger, J.; Sollogoub, C.; Maconachie, T.; Leary, M.; Molotnikov, A. Experimental and computational analysis of the mechanical properties of composite auxetic lattice structures. Addit. Manuf. 2021, 47, 102351. [Google Scholar] [CrossRef]
- Günaydın, K.; Rea, C.; Kazancı, Z. Energy absorption enhancement of additively manufactured hexagonal and re-entrant (auxetic) lattice structures by using multi-material reinforcements. Addit. Manuf. 2022, 59, 103076. [Google Scholar] [CrossRef]
- Kahraman, M.F.; İriç, S.; Genel, K. Comparative failure behavior of metal honeycomb structures under bending: A finite element-based study. Eng. Fail. Anal. 2024, 157, 107963. [Google Scholar] [CrossRef]
- Liu, H.-T.; An, M.-R. In-plane crushing behaviors of a new-shaped auxetic honeycomb with thickness gradient based on additive manufacturing. Mater. Lett. 2022, 318, 132208. [Google Scholar] [CrossRef]
- Ma, N.; Han, S.; Han, Q.; Li, C. Design and compressive behaviors of the gradient re-entrant origami honeycomb metamaterials. Thin-Walled Struct. 2024, 198, 111652. [Google Scholar] [CrossRef]
- Jiang, W.Z.; Teng, X.C.; Ni, X.H.; Zhang, X.G.; Cheng, X.; Han, D.; Zhang, Y.; Ren, X. An improved re-entrant honeycomb with programmable densification and multistage energy-absorbing performance. Eng. Struct. 2024, 301, 117318. [Google Scholar] [CrossRef]
- Štambuk, I.; Konjevod, J.; Malarić, R. Design, Production and Analysis of Cylindrical, Coaxial and Alternating Current Shunts, using ANSYS. Acta Polytech. Hung. 2023, 20, 131–143. [Google Scholar] [CrossRef]
- Ibrahim, S.K.; Rad, M.M.; Fischer, S. Optimal Elasto-Plastic Analysis of Reinforced Concrete Structures under Residual Plastic Deformation Limitations. Acta Polytech. Hung. 2023, 20, 45–62. [Google Scholar] [CrossRef]
- Koch, E.; Ray, R.P. Impact Assessment of Railway Bridge Construction Schedule, based on 3D Geotechnical Finite Element Modeling. Acta Polytech. Hung. 2024, 21, 187–205. [Google Scholar] [CrossRef]
- Albert, J.; Takács, Á. Optimization Methodology of Thermoelectric Peltier-Modules, for Structural Design and Material Selection, using MCDM and FEM Modelling. Acta Polytech. Hung. 2024, 21, 217–229. [Google Scholar] [CrossRef]
- He, P.; Wang, S.; Zhang, M.; Sang, L.; Tong, L.; Hou, W. Compression performance of 3D-printed thermoplastic auxetic structures. Thin-Walled Struct. 2024, 197, 111558. [Google Scholar] [CrossRef]
- ISO 527-2:2012; Determination of Tensile Properties—Part 2: Test Conditions for Moulding and Extrusion Plastics. International Organization for Standardization: Geneva, Switzerland, 2012.
- Van De Velde, F.; De Baets, P. The friction and wear behaviour of polyamide 6 sliding against steel at low velocity under very high contact pressures. Wear 1997, 209, 106–114. [Google Scholar] [CrossRef]
- Mooney, M. A Theory of Large Elastic Deformation. J. Appl. Phys. 1940, 11, 582–592. [Google Scholar] [CrossRef]
- Rivlin, R.S. Large elastic deformations of isotropic materials IV. further developments of the general theory. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1948, 241, 379–397. [Google Scholar] [CrossRef]
- Euler, L.; Daudet, R.; Delamonce, F.P.J.I.; Dibner, B. Methodus Inveniendi Lineas Curvas Maximi Minimive Proprietate Gaudentes, Sive, Solutio Problematis Isoperimetrici Latissimo Sensu Accepti; Apud Marcum-Michaelem Bousquet & Socios: Geneva, Switzerland, 1744. [Google Scholar] [CrossRef]
- Jones, R.M. Buckling of Bars, Plates, and Shells; Bull Ridge Publishing: Blacksburg, VA, USA, 2006. [Google Scholar]
- Harrington, E.C. The desirability function. Ind. Qual. Control 1965, 21, 494–498. [Google Scholar]
- Myers, R.H. Classical and Modern Regression with Applications; Duxbury Press: Belmont, CA, USA, 1990. [Google Scholar]
- Anderson, M.J.; Whitcomb, P.J. RSM Simplified; Productivity Press: New York, NY, USA, 2016. [Google Scholar] [CrossRef]
- Myers, R.H.; Montgomery, D.C.; Anderson-Cook, C.M. Response Surface Methodology: Process and Product Optimization Using Designed Experiments, 4th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Liu, K.; Zong, S.; Li, Y.; Wang, Z.; Hu, Z.; Wang, Z. Structural response of the U-type corrugated core sandwich panel used in ship structures under the lateral quasi-static compression load. Mar. Struct. 2022, 84, 103198. [Google Scholar] [CrossRef]
- Wang, S.; Deng, C.; Ojo, O.; Akinrinlola, B.; Kozub, J.; Wu, N. Design and modeling of a novel three dimensional auxetic reentrant honeycomb structure for energy absorption. Compos. Struct. 2022, 280, 114882. [Google Scholar] [CrossRef]






| Specimen No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| d0 (mm) | 0.6 | 0.6 | 0.6 | 1 | 1 | 1 | 1.4 | 1.4 | 1.4 |
| 30 | 35 | 40 | 30 | 35 | 40 | 30 | 35 | 40 | |
| Relative density (-) | 0.416 | 0.413 | 0.409 | 0.436 | 0.433 | 0.431 | 0.458 | 0.456 | 0.457 |
| ) | 457.8 | 454.5 | 449.9 | 479.4 | 475.9 | 473.7 | 503.6 | 502.1 | 503.3 |
| Specimen No. | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|
| (°) (mm) | 30 1.4 | 35 1.4 | 40 1.4 | 30 1 | 35 1 | 40 1 | 30 0.6 | 35 0.6 | 40 0.6 |
| (mm) | 4.792 | 5.066 | 5.417 | 4.330 | 4.578 | 4.895 | 3.868 | 4.089 | 4.373 |
| (mm) | 2.743 | 2.326 | 1.898 | 2.784 | 2.360 | 1.901 | 2.892 | 2.491 | 2.042 |
| (°) | 89.31 | 87.99 | 82.47 | 98.94 | 99.93 | 98.26 | 108.1 | 111.06 | 112.9 |
| (mm) | 0.708 | 0.437 | 0.129 | 1.223 | 0.985 | 0.656 | 1.798 | 1.684 | 1.471 |
| (mm) | 2.692 | 2.149 | 1.188 | 3.461 | 3.117 | 2.849 | 4.089 | 3.960 | 3.744 |
| 43.40 | 54.82 | 75.02 | 27.24 | 34.46 | 40.11 | 14.05 | 16.75 | 21.29 | |
| 6.197 | 4.957 | 2.744 | 7.914 | 7.154 | 6.561 | 9.245 | 8.978 | 8.525 | |
| Expected behavioural mechanism | Buckling | Cont. aux | Cont. aux | Buckling | Buckling | Buckling | Buckling | Buckling | Buckling |
| No. | Offset Parameter [mm] | Deg Parameter | Analytical Prediction | Real (and FEM) | |
|---|---|---|---|---|---|
| Behavioural Mechanism | Critical Strain Value | Behavioural Mechanism | |||
| 1 | 1.4 | 40 | cont. auxetic | 75.1% | cont. auxetic |
| 2 | 1.4 | 35 | cont. auxetic | 54.8% | cont. auxetic |
| 3 | 1.4 | 30 | buckling | 43.4% | cont. auxetic |
| 4 | 1 | 40 | buckling | 40.1% | cont. auxetic |
| 5 | 1 | 35 | buckling | 34.5% | cont. auxetic |
| 6 | 1 | 30 | buckling | 27.2% | buckling |
| 7 | 0.6 | 40 | buckling | 21.3% | buckling |
| 8 | 0.6 | 35 | buckling | 16.8% | buckling |
| 9 | 0.6 | 30 | buckling | 14.1% | buckling |
| 10 | Etalon | 0 | buckling | ||
| Specimen No. | 7 | 8 | 9 | |
|---|---|---|---|---|
| (°) (mm) | 30 1.0 | 30 0.6 | 35 0.6 | 40 0.6 |
| 139.4 | 151.6 | 123.4 | 117.4 |
| Specimen No. | ETA | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| d0 (mm) | 0 | 0.6 | 0.6 | 0.6 | 1 | 1 | 1 | 1.4 | 1.4 | 1.4 |
| 0 | 30 | 35 | 40 | 30 | 35 | 40 | 30 | 35 | 40 | |
| 43.49 | 28.88 | 32.00 | 31.01 | 27.75 | 27.64 | 27.83 | 26.10 | 26.63 | 26.41 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Széles, L.; Horváth, R.; Cveticanin, L. Analysis of Mechanical Properties and Parameter Dependency of Novel, Doubly Re-Entrant Auxetic Honeycomb Structures. Polymers 2024, 16, 2524. https://doi.org/10.3390/polym16172524
Széles L, Horváth R, Cveticanin L. Analysis of Mechanical Properties and Parameter Dependency of Novel, Doubly Re-Entrant Auxetic Honeycomb Structures. Polymers. 2024; 16(17):2524. https://doi.org/10.3390/polym16172524
Chicago/Turabian StyleSzéles, Levente, Richárd Horváth, and Lívia Cveticanin. 2024. "Analysis of Mechanical Properties and Parameter Dependency of Novel, Doubly Re-Entrant Auxetic Honeycomb Structures" Polymers 16, no. 17: 2524. https://doi.org/10.3390/polym16172524
APA StyleSzéles, L., Horváth, R., & Cveticanin, L. (2024). Analysis of Mechanical Properties and Parameter Dependency of Novel, Doubly Re-Entrant Auxetic Honeycomb Structures. Polymers, 16(17), 2524. https://doi.org/10.3390/polym16172524







