A Description of the Isothermal Ageing Creep Process in Polymethyl Methacrylate Using Fractional Differential Models
Abstract
:1. Introduction
2. Materials and Methods
2.1. Definition of Fractional Calculus
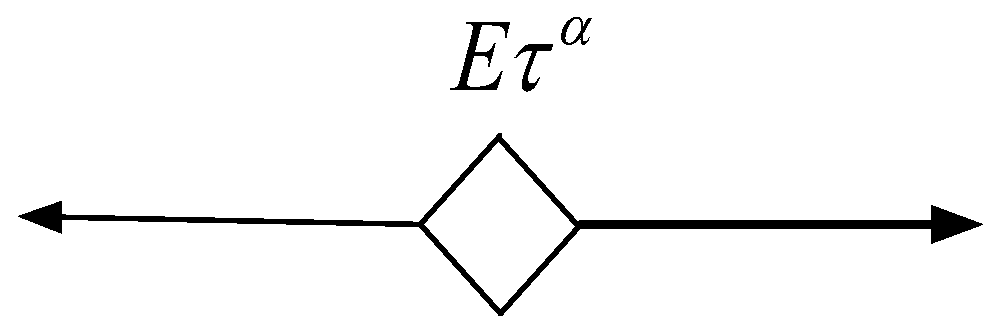
2.2. Spring-Pot Model
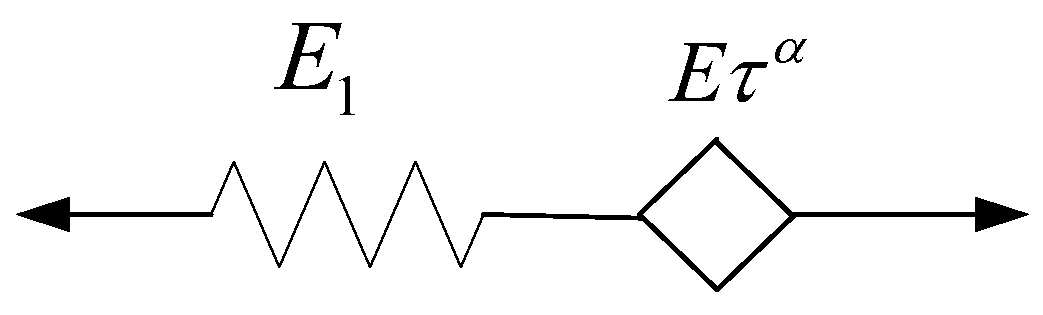
2.3. Fractional Differential Maxwell Model
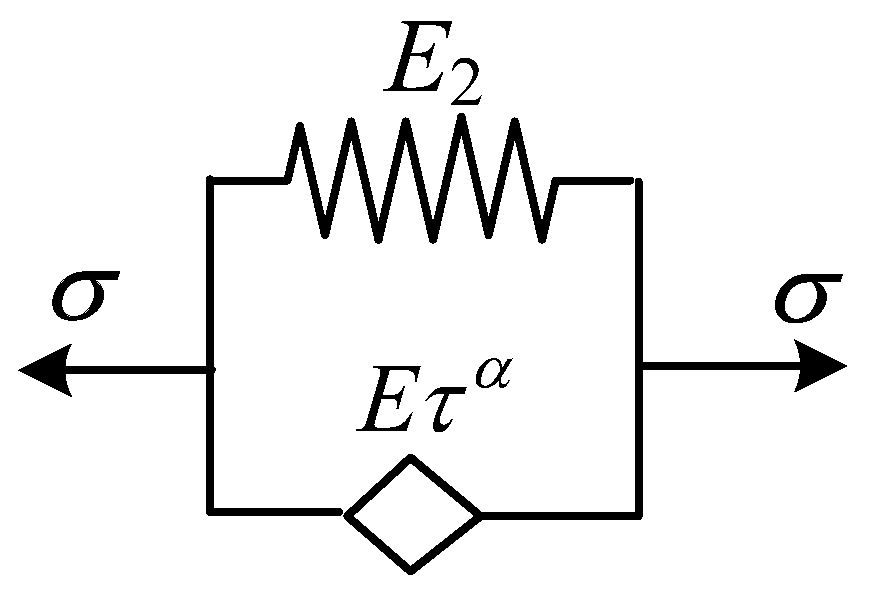
2.4. Fractional Differential Kelvin Model
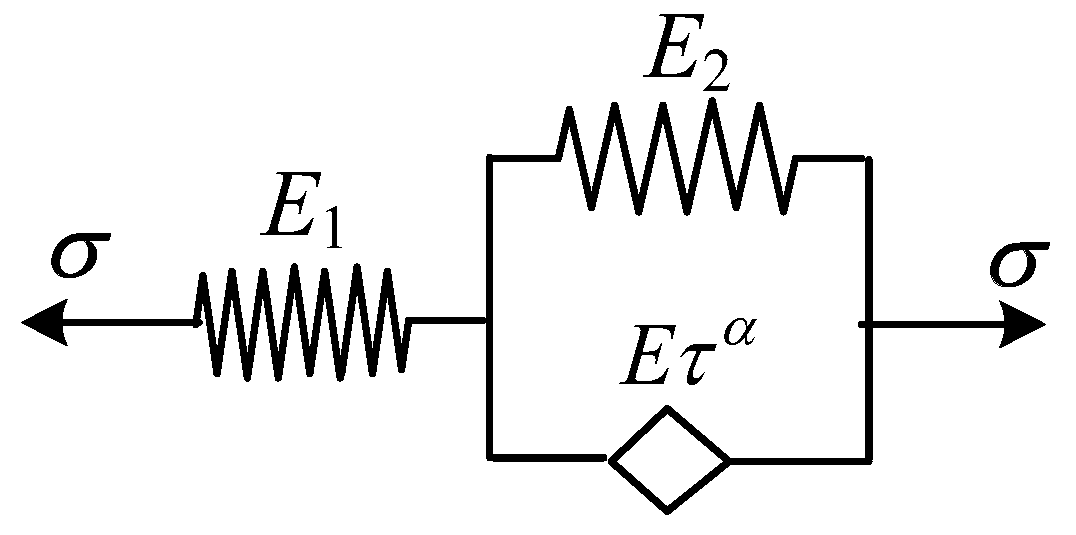
2.5. Fractional Differential Zener Model
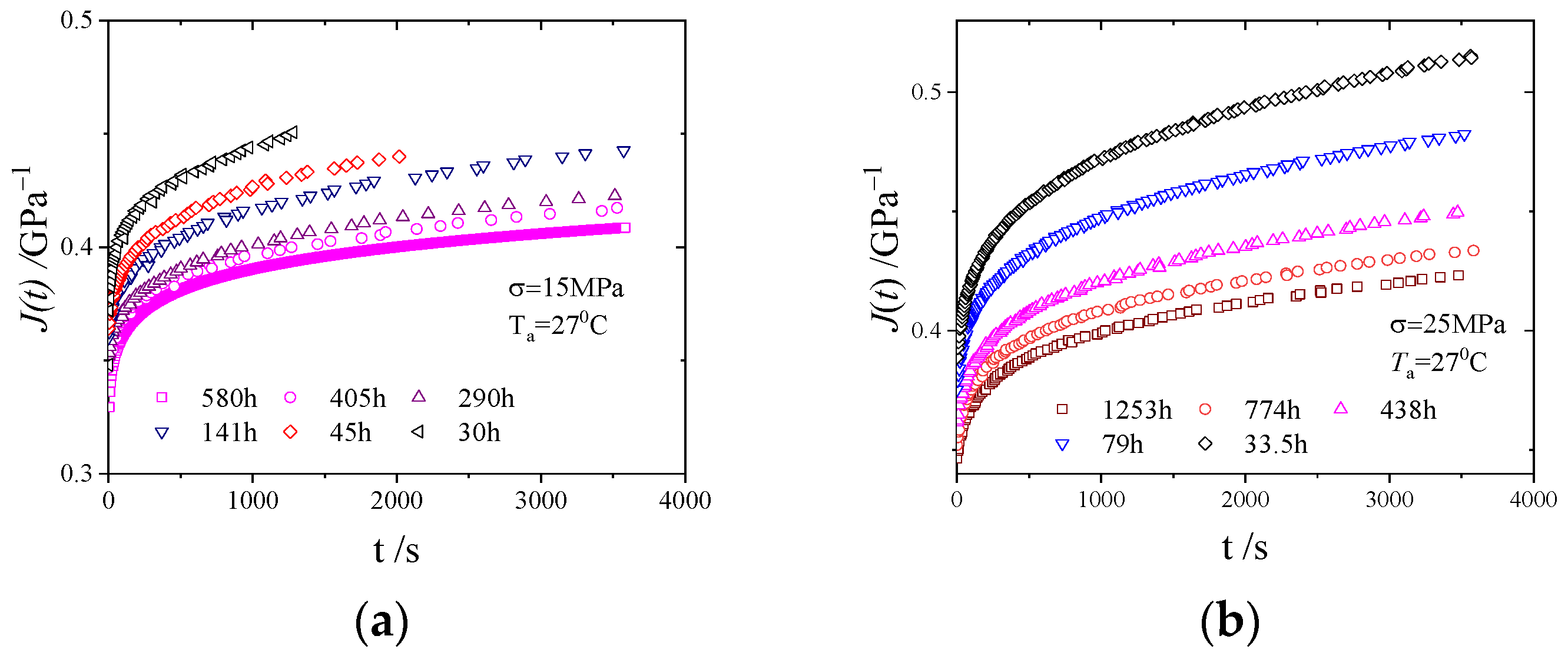
2.6. Materials and Experiments
3. Results
4. Discussion
5. Conclusions
- (1)
- When fitting the creep data of PMMA at different ageing times with the fractional differential model, the Marquardt method (Levenberg–Marquardt) and a general global optimisation method were used to optimise the parameters, with the smallest error of the experimental data fitting as the criterion. The model fitting matched the experimental data well.
- (2)
- As the ageing time increased, the fractional differential Zener model showed a relative increase in the modulus parameter of the spring and a relative decrease in the modulus parameter reflecting the viscosity of the spring-pot, which indicated that physical ageing made the material more elastic. The relaxation time of the material increased, which indicated that the physical ageing reduced the free volume of the material, hindered the movement of molecules/segments, and increased the time required for the material to reach equilibrium. The fractional order of the model decreased, which reflected the phenomenon that physical ageing reduced the creep compliance of the material.
- (3)
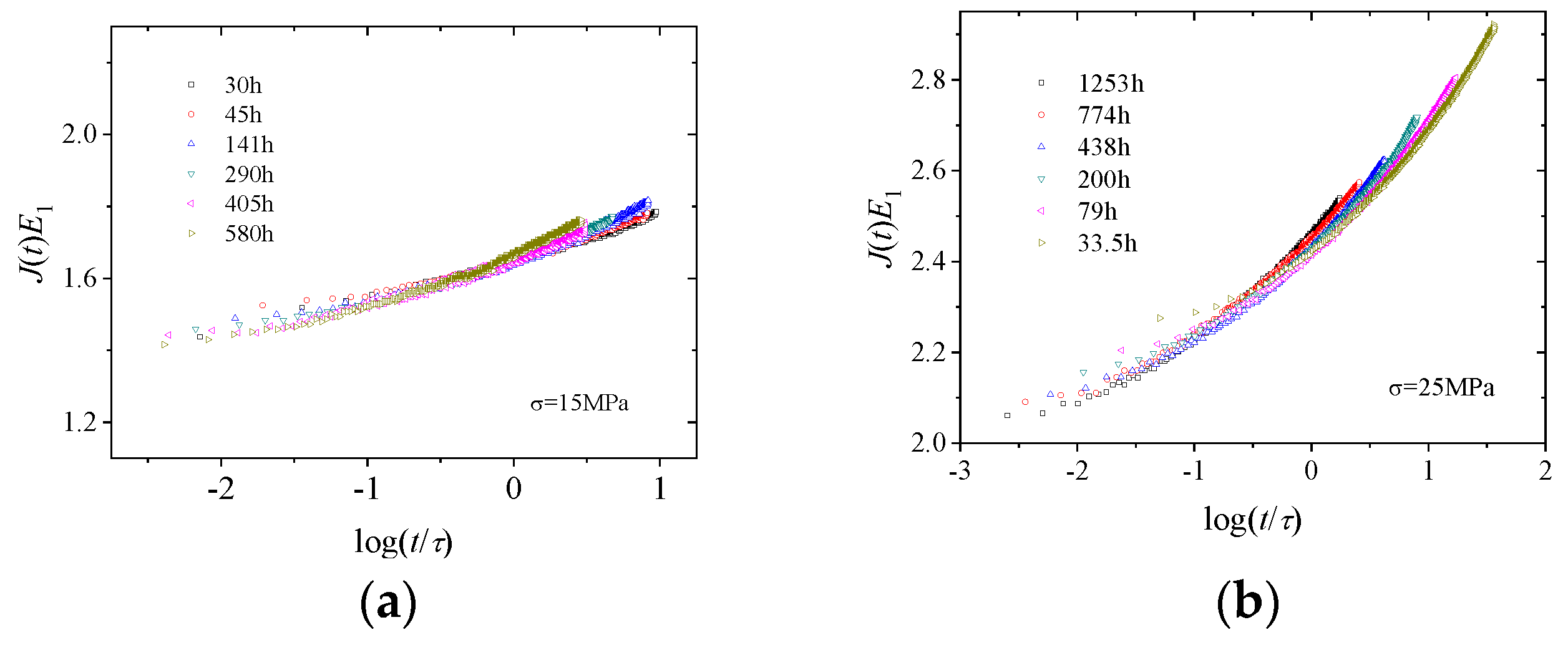
- By plotting the relaxation time obtained from the fitting of the fractional differential Zener model and the physical ageing time in a double-logarithmic coordinate system, a linear relationship was obtained.
- (4)
- Using the relaxation time as the time scale, the creep curves at different ageing times under the same stress level could be superimposed, naturally presenting the time–ageing time equivalence principle.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, Z.; Guo, J.; Seppala, J.E.; Nguyen, T.D. Extending the effective temperature model to the large strain hardening behavior of glassy polymers. J. Mech. Phys. Solids 2021, 146, 104175. [Google Scholar] [CrossRef]
- Liu, F.; Wang, J.; Long, S.; Zhang, H.; Yao, X. Experimental and modeling study of the viscoelastic-viscoplastic deformation behavior of amorphous polymers over a wide temperature range. Mech. Mater. 2022, 167, 104246. [Google Scholar] [CrossRef]
- Lan, T.; Jiang, Y.; Wu, P. A constitutive model for poly-methyl-methacrylate over a wide range of strain rates and temperatures. Polymer 2022, 240, 124524. [Google Scholar] [CrossRef]
- Pedoto, G.; Grandidier, J.C.; Gigliotti, M.; Vinet, A. Characterization and modelling of the PEKK thermomechanical and creep behavior above the glass transition temperature. Mech. Mater. 2022, 166, 104189. [Google Scholar] [CrossRef]
- Holm, S. Justification for power laws and fractional models. J. Acoust. Soc. Am. 2020, 148, 2601. [Google Scholar] [CrossRef]
- Sheikh, N.A.; Ching DL, C.; Khan, I.; Sakidin, H.B.; Jamil, M.; Khalid, H.U.; Ahmed, N. Fractional model for MHD flow of Casson fluid with cadmium telluride nanoparticles using the generalized Fourier’s law. Sci. Rep. UK 2021, 11, 16117. [Google Scholar] [CrossRef]
- Hamid, M.; Usman, M.; Haq, R.; Wang, W. A Chelyshkov polynomial based algorithm to analyze the transport dynamics and anomalous diffusion in fractional model. Phys. A 2020, 551, 124227. [Google Scholar] [CrossRef]
- Maiti, S.; Shaw, S.; Shit, G. Caputo–Fabrizio fractional order model on MHD blood flow with heat and mass transfer through a porous vessel in the presence of thermal radiation. Phys. A 2020, 540, 123149. [Google Scholar] [CrossRef]
- Bahloul, M.A.; Laleg-Kirati, T.M. Assessment of fractional-order arterial windkessel as a model of aortic input impedance. IEEE Open J. Eng. Med. Biol. 2020, 1, 123–132. [Google Scholar] [CrossRef]
- Yusuf, A.; Qureshi, S.; Aliyu, A.I.; Baleanu, D.; Shaikh, A.A. Two-strain epidemic model involving fractional derivative with Mittag–Leffler kernel. Chaos 2018, 28, 123121. [Google Scholar] [CrossRef]
- Jain, M.; Gupta, M. Design of fractional order recursive digital differ integrators using different approximation techniques. Int. J. Intell. Syst. 2020, 12, 33–42. [Google Scholar]
- Meng, R.; Yin, D.; Drapaca, C.S. A variable order fractional constitutive model of the viscoelastic behavior of polymers. Int. J. Nonlinear Mech. 2019, 113, 171–177. [Google Scholar] [CrossRef]
- Wu, F.; Gao, R.; Liu, J.; Li, C. New fractional variable-order creep model with short memory. Appl. Math. Comput. 2020, 380, 125278. [Google Scholar] [CrossRef]
- Ross, B.; Samko, S.G.; Love, E.R. Functions that have no first order derivative might have fractional derivatives of all orders less than one. Real. Anal. Exch 1994, 20, 140–157. [Google Scholar] [CrossRef]
- Cai, W.; Wang, P.; Fan, J. A variable-order fractional model of tensile and shear behaviors for sintered nano-silver paste used in high power electronics. Mech. Mater 2020, 145, 103391. [Google Scholar] [CrossRef]
- Meng, R.; Yin, D.; Chao, Z.; Hao, W. Fractional description of time-dependent mechanical property evolution in materials with strain softening behavior. Appl. Math. Model 2016, 40, 398–406. [Google Scholar] [CrossRef]
- Cai, W.; Wang, P. A nonlinear strain-dependent variable-order fractional model with applications to aluminum foams. Fractals 2021, 30, 2250021. [Google Scholar] [CrossRef]
- Xu, M.; Tan, W. A fractional-order viscoelastic model for polymer physical aging. J. Appl. Polym. Sci. 2019, 136, 48104. [Google Scholar]
- Li, B.; Hu, H. Modeling the physical aging of polymers using a fractional calculus approach. Polymers 2020, 12, 1577. [Google Scholar]
- Zhang, R.; Sun, X. Fractional calculus based model for the time-dependent behavior of polymers. Eur. Polym. J. 2018, 99, 8–16. [Google Scholar]
- Li, X.; Liu, Y. A fractional-order model for the physical aging of polymers: Experiments and simulations. Polym. Test. 2021, 94, 107072. [Google Scholar]
- Mao, J.; Xu, M. Fractional-order dynamic mechanical analysis of polymer physical aging. Polymers 2019, 11, 1799. [Google Scholar]
- Wang, L.; Wang, H. A fractional-order model for the prediction of polymer physical aging. J. Appl. Mech. Tech. Phys. 2020, 61, 280–286. [Google Scholar]
- Nonnenmacher, T.F.; Metzler, R. On the Riemann-Liouville fractional calculus and some recent applications. Fractals 1995, 3, 557–566. [Google Scholar] [CrossRef]
- Koeller, R.C. Applications of fractional calculus to the theory of viscoelasticity. J. Appl. Mech. 1984, 51, 299–307. [Google Scholar] [CrossRef]
- Fa, W. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Wu, F.; Liu, J.F.; Wang, J. An improved Maxwell creep model for rock based on variable-order fractional derivatives. Environ. Earth Sci. 2015, 73, 6965–6971. [Google Scholar] [CrossRef]
- Hou, T.; Chen, H. Isothermal physical aging of PEEK and PPS investigated by fractional Maxwell model. Polymer 2012, 53, 2509–2518. [Google Scholar] [CrossRef]
- Chen, H.S.; Jia, Y.Y. The application of the fractional Maxwell model in the creep of high-density polyethylene. J. Northwest Norm. Univ. 2012, 48, 32–35. [Google Scholar]
- Karner, T.; Belšak, R.; Gotlih, J. Used a fully fractional generalised Maxwell model for describing the time dependent sinusoidal creep of a dielectric elastomer actuator. Fractal Fract. 2022, 6, 720. [Google Scholar] [CrossRef]
- GB/T1040-2006; Plastics—Determination of Tensile Properties—Part 2: Test Conditions for Moulding and Extrusion Plastics. Standardization Administration of China: Beijing, China, 2006.
- Wang, P.; Cai, W.; Zhang, Y.; Wang, Z. A fractional rheological model for loading-dependent rheological behavior of polymers. Mech. Time Depend. Mater. 2023, 1–12. [Google Scholar] [CrossRef]
- Patnaik, S.; Sidhardh, S.; Semperlotti, F. A Ritz-based finite element method for a fractional-order boundary value problem of nonlocal elasticity. Int. J. Solids Struct 2020, 202, 398–417. [Google Scholar] [CrossRef]
- Patnaik, S.; Sidhardh, S.; Semperlotti, F. Nonlinear thermoelastic fractional-order model of nonlocal plates: Application to postbuckling and bending response. Thin Wall Struct. 2021, 164, 107809. [Google Scholar] [CrossRef]
- Sun, Y.; Gao, Y.; Song, S.; Chen, C. Three-dimensional state-dependent fractional plasticity model for soils. Int. J. Geomech. 2020, 20, 04019161. [Google Scholar] [CrossRef]


| °C | RMSE | R | |||||
|---|---|---|---|---|---|---|---|
| 15 MPa | 30 | 4.383 | 7.31 | 24.972 | 0.441 | 0.0013 | 0.9968 |
| 45 | 3.504 | 9.0 | 21.415 | 0.338 | 0.0041 | 0.9691 | |
| 141 | 4.105 | 6.67 | 37.65 | 0.438 | 0.0048 | 0.9619 | |
| 290 | 4.526 | 4.943 | 33.95 | 0.239 | 0.0051 | 0.9445 | |
| 405 | 2.684 | 5.687 | 36.574 | 0.434 | 0.0054 | 0.9317 | |
| 580 | 4.315 | 6.049 | 4.255 | 0.165 | 0.0061 | 0.9169 | |
| 25 MPa | 33.5 | 5.283 | 4.888 | 0.679 | 0.461 | 0.009 | 0.9724 |
| 79 | 6.813 | 3.488 | 28.2 | 0.463 | 0.0091 | 0.9633 | |
| 438 | 5.924 | 4.203 | 834.26 | 0.459 | 0.0077 | 0.9376 | |
| 774 | 5.168 | 3.109 | 33.367 | 0.448 | 0.0073 | 0.9179 | |
| 1253 | 6.496 | 4.029 | 0.699 | 0.454 | 0.0075 | 0.9054 |
| °C | RMSE | R | |||||
|---|---|---|---|---|---|---|---|
| 15 MPa | 30 | 2.564 | 2.569 | 4.881 | 0.075 | 0.0105 | 0.9152 |
| 45 | 2.801 | 2.939 | 3.139 | 0.103 | 0.018 | 0.926 | |
| 141 | 2.833 | 3.01 | 2.946 | 0.101 | 0.014 | 0.9944 | |
| 290 | 2.924 | 3.069 | 3.038 | 0.096 | 0.0135 | 0.9912 | |
| 405 | 2.921 | 3.044 | 3.144 | 0.087 | 0.0133 | 0.9411 | |
| 580 | 2.982 | 3.102 | 3.294 | 0.092 | 0.0071 | 0.9757 | |
| 25 MPa | 33.5 | 1.294 | 2.945 | 2.338 | 0.051 | 0.0348 | 0.9217 |
| 79 | 7.662 | 10.439 | 9.574 | 0.011 | 0.0363 | 0.916 | |
| 438 | 0.003 | 3.039 | 2.761 | 0.039 | 0.0375 | 0.9829 | |
| 774 | 0.005 | 3.043 | 3.364 | 0.036 | 0.0397 | 0.9481 | |
| 1253 | 1.404 | 3.109 | 3.063 | 0.035 | 0.0389 | 0.9168 |
| °C | RMSE | R | ||||||
|---|---|---|---|---|---|---|---|---|
| 15 MPa | 30 | 2.774 | 2.131 | 36.89 | 139.872 | 0.1287 | 0.0018 | 0.961 |
| 45 | 2.794 | 2.962 | 36.753 | 259.998 | 0.1248 | 0.0016 | 0.9023 | |
| 141 | 2.858 | 6.942 | 33.964 | 431.502 | 0.1008 | 0.0021 | 0.9546 | |
| 290 | 2.898 | 7.331 | 29.306 | 754.175 | 0.0826 | 0.0015 | 0.9424 | |
| 405 | 5.344 | 8.052 | 4.378 | 1152.72 | 0.0766 | 0.0021 | 0.9686 | |
| 580 | 6.232 | 8.574 | 2.991 | 1239.575 | 0.0677 | 0.0006 | 0.9581 | |
| 25 MPa | 33.5 | 2.591 | 4.847 | 200.39 | 98.698 | 0.1134 | 0.0032 | 0.9675 |
| 79 | 2.669 | 5.879 | 137.5 | 208.704 | 0.0993 | 0.0026 | 0.9728 | |
| 438 | 2.771 | 6.921 | 33.49 | 848.867 | 0.0797 | 0.0022 | 0.9234 | |
| 774 | 2.839 | 7.708 | 28.88 | 1394.35 | 0.0673 | 0.0019 | 0.9934 | |
| 1253 | 2.896 | 8.277 | 7.494 | 1992.949 | 0.0635 | 0.0019 | 0.9671 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Chen, X. A Description of the Isothermal Ageing Creep Process in Polymethyl Methacrylate Using Fractional Differential Models. Polymers 2024, 16, 2725. https://doi.org/10.3390/polym16192725
Wang C, Chen X. A Description of the Isothermal Ageing Creep Process in Polymethyl Methacrylate Using Fractional Differential Models. Polymers. 2024; 16(19):2725. https://doi.org/10.3390/polym16192725
Chicago/Turabian StyleWang, Chuhong, and Xin Chen. 2024. "A Description of the Isothermal Ageing Creep Process in Polymethyl Methacrylate Using Fractional Differential Models" Polymers 16, no. 19: 2725. https://doi.org/10.3390/polym16192725





