Using Thin Ultra-High-Molecular-Weight Polyethylene Coatings to Reduce Friction in Frost-Resistant Rubbers
Abstract
:1. Introduction
2. Materials and Experimental Methods
2.1. Materials
2.2. Methods for Determining Tensile Strength and Elongation
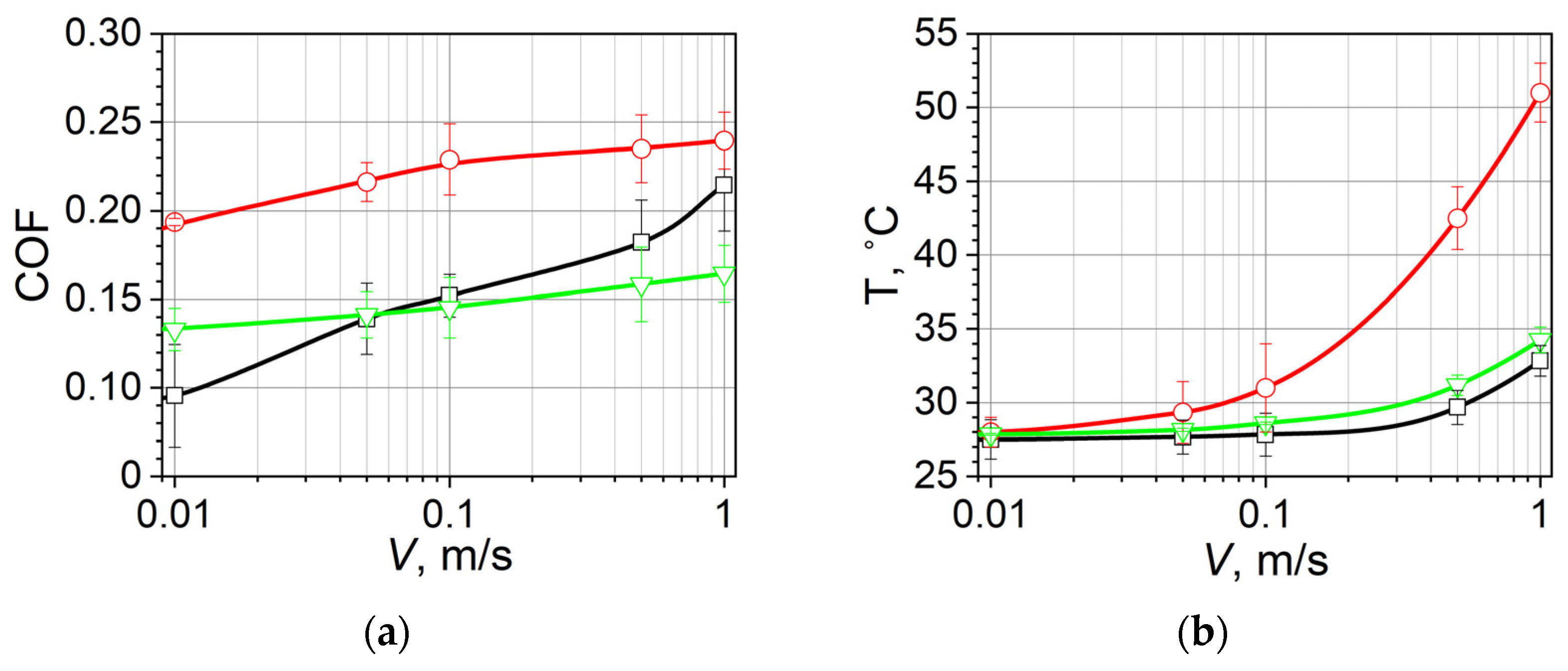
2.3. Friction Tests
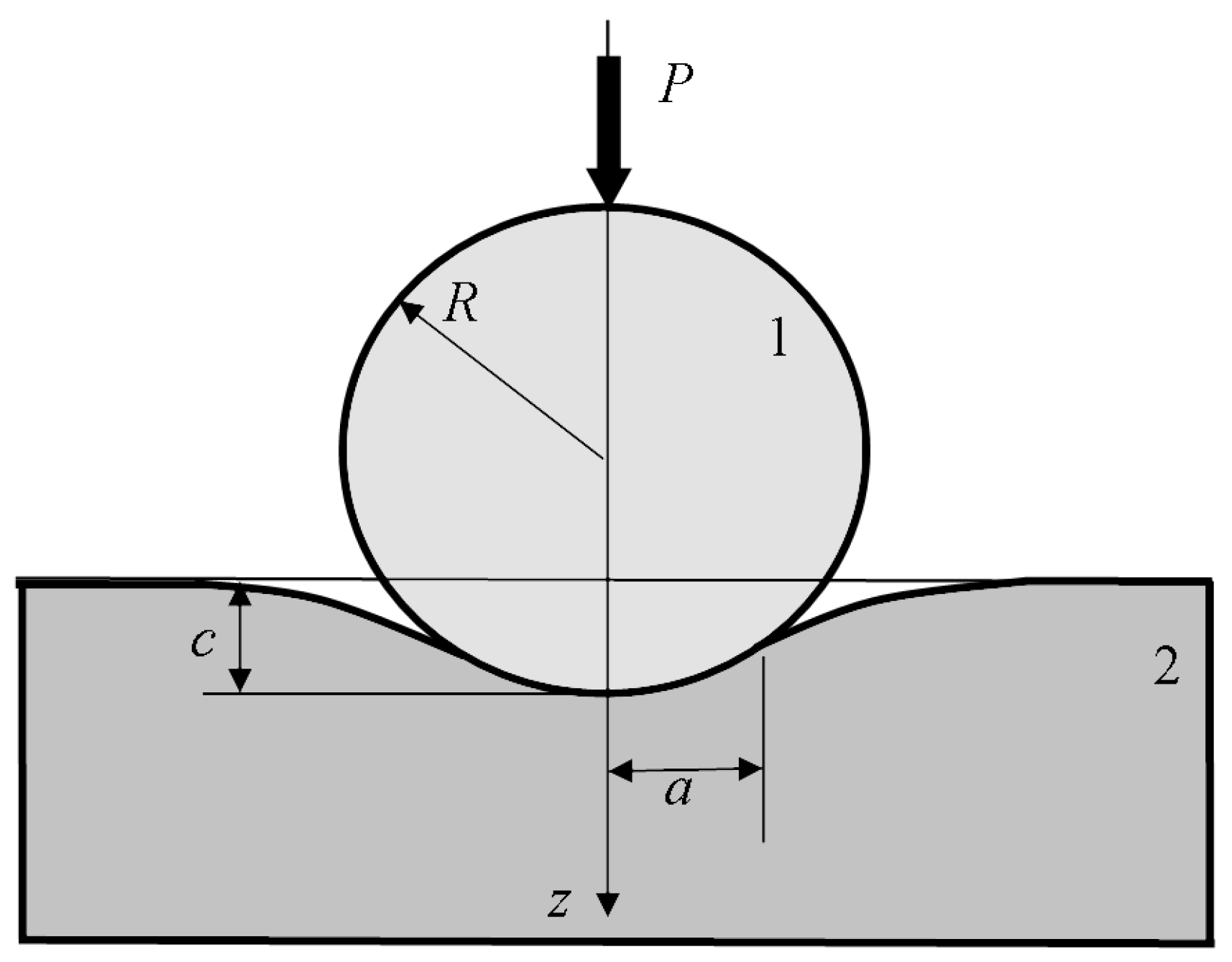
3. Models
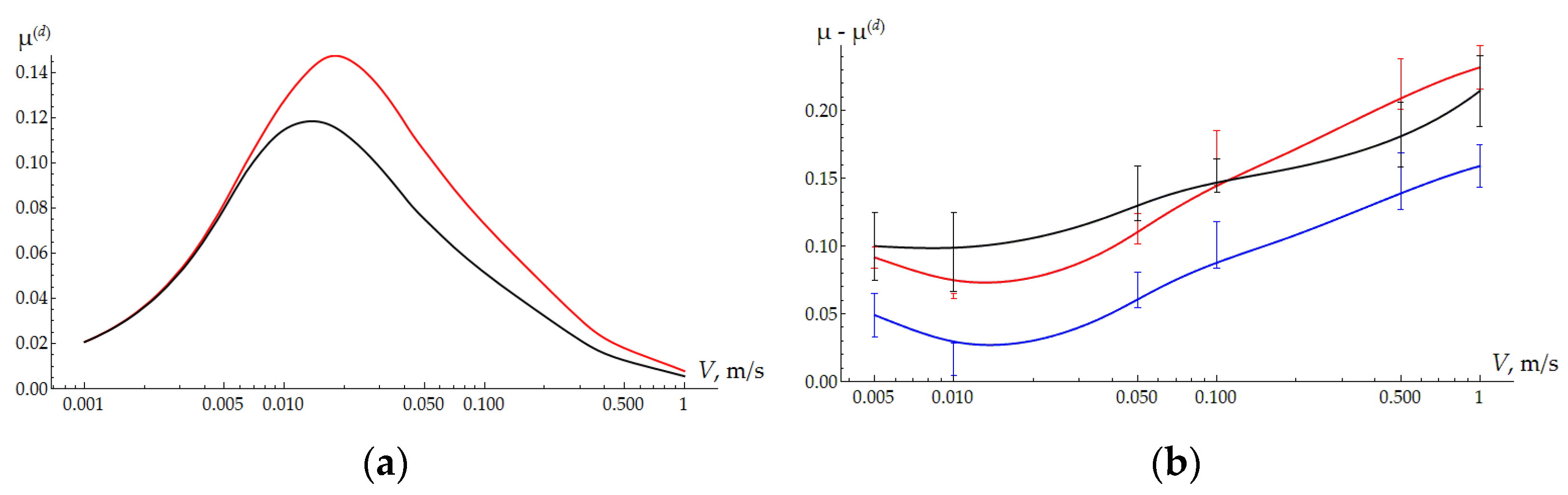
3.1. Contact Problem
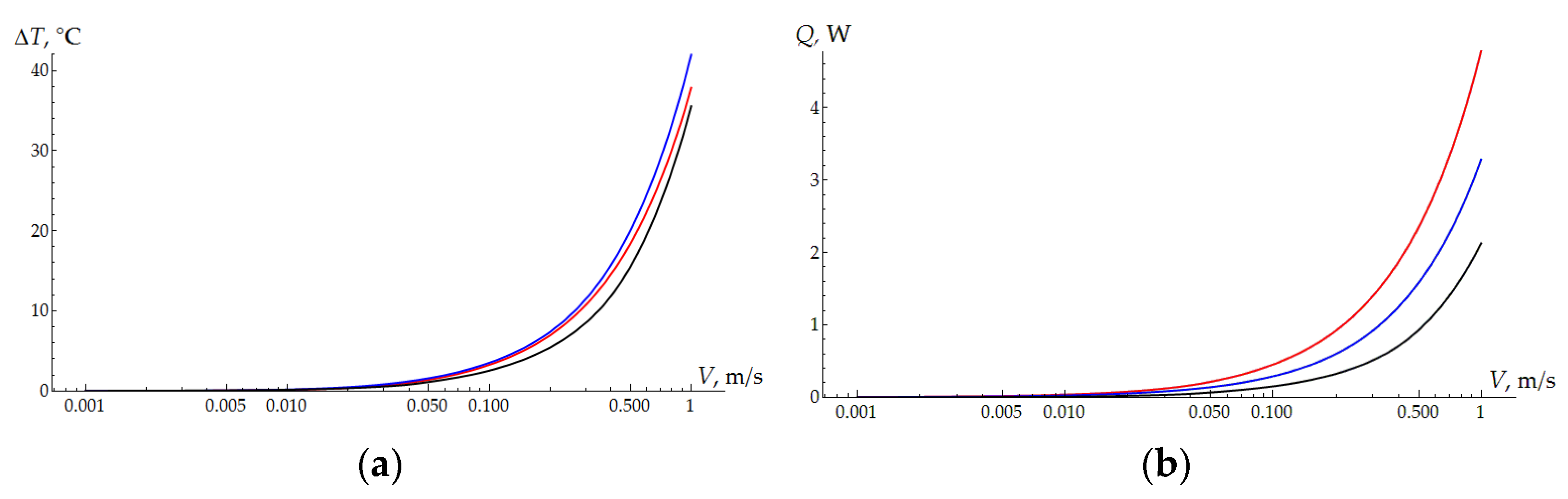
3.2. Thermal Problem
4. Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A

| , Hz | , nm | , nm | , rad | |
|---|---|---|---|---|
| 1 | 0.1 | 87,493 | 7033 | 0.138 |
| 2 | 0.2 | 85,832 | 6993 | 0.126 |
| 3 | 0.5 | 84,761 | 6317 | 0.044 |
| 4 | 1 | 83,525 | 6018 | 0.038 |
| 5 | 6 | 83,607 | 5333 | 0.057 |
| 6 | 30 | 83,607 | 6700 | 0.161 |
| , s | , s | , MPa | ||||
|---|---|---|---|---|---|---|
| 1 | 4.77 | 0.14 | 0.030 | 5.54 | 2.76 | 5.03 |
| 2 | 0.025 | 5.59 | 20.67 | 0.18 |
References
- Feng, W.; Patel, S.H.; Young, M.; Zunino, J.L.; Xanthos, M. Smart Polymeric Coatings—Recent Advances. Adv. Polym. Technol. 2007, 26, 1–13. [Google Scholar] [CrossRef]
- Martínez-Martínez, D.; Tiss, B.; Glanzmann, L.N.; Wolthuizen, D.J.; Cunha, L.; Mansilla, C.; De Hosson, J.T.M. Protective Films on Complex Substrates of Thermoplastic and Cellular Elastomers: Prospective Applications to Rubber, Nylon and Cork. Surf. Coat. Technol. 2022, 442, 128405. [Google Scholar] [CrossRef]
- Zhou, B.; Liu, Z.; Xu, B.; Rogachev, A.V.; Yarmolenko, M.A.; Rogachev, A.A. Modification of Cu-PE-PTFE Composite Coatings on Rubber Surface by Low-energy Electron Beam Dispersion with Glow Discharge. Polym. Eng. Sci. 2018, 58, 103–111. [Google Scholar] [CrossRef]
- Liu, Y.; Bian, D.; Wang, J.; Zhao, Y. Influence of Pore-Forming Agent on Wear Resistance of Composite Coating. Surf. Eng. 2022, 38, 208–215. [Google Scholar] [CrossRef]
- Aliyu, I.K.; Samad, M.A.; Al-Qutub, A. Tribological Characterization of a Bearing Coated with UHMWPE/GNPs Nanocomposite Coating. Surf. Eng. 2021, 37, 60–69. [Google Scholar] [CrossRef]
- Smith, J.R.; Lamprou, D.A. Polymer Coatings for Biomedical Applications: A Review. Trans. IMF 2014, 92, 9–19. [Google Scholar] [CrossRef]
- Abdul Samad, M. Recent Advances in UHMWPE/UHMWPE Nanocomposite/UHMWPE Hybrid Nanocomposite Polymer Coatings for Tribological Applications: A Comprehensive Review. Polymers 2021, 13, 608. [Google Scholar] [CrossRef]
- Surikov, V.I.; Nikolaev, I.V.; Polonyankin, D.A.; Tselykh, E.P.; Rogachev, E.A.; Surikov, V.I. Morphology, Composition and Tribological Properties of Tantalum Coatings Deposited onto a Rubber Substrate. J. Phys. Conf. Ser. 2017, 858, 012034. [Google Scholar] [CrossRef]
- Tikhomirov, L.A.; Tarasenko, V.A.; Kostina, T.Y.; Dorofeeva, L.V. The Effect of Molybdenum Disulphide on the Tribotechnical Characteristics of Polyamide Coatings on Nitrile Rubber Compounds. Int. Polym. Sci. Technol. 2015, 42, 31–34. [Google Scholar] [CrossRef]
- Ning, K.; Lu, J.; Xie, P.; Hu, J.; Huang, J.; Sheng, K. Study on Surface Modification of Silicone Rubber for Composite Insulator by Electron Beam Irradiation. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2021, 499, 7–16. [Google Scholar] [CrossRef]
- Jin, M.; Zhang, X.; Emeline, A.V.; Numata, T.; Murakami, T.; Fujishima, A. Surface Modification of Natural Rubber by TiO2 Film. Surf. Coat. Technol. 2008, 202, 1364–1370. [Google Scholar] [CrossRef]
- Dyakonov, A.A.; Shadrinov, N.V.; Sokolova, M.D.; Fedorov, A.L.; Sleptsova, S.A.; Okhlopkova, A.A. Research of the Effect of Diphenylguanidine on the Adhesive Interaction of Elastomers with Ultrahigh Molecular Weight Polyethylene. J. Sib. Fed. University. Eng. Technol. 2019, 12, 476–487. [Google Scholar] [CrossRef]
- Dyakonov, A.A.; Vasilev, A.P.; Danilova, S.N.; Okhlopkova, A.A.; Tarasova, P.N.; Lazareva, N.N.; Ushkanov, A.A.; Tuisov, A.G.; Kychkin, A.K.; Vinokurov, P.V. Two-Layer Rubber-Based Composite Material and UHMWPE with High Wear Resistance. Materials 2022, 15, 4678. [Google Scholar] [CrossRef]
- Shadrinov, N.V.; Sokolova, M.D.; Dyakonov, A.A. Mechanical Properties and Deformation Features of Nitrile Butadiene Rubber with Protective Coating from Ultra High-Molecular Weight Polyethylene. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1079, 042015. [Google Scholar] [CrossRef]
- Petrica, M.; Duscher, B.; Koch, T.; Archodoulaki, V.-M. Studies on Tribological Behavior of PEEK and PE-UHMW. In Proceedings of the Regional Conference Graz 2015–Polymer Processing Society, Graz, Austria, 21–25 September 2015; p. 070001. [Google Scholar]
- Han, Y.; Chen, J. Experimental Investigation on Tribological Properties of UHMWPE with the Addition of Basalt Fiber. Adv. Compos. Lett. 2019, 28. [Google Scholar] [CrossRef]
- Wang, Y.; Yin, Z.; Li, H.; Gao, G.; Zhang, X. Friction and Wear Characteristics of Ultrahigh Molecular Weight Polyethylene (UHMWPE) Composites Containing Glass Fibers and Carbon Fibers under Dry and Water-Lubricated Conditions. Wear 2017, 380–381, 42–51. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, Y.; Wang, H.; Fan, N.; Yan, F. Fretting Wear Behavior of UHMWPE Under Different Temperature Conditions. J. Macromol. Sci. Part B 2017, 56, 493–504. [Google Scholar] [CrossRef]
- Alam, F.; Choosri, M.; Gupta, T.K.; Varadarajan, K.M.; Choi, D.; Kumar, S. Electrical, Mechanical and Thermal Properties of Graphene Nanoplatelets Reinforced UHMWPE Nanocomposites. Mater. Sci. Eng. B 2019, 241, 82–91. [Google Scholar] [CrossRef]
- Saikko, V.; Morad, O.; Viitala, R. Effect of Temperature on UHMWPE and VEXLPE Friction and Wear against CoCr in Noncyclic Tests. Wear 2022, 490–491, 204190. [Google Scholar] [CrossRef]
- Cao, M.; Chen, L.; Xu, R.; Fang, Q. Effect of the Temperature on Ballistic Performance of UHMWPE Laminate with Limited Thickness. Compos. Struct. 2021, 277, 114638. [Google Scholar] [CrossRef]
- Imado, K.; Miura, A.; Nagatoshi, M.; Kido, Y.; Miyagawa, H.; Higaki, H. A Study of Contact Temperature Due to Frictional Heating of UHMWPE. Tribol. Lett. 2004, 16, 265–273. [Google Scholar] [CrossRef]
- Tabor, D. The Mechanism of Rolling Friction II. The Elastic Range. Proc. R. Soc. Lond. A 1955, 229, 198–220. [Google Scholar] [CrossRef]
- Greenwood, J.A.; Tabor, D. The Friction of Hard Sliders on Lubricated Rubber: The Importance of Deformation Losses. Proc. Phys. Soc. 1958, 71, 989–1001. [Google Scholar] [CrossRef]
- Grosch, K.A. The Relation between the Friction and Visco-Elastic Properties of Rubber. Proc. R. Soc. Lond. A 1963, 274, 21–39. [Google Scholar] [CrossRef]
- Aleksandrov, V.M.; Goryacheva, I.G.; Torskaya, E.V. Sliding Contact of a Smooth Indenter and a Viscoelastic Half-Space (3D Problem). Dokl. Phys. 2010, 55, 77–80. [Google Scholar] [CrossRef]
- Goryacheva, I.G.; Stepanov, F.I.; Torskaya, E.V. Sliding of a Smooth Indentor over a Viscoelastic Half-Space When There Is Friction. J. Appl. Math. Mech. 2015, 79, 596–603. [Google Scholar] [CrossRef]
- Goryacheva, I.; Stepanov, F.; Torskaya, E. Effect of Friction in Sliding Contact of a Sphere Over a Viscoelastic Half-Space. In Mathematical Modeling and Optimization of Complex Structures; Computational Methods in Applied Sciences, Neittaanmäki, P., Repin, S., Tuovinen, T., Eds.; Springer International Publishing: Cham, Switzerland, 2016; Volume 40, pp. 93–103. ISBN 978-3-319-23563-9. [Google Scholar]
- Koumi, K.E.; Chaise, T.; Nelias, D. Rolling Contact of a Rigid Sphere/Sliding of a Spherical Indenter upon a Viscoelastic Half-Space Containing an Ellipsoidal Inhomogeneity. J. Mech. Phys. Solids 2015, 80, 1–25. [Google Scholar] [CrossRef]
- Aleksandrov, V.M.; Goryacheva, I.G. Motion with a Constant Velocity of a Distributed Load over a Viscoelastic Half-Space. In Proceedings of the 5th Russian Conference “Mixed Problems of Deformable Body Mechanics”; Saratov University: Saratov, Russia, 2005; pp. 23–25. [Google Scholar]
- Torskaya, E.V.; Stepanov, F.I. Effect of Surface Layers in Sliding Contact of Viscoelastic Solids (3-D Model of Material). Front. Mech. Eng. 2019, 5, 26. [Google Scholar] [CrossRef]
- ISO 37:2024; Rubber, Vulcanized or Thermoplastic—Determination of Tensile Stress-Strain Properties. ISO: Geneva, Switzerland, 2024.
- ISO 1817:2024; Rubber, Vulcanized or Thermoplastic—Determination of the Effect of Liquids. ISO: Geneva, Switzerland, 2024.
- ISO 23529:2016; Rubber—General Procedures for Preparing and Conditioning Test Pieces for Physical Test Methods. ISO: Geneva, Switzerland, 2016.
- Wypych, G. UHMWPE Ultrahigh Molecular Weight Polyethylene. In Handbook of Polymers; Elsevier: Berlin/Heidelberg, Germany, 2016; pp. 693–697. ISBN 978-1-895198-92-8. [Google Scholar]
- Morozov, A.V.; Murav’eva, T.I.; Petrova, N.N.; Portnyagina, V.V.; Ammosova, V.N.; Zagorskii, D.L. Investigation of the Tribological and Adhesive Properties of Cold-Resistant Rubbers. Int. Polym. Sci. Technol. 2016, 43, 27–32. [Google Scholar] [CrossRef]
- Bukovskiy, P.O.; Morozov, A.V.; Petrova, N.N.; Timofeeva, E.V. Study on the Influence of Activated Carbon Nanotubes on the Tribological Properties of Frost-Resistant Rubber. Mech. Solids 2019, 54, 1250–1255. [Google Scholar] [CrossRef]
- ASTM G99-23; Standard Test Method for Wear and Friction Testing with a Pin-on-Disk or Ball-on-Disk Apparatus. ASTM International: West Conshohocken, PA, USA, 2023.
- Nikishin, V.S.; Shapiro, G.S. Space Problems of Elasticity Theory for Multilayered Media; VTs AN SSSR: Moscow, Russia, 1970. [Google Scholar]
- Liu, S.; Wang, Q.; Liu, G. A Versatile Method of Discrete Convolution and FFT (DC-FFT) for Contact Analyses. Wear 2000, 243, 101–111. [Google Scholar] [CrossRef]
- Evtushenko, A.A.; Ivanik, E.G.; Evtushenko, E.A. Approximate Method for Determining the Maximum Temperature during Quasistationary Heating of a Piecewise-Homogeneous Half-Space. J. Appl. Mech. Technol. Phys. 2005, 46, 375–385. [Google Scholar] [CrossRef]
- Macuvele, D.L.P.; Nones, J.; Matsinhe, J.V.; Lima, M.M.; Soares, C.; Fiori, M.A.; Riella, H.G. Advances in Ultra High Molecular Weight Polyethylene/Hydroxyapatite Composites for Biomedical Applications: A Brief Review. Mater. Sci. Eng. C 2017, 76, 1248–1262. [Google Scholar] [CrossRef]
- Goryacheva, I.G.; Makhovskaya, Y. Discrete Contact Mechanics with Applications in Tribology; Elsevier: Berlin/Heidelberg, Germany, 2022; ISBN 978-0-12-821799-3. [Google Scholar]
- Torskaya, E.V.; Stepanov, F.I. Effect of Friction in Sliding Contact of Layered Viscoelastic Solids. In Advanced Problem in Mechanics II; Lecture Notes in Mechanical Engineering, Indeitsev, D.A., Krivtsov, A.M., Eds.; Springer International Publishing: Cham, Switzerland, 2022; pp. 320–330. ISBN 978-3-030-92143-9. [Google Scholar]
- Rabotnov, Y.N. Creep of Structural Elements; Nauka Publ.: Moscow, Russia, 1966. [Google Scholar]
- Christensen, R.M. Theory of Viscoelasticity: An Introduction; Academic Press: New York, NY, USA, 1971. [Google Scholar]
- Johnson, K.L. Contact Mechanics, 1st ed.; Cambridge University Press: Cambridge, UK, 1985; ISBN 978-0-521-25576-9. [Google Scholar]
- Sneddon, I. Fourier Transforms; McGraw Hill: New York, NY, USA, 1951. [Google Scholar]
- Haiat, G.; Phan Huy, M.C.; Barthel, E. The Adhesive Contact of Viscoelastic Spheres. J. Mech. Phys. Solids 2003, 51, 69–99. [Google Scholar] [CrossRef]
- Argatov, I.I.; Popov, V.L. Rebound Indentation Problem for a Viscoelastic Half-space and Axisymmetric Indenter—Solution by the Method of Dimensionality Reduction. Z. Angew. Math. Mech. 2016, 96, 956–967. [Google Scholar] [CrossRef]
- Baumgaertel, M.; Winter, H.H. Determination of Discrete Relaxation and Retardation Time Spectra from Dynamic Mechanical Data. Rheol. Acta 1989, 28, 511–519. [Google Scholar] [CrossRef]



| Input | Q, N | Vertical load | 10; 20 |
| R, m | Radius of ball | 0.005 | |
| E(0), MPa | Young modulus of ball | 210,000 | |
| ν(0) | Poisson ratio of ball | 0.3 | |
| E(1), MPa | Young modulus of coating | 1000 | |
| ν(1) | Poisson ratio of coating | 0.35 | |
| E(2), MPa | Young modulus of substrate | 13.8 | |
| ν(2) | Poisson ratio of substrate | 0.45 | |
| µi, s | Spectrum of retardation times | 0.13 | |
| 1/ki, s | Spectrum of relaxation times | 1/40.14 | |
| H, m | Coating thickness | 0.0003; 0.0006 | |
| λ(0), W/(m·K) | Coefficient of thermal conductivity of indenter | 50 | |
| λ(1), W/(m·K) | Coefficient of thermal conductivity of coating | 0.4 | |
| λ(2), W/(m·K) | Coefficient of thermal conductivity of substrate | 0.15 | |
| µ | Friction coefficient | from the tests | |
| V, m/s | Sliding velocity | from the tests | |
| Output | P(x,y), Pa | Contact pressure distribution | |
| D, m | Approach of indentor | ||
| µ(d) | Deformation component of friction coefficient | ||
| µ(a) | Adhesion component of friction coefficient | ||
| T(x,y,z), °C | Temperature |
| Properties | Tensile Strength, MPa, | Relative Elongation, % | The Degree of Swelling in Oil (AMG-10), % | Tg, °C |
|---|---|---|---|---|
| NBR, (sample 1) | 11.7 ± 0.95 | 273 ± 21 | 15.5 ± 0.5 | −44.3 |
| NBR, (sample 2) | 12.3 ± 0.8 | 238 ± 18 | 14.6 ± 0.4 | −45.4 |
| UHMWPE | 37.4 ± 1.0 | 324 ± 24 | 0 | −120 [15] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Torskaya, E.; Shkalei, I.; Stepanov, F.; Makhovskaya, Y.; Dyakonov, A.; Petrova, N. Using Thin Ultra-High-Molecular-Weight Polyethylene Coatings to Reduce Friction in Frost-Resistant Rubbers. Polymers 2024, 16, 2870. https://doi.org/10.3390/polym16202870
Torskaya E, Shkalei I, Stepanov F, Makhovskaya Y, Dyakonov A, Petrova N. Using Thin Ultra-High-Molecular-Weight Polyethylene Coatings to Reduce Friction in Frost-Resistant Rubbers. Polymers. 2024; 16(20):2870. https://doi.org/10.3390/polym16202870
Chicago/Turabian StyleTorskaya, Elena, Ivan Shkalei, Fedor Stepanov, Yulia Makhovskaya, Afanasy Dyakonov, and Natalia Petrova. 2024. "Using Thin Ultra-High-Molecular-Weight Polyethylene Coatings to Reduce Friction in Frost-Resistant Rubbers" Polymers 16, no. 20: 2870. https://doi.org/10.3390/polym16202870
APA StyleTorskaya, E., Shkalei, I., Stepanov, F., Makhovskaya, Y., Dyakonov, A., & Petrova, N. (2024). Using Thin Ultra-High-Molecular-Weight Polyethylene Coatings to Reduce Friction in Frost-Resistant Rubbers. Polymers, 16(20), 2870. https://doi.org/10.3390/polym16202870







