Glass Transition Temperatures and Thermal Conductivities of Polybutadiene Crosslinked with Randomly Distributed Sulfur Chains Using Molecular Dynamic Simulation
Abstract
:1. Introduction
2. Methods and Theoretical Formulations
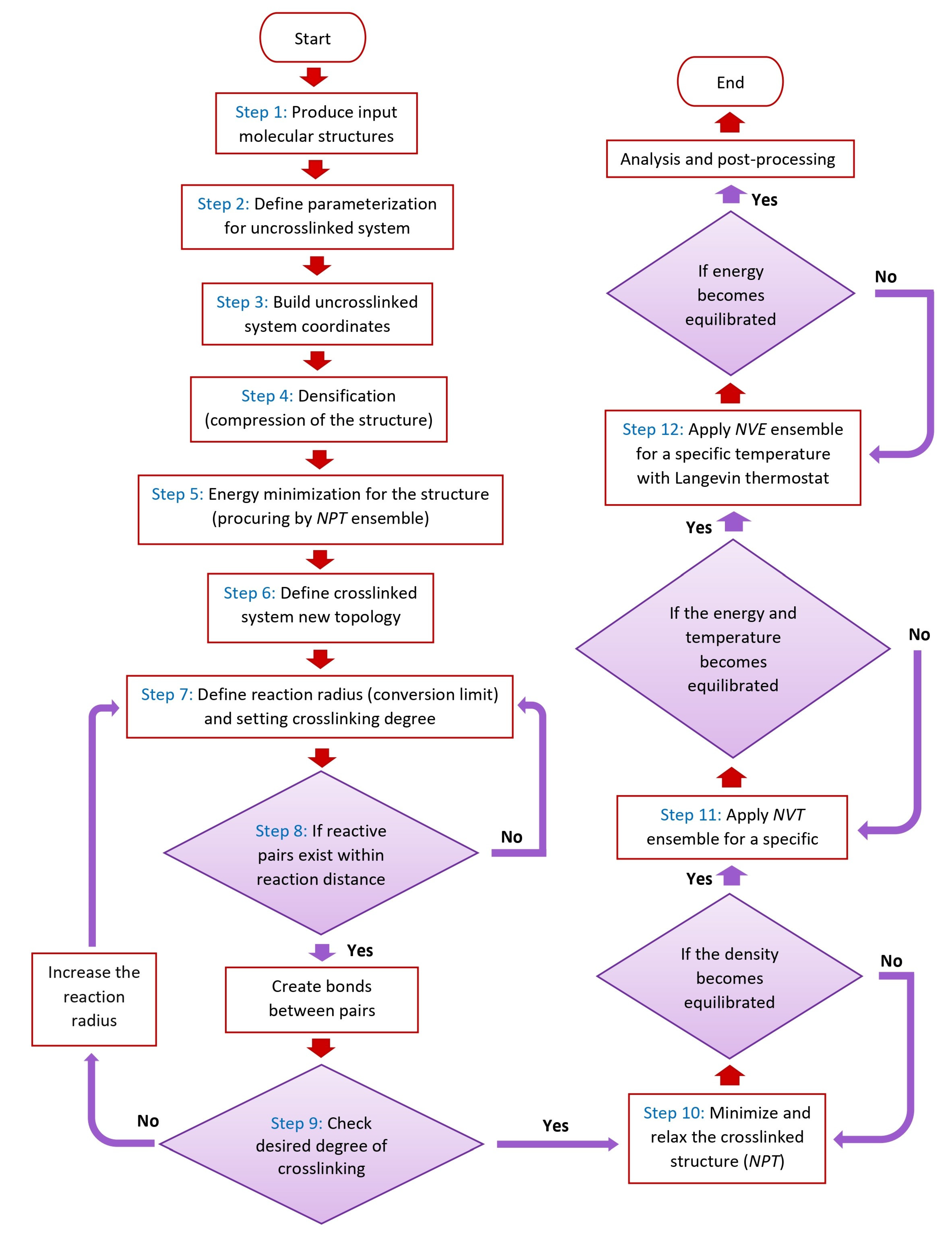
2.1. Set-Up of Simulation
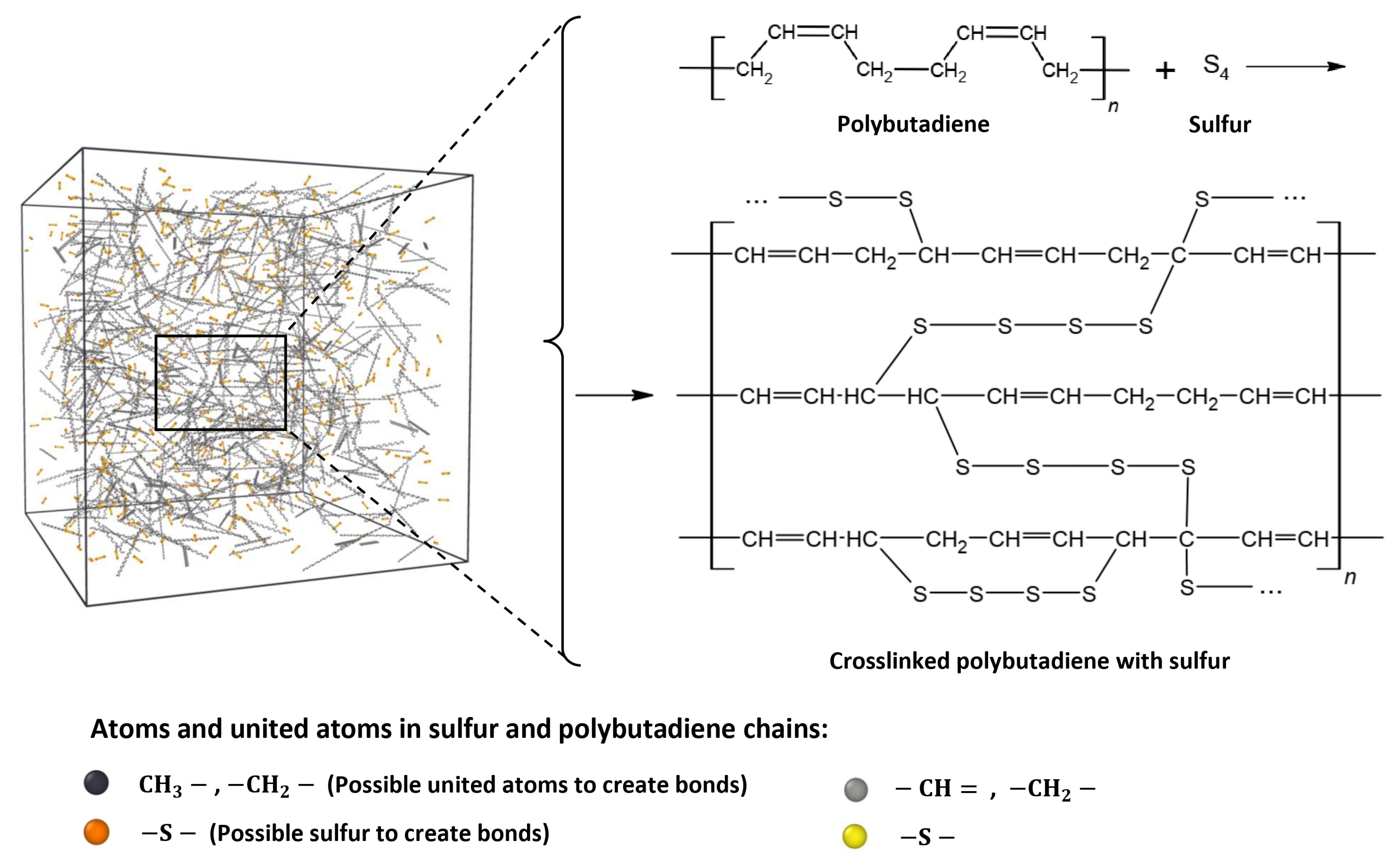
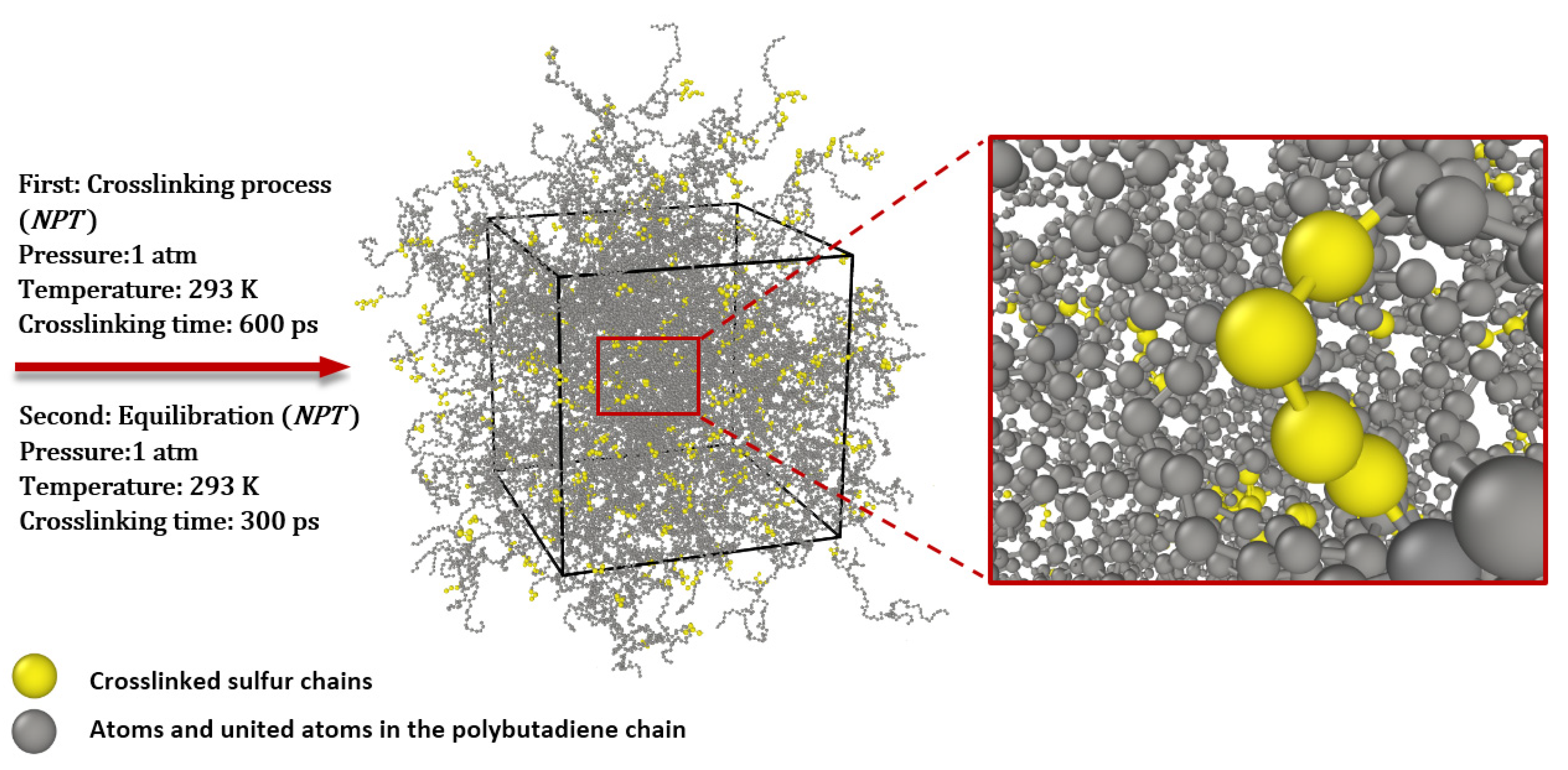
2.1.1. Mechanism of Chemical Bond Formation and Crosslinking
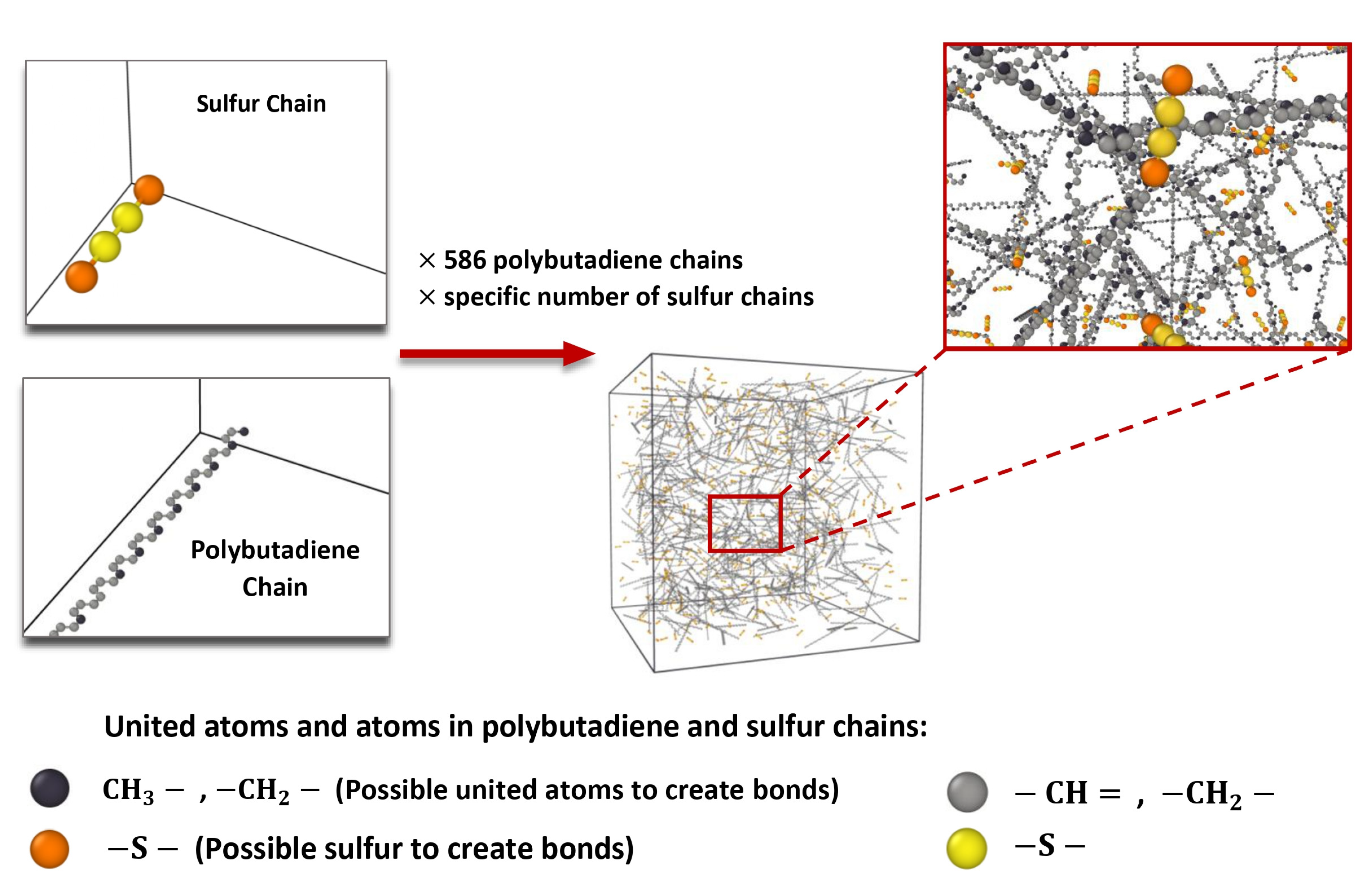
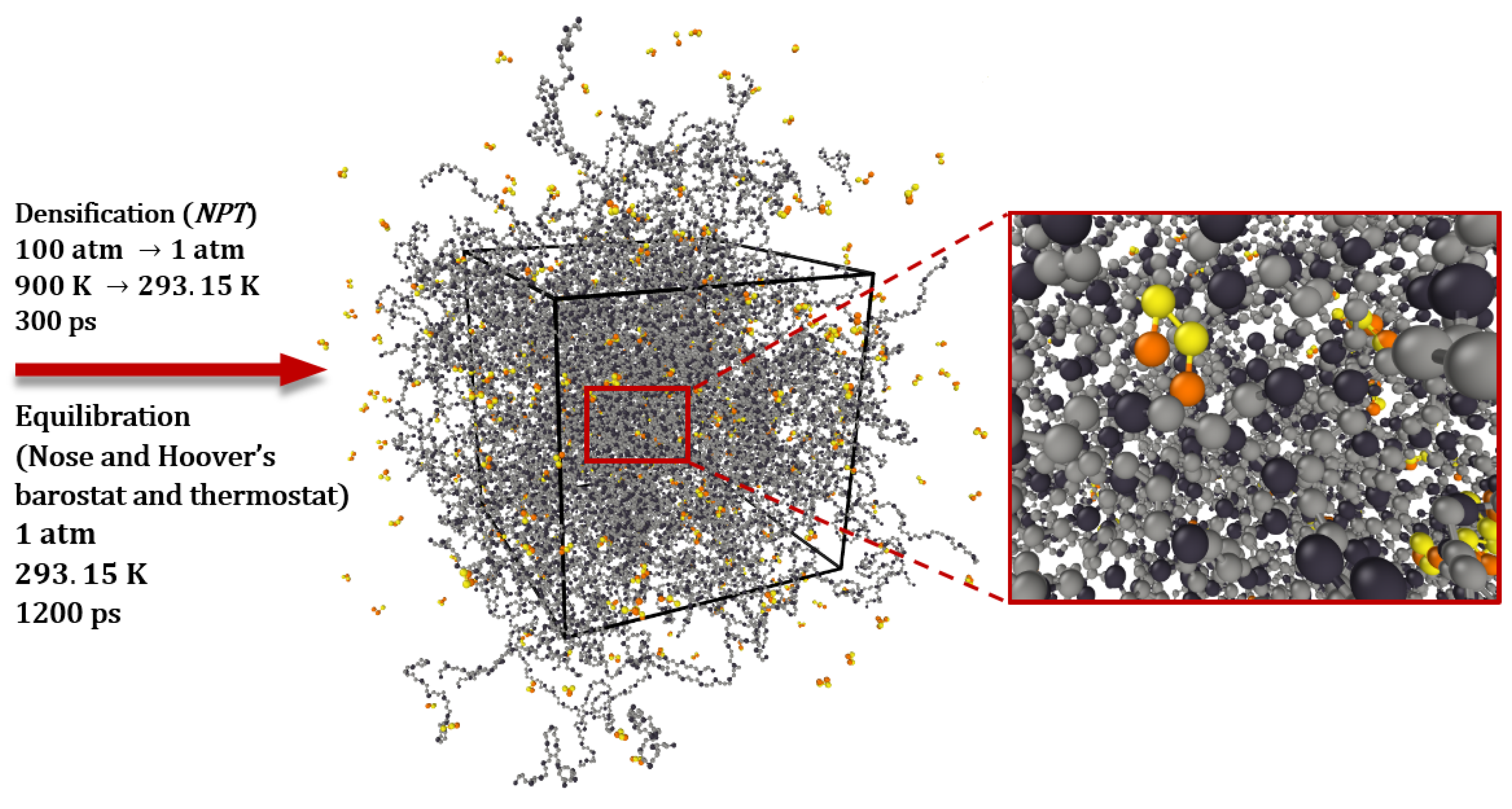
2.1.2. Simulation and Creation of Model Systems
2.2. Green–Kubo Method and Heat Flux Formulation
3. Results and Discussion
3.1. Representation of Cis-1,4-Polybutadiene in MD Simulations
3.2. Cis-1,4-Polybutadiene Crosslinked with Randomly Distributed Sulfur Chains of Different Lengths with a Constant Degree of Crosslinking in All Models
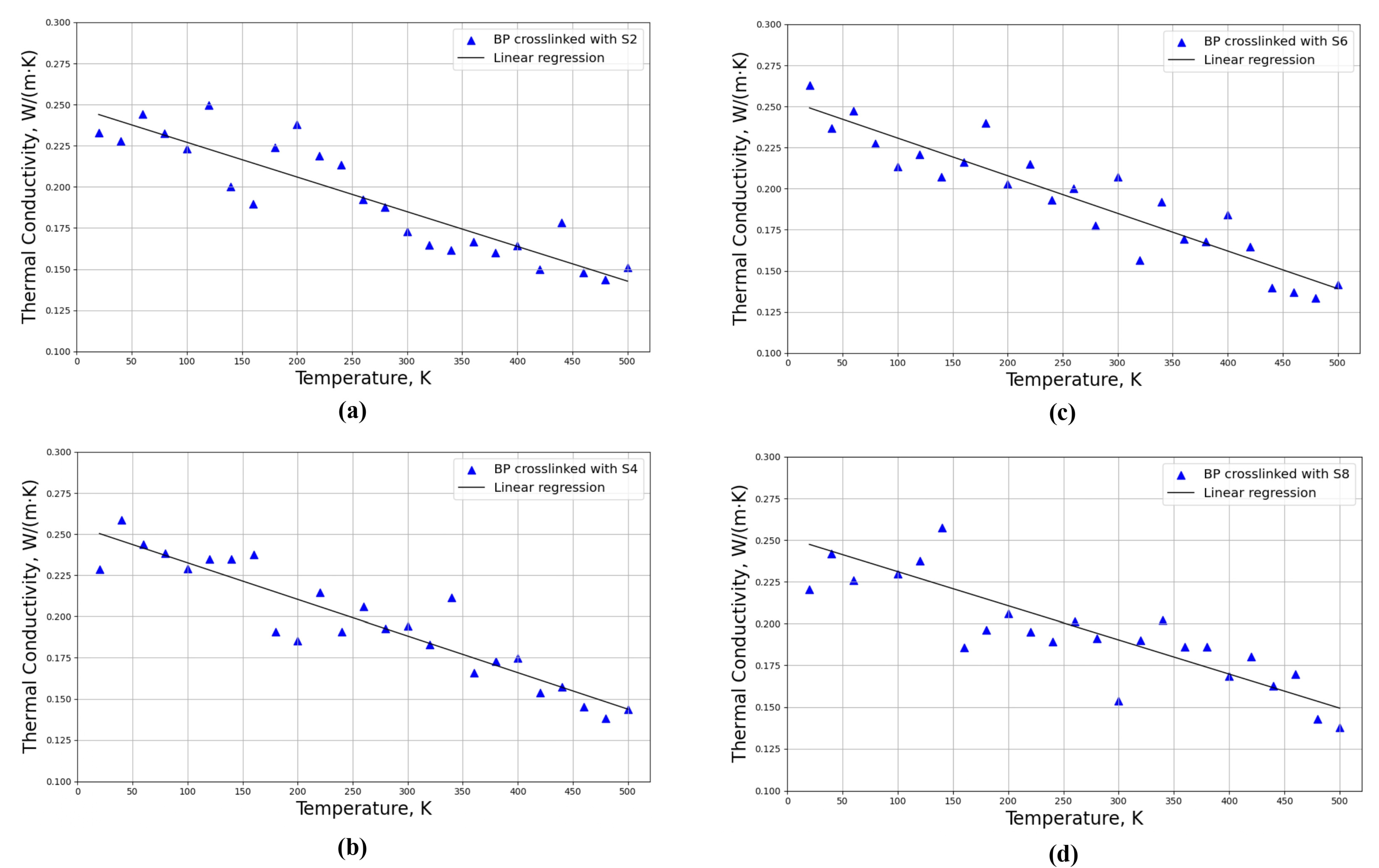
3.2.1. Determination of Thermal Conductivity with Constant Crosslinking Degree of Sulfur Bridges
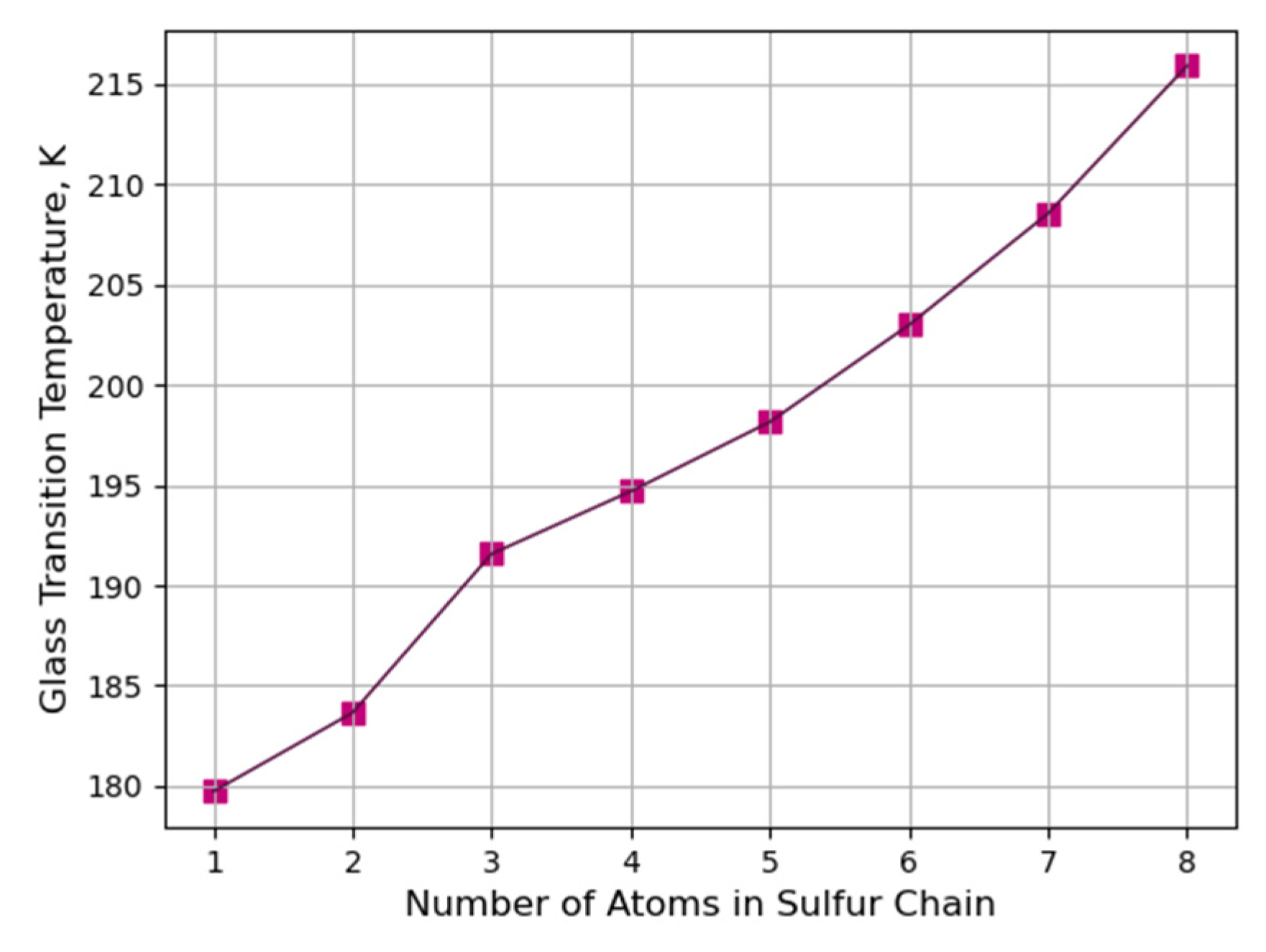
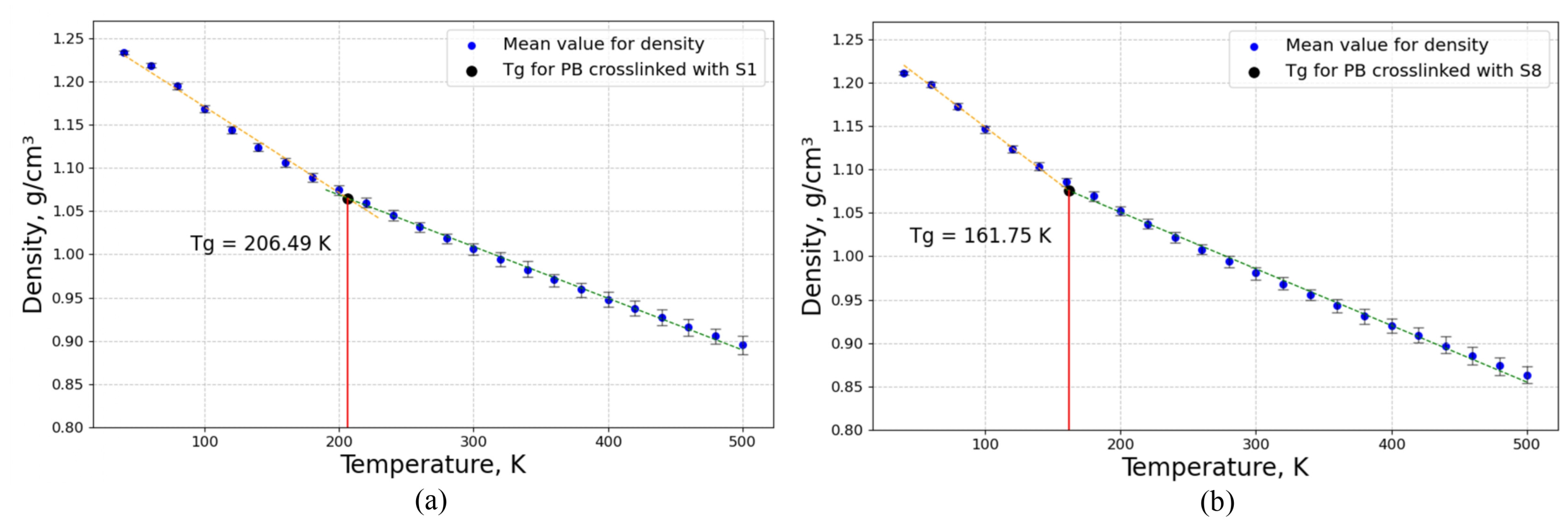
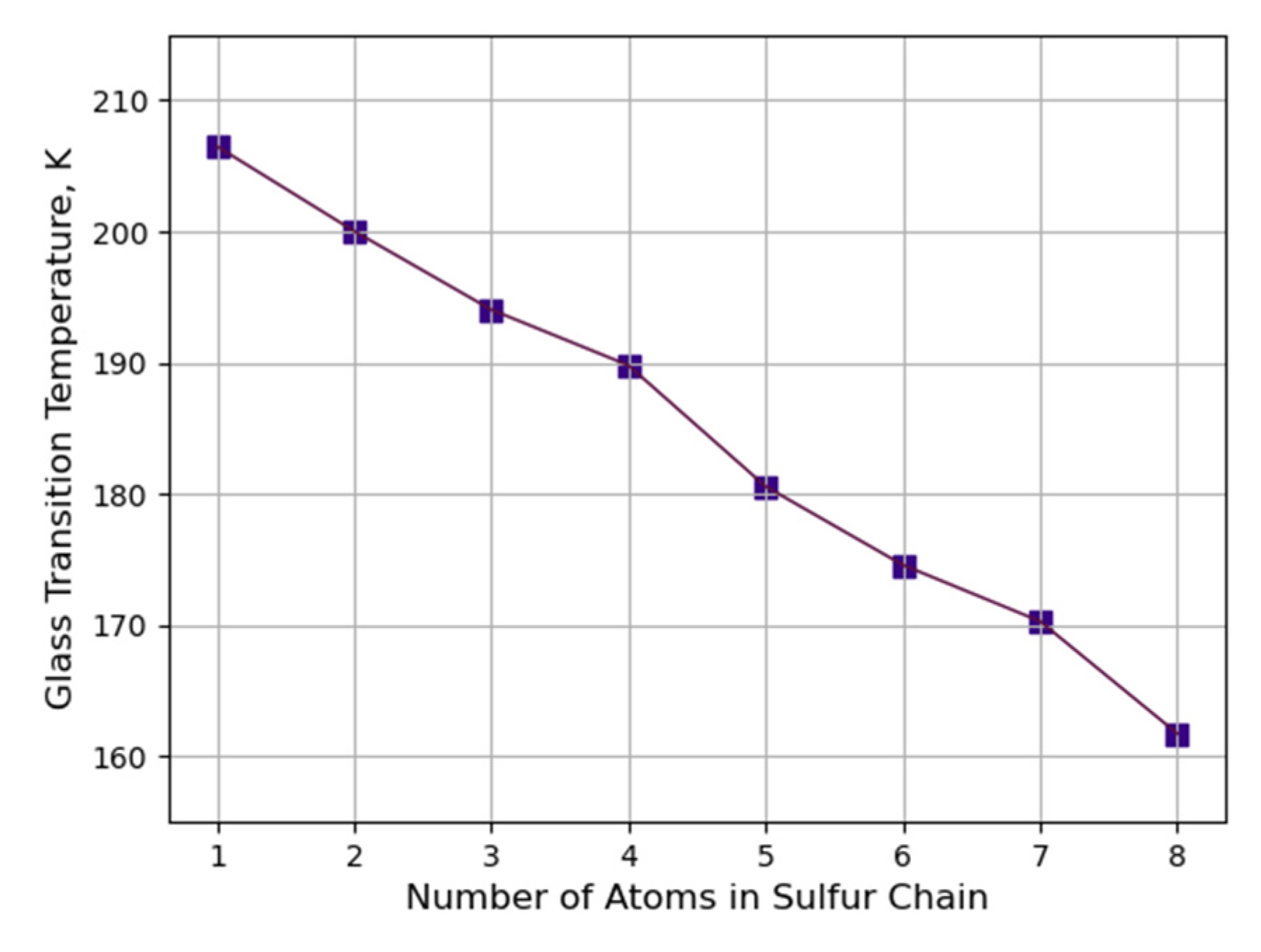
3.2.2. Determination of Glass Transition Temperature with Constant Crosslinking Degree of Sulfur Bridges
3.3. Polybutadiene Crosslinked with Randomly Distributed Sulfur of Different Lengths with Constant Molar Mass of Sulfur in All Models
3.3.1. Determination of Thermal Conductivities with Constant Molar Mass of Sulfur
3.3.2. Determination of Glass Transition Temperature with a Constant Molar Mass of Sulfur
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bedrov, D.; Piquemal, J.-P.; Borodin, O.; MacKerell, A.D., Jr.; Roux, B.; Schröder, C. Molecular Dynamics Simulations of Ionic Liquids and Electrolytes Using Polarizable Force Fields. Chem. Rev. 2019, 119, 7940–7995. [Google Scholar] [CrossRef]
- Noé, F.; Tkatchenko, A.; Müller, K.-R.; Clementi, C. Machine Learning for Molecular Simulation. Annu. Rev. Phys. Chem. 2020, 71, 361–390. [Google Scholar] [CrossRef]
- Asandulesa, M.; Kostromin, S.; Tameev, A.; Aleksandrov, A.; Bronnikov, S. Molecular Dynamics and Conductivity of a PTB7:PC71BM Photovoltaic Polymer Blend: A Dielectric Spectroscopy Study. ACS Appl. Polym. Mater. 2021, 3, 4869–4878. [Google Scholar] [CrossRef]
- Niu, W.; Nie, W.; Yuan, M.; Bao, Q.; Zhou, W.; Yan, J.; Yu, F.; Liu, C.; Sun, N.; Xue, Q. Study of the Microscopic Mechanism of Lauryl Glucoside Wetting Coal Dust: Environmental Pollution Prevention and Control. J. Hazard. Mater. 2021, 412, 125223. [Google Scholar] [CrossRef]
- Bhatt, P.; Joshi, T.; Bhatt, K.; Zhang, W.; Huang, Y.; Chen, S. Binding Interaction of Glyphosate with Glyphosate Oxidoreductase and C-P Lyase: Molecular Docking and Molecular Dynamics Simulation Studies. J. Hazard. Mater. 2021, 409, 124927. [Google Scholar] [CrossRef]
- Takari, A.; Ghasemi, A.R.; Hamadanian, M.; Sarafrazi, M.; Najafidoust, A. Molecular Dynamics Simulation and Thermo-Mechanical Characterization for Optimization of Three-Phase Epoxy/TiO2/SiO2 Nano-Composites. Polym. Test. 2021, 93, 106890. [Google Scholar] [CrossRef]
- Salmaso, V.; Moro, S. Bridging Molecular Docking to Molecular Dynamics in Exploring Ligand-Protein Recognition Process: An Overview. Front. Pharmacol. 2018, 9, 923. [Google Scholar] [CrossRef] [PubMed]
- Jing, Z.; Liu, C.; Cheng, S.Y.; Qi, R.; Walker, B.D.; Piquemal, J.-P.; Ren, P. Polarizable Force Fields for Biomolecular Simulations: Recent Advances and Applications. Annu. Rev. Biophys. 2019, 48, 371–394. [Google Scholar] [CrossRef] [PubMed]
- Guo, F.; Zhang, J.; Pei, J.; Ma, W.; Hu, Z.; Guan, Y. Evaluation of the Compatibility between Rubber and Asphalt Based on Molecular Dynamics Simulation. Front. Struct. Civ. Eng. 2020, 14, 435–445. [Google Scholar] [CrossRef]
- Ganazzoli, F.; Raffaini, G. Dendrimer Dynamics: A Review of Analytical Theories and Molecular Simulation Methods. Polymers 2020, 12, 1387. [Google Scholar] [CrossRef]
- Rohr, D.F.; Klein, M.T. Modeling Diffusion and Reaction in Crosslinking Epoxy-Amine Cure Kinetics: A Dynamic Percolation Approach. Ind. Eng. Chem. Res. 1990, 29, 1210–1218. [Google Scholar] [CrossRef]
- Shy, L.Y.; Leung, Y.K.; Eichinger, B.E. Critical Exponents for Off-Lattice Gelation of Polymer Chains. Macromolecules 1985, 18, 983–986. [Google Scholar] [CrossRef]
- Chen, Y.-C.; Chiu, W.-Y. Polymer Chain Buildup and Network Formation of Imidazole-Cured Epoxy/Phenol Resins. Macromolecules 2000, 33, 6672–6684. [Google Scholar] [CrossRef]
- Doherty, D.C.; Holmes, B.N.; Leung, P.; Ross, R.B. Polymerization Molecular Dynamics Simulations. I. Cross-Linked Atomistic Models for Poly(Methacrylate) Networks. Comput. Theor. Polym. Sci. 1998, 8, 169–178. [Google Scholar] [CrossRef]
- Gestoso, P.; Nicol, E.; Doxastakis, M.; Theodorou, D.N. Atomistic Monte Carlo Simulation of Polybutadiene Isomers: Cis-1,4-Polybutadiene and 1,2-Polybutadiene. Macromolecules 2003, 36, 6925–6938. [Google Scholar] [CrossRef]
- Tsolou, G.; Mavrantzas, V.G.; Theodorou, D.N. Detailed Atomistic Molecular Dynamics Simulation of Cis-1,4-Poly(Butadiene). Macromolecules 2005, 38, 1478–1492. [Google Scholar] [CrossRef]
- Narros, A.; Arbe, A.; Alvarez, F.; Colmenero, J.; Zorn, R.; Schweika, W.; Richter, D. Partial Structure Factors in 1,4-Polybutadiene. A Combined Neutron Scattering and Molecular Dynamics Simulations Study. Macromolecules 2005, 38, 9847–9853. [Google Scholar] [CrossRef]
- Maurel, G.; Schnell, B.; Goujon, F.; Couty, M.; Malfreyt, P. Multiscale Modeling Approach toward the Prediction of Viscoelastic Properties of Polymers. J. Chem. Theory Comput. 2012, 8, 4570–4579. [Google Scholar] [CrossRef] [PubMed]
- Maurel, G.; Goujon, F.; Schnell, B.; Malfreyt, P. Prediction of Structural and Thermomechanical Properties of Polymers from Multiscale Simulations. RSC Adv. 2015, 5, 14065–14073. [Google Scholar] [CrossRef]
- Maurel, G.; Goujon, F.; Schnell, B.; Malfreyt, P. Multiscale Modeling of the Polymer—Silica Surface Interaction: From Atomistic to Mesoscopic Simulations. J. Phys. Chem. C 2015, 119, 4817–4826. [Google Scholar] [CrossRef]
- Sharma, P.; Roy, S.; Karimi-Varzaneh, H.A. Validation of Force Fields of Rubber through Glass-Transition Temperature Calculation by Microsecond Atomic-Scale Molecular Dynamics Simulation. J. Phys. Chem. B 2016, 120, 1367–1379. [Google Scholar] [CrossRef]
- Krejsa, M.R.; Koenig, J.L. A Review of Sulfur Crosslinking Fundamentals for Accelerated and Unaccelerated Vulcanization. Rubber Chem. Technol. 1993, 66, 376–410. [Google Scholar] [CrossRef]
- Akiba, M.; Hashim, A.S. Vulcanization and Crosslinking in Elastomers. Prog. Polym. Sci. 1997, 22, 475–521. [Google Scholar] [CrossRef]
- Bhowmick, A.K.; Mukhopadhyay, R.; De, S.K. High Temperature Vulcanization of Elastomers. Rubber Chem. Technol. 1979, 52, 725–734. [Google Scholar] [CrossRef]
- Mark, J.E.; Erman, B.; Eirich, F.R. (Eds.) Science and Technology of Rubber, 2nd ed.; Academic Press: San Diego, CA, USA, 1994; ISBN 978-0-12-472525-6. [Google Scholar]
- Boonkerd, K.; Deeprasertkul, C.; Boonsomwong, K. Effect of Sulfur to Accelerator Ratio on Crosslink Structure, Reversion, and Strength in Natural Rubber. Rubber Chem. Technol. 2016, 89, 450–464. [Google Scholar] [CrossRef]
- Zaper, A.M.; Koenig, J.L. Solid State Carbon-13 NMR Studies of Vulcanized Elastomers. III, Accelerated Sulfur Vulcanization of Natural Rubber. Rubber Chem. Technol. 1987, 60, 278–297. [Google Scholar] [CrossRef]
- Sombatsompop, N. Analysis of Cure Characteristics on Cross-Link Density and Type, and Viscoelastic Properties of Natural Rubber. Polym.—Plast. Technol. Eng. 1998, 37, 333–349. [Google Scholar] [CrossRef]
- Marzocca, Á.; Mansilla, M. Analysis of Network Structure Formed in Styrene–Butadiene Rubber Cured with Sulfur/TBBS System. J. Appl. Polym. Sci. 2007, 103, 1105–1112. [Google Scholar] [CrossRef]
- Mukhopadhyay, R.; Bhowmick, A.K.; De, S.K. Effect of Vulcanization Temperature and Synergism of Accelerators on the Network and Technical Properties of Efficiently Vulcanized Natural Rubber Mixes. Polymer 1978, 19, 1176–1180. [Google Scholar] [CrossRef]
- Mukhopadhyay, R.; De, S.K.; Chakraborty, S.N. Effect of Vulcanization Temperature and Vulcanization Systems on the Structure and Properties of Natural Rubber Vulcanizates. Polymer 1977, 18, 1243–1249. [Google Scholar] [CrossRef]
- Liu, Y.; Wu, Q.; Wang, C.; Zhou, D.; Liang, R.; Kang, Y. Curing Behaviors’ Characterization of Strong and Weak Crosslinking Systems by Thermal and Dynamic Mechanical Methods. Polym. Test. 2018, 70, 1–7. [Google Scholar] [CrossRef]
- Du, Y.; Zhao, G.; Shi, G.; Wang, Y.; Li, W.; Ren, S. Effect of Crosslink Structure on Mechanical Properties, Thermal Stability and Flame Retardancy of Natural Flavonoid Based Epoxy Resins. Eur. Polym. J. 2022, 162, 110898. [Google Scholar] [CrossRef]
- Djemour, A.; Sanctuary, R.; Baller, J. Mobility Restrictions and Glass Transition Behaviour of an Epoxy Resin under Confinement. Soft Matter 2015, 11, 2683–2690. [Google Scholar] [CrossRef] [PubMed]
- Huang, M.; Tunnicliffe, L.B.; Thomas, A.G.; Busfield, J.J.C. The Glass Transition, Segmental Relaxations and Viscoelastic Behaviour of Particulate-Reinforced Natural Rubber. Eur. Polym. J. 2015, 67, 232–241. [Google Scholar] [CrossRef]
- Samith, V.D.; Ramos-Moore, E. Study of Glass Transition in Functionalized Poly(Itaconate)s by Differential Scanning Calorimetry, Raman Spectroscopy and Thermogravimetric Analysis. J. Non-Cryst. Solids 2015, 408, 37–42. [Google Scholar] [CrossRef]
- Hagita, K.; Morita, H.; Doi, M.; Takano, H. Coarse-Grained Molecular Dynamics Simulation of Filled Polymer Nanocomposites under Uniaxial Elongation. Macromolecules 2016, 49, 1972–1983. [Google Scholar] [CrossRef]
- Fu, Y.; Michopoulos, J.; Song, J.-H. Coarse-Grained Molecular Dynamics Simulations of Epoxy Resin during the Curing Process. Comput. Mater. Sci. 2015, 107, 24–32. [Google Scholar] [CrossRef]
- Huo, R.; Zhang, Z.; Athir, N.; Fan, Y.; Liu, J.; Shi, L. Designing High Thermal Conductivity of Cross-Linked Epoxy Resin via Molecular Dynamics Simulations. Phys. Chem. Chem. Phys. 2020, 22, 19735–19745. [Google Scholar] [CrossRef]
- Fan, H.B.; Yuen, M.M.F. Material Properties of the Cross-Linked Epoxy Resin Compound Predicted by Molecular Dynamics Simulation. Polymer 2007, 48, 2174–2178. [Google Scholar] [CrossRef]
- D’Escamard, G.; De Rosa, C.; Auriemma, F. Predicting the Glass Transition Temperature as Function of Crosslink Density and Polymer Interactions in Rubber Compounds; AIP Publishing: Naples, Italy, 2016; p. 020176. [Google Scholar]
- Yang, Q.; Chen, X.; He, Z.; Lan, F.; Liu, H. The Glass Transition Temperature Measurements of Polyethylene: Determined by Using Molecular Dynamic Method. RSC Adv. 2016, 6, 12053–12060. [Google Scholar] [CrossRef]
- Donth, E.-J. The Glass Transition: Relaxation Dynamics in Liquids and Disordered Materials; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2001; ISBN 978-3-540-41801-6. [Google Scholar]
- Alamfard, T.; Lorenz, T.; Breitkopf, C. Thermal Conductivities of Uniform and Random Sulfur Crosslinking in Polybutadiene by Molecular Dynamic Simulation. Polymers 2023, 15, 2058. [Google Scholar] [CrossRef] [PubMed]
- Thompson, A.P.; Aktulga, H.M.; Berger, R.; Bolintineanu, D.S.; Brown, W.M.; Crozier, P.S.; in ’t Veld, P.J.; Kohlmeyer, A.; Moore, S.G.; Nguyen, T.D.; et al. LAMMPS—A Flexible Simulation Tool for Particle-Based Materials Modeling at the Atomic, Meso, and Continuum Scales. Comput. Phys. Commun. 2022, 271, 108171. [Google Scholar] [CrossRef]
- Kubo, R.; Toda, M.; Hashitsume, N.; Saito, N. Statistical Physics II: Nonequilibrium Statistical Mechanics; Springer: Berlin/Heidelberg, Germany, 1985. [Google Scholar]
- McQuarrie, D.A. Mathematical Methods for Scientists and Engineers; University Science Books: Herndon, VA, USA, 2003; ISBN 978-1-891389-24-5. [Google Scholar]
- Ladd, A.J.C.; Moran, B.; Hoover, W.G. Lattice Thermal Conductivity: A Comparison of Molecular Dynamics and Anharmonic Lattice Dynamics. Phys. Rev. B 1986, 34, 5058–5064. [Google Scholar] [CrossRef] [PubMed]
- Kumar, A.; Sundararaghavan, V.; Browning, A.R. Study of Temperature Dependence of Thermal Conductivity in Cross-Linked Epoxies Using Molecular Dynamics Simulations with Long Range Interactions. Model. Simul. Mater. Sci. Eng. 2014, 22, 025013. [Google Scholar] [CrossRef]
- Jewett, A.I.; Stelter, D.; Lambert, J.; Saladi, S.M.; Roscioni, O.M.; Ricci, M.; Autin, L.; Maritan, M.; Bashusqeh, S.M.; Keyes, T.; et al. Moltemplate: A Tool for Coarse-Grained Modeling of Complex Biological Matter and Soft Condensed Matter Physics. J. Mol. Biol. 2021, 433, 166841. [Google Scholar] [CrossRef]
- Dai, L.; Rutkevych, P.P.; Chakraborty, S.; Wu, G.; Ye, J.; Lau, Y.H.; Ramanarayan, H.; Wu, D.T. Molecular Dynamics Simulation of Octacosane for Phase Diagrams and Properties via the United-Atom Scheme. Phys. Chem. Chem. Phys. 2021, 23, 21262–21271. [Google Scholar] [CrossRef]
- Martínez, L.; Andrade, R.; Birgin, E.G.; Martínez, J.M. PACKMOL: A Package for Building Initial Configurations for Molecular Dynamics Simulations. J. Comput. Chem. 2009, 30, 2157–2164. [Google Scholar] [CrossRef]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Vasilev, A.; Lorenz, T.; Kamble, V.G.; Wießner, S.; Breitkopf, C. Thermal Conductivity of Polybutadiene Rubber from Molecular Dynamics Simulations and Measurements by the Heat Flow Meter Method. Materials 2021, 14, 7737. [Google Scholar] [CrossRef]
- Nosé, S. A Molecular Dynamics Method for Simulations in the Canonical Ensemble. Mol. Phys. 1984, 52, 255–268. [Google Scholar] [CrossRef]
- Hoover, W.G. Canonical Dynamics: Equilibrium Phase-Space Distributions. Phys. Rev. A 1985, 31, 1695–1697. [Google Scholar] [CrossRef] [PubMed]
- Schneider, T.; Stoll, E. Molecular-Dynamics Study of a Three-Dimensional One-Component Model for Distortive Phase Transitions. Phys. Rev. B 1978, 17, 1302–1322. [Google Scholar] [CrossRef]
- Bai, L.; Zhao, X.; Bao, R.-Y.; Liu, Z.-Y.; Yang, M.-B.; Yang, W. Effect of Temperature, Crystallinity and Molecular Chain Orientation on the Thermal Conductivity of Polymers: A Case Study of PLLA. J. Mater. Sci. 2018, 53, 10543–10553. [Google Scholar] [CrossRef]
- Gregg, E.C., Jr.; Lattimer, R.P. Polybutadiene Vulcanization. Chemical Structures from Sulfur-Donor Vulcanization of an Accurate Model. Rubber Chem. Technol. 1984, 57, 1056–10971. [Google Scholar] [CrossRef]
- Luo, Z.; Yang, Z.; Fei, Z.; Li, K. Effect of Crosslinking Rate on the Glass Transition Temperature of Polyimide Cross-Linked Silica Aerogels. J. Polym. Res. 2020, 27, 255. [Google Scholar] [CrossRef]
- Nardelli, F.; Calucci, L.; Carignani, E.; Borsacchi, S.; Cettolin, M.; Arimondi, M.; Giannini, L.; Geppi, M.; Martini, F. Influence of Sulfur-Curing Conditions on the Dynamics and Crosslinking of Rubber Networks: A Time-Domain NMR Study. Polymers 2022, 14, 767. [Google Scholar] [CrossRef]
- Glass-Transition Temperature and Microstructure of Polybutadienes. Available online: https://ouci.dntb.gov.ua/en/works/4ben3zv7/ (accessed on 22 January 2024).



| Force Field Parameters for Polybutadiene Crosslinked with Sulfur | ||
|---|---|---|
| 0.209 | 3.723 | |
| 0.172 | 3.723 | |
| 0.170 | 3.673 | |
| 0.128 | 3.525 | |
| 0.250 | 3.550 | |
| 0.250 | 3.550 | |
| 317.0 | 1.500 | |
| 260.0 | 1.526 | |
| 317.0 | 1.500 | |
| 222.0 | 1.810 | |
| 70.0 | 118.0 | |
| 68.0 | 103.7 | |
| 62.0 | 98.9 | |
| 62.0 | 98.9 | |
| --- | --- | |
| --- | --- | |
| --- | --- | |
| --- | --- | |
| Type of Sulfur | Number of Sulfur Chains | Number of Sulfur Atoms in the Structure | PB Content (phr) | Sulfur Content (phr) | Molar Mass of Sulfur (g/mol) |
|---|---|---|---|---|---|
| Mono-sulfur (S1) | 396 | 396 | 96.5 | 3.5 | 12,697 |
| Di-sulfur (S2) | 396 | 792 | 93.0 | 7.0 | 25,395 |
| Tri-sulfur (S3) | 396 | 1188 | 89.5 | 10.5 | 38,093 |
| Tetra-sulfur (S4) | 396 | 1584 | 86.0 | 14.0 | 50,790 |
| Penta-sulfur (S5) | 396 | 1980 | 82.5 | 17.5 | 63,488 |
| Hexa-sulfur (S6) | 396 | 2376 | 79.0 | 21.0 | 76,186 |
| Hepta-sulfur (S7) | 396 | 2772 | 75.5 | 24.5 | 88,884 |
| Octa-sulfur (S8) | 396 | 3168 | 72.0 | 28.0 | 101,581 |
| Number of Sulfur Atoms | S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 |
|---|---|---|---|---|---|---|---|---|
| Thermal Conductivity (W/m·K) | 0.176 | 0.189 | 0.185 | 0.189 | 0.195 | 0.201 | 0.204 | 0.213 |
| Type of Sulfur | Number of Sulfur Chains | Number of Sulfur Atoms in the Structure | Molar Mass of Sulfur (g/mol) |
|---|---|---|---|
| Mono-sulfur (S1) | 396 | 396 | 12,697 |
| Di-sulfur (S2) | 198 | 396 | 12,697 |
| Tri-sulfur (S3) | 132 | 396 | 12,697 |
| Tetra-sulfur (S4) | 99 | 396 | 12,697 |
| Penta-sulfur (S5) | 79 | 395 | 12,665 |
| Hexa-sulfur (S6) | 66 | 396 | 12,697 |
| Hepta-sulfur (S7) | 57 | 399 | 12,793 |
| Octa-sulfur (S8) | 50 | 400 | 12,826 |
| Number of Sulfur Atoms | S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 |
|---|---|---|---|---|---|---|---|---|
| Thermal Conductivity (W/m·K) | 0.186 | 0.192 | 0.191 | 0.189 | 0.187 | 0.189 | 0.194 | 0.190 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alamfard, T.; Lorenz, T.; Breitkopf, C. Glass Transition Temperatures and Thermal Conductivities of Polybutadiene Crosslinked with Randomly Distributed Sulfur Chains Using Molecular Dynamic Simulation. Polymers 2024, 16, 384. https://doi.org/10.3390/polym16030384
Alamfard T, Lorenz T, Breitkopf C. Glass Transition Temperatures and Thermal Conductivities of Polybutadiene Crosslinked with Randomly Distributed Sulfur Chains Using Molecular Dynamic Simulation. Polymers. 2024; 16(3):384. https://doi.org/10.3390/polym16030384
Chicago/Turabian StyleAlamfard, Tannaz, Tommy Lorenz, and Cornelia Breitkopf. 2024. "Glass Transition Temperatures and Thermal Conductivities of Polybutadiene Crosslinked with Randomly Distributed Sulfur Chains Using Molecular Dynamic Simulation" Polymers 16, no. 3: 384. https://doi.org/10.3390/polym16030384
APA StyleAlamfard, T., Lorenz, T., & Breitkopf, C. (2024). Glass Transition Temperatures and Thermal Conductivities of Polybutadiene Crosslinked with Randomly Distributed Sulfur Chains Using Molecular Dynamic Simulation. Polymers, 16(3), 384. https://doi.org/10.3390/polym16030384










