Computational Analysis of Mechanical Properties in Polymeric Sandwich Composite Materials
Abstract
1. Introduction
2. Materials and Methods
2.1. First Step: Preparation of the Input Material
2.2. Second Step: Preparation of Composite Laminates
2.3. Third Step: Preparation of the Finished Product from Composite Laminates
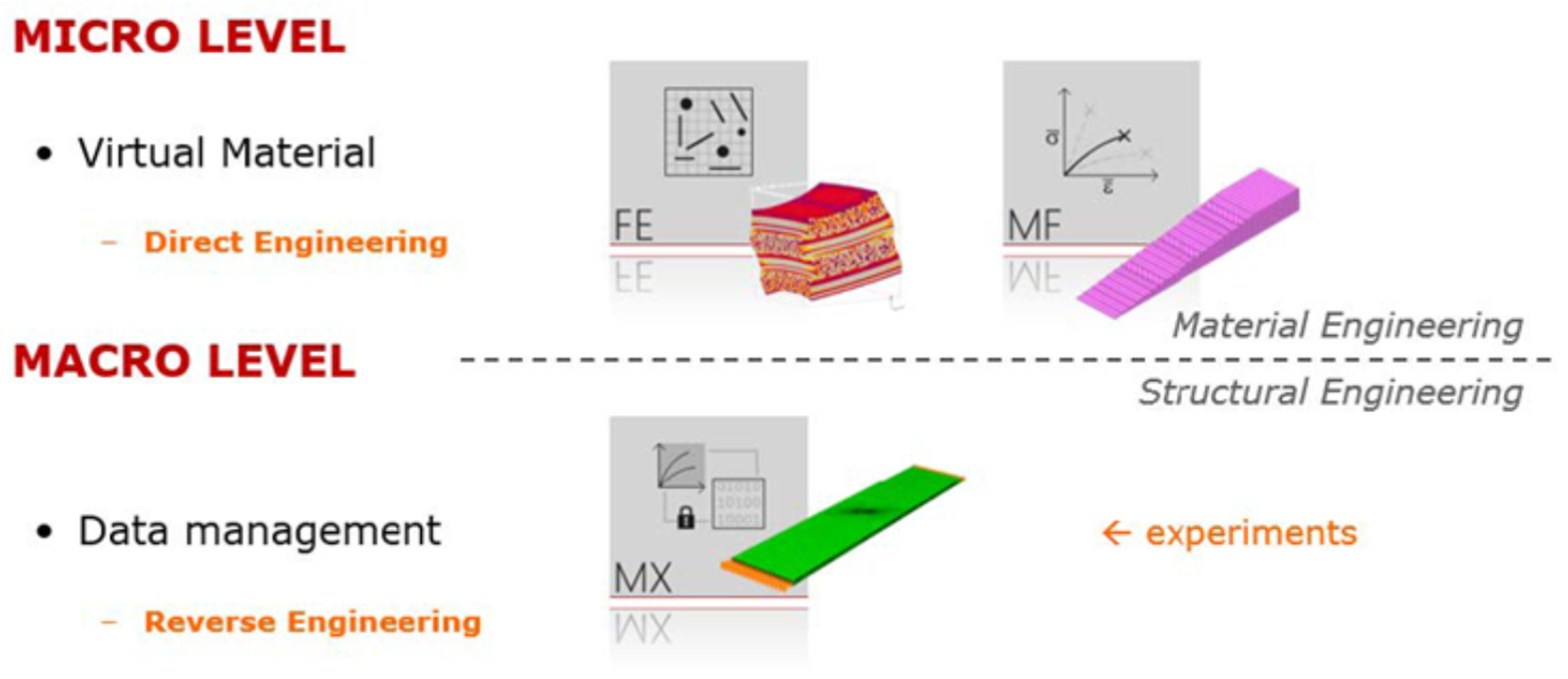
2.4. Modeling of Composite Materials
- macro material point: center of the representative volume element (RVE);
- on a microscale: the RVE contains a finite number of components;
- a constitutive model is needed for each of the components;
- micro/macro transition: homogenization method to find the macro-constitutive response of the RVE;
- Tools: A set of interoperable software products aimed at professional use for material or structural engineering purposes (MF, FE, MAP, CAE) (Figure 4).
- Solutions: Use of Digimat technology in a fully integrated GUI-controlled environment for specific tasks (RP, VA, AM).
- Expertise: Knowledge transfer from 10+ years of experience in micromechanical modeling. It includes a documentation file and a collection of examples.
2.5. Design of a Composite Part for a Luggage Compartment
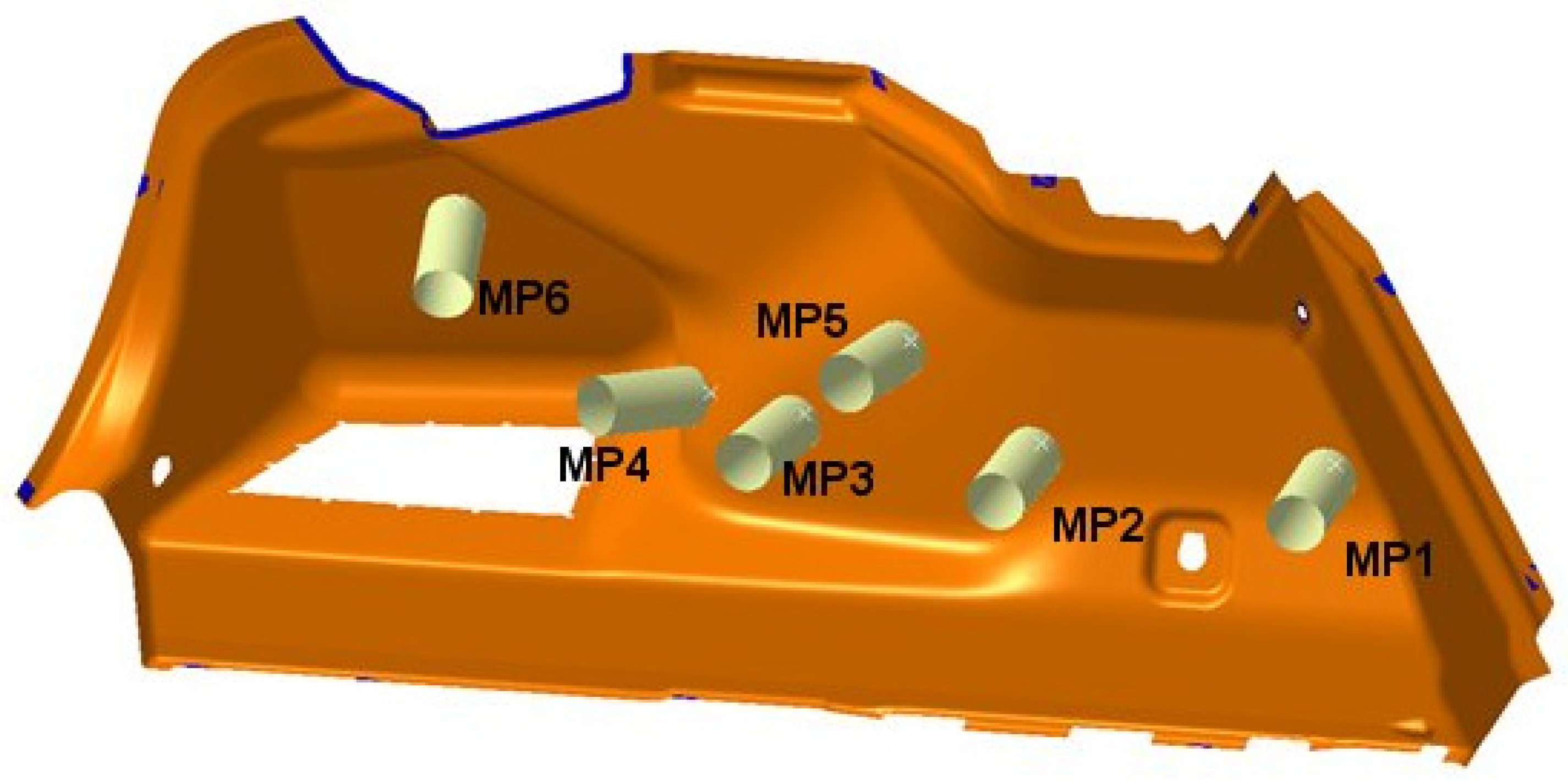
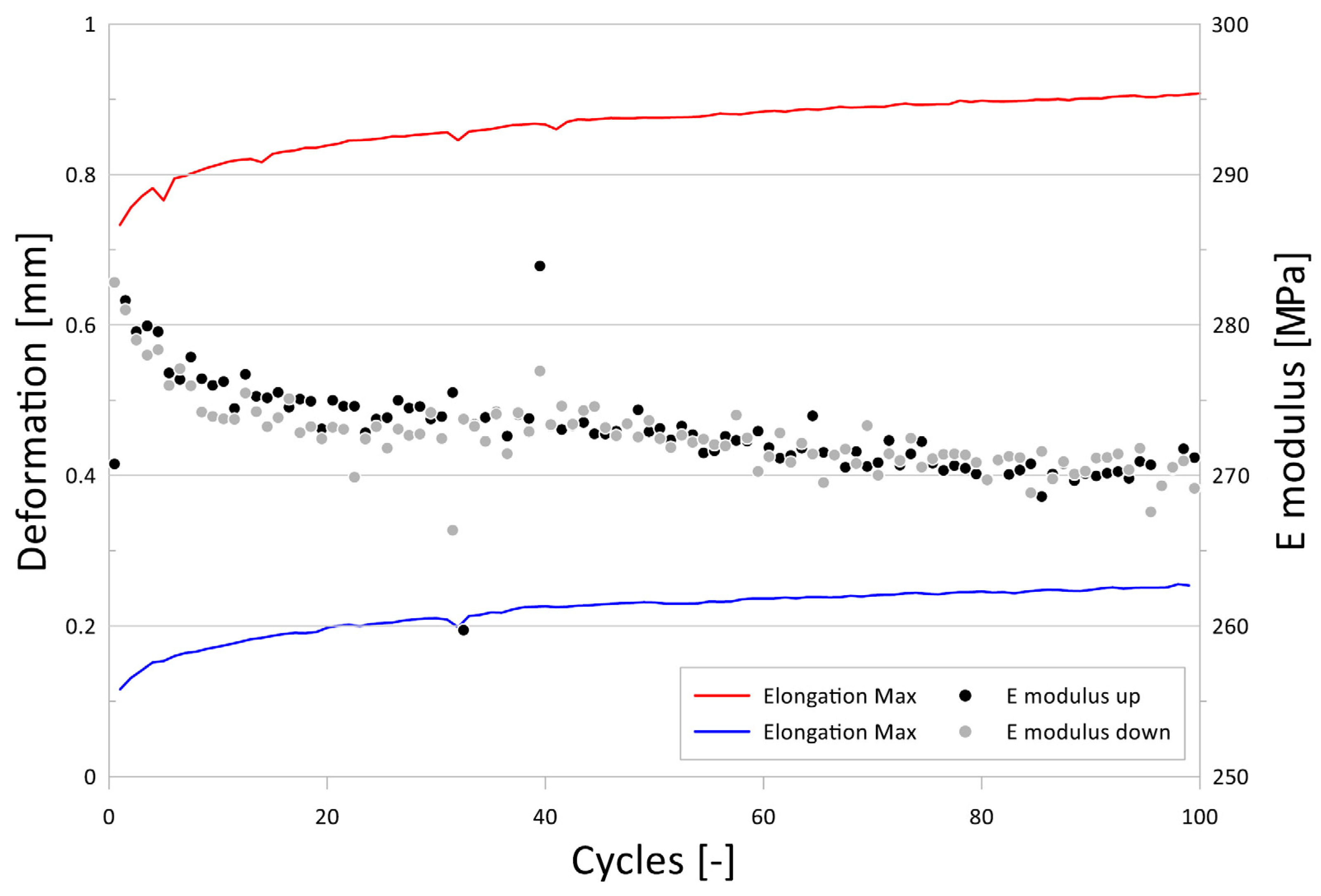
2.6. Tests for the Experimental Verification of the Calculated Values
3. Results and Discussion
3.1. Analysis of the Geometric Surface for a Quality Compartment
- checking the connection of surfaces—the design of surfaces takes place in special programs for creating designs such as, for example, Maya/Autedesk, where the output surface must be further modified for the needs of FEM. The most important parameter is the “connexity check” to 0.001 mm. This treatment of the surfaces will prevent the overlapping of the surfaces as well as remove the micro-gaps between the surfaces;
- creating a central zero surface; then, the ability of the surface to offset the required thickness is checked in both directions. Here, it is necessary to replace problematic surfaces with new ones, similar in shape to the original design;
- due to the production technology for the side lining, there is a difference in material thickness. The expected course of the material thickness in the final product needs to be defined for the FEM model. Figure 10 shows the model.
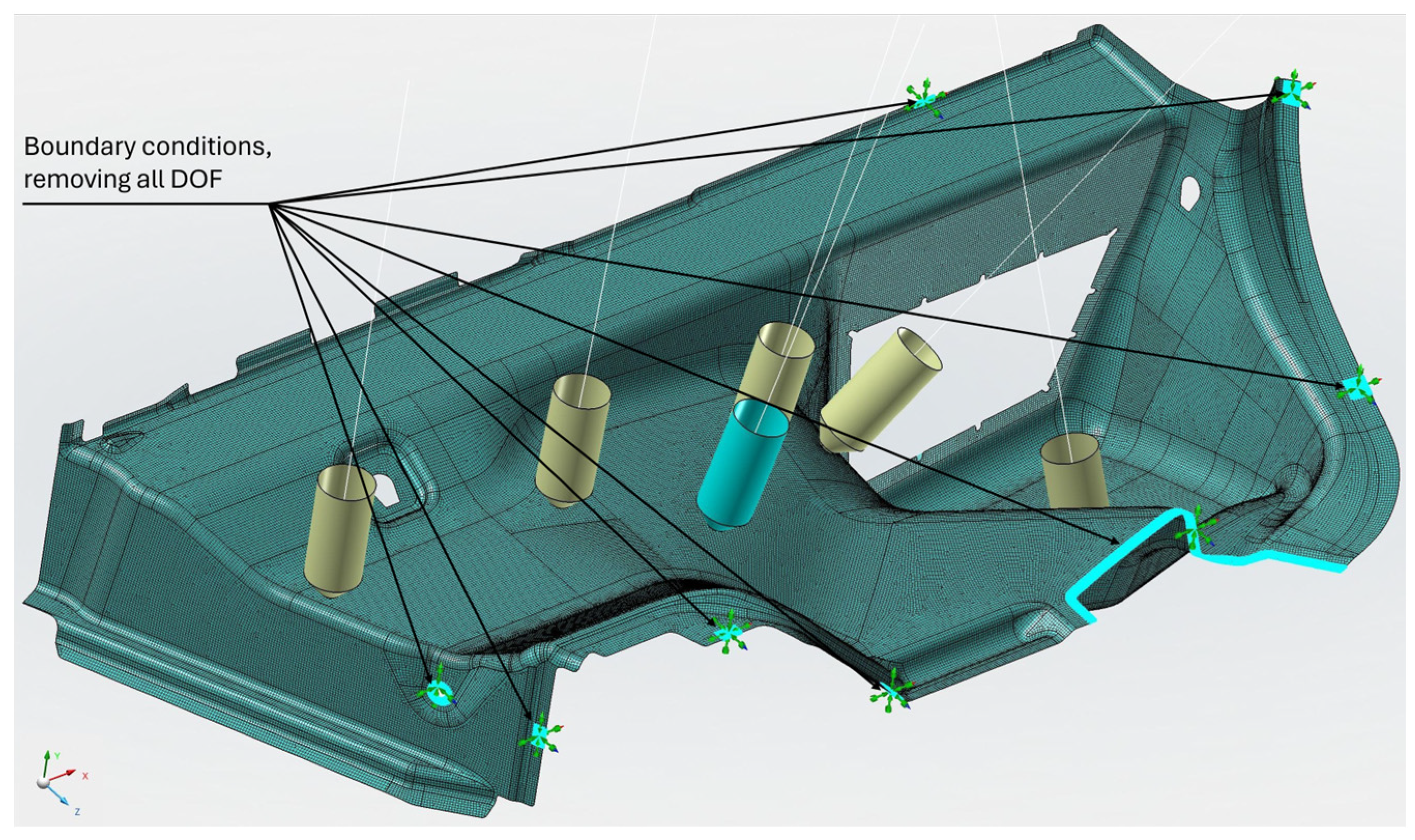
3.2. FEM Analysis of the Model for the Luggage Compartment
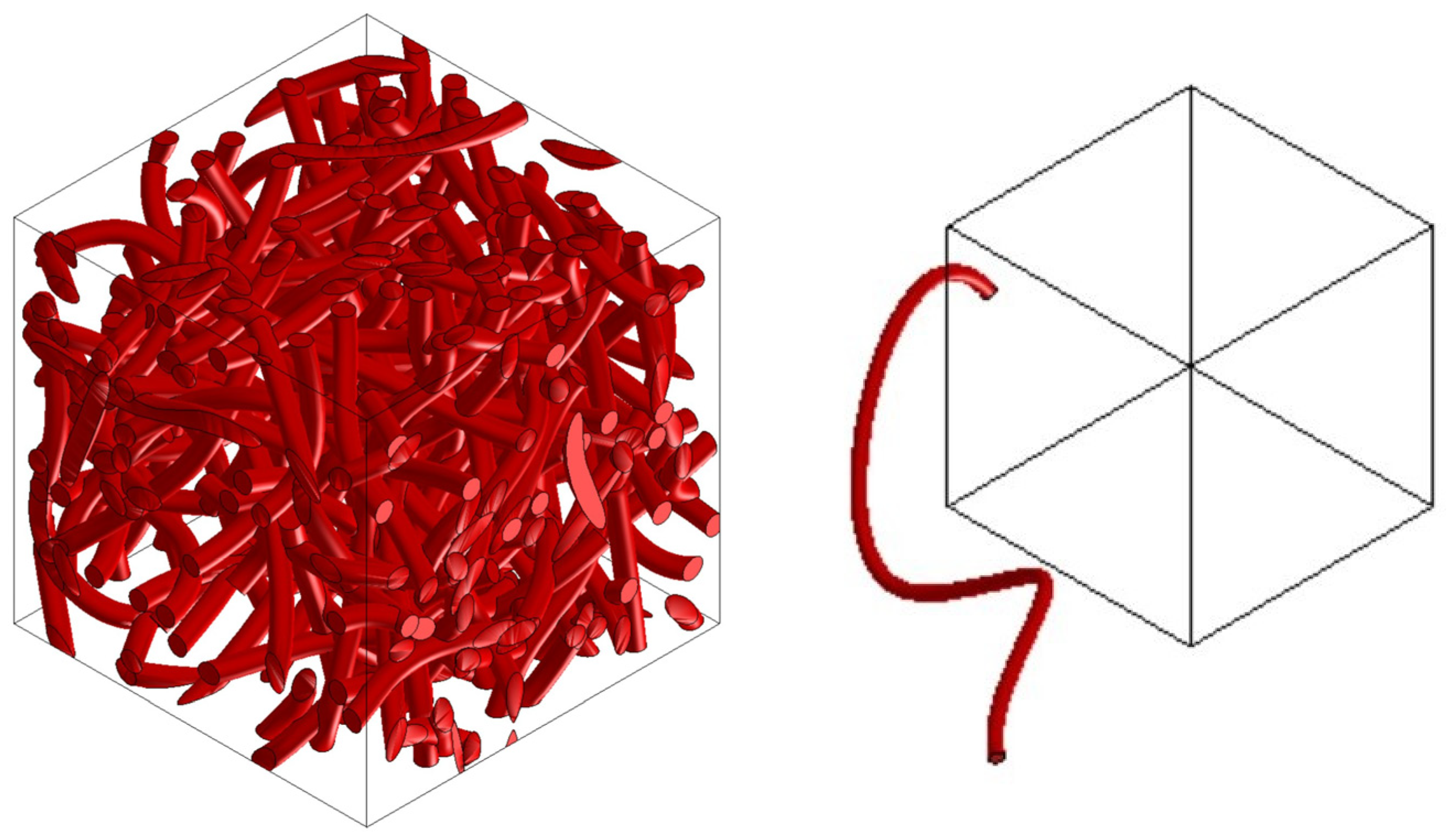
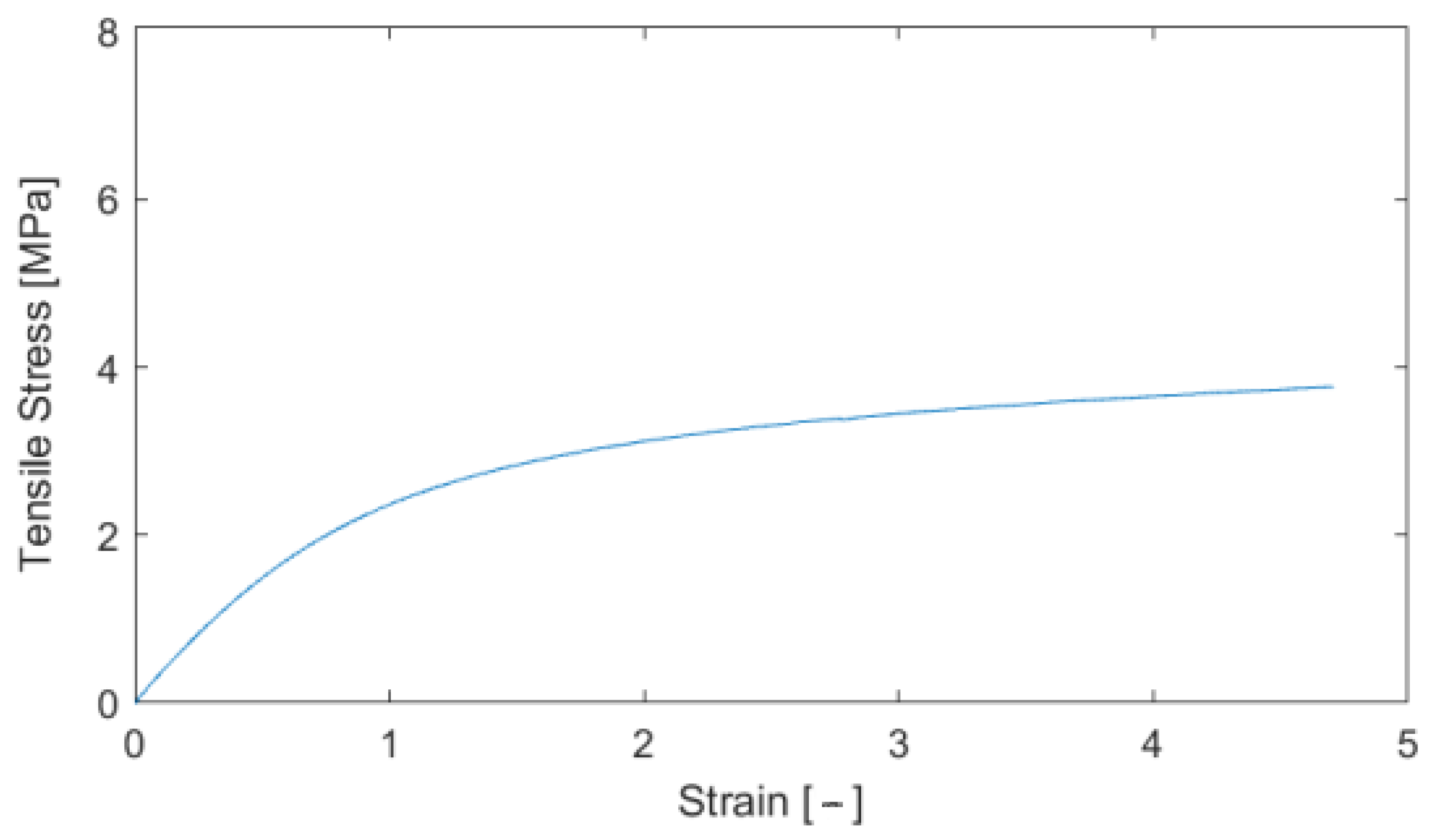
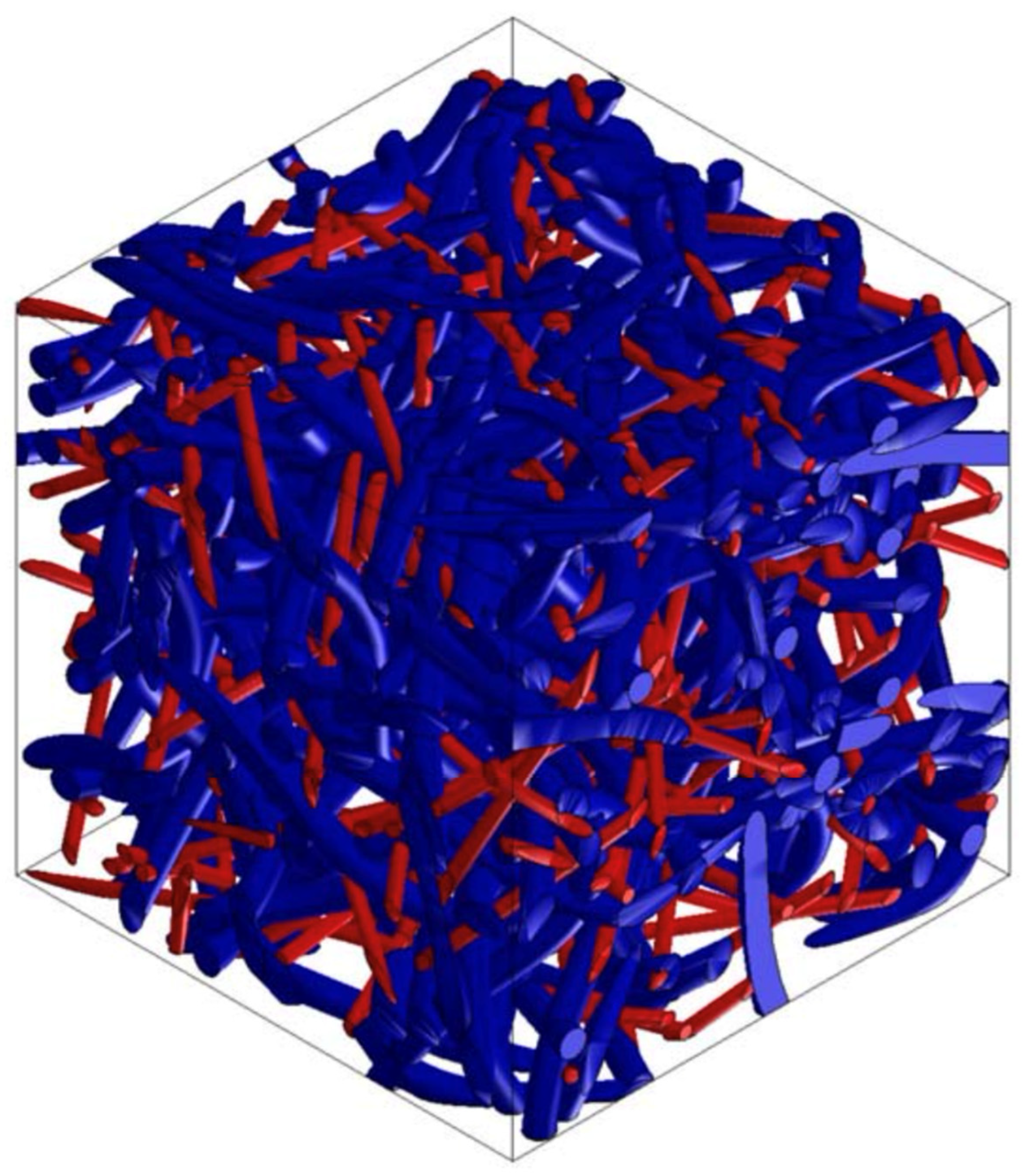
- Material preparation was performed using MSC.Digimat FE. The standard material used in the design of these components was a combination of PP/PET fibers in a ratio of 50:50. A material with a thickness of 5 mm and a density of up to 450 kg/m3 was designed for this component. After defining the basic material properties (Table 1), the type, shape, and dimensions of the volume elements were defined. Subsequently, the RVE was generated (Figure 13). To obtain the properties of the composite, a finite element mesh of the RVE model was generated using 512,000 elements and 531,444 nodes (Figure 14). Using the function “Automatic properties evaluation”, six loading steps were applied by Digimat FE to the prepared FEM model to obtain all the material properties (Table 2). As a solver, the MSC Marc CASI Iterative solver was selected, and the contact algorithm node-to-segment was applied.
3.3. Experimental Verification of Calculated Values
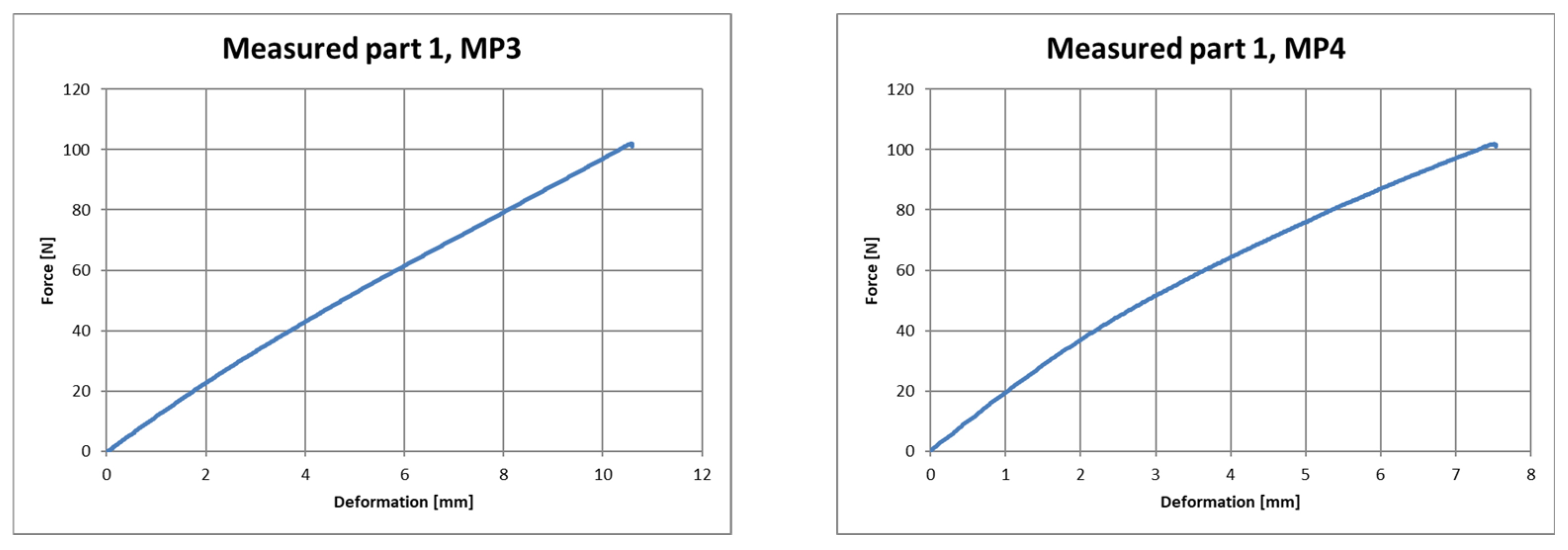
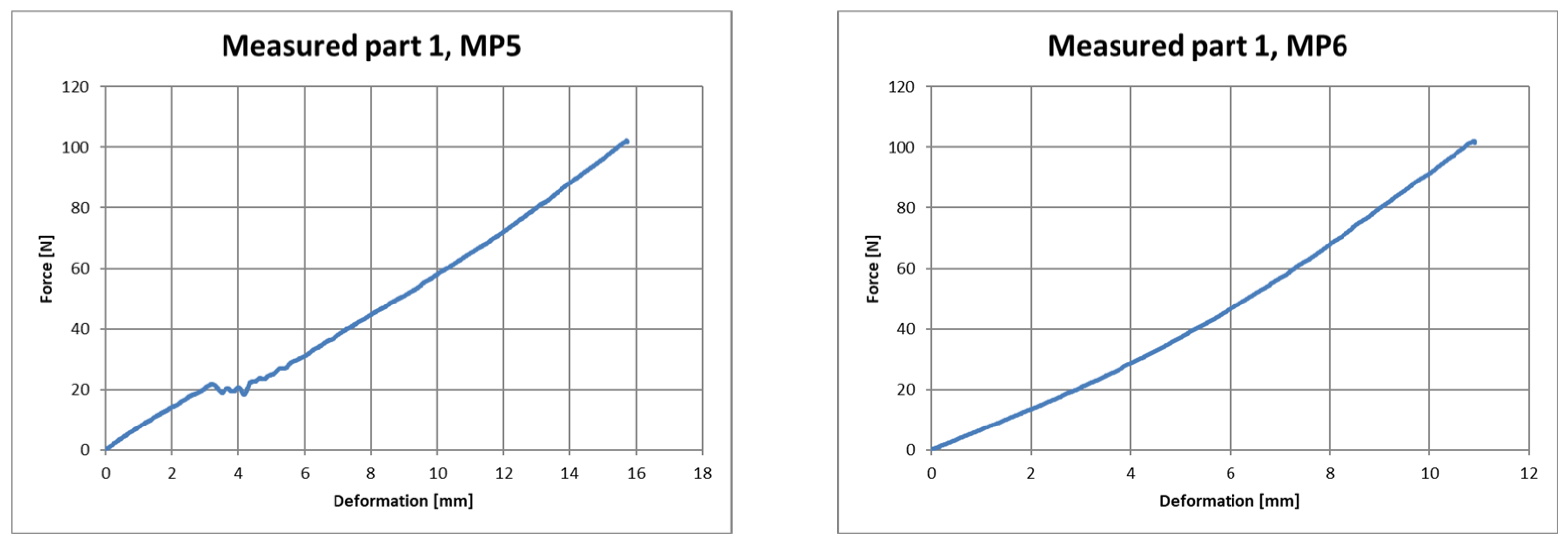
3.4. Comparison of Measured Data and Calculated Values
3.5. PP/PET/Cotton Material Design
3.6. PP/PET/Glass Fiber-Based Material Design
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hagnell, M.; Kumaraswamy, S.; Nyman, T.; Åkermo, M. From aviation to automotive—A study on material selection and its implication on cost and weight efficient structural composite and sandwich designs. Heliyon 2020, 6, e03716. [Google Scholar] [CrossRef]
- Stylios, G.K. Novel Smart Textiles. Materials 2020, 13, 950. [Google Scholar] [CrossRef] [PubMed]
- Irez, A.B.; Bayraktar, E.; Miskioglu, I. Fracture Toughness Analysis of Epoxy-Recycled Rubber-Based Composite Reinforced with Graphene Nanoplatelets for Structural Applications in Automotive and Aeronautics. Polymers 2020, 12, 448. [Google Scholar] [CrossRef]
- Šteininger, J.; Hrček, S.; Smetanka, L.; Skyba, R. Optimisation procedure of inner geometry in spherical roller bearings with regard to their durability. Sci. J. Silesian Univ. Technol. Ser. Transp. Access 2020, 106, 173–181. [Google Scholar] [CrossRef]
- Sharma, S.; Sudhakara, P.; Misra, S.; Singh, J. A comprehensive review of current developments on the waste-reinforced polymer- matrix composites for automotive, sports goods and construction applications: Materials, processes and properties. Mater. Today Proc. 2020, 33, 1671–1679. [Google Scholar] [CrossRef]
- Alhijazi, M.; Zeeshan, Q.; Qin, Z.; Safaei, B.; Asmael, M. Finite element analysis of natural fibers composites: A review. Nanotechnol. Rev. 2020, 9, 853–875. [Google Scholar] [CrossRef]
- Müller, U.; Jost, T.; Kurzböck, C.; Stadlmann, A.; Wagner, W.; Kirschbichler, S.; Baumann, G.; Pramreiter, M.; Feist, F. Crash simulation of wood and composite wood for future automotive engineering. Wood Mater. Sci. Eng. 2019, 15, 312–324. [Google Scholar] [CrossRef]
- Lixandrão, K.C.D.L.; Ferreira, F.F. Polypropylene and tire powder composite for use in automotive industry. Heliyon 2019, 5, e02405. [Google Scholar] [CrossRef] [PubMed]
- Bašťovanský, R.; Konstantová, V.; Bronček, J.; Kučera, Ľ. Flexural testing of carbon FLP composite bars with annular and square cross section. Prod. Eng. Arch. 2020, 26, 138–143. [Google Scholar] [CrossRef]
- Jędral, A. Review of Testing Methods Dedicated for Sandwich Structures with Honeycomb Core. Trans. Aerosp. Res. 2019, 2019, 1–14. [Google Scholar] [CrossRef]
- Ueki, Y. High-speed bending-fatigue testing of composite materials, 39th Risø International Symposium on Materials Science. IOP Publ. IOP Conf. Ser. Mater. Sci. Eng. 2018, 388, 012008. [Google Scholar] [CrossRef]
- Gautrelet, C.H.; Khalij, L.; Machado, M.R. Resonance track-and-dwell testing for crack length measurement on 304L stainless steel. Mech. Ind. 2020, 21, 617. [Google Scholar] [CrossRef]
- Chauhan, V.; Käki, T.; Varis, J. Review of natural fiber-reinforced engineering plastic composites, their applications in the transportation sector and processing techniques. J. Thermoplast. Compos. Mater. 2019, 35, 1169–1209. [Google Scholar] [CrossRef]
- Duan, S.Y.; Han, X.; Liu, G.R. Structural Optimization and Reliability Analysis of Automotive Composite Bumper Against Low-Velocity Longitudinal and Corner Pendulum Impacts. Int. J. Comput. Methods 2019, 16, 1841003. [Google Scholar] [CrossRef]
- Nunna, S.; Blanchard, P.; Buckmaster, D.; Davis, S.; Naebe, M. Development of a cost model for the productionof carbon fibres. Heliyon 2019, 5, e02698. [Google Scholar] [CrossRef] [PubMed]
- Datar, R.; Kim, S.; Jeon, S.; Hesketh, P.; Manalis, S.R.; Boisen, A.; Thundat, T. Cantilever Sensors: Nanomechanical Tools for Diagnostics. MRS Bull. 2009, 34, 449–454. [Google Scholar] [CrossRef]
- Bohayra, M.; Majid, B.; Bardon, J.; Ahzi, S. Modeling of two-phase random composite materials by finite element, Mori–Tanaka and strong contrast methods. Compos. Part B Eng. 2013, 45, 1117–1125. [Google Scholar]
- Gangloff, J., Jr.; Claire, D.; Suresh, G.A. A model of two-phase resin and void flow during composites processing. Int. J. Multiph. Flow 2014, 65, 51–60. [Google Scholar] [CrossRef]
- Avtar, S.; Siladitya, P. Multi-phase field modeling for various fracture mechanisms in composites. Eng. Fract. Mech. 2021, 241, 107348. [Google Scholar]
- Lu, X.; Hou, Y.; Tie, Y.; Li, C.; Zhang, C. Crack nucleation and propagation simulation in brittle two-phase perforated/particulate composites by a phase field model. Acta Mech. Sin. 2020, 36, 493–512. [Google Scholar] [CrossRef]
- Eshelby, J. The determination of the elastic field of an ellipsoidal inclusion and related problems. Proc. R. Soc. Lond. 1957, 241, 376–396. [Google Scholar]
- Hashin, Z.; Shtrikman, S. A variational approach to the theory of the effective magnetic permeability of multiphase materials. J. Appl. Phys. 1962, 33, 3125–3131. [Google Scholar] [CrossRef]
- Benveniste, Y. A new approach to the application of Mori-Tanaka theory in composite materials. Mech. Mater. 1987, 6, 147–157. [Google Scholar] [CrossRef]
- Mori, T.; Tanaka, K. Average stress in the matrix and average elastic energy of materials with misfitting inclusions. Acta Metall. Mater. 1973, 21, 571–574. [Google Scholar] [CrossRef]
- Yıldırım, F.; Demirel, B.; Bulucu, E.D. Investigation of the mechanical properties of calcite reinforced polypropylene by using digimat-mean field homogenization and ansys FEM. Mater. Today Commun. 2022, 33, 105023. [Google Scholar] [CrossRef]
- Yun, J.H.; Jeon, Y.J.; Kang, M.S. Effective Properties for the Design of Basalt Particulate-Polymer Composites. Polymers 2023, 15, 4125. [Google Scholar] [CrossRef] [PubMed]
- Yun, J.-H.; Jeon, Y.-J.; Kang, M.-S. Prediction of the Elastic Properties of Ultra High Molecular-Weight Polyethylene Particle-Reinforced Polypropylene Composite Materials through Homogenization. Appl. Sci. 2022, 12, 7699. [Google Scholar] [CrossRef]
- Ma, D.; González-Jiménez, Á.; Giglio, M.; Cougo, C.M.d.S.; Amico, S.C.; Manes, A. Multiscale modelling approach for simulating low velocity impact tests of aramid-epoxy composite with nanofillers. Eur. J. Mech. A Solids 2021, 90, 104286. [Google Scholar] [CrossRef]
- Rayhan, S.B.; Rahman, M.M. Modeling elastic properties of unidirectional composite materials using Ansys Material Designer. Procedia Struct. Integr. 2020, 28, 1892–1900. [Google Scholar] [CrossRef]
- Isaincu, A.; Dan, M.; Ungureanu, V.; Marsavina, L. Numerical investigation on the influence of fiber orientation mapping procedure to the mechanical response of short-fiber reinforced composites using Moldflow, Digimat and Ansys software. Mater. Today Proc. 2020, 45, 4304–4309. [Google Scholar] [CrossRef]
- Nayak, B.; Sahu, R.K. Experimental and digimat-FE based representative volume element analysis of exceptional graphene flakes/aluminium alloy nanocomposite characteristics. Mater. Res. Express 2019, 6, 116593. [Google Scholar] [CrossRef]
- Trzepieciński, T.; Ryzińska, G.; Biglar, M.; Gromada, M. Modelling of multilayer actuator layers by homogenisation technique using Digimat software. Ceram. Int. 2016, 43, 3259–3266. [Google Scholar] [CrossRef]
- PR 375; Steifigkeitsmessung an Gepäckraumverkleidungen. BMW: Munich, Germany, 2016.
- Nemat-Nasser, S.; Hori, M. Micromechanics: Overall Properties of Heterogeneous Solids; Elsevier Science: Amsterdam, The Netherlands, 1993. [Google Scholar]
- Verga, C. Enhancing Composite Material Structures Simulation with Multi-Scale Approach. Politecnico di Torino, Corso di Laurea Magistrale in Automotive Engineering (Ingegneria Dell’Autoveicolo). Master’s Thesis, Politecnico di Torino, Torino, Italy, 2020. [Google Scholar]
- Hexagon, A.B. Digimat MF User’s Guide, Heterogeneous Composite Materials. 2022. Available online: https://simcompanion.hexagon.com/customers/s/article/Digimat-Support-Home-Page (accessed on 29 February 2024).
- ASTM D 3039-00; Standard Test Method for Tensile Properties of Polymer Matrix Composite Materials. ASTM: West Conshohocken, PA, USA, 2014.
- ASTM D3479; Standard Test Method for Tention-Tension Fatigue of Polymer Matrix Composite Materials. ASTM: West Conshohocken, PA, USA, 2023.

















| Material | Modulus of Elasticity E [MPa] | Poisson’s Ratio µ | Density ρ [kg·m−3] | Fiber Diameter [mm] | Fiber Length [mm] |
|---|---|---|---|---|---|
| Polypropylene PP | 1450 | 0.4 | 910 | 0.025 | 10 |
| Thermoplastic polyester PET | 1300 | 0.4 | 1300 | 0.020 | 10 |
| Material | PP/PET 50:50 |
|---|---|
| Modulus of elasticity E11 [MPa] | 370.3 |
| Modulus of elasticity E22 [MPa] | 366 |
| Modulus of elasticity E33 [MPa] | 386.9 |
| Poisson’s ratio µ12 | 0.287 |
| Poisson’s ratio µ21 | 0.284 |
| Poisson’s ratio µ13 | 0.276 |
| Poisson’s ratio µ31 | 0.289 |
| Poisson’s ratio µ23 | 0.274 |
| Poisson’s ratio µ32 | 0.289 |
| Modulus of elasticity in shear G12 [MPa] | 139.5 |
| Modulus of elasticity in shear G23 [MPa] | 141.2 |
| Modulus of elasticity in shear G13 [MPa] | 142.4 |
| Bulk density ρ [kg·m−3] | 442.4 |
| a [mm] | b [mm] | L0 [mm] | E [MPa] | E_avg [MPa] | E_sd [MPa] | |
|---|---|---|---|---|---|---|
| Tensile test type I | 50.21 | 1.78 | 100 | 380 | 373 | 11.9 |
| 50.02 | 1.79 | 100 | 358 | |||
| 50.14 | 1.80 | 100 | 365 | |||
| 49.78 | 1.81 | 100 | 371 | |||
| 50.09 | 1.84 | 100 | 392 | |||
| 49.74 | 1.82 | 100 | 389 | |||
| 49.75 | 1.73 | 100 | 361 |
| a [mm] | b [mm] | L0 [mm] | E [MPa] | E_avg [MPa] | E_sd [MPa] | |
|---|---|---|---|---|---|---|
| Tensile test type II | 50.03 | 1.84 | 100 | 375 | 375 | 11.4 |
| 49.74 | 1.82 | 100 | 389 | |||
| 49.75 | 1.73 | 100 | 361 |
| MP1 | MP2 | MP3 | MP4 | MP5 | MP6 | |
|---|---|---|---|---|---|---|
| Measured deformation (mm) | 5.31 | 9.53 | 10.28 | 6.31 | 14.49 | 10.71 |
| Calculated deformation (mm) | 3.52 | 9.96 | 10.63 | 4.76 | 9.49 | 9.61 |
| Difference [%] | 33.71 | 4.51 | 3.40 | 24.56 | 34.51 | 9.34 |
| DIGIMAT FE | ||
|---|---|---|
| PP/PET/Cotton | 60/0/40 | 50/25/25 |
| Modulus of elasticity E11/E22/E33 [MPa] | 470/477/482 | 509/5121/556 |
| Poisson’s ratio µ12, µ23, µ31 | 0.27/0.26/0.26 | 0.28/0.28/0.26 |
| Modulus of elasticity in shear G12, G23, G31 [MPa] | 180/183/181 | 207/210/211 |
| Density ρ [kg·m−3] | 442 | 521 |
| DIGIMAT FE | |||
|---|---|---|---|
| PP/PET/glass fibers | 60/0/40 | 50/25/25 | 50/45/5 |
| Modulus of elasticity E11/E22/E33 [MPa] | 1809/1360/2302 | 1445/1360/1472 | 620/529/553 |
| Poisson’s ratio µ12, µ23, µ31 | 0.27/0.25/0.23 | 0.27/0.25/0.24 | 0.32/0.29/0.25 |
| Modulus of elasticity in shear G12, G23, G31 [MPa] | 854/962/771 | 579/577/576 | 247/231/241 |
| Density ρ [kg·m−3] | 640 | 651 | 527 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kohar, R.; Miskolci, J.; Pompas, L.; Kucera, L.; Stevko, P.; Petru, M.; Mishra, R.K. Computational Analysis of Mechanical Properties in Polymeric Sandwich Composite Materials. Polymers 2024, 16, 673. https://doi.org/10.3390/polym16050673
Kohar R, Miskolci J, Pompas L, Kucera L, Stevko P, Petru M, Mishra RK. Computational Analysis of Mechanical Properties in Polymeric Sandwich Composite Materials. Polymers. 2024; 16(5):673. https://doi.org/10.3390/polym16050673
Chicago/Turabian StyleKohar, Robert, Jaroslav Miskolci, Lukas Pompas, Lubos Kucera, Peter Stevko, Michal Petru, and Rajesh Kumar Mishra. 2024. "Computational Analysis of Mechanical Properties in Polymeric Sandwich Composite Materials" Polymers 16, no. 5: 673. https://doi.org/10.3390/polym16050673
APA StyleKohar, R., Miskolci, J., Pompas, L., Kucera, L., Stevko, P., Petru, M., & Mishra, R. K. (2024). Computational Analysis of Mechanical Properties in Polymeric Sandwich Composite Materials. Polymers, 16(5), 673. https://doi.org/10.3390/polym16050673








