Investigation of Cellulose-Based Materials Applied in Life Sciences Using Laser Light Scattering Methods
Abstract
:1. Introduction
2. Theory of the Light Scattering Phenomena
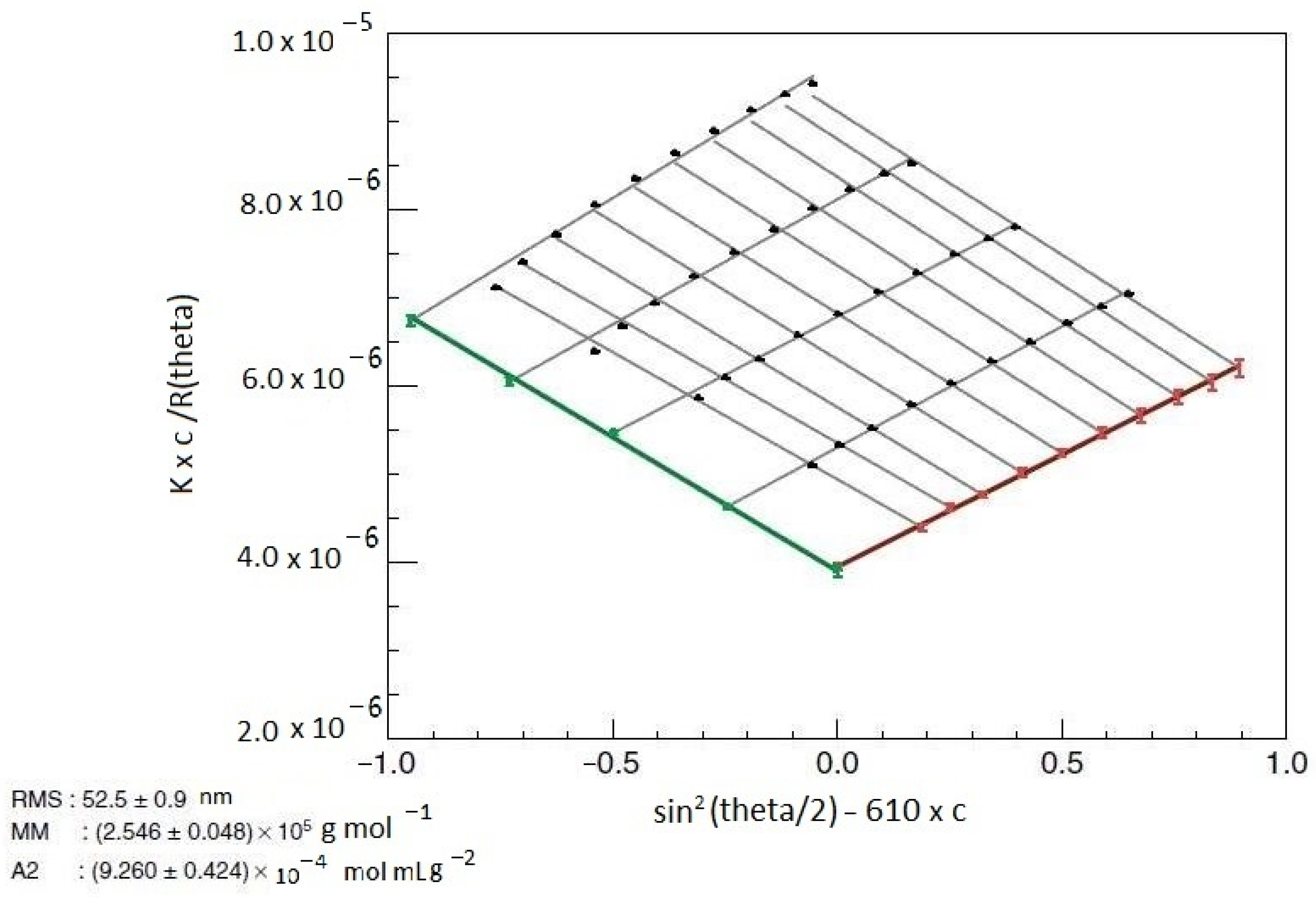
2.1. Static Light Scattering
2.2. Dynamic Light Scattering
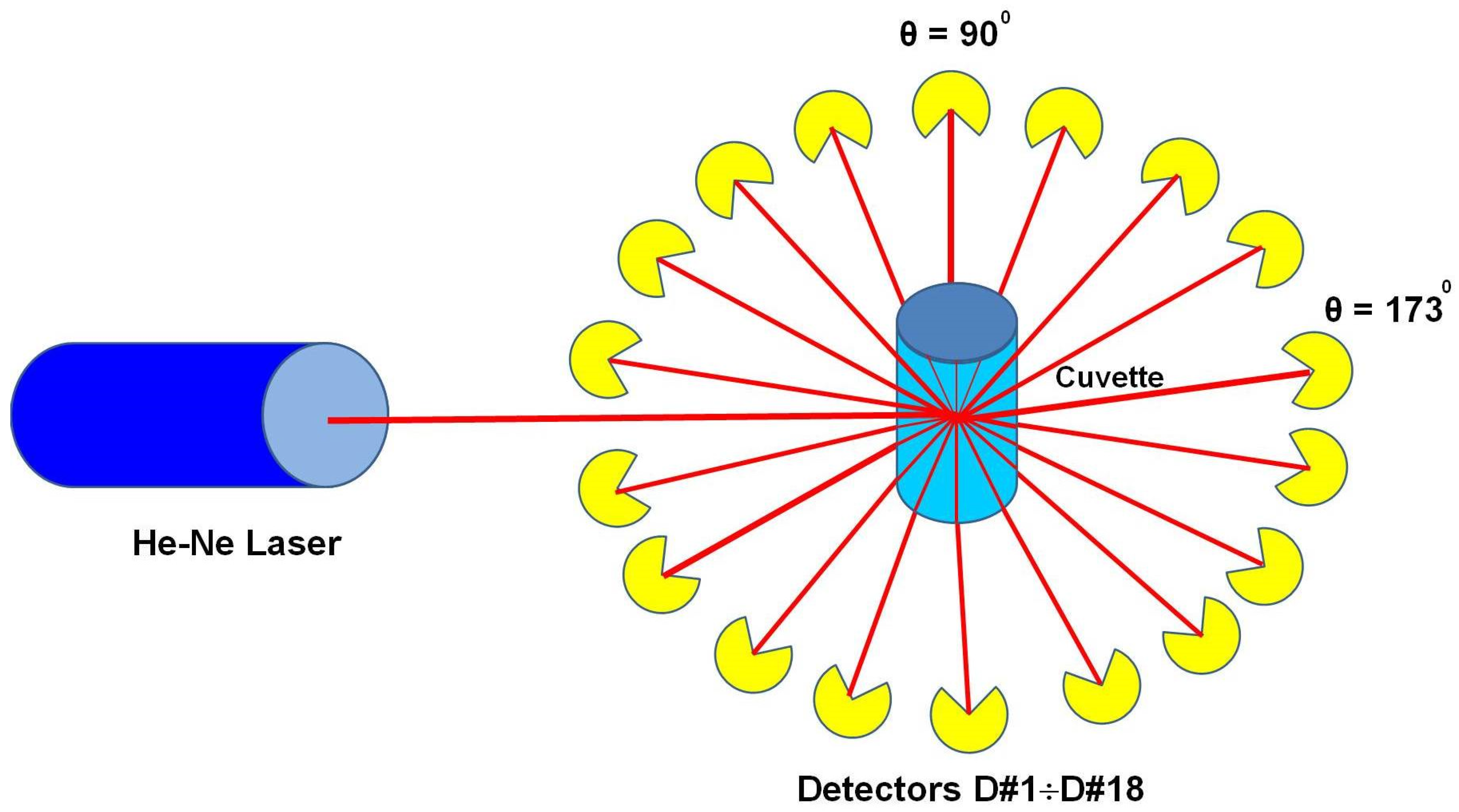
3. Laser Light Scattering Instrumentation and Detectors
4. Data Analysis of Light Scattering Signals
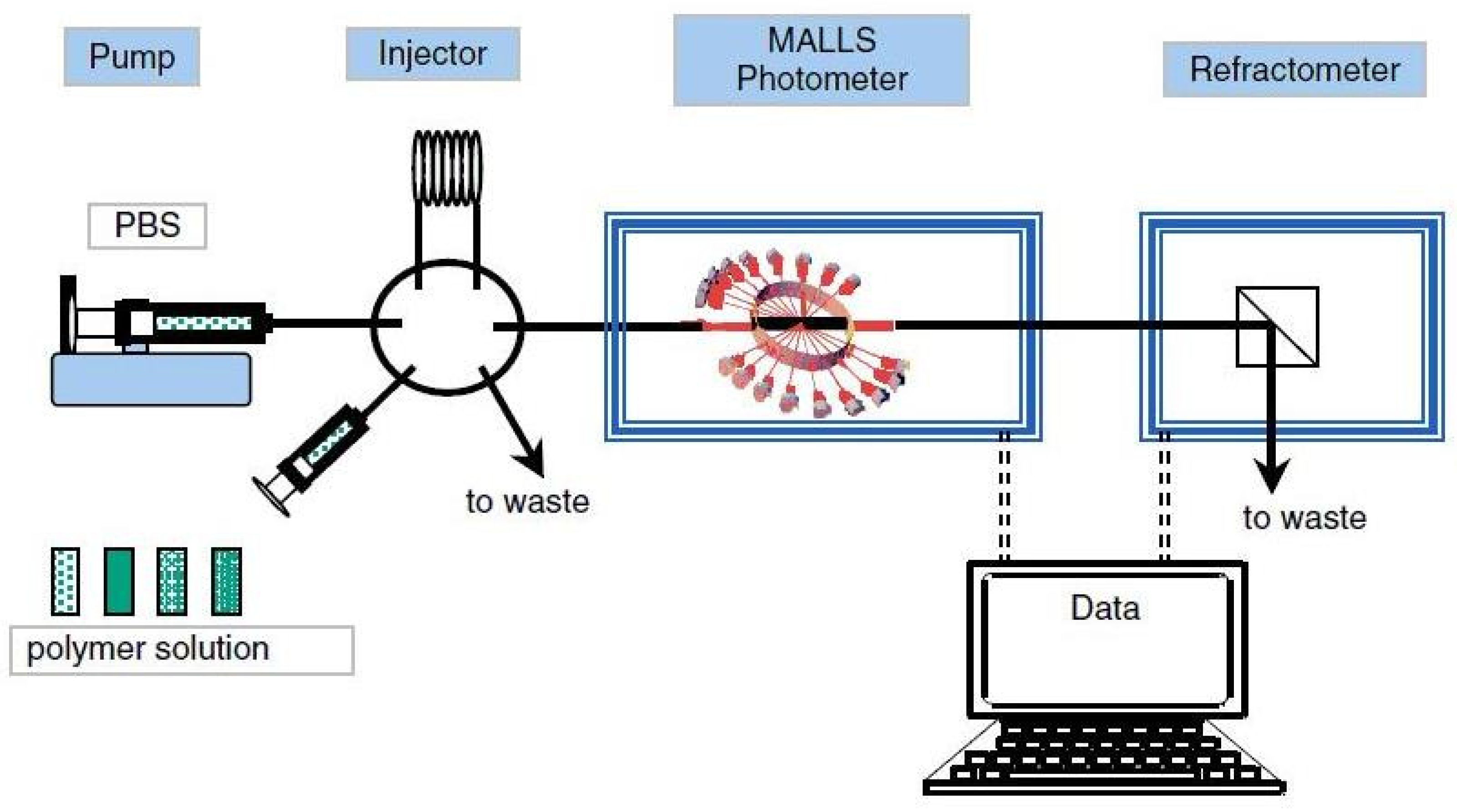
5. Detector-Coupling Techniques That Include a Light Scattering Detector
6. Molecular Weights, Particle Size, Molecular Weight Distributions, Particle Size Distributions, and Conformation for Cellulose-Based Materials in Various Solvents
6.1. Celluloses
6.2. Esters of Cellulose
6.3. Co-Esters of Cellulose
6.4. Alkyl Esters of Cellulose
6.5. Ethers of Cellulose
6.6. Other Heterogeneous Cellulose Derivatives
7. Applications of Cellulosic Materials in Life Sciences
7.1. Wastewater Treatment
7.2. Pharmaceutical Industry
7.3. Personal and Health Care Industry
7.4. Food-Packing Materials
7.5. Restoration of Heritage Objects
8. Conclusions and Future Perspectives
- In the case of cellulose-based materials, the optimization of the final properties is closely related to the specific parameters of the macromolecules in solution: the average molecular weights Mw, Mn, and Mv, the second virial coefficient A2, the radius of gyration Rg, the hydrodynamic radius Rh, the molecular weight distributions, the particle size distributions, and the conformation. These parameters are considered when the reproducibility of the polymer behavior in solution is sought.
- Determining the characteristic parameters of cellulosic compounds in solution using laser light scattering methods requires rigorous experimental conditions.
- Because no ideal GPC standards for molecular weights of cellulose-based materials are available, laser light scattering measurements are recommended in batch mode or online coupled mode as a function of the filtration grade and the polydispersity of the sample.
- Laser light scattering methods are absolute methods that provide direct information on cellulose-based materials. The main advantages of SLS and DLS are their high sensitivity, the possibility to use the same species before and after the experiment, and their compatibility with detectors like SEC, VISC, FFFF, UV-Vis, or dRI for completely characterizing macromolecules in solution. In addition, laser light scattering measurements allow the analysis of unfractionated samples in batch mode configuration. In practice, the molecular masses and MWDs from laser light scattering are compared with the values from viscometry and chromatography. Also, the Rg and Rh are compared with macromolecular sizes from TEM, AFM, or different theoretical models.
- A rigorous dissolution of cellulosic materials will prevent their aggregation in the solution at the molecular level and favor obtaining values as close as possible to reality for Mw, Rg, Rh, and A2. In practice, the solvents or binary solvent systems are used at temperatures close to room temperature (aprotic dipolar solvents with a small concentration of added LiCl; ionic liquids) or below 0 °C (aqueous solutions of urea/thiourea with the addition of NaOH or LiOH). In some cases, the pretreatment of cellulose is required to dissolve cellulose in appropriate solvents. The A2 values represent an indication for choosing the right solvent.
- Since dn/dc is part of the equation of static light scattering, experimentally determining this parameter as precisely as possible is recommended.
- Sample fractionation is recommended to ensure that monodisperse samples are obtained and the Rg, Rh, A2, Mw, and dn/dc values are determined with increased accuracy.
- When the light scattering detector is part of a chromatographic system, it is desired in the future to design new materials for chromatographic columns that can withstand for a long time the action of organic solvents usually used to dissolve cellulosic substances.
- If the intention is to compare the data obtained by several laboratories using laser light scattering or to confirm the data with those provided by other characterization methods, using the same experimental variables like solvent or the wavelength of the incident light would be ideal.
- Being biodegradable and biocompatible, cellulose-based materials are safely applied to living organisms. The practical applications of light scattering methods concern wastewater treatment, the pharmaceutical industry, the personal and healthcare industry, food-packing materials, and the restoration of heritage objects. To begin with, researchers were interested in light scattering studies regarding the solubility of cellulosic substances in various solvents and the phenomena of aggregation or self-assembly in solution. Other light scattering research has focused on the influence of different chemical and physical treatments on aging and implicitly on the depolymerization of cellulosic materials. Also, laser light scattering studies contributed to the elucidation of the interactions of cellulosic materials with various dispersants, plasticizers, surfactants, or inorganic particles in pharmaceutical and cosmetic formulas or drug delivery systems. Cellulose-based materials used as defoaming surfactants, adsorbents, and flocculants for pollutants, platforms for nanoparticle synthesis, and food packaging were also analyzed using laser light scattering.
Funding
Data Availability Statement
Conflicts of Interest
References
- Poletto, M.; Heitor, L.O., Jr.; Zattera, A.J. Native cellulose: Structure, characterization and thermal properties. Materials 2014, 7, 6105–6119. [Google Scholar] [CrossRef] [PubMed]
- Jonoobi, M.; Oladi, R.; Davoudpour, Y.; Oksman, K.; Dufresne, A.; Hamzeh, Y.; Davoodi, R. Different preparation methods and properties of nanostructured cellulose from various natural resources and residues: A review. Cellulose 2015, 22, 935–969. [Google Scholar] [CrossRef]
- Eichhorn, S.J.; Dufresne, A.; Aranguren, M.; Marcovich, N.E.; Capadona, J.R.; Rowan, S.J.; Weder, C.; Thielemans, W.; Roman, M.; Renneckar, S.; et al. Review: Current international research into cellulose nanofibers and nanocomposites. J. Mater. Sci. 2010, 45, 1–33. [Google Scholar] [CrossRef]
- Gatenholm, P.; Klemm, D. Bacterial nanocellulose as a renewable material for biomedical applications. MRS Bull. 2010, 35, 208–213. [Google Scholar] [CrossRef]
- Klemm, D.; Heublein, B.; Fink, H.P.; Bohn, A. Cellulose: Fascinating biopolymer and sustainable raw material. Angew. Chem. Int. Ed. 2005, 44, 3358–3393. [Google Scholar] [CrossRef]
- Ullah, H.; Santos, H.A.; Khan, T. Applications of bacterial cellulose in food, cosmetics and drug delivery. Cellulose 2016, 23, 2291–2314. [Google Scholar] [CrossRef]
- Shokri, J.; Adibki, K. Application of cellulose and cellulose derivatives in pharmaceutical industries. In Cellulose—Medical, Pharmaceutical and Electronic Applications; van de Ven, T., Godbout, L., Eds.; InTech: London, UK, 2013; pp. 47–66. [Google Scholar]
- Sun, Y.; Wang, J.; Li, D.; Cheng, F. The recent progress of the cellulose-based antibacterial hydrogel. Gels 2024, 10, 109. [Google Scholar] [CrossRef]
- Chen, C.; Xi, Y.; Weng, Y. Recent advances in cellulose-based hydrogels for tissue engineering applications. Polymers 2022, 14, 3335. [Google Scholar] [CrossRef]
- Nath, P.C.; Debnath, S.; Sharma, M.; Sridhar, K.; Nayak, P.K.; Inbaraj, B.S. Recent advances in cellulose-based hydrogels: Food applications. Foods 2023, 12, 350. [Google Scholar] [CrossRef]
- Singh, A.K.; Itkor, P.; Lee, Y.S. State-of-the-art insights and potential applications of cellulose-based hydrogels in food packaging: Advances towards sustainable trends. Gels 2023, 9, 433. [Google Scholar] [CrossRef]
- Nocca, G.; Arcovito, A.; Elkasabgy, N.A.; Basha, M.; Giacon, N.; Mazzinelli, E.; Abdel Maksoud, M.S.; Kamel, R. Cellulosic textiles—An appealing trend for different pharmaceutical applications. Pharmaceutics 2023, 15, 2738. [Google Scholar] [CrossRef] [PubMed]
- Omidian, H.; Akhzarmehr, A.; Chowdhury, S.D. Advancements in cellulose-based superabsorbent hydrogels: Sustainable solutions across industries. Gels 2024, 10, 174. [Google Scholar] [CrossRef] [PubMed]
- Ma, J.; Li, X.; Bao, Y. Advances in cellulose-based superabsorbent hydrogels. RSC Adv. 2015, 5, 59745. [Google Scholar] [CrossRef]
- Mikhailidi, A.; Volf, I.; Belosinschi, D.; Tofanica, B.-M.; Ungureanu, E. Cellulose-based metallogels—Part 2: Physico-chemical properties and biological stability. Gels 2023, 9, 633. [Google Scholar] [CrossRef] [PubMed]
- Teng, C.P.; Tan, M.Y.; Toh, J.P.W.; Lim, Q.F.; Wang, X.; Ponsford, D.; Lin, E.M.J.; Thitsartarn, W.; Tee, S.Y. Advances in cellulose-based composites for energy applications. Materials 2023, 16, 3856. [Google Scholar] [CrossRef]
- Wang, D.-C.; Lei, S.-N.; Zhong, S.; Xiao, X.; Guo, Q.-H. Cellulose-based conductive materials for energy and sensing applications. Polymers 2023, 15, 4159. [Google Scholar] [CrossRef] [PubMed]
- Kulicke, W.-M.; Clasen, C.; Lohman, C. Characterization of water-soluble cellulose derivatives in terms of the molar mass and particle size as well as their distribution. Macromol. Symp. 2005, 223, 151–174. [Google Scholar] [CrossRef]
- Budtova, T.; Navard, P. Cellulose in NaOH–water based solvents: A review. Cellulose 2016, 23, 5–55. [Google Scholar] [CrossRef]
- Dibrova, A.K.; Khanchich, O. Cellulose solutions in dipolar aprotic solvents. Polym. Sci. Ser. A 2010, 52, 1264–1269. [Google Scholar] [CrossRef]
- Moon, R.J.; Martini, A.; Nairn, J.; Simonsenf, J.; Youngblood, J. Cellulose nanomaterials review: Structure, properties and nanocomposites. Chem. Soc. Rev. 2011, 40, 3941–3994. [Google Scholar] [CrossRef]
- Terinte, N.; Ibbett, R.; Schuster, K.C. Overview on native cellulose and microcrystalline cellulose I structure studied by X-ray diffraction (WAXD): Comparison between measurements techniques. Lenzing. Berichte 2011, 89, 118–131. [Google Scholar]
- Ummartyotin, S.; Manuspiya, H. A critical review on cellulose: From fundamental to an approach on sensor technology. Renew. Sustain. Energy Rev. 2015, 41, 402–412. [Google Scholar] [CrossRef]
- Lang, P. Scattering Methods: Basic Principles and Application to Polymer and Colloidal Solutions, Part I, (Summer Term, 2004). Available online: https://www.yumpu.com/en/document/read/33367130/basic-principles-and-application-to-polymer-and-colloidal-solutions- (accessed on 28 March 2023).
- Braun, B.; Dorgan, J.R.; Chandler, J.P. Cellulosic nanowhiskers. Theory and application of light scattering from polydisperse spheroids in the Rayleigh-Gans-Debye regime. Biomacromolecules 2008, 9, 1255–1263. [Google Scholar] [CrossRef] [PubMed]
- Gao, W.; Liu, X.M.; Gross, R.A. Determination of molar mass and solution properties of cationic hydroxyethyl cellulose derivatives by multi-angle laser light scattering with simultaneous refractive index detection. Polym. Int. 2009, 58, 1115–1119. [Google Scholar] [CrossRef]
- Podzimek, S. Light Scattering, Size Exclusion Chromatography and Asymmetric Flow Field Flow Fractionation: Powerful Tools for Characterization of Polymers, Proteins and Nanoparticles; John Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Schäertl, W. Light Scattering from Polymer Solutions and Nanoparticle Dispersions; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Potthast, A.; Rosenau, T.; Buchner, R.; Röder, T.; Ebner, G.; Bruglachner, H.; Sixta, H.; Kosma, P. The cellulose solvent system N,N-dimethylacetamide/lithium chloride revisited: The effect of water on physicochemical properties and chemical stability. Cellulose 2002, 9, 41–53. [Google Scholar] [CrossRef]
- Lima, M.M.D.; Wong, J.T.; Paillet, M.; Borsali, R.; Pecora, R. Translational and rotational dynamics of rodlike cellulose whiskers. Langmuir 2003, 19, 24–29. [Google Scholar] [CrossRef]
- van der Zande, B.M.I.; Dhont, J.K.G.; Bohmer, M.R.; Philipse, A.P. Colloidal dispersions of gold rods characterized by dynamic light scattering and electrophoresis. Langmuir 2000, 16, 459–464. [Google Scholar] [CrossRef]
- de la Torre, J.G.; Carrasco, B. Intrinsic viscosity and rotational diffusion of bead models for rigid macromolecules and bioparticles. Eur. Biophys. J. 1998, 27, 549–557. [Google Scholar] [CrossRef]
- Broersma, S. Rotational diffusion constant of a cylindrical particle. J. Chem. Phys. 1960, 32, 1626–1631. [Google Scholar] [CrossRef]
- Broersma, S. Viscous force and torque constants for a cylinder. J. Chem. Phys. 1981, 74, 6989–6990. [Google Scholar] [CrossRef]
- de la Torre, J.G.; Bloomfield, V.A. Hydrodynamic properties of complex, rigid, biological macromolecules: Theory and applications. Q. Rev. Biophys. 1981, 14, 81–139. [Google Scholar] [CrossRef] [PubMed]
- Dreux, M.; Lafosse, M. Evaporative light scattering detection of carbohydrates in HPLC. In Carbohydrate Analysis: High Performance Liquid Chromatography and Capillary Electrophoresis; Journal of Chromatography Library Book Series; El Rassi, Z., Ed.; Elsevier: Amsterdam, The Netherlands, 1995; Volume 58. [Google Scholar]
- Douville, V.; Lodi, A.; Miller, J.; Nicolas, A.; Clarot, I.; Prilleux, B.; Megoulas, N.; Koupparis, M. Evaporative light scattering detection (ELSD): A tool for improved quality control of drug substances. Pharmeur. Sci. Notes 2006, 1, 9–15. [Google Scholar] [PubMed]
- Shakun, M.; Maier, H.; Heinze, T.; Kilz, P.; Radke, W. Molar mass characterization of sodium carboxymethyl cellulose by SEC-MALLS. Carbohyd. Polym. 2013, 95, 550–559. [Google Scholar] [CrossRef] [PubMed]
- Rashan, J., Jr.; Chen, R. Developing a versatile gradient elution LC/ELSD method for analyzing cellulose derivatives in pharmaceutical formulations. J. Pharmaceut. Biomed. Anal. 2007, 44, 23–28. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Liu, C.; Chen, Y.; Zhang, Z.; Zhu, A.; Qian, F. A high-sensitivity HPLC-ELSD method for HPMC-AS quantification and its application in elucidating the release mechanism of HPMC-AS based amorphous solid dispersions. Eur. J. Pharmaceut. Sci. 2018, 122, 303–310. [Google Scholar] [CrossRef] [PubMed]
- ASTRA for Windows User’s Guide, Version 4.90; Wyatt Technology Corporation: Santa Barbara, CA, USA, 2002.
- Gamelas, J.A.F.; Pedrosa, J.; Lourenc, A.F.; Mutjé, P.; González, I.; Chinga-Carrasco, G.; Singh, G.; Ferreir, P.J.T. On the morphology of cellulose nanofibrils obtained by TEMPO-mediated oxidation and mechanical treatment. Micron 2015, 72, 28–33. [Google Scholar] [CrossRef] [PubMed]
- Potthast, A.; Radosta, S.; Saake, B.; Lebioda, S.; Heinze, T.; Henniges, U.; Isogai, A.; Koschella, A.; Kosma, P.; Rosenau, T.; et al. Comparison testing of methods for gel permeation chromatography of cellulose: Coming closer to a standard protocol. Cellulose 2015, 22, 1591–1613. [Google Scholar] [CrossRef]
- Jeong, M.J.; Bogolitsyna, A.; Jo, B.M.; Kang, K.Y.; Rosenau, T.; Potthast, A. Deterioration of ancient Korean paper (Hanji), treated with beeswax: A mechanistic study. Carbohyd. Polym. 2014, 101, 1249–1254. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.M.; Gao, W.; Maziarz, E.P.; Salamone, J.C.; Duex, J.; Xia, E. Detailed characterization of cationic hydroxyethylcellulose derivatives using aqueous size-exclusion chromatography with on-line triple detection. J. Chromatogr. A 2006, 1104, 145–153. [Google Scholar] [CrossRef]
- Kacík, F.; Podzimek, S.; Vizarova, K.; Kacikova, D.; Cabalova, I. Characterization of cellulose degradation during accelerated ageing by SEC-MALS, SEC-DAD, and A4F-MALS methods. Cellulose 2016, 23, 357–366. [Google Scholar] [CrossRef]
- Guan, X.; Cueto, R.; Russo, P.; Qi, Y.; Wu, Q. Asymmetric flow field-flow fractionation with multiangle light scattering detection for characterization of cellulose nanocrystals. Biomacromolecules 2012, 13, 2671–2679. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Z.; Lu, A.; Zhou, J.; Zhang, L. Interaction between –OH groups of methylcellulose and solvent in NaOH/urea aqueous system at low temperature. Cellulose 2012, 19, 671–678. [Google Scholar] [CrossRef]
- Striegel, A.M.; Isenberg, S.L.; Cote, G.L. An SEC/MALS study of alternan degradation during size-exclusion chromatographic analysis. Anal. Bioanal. Chem. 2009, 394, 1887–1893. [Google Scholar] [CrossRef] [PubMed]
- Strlic, M.; Kolar, J. Size exclusion chromatography of cellulose in LiCl/N,N-dimethylacetamide. J. Biochem. Bioph. Meth. 2003, 56, 265–279. [Google Scholar] [CrossRef] [PubMed]
- Berggren, R.; Berthold, F.; Sjöholm, E.; Lindström, M. Improved methods for evaluating the molar mass distributions of cellulose in Kraft pulp. J. Appl. Polym. Sci. 2003, 88, 1170–1179. [Google Scholar] [CrossRef]
- Saito, T.; Yanagisawa, M.; Isogai, A. TEMPO-mediated oxidation of native cellulose: SEC–MALLS analysis of water-soluble and -insoluble fractions in the oxidized products. Cellulose 2005, 12, 305–315. [Google Scholar] [CrossRef]
- Dupont, A.-L.; Harrison, G. Conformation and dn/dc determination of cellulose in N,N-dimethylacetamide containing lithium chloride. Carbohyd. Polym. 2004, 58, 233–243. [Google Scholar] [CrossRef]
- Yanagisawa, M.; Shibata, I.; Isogai, A. SEC–MALLS analysis of cellulose using LiCl/1,3-dimethyl-2-imidazolidinone as an eluent. Cellulose 2004, 11, 169–176. [Google Scholar] [CrossRef]
- Yanagisawa, M.; Isogai, A. SEC−MALS−QELS study on the molecular conformation of cellulose in LiCl/amide solutions. Biomacromolecules 2005, 6, 1258–1265. [Google Scholar] [CrossRef]
- Lojewski, T.; Zieba, K.; Lojewska, J. Size exclusion chromatography and viscometry in paper degradation studies. New Mark-Houwink coefficients for cellulose in cupri-ethylenediamine. J. Chromatogr. A 2010, 1217, 6462–6468. [Google Scholar] [CrossRef]
- Yamamoto, M.; Kuramae, R.; Yanagisawa, M.; Ishii, D.; Isogai, A. Light-scattering analysis of native wood holocelluloses totally dissolved in LiCl–DMI solutions: High probability of branched structures in inherent cellulose. Biomacromolecules 2011, 12, 3982–3988. [Google Scholar] [CrossRef] [PubMed]
- Kes, M.; Christensen, B.E. Degradation of cellulosic insulation in power transformers: A SEC–MALLS study of artificially aged transformer papers. Cellulose 2013, 20, 2003–2011. [Google Scholar] [CrossRef]
- Pawcenis, D.; Thomas, J.L.; Lojewski, T.; Milczarek, J.M.; Lojewska, J. Towards determination of absolute molar mass of cellulose polymer by size exclusion chromatography with mulitple angle laser light scattering detection. J. Chromatogr. A 2015, 1409, 53–59. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, W.; Kuitunen, S.; Sixta, H.; Alopaeus, V. Population balance based modeling of changes in cellulose molecular weight distribution during ageing. Cellulose 2015, 22, 151–163. [Google Scholar] [CrossRef]
- Hiraoki, R.; Fukuzumi, H.; Ono, Y.; Saito, T.; Isogai, A. SEC-MALLS analysis of TEMPO-oxidized celluloses using methylation of carboxyl groups. Cellulose 2014, 21, 167–176. [Google Scholar] [CrossRef]
- Ono, Y.; Tanaka, R.; Funahashi, R.; Takeuchi, M.; Saito, T.; Isogai, A. SEC–MALLS analysis of ethylenediamine-pretreated native celluloses in LiCl/N,N-dimethylacetamide: Softwood Kraft pulp and highly crystalline bacterial, tunicate, and algal celluloses. Cellulose 2016, 23, 1639–1647. [Google Scholar] [CrossRef]
- Ono, Y.; Ishida, T.; Soeta, H.; Saito, T.; Isogai, A. Reliable dn/dc values of cellulose, chitin, and cellulose triacetate dissolved in LiCl/N,N-dimethylacetamide for molecular mass analysis. Biomacromolecules 2016, 17, 192–199. [Google Scholar] [CrossRef] [PubMed]
- Aono, H.; Tatsumi, D.; Matsumoto, T. Scaling analysis of cotton cellulose/LiCl·DMAc solution using light scattering and rheological measurements. J. Polym. Sci. Pol. Phys. 2006, 44, 2155–2160. [Google Scholar] [CrossRef]
- Aono, H.; Tatsumi, D.; Matsumoto, T. Characterization of aggregate structure in mercerized cellulose/LiCl·DMAc solution using light scattering and rheological measurements. Biomacromolecules 2006, 7, 1311–1317. [Google Scholar] [CrossRef]
- Mandal, A.; Chakrabarty, D. Isolation of nanocellulose from waste sugarcane bagasse (SCB) and its characterization. Carbohyd. Polym. 2011, 86, 1291–1299. [Google Scholar] [CrossRef]
- Lue, A.; Zhang, L. Effects of carbon nanotubes on rheological behavior in cellulose solution dissolved at low temperature. Polymer 2010, 51, 2748–2754. [Google Scholar] [CrossRef]
- Zhang, J.; Cao, Y.; Feng, J.; Wu, P. Graphene-oxide-sheet-induced gelation of cellulose and promoted mechanical properties of composite aerogels. J. Phys. Chem. C 2012, 116, 8063–8068. [Google Scholar] [CrossRef]
- Ishii, D.; Kanazawa, Y.; Tatsumi, D.; Matsumoto, T. Effect of solvent exchange on the pore structure and dissolution behavior of cellulose. J. Appl. Polym. Sci. 2007, 103, 3976–3984. [Google Scholar] [CrossRef]
- Zhao, G.H.; Kapur, N.; Carlin, B.; Selinger, E.; Guthrie, J.T. Characterization of the interactive properties of microcrystalline cellulose-carboxymethyl cellulose hydrogels. Int. J. Pharm. 2011, 415, 95–101. [Google Scholar] [CrossRef] [PubMed]
- Troshenkova, S.V.; Sashina, E.S.; Novoselov, N.P.; Arndt, K.-F. Light scattering in diluted solutions of cellulose and hydroxypropylcellulose in 1-ethyl-3-methylimidazolium acetate. Russ. J. Gen. Chem. 2010, 80, 501–506. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, Y.; Ke, F.; Zhou, J.; Wang, H.; Liang, D. Solubility of neutral and charged polymers in ionic liquids studied by laser light scattering. Polymer 2011, 52, 481–488. [Google Scholar] [CrossRef]
- Boluk, Y.; Danumah, C. Analysis of cellulose nanocrystal rod lengths by dynamic light scattering and electron microscopy. J. Nanopart. Res. 2014, 16, 2174. [Google Scholar] [CrossRef]
- Khouri, S.; Shams, M.; Tam, K.C. Determination and prediction of physical properties of cellulose nanocrystals from dynamic light scattering measurements. J. Nanopart. Res. 2014, 16, 2499. [Google Scholar] [CrossRef]
- Chen, D.; Ven, T.G.M. Morphological changes of sterically stabilized nanocrystalline cellulose after periodate oxidation. Cellulose 2016, 23, 1051–1059. [Google Scholar] [CrossRef]
- Zoppe, J.O.; Johansson, L.S.; Seppala, J. Manipulation of cellulose nanocrystal surface sulfate groups toward biomimetic nanostructures in aqueous media. Carbohyd. Polym. 2015, 126, 23–31. [Google Scholar] [CrossRef]
- Qin, X.; Lu, A.; Cai, J.; Zhang, L. Stability of inclusion complex formed by cellulose in NaOH/urea aqueous solution at low temperature. Carbohyd. Polym. 2013, 92, 1315–1320. [Google Scholar] [CrossRef]
- do Nascimento, J.H.O.; Luz, R.F.; Galvao, F.M.F.; Melo, J.D.D.; Oliveira, F.R.; Ladchumananandasivam, R.; Zille, A. Extraction and characterization of cellulosic nanowhisker obtained from discarded cotton fibers. Mater. Today-Proc. 2015, 2, 1–7. [Google Scholar] [CrossRef]
- Zhong, L.; Fu, S.; Peng, X.; Zhan, H.; Sun, R. Colloidal stability of negatively charged cellulose nanocrystalline in aqueous systems. Carbohyd. Polym. 2012, 90, 644–649. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Kang, H.; Li, P.; Liu, Z.; Zhang, Y.; Liu, R.; Xiang, J.-F.; Huang, Y. Dual effects of dimethylsulfoxide on cellulose solvating ability of 1-allyl-3-methylimidazolium chloride. Cellulose 2016, 23, 1165–1175. [Google Scholar] [CrossRef]
- Rinaldi, R. Instantaneous dissolution of cellulose in organic electrolyte solutions. Chem. Commun. 2011, 47, 511–513. [Google Scholar] [CrossRef]
- Lin, L.Z.; Yamaguchi, H.; Suzuki, A. Dissolution of cellulose in the mixed solvent of [bmim]Cl-DMAc and its application. RSC Adv. 2013, 3, 14379–14384. [Google Scholar] [CrossRef]
- Bardet, R.; Belgacem, N.; Bras, J. Flexibility and color monitoring of cellulose nanocrystal iridescent solid films using anionic or neutral polymers. ACS Appl. Mater. Interfaces 2015, 7, 4010–4018. [Google Scholar] [CrossRef]
- Engel, P.; Hein, L.; Spiess, A. Derivatization-free gel permeation chromatography elucidates enzymatic cellulose hydrolysis. Biotechnol. Biofuels 2012, 5, 77. [Google Scholar] [CrossRef]
- Rein, D.M.; Khalfin, R.; Szekely, N.; Cohen, Y. True molecular solutions of natural cellulose in the binary ionic liquid-containing solvent mixtures. Carbohyd. Polym. 2014, 112, 125–133. [Google Scholar] [CrossRef]
- Zhou, J.; Zhang, L.; Cai, J. Behavior of cellulose in NaOH/urea aqueous solution characterized by light scattering and viscometry. J. Polym. Sci. Part B Polym. Phys. 2004, 42, 347–353. [Google Scholar] [CrossRef]
- Alves, L.; Medronho, B.; Antunes, F.E.; Fernández-García, M.P.; Ventura, J.; Araújo, J.P.; Romano, A.; Lindman, B. Unusual extraction and characterization of nanocrystalline cellulose from cellulose derivatives. J. Mol. Liq. 2015, 210, 106–112. [Google Scholar] [CrossRef]
- Saake, B.; Zenker, M.; Stein, A.; Puls, J. Studies on pre-hump and main fractions of cellulose-2,5-acetate in acetone. Cellulose 2006, 13, 449–458. [Google Scholar] [CrossRef]
- Ramos, L.A.; Morgado, D.L.; El Seoud, O.A.; da Silva, V.C.; Frollini, E. Acetylation of cellulose in LiCl-N,N-dimethylacetamide: First report on the correlation between the reaction efficiency and the aggregation number of dissolved cellulose. Cellulose 2011, 18, 385–392. [Google Scholar] [CrossRef]
- Ghareeb, H.O.; Malz, F.; Kilz, P.; Radke, W. Molar mass characterization of cellulose acetates over a wide range of high DS by size exclusion chromatography with multi-angle laser light scattering detection. Carbohyd. Polym. 2012, 88, 96–102. [Google Scholar] [CrossRef]
- Tsunashima, Y.; Ikuno, M.; Onodera, G.; Horii, F. Low-temperature dynamic light scattering. I. Structural reorganization and physical gel formation in cellulose triacetate/methyl acetate dilute solution at −99–45 °C. Biopolymers 2006, 82, 222–233. [Google Scholar] [CrossRef]
- Porsch, B.; Hillang, I.; Karlsson, A.; Sundelöf, L.-O. Distribution analysis of cellulose acetate phthalate by ion-exclusion-moderated size exclusion chromatography. Carbohyd. Polym. 2002, 48, 379–384. [Google Scholar] [CrossRef]
- ASTM D5226-98; Standard Practice for Dissolving Polymer Material. ASTM International: West Conshohocken, PA, USA, 2003. Available online: https://www.astm.org/d5226-98.html (accessed on 28 March 2023).
- Grigoras, A.G.; Olaru, N. Solubility behavior of cellulose acetate butyrate in mixture of solvents. Rev. Chim. Buchar. 2017, 68, 1379–1382. [Google Scholar] [CrossRef]
- Olaru, N.; Anghel, N.; Pascariu, P.; Ailiesei, G. Synthesis and testing of cellulose acetate nicotinate as adsorbent for Rhodamine B dye. J. Appl. Polym. Sci. 2019, 136, 47772. [Google Scholar] [CrossRef]
- Grigoras, A.G.; Grigoras, V.C. Investigation of cellulose derivatives in solution: Laser light scattering and gel permeation chromatography studies. Rom. J. Phys. 2021, 66, 903. [Google Scholar]
- Zhang, K.; Geissler, A.; Heinze, T. Reversibly crystalline nanoparticles from cellulose alkyl esters via nanoprecipitation. Part. Part. Syst. Charact. 2015, 32, 258–266. [Google Scholar] [CrossRef]
- Adden, R.; Melander, C.; Brinkmalm, G.; Knarr, M.; Engelhardt, J.; Mischnick, P. The applicability of enzymes in cellulose ether analysis. Macromol. Symp. 2009, 280, 36–44. [Google Scholar] [CrossRef]
- Goodwin, D.J.; Picout, D.R.; Ross-Murphy, S.B.; Holland, S.J.; Martini, L.G.; Lawrence, M.J. Ultrasonic degradation for molecular weight reduction of pharmaceutical cellulose ethers. Carbohyd. Polym. 2011, 83, 843–851. [Google Scholar] [CrossRef]
- Pfefferkorn, P.; Beister, J.; Hild, A.; Thielking, H.; Kulicke, W.-M. Determination of the molar mass and the radius of gyration, together with their distributions for methylhydroxyethylcelluloses. Cellulose 2003, 10, 27–36. [Google Scholar] [CrossRef]
- Porsch, B.; Andersson, M.; Wittgren, B.; Wahlund, K.-G. Molecular mass distribution analysis of ethyl(hydroxyethyl)cellulose by size-exclusion chromatography with dual light-scattering and refractometric detection. J. Chromatogr. A 2002, 946, 69–81. [Google Scholar] [CrossRef]
- Allabash, S.; Nicolai, T.; Benyahia, L.; Tassin, J.-F.; Chassenieux, C. Evidence for the co-existence of interpenetrating permanent and transient networks of hydroxypropyl methyl cellulose. Biomacromolecules 2014, 15, 311–318. [Google Scholar] [CrossRef]
- Fettaka, M.; Issaadi, R.; Moulai-Mostefa, N.; Dez, I.; Cerf, D.L.; Picton, L. Thermo sensitive behavior of cellulose derivatives in dilute aqueous solutions: From macroscopic to mesoscopic scale. J. Colloid. Interf. Sci. 2011, 357, 372–378. [Google Scholar] [CrossRef]
- Marcelo, G.; Saiz, E.; Tarazona, M.P. Determination of molecular parameters of hydroxyethyl and hydroxypropyl celluloses by chromatography with dual detection. J. Chromatogr. A 2007, 1165, 45–51. [Google Scholar] [CrossRef]
- Dogsa, I.; Tomsic, M.; Orehek, J.; Benigar, E.; Jamnik, A.; Stopar, D. Amorphous supramolecular structure of carboxymethyl cellulose in aqueous solution at different pH values as determined by rheology, small angle X-ray and light scattering. Carbohyd. Polym. 2014, 111, 492–504. [Google Scholar] [CrossRef]
- Wittgren, B.; Stefansson, M.; Porsch, B. Interactions between sodium dodecyl sulphate and non-ionic cellulose derivatives studied by size exclusion chromatography with online multi-angle light scattering and refractometric detection. J. Chromatogr. A 2005, 1082, 166–175. [Google Scholar] [CrossRef]
- Lauten, R.A.; Nyström, B. Time dependent association phenomena in dilute aqueous mixtures of a hydrophobically modified cellulose derivative and an anionic surfactant. Colloid. Surf. A 2003, 219, 45–53. [Google Scholar] [CrossRef]
- de Martins, R.M.; Silva, C.A.; Becker, C.M.; Samios, D.; Christoff, M.; Bica, C.I.D. Interaction of (hydroxypropyl) cellulose with anionic surfactants in dilute regime. Colloid. Polym. Sci. 2006, 284, 1353–1361. [Google Scholar] [CrossRef]
- de Martins, R.M.; Becker, C.M.; Samios, D.; Bica, C.I.D. Interaction of (hydroxypropylmethyl)cellulose with anionic surfactants. Macromol. Symp. 2007, 245–246, 287–296. [Google Scholar] [CrossRef]
- Beheshti, N.; Nguyen, G.T.M.; Kjøniksen, A.-L.; Knudsen, K.D.; Nyström, B. Structure and dynamics of aqueous mixtures of an anionic cellulose derivative and anionic or cationic surfactants. Colloid. Surf. A 2006, 279, 40–49. [Google Scholar] [CrossRef]
- Chen, R.; Ilasi, N.; Sekulic, S.S. Absolute molecular weight determination of hypromellose acetate succinate by size exclusion chromatography: Use of a multiangle laser light scattering detector and a mixed solvent. J. Pharmaceut. Biomed. Anal. 2011, 56, 743–748. [Google Scholar] [CrossRef] [PubMed]
- Fischer, K.; Krasselt, K.; Schmidt, I.; Weightman, D. Distribution of substituents along the cellulose chain on cellulose xanthate and carboxymethyl cellulose. Macromol. Symp. 2005, 223, 109–120. [Google Scholar] [CrossRef]
- Li, Q.; Wu, P.; Zhou, J.; Zhang, L. Structure and solution properties of cyanoethyl celluloses synthesized in LiOH/urea aqueous solution. Cellulose 2012, 19, 161–169. [Google Scholar] [CrossRef]
- Song, Y.; Zhang, L.; Gan, W.; Zhou, J.; Zhang, L. Self-assembled micelles based on hydrophobically modified quaternized cellulose for drug delivery. Colloid. Surf. B 2011, 83, 313–320. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Wu, B.; Mu, C.; Lin, W. Concomitant degradation in periodate oxidation of carboxymethyl cellulose. Carbohyd. Polym. 2011, 84, 881–886. [Google Scholar] [CrossRef]
- Tan, H.; Wu, B.; Li, C.; Mu, C.; Li, H.; Lin, W. Collagen cryogel cross-linked by naturally derived dialdehyde carboxymethyl cellulose. Carbohyd. Polym. 2015, 129, 17–24. [Google Scholar] [CrossRef]
- Demeter, J.; Mormann, W.; Schmidt, J.; Burchard, W. Solution behavior of trimethylsilyl cellulose of different degrees of substitution, studied by static and dynamic light scattering. Macromolecules 2003, 36, 5297–5303. [Google Scholar] [CrossRef]
- Mhlanga, S.S. Investigating the Relative Adsorption of Polymeric Depressants on Pure Minerals. Master’s Thesis, University of Cape Town, Cape Town, South Africa, 2011. [Google Scholar]
- Parolis, L.A.S.; van der Merwe, R.; Groenmeyer, G.V.; Harris, P.J. The influence of metal cations on the behavior of carboxymethyl celluloses as talc depressants. Colloid. Surf. A 2008, 317, 109–115. [Google Scholar] [CrossRef]
- Smiechowicz, E.; Kulpinski, P.; Niekraszewicz, B.; Bacciarelli, A. Cellulose fibers modified with silver nanoparticles. Cellulose 2011, 18, 975–985. [Google Scholar] [CrossRef]
- Sharma, P.R.; Kamble, S.; Sarkar, D.; Anand, A.; Varma, A.J. Shape and size engineered cellulosic nanomaterials as broad spectrum anti-microbial compounds. Int. J. Biol. Macromol. 2016, 87, 460–465. [Google Scholar] [CrossRef] [PubMed]
- Rowe, R.C.; Sheskey, P.J.; Owen, S.C. Handbook of Pharmaceutical Excipients; Pharmaceutical Press: London, UK, 2006. [Google Scholar]
- Shukla, R.K.; Tiwari, A. Carbohydrate polymers: Applications and recent advances in delivering drugs to the colon. Carbohyd. Polym. 2012, 88, 399–416. [Google Scholar] [CrossRef]
- Ramesh Babu, V.; Krishna Rao, K.S.V.; Lee, Y.I. Preparation and characterization of nifedipine-loaded cellulose acetate butyrate based microspheres and their controlled release behavior. Polym. Bull. 2010, 65, 157–167. [Google Scholar] [CrossRef]
- Rokhade, A.P.; Agnihotri, S.A.; Patil, S.A.; Mallikarjuna, N.N.; Kulkarni, P.V.; Aminabhavi, T.M. Semi-interpenetrating polymer network microspheres of gelatin and sodium carboxymethyl cellulose for controlled release of ketorolac tromethamine. Carbohyd. Polym. 2006, 65, 243–252. [Google Scholar] [CrossRef]
- Grishkewich, N.; Mohammed, N.; Tang, J.; Tam, K.C. Recent advances in the application of cellulose nanocrystals. Curr. Opin. Colloid. Interface Sci. 2017, 29, 32–45. [Google Scholar] [CrossRef]
- Yu, H.; Yan, C.; Yao, J. Fully biodegradable food packaging materials based on functionalized cellulose nanocrystals/poly(3-hydroxybutyrate-co-3-hydroxyvalerate) nanocomposites. RSC Adv. 2014, 4, 59792–59802. [Google Scholar] [CrossRef]
- Cheng, S.; Zhang, Y.; Cha, R.; Yang, J.; Jiang, X. Water-soluble nanocrystalline cellulose films with highly transparent and oxygen barrier properties. Nanoscale 2016, 8, 973–978. [Google Scholar] [CrossRef]
- Ioelovich, M.; Figovsky, O. Structure and properties of nanoparticles used in paper compositions. Mech. Compos. Mater. 2010, 46, 435–442. [Google Scholar] [CrossRef]



| Sample | Asingle/Aagg | Mw,app (×104 g/mol) | Ωsingle | Nagg |
|---|---|---|---|---|
| Na7Ur12 | 0.32 | 19.6 | 0.63 | 5.5 |
| Na8Ur12 | 0.43 | 16.3 | 0.67 | 4.6 |
| Na9Ur12 | 0.84 | 10.6 | 0.86 | 4.1 |
| Na12Ur12 | - | 139 | - | - |
| Na7Ur13 | 0.34 | 18.9 | 0.65 | 5.4 |
| Na7Ur15 | 0.33 | 18.8 | 0.65 | 5.4 |
| Na9Ur13 | 1.40 | 8.1 | 0.96 | 3.6 |
| Type of Electrolytes | Ionic Strength | Particle Size (nm) | Zeta Potential (mV) | Interpretation of Data | |
|---|---|---|---|---|---|
| Inorganic electrolytes | Na+/NaCl | 2.5 or 5.0 mM | 118–120 | −38 to −32 | Electrostatic screening effect of Na+ |
| 10 mM–50 mM | 151–980 | −25.8 to −16.5 | Particle aggregation | ||
| Ca2+/CaCl2 | ≤1 mM | 116–119 | >30 mV | Little aggregation | |
| 2.5–5.0 mM | 325–752 | −15.6 to −7.8 | Particles tended to aggregate | ||
| Organic electrolytes | Anionic sodium dodecyl sulfate (SDS) | 0.0–5.0 g/L | 116–119 | −55 to −75 | Electrostatic repulsion between negatively charged SDS and CNCs |
| 15.0 g/L | 105 | −75 | Low absorption of SDS on CNC surface | ||
| Anionic sodium carboxymethyl cellulose (CMC) | 0.0–2.5 g/L | 100–600 | −55 to −105 | Larger aggregates | |
| Cationic poly(acrylamide) (CPAM) | 0.5 g/L | - | - | Started aggregation |
| Sample | Length (L) (nm) | Average Width (d) (nm) | Average Aspect Ratio (L/d) | Zeta Potential (mV) | |
|---|---|---|---|---|---|
| SEM | DLS | SEM | |||
| CNCHPMC | 300–400 | 260 | 50–100 | 3–8 | −8.6 |
| CNCMCC | 1000 | 820 | 100–300 | 3.3–10 | −51.5 |
| CNCCMC | 300–600 | 218 | 50–100 | 3–6 | −33.2 |
| CAP Sample | LiCl Content (M) | |||
|---|---|---|---|---|
| 0.005 | 0.0075 | |||
| Mw | Mw/Mn | Mw | Mw/Mn | |
| Wako | 56,900 | 1.5 | 53,300 | 1.6 |
| Eastman | 54,400 | 1.6 | 54,700 | 1.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grigoras, A.-G. Investigation of Cellulose-Based Materials Applied in Life Sciences Using Laser Light Scattering Methods. Polymers 2024, 16, 1170. https://doi.org/10.3390/polym16081170
Grigoras A-G. Investigation of Cellulose-Based Materials Applied in Life Sciences Using Laser Light Scattering Methods. Polymers. 2024; 16(8):1170. https://doi.org/10.3390/polym16081170
Chicago/Turabian StyleGrigoras, Anca-Giorgiana. 2024. "Investigation of Cellulose-Based Materials Applied in Life Sciences Using Laser Light Scattering Methods" Polymers 16, no. 8: 1170. https://doi.org/10.3390/polym16081170
APA StyleGrigoras, A. -G. (2024). Investigation of Cellulose-Based Materials Applied in Life Sciences Using Laser Light Scattering Methods. Polymers, 16(8), 1170. https://doi.org/10.3390/polym16081170






