Crystallization Behavior of Copolyesters Containing Sulfonates
Abstract
1. Introduction
2. Materials and Methods
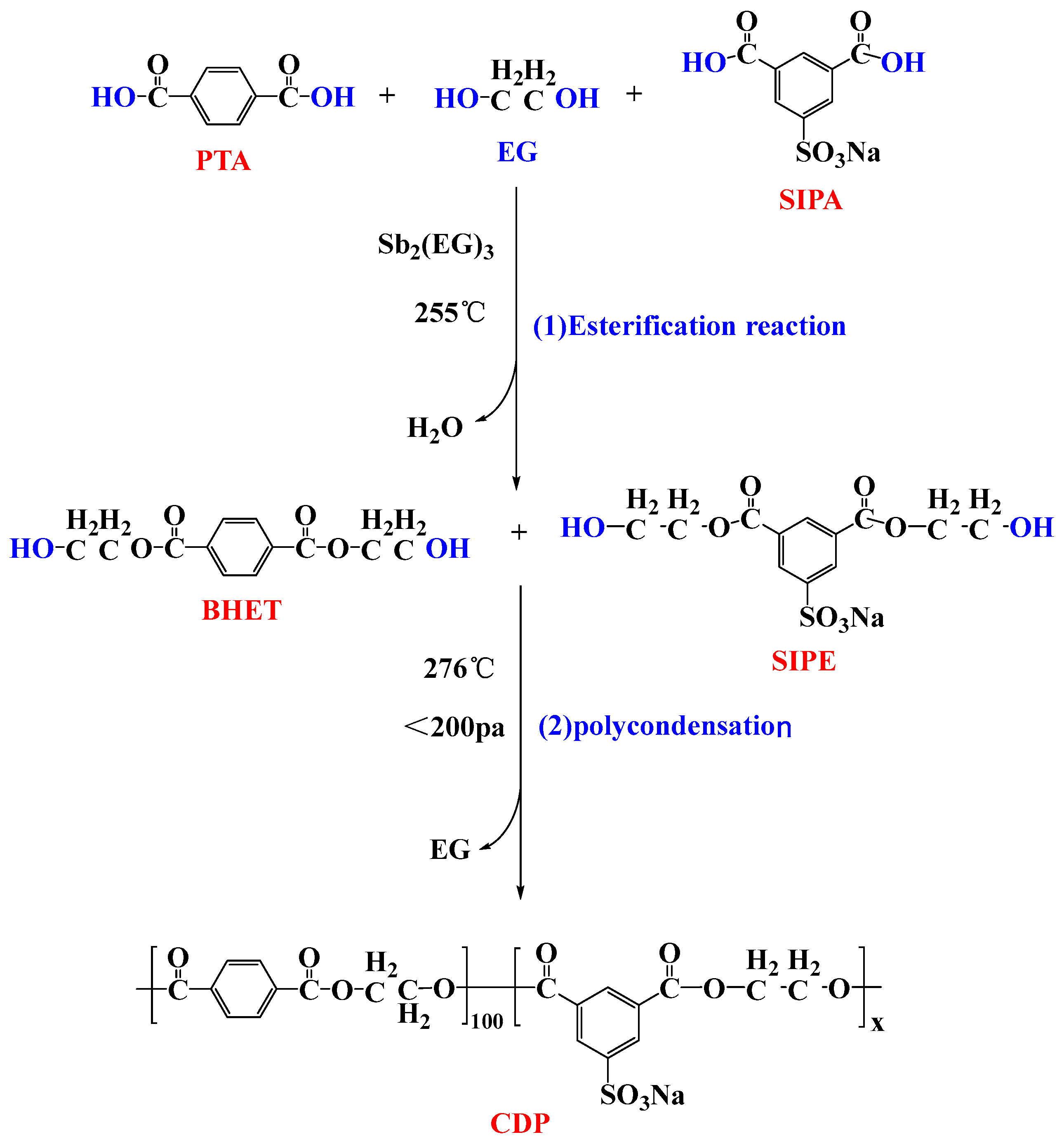
2.1. Materials and Synthesis
2.1.1. Materials
2.1.2. Synthesis
2.2. Characterization
2.2.1. Intrinsic Viscosity
2.2.2. Non-Isothermal Crystallization
3. Results and Discussion
3.1. Intrinsic Viscosity
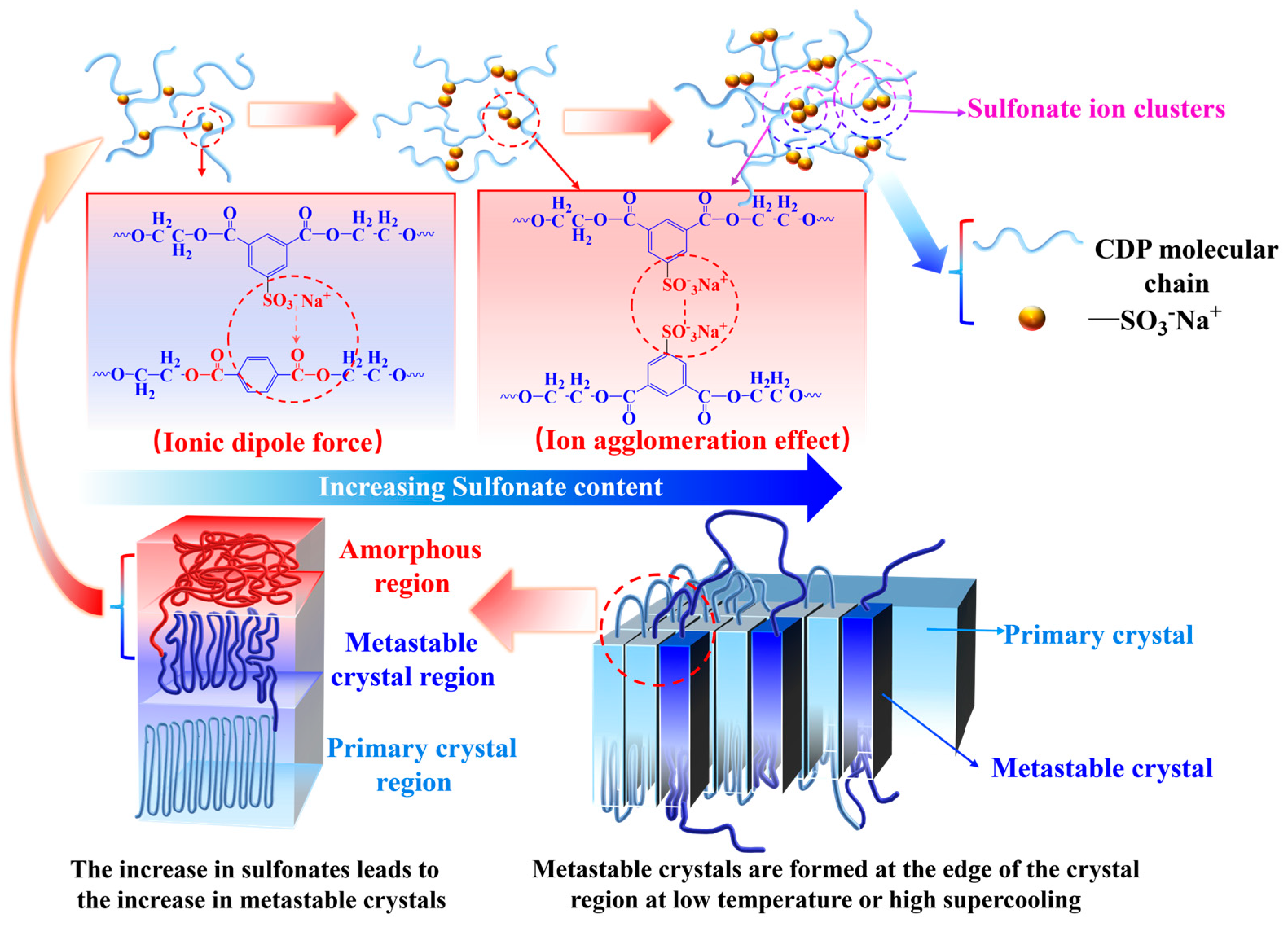
3.2. Non-Isothermal Crystallization
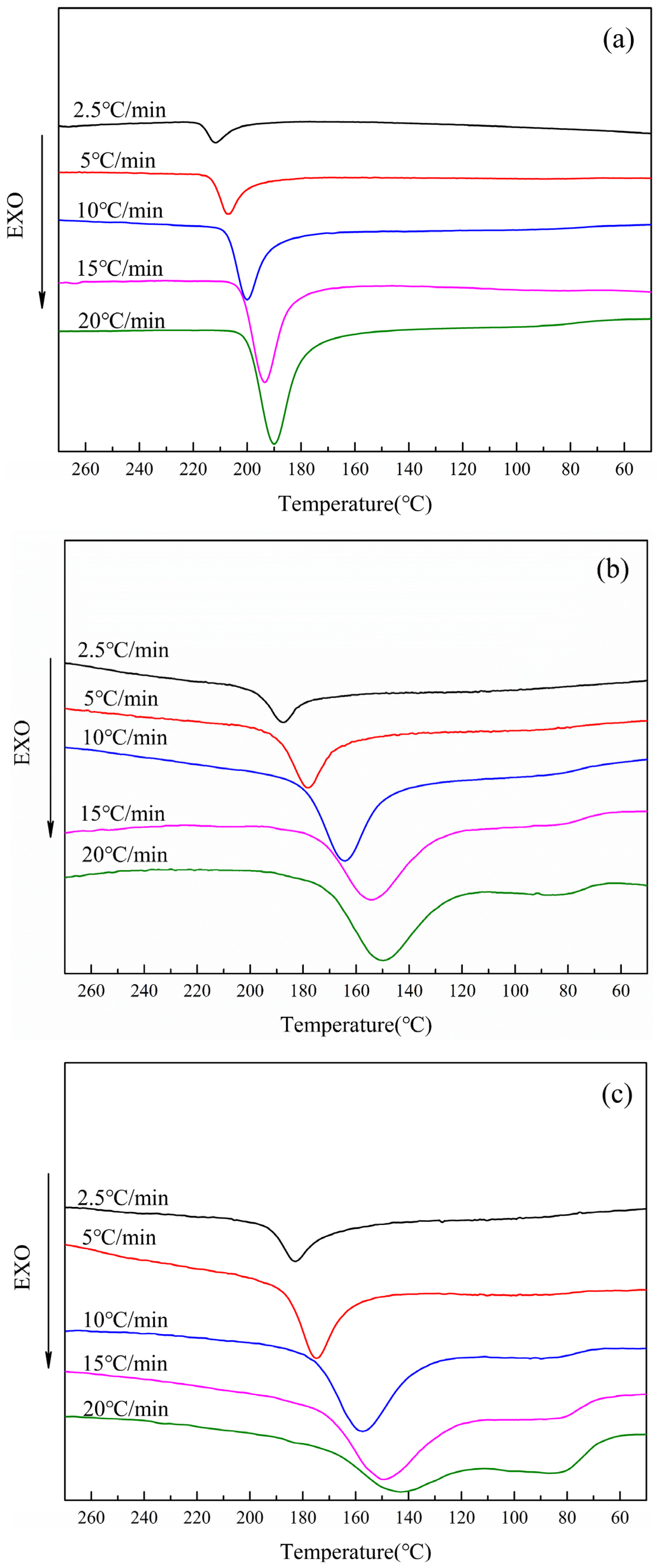
3.2.1. Non-Isothermal Crystallization Behavior of CDP at Different Cooling Rates
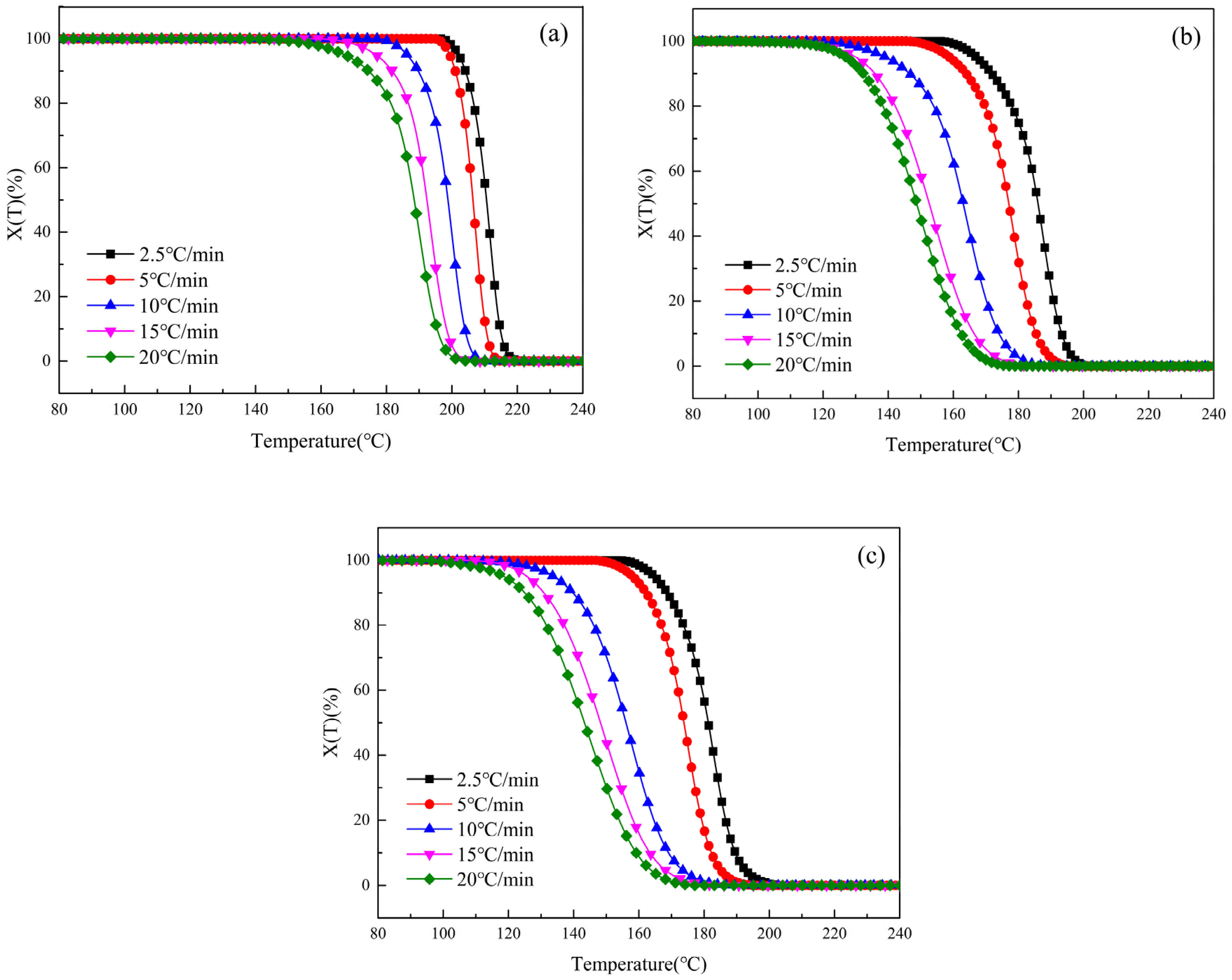
3.2.2. Variation in Relative Crystallinity (X(T)) with Temperature (T)
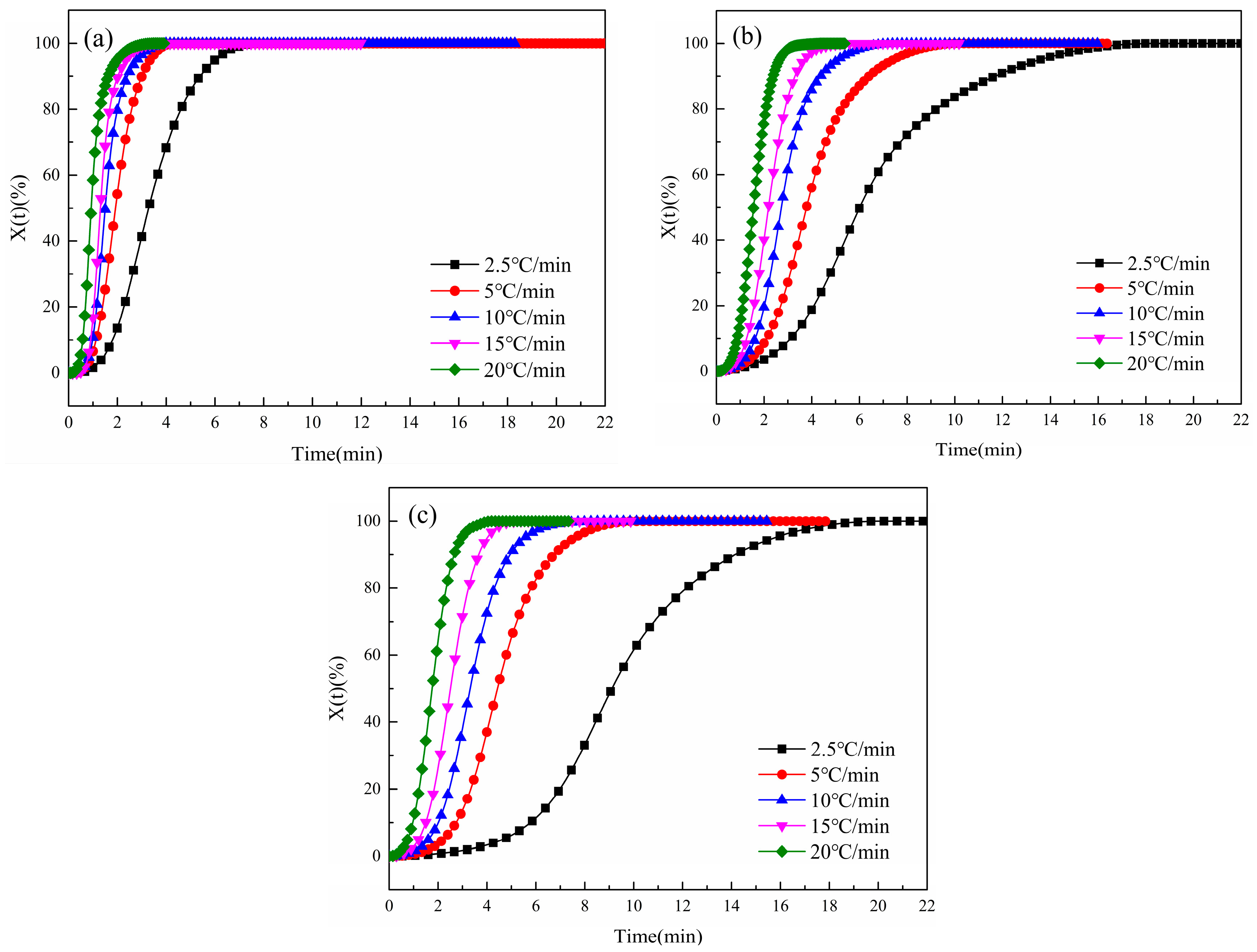
3.2.3. Variation in Relative Crystallinity (X(t)) with Time (t)
3.2.4. Melting Temperature Curve of CDP at Different Cooling Rates
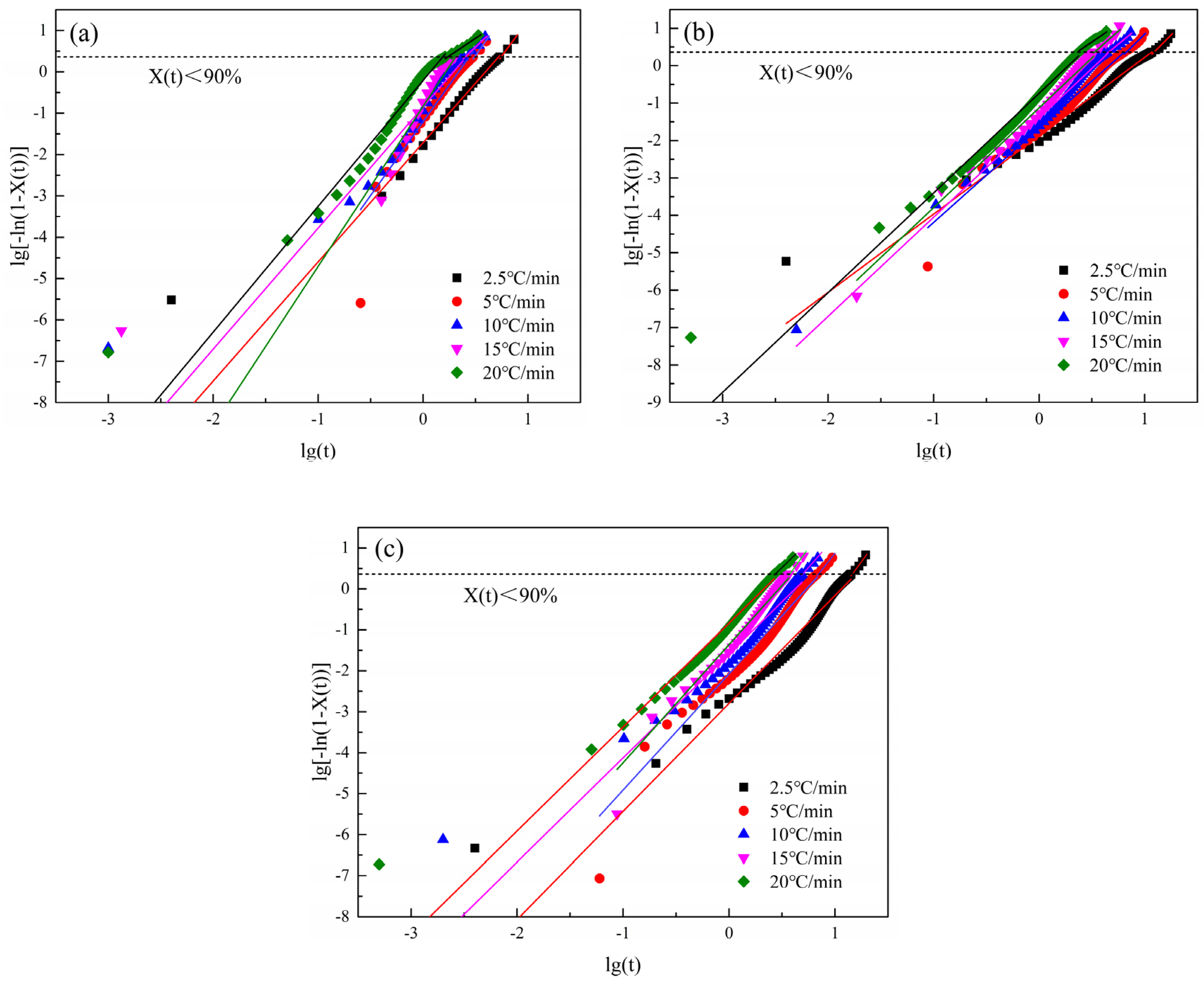
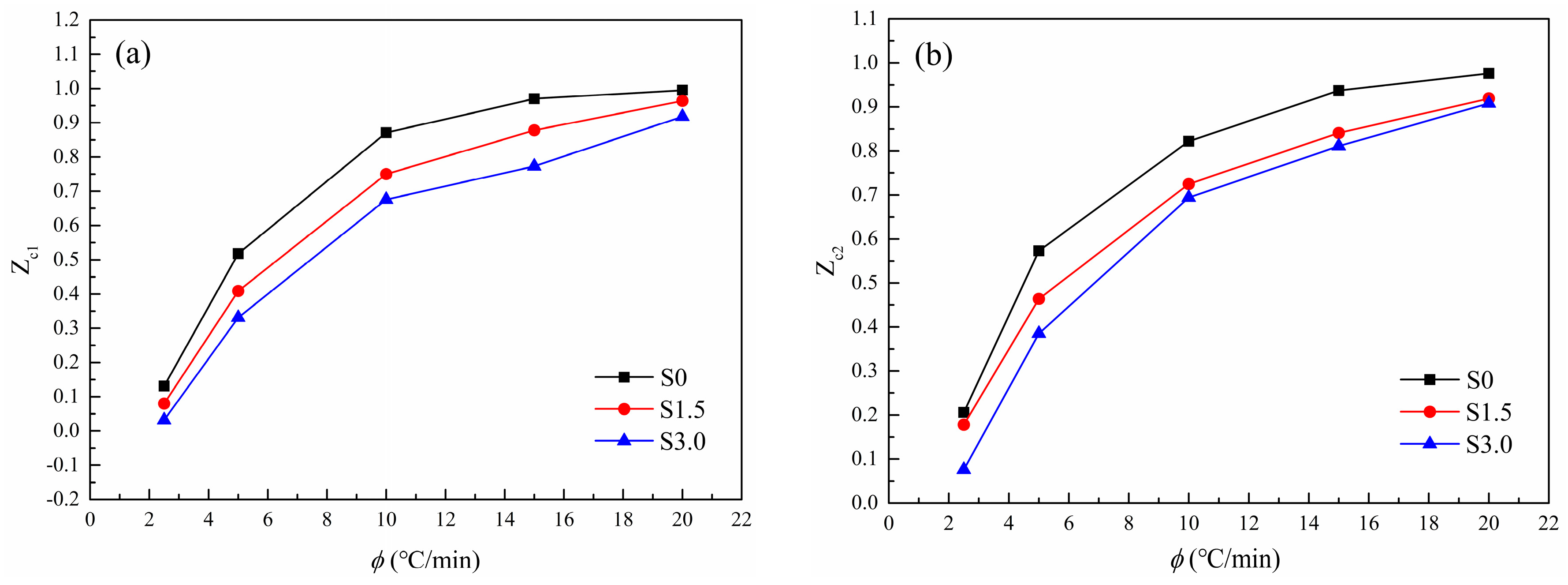
3.2.5. Jeziorny Method
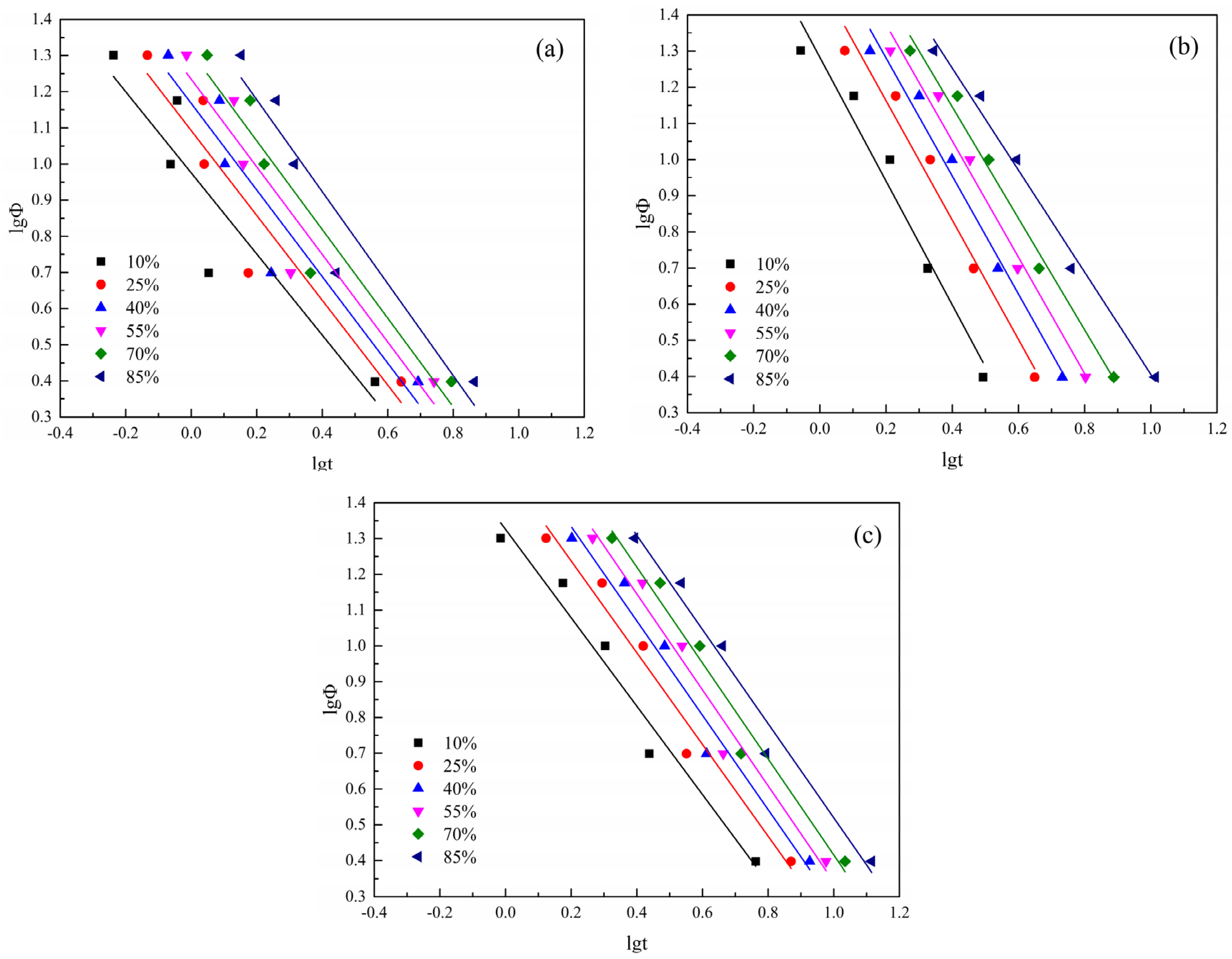
3.2.6. Ozawa Method
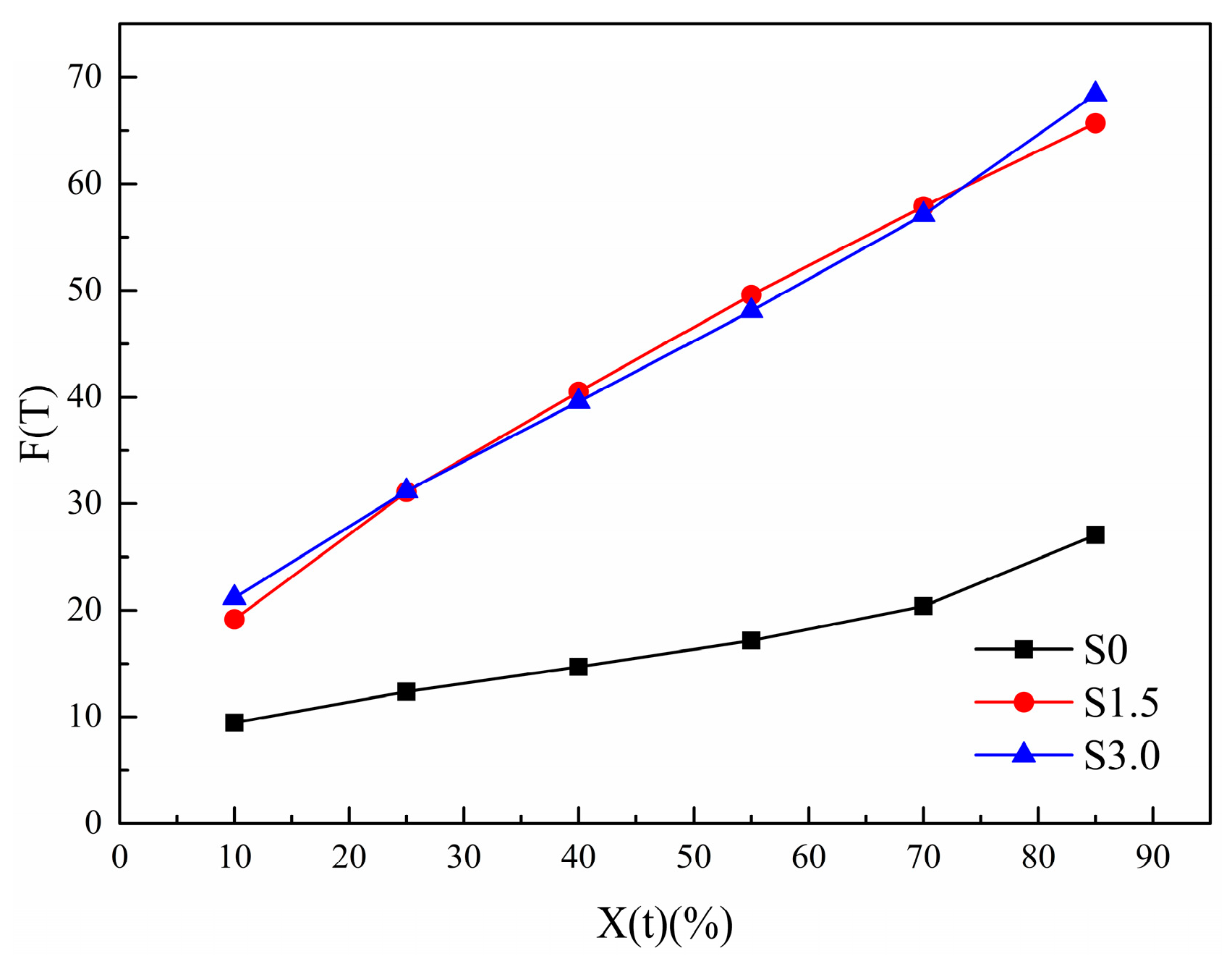
3.2.7. Mo Method
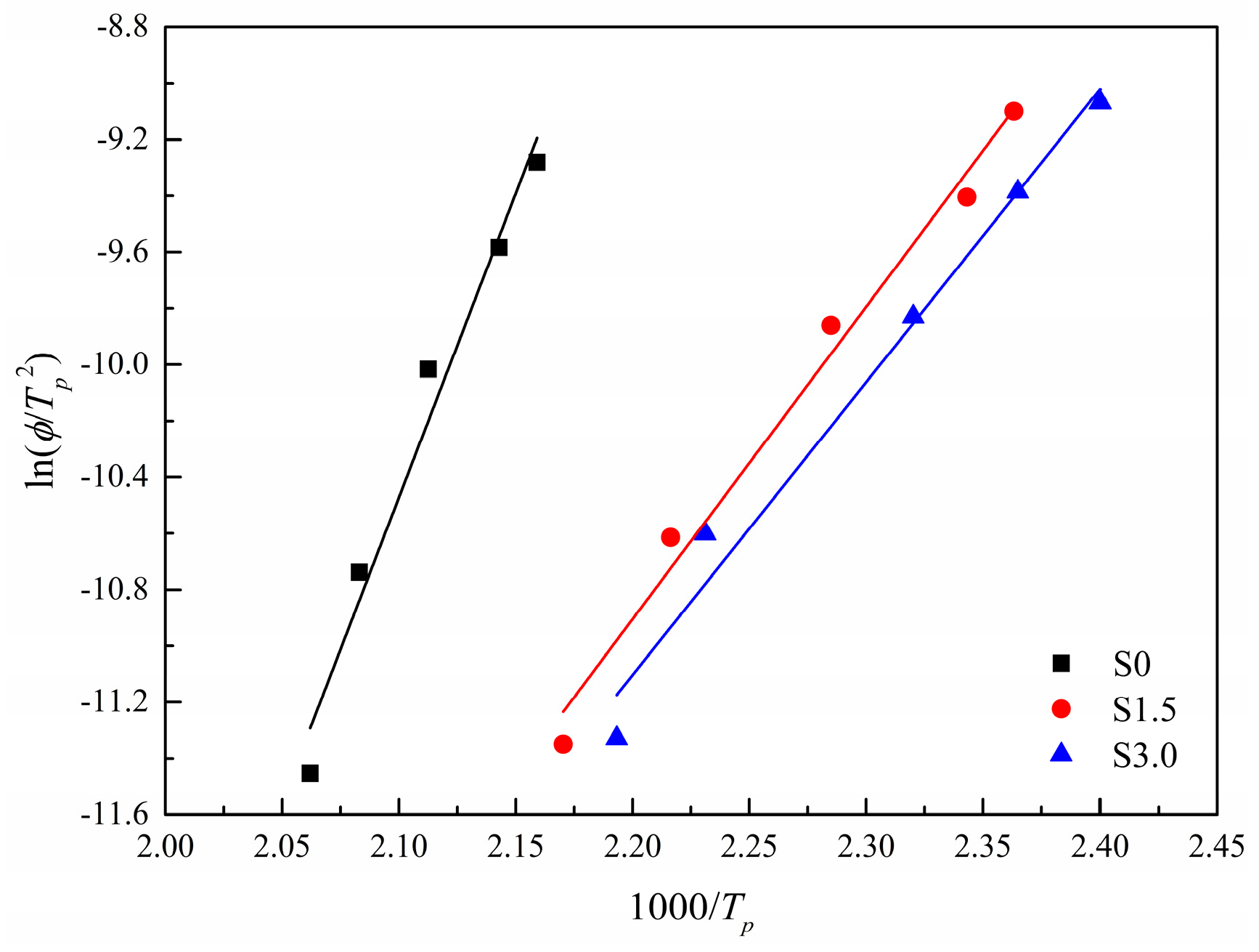
3.2.8. Kissinger Method
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Strobl, G.R. The Physics of Polymers: Concepts for Understanding Their Structures and Behavior; Springer: Berlin/Heidelberg, Germany, 1998; Volume 206, pp. 274–276. [Google Scholar]
- Singh, A.K.; Bedi, R.; Kaith, B.S. Composite materials based on recycled polyethylene terephthalate and their properties—A comprehensive review. Compos. Part B Eng. 2021, 219, 108928. [Google Scholar] [CrossRef]
- Nisticò, R. Polyethylene terephthalate (PET) in the packaging industry. Polym. Test. 2020, 90, 106707. [Google Scholar] [CrossRef]
- Jaffe, M.; Easts, A.J.; Feng, X. Polyester Fibers, Thermal Analysis of Textiles and Fibers; Elsevier: Amsterdam, The Netherlands, 2020; pp. 133–149. [Google Scholar]
- Chen, S.; Zhang, S.; Galluzzi, M.; Li, F.; Zhang, X.; Yang, X.; Liu, X.; Cai, X.; Zhu, X.; Du, B.; et al. Insight into multifunctional polyester fabrics finished by one-step eco-friendly strategy. Chem. Eng. J. 2019, 358, 634–642. [Google Scholar] [CrossRef]
- Sfameni, S.; Lawnick, T.; Rando, G.; Visco, A.; Textor, T.; Plutino, M.R. Super-hydrophobicity of polyester fabrics driven by functional sustainable fluorine-free silane-based coatings. Gels 2023, 9, 109. [Google Scholar] [CrossRef] [PubMed]
- Ketema, A.; Worku, A. Review on intermolecular forces between dyes used for polyester dyeing and polyester fiber. J. Chem. 2020, 2020, 6628404. [Google Scholar] [CrossRef]
- John, M.G. Sulfinate Containing Polyesters Dyeable with Basic Dyes. U.S. Patent 3,057,827, 9 October 1962. [Google Scholar]
- Wang, J.; Li, X.; Cai, Z.; Gu, L. Absorption kinetics and thermodynamics of cationic dyeing on easily dyeable copolyester modified by 2-methyl-1, 3-propanediol. Fibers Polym. 2015, 16, 2384–2390. [Google Scholar] [CrossRef]
- Shaki, H. Color, fastness, antibacterial, and skin sensitivity properties of high lightfastness azo disperse dyes incorporating sulfamide groups. Fibers Polym. 2020, 21, 2530–2538. [Google Scholar] [CrossRef]
- Lillwitz, L. Production of dimethyl-2, 6-naphthalenedicarboxylate: Precursor to polyethylene naphthalate. Appl. Catal. A Gen. 2001, 221, 337–358. [Google Scholar] [CrossRef]
- Sun, L.; Huang, L.; Wang, X.; Hu, H.; Zhu, R.; He, M. Absorption kinetics and thermodynamics of cationic dyeing for poly (ethylene terephthalate) copolyester modified by 2, 2-dimethyl-1, 3-propylene glycol (NPG). J. Text. Inst. 2022, 113, 2808–2815. [Google Scholar] [CrossRef]
- Wang, J.; Li, X.; Ge, F.; Cai, Z.; Gu, L. Carrier-Free and Low-Temperature Ultradeep Dyeing of Poly (ethylene terephthalate) Copolyester Modified with Sodium-5-sulfo-bis (hydroxyethyl)-isophthalate and 2-Methyl-1, 3-propanediol. ACS Sustain. Chem. Eng. 2016, 4, 3285–3291. [Google Scholar] [CrossRef]
- Hu, Y.; Wang, Y.; Zhang, X.; Qian, J.; Xing, X.; Wang, X. Regenerated cationic dyeable polyester deriving from poly (ethylene terephthalate) waste. Polym. Degrad. Stab. 2020, 179, 109261. [Google Scholar] [CrossRef]
- Rao, B.R.; Datye, K.V. lonomeric Polyester Fiber. Text. Chem. Color. 1996, 28, 17. [Google Scholar]
- Xiong, L.-K.; Fu, Y.-F.; Zhang, S.-Y.; Yin, C.-Y. Investigation of stain-resistant cationic dyeable nylon 6 modified with sodium salt of 5-sulfoisophthalic acid and polyethylene glycol. Fibers Polym. 2016, 17, 984–991. [Google Scholar] [CrossRef]
- Yang, W.; Li, A.; Zhang, Q.; Fei, Z.; Liu, F. Adsorption of 5-sodiosulfoisophthalic acids from aqueous solutions onto acrylic ester polymer YWB-7 resin. Sep. Purif. Technol. 2005, 46, 161–167. [Google Scholar] [CrossRef]
- Eisenberg, A.; Hird, B.; Moore, R.B. A new multiplet-cluster model for the morphology of random ionomers. Macromolecules 1990, 23, 4098–4107. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, Z.; Chen, Q.; Matsumiya, Y.; Watanabe, H. Nonlinear rheology of telechelic ionomers based on sodium sulfonate and carboxylate. Macromolecules 2021, 54, 9724–9738. [Google Scholar] [CrossRef]
- Pawlak, A. The entanglements of macromolecules and their influence on the properties of polymers. Macromol. Chem. Phys. 2019, 220, 1900043. [Google Scholar] [CrossRef]
- Yin, Y.; Jiang, B.; Meng, L. Research on synthesis and thermal properties of poly (ethylene terephthalate) sulfonate group containing ionomer. J. Appl. Polym. Sci. 2021, 138, 49966. [Google Scholar] [CrossRef]
- Huang, Z.; Bao, J.; Zhang, X.; Chen, W. New Insights in Structures, Properties, and Rheological Behaviors of Cationic Dyeable Polyesters. Ind. Eng. Chem. Res. 2023, 62, 14648–14656. [Google Scholar] [CrossRef]
- Zhao, Z.; Wu, Y.; Wang, K.; Xia, Y.; Gao, H.; Luo, K.; Cao, Z.; Qi, J. Effect of the trifunctional chain extender on intrinsic viscosity, crystallization behavior, and mechanical properties of poly (ethylene terephthalate). ACS Omega 2020, 5, 19247–19254. [Google Scholar] [CrossRef] [PubMed]
- Zhou, T.; Wang, X.; Liu, Y.; Zheng, L. A green and efficient synthetic strategy for the preparation of PBS ionomers with high molecular weight, high ionic group content and good combined properties. Chem. Eng. J. 2023, 477, 146275. [Google Scholar] [CrossRef]
- Khanna, Y. A barometer of crystallization rates of polymeric materials. Polym. Eng. Sci. 1990, 30, 1615–1619. [Google Scholar] [CrossRef]
- Sheikh Nezhad Moghadam, A.; Rafizadeh, M.; Afshar Taromi, F. Non-isothermal crystallization kinetics of polyethylene terephthalate: A study based on Tobin, Hay and Nakamura models. Iran. Polym. J. 2023, 32, 125–137. [Google Scholar] [CrossRef]
- Eisenberg, A. Ion-Containing Polymers: Physical Properties and Structure; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Middleton, L.R.; Winey, K.I. Nanoscale aggregation in acid-and ion-containing polymers. Annu. Rev. Chem. Biomol. Eng. 2017, 8, 499–523. [Google Scholar] [CrossRef] [PubMed]
- Yao, S.-F.; Chen, X.-T.; Ye, H.-M. Investigation of structure and crystallization behavior of poly (butylene succinate) by fourier transform infrared spectroscopy. J. Phys. Chem. B 2017, 121, 9476–9485. [Google Scholar] [CrossRef] [PubMed]
- Toda, A.; Androsch, R.; Schick, C. Melting kinetics of superheated polymer crystals examined by isothermal and nonisothermal fast scanning calorimetry. Macromolecules 2021, 54, 8770–8779. [Google Scholar] [CrossRef]
- Li, S.; Chen, T.; Liao, X.; Han, W.; Yan, Z.; Li, J.; Li, G. Effect of macromolecular chain movement and the interchain interaction on crystalline nucleation and spherulite growth of polylactic acid under high-pressure CO2. Macromolecules 2019, 53, 312–322. [Google Scholar] [CrossRef]
- Zhang, X.; Zhao, S.; Mohamed, M.G.; Kuo, S.-W.; Xin, Z. Crystallization behaviors of poly (ethylene terephthalate)(PET) with monosilane isobutyl-polyhedral oligomeric silsesquioxanes (POSS). J. Mater. Sci. 2020, 55, 14642–14655. [Google Scholar] [CrossRef]
- Bianchi, O.; Oliveira, R.V.B.; Fiorio, R.; Martins, J.D.N.; Zattera, A.J.; Canto, L.B. Assessment of Avrami, Ozawa and Avrami–Ozawa equations for determination of EVA crosslinking kinetics from DSC measurements. Polym. Test. 2008, 27, 722–729. [Google Scholar] [CrossRef]
- Toda, A. Effect of a nucleating agent on polymer crystallization analyzed using the original Avrami model. Macromolecules 2022, 55, 2202–2209. [Google Scholar] [CrossRef]
- Sangroniz, L.; Cavallo, D.; Müller, A.J. Self-nucleation effects on polymer crystallization. Macromolecules 2020, 53, 4581–4604. [Google Scholar] [CrossRef]
- Hu, W. The physics of polymer chain-folding. Phys. Rep. 2018, 747, 1–50. [Google Scholar] [CrossRef]
- Lotz, B. Fold Surfaces of Polymer Crystals Are Nucleation Sites: The Link between Polymer Decoration, Secondary Crystallization, and the Rigid Amorphous Fraction (RAF). Macromolecules 2023, 56, 4135–4152. [Google Scholar] [CrossRef]
- Xu, S.; Zhou, J.; Pan, P. Structural Evolutions of Initially Amorphous Polymers during Near-Tg Stretching: A Minireview of Recent Progresses. Macromol. Chem. Phys. 2022, 223, 2100427. [Google Scholar] [CrossRef]
- Righetti, M.C.; Di Lorenzo, M.L.; Tombari, E.; Angiuli, M. The low-temperature endotherm in poly (ethylene terephthalate): Partial melting and rigid amorphous fraction mobilization. J. Phys. Chem. B 2008, 112, 4233–4241. [Google Scholar] [CrossRef] [PubMed]
- Ronkay, F.; Molnár, B.; Nagy, D.; Szarka, G.; Iván, B.; Kristály, F.; Mertinger, V.; Bocz, K. Melting temperature versus crystallinity: New way for identification and analysis of multiple endotherms of poly (ethylene terephthalate). J. Polym. Res. 2020, 27, 372. [Google Scholar] [CrossRef]
- Bazuin, C.G.; Eisenberg, A. Modification of polymer properties through ion incorporation. Ind. Eng. Chem. Prod. Res. Dev. 1981, 20, 271–286. [Google Scholar] [CrossRef]
- Gaonkar, A.A.; Murudkar, V.V.; Deshpande, V.D. Comparison of crystallization kinetics of polyethylene terephthalate (PET) and reorganized PET. Thermochim. Acta 2020, 683, 178472. [Google Scholar] [CrossRef]
- Shirzad, K.; Viney, C. A critical review on applications of the Avrami equation beyond materials science. J. R. Soc. Interface 2023, 20, 20230242. [Google Scholar] [CrossRef] [PubMed]
- Kourtidou, D.; Tarani, E.; Chrysafi, I.; Menyhard, A.; Bikiaris, D.N.; Chrissafis, K. Non-isothermal crystallization kinetics of graphite-reinforced crosslinked high-density polyethylene composites. J. Therm. Anal. Calorim. 2020, 142, 1849–1861. [Google Scholar] [CrossRef]
- Li, Y.; Duan, L.; Cheng, L.; Yang, Y.; Li, Y.; Cheng, Y.; Song, D. Thermal analysis and crystallization kinetics of polyurethane. J. Therm. Anal. Calorim. 2019, 135, 2843–2848. [Google Scholar] [CrossRef]
- Dingler, C.; Dirnberger, K.; Ludwigs, S. Semiconducting polymer spherulites—From fundamentals to polymer electronics. Macromol. Rapid Commun. 2019, 40, 1800601. [Google Scholar] [CrossRef] [PubMed]
- Qu, D.; Gao, H.; Wang, Q.; Bai, Y.; Li, N. Non-isothermal crystallization kinetics of bio-based poly (butylene-co-isosorbide succinate)(PBIS). J. Therm. Anal. Calorim. 2020, 139, 1931–1939. [Google Scholar] [CrossRef]
- Barati, A.; Wang, P.; Liu, S.; Dashtimoghadam, E. Reactive Blending of Recycled Poly (ethylene terephthalate)/Recycled Polypropylene: Kinetics Modeling of Non-Isothermal Crystallization. ACS Omega 2023, 8, 15062–15074. [Google Scholar] [CrossRef] [PubMed]
- Ozawa, T. Kinetics of non-isothermal crystallization. Polymer 1971, 12, 150–158. [Google Scholar] [CrossRef]
- Di Lorenzo, M.; Silvestre, C. Non-isothermal crystallization of polymers. Prog. Polym. Sci. 1999, 24, 917–950. [Google Scholar] [CrossRef]
- Zhishen, M.O. A method for the non-isothermal crystallization kinetics of polymers. Acta Polym. Sin. 2008, 7, 656–661. [Google Scholar]
- Chen, L.; Dou, Q. Influence of the combination of nucleating agent and plasticizer on the non-isothermal crystallization kinetics and activation energies of poly (lactic acid). J. Therm. Anal. Calorim. 2020, 139, 1069–1090. [Google Scholar] [CrossRef]


| Sample | SIPA Content/mol% | [η]/dL·g−1 |
|---|---|---|
| S0 | 0 | 0.681 |
| S1.5 | 1.5 | 0.566 |
| S3.0 | 3.0 | 0.494 |
| Sample | (°C/min) | /°C | /°C | /°C | /(J/g) | ORC |
|---|---|---|---|---|---|---|
| S0 | 2.5 | 223.9 | 211.8 | 197.0 | 25.52 | −0.802 |
| 5 | 216.1 | 206.9 | 194.7 | 26.48 | ||
| 10 | 212.6 | 200.2 | 176.3 | 33.16 | ||
| 15 | 208.9 | 193.5 | 156.6 | 33.61 | ||
| 20 | 207.1 | 190.0 | 135.9 | 32.66 | ||
| S1.5 | 2.5 | 201.1 | 187.6 | 155.3 | 30.84 | −0.465 |
| 5 | 196.0 | 178.1 | 145.0 | 35.40 | ||
| 10 | 192.0 | 164.5 | 114.8 | 31.60 | ||
| 15 | 185.4 | 153.6 | 97.4 | 23.09 | ||
| 20 | 179.9 | 150.0 | 92.6 | 18.68 | ||
| S3.0 | 2.5 | 204.1 | 182.8 | 154.1 | 29.54 | −0.446 |
| 5 | 196.0 | 175.1 | 145.9 | 27.69 | ||
| 10 | 189.2 | 157.9 | 114.0 | 24.23 | ||
| 15 | 185.8 | 149.7 | 105.7 | 16.65 | ||
| 20 | 178.5 | 143.5 | 92.9 | 6.99 |
| Sample | (°C/min) | /°C | /°C | /°C | /°C | /(J/g) | /(J/g) |
|---|---|---|---|---|---|---|---|
| S0 | 2.5 | 79.5 | 245.0 | / | / | / | 39.60 |
| 5 | 80.5 | 244.3 | / | / | / | 38.09 | |
| 10 | 79.9 | 242.7 | 249.8 | / | / | 37.46 | |
| 15 | 78.9 | 240.2 | 248.8 | / | / | 37.22 | |
| 20 | 81.6 | 239.1 | 249.8 | / | / | 36.80 | |
| S1.5 | 2.5 | 79.5 | 234.3 | 238.8 | / | / | 35.06 |
| 5 | 79.7 | / | 240.4 | / | / | 37.01 | |
| 10 | 79.4 | / | 239.6 | / | / | 33.96 | |
| 15 | 78.4 | / | 239.3 | 157.4 | 2.68 | 38.80 | |
| 20 | 77.7 | / | 240.3 | 153.2 | 6.38 | 36.66 | |
| S3.0 | 2.5 | 81.5 | 231.6 | 237.5 | / | / | 33.68 |
| 5 | 81.1 | / | 239.3 | / | / | 30.86 | |
| 10 | 79.7 | / | 238.8 | / | / | 35.92 | |
| 15 | 78.9 | / | 239.5 | 155.5 | 10.96 | 36.11 | |
| 20 | 78.5 | / | 239.7 | 157.1 | 18.65 | 35.58 |
| Sample | ϕ (°C/min) | n1 | R12 | n2 | R22 | ||
|---|---|---|---|---|---|---|---|
| S0 | 2.5 | 3.450 | 0.131 | 0.966 | 2.882 | 0.206 | 0.965 |
| 5 | 3.639 | 0.518 | 0.935 | 3.564 | 0.573 | 0.987 | |
| 10 | 2.400 | 0.871 | 0.931 | 2.929 | 0.822 | 0.951 | |
| 15 | 2.101 | 0.970 | 0.941 | 3.872 | 0.937 | 0.991 | |
| 20 | 1.703 | 0.995 | 0.954 | 3.043 | 0.976 | 0.976 | |
| S1.5 | 2.5 | 2.846 | 0.080 | 0.942 | 2.094 | 0.178 | 0.978 |
| 5 | 2.784 | 0.409 | 0.932 | 2.520 | 0.464 | 0.988 | |
| 10 | 2.315 | 0.750 | 0.956 | 2.651 | 0.725 | 0.982 | |
| 15 | 2.328 | 0.878 | 0.984 | 2.666 | 0.841 | 0.984 | |
| 20 | 1.911 | 0.964 | 0.978 | 2.665 | 0.919 | 0.986 | |
| S3.0 | 2.5 | 3.523 | 0.032 | 0.945 | 2.636 | 0.076 | 0.970 |
| 5 | 3.274 | 0.331 | 0.927 | 2.840 | 0.385 | 0.980 | |
| 10 | 2.961 | 0.676 | 0.973 | 2.541 | 0.694 | 0.963 | |
| 15 | 3.562 | 0.773 | 0.976 | 2.886 | 0.811 | 0.986 | |
| 20 | 2.525 | 0.918 | 0.936 | 2.563 | 0.908 | 0.989 |
| Sample | T (°C) | m | lgk(T)/(K/min)m | R2 |
|---|---|---|---|---|
| S0 | 198 | 2.409 | 1.980 | 0.862 |
| 200 | 2.741 | 2.020 | 0.851 | |
| 202 | 3.213 | 2.152 | 0.862 | |
| 204 | 3.825 | 2.341 | 0.876 | |
| 206 | 4.888 | 2.759 | 0.879 | |
| S1.5 | 164 | 1.902 | 1.499 | 0.919 |
| 166 | 2.050 | 1.523 | 0.919 | |
| 168 | 2.218 | 1.557 | 0.919 | |
| 170 | 2.410 | 1.604 | 0.921 | |
| 172 | 2.640 | 1.667 | 0.922 | |
| 174 | 2.909 | 1.747 | 0.921 | |
| S3.0 | 158 | 1.854 | 1.573 | 0.954 |
| 160 | 1.931 | 1.544 | 0.947 | |
| 162 | 2.035 | 1.538 | 0.943 | |
| 164 | 2.154 | 1.538 | 0.941 | |
| 166 | 2.283 | 1.541 | 0.940 | |
| 168 | 2.427 | 1.550 | 0.941 |
| Sample | X(t) (%) | α | F(T) | R2 |
|---|---|---|---|---|
| S0 | 10 | 1.122 | 9.45 | 0.805 |
| 25 | 1.174 | 12.37 | 0.852 | |
| 40 | 1.198 | 14.71 | 0.872 | |
| 55 | 1.212 | 17.16 | 0.886 | |
| 70 | 1.227 | 20.40 | 0.895 | |
| 85 | 1.272 | 27.07 | 0.891 | |
| S1.5 | 10 | 1.712 | 19.17 | 0.950 |
| 25 | 1.651 | 31.11 | 0.968 | |
| 40 | 1.633 | 40.50 | 0.975 | |
| 55 | 1.610 | 49.59 | 0.979 | |
| 70 | 1.542 | 57.89 | 0.983 | |
| 85 | 1.412 | 65.69 | 0.986 | |
| S3.0 | 10 | 1.235 | 21.18 | 0.960 |
| 25 | 1.282 | 31.19 | 0.963 | |
| 40 | 1.319 | 39.57 | 0.964 | |
| 55 | 1.341 | 48.08 | 0.964 | |
| 70 | 1.341 | 57.09 | 0.965 | |
| 85 | 1.315 | 68.40 | 0.968 |
| Sample | /(°C·min) | /°C | ||
|---|---|---|---|---|
| S0 | 2.5 | 211.8 | −179.7 | 0.967 |
| 5 | 206.9 | |||
| 10 | 200.2 | |||
| 15 | 193.5 | |||
| 20 | 190.0 | |||
| S1.5 | 2.5 | 187.6 | −92.3 | 0.983 |
| 5 | 178.1 | |||
| 10 | 164.5 | |||
| 15 | 153.6 | |||
| 20 | 150.0 | |||
| S3.0 | 2.5 | 182.8 | −86.5 | 0.977 |
| 5 | 175.1 | |||
| 10 | 157.9 | |||
| 15 | 149.7 | |||
| 20 | 143.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Chu, Y.; Huang, Q.; Jin, X.; Qiu, Z.; Jin, J. Crystallization Behavior of Copolyesters Containing Sulfonates. Polymers 2024, 16, 1177. https://doi.org/10.3390/polym16081177
Li Z, Chu Y, Huang Q, Jin X, Qiu Z, Jin J. Crystallization Behavior of Copolyesters Containing Sulfonates. Polymers. 2024; 16(8):1177. https://doi.org/10.3390/polym16081177
Chicago/Turabian StyleLi, Zhiyong, Yongjing Chu, Qing Huang, Xiaopei Jin, Zhicheng Qiu, and Jian Jin. 2024. "Crystallization Behavior of Copolyesters Containing Sulfonates" Polymers 16, no. 8: 1177. https://doi.org/10.3390/polym16081177
APA StyleLi, Z., Chu, Y., Huang, Q., Jin, X., Qiu, Z., & Jin, J. (2024). Crystallization Behavior of Copolyesters Containing Sulfonates. Polymers, 16(8), 1177. https://doi.org/10.3390/polym16081177





