Enhanced Lightweight Structures Through Brachistochrone-Inspired Lattice Design
Abstract
1. Introduction
2. Brachistochrone-Based TPMS Lattice Structures
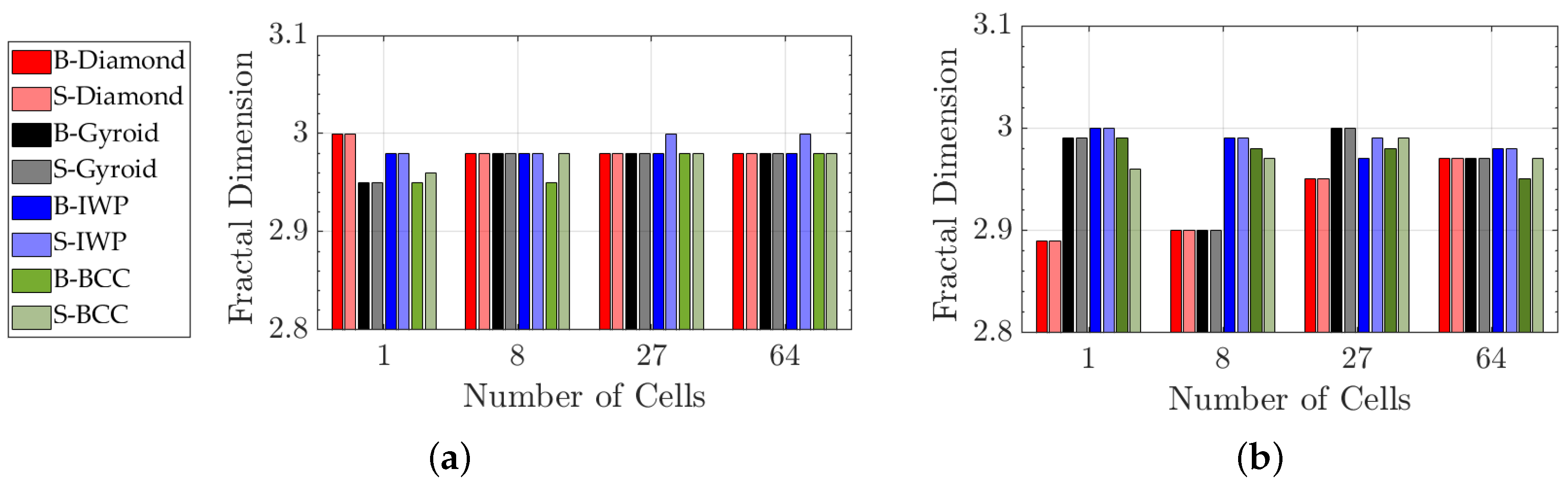
2.1. Fractal Dimension
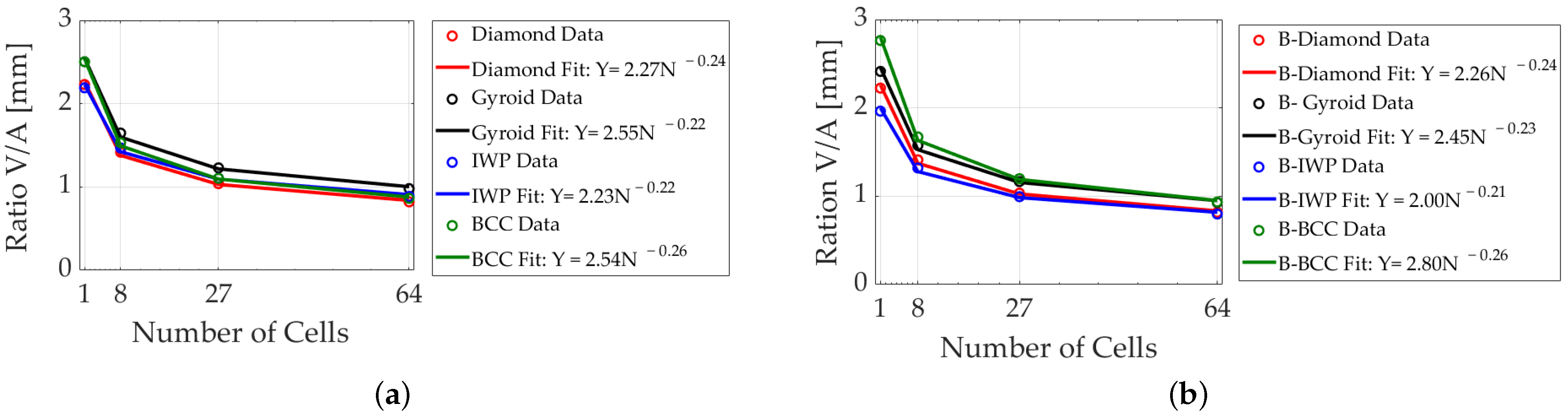
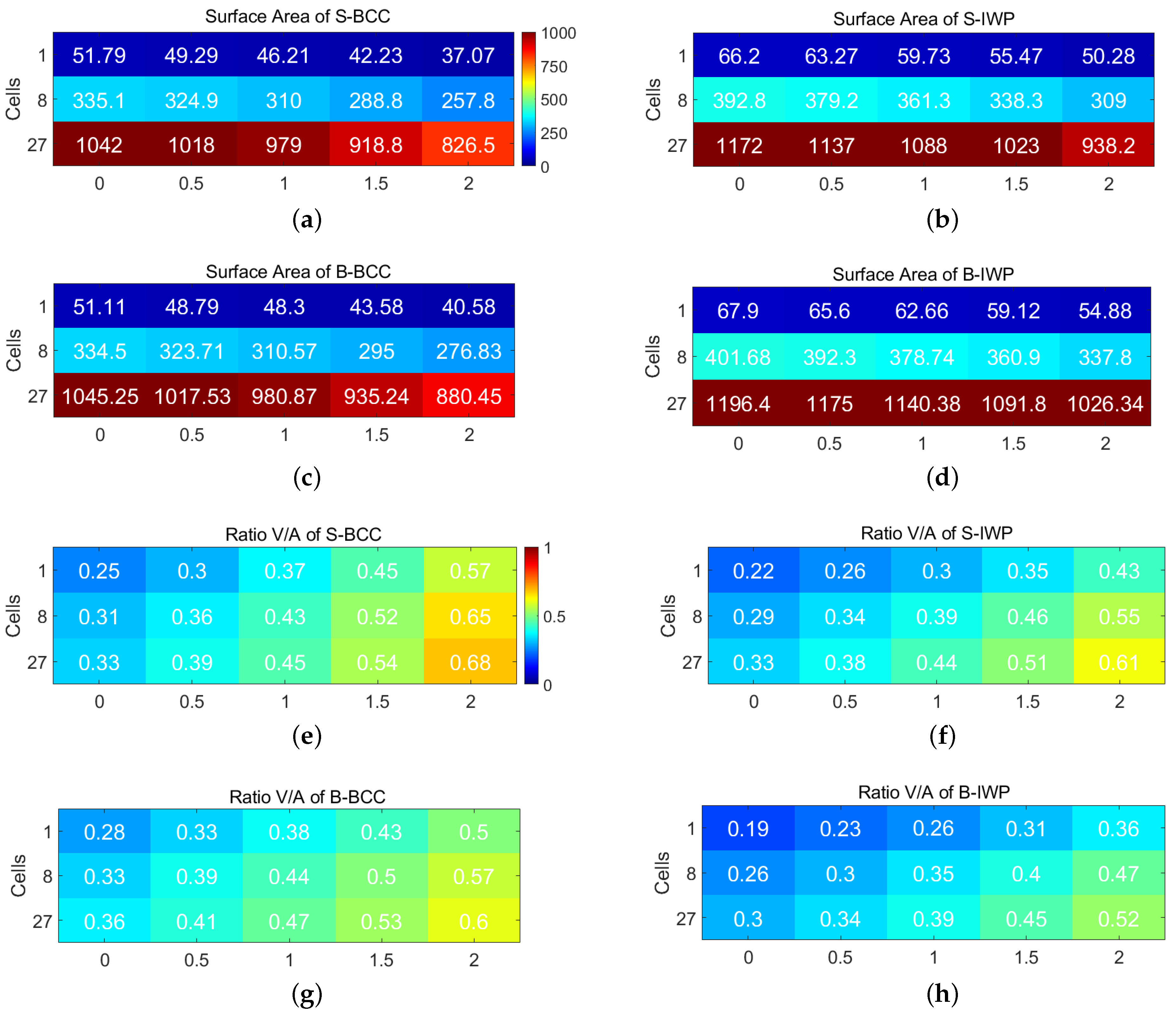
2.2. Ratio Volume to Surface Area
3. Experimental Measurements and Numerical Results
3.1. Manufacturing of Lattice Structures for Compressive Test
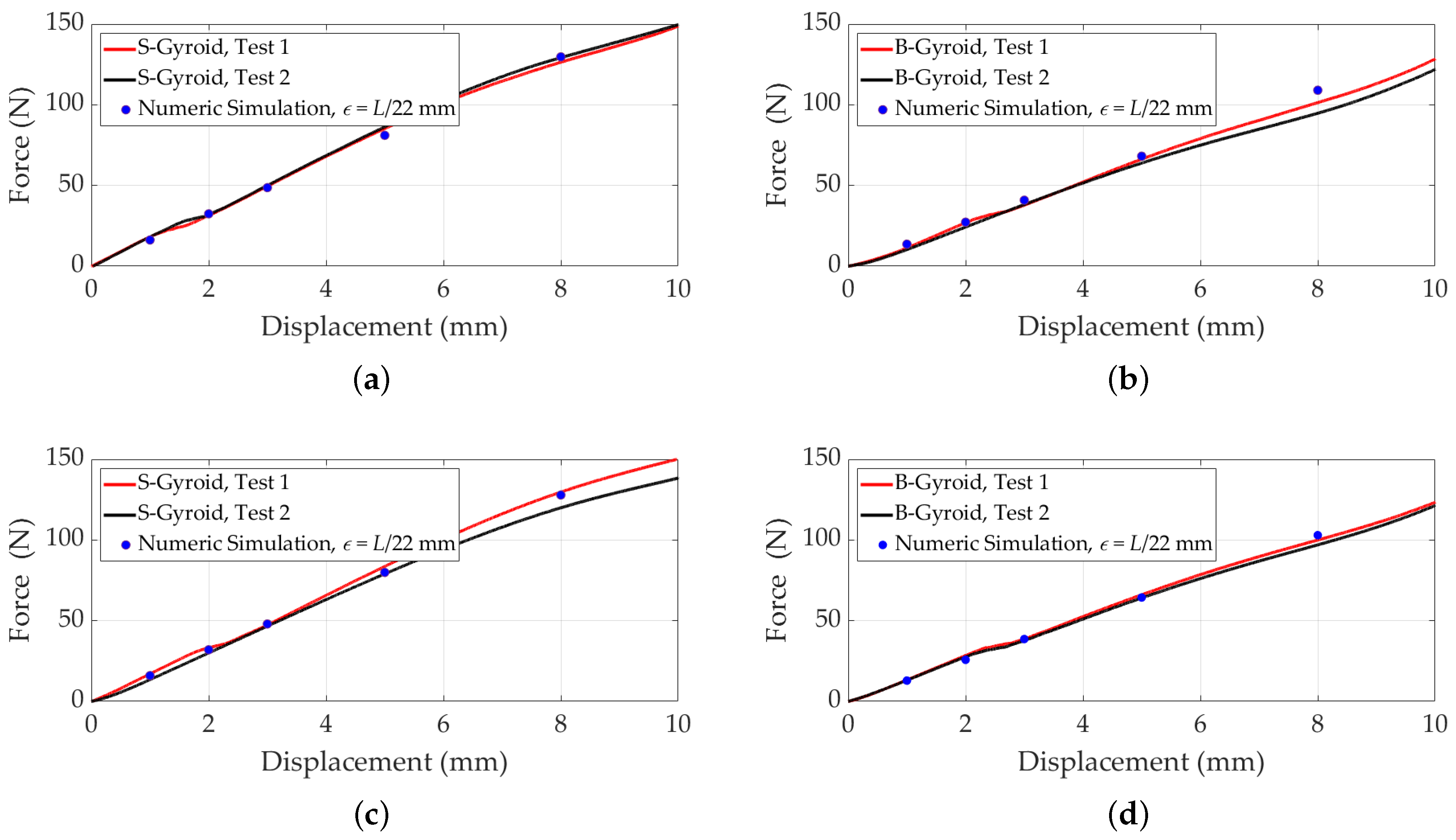
3.2. Numerical Simulation via Finite Element Method
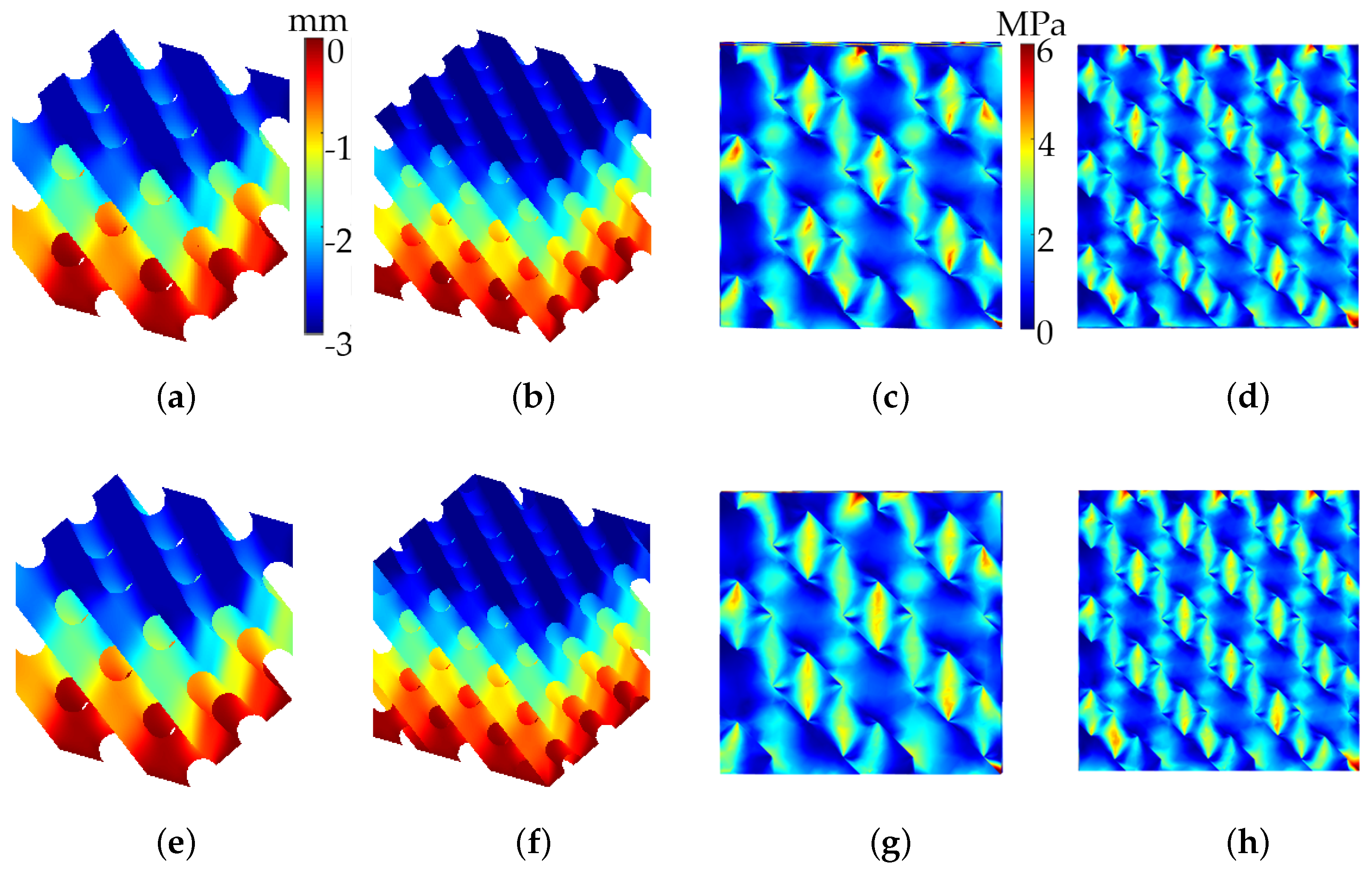
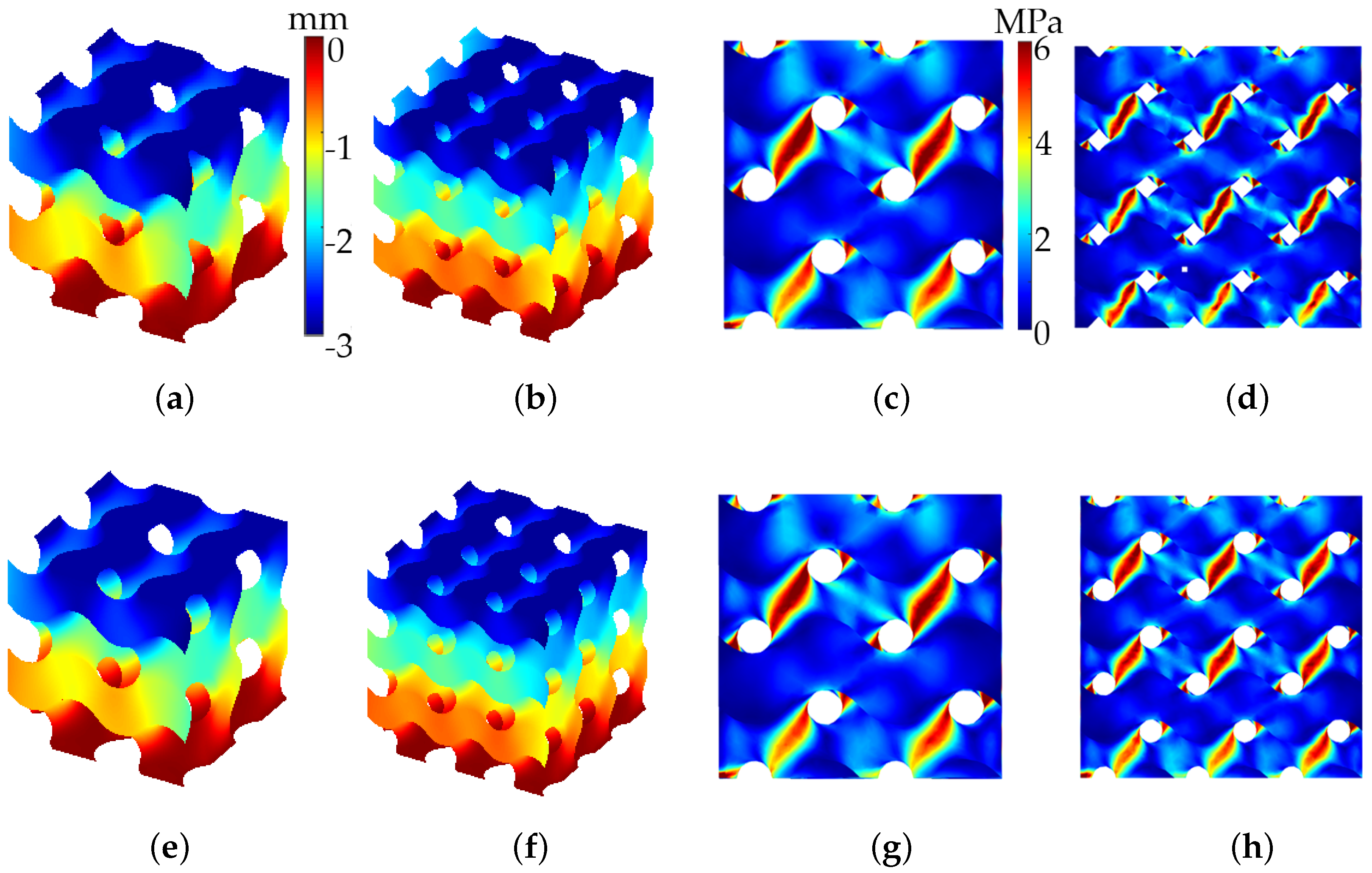
3.2.1. Diamond Lattice Structures
3.2.2. Gyroid Lattice Structures
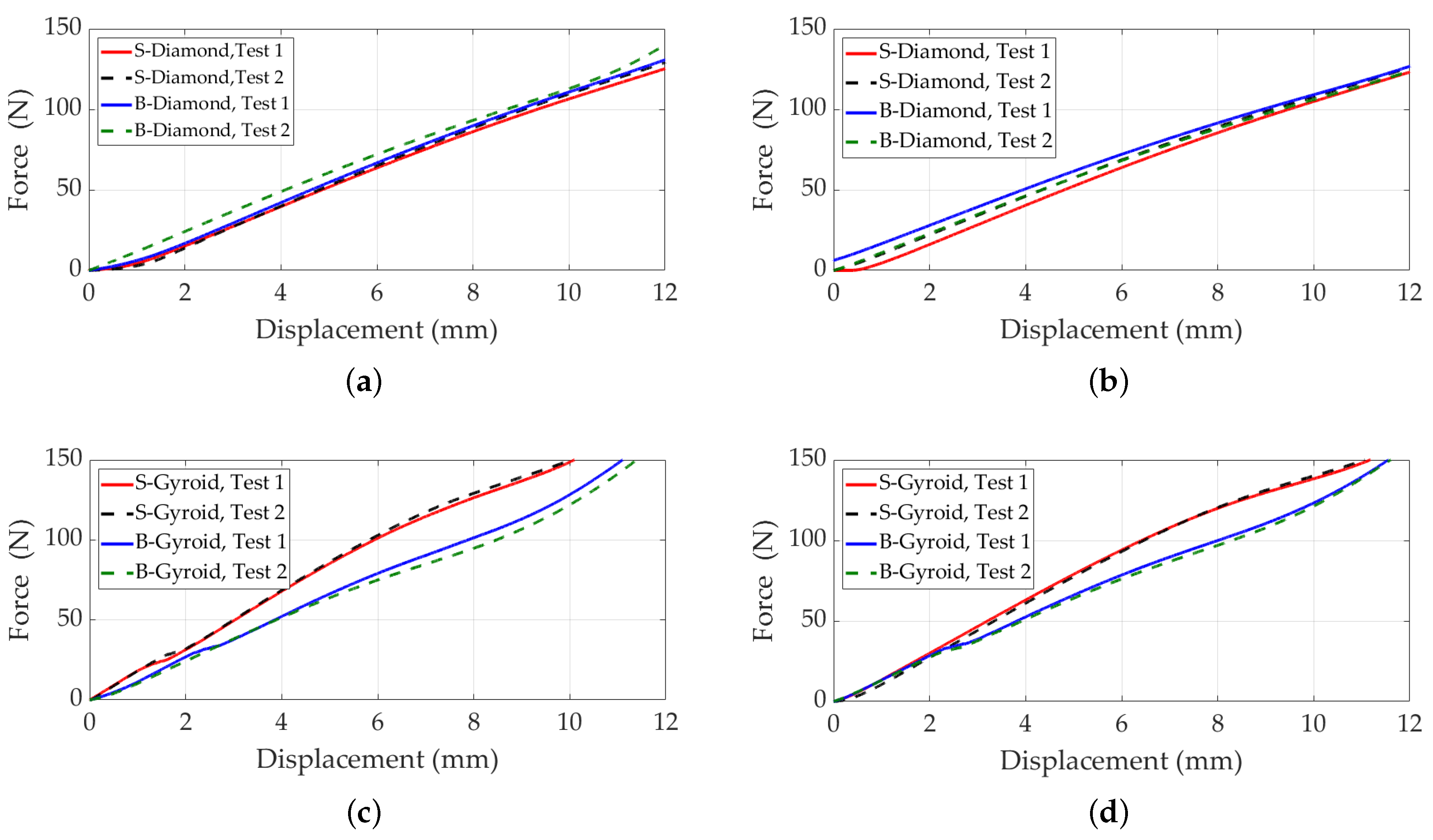
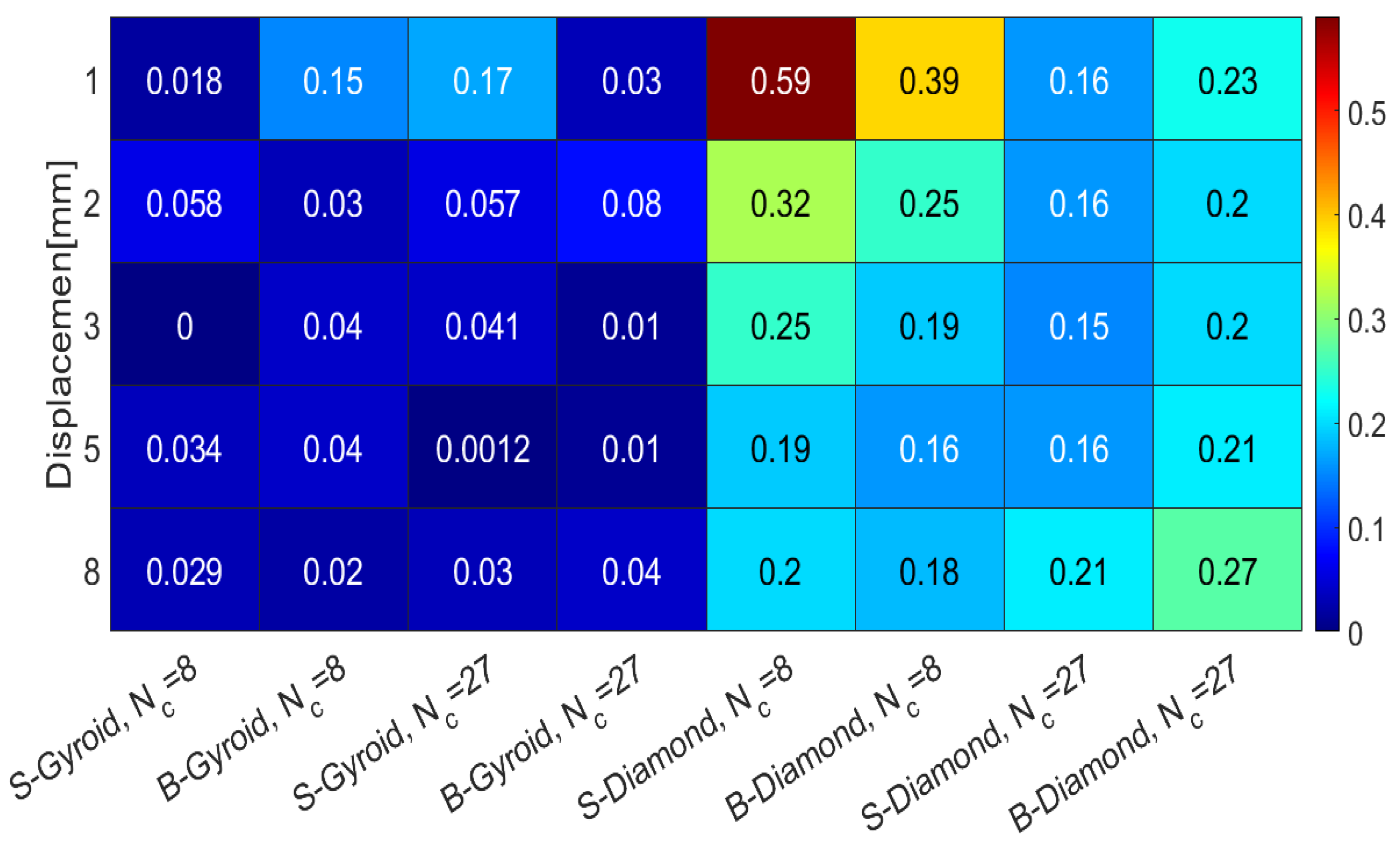
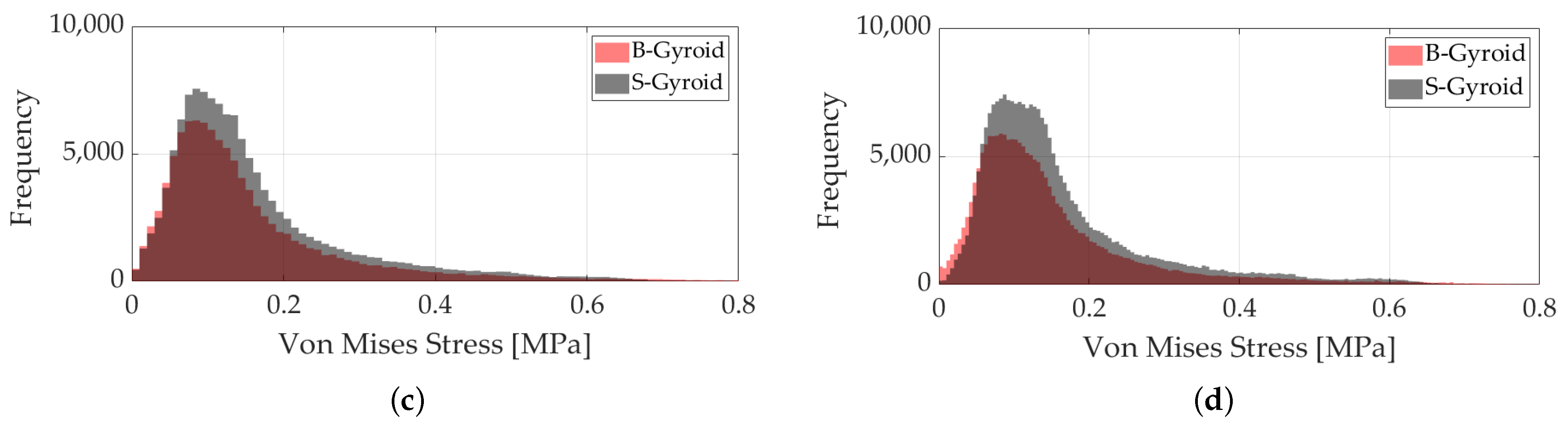
3.2.3. Results Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Aslan, B.; Yıldız, A.R. Optimum design of automobile components using lattice structures for additive manufacturing. Mater. Test. 2020, 62, 633–639. [Google Scholar] [CrossRef]
- Morciano, M.; Alberghini, M.; Fasano, M.; Almiento, M.; Calignano, F.; Manfredi, D.; Asinari, P.; Chiavazzo, E. 3D printed lattice metal structures for enhanced heat transfer in latent heat storage systems. J. Energy Storage 2023, 65, 107350. [Google Scholar] [CrossRef]
- Khosroshahi, S.F.; Tsampas, S.; Galvanetto, U. Feasibility study on the use of a hierarchical lattice architecture for helmet liners. Mater. Today Commun. 2018, 14, 312–323. [Google Scholar] [CrossRef]
- Nasim, M.; Hasan, M.J.; Galvanetto, U. Impact behavior of energy absorbing helmet liners with PA12 lattice structures: A computational study. Int. J. Mech. Sci. 2022, 233, 107673. [Google Scholar] [CrossRef]
- Decker, T.; Kedziora, S. Optimizing the Thickness of Functionally Graded Lattice Structures for High-Performance Energy Absorption: A Case Study Based on a Bicycle Helmet. Appl. Sci. 2024, 14, 2788. [Google Scholar] [CrossRef]
- Bazyar, P.; Sheidaee, E. Design and simulating lattice structures in the FE analysis of the femur bone. Bioprinting 2023, 37, e00326. [Google Scholar] [CrossRef]
- Seharing, A.; Azman, A.H.; Abdullah, S. Finite element analysis of gradient lattice structure patterns for bone implant design. Int. J. Struct. Integr. 2020, 11, 535–545. [Google Scholar] [CrossRef]
- Oladapo, B.I.; Ismail, S.O.; Ikumapayi, O.M.; Karagiannidis, P.G. Impact of rGO-coated PEEK and lattice on bone implant. Colloids Surfaces B Biointerfaces 2022, 216, 112583. [Google Scholar] [CrossRef]
- Ma, X.; Zhang, D.Z.; Zheng, X. Revealing the excellent properties of minimal surface lattice structures based on additive manufacturing through the principle of least action. Int. J. Adv. Manuf. Technol. 2022, 121, 1575–1588. [Google Scholar] [CrossRef]
- Wang, W.; Lin, Y.; Hu, Y.; Yang, L.; Lin, D.; Ma, J.; Zhou, L.; Liu, B.; Cai, X.; Yan, C.; et al. The effect of fatigue loading on the mechanical properties of additively manufactured continuous carbon fiber-reinforced composites. Compos. Commun. 2025, 53, 102231. [Google Scholar] [CrossRef]
- Abou-Ali, A.M.; Lee, D.W.; Abu Al-Rub, R.K. On the effect of lattice topology on mechanical properties of SLS additively manufactured sheet-, ligament-, and strut-based polymeric metamaterials. Polymers 2022, 14, 4583. [Google Scholar] [CrossRef] [PubMed]
- Germain, L.; Fuentes, C.A.; van Vuure, A.W.; des Rieux, A.; Dupont-Gillain, C. 3D-printed biodegradable gyroid scaffolds for tissue engineering applications. Mater. Des. 2018, 151, 113–122. [Google Scholar] [CrossRef]
- Akbar, S.; Squires, A.M.; Elliott, J.M. Production of a Metallic Single Gyroid with a Tunable Sub-10-nm Unit Cell Size via Lipid-Cubic-Phase Templating: Chiral Nanomaterials for Catalytic and Optical Applications. ACS Appl. Nano Mater. 2024, 7, 9809–9815. [Google Scholar] [CrossRef]
- Su, L.; Lu, F.; Li, Y.; Wang, Y.; Li, X.; Zheng, L.; Gao, X. Gyroid Liquid Crystals as Quasi-Solid-State Electrolytes Toward Ultrastable Zinc Batteries. ACS Nano 2024, 18, 7633–7643. [Google Scholar] [CrossRef]
- Lee, J.; Moon, J.; Han, S.A.; Kim, J.; Malgras, V.; Heo, Y.U.; Kim, H.; Lee, S.M.; Liu, H.K.; Dou, S.X.; et al. Everlasting living and breathing gyroid 3D network in Si@ SiOx/C nanoarchitecture for lithium ion battery. ACS Nano 2019, 13, 9607–9619. [Google Scholar] [CrossRef]
- Choudhury, S.; Agrawal, M.; Formanek, P.; Jehnichen, D.; Fischer, D.; Krause, B.; Albrecht, V.; Stamm, M.; Ionov, L. Nanoporous cathodes for high-energy Li–S batteries from gyroid block copolymer templates. ACS Nano 2015, 9, 6147–6157. [Google Scholar] [CrossRef]
- Zhang, M.; Hu, T.; Wang, X.; Chang, P.; Jin, Z.; Pan, L.; Mei, H.; Cheng, L.; Zhang, L. Boosting uniform charge distribution using 3D rigid electrodes with interconnected gyroid channels to achieve stable and reliable zinc-ion batteries. J. Mater. Chem. A 2022, 10, 7195–7206. [Google Scholar] [CrossRef]
- Nguyen, N.V.; Tran, K.Q.; Do, D.T.; Thai, C.H.; Żur, K.K.; Nguyen-Xuan, H. An isogeometric analysis of solar panels with a bio-inspired substrate. Eng. Anal. Bound. Elem. 2024, 166, 105854. [Google Scholar] [CrossRef]
- Wu, S.; Yang, L.; Yang, X.; Chen, P.; Su, J.; Wu, H.; Liu, Z.; Wang, H.; Wang, C.; Yan, C.; et al. Mechanical properties and energy absorption of AlSi10Mg Gyroid lattice structures fabricated by selective laser melting. Smart Manuf. 2022, 1, 2150001. [Google Scholar] [CrossRef]
- Zhang, C.; Zheng, H.; Yang, L.; Li, Y.; Jin, J.; Cao, W.; Yan, C.; Shi, Y. Mechanical responses of sheet-based gyroid-type triply periodic minimal surface lattice structures fabricated using selective laser melting. Mater. Des. 2022, 214, 110407. [Google Scholar] [CrossRef]
- Du Plessis, A.; Razavi, N.; Berto, F. The effects of microporosity in struts of gyroid lattice structures produced by laser powder bed fusion. Mater. Des. 2020, 194, 108899. [Google Scholar] [CrossRef]
- Jivrakh, K.B.; Varghese, A.M.; Ehrling, S.; Kuppireddy, S.; Polychronopoulou, K.; Al-Rub, R.K.A.; Alamoodi, N.; Karanikolos, G.N. 3D-Printed zeolite 13X gyroid monolith adsorbents for CO2 capture. Chem. Eng. J. 2024, 497, 154674. [Google Scholar] [CrossRef]
- Ho, J.Y.; Chang, T.T.; Ho, P.C.; Chang, H.K.; Chen, P.Y. Fabrication of gyroid-structured, hierarchically-porous hydroxyapatite scaffolds by a dual-templating method. Mater. Chem. Phys. 2024, 314, 128854. [Google Scholar] [CrossRef]
- Fina, F.; Goyanes, A.; Madla, C.M.; Awad, A.; Trenfield, S.J.; Kuek, J.M.; Patel, P.; Gaisford, S.; Basit, A.W. 3D printing of drug-loaded gyroid lattices using selective laser sintering. Int. J. Pharm. 2018, 547, 44–52. [Google Scholar] [CrossRef]
- Alizadeh-Osgouei, M.; Li, Y.; Vahid, A.; Ataee, A.; Wen, C. High strength porous PLA gyroid scaffolds manufactured via fused deposition modeling for tissue-engineering applications. Smart Mater. Med. 2021, 2, 15–25. [Google Scholar] [CrossRef]
- Salaha, Z.F.M.; Ammarullah, M.I.; Abdullah, N.N.A.A.; Aziz, A.U.A.; Gan, H.S.; Abdullah, A.H.; Abdul Kadir, M.R.; Ramlee, M.H. Biomechanical effects of the porous structure of gyroid and voronoi hip implants: A finite element analysis using an experimentally validated model. Materials 2023, 16, 3298. [Google Scholar] [CrossRef]
- Higuchi, T. Relationship between the fractal dimension and the power law index for a time series: A numerical investigation. Phys. D Nonlinear Phenom. 1990, 46, 254–264. [Google Scholar] [CrossRef]
- Beer, T.; Enting, I.G. Fractals, lattice models, and environmental systems. Environ. Int. 1991, 17, 519–533. [Google Scholar] [CrossRef]
- Gefen, Y.; Mandelbrot, B.B.; Aharony, A. Critical phenomena on fractal lattices. Phys. Rev. Lett. 1980, 45, 855. [Google Scholar] [CrossRef]
- Manna, S.; Nandy, S.; Roy, B. Higher-order topological phases on fractal lattices. Phys. Rev. B 2022, 105, L201301. [Google Scholar] [CrossRef]
- Kosior, A.; Sacha, K. Localization in random fractal lattices. Phys. Rev. B 2017, 95, 104206. [Google Scholar] [CrossRef]
- Zierenberg, J.; Fricke, N.; Marenz, M.; Spitzner, F.; Blavatska, V.; Janke, W. Percolation thresholds and fractal dimensions for square and cubic lattices with long-range correlated defects. Phys. Rev. E 2017, 96, 062125. [Google Scholar] [CrossRef]
- Zhang, Z.; Scarpa, F.; Bednarcyk, B.A.; Chen, Y. Harnessing fractal cuts to design robust lattice metamaterials for energy dissipation. Addit. Manuf. 2021, 46, 102126. [Google Scholar] [CrossRef]
- Nguyen-Van, V.; Wu, C.; Vogel, F.; Zhang, G.; Nguyen-Xuan, H.; Tran, P. Mechanical performance of fractal-like cementitious lightweight cellular structures: Numerical investigations. Compos. Struct. 2021, 269, 114050. [Google Scholar] [CrossRef]
- Rian, I.M.; Sassone, M.; Asayama, S. From fractal geometry to architecture: Designing a grid-shell-like structure using the Takagi–Landsberg surface. Comput.-Aided Des. 2018, 98, 40–53. [Google Scholar] [CrossRef]
- Cooper, J.M. Introduction to Partial Differential Equations with MATLAB; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Li, J.; Chen, Y.T. Computational Partial Differential Equations Using MATLAB®; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Pepper, D.W.; Heinrich, J.C. The Finite Element Method: Basic Concepts and Applications with MATLAB, MAPLE, and COMSOL; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Carpinteri, A. Fractal nature of material microstructure and size effects on apparent mechanical properties. Mech. Mater. 1994, 18, 89–101. [Google Scholar] [CrossRef]
- Xie, H.; Wang, J.A.; Xie, W.H. Fractal effects of surface roughness on the mechanical behavior of rock joints. Chaos Solitons Fractals 1997, 8, 221–252. [Google Scholar] [CrossRef]
- Yang, X.; Dai, H. Effect of geometric form of concrete meso-structure on its mechanical behavior under compression. Powder Technol. 2020, 360, 372–382. [Google Scholar] [CrossRef]
- Sanchez-Molina, D.; Velazquez-Ameijide, J.; Quintana, V.; Arregui-Dalmases, C.; Crandall, J.R.; Subit, D.; Kerrigan, J.R. Fractal dimension and mechanical properties of human cortical bone. Med Eng. Phys. 2013, 35, 576–582. [Google Scholar] [CrossRef]
- Elías-Zúñiga, A.; Martínez-Romero, O.; Trejo, D.O.; Palacios-Pineda, L.M. An Efficient Approach for Solving the Fractal, Damped Cubic-Quintic DUFFING’S Equation. Fractals 2024, 32, 1–10. [Google Scholar] [CrossRef]
- Elias-Zuniga, A.; Martinez-Romero, O.; Olvera-Trejo, D.; Perales-Martínez, I.A.; Palacios-Pineda, L.M. Exploring Insects Free Flight: Enhancing the Dipteran Flight Model to Include Fractal Effects. Fractals 2024, 32, 2450015. [Google Scholar] [CrossRef]
- Chen, R.; Zhang, W.; Jia, Y.; Wang, S.; Cao, B.; Li, C.; Du, J.; Yu, S.; Wei, J. Ultra-stiff and quasi-elastic-isotropic triply periodic minimal surface structures designed by deep learning. Mater. Des. 2024, 244, 113107. [Google Scholar] [CrossRef]
- Zhao, M.; Liu, F.; Fu, G.; Zhang, D.Z.; Zhang, T.; Zhou, H. Improved mechanical properties and energy absorption of BCC lattice structures with triply periodic minimal surfaces fabricated by SLM. Materials 2018, 11, 2411. [Google Scholar] [CrossRef] [PubMed]
- Lu, J.Y.; Silva, T.; Alzaabi, F.; Abu Al-Rub, R.K.; Lee, D.W. Insights into acoustic properties of seven selected triply periodic minimal surfaces-based structures: A numerical study. J. Low Freq. Noise Vib. Act. Control 2024, 43, 208–219. [Google Scholar] [CrossRef]
- Fu, H.; Kaewunruen, S. Experimental and DEM investigation of axially-loaded behaviours of IWP-based structures. Int. J. Mech. Sci. 2022, 235, 107738. [Google Scholar] [CrossRef]
- Elias-Zuniga, A.; Palacios-Pineda, L.M.; Jimenez-Cedeno, I.H.; Martinez-Romero, O.; Olvera-Trejo, D. A fractal model for current generation in porous electrodes. J. Electroanal. Chem. 2021, 880, 114883. [Google Scholar] [CrossRef]
- Liu, F.; Mao, Z.; Zhang, P.; Zhang, D.Z.; Jiang, J.; Ma, Z. Functionally graded porous scaffolds in multiple patterns: New design method, physical and mechanical properties. Mater. Des. 2018, 160, 849–860. [Google Scholar] [CrossRef]
- Naghavi, S.A.; Tamaddon, M.; Marghoub, A.; Wang, K.; Babamiri, B.B.; Hazeli, K.; Xu, W.; Lu, X.; Sun, C.; Wang, L.; et al. Mechanical characterisation and numerical modelling of TPMS-based gyroid and diamond Ti6Al4V scaffolds for bone implants: An integrated approach for translational consideration. Bioengineering 2022, 9, 504. [Google Scholar] [CrossRef]
- Maskery, I.; Aremu, A.O.; Parry, L.; Wildman, R.D.; Tuck, C.J.; Ashcroft, I.A. Effective design and simulation of surface-based lattice structures featuring volume fraction and cell type grading. Mater. Des. 2018, 155, 220–232. [Google Scholar] [CrossRef]
- Haney, C.W.; Siller, H.R. Anthropo-fidelic behavior of elastic-plastic lattice structures. Polym. Test. 2023, 120, 107970. [Google Scholar] [CrossRef]
- De Groot, R.; Peters, M.; De Haan, Y.; Dop, G.; Plasschaert, A. Failure stress criteria for composite resin. J. Dent. Res. 1987, 66, 1748–1752. [Google Scholar] [CrossRef]
- Ausiello, P.; Rengo, S.; Davidson, C.L.; Watts, D.C. Stress distributions in adhesively cemented ceramic and resin-composite Class II inlay restorations: A 3D-FEA study. Dent. Mater. 2004, 20, 862–872. [Google Scholar] [CrossRef] [PubMed]
- Shim, J.S.; Watts, D.C. An examination of the stress distribution in a soft-lined acrylic resin mandibular complete denture by finite element analysis. Int. J. Prosthodont. 2000, 13, 19. [Google Scholar] [PubMed]
- Ashok, D.; Bahubalendruni, M.R.; Mhaskar, A.; Choudhary, V.; Balamurali, G.; Turaka, S. Experimental and numerical investigation on 2.5-dimensional nature-inspired infill structures under out-plane quasi-static loading. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2023, 09544089231197853. [Google Scholar] [CrossRef]





| Lattice | Equation |
|---|---|
| Diamond | |
| Gyroid | |
| BCC | |
| IWP |
| Diamond | Gyroid | IWP | BCC | |
|---|---|---|---|---|
| B-lattice | 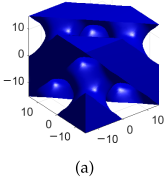 | 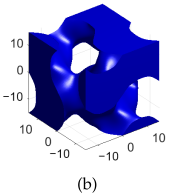 | 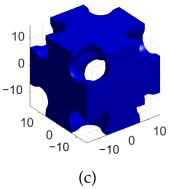 |  |
| B- subs S- lattice |  | 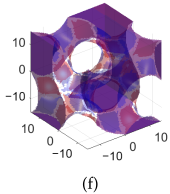 | 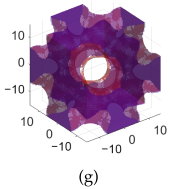 | 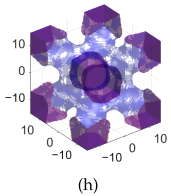 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Majari, P.; Olvera-Trejo, D.; Estrada-Díaz, J.A.; Elías-Zúñiga, A.; Martinez-Romero, O.; Ramírez-Herrera, C.A.; Perales-Martínez, I.A. Enhanced Lightweight Structures Through Brachistochrone-Inspired Lattice Design. Polymers 2025, 17, 654. https://doi.org/10.3390/polym17050654
Majari P, Olvera-Trejo D, Estrada-Díaz JA, Elías-Zúñiga A, Martinez-Romero O, Ramírez-Herrera CA, Perales-Martínez IA. Enhanced Lightweight Structures Through Brachistochrone-Inspired Lattice Design. Polymers. 2025; 17(5):654. https://doi.org/10.3390/polym17050654
Chicago/Turabian StyleMajari, Parisa, Daniel Olvera-Trejo, Jorge A. Estrada-Díaz, Alex Elías-Zúñiga, Oscar Martinez-Romero, Claudia A. Ramírez-Herrera, and Imperio Anel Perales-Martínez. 2025. "Enhanced Lightweight Structures Through Brachistochrone-Inspired Lattice Design" Polymers 17, no. 5: 654. https://doi.org/10.3390/polym17050654
APA StyleMajari, P., Olvera-Trejo, D., Estrada-Díaz, J. A., Elías-Zúñiga, A., Martinez-Romero, O., Ramírez-Herrera, C. A., & Perales-Martínez, I. A. (2025). Enhanced Lightweight Structures Through Brachistochrone-Inspired Lattice Design. Polymers, 17(5), 654. https://doi.org/10.3390/polym17050654








