A Surface-Enabled Computational Homogenization Method for Variable-Density Polymer Lattice Metastructures
Abstract
:1. Introduction
2. Problem Statement
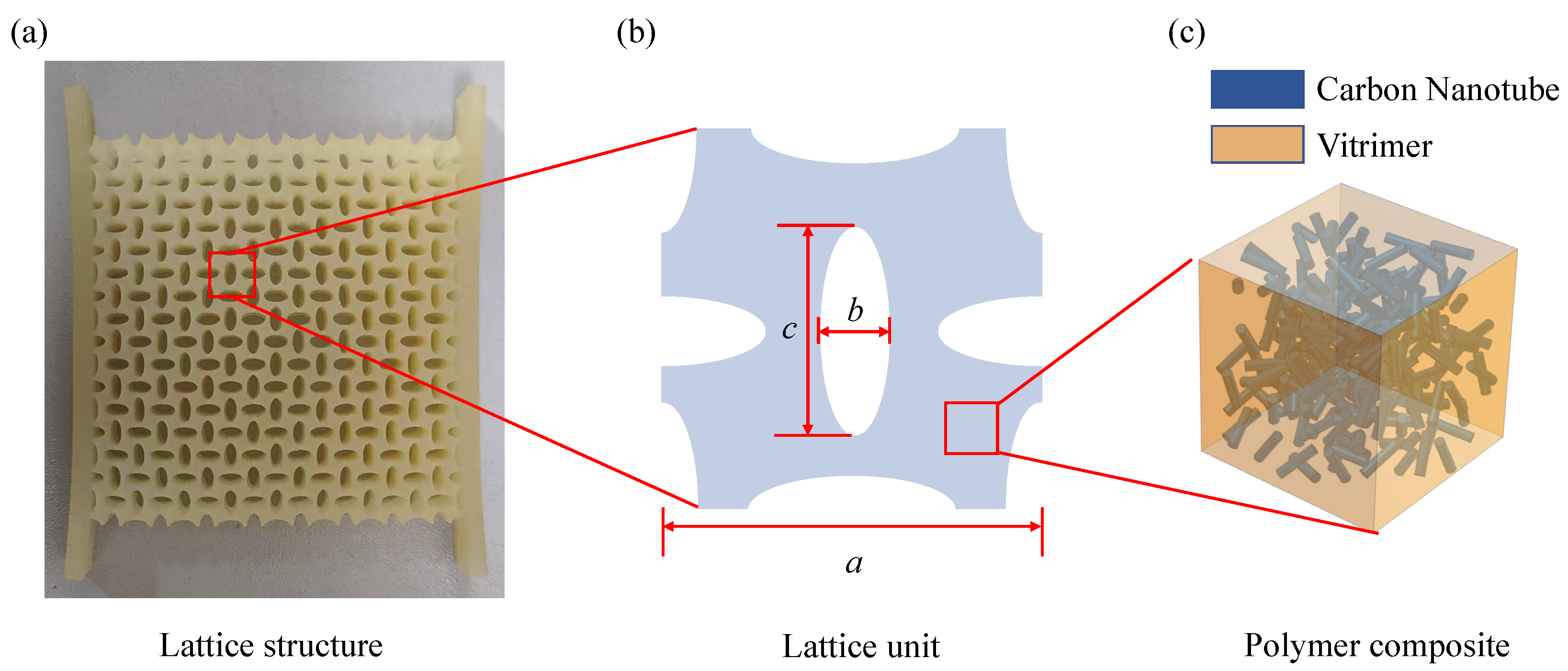
2.1. Importance of the Variable-Density Surface Effect
2.2. Key Problems and Contributions
- (1)
- VDPLMs exhibit an obvious surface effect when the lattice constant and the macroscopic size of the metastructure are of the same order of magnitude. However, the relationship between the microstructure and surface thickness is unclear, limiting their design and application. Therefore, at the scientific level, this paper aims to uncover the variable-density surface law governing the surface thickness of polymer metastructures with variable density.
- (2)
- Existing surface models that assume a constant surface thickness cannot accurately describe their size-dependent mechanical behavior. Therefore, at the theoretical level, it is necessary to establish a variable-density surface elastic model to describe the mechanical behavior of variable-density microstructures.
- (3)
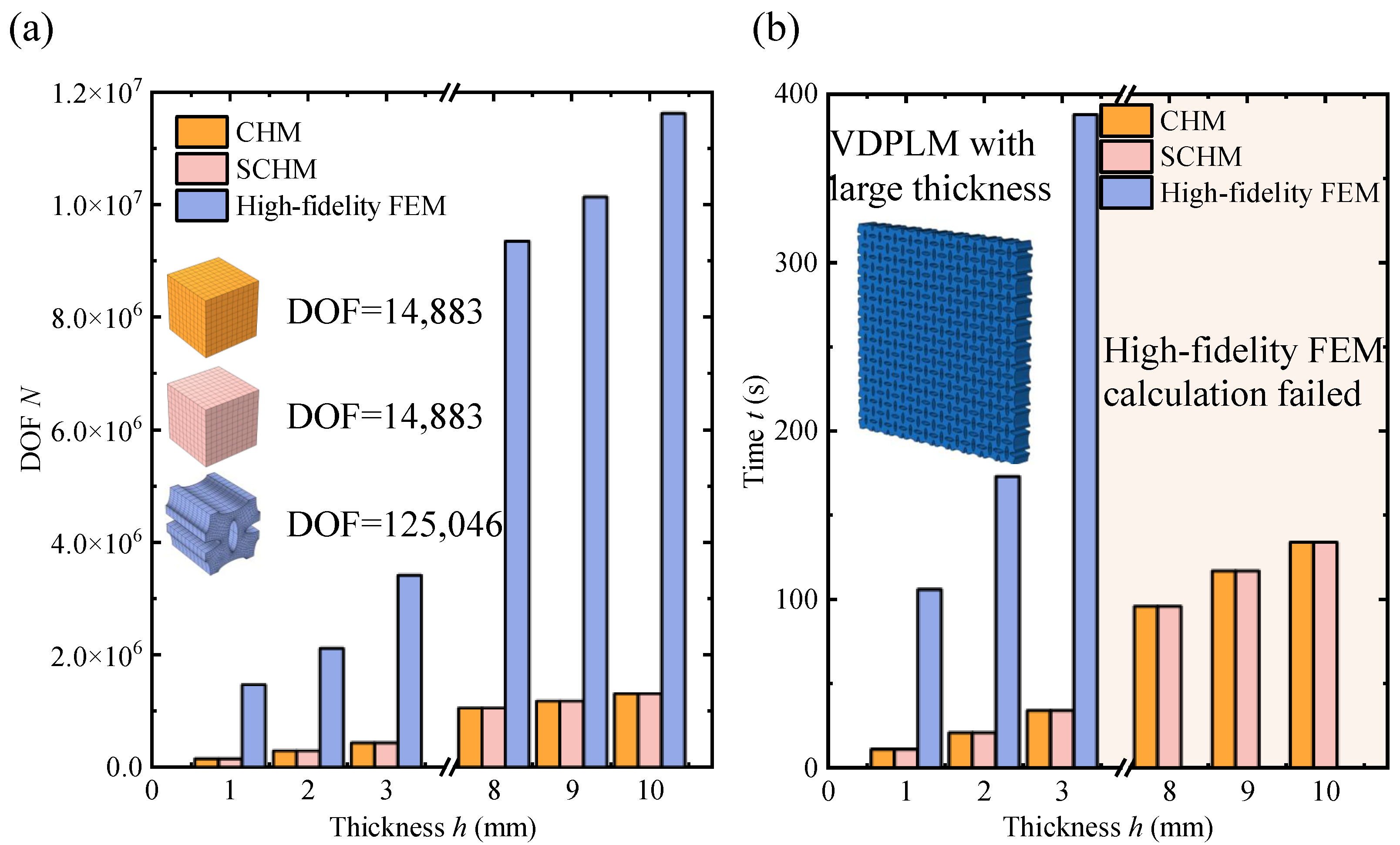
- VDPLMs have complex microstructures, and using the high-fidelity FEM to fully resolve these microstructures requires substantial computational resources and time. Therefore, to predict the mechanical properties of polymer metastructures incorporating surface effect due to the surface effect with both high efficiency and accuracy, at the technical level, it is essential to develop a homogenization method that accounts for the variable-density surface effect.
- (a)
- Scientific breakthrough: Current limitations in predicting mechanical performance stem from incomplete knowledge of surface-induced size effects of variable-density polymer lattice metastructures. By employing high-fidelity finite element simulations, we reveal a novel variable-density surface law governing the surface intrinsic length at macroscopic scales, which is fundamentally determined by the lattice configuration.
- (b)
- Methodological innovation: Traditional homogenization methods based on scale separation prove inadequate when macroscopic dimensions approach surface intrinsic lengths. To overcome this, we develop a surface-enabled computational homogenization framework informed by our variable-density surface law discovery. This new approach enables efficient macroscopic prediction of mechanical behaviors while preserving critical configuration-dependent surface effects.
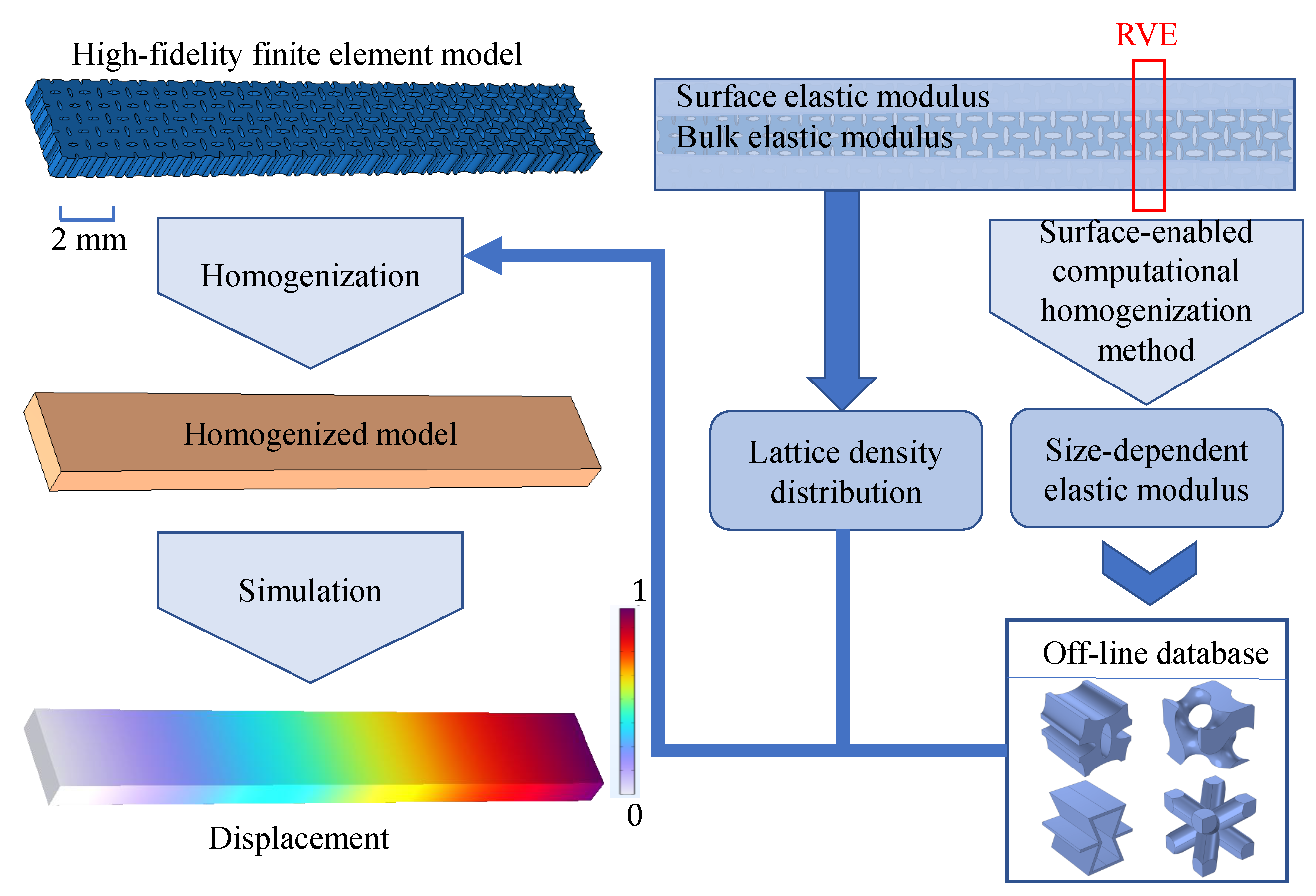
3. A Homogenization Method for the VDPLM Incorporating the Surface Effect
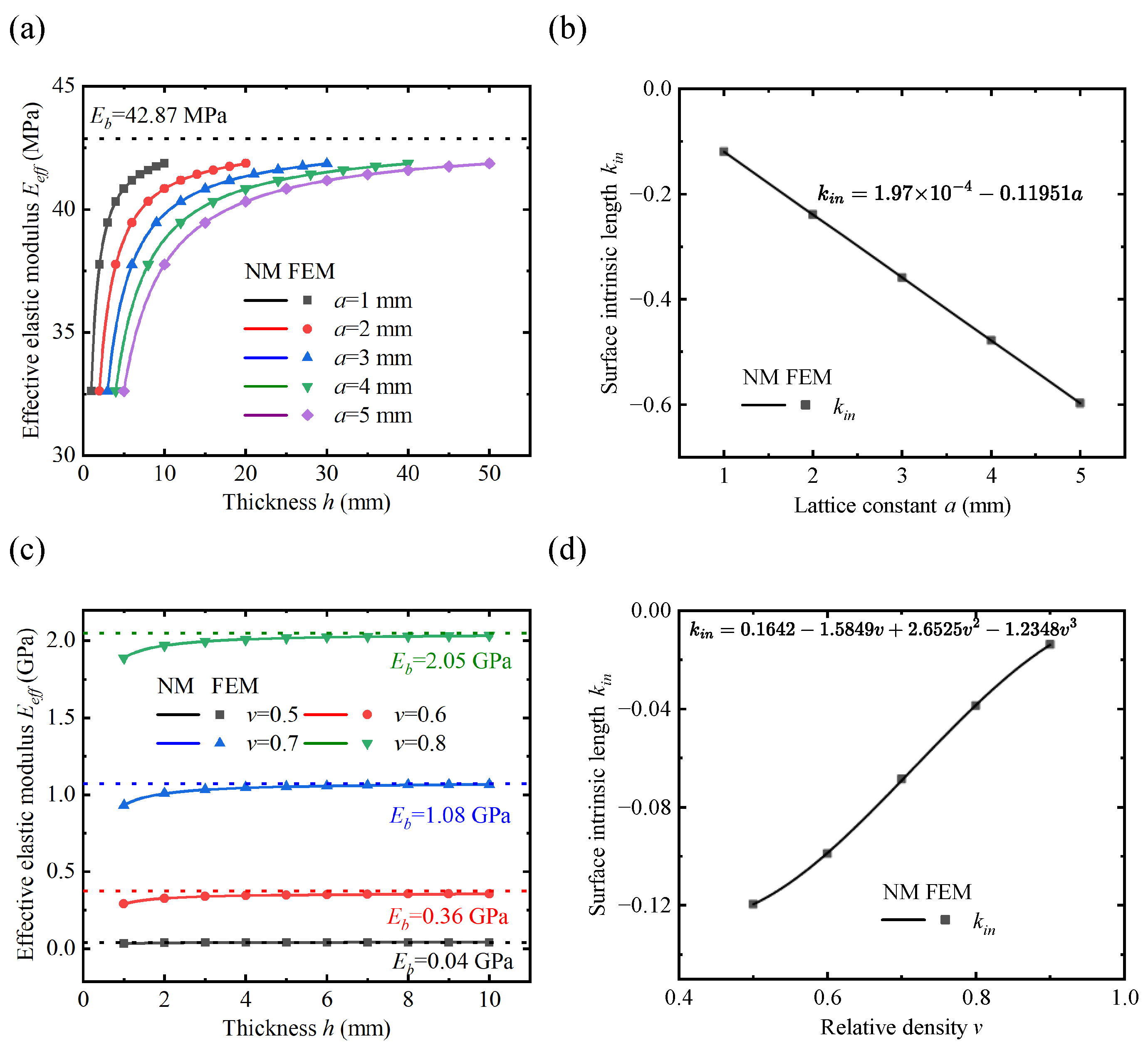
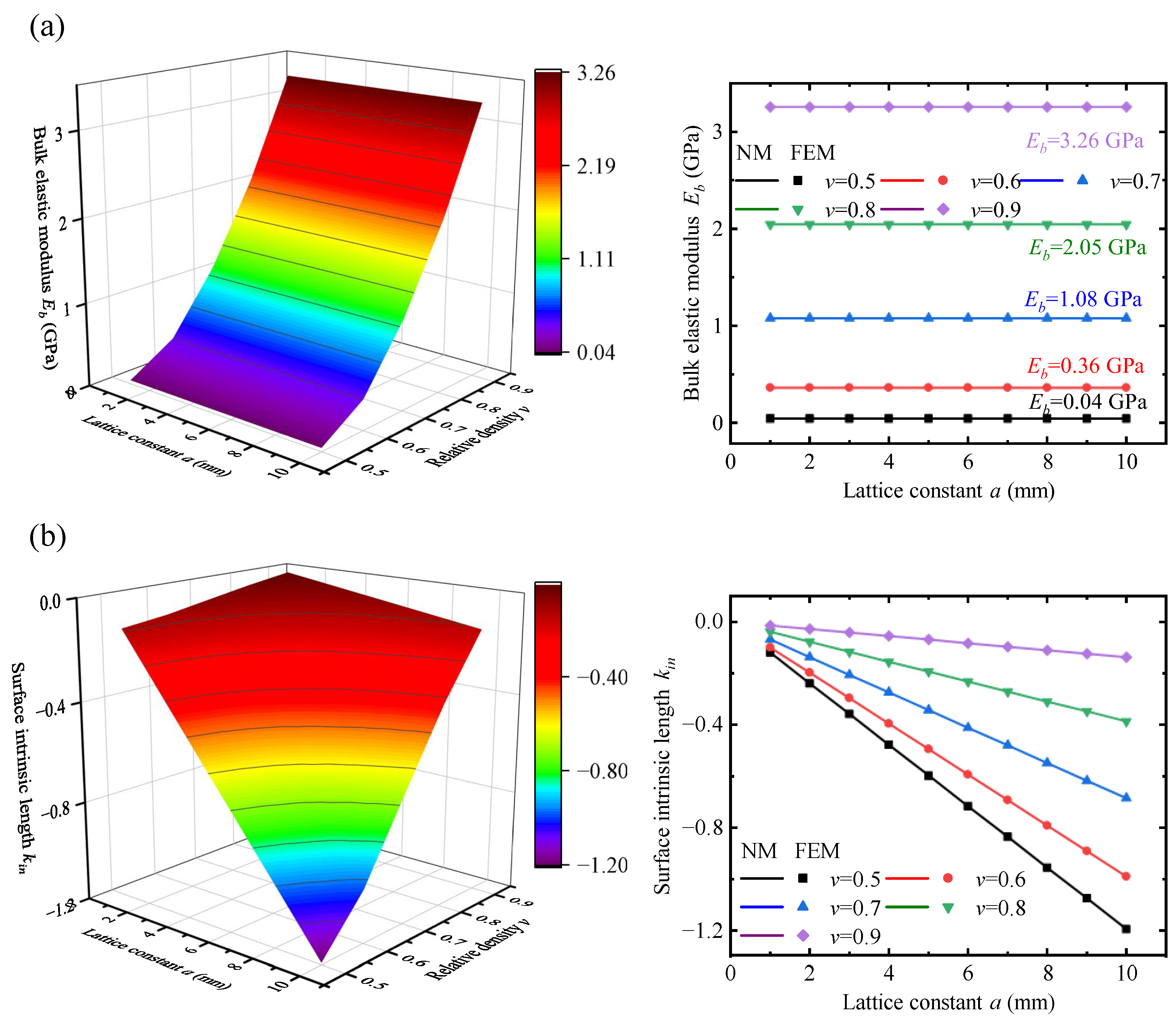
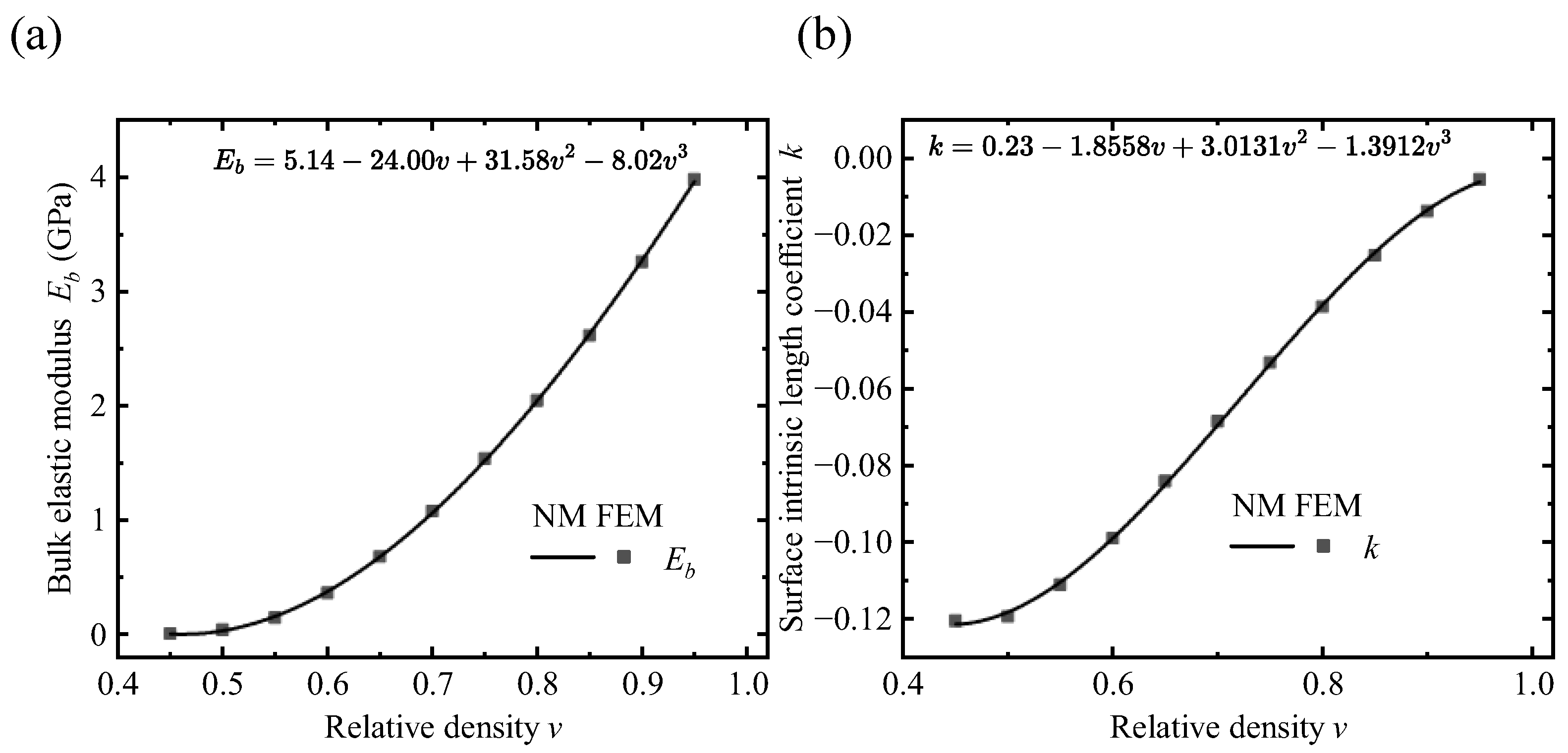
3.1. A Variable-Density Surface Law
3.2. Effective Elastic Modulus Incorporating the Surface Effect of the
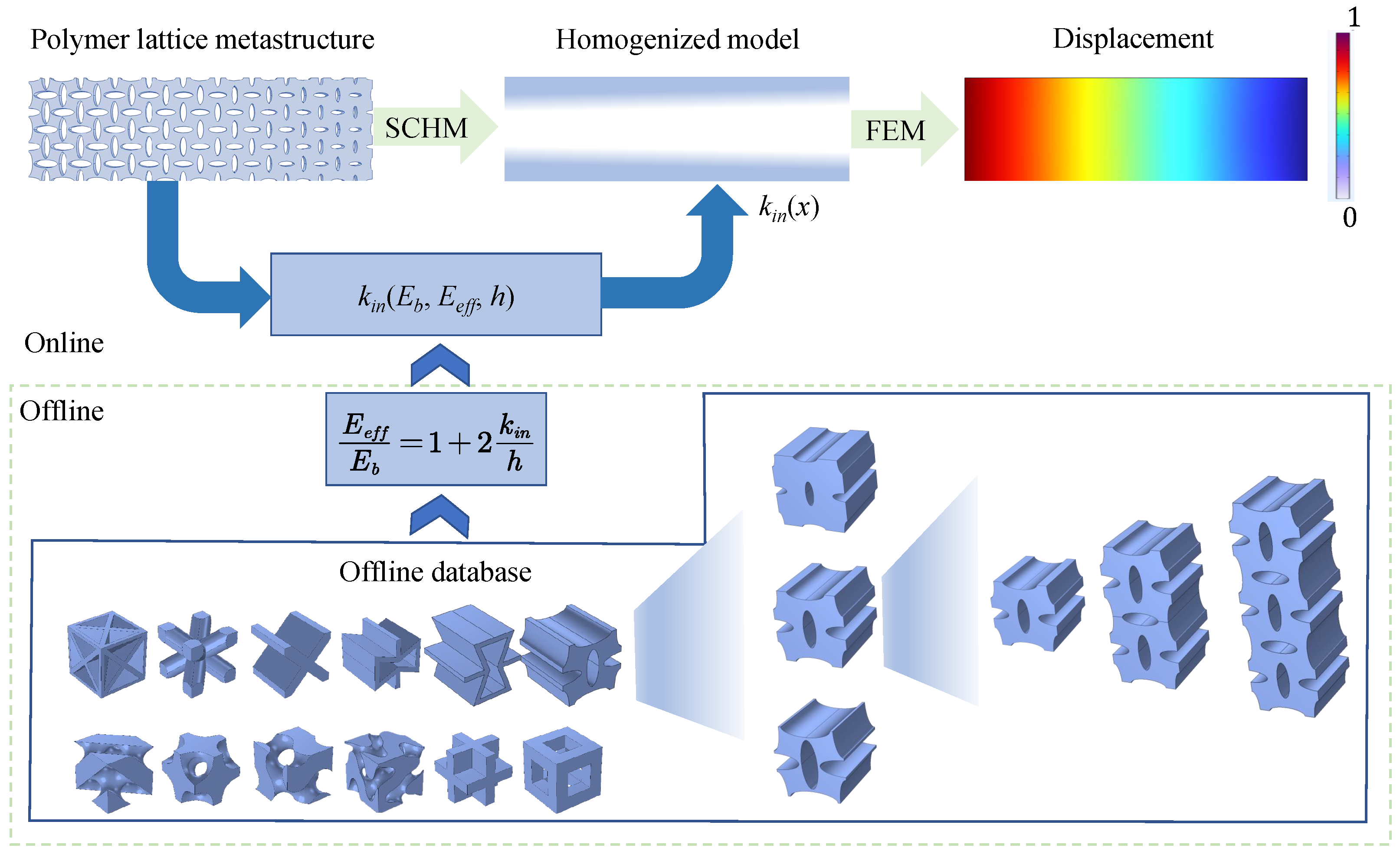
3.3. Surface-Enabled Computational Homogenization Method
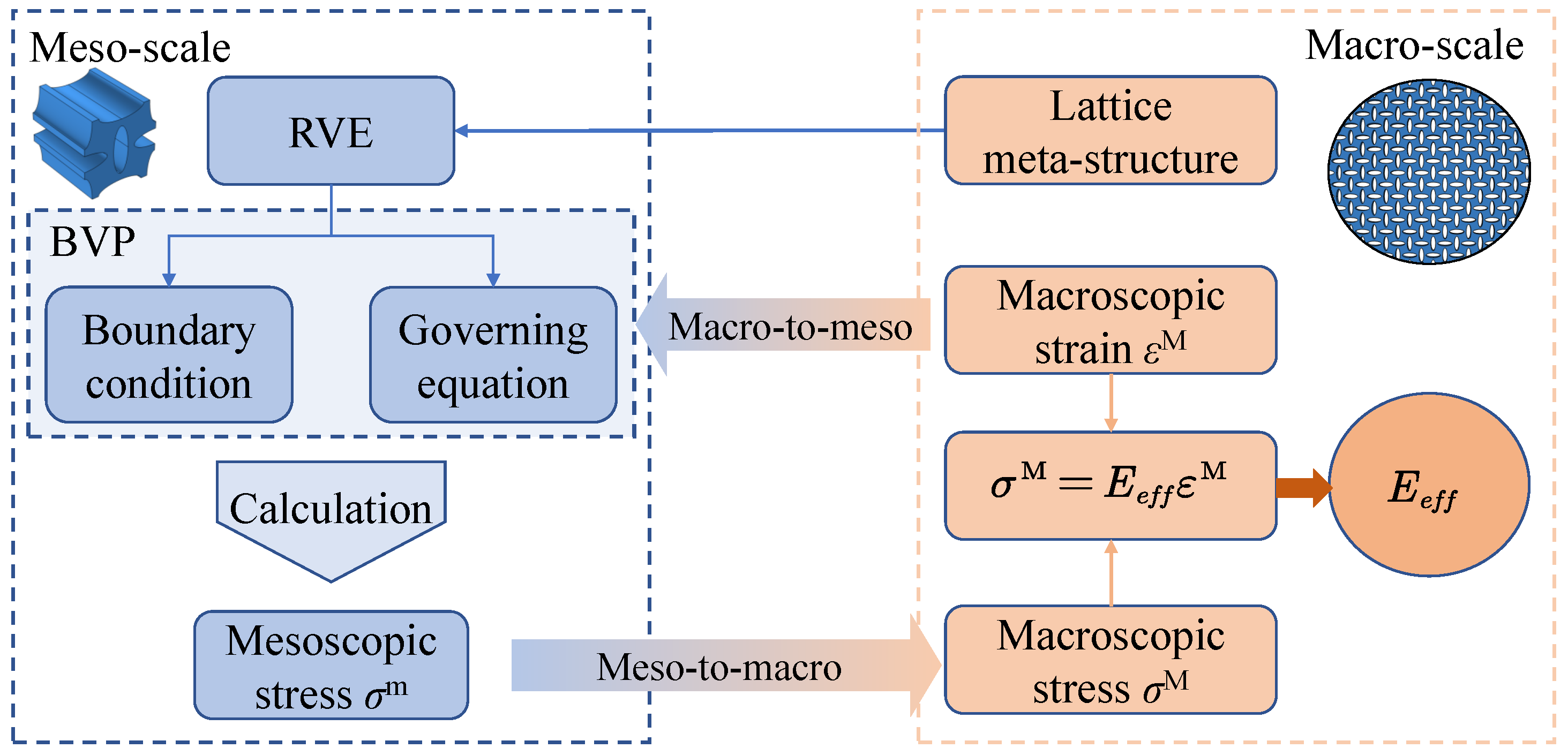
3.3.1. Macro-to-Meso Scale Transition
3.3.2. Meso-to-Macro Scale Transition Using the Hill–Mandel Condition
3.4. Calibration Method for the Surface Intrinsic Length
3.4.1. Effective Elastic Modulus
3.4.2. Implementation of the FEM-Based Homogenization Method
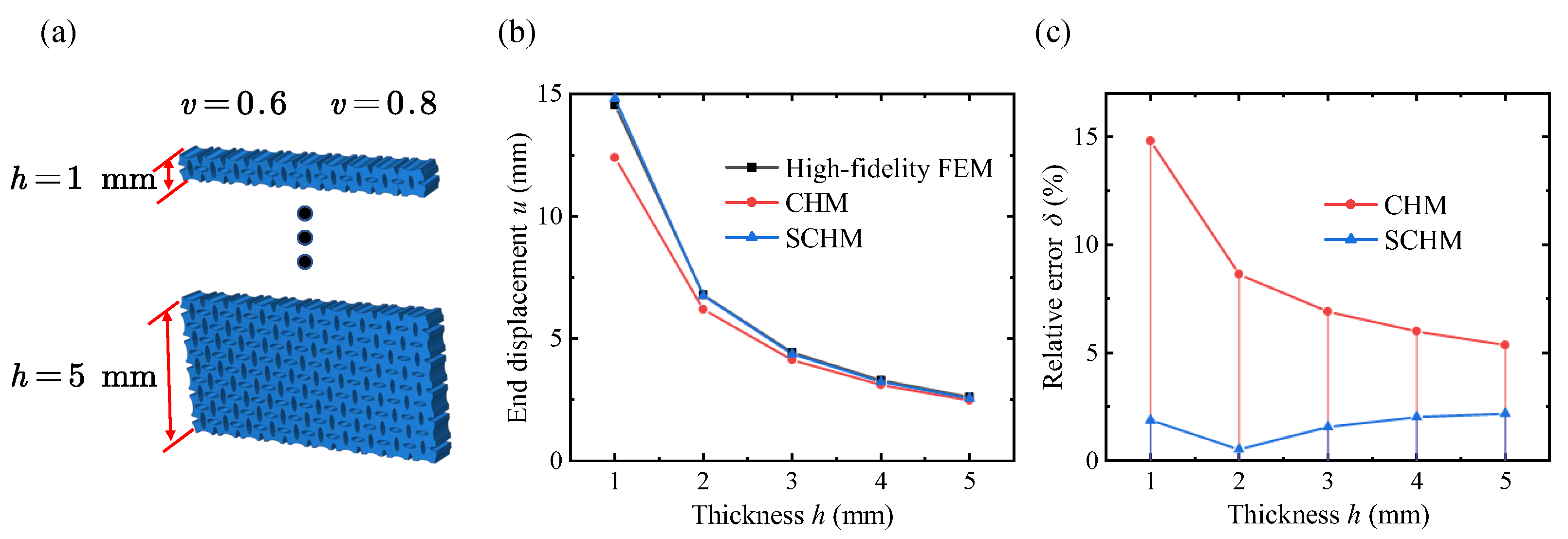
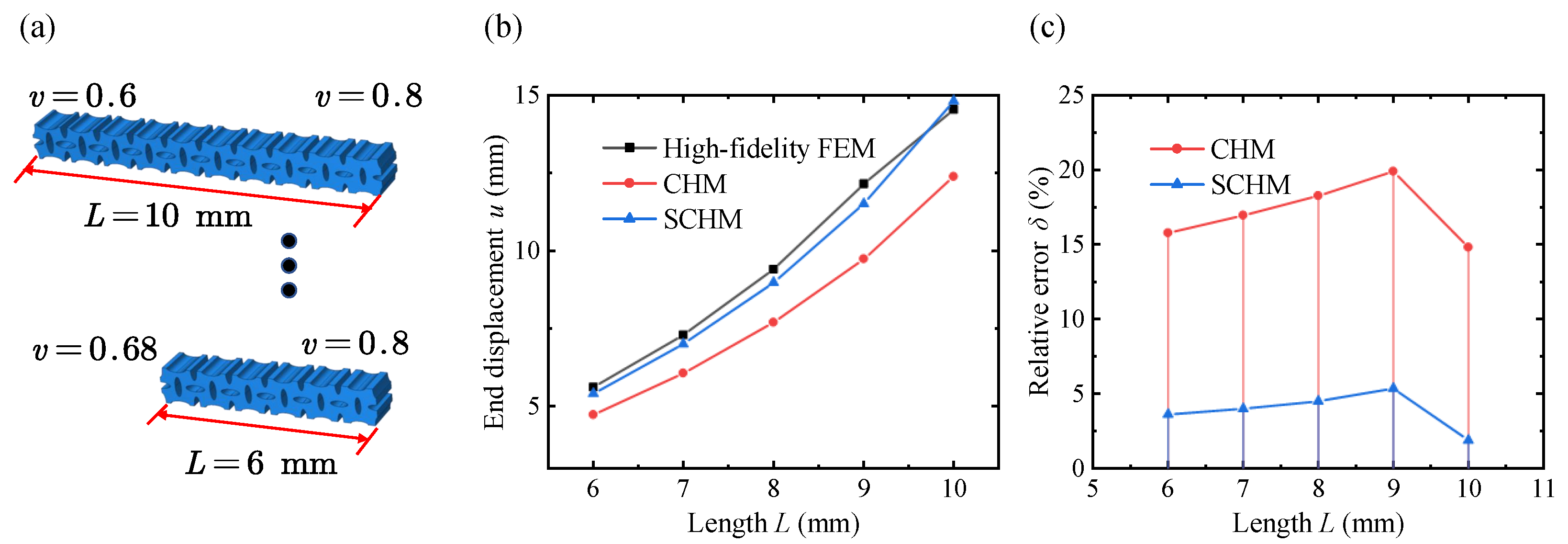
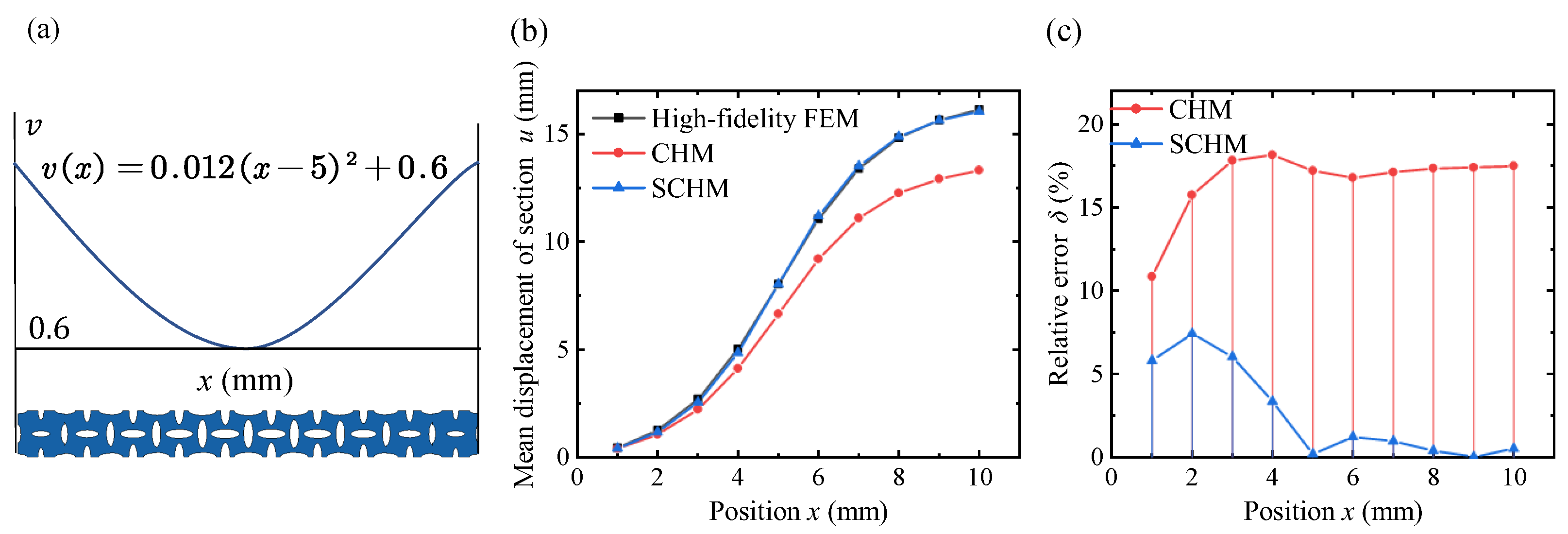
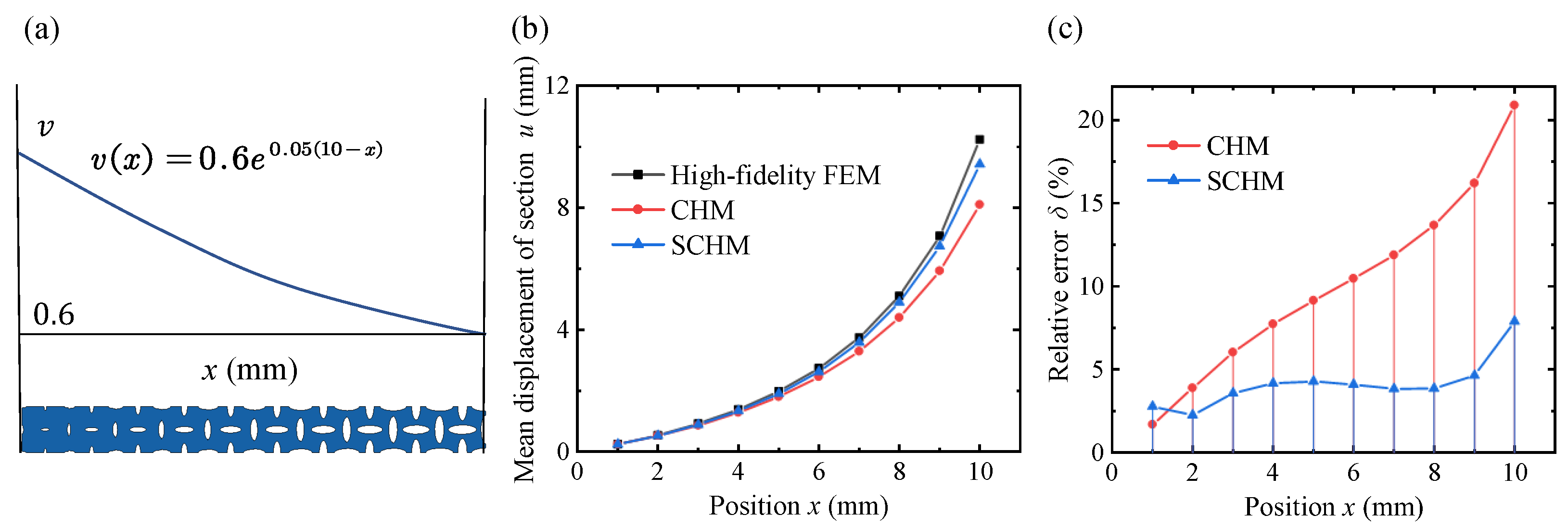
4. Results and Discussion
4.1. Effect of Material Parameters on the Effective Elastic Modulus
4.2. Effect of Lattice Geometry on the Effective Elastic Modulus
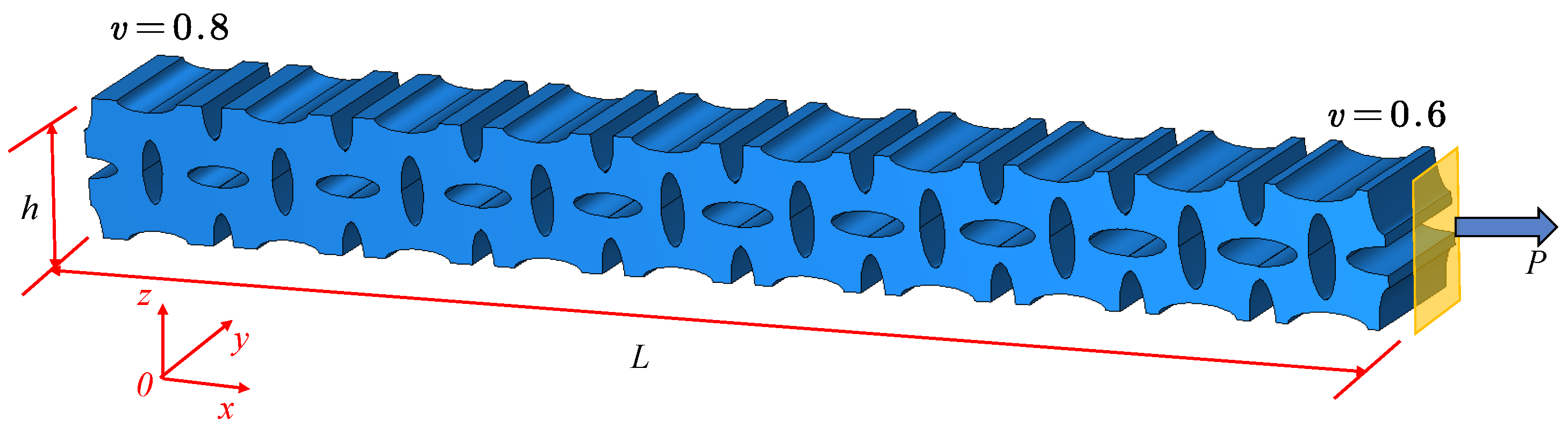
4.3. Application of the VDPLM Under Tension
5. Conclusions
- (1)
- Compared with the bulk lattices, the lattices in the surface region lack the interaction of adjacent lattices. Therefore, the effective elastic modulus of lattices in the surface region is different from that in the bulk region, which is known as the surface effect. The varying volume occupancy and elasticity of these two regions contribute to the size-dependent effective elasticity of the lattice metastructure. In the VDPLM, the lattice density is position-dependent, which in turn causes the effective elasticity to also vary with position. Therefore, the VDPLM shows microstructure-dependent variable-density surface effects.
- (2)
- To predict the mechanical properties of the VDPLM with high accuracy and efficiency, an FEM-based homogenization method for the VDPLM incorporating surface effect was proposed. An offline database of effective elastic modulus was established through the proposed method. According to the offline database, we revealed the variable-density surface law of the surface intrinsic length. The variable-density surface law shows that the surface intrinsic length is related to the lattice type, relative density, and lattice constant, where it shows a clear linear relationship with the lattice constant.
- (3)
- An efficient and high-precision surface elastic model was proposed, which overcomes the inaccuracy of the classical model by inducing a surface intrinsic length obeying the variable-density surface law and the time-consuming problem of high-fidelity finite element analysis.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kangishwar, S.; Radhika, N.; Sheik, A.A.; Chavali, A.; Hariharan, S. A comprehensive review on polymer matrix composites: Material selection, fabrication, and application. Polym. Bull. 2022, 80, 47–87. [Google Scholar] [CrossRef]
- Rajak, D.; Pagar, D.; Menezes, P.; Linul, E. Fiber-Reinforced Polymer Composites: Manufacturing, Properties, and Applications. Polymers 2019, 11, 1667. [Google Scholar] [CrossRef] [PubMed]
- Veerabagu, U.; Palza, H.; Quero, F. Review: Auxetic Polymer-Based Mechanical Metamaterials for Biomedical Applications. ACS Biomater. Sci. Eng. 2022, 8, 2798–2824. [Google Scholar] [CrossRef] [PubMed]
- Garg, A.; Sharma, A.; Zheng, W.; Li, L. A review on artificial intelligence-enabled mechanical analysis of 3D printed and FEM-modelled auxetic metamaterials. Virtual Phys. Prototyp. 2025, 20, e2445712. [Google Scholar] [CrossRef]
- Li, S.; Zheng, W.; Li, L. Spatiotemporally nonlocal homogenization method for viscoelastic porous metamaterial structures. Int. J. Mech. Sci. 2024, 282, 109572. [Google Scholar] [CrossRef]
- Li, S.; Duan, K.; He, Y.; Li, L. A configuration-driven nonlocal model for functionally graded lattices. Int. J. Eng. Sci. 2025, 209, 104222. [Google Scholar] [CrossRef]
- Brunet, T.; Merlin, A.; Mascaro, B.; Zimny, K.; Leng, J.; Poncelet, O.; Aristégui, C.; Mondain-Monval, O. Soft 3D acoustic metamaterial with negative index. Nat. Mater. 2014, 14, 384–388. [Google Scholar] [CrossRef]
- Padilla, W.J.; Basov, D.N.; Smith, D.R. Negative refractive index metamaterials. Mater. Today 2006, 9, 28–35. [Google Scholar] [CrossRef]
- Li, S.; Li, L. A homogenization method incorporating surface effect for thin metamaterial structure. Int. J. Eng. Sci. 2024, 201, 104093. [Google Scholar] [CrossRef]
- Yang, H.; Ganzosch, G.; Giorgio, I.; Abali, B.E. Material characterization and computations of a polymeric metamaterial with a pantographic substructure. Z. Angew. Math. Phys. 2018, 69, 105. [Google Scholar] [CrossRef]
- Truszkiewicz, E.; Thalhamer, A.; Rossegger, M.; Vetter, M.; Meier, G.; Rossegger, E.; Fuchs, P.; Schlögl, S.; Berer, M. Mechanical behavior of 3D-printed polymeric metamaterials for lightweight applications. J. Appl. Polym. Sci. 2021, 139, 51618. [Google Scholar] [CrossRef]
- Panirani, P.N.; Ghanbari, J. Design and optimization of bio-inspired thin-walled structures for energy absorption applications. Int. J. Crashworthiness 2022, 28, 1–12. [Google Scholar] [CrossRef]
- Song, J.; Huo, Q.; Li, D.; Chen, B.; Zhang, J. Energy-Absorption Behavior of Novel Bio-Inspired Thin-Walled Honeycomb Tubes Filled with TPMS Structure. Coatings 2024, 14, 675. [Google Scholar] [CrossRef]
- Du, J.; Hao, P.; Liu, M.; Xue, R.; Li, L. Energy absorbed ability and damage analysis for honeycomb sandwich material of bio-inspired micro aerial vehicle under low velocity impact. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2020, 237, 4175–4186. [Google Scholar] [CrossRef]
- Yadav, R.; Tirumali, M.; Wang, X.; Naebe, M.; Kandasubramanian, B. Polymer composite for antistatic application in aerospace. Def. Technol. 2020, 16, 107–118. [Google Scholar] [CrossRef]
- Raja, S.; AhmedMustafa, M.; KamilGhadir, G.; MusaadAl-Tmimi, H.; KhalidAlani, Z.; AliRusho, M.; Rajeswari, N. An analysis of polymer material selection and design optimization to improve Structural Integrity in 3D printed aerospace components. Appl. Chem. Eng. 2024, 7, 1875. [Google Scholar] [CrossRef]
- Lyu, M.Y.; Choi, T.G. Research trends in polymer materials for use in lightweight vehicles. Int. J. Precis. Eng. Manuf. 2015, 16, 213–220. [Google Scholar] [CrossRef]
- Volpe, V.; Lanzillo, S.; Affinita, G.; Villacci, B.; Macchiarolo, I.; Pantani, R. Lightweight High-Performance Polymer Composite for Automotive Applications. Polymers 2019, 11, 326. [Google Scholar] [CrossRef]
- Rossignolo, J.A.; Agnesini, M.V. Mechanical properties of polymer-modified lightweight aggregate concrete. Cem. Concr. Res. 2002, 32, 329–334. [Google Scholar] [CrossRef]
- Liu, L.; Zhu, M.; Feng, J.; Peng, H.; Shi, Y.; Gao, J.; Tang, L.; Song, P. Fire-retardant and high-strength polymeric materials enabled by supramolecular aggregates: Special Collection: Distinguished Australian Researchers. Aggregate 2024, 5, e494. [Google Scholar] [CrossRef]
- Yao, Y.; Jin, S.; Zou, H.; Li, L.; Ma, X.; Lv, G.; Gao, F.; Lv, X.; Shu, Q. Polymer-based lightweight materials for electromagnetic interference shielding: A review. J. Mater. Sci. 2021, 56, 6549–6580. [Google Scholar] [CrossRef]
- Oda, H.; Konno, T.; Ishihara, K. Efficient differentiation of stem cells encapsulated in a cytocompatible phospholipid polymer hydrogel with tunable physical properties. Biomaterials 2015, 56, 86–91. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Xie, B.; Liu, Q.; Kong, B.; Wang, H. Fabrication and characterization of a novel polysaccharide based composite nanofiber films with tunable physical properties. Carbohydr. Polym. 2020, 236, 116054. [Google Scholar] [CrossRef]
- Fadeev, A.A.; Bím, D.; Císařová, I.; Kotora, M. Bioinspired intramolecular spirocyclopropanation of quinones as an interrupted photoredox process. Org. Chem. Front. 2024, 11, 5703–5711. [Google Scholar] [CrossRef]
- An, X.; Sun, G.; Yuan, X.; Tian, Y.; Hou, X.; Fan, H. Design of Kagome lattice composite sandwich metastructures with high load bearing and low frequency vibration reduction properties. Compos. Part A Appl. Sci. Manuf. 2023, 174, 107716. [Google Scholar] [CrossRef]
- Ashby, M.F.; Evans, A.; Fleck, N.A.; Gibson, L.J.; Hutchinson, J.W.; Wadley, H.N. Metal foams: A design guide. Mater. Des. 2002, 23, 119. [Google Scholar] [CrossRef]
- Deshpande, V.; Fleck, N. Collapse of truss core sandwich beams in 3-point bending. Int. J. Solids Struct. 2001, 38, 6275–6305. [Google Scholar] [CrossRef]
- Deshpande, V.; Fleck, N.; Ashby, M. Effective properties of the octet-truss lattice material. J. Mech. Phys. Solids 2001, 49, 1747–1769. [Google Scholar] [CrossRef]
- Gu, D. Material-structure-performance integrated laser-metal additive manufacturing. In Laser Additive Manufacturing of Metallic Materials and Components; Elsevier: Amsterdam, The Netherlands, 2023; pp. 1–33. [Google Scholar] [CrossRef]
- Wong, K.V.; Hernandez, A. A Review of Additive Manufacturing. ISRN Mech. Eng. 2012, 2012, 1–10. [Google Scholar] [CrossRef]
- Gibson, I.; Rosen, D.W.; Stucker, B.; Khorasani, M.; Rosen, D.; Stucker, B.; Khorasani, M. Additive Manufacturing Technologies; Springer: Berlin/Heidelberg, Germany, 2021; Volume 17. [Google Scholar] [CrossRef]
- Evans, A.; Hutchinson, J.; Fleck, N.; Ashby, M.; Wadley, H. The topological design of multifunctional cellular metals. Prog. Mater. Sci. 2001, 46, 309–327. [Google Scholar] [CrossRef]
- Murr, L.E.; Gaytan, S.M.; Medina, F.; Lopez, H.; Martinez, E.; Machado, B.I.; Hernandez, D.H.; Martinez, L.; Lopez, M.I.; Wicker, R.B.; et al. Next-generation biomedical implants using additive manufacturing of complex, cellular and functional mesh arrays. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2010, 368, 1999–2032. [Google Scholar] [CrossRef] [PubMed]
- Murr, L.; Amato, K.; Li, S.; Tian, Y.; Cheng, X.; Gaytan, S.; Martinez, E.; Shindo, P.; Medina, F.; Wicker, R. Microstructure and mechanical properties of open-cellular biomaterials prototypes for total knee replacement implants fabricated by electron beam melting. J. Mech. Behav. Biomed. Mater. 2011, 4, 1396–1411. [Google Scholar] [CrossRef] [PubMed]
- Jafferson, J.; Chatterjee, D. A review on polymeric materials in additive manufacturing. Mater. Today Proc. 2021, 46, 1349–1365. [Google Scholar] [CrossRef]
- Tan, L.J.; Zhu, W.; Zhou, K. Recent progress on polymer materials for additive manufacturing. Adv. Funct. Mater. 2020, 30, 2003062. [Google Scholar] [CrossRef]
- Bourell, D.; Kruth, J.P.; Leu, M.; Levy, G.; Rosen, D.; Beese, A.M.; Clare, A. Materials for additive manufacturing. CIRP Ann. 2017, 66, 659–681. [Google Scholar] [CrossRef]
- Lendlein, A.; Kelch, S. Shape-Memory Polymers. Angew. Chem. Int. Ed. 2002, 41, 2034. [Google Scholar] [CrossRef]
- Rahmatabadi, D.; Khajepour, M.; Bayati, A.; Mirasadi, K.; Amin Yousefi, M.; Shegeft, A.; Ghasemi, I.; Baniassadi, M.; Abrinia, K.; Bodaghi, M.; et al. Advancing sustainable shape memory polymers through 4D printing of polylactic acid-polybutylene adipate terephthalate blends. Eur. Polym. J. 2024, 216, 113289. [Google Scholar] [CrossRef]
- Mukherjee, C.; Varghese, D.; Krishna, J.; Boominathan, T.; Rakeshkumar, R.; Dineshkumar, S.; Brahmananda Rao, C.; Sivaramakrishna, A. Recent advances in biodegradable polymers – Properties, applications and future prospects. Eur. Polym. J. 2023, 192, 112068. [Google Scholar] [CrossRef]
- Dananjaya, S.; Chevali, V.; Dear, J.; Potluri, P.; Abeykoon, C. 3D printing of biodegradable polymers and their composites – Current state-of-the-art, properties, applications, and machine learning for potential future applications. Prog. Mater. Sci. 2024, 146, 101336. [Google Scholar] [CrossRef]
- Jin, X.; Li, G.; Gong, J. Optimal design and modeling of 3D variable-density lattice structures. In Proceedings of the 2017 8th International Conference on Mechanical and Aerospace Engineering (ICMAE), Prague, Czech Republic, 22–25 July 2017; IEEE: New York, NY, USA, 2017; pp. 320–325. [Google Scholar] [CrossRef]
- McConaha, M.; Venugopal, V.; Anand, S. Design Tool for Topology Optimization of Self Supporting Variable Density Lattice Structures for Additive Manufacturing. J. Manuf. Sci. Eng. 2021, 143, 071001. [Google Scholar] [CrossRef]
- Cheng, L.; Liang, X.; Belski, E.; Wang, X.; Sietins, J.M.; Ludwick, S.; To, A. Natural Frequency Optimization of Variable-Density Additive Manufactured Lattice Structure: Theory and Experimental Validation. J. Manuf. Sci. Eng. 2018, 140, 105002. [Google Scholar] [CrossRef]
- Nazir, A.; Arshad, A.B.; Jeng, J.Y. Buckling and Post-Buckling Behavior of Uniform and Variable-Density Lattice Columns Fabricated Using Additive Manufacturing. Materials 2019, 12, 3539. [Google Scholar] [CrossRef] [PubMed]
- Takezawa, A.; Chen, Q.; To, A.C. Optimally variable density lattice to reduce warping thermal distortion of laser powder bed fusion. Addit. Manuf. 2021, 48, 102422. [Google Scholar] [CrossRef]
- Traxel, K.D.; Groden, C.; Valladares, J.; Bandyopadhyay, A. Mechanical properties of additively manufactured variable lattice structures of Ti6Al4V. Mater. Sci. Eng. A 2021, 809, 140925. [Google Scholar] [CrossRef]
- Tang, Y.; Dong, G.; Zhou, Q.; Zhao, Y.F. Lattice structure design and optimization with additive manufacturing constraints. IEEE Trans. Autom. Sci. Eng. 2017, 15, 1546–1562. [Google Scholar] [CrossRef]
- Takezawa, A.; To, A.C.; Chen, Q.; Liang, X.; Dugast, F.; Zhang, X.; Kitamura, M. Sensitivity analysis and lattice density optimization for sequential inherent strain method used in additive manufacturing process. Comput. Methods Appl. Mech. Eng. 2020, 370, 113231. [Google Scholar] [CrossRef]
- Ueno, A.; Guo, H.; Takezawa, A.; Moritoyo, R.; Kitamura, M. Temperature Distribution Design Based on Variable Lattice Density Optimization and Metal Additive Manufacturing. Symmetry 2021, 13, 1194. [Google Scholar] [CrossRef]
- Cheng, L.; Liu, J.; To, A.C. Concurrent lattice infill with feature evolution optimization for additive manufactured heat conduction design. Struct. Multidiscip. Optim. 2018, 58, 511–535. [Google Scholar] [CrossRef]
- Shu, W.; Stanciulescu, I. Computational modeling and multiscale homogenization of short fiber composites considering complex microstructure and imperfect interfaces. Compos. Struct. 2023, 306, 116592. [Google Scholar] [CrossRef]
- Shu, W.; Stanciulescu, I. Multiscale homogenization method for the prediction of elastic properties of fiber-reinforced composites. Int. J. Solids Struct. 2020, 203, 249–263. [Google Scholar] [CrossRef]
- Bishara, D.; Xie, Y.; Liu, W.K.; Li, S. A State-of-the-Art Review on Machine Learning-Based Multiscale Modeling, Simulation, Homogenization and Design of Materials. Arch. Comput. Methods Eng. 2022, 30, 191–222. [Google Scholar] [CrossRef]
- Akinbade, Y.; Harries, K.A. Is the rule of mixture appropriate for assessing bamboo material properties? Constr. Build. Mater. 2021, 267, 120955. [Google Scholar] [CrossRef]
- Luo, Y. Isotropized Voigt-Reuss model for prediction of elastic properties of particulate composites. Mech. Adv. Mater. Struct. 2021, 29, 3934–3941. [Google Scholar] [CrossRef]
- Hershey, A.V. The Elasticity of an Isotropic Aggregate of Anisotropic Cubic Crystals. J. Appl. Mech. 1954, 21, 236–240. [Google Scholar] [CrossRef]
- Hill, R. A self-consistent mechanics of composite materials. J. Mech. Phys. Solids 1965, 13, 213–222. [Google Scholar] [CrossRef]
- Mori, T.; Tanaka, K. Average stress in matrix and average elastic energy of materials with misfitting inclusions. Acta Metall. 1973, 21, 571–574. [Google Scholar] [CrossRef]
- Song, Z.; Peng, X.; Tang, S.; Fu, T. A homogenization scheme for elastoplastic composites using concept of Mori-Tanaka method and average deformation power rate density. Int. J. Plast. 2020, 128, 102652. [Google Scholar] [CrossRef]
- Needleman, A. Computational mechanics at the mesoscale. Acta Mater. 2000, 48, 105–124. [Google Scholar] [CrossRef]
- Zhou, H.; Zhu, J.; Wang, C.; Zhang, Y.; Wang, J.; Zhang, W. Hierarchical structure optimization with parameterized lattice and multiscale finite element method. Struct. Multidiscip. Optim. 2022, 65, 39. [Google Scholar] [CrossRef]
- Dong, Z.; Quan, W.; Ma, X.; Li, X.; Zhou, J. Asymptotic homogenization of effective thermal-elastic properties of concrete considering its three-dimensional mesostructure. Comput. Struct. 2023, 279, 106970. [Google Scholar] [CrossRef]
- Aboudi, J. Generalized effective stiffness theory for the modeling of fiber-reinforced composites. Int. J. Solids Struct. 1981, 17, 1005–1018. [Google Scholar] [CrossRef]
- Ghosh, S.; Mallett, R. Voronoi cell finite elements. Comput. Struct. 1994, 50, 33–46. [Google Scholar] [CrossRef]
- Mao, C.; Zhang, R.; Guo, R.; Zhao, X. Two-scale modeling of particle crack initiation and propagation in particle-reinforced composites by using microscale analysis based on Voronoi cell finite element model. Compos. Struct. 2023, 316, 116989. [Google Scholar] [CrossRef]
- Geers, M.; Kouznetsova, V.; Brekelmans, W. Multi-scale computational homogenization: Trends and challenges. J. Comput. Appl. Math. 2010, 234, 2175–2182. [Google Scholar] [CrossRef]
- Thai, C.H.; Ferreira, A.; Tran, T.; Phung-Van, P. A size-dependent quasi-3D isogeometric model for functionally graded graphene platelet-reinforced composite microplates based on the modified couple stress theory. Compos. Struct. 2020, 234, 111695. [Google Scholar] [CrossRef]
- Plocher, J.; Panesar, A. Effect of density and unit cell size grading on the stiffness and energy absorption of short fibre-reinforced functionally graded lattice structures. Addit. Manuf. 2020, 33, 101171. [Google Scholar] [CrossRef]
- Li, D.; Li, S.; Zhang, C.; Chen, W. Propagation characteristics of shear horizontal waves in piezoelectric semiconductor nanoplates incorporating surface effect. Int. J. Mech. Sci. 2023, 247, 108201. [Google Scholar] [CrossRef]
- Le, K. An asymptotically exact first-order shear deformation theory for functionally graded plates. Int. J. Eng. Sci. 2023, 190, 103875. [Google Scholar] [CrossRef]
- Vidal, A.; Fung, S.W.; Osher, S.; Tenorio, L.; Nurbekyan, L. Kernel Expansions for High-Dimensional Mean-Field Control with Non-local Interactions. arXiv 2024, arXiv:2405.10922. [Google Scholar] [CrossRef]
- Mo, Y.; Tang, X.; Meng, L.; Yao, X. A general finite element based non-local theory for the medium-long-range correlation of metallic glasses. Int. J. Plast. 2023, 168, 103673. [Google Scholar] [CrossRef]
- Tarasov, V.E. General Non-Local Continuum Mechanics: Derivation of Balance Equations. Mathematics 2022, 10, 1427. [Google Scholar] [CrossRef]
- Shishesaz, M.; Shariati, M.; Hosseini, M. Size-Effect Analysis on Vibrational Response of Functionally Graded Annular Nano-Plate Based on Nonlocal Stress-Driven Method. Int. J. Struct. Stab. Dyn. 2022, 22, 2250098. [Google Scholar] [CrossRef]
- Li, L.; Hu, Y.; Li, X. Longitudinal vibration of size-dependent rods via nonlocal strain gradient theory. Int. J. Mech. Sci. 2016, 115, 135–144. [Google Scholar] [CrossRef]
- Li, L.; Hu, Y. Buckling analysis of size-dependent nonlinear beams based on a nonlocal strain gradient theory. Int. J. Eng. Sci. 2015, 97, 84–94. [Google Scholar] [CrossRef]
- Gurtin, M.E.; Ian Murdoch, A. A continuum theory of elastic material surfaces. Arch. Ration. Mech. Anal. 1975, 57, 291–323. [Google Scholar] [CrossRef]
- Lu, P.; He, L.; Lee, H.; Lu, C. Thin plate theory including surface effects. Int. J. Solids Struct. 2006, 43, 4631–4647. [Google Scholar] [CrossRef]
- Wang, J.; Duan, H.; Huang, Z.; Karihaloo, B. A scaling law for properties of nano-structured materials. Proc. R. Soc. A Math. Phys. Eng. Sci. 2006, 462, 1355–1363. [Google Scholar] [CrossRef]
- Xu, X.; Li, J.; Wu, X.; Ling, L.; Li, L. Size-dependent heat conduction of thermal cellular structures: A surface-enriched multiscale method. Def. Technol. 2025, in press. [Google Scholar] [CrossRef]
- March, N.G.; Gunasegaram, D.R.; Murphy, A.B. Evaluation of computational homogenization methods for the prediction of mechanical properties of additively manufactured metal parts. Addit. Manuf. 2023, 64, 103415. [Google Scholar] [CrossRef]
- Galadima, Y.K.; Oterkus, S.; Oterkus, E.; Amin, I.; El-Aassar, A.H.; Shawky, H. A nonlocal method to compute effective properties of viscoelastic composite materials based on peridynamic computational homogenization theory. Compos. Struct. 2023, 319, 117147. [Google Scholar] [CrossRef]
- Stoll, A.; Benner, P. Machine learning for material characterization with an application for predicting mechanical properties. GAMM-Mitteilungen 2021, 44, e202100003. [Google Scholar] [CrossRef]
- Durodola, J. Machine learning for design, phase transformation and mechanical properties of alloys. Prog. Mater. Sci. 2022, 123, 100797. [Google Scholar] [CrossRef]
- Kouznetsova, V.G. Computational Homogenization for the Multi-Scale Analysis of Multi-Phase Materials. Ph.D. Thesis, Technische Universiteit Eindhoven, Eindhoven, The Netherlands, 2002. [Google Scholar] [CrossRef]
- Nemat-Nasser, S. Averaging theorems in finite deformation plasticity. Mech. Mater. 1999, 31, 493–523. [Google Scholar] [CrossRef]




| Homogenization Methods | Advantages | Limitations |
|---|---|---|
| Rule of mixture | Simple model | Only the volume fraction is considered, not the specific geometry |
| Voigt–Reuss model | A simple manner to provide a reasonable estimate of the effective performance range | The range is too wide and is mainly used to test the correctness |
| Self-consistent method | Suitable for high volume fraction inclusions | Difficult to solve and usually no analytical solution can be obtained |
| Mori–Tanaka method | Simple calculation, suitable for low volume dispersed inclusions | Difficult to handle complex microstructures |
| Asymptotic homogenization method | Provides effective overall properties as well as local stress and strain values | The calculation is complicated |
| Method of cells | Computational efficiency is greatly improved | A loss of local field accuracy |
| Voronoi cell finite element method | Reduce the number of finite elements and the difficulty of calculation | Irregular finite element shapes, which increase errors |
| Lattice Type | Mapping | Lattice Unit |
|---|---|---|
| Crisscrossed elliptical holes |  | |
| Two-dimensional re-entrant hexagonal honeycomb in x |  | |
| Two-dimensional re-entrant hexagonal honeycomb in z |  | |
| Square honeycomb rotated |  | |
| Body centered cubic |  | |
| Body centered cubic foam |  | |
| Cube |  | |
| Cubic plate lattice |  | |
| Fisher–KochS |  | |
| Gyroid |  | |
| I-WP |  | |
| Diamond |  | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, A.; Li, S.; Ling, L.; Li, L. A Surface-Enabled Computational Homogenization Method for Variable-Density Polymer Lattice Metastructures. Polymers 2025, 17, 769. https://doi.org/10.3390/polym17060769
Zhang A, Li S, Ling L, Li L. A Surface-Enabled Computational Homogenization Method for Variable-Density Polymer Lattice Metastructures. Polymers. 2025; 17(6):769. https://doi.org/10.3390/polym17060769
Chicago/Turabian StyleZhang, Aofei, Shuo Li, Ling Ling, and Li Li. 2025. "A Surface-Enabled Computational Homogenization Method for Variable-Density Polymer Lattice Metastructures" Polymers 17, no. 6: 769. https://doi.org/10.3390/polym17060769
APA StyleZhang, A., Li, S., Ling, L., & Li, L. (2025). A Surface-Enabled Computational Homogenization Method for Variable-Density Polymer Lattice Metastructures. Polymers, 17(6), 769. https://doi.org/10.3390/polym17060769







