Evolutionary Algorithm-Based Design and Performance Evaluation of Wood–Plastic Composite Roof Panels for Low-Cost Housing
Abstract
:1. Introduction
2. Materials and Experimental Methods
2.1. Material Preparation and Manufacturing Process
2.2. Three-Point Bending Test
3. Optimization Algorithms and Problem Formulation
3.1. Genetic Algorithm (GA)
3.2. Particle Swarm Optimization (PSO)
3.3. Design Problem Formulation
3.3.1. Sinusoidal Wave Panel
3.3.2. Triangular and Trapezoidal Panels
3.4. Finite Element Analysis (FEA) of the Panels
3.5. WPC Panels’ Optimization Framework
| Algorithm 1. WPC Roof Panel Optimization | |||
| Input: | |||
| Panel dimensions Applied loads Material properties Constraints | |||
| Output: | |||
| Optimal shape parameters | |||
| 1 | Initialization:Generate the initial set of random shape parameters S | ||
| 2 | while (Maximum generations not met) | ||
| 3 | for each parameter set x in S do | ||
| 4 | Generate panel using shape parameters x | ||
| 5 | Apply loads and boundary conditions | ||
| 6 | Perform finite element analysis | ||
| 7 | Evaluate objective function and apply penalties for constraint violation | ||
| 8 | end for | ||
| 9 | Generate new solutions set and update S | ||
| 10 | end while | ||
| 11 | return Optimal set of shape parameters | ||
4. Results
4.1. Experimental Results
4.2. Computational Design and Optimization Results
5. Discussion
5.1. Comparative Structural Analysis of Sinusoidal and Trapezoidal Panels
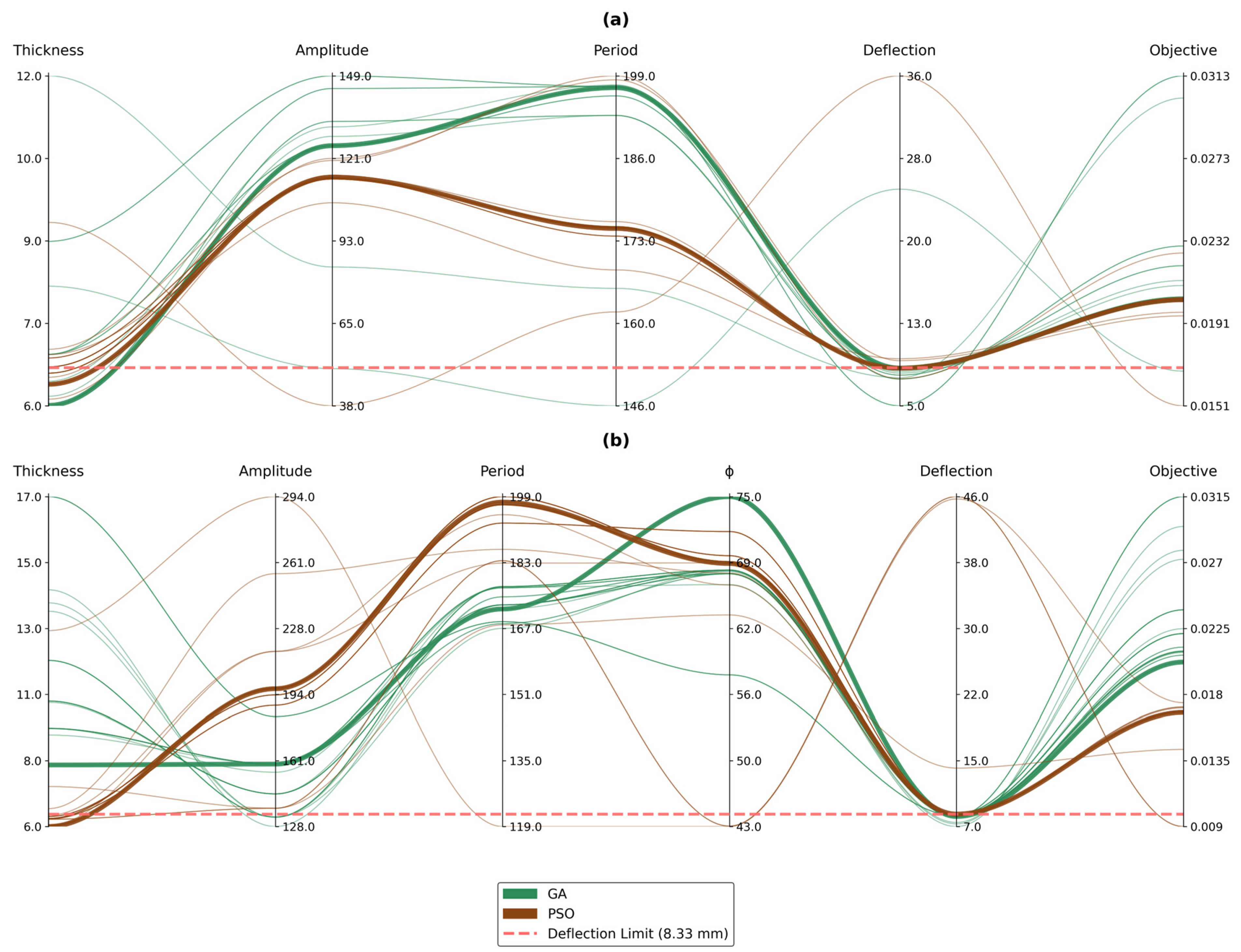
5.2. Algorithmic Convergence and Solution Quality Assessment
6. Conclusions
- Three-point bending tests showed that the WPC material, which is made up of 60% HDPE and 40% sawdust, had consistent mechanical properties. Its average modulus of rupture was 42.7 MPa and its average modulus of elasticity was 2.46 GPa.
- A range of cross-sectional geometries, such as sinusoidal, trapezoidal, and triangular profiles, was assessed. The trapezoidal shape was seen as the best balance between material efficiency and structural rigidity, so it was chosen as the best option for further development.
- Particle swarm optimization (PSO) exhibited enhanced efficacy relative to the genetic algorithm (GA) by achieving faster convergence and meeting the deflection constraints in fewer iterations. This efficiency diminishes computational time while preserving the accuracy of the optimization process.
- Finite element analysis demonstrated unique stress distribution characteristics across the profiles. The sinusoidal profile demonstrated more gradual stress transitions, potentially decreasing the risk of failures associated with stress concentration. Conversely, the trapezoidal profile exhibited elevated peak stresses concentrated in flat areas. Still, these stress levels stayed within the WPC material’s acceptable range, which meant that the structure would remain strong under the expected loading conditions.
- These findings underscore the effectiveness of integrating experimental characterization, computational modeling, and sophisticated optimization algorithms to improve the performance and manufacturability of WPC roof panels. To make the best use of WPC materials in long-lasting, low-cost housing solutions, future research may focus on improving the way the materials are made and looking into how long they last in different environments.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| EA | Evolutionary algorithms |
| FEA | Finite element analysis |
| GA | Genetic algorithm |
| HDPE | High-density polyethylene |
| PSO | Particle swarm optimization |
| WPC | Wood–plastic composite |
References
- Xu, K.; Du, G.; Wang, S.; Xu, K.; Du, G.; Wang, S. Wood Plastic Composites: Their Properties and Applications. In Engineered Wood Products for Construction; IntechOpen: London, UK, 2021; ISBN 978-1-83962-772-9. [Google Scholar]
- Shih, Y.-F.; Chang, C.-W.; Hsu, T.-H.; Dai, W.-Y. Application of Sustainable Wood-Plastic Composites in Energy-Efficient Construction. Buildings 2024, 14, 958. [Google Scholar] [CrossRef]
- Lin, Z.; Xiang, Q.; Dongmei, X. Study on Water Resistance of Polypropylene Based Wood-Plastic Composites Used in Building. Compos. Adv. Mater. 2023, 32, 26349833231218017. [Google Scholar] [CrossRef]
- Ratanawilai, T.; Taneerat, K. Alternative Polymeric Matrices for Wood-Plastic Composites: Effects on Mechanical Properties and Resistance to Natural Weathering. Constr. Build. Mater. 2018, 172, 349–357. [Google Scholar] [CrossRef]
- Vedrtnam, A.; Kumar, S.; Chaturvedi, S. Experimental Study on Mechanical Behavior, Biodegradability, and Resistance to Natural Weathering and Ultraviolet Radiation of Wood-Plastic Composites. Compos. Part B Eng. 2019, 176, 107282. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, Z.; Du, K.; Bi, Y.; Su, J.; Zhang, Y.; Shen, Y.; Zhang, S. Functional Natural Wood-Plastic Composites: A Review of Antimicrobial Properties and Their Influencing Factors. Ind. Crops Prod. 2023, 201, 116705. [Google Scholar] [CrossRef]
- Lopez, Y.M.; Gonçalves, F.G.; Paes, J.B.; Gustave, D.; Theodoro Nantet, A.C.; Sales, T.J. Resistance of Wood Plastic Composite Produced by Compression to Termites Nasutitermes Corniger (Motsch.) and Cryptotermes Brevis (Walker). Int. Biodeterior. Biodegrad. 2020, 152, 104998. [Google Scholar] [CrossRef]
- Mitaľová, Z.; Mitaľ, D.; Berladir, K. A Concise Review of the Components and Properties of Wood–Plastic Composites. Polymers 2024, 16, 1556. [Google Scholar] [CrossRef]
- Jian, B.; Mohrmann, S.; Li, H.; Li, Y.; Ashraf, M.; Zhou, J.; Zheng, X. A Review on Flexural Properties of Wood-Plastic Composites. Polymers 2022, 14, 3942. [Google Scholar] [CrossRef]
- Hugot, F.; Cazaurang, G. Mechanical Properties of an Extruded Wood Plastic Composite. Mécanique Ind. 2009, 10, 519–524. [Google Scholar] [CrossRef]
- Frącz, W.J.; Janowski, G. Analysis of Fiber Orientation in the Wood-Polymer Composites (WPC) on Selected Examples. Adv. Sci. Technol. Res. J. 2017, 11, 122–129. [Google Scholar] [CrossRef]
- de Prá Andrade, M.; Poletto, M. Wood Treatments and Interfacial Bonding in Wood-Plastic Composites. In Wood Polymer Composites: Recent Advancements and Applications; Mavinkere Rangappa, S., Parameswaranpillai, J., Kumar, M.H., Siengchin, S., Eds.; Springer: Singapore, 2021; pp. 43–65. ISBN 9789811616068. [Google Scholar]
- Rezaee Niaraki, P.; Krause, A. Correlation between Physical Bonding and Mechanical Properties of Wood–Plastic Composites: Part 2: Effect of Thermodynamic Factors on Interfacial Bonding at Wood–Polymer Interface. J. Adhes. Sci. Technol. 2020, 34, 756–768. [Google Scholar] [CrossRef]
- Hamel, S.E.; Hermanson, J.C.; Cramer, S.M. Mechanical and Time-Dependent Behavior of Wood–Plastic Composites Subjected to Tension and Compression. J. Thermoplast. Compos. Mater. 2013, 26, 968–987. [Google Scholar] [CrossRef]
- Hao, X.; Yi, X.; Sun, L.; Tu, D.; Wang, Q.; Ou, R. Mechanical Properties, Creep Resistance, and Dimensional Stability of Core/Shell Structured Wood Flour/Polyethylene Composites with Highly Filled Core Layer. Constr. Build. Mater. 2019, 226, 879–887. [Google Scholar] [CrossRef]
- Feng, L.; Zhao, C. Analysis of Creep Properties and Factors Affecting Wood Plastic Composites. Polymers 2022, 14, 2814. [Google Scholar] [CrossRef]
- Ratanawilai, T.; Srivabut, C. Physico-Mechanical Properties and Long-Term Creep Behavior of Wood-Plastic Composites for Construction Materials: Effect of Water Immersion Times. Case Stud. Constr. Mater. 2022, 16, e00791. [Google Scholar] [CrossRef]
- Hamel, S.E.; Hermanson, J.C.; Cramer, S.M. Predicting the Flexure Response of Wood-Plastic Composites from Uni-Axial and Shear Data Using a Finite-Element Model. J. Mater. Civ. Eng. 2014, 26, 04014098. [Google Scholar] [CrossRef]
- Nukala, S.G.; Kong, I.; Kakarla, A.B.; Patel, V.I.; Abuel-Naga, H. Simulation of Wood Polymer Composites with Finite Element Analysis. Polymers 2023, 15, 1977. [Google Scholar] [CrossRef]
- Liu, H.-H.; Dong, C.; Xiong, P.-Q.; Nan, H.-F.; Yan, D.-X.; Li, R.-Q.; An, Y.-P.; Lei, J.; Li, Z.-M. Triple Thermal Management Wood–Plastic Composite Plate with Excellent Waterproof and Mechanical Properties. Ind. Eng. Chem. Res. 2025, 64, 453–465. [Google Scholar] [CrossRef]
- He, Z.; Fang, H.; Zhang, X.; Shen, C. Lateral Behavior of Wood Frame Shear Wall Using PVC Wood-Plastic Composite (WPC) Veneer Panels. J. Build. Eng. 2024, 89, 109367. [Google Scholar] [CrossRef]
- Eakintumas, W.; Pulngern, T.; Rosarpitak, V.; Sombatsompop, N. Load-Bearing Capacity of Wood Polyvinyl Chloride Composite Log-Walls with Openings Strengthened with Steel Flat Bars via Experimental and Numerical Studies. Structures 2022, 37, 242–254. [Google Scholar] [CrossRef]
- Zhao, L.; Li, H.; Wei, Y.; Xi, F. Experimental Study on the Axial Compression Performance of CFRP Wrapped Wood Plastic Composite Hollow Short Columns. Thin-Walled Struct. 2025, 209, 112887. [Google Scholar] [CrossRef]
- Fei, G.; Yuyu, L.I.; Wenhui, H.E.; Xiaolong, H.; Rongxian, O.U.; Qingwen, W. Experimental Study and Finite Element Analysis of Wood-Plastic Composite Hollow Columns Subjected to Axial Compression. Chin. J. Wood Sci. Technol. 2024, 38, 40–48. [Google Scholar] [CrossRef]
- Darwish, M.; Elnakeb, M.; Moawad, M.; Shawki, M.M.; Abdelhamid, E.; Eldwib, D.; Abouzeid, M.N.; Saudy, M.; Khedr, S.; Nassar, K. Design and Characteristics of a Single-Story Building Model Incorporating Waste. Buildings 2025, 15, 177. [Google Scholar] [CrossRef]
- Haftka, R.T.; Gürdal, Z. Introduction. In Elements of Structural Optimization; Haftka, R.T., Gürdal, Z., Eds.; Springer: Dordrecht, The Netherlands, 1992; pp. 1–21. ISBN 978-94-011-2550-5. [Google Scholar]
- Kobelev, V. Fundamentals of Structural Optimization (II): Shape, Anisotropy, Topology; Mathematical Engineering; Springer International Publishing: Cham, Switzerland, 2024; ISBN 978-3-031-59139-6. [Google Scholar]
- Liu, S.; Li, Q.; Hu, J.; Chen, W.; Zhang, Y.; Luo, Y.; Wang, Q. A Survey of Topology Optimization Methods Considering Manufacturable Structural Feature Constraints for Additive Manufacturing Structures. Addit. Manuf. Front. 2024, 3, 200143. [Google Scholar] [CrossRef]
- Mei, L.; Wang, Q. Structural Optimization in Civil Engineering: A Literature Review. Buildings 2021, 11, 66. [Google Scholar] [CrossRef]
- Saka, M.P.; Geem, Z.W. Mathematical and Metaheuristic Applications in Design Optimization of Steel Frame Structures: An Extensive Review. Math. Probl. Eng. 2013, 2013, 271031. [Google Scholar] [CrossRef]
- Prayogo, D.; Sebastian; Hauwing, W.; Wong, F.T.; Tjandra, D. Structural Design Optimization Using Particle Swarm Optimization and Its Variants. IOP Conf. Ser. Earth Environ. Sci. 2020, 506, 012048. [Google Scholar] [CrossRef]
- Guo, P.; Wang, X.; Han, Y. A Hybrid Genetic Algorithm for Structural Optimization with Discrete Variables. In Proceedings of the 2011 International Conference on Internet Computing and Information Services, Hong Kong, China, 17–18 September 2011; pp. 223–226. [Google Scholar]
- Kaveh, A. Advances in Metaheuristic Algorithms for Optimal Design of Structures; Springer International Publishing: Cham, Switzerland, 2014; ISBN 978-3-319-05548-0. [Google Scholar]
- Xie, J.; Yan, J.; Zhang, J.Y.; Xu, Y.F.; Chen, M. Application of Improved Combined Shape Genetic Algorithm on Structural Optimization. Appl. Mech. Mater. 2014, 602–605, 3119–3122. [Google Scholar] [CrossRef]
- Perez, R.E.; Behdinan, K. Particle Swarm Approach for Structural Design Optimization. Comput. Struct. 2007, 85, 1579–1588. [Google Scholar] [CrossRef]
- Kashani, A.R.; Camp, C.V.; Rostamian, M.; Azizi, K.; Gandomi, A.H. Population-Based Optimization in Structural Engineering: A Review. Artif. Intell. Rev. 2022, 55, 345–452. [Google Scholar] [CrossRef]
- Kayabekir, A.E.; Bekdaş, G.; Nigdeli, S.M. Developments on Metaheuristic-Based Optimization in Structural Engineering. In Advances in Structural Engineering—Optimization: Emerging Trends in Structural Optimization; Nigdeli, S.M., Bekdaş, G., Kayabekir, A.E., Yucel, M., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 1–22. ISBN 978-3-030-61848-3. [Google Scholar]
- Lagaros, N.D.; Plevris, V.; Kallioras, N.A. The Mosaic of Metaheuristic Algorithms in Structural Optimization. Arch. Comput. Methods Eng. 2022, 29, 5457–5492. [Google Scholar] [CrossRef]
- Saka, M.P.; Hasançebi, O.; Geem, Z.W. Metaheuristics in Structural Optimization and Discussions on Harmony Search Algorithm. Swarm Evol. Comput. 2016, 28, 88–97. [Google Scholar] [CrossRef]
- Awad, Z.K.; Aravinthan, T.; Zhuge, Y.; Gonzalez, F. A Review of Optimization Techniques Used in the Design of Fibre Composite Structures for Civil Engineering Applications. Mater. Des. 2012, 33, 534–544. [Google Scholar] [CrossRef]
- Martins, G.; Antunes, F.; Mateus, A.; Baptista, S.; Malça, C. Optimization of a Wood Plastic Composite to Produce a New Dynamic Shading System. In Natural Fibres: Advances in Science and Technology Towards Industrial Applications; Fangueiro, R., Rana, S., Eds.; Springer: Dordrecht, The Netherlands, 2016; pp. 343–350. [Google Scholar]
- Martins, G.; Antunes, F.; Mateus, A.; Malça, C. Optimization of a Wood Plastic Composite for Architectural Applications. Procedia Manuf. 2017, 12, 203–220. [Google Scholar] [CrossRef]
- Javier, C.-S. Optimization of the Tensile and Flexural Strength of a Wood-PET Composite. Ing. Investig. Y Technol. 2015, 16, 105–112. [Google Scholar] [CrossRef]
- Ji, F. Optimization of Wood-Plastic Composites by Response Surface Method. BioRes 2024, 19, 5949–5960. [Google Scholar] [CrossRef]
- Ndiaye, A.; Michaud, F.; Castéra, P.; Fernandez, C. Metaheuristic Methods Applied to the Environmentally Conscious Optimization of Wood-Plastic Composites. In Proceedings of the 22nd Annual American Society for Composites Technical Conference of the American Society for Composites, Seattle, WA, USA, 17–19 September 2007; Volume 3, pp. 2123–2137. [Google Scholar]
- Zhang, Y.; Xue, P.; Ding, Y.; Jia, M.; Cai, J.; Jin, X. Improvement of Mechanical Properties of Wood-Plastic Composite Floors Based on the Optimum Structural Design. Acta Mech. Solida Sin. 2016, 29, 444–454. [Google Scholar] [CrossRef]
- Ravivarman, S.; Venkatesh, G.S.; Karmarkar, A.; Shivkumar, N.D.; Abhilash, R.M. Optimization of Wood Plastic Composite Decks. AIP Conf. Proc. 2018, 1943, 020005. [Google Scholar] [CrossRef]
- Soury, E.; Behravesh, A.H.; Rouhani Esfahani, E.; Zolfaghari, A. Design, Optimization and Manufacturing of Wood–Plastic Composite Pallet. Mater. Des. 2009, 30, 4183–4191. [Google Scholar] [CrossRef]
- ASTM D1037; Standard Test Methods for Evaluating Properties of Wood-Base Fiber and Particle Panel Materials. ASTM International: West Conshohocken, PA, USA, 2020. [CrossRef]
- Blank, J.; Deb, K. Pymoo: Multi-Objective Optimization in Python. IEEE Access 2020, 8, 89497–89509. Available online: https://ieeexplore.ieee.org/document/9078759 (accessed on 15 February 2025). [CrossRef]
- Holland, J.H. Genetic Algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Hassanat, A.; Almohammadi, K.; Alkafaween, E.; Abunawas, E.; Hammouri, A.; Prasath, V.B.S. Choosing Mutation and Crossover Ratios for Genetic Algorithms—A Review with a New Dynamic Approach. Information 2019, 10, 390. [Google Scholar] [CrossRef]
- Deb, K.; Agrawal, S. Understanding Interactions among Genetic Algorithm Parameters. Found. Genet. Algorithms 1999, 5, 265–286. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 October–1 November 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Shi, Y.; Eberhart, R. A Modified Particle Swarm Optimizer. In Proceedings of the 1998 IEEE International Conference on Evolutionary Computation Proceeding, IEEE World Congress on Computational Intelligence (Cat. No. 98TH8360), Anchorage, AK, USA, 4–9 May 1998; pp. 69–73. [Google Scholar]
- NHBRC. Egyptian Code for Design and Construction of Reinforced Concrete Structures (ECP 203:2020); National Housing and Building Research Center: Giza Governorate, Egypt, 2020; Volume 203. [Google Scholar]
- Riegel, J.; Mayer, W.; van Havre, Y. FreeCAD 2001. Available online: http://www.freecadweb.org (accessed on 15 January 2025).
- Dhondt, G.; Wittig, K. CalculiX 1998. Available online: https://www.tms.org/forum/messageview.aspx?catid=113&threadid=1316&enterthread=y (accessed on 15 January 2025).
- NHBRC. Egyptian Code of Practice for Calculation of Loads and Forces in Structures and Buildings (ECP-201:2012); National Housing and Building Research Center: Giza Governorate, Egypt, 2012; Volume 201. [Google Scholar]

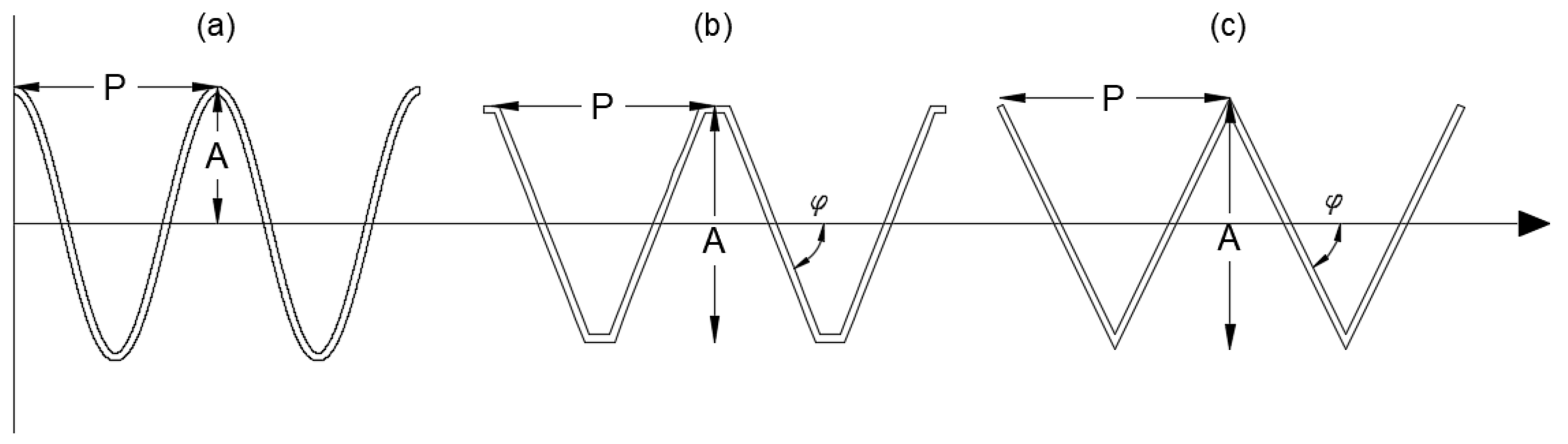


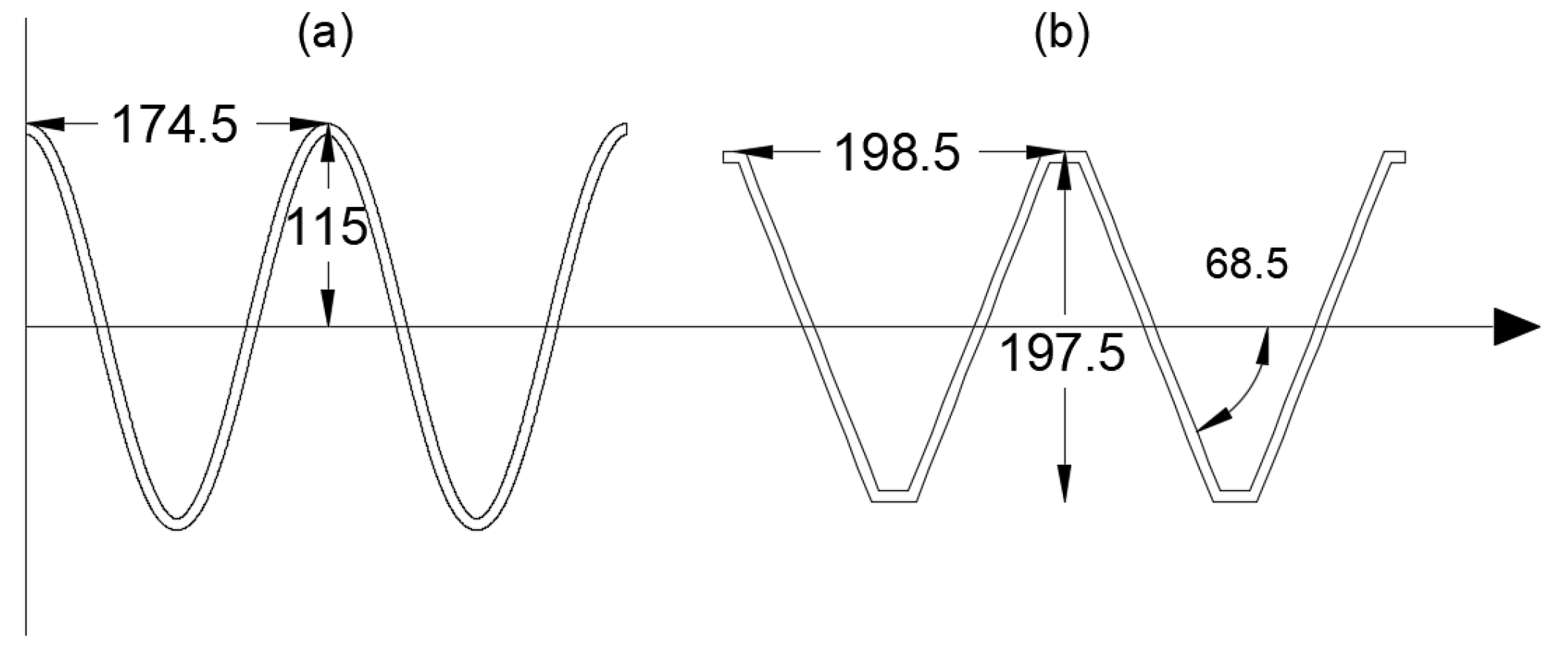
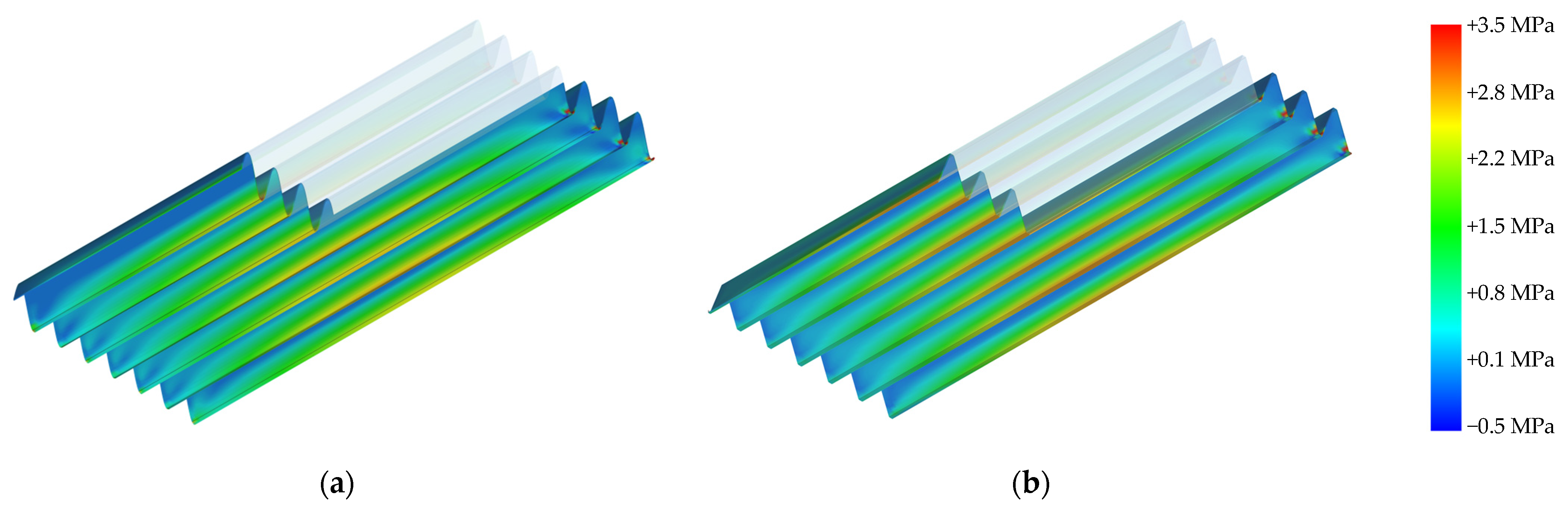
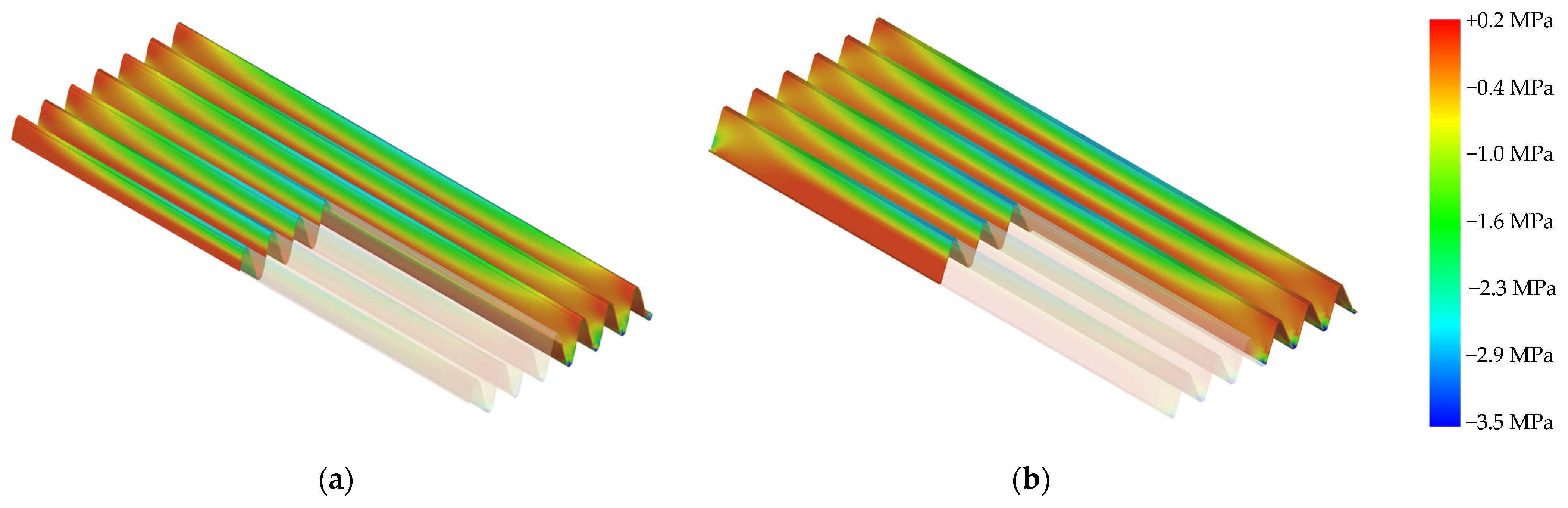

| Parameter | Lower Bound | Upper Bound |
|---|---|---|
| 20 mm | 300 mm | |
| 50 mm | 200 mm | |
| 20 | 85 | |
| 6 | 50 |
| Shape | Parameters | Cross-Sectional Properties | |||
|---|---|---|---|---|---|
| Amplitude | Period | Area (mm2) | (mm4) | ||
| Sinusoidal | 230 | 174.5 | - | 22,054 | 108,328,378 |
| Trapezoidal | 197.5 | 198.5 | 197.5 | 17,444 | 67,553,565 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdelshahid, B.; Nassar, K.; Youssef, P.; Sayed-Ahmed, E.; Darwish, M. Evolutionary Algorithm-Based Design and Performance Evaluation of Wood–Plastic Composite Roof Panels for Low-Cost Housing. Polymers 2025, 17, 795. https://doi.org/10.3390/polym17060795
Abdelshahid B, Nassar K, Youssef P, Sayed-Ahmed E, Darwish M. Evolutionary Algorithm-Based Design and Performance Evaluation of Wood–Plastic Composite Roof Panels for Low-Cost Housing. Polymers. 2025; 17(6):795. https://doi.org/10.3390/polym17060795
Chicago/Turabian StyleAbdelshahid, Bassel, Khaled Nassar, Passant Youssef, Ezzeldin Sayed-Ahmed, and Mohamed Darwish. 2025. "Evolutionary Algorithm-Based Design and Performance Evaluation of Wood–Plastic Composite Roof Panels for Low-Cost Housing" Polymers 17, no. 6: 795. https://doi.org/10.3390/polym17060795
APA StyleAbdelshahid, B., Nassar, K., Youssef, P., Sayed-Ahmed, E., & Darwish, M. (2025). Evolutionary Algorithm-Based Design and Performance Evaluation of Wood–Plastic Composite Roof Panels for Low-Cost Housing. Polymers, 17(6), 795. https://doi.org/10.3390/polym17060795






