A Review on Advances in the Use of Raw and Modified Agricultural Lignocellulosic Residues in Mono- and Multicomponent Continuous Adsorption of Inorganic Pollutants for Upscaling Technologies
Abstract
:1. Introduction
- The main bottlenecks that prevent major advances in the technology readiness level (TRL > 5, at mini-pilot or pilot scales in a relevant environment) and upscaling of the technologies.
- The influence of chemical modifications on the physicochemical properties and behaviors of bioadsorbents in fixed-bed columns.
- The problem of using simplified model equations for modeling monocomponent adsorption in fixed-bed columns.
- The complexity of competitive adsorption and column behavior in multicomponent adsorption, with possible solutions arising in the near future due to the introduction of artificial neural networks and machine learning methods to simulate adsorption operation, including efficiency of separation.
- The recovery and destination of depleted bioadsorbents after the treatment of water containing inorganic contaminants, with possible second uses in industry, strengthening the concepts of a circular bioeconomy.
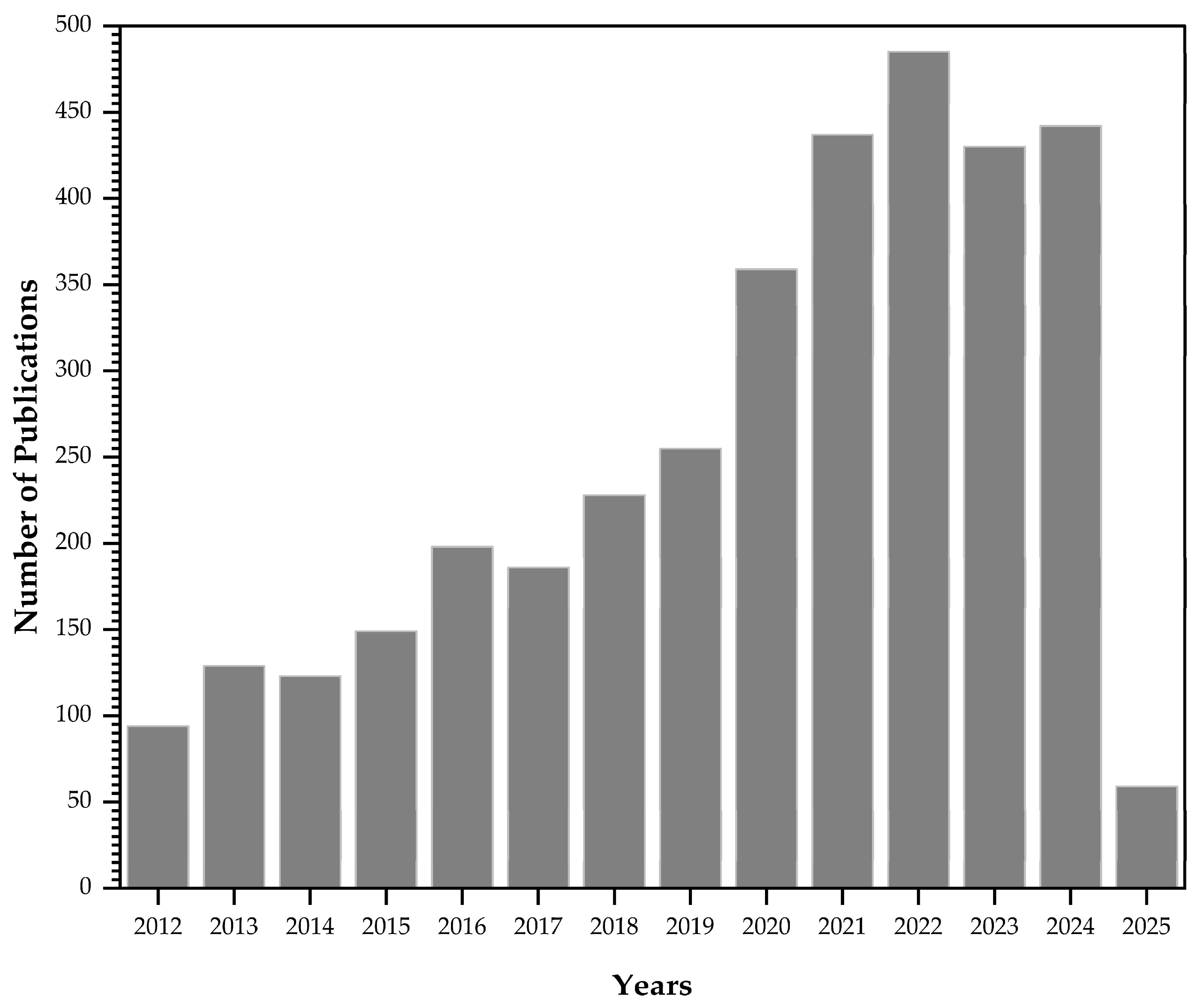
2. Methodology: A Bibliometric Approach
3. Technologies for Removal of Inorganic Pollutants from Water
| Method | Material | Advantages | Disadvantages | Reference |
|---|---|---|---|---|
| Chemical precipitation | Precipitants (lime, alkalis, sulfides) | Low concentrations of toxic inorganic species in the treated effluent Treatment of high volumes of water Simple to implement and operate | High demand for chemicals Strict control of pH and temperature for correct operation Generation of toxic sludge to be disposed of safely Low efficiency for removal of trace-level inorganic species | [2,19,20,22] |
| Ion exchange | Ion exchange resins | Treatment of high volumes of water/effluent Allows medium filtration rates Simple to implement and operate | Requires chemicals for regeneration and reuse High cost for acquisition of resins Exhausted resins need to be disposed of safely | [2,19,20,22] |
| Membrane filtration | Membranes | Enables reuse of water/effluent Produces high-quality treated water Strict limits of pollutant concentrations in effluents can be met | Membrane fouling High investment in equipment High costs of membranes, maintenance, and operation | [2,19,20,22] |
| Coagulation/flocculation | CaO, Al2(SO4)3, aluminum polychloride, FeSO4, FeCl3 | Treatment of high volumes of water/effluent Supports high flow rates Simple to implement and operate | High demand for chemicals Strict control of pH and temperature for correct operation Generation of toxic sludge to be disposed of safely Low efficiency for removal of trace-level inorganic species | [2,19,20,22] |
| Electrolytic recovery | Electrodes and electrolytes | Recovery of pure metal High selectivity for target compounds High metal removal rates | High demand for chemicals (electrolytes) High operating cost (electrodes) Reduced efficiency for very diluted pollutants High cost for large-scale implementation | [19,20] |
| Reverse osmosis | Membranes | Medium to high removal rates for toxic inorganic species Meets strict concentration limits for target pollutants | High investment in equipment High costs of membranes, maintenance, and operation Membrane fouling | [19,20] |
| Adsorption | Adsorbents | Highly efficient for low and high concentrations of inorganic pollutants Low cost for acquisition of adsorbents and operation Meets strict concentration limits for pollutants Simple to implement and operate | Requires chemicals for regeneration and reuse Exhausted adsorbents need to be disposed of safely | [19,20,22] |
4. Adsorption
4.1. Adsorption Phenomenon
4.2. Adsorption Mechanisms
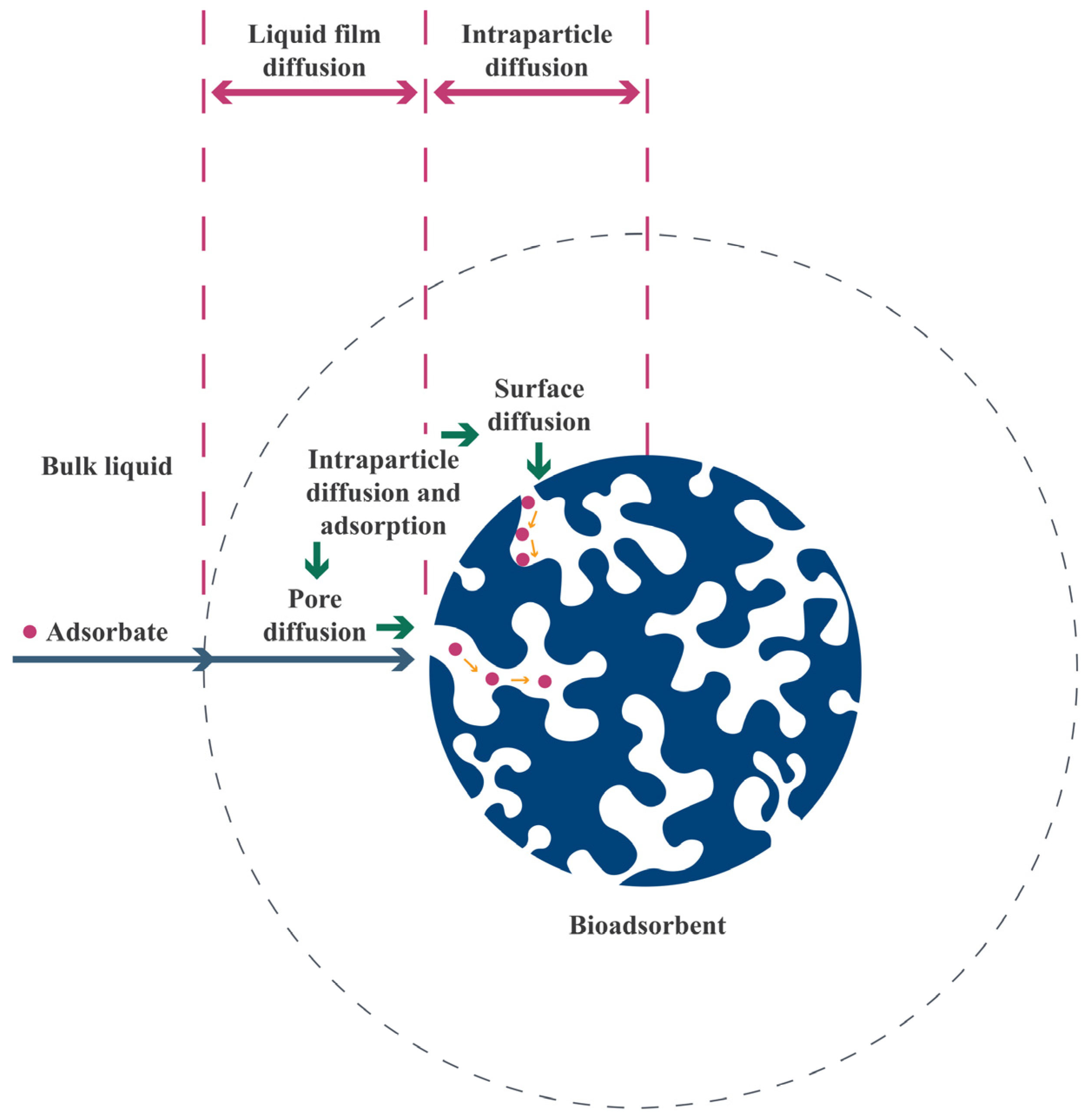
4.3. Batch and Continuous Adsorption
5. Fixed-Bed Column Adsorption Studies with Raw and Modified Lignocellulosic Residues
5.1. Overview
| Matrix | MA | pH | Ion | C0 /mg L−1 | Z /cm | Q /mL min−1 | Qe /mg g−1 | Qe /mmol g−1 | Model | Ze/% | Performance Parameters for Regeneration | Reference | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Number of Cycles | Eads/% | Edes/% | Ere-ads/% | Eluent | ||||||||||||
| Coconut leaves (Cocos nucifera) | - | 1 | Cr(VI) | 100 | 20 | 4 | 4.88 | 0.98 | Tho, YN, MDR | 58.3 | - | - | - | - | - | [86] |
| 2 | V(V) | 100 | 20 | 4 | 4.89 | 1.11 | 57.9 | |||||||||
| Hazelnut shell (Corylus spp.) | H3PO4 Urea | 6.27 | Li | 10 | 1.5 | 0.25 | 22.29 | 3.21 | Tho, YN, MDR | 81.20 | 5 | - | 100 | - | H2SO4 | [87] |
| Pine cone shell (Pinus sylvestris) | - | 5.6 | Cu(II) | 120.9 | 20 | 2.65 | 11.1 | 0.17 | Sips | - | - | - | - | - | HCl | [88] |
| Pb(II) | 96.7 | 0.7 | 55.57 | 0.27 | ||||||||||||
| Fibers, coniferous trees (Pinus spp.) | H3PO4 | Fe | 1420 | 60 (4 columns) | 1000 | 1635.0 | 29.27 | - | - | - | - | - | - | - | [89] | |
| Mn(II) | 18.3 | 23.1 | 0.42 | |||||||||||||
| Zn(II) | 19.2 | 18.1 | 0.28 | |||||||||||||
| Sugarcane bagasse (Saccharum officinarum) | BAD | 5.75 | Cd(II) | 56.2 | 3.1 | 2.5 | 65 | 0.58 | - | 16 | 4 | - | 99.4–92.8 | 94.3–90.1 | HNO3 | [90] |
| 5.25 | Pb(II) | 207.2 | 153 | 0.71 | 15 | - | 100.5–98.7 | 108.3–91.2 | ||||||||
| Gundelia tournefortii | EDTAD | 6 | Cu(II) | 10 | 2 | 7 | 15.61 | 0.25 | BA, Tho, YN | 53.8 | [91] | |||||
| Ramie stalk (Boehmeria nivea) | H3PO4 | 5.5 | Zn(II) | 32.7 | 5 | 5 | 32.4 | 0.495 | BA, Tho, YN, BDST | 71 | 5 | - | 98.5–97.1 | 99–90 | HCl | [92] |
| Cucumber peel (Cucumis sativus) | - | 5 | Cd(II) | 50 | 8 | 20 | 300.26 | 2.67 | Tho, YN, BDST | - | 3 | - | 97–95 | - | HCl | [93] |
| Walnut shell (Juglans regia) | ECH TEA DETA | 3 | Cr(VI) | 200 | 3 | 10 | 308.4 | 5.76 | Tho, Ck | - | 2 | - | - | 83 | NaOH | [94] |
| Palm bagasse Opuntia ficus-indica | - | 2 | Cr(VI) | 100 | - | 45 | 111.45 | 2.1434 | BA, Tho, YN, BDST | - | - | 99–100 | - | - | - | [70] |
| 6 | Ni(II) | 103.49 | 1.7633 | 87–100 | ||||||||||||
| Yam peels (Dioscorea alata) | 2 | Cr(VI) | 50.12 | 0.9641 | 65–100 | |||||||||||
| 6 | Ni(II) | 30.04 | 0.5118 | 87–99 | ||||||||||||
| Plantain (Musa paradisiaca) | NaOH | 2 | Cr(VI) | 100 | 11.4 | 45 | 18.25 | 0.351 | - | - | - | - | - | - | - | [95] |
| 6 | Ni(II) | 22.08 | 0.376 | |||||||||||||
| Yam (Dioscorea alata) | NaOH | 2 | Cr(VI) | 100 | 9.0 | 45 | 28.01 | 0.539 | - | - | - | - | - | - | - | |
| 6 | Ni(II) | 28.01 | 0.477 | |||||||||||||
| Moringa oleifera seed | - | 7.0 | Cd(II) | 0.3 | 32.1 | 2.0 | 0.065 | 5.82 × 10−4 | Tho | 80 | - | - | - | - | - | [51] |
| Sugarcane bagasse (Saccharum officinarum) | - | 4 | Zr(IV) | 75 | 3 | 1.8 | 20.32 | 0.223 | Tho, BDST | 59 | - | 15–26 | - | - | - | [65] |
| Sugarcane bagasse (Saccharum officinarum) | H3PO4 NaNO2 | 5 | Co(II) | 1.26 | 3.8 | 1.4 | 13.20 | 0.224 | BA | 39 | - | - | 85 | 93 | - | [67] |
| Cu(II) | 0.68 | 35.20 | 0.554 | 18 | - | 98 | 104 | |||||||||
| Orange peel (Citrus sinensis) | - | 2 | Se(IV) | 140 | 9 | 1 | 3.37 | 0.043 | Tho, BDST | 25 | 2 | 87 | 70 | 45 | NaOH | [77] |
| Cariaquillo (Lantana camara) | H2SO4 | 1.5 | Cr(VI) | 300 | 4 | 4 | 362.8 | 6.98 | Tho, BDST | 9 | 3 | 53 | - | 30–71 | NaOH | [96] |
| Almond shell (Prunus dulcis) | - | 3.7 | Cr(VI) | 67.5 | 7 | 3 | 21.92 | 0.422 | Tho, YN, MDR | - | - | 66 | - | - | - | [49] |
| Cu(II) | 7.0 | 2.39 | 0.038 | - | 70 | - | - | |||||||||
| Cashew nut shell (Anacardium occidentale) | H2SO4 | Cr(VI) | 21.05 | 10 | 5 | 10.79 | 0.208 | BA, YN, Ck | - | - | 56 | - | - | - | [50] | |
| Mg(II) | 20.3 | 9.82 | 0.179 | - | 53 | - | - | |||||||||
| Walnut shell (Juglans regia) | NaOH ECH DETA | 3 | Cr(VI) | 30 | 2 | 8.0 | 28.1 | 0.540 | YAN | 6.5 | 3 | 49 | 18–21 | 51–72 | NaOH | [45] |
| Sugarcane bagasse (Saccharum officinarum) | ECH TEPA | 5 | Cu(II) | 20 | - | 6.25 | 16.51 | 0.26 | - | 38 | - | 52 | >95 | - | EDTA-2Na | [62] |
| Cd(II) | 11.24 | 0.10 | 33 | 75 | ||||||||||||
| Sugarcane bagasse (Saccharum officinarum) | ECH TEPA | 4.5 | Cu(II) | 12.5 | - | 6.25 | 10.8 | 0.170 | YN | 48 | 5 | 26 | >95 | - | EDTA-2Na | [73] |
| H3PO4 Urea | 4.5 | Pb(II) | 20.8 | - | 6.25 | 64.2 | 0.310 | YN | 19 | 5 | 80 | >95 | - | |||
| Olive oil residues (Olea europaea) | - | 6.0 | Pb(II) | 10 | 9.2 | 5 | 8.15 | 0.04 | - | - | - | - | - | - | - | [97] |
| Cd(II) | 3.50 | 0.03 | ||||||||||||||
| Ni(II) | 2.90 | 0.05 | ||||||||||||||
| Breadfruit (Artocarpus nobilis) | - | - | Ni(II) | 10.0 | 10 | 8.4 | 4.19 | 0.071 | Tho, BA, YN | - | - | 93 | - | - | - | [98] |
| Sugarcane bagasse (Saccharum officinarum) | H3PO4 Urea | 5 | Pb(II) | 103.6 | - | 6.25 | 76.5 | 0.369 | BA, YN | - | - | - | 90–99 | - | EDTA-2Na | [71] |
| Cu(II) | 31.78 | 23.1 | 0.363 | |||||||||||||
| Zn(II) | 32.69 | 21.7 | 0.332 | |||||||||||||
| Cd(II) | 56.21 | 30.3 | 0.270 | |||||||||||||
| Ca(II) | 20 | 17.9 | 0.447 | |||||||||||||
| Sugarcane bagasse (Saccharum officinarum) | PMDA DMAc | 5 | Pb(II) | 25 | 12.1 | 6.25 | 163.69 | 0.79 | BA, modified BA | - | - | - | >99 | - | EDTA-2Na | [64] |
| Waste tea (Camellia sinensis) | - | 2 | Cr(VI) | 100 | - | 300 | 94.34 | 1.81 | - | >80 | 4 | 30–90 | 10–20 | >50 | NaOH | [99] |
| Sugarcane bagasse (Saccharum officinarum) | TA SA | 5.75 | Co(II) | 123.8 | 3.1 | 2.5 | 59.52 | 1.01 | BA | 23 | 5 | - | 93 | 100 | HNO3 | [61] |
| Ni(II) | 123.3 | 61.03 | 1.04 | 29 | - | 93 | 100 | |||||||||
| Sugarcane bagasse (Saccharum officinarum) | CA | 5 | Pb(II) | 99.87 | 7 | 1.5 | 158.9 | 0.767 | Tho, YN | - | 4 | - | 10–95 | >80 | HCl, HNO3, NaOH, NaCl | [63] |
| Guava leaves (Psidium guajava) | - | - | Cr(VI) | 20 | 10 | 40 | 8.72 | 0.168 | Tho, BA | 77 | - | 0.168 | - | - | - | [59] |
| Tea tree shell (Melaleuca alternifolia) | - | - | Cu(II) | 28.82 | - | 7.4 | 7.42 | 0.117 | Tho | <30 | - | 90–95 | - | - | - | [46] |
| Pb(II) | 150.66 | 8.0 | 4.17 | 0.020 | ||||||||||||
| Cd(II) | 80.59 | 7.4 | 18.02 | 0.160 | ||||||||||||
| Eucalyptus leaf (Eucalyptus globulus) | - | 3.8 | Pb(II) | 20.72 | 24 | 10 | 32.74 | 0.158 | - | 51 | 3 | 30–50 | >80 | >75 | HNO3 | [57] |
| Cd(II) | 11.24 | 7.24 | 0.064 | 48 | >54 | |||||||||||
| Ni(II) | 5.87 | 1.77 | 0.030 | 33 | >43 | |||||||||||
| Coconut coir (Cocos nucifera) | H2O2 | 6 | Cd(II) | 30 | 21 | 15 | 7.22 | 0.642 | BDST | 37 | 3 | 70–77 | >94 | >93 | HCl | [100] |
| Pine bark (Pinus pinaster) | NaOH CS2 | 5 | Cr(III) | 500 | 2.5 | 10 | 53.04 | 0.78 | Tho, BA, YN | 47 | 1 | 79 | 53–68 | - | H2SO4 | [101] |
| Olive cake (Olea europaea) | NaOH | 4.5–5 | Pb(II) | 200 | - | 4.0 | 13.21 | 0.064 | Tho, YN, BDST | 45 | - | - | - | - | - | [102] |
| Cu(II) | 5.17 | 0.082 | 28 | |||||||||||||
| Cr(VI) | 3.08 | 0.059 | 13 | |||||||||||||
| Zn(II) | 5.51 | 0.843 | 21 | |||||||||||||
| Lentil husk | - | 5 | Pb(II) | 100 | 10 | 20 | 205.87 | 0.993 | Tho, BA, YN | 63 | 3 | 96 | 96–98 | >95 | HNO3 | [53] |
| Fig leaf (Ficus carica) | - | 5.5 | Co(II) | 5.4 | 2 | 1 | 11.09 | 0.188 | Tho, BA, YN | 22 | - | 50 | - | - | - | [58] |
| Pb(II) | 12.27 | 0.059 | 24 | |||||||||||||
| Pine nuts shell (Pinus pinea) | - | 5 | Cu(II) | 100 | 3.80 | 6 | 7.14 | 0.112 | Tho, YN, BDST | - | 19–99 | - | - | - | [42] | |
| Pb(II) | 20.25 | 0.098 | 51–100 | |||||||||||||
| Sugarcane bagasse (Saccharum officinarum) | - | 5 | Cd(II) | 10 | 28 | 1.6 | 0.146 | 1.30 × 10−3 | YN, Tho, BDST | 44 | - | 91 | - | - | - | [69] |
| Pb(II) | 0.154 | 7.43 × 10−4 | 55 | 90 | ||||||||||||
| Ramie stalk (Boehmeria nivea) | EPH NaOH Na2CO3 TEPA | 5 | Cu(II) | 44.49 | 10 | 5 | 34.0 | 0.535 | BA, Tho, YN, BDST | 81 | 5 | 82 | 97–98 | 100 | EDTA-2Na | [32] |
| Apple pomace (Malus domestica Borkh) | H2SO4 CS2 | 4 | Pb(II) | 50 | 7 | 60 | 192 | 0.927 | Tho | 53 | 5 | 18–70 | 75–100 | >80 | HNO3 | [103] |
| Mercerizing pine bark (Pinus pinaster) | NaOH | 5 | Cr(III) | 100 | 7.5 | 10 | 35.35 | 0.680 | Mech, BA, Tho, YN | 53 | 1 | 50 | 47 | - | HNO3 | [104] |
| Sugarcane bagasse (Saccharum officinarum) | TA | 5.5 | Cu(II) | 60.37 | 3.2 | 1.7 | 67.36 | 1.06 | BA, Tho | 58 | 3 | 60 | >95 | >92 | HNO3 | [105] |
| Co(II) | 64.83 | 44.79 | 0.76 | 61 | 62 | |||||||||||
| Ni(II) | 204.84 | 57.52 | 0.98 | 50 | 55 | |||||||||||
| Sugarcane bagasse (Saccharum officinarum) | PMDA | 5 | Pb(II) | 80 | - | 6.25 | 258 | 1.25 | YN, modified YN | 56 | - | >99 | 98 | - | HNO3 | [68] |
| Pongamia oil cake (Millettia pinnata) | - | 4.5 | Zn(II) | 100 | 14.8 | 5.6 | 85.98 | 1.315 | Tho, BDST | 35 | 6 | 86 | - | - | EDTA | [106] |
| Raw watermelon rind (Citrullus lanatus) | H3PO4 | 6 | Ni(II) | 75 | 5 | 5 | 33.12 | 0.564 | BA, Tho, YN | 1 | - | 44 | 80 | - | HCl | [107] |
| Tarap leaves (Corchorus capsularis) | NaOH EDTA | 5 | Pb(II) | 100 | 10 | 8.33 | 109.70 | 0.529 | - | 77 | 4 | 85 | 20–95 | 100 | Acid, base, water | [108] |
| Jute fiber (Corchorus capsularis) | PMDA | 6 | Cu(II) | 100 | 12 | 54.78 | 40.05 | 0.630 | Tho, YN, BDST | 34 | - | 59 | - | - | - | [80] |
| Sugarcane bagasse (Saccharum officinarum) | - | 2 | Cr(VI) | 15 | 20 | 2 | 1.99 | 0.038 | - | 12 | - | 98 | - | - | - | [66] |
| 5 | Ni(II) | 3.43 | 0.058 | 39 | 96 | |||||||||||
| Olive oil residues (Olea europaea) | - | 6 | Pb(II) | 10 | - | 11.67 | 5.33 | 0.026 | - | 34 | - | - | - | - | - | [109] |
| Cd(II) | 2.71 | 0.024 | 14 | |||||||||||||
| Ni(II) | 1.98 | 0.034 | 10 | |||||||||||||
| Calabasa (Cucurbita moschata) | Na2CO3 | 5 | Cu(II) | 50 | - | 1.0 | 5.0 | 0.08 | - | - | - | 10 | 87.82 | - | HCl | [110] |
| Ni(II) | 6.0 | 0.10 | 12 | 81.57 | ||||||||||||
| Olive stone (Olea europaea) | - | 5 | Cu(II) | 100 | 13.4 | 6.0 | 5.06 | 0.080 | BA, Tho, YN, BDST, ANFIS | - | - | 20–100 | - | - | - | [43] |
| Pine shell (Pinus pinea) | 7.14 | 0.112 | 10–81 | |||||||||||||
| Grapefruit peel (Vitis vinifera) | CA | 5 | Cu(II) | 266 | 16 | 1.3 | 48.54 | 0.764 | BA, Tho, YN, BDST | 0 | - | - | - | - | - | [78] |
| Tea waste (Camellia sinensis); mapleleaves (Acer pseudoplatanus; mandarin peel (Citrus reticulata) | NaOH CaCl2 | 5.5 | Cd(II) | 20 | 31 | 10 | 38.25 | 0.340 | Tho, BDST | 61 | 3 | 47–50 | 22–49 | >99 | HCl | [56] |
| Cu(II) | 63.37 | 0.997 | 61 | 48–51 | 23–48 | |||||||||||
| Pb(II) | 108.12 | 0.522 | 61 | 56–57 | 34–58 | |||||||||||
| Zn(II) | 35.23 | 0.539 | 60 | 52–54 | 23–46 | |||||||||||
| Cucumber peel (Cucumis sativus) | - | 5 | Cd(II) | 100 | 8 | 20 | 180.53 | 1.61 | BA, Tho, YN | 36 | 3 | 77–85 | 94–98 | - | HCl | [75] |
| Sugar beet pulp (Beta vulgaris) | - | 5 | Zn(II) | 500 | 66 | 50 | 5.23 | 0.08 | BA | 35 | 3 | - | - | - | H2SO4, HCl, HNO3, EDTA-2Na | [111] |
| Pine cone shell (Pinus halepensis) | - | 5 | Pb(II) | 100 | 14.3 | 2 | 8.09 | 0.175 | - | 0 | 4 | 92 | 14–64 | 83 | HCl | [47] |
| Cu(II) | 36.19 | 0.127 | 0 | 23 | 19–63 | 100 | ||||||||||
| Litchi peels (Litchi chinensis) | - | 3 | Cr(VI) | 50 | 5 | 1.5 | 41.2 | 0.65 | BDST | 40 | 3 | - | >99 | >94 | HNO3 | [74] |
| Maple tree leaves (Acer pseudoplatanus) | - | 5 | Cu(II) | 55.0 | 21 | 21 | 18.3 | 0.288 | SREQ | 21 | 8 | 53 | 93–99 | 100 | H2SO4 | [37] |
| Java jute (Hibiscus cannabinus) | NaClO NaOH HCl | 7 | Cr(VI) | 0.5 | 15 | 2.2 | 0.021 | 4.04 × 10−4 | YN, Tho, BA | 25 | - | 52 | 88–92 | 78–98 | NaOH, HCl | [112] |
| Spent coffee grounds (Coffea) | - | 4.5 | Cd(II) | 11.41 | 14 | 5.5 | 13.49 | 0.12 | - | 13 | 4 | <50 | 60–100 | >99 | HNO3, CaCl2, AC | [113] |
| Cu(II) | 6.35 | 13.34 | 0.21 | 21 | ||||||||||||
| Pb(II) | 20.72 | 66.30 | 0.32 | 20 | ||||||||||||
| Grapefruit peel (Vitis vinifera) | H2O2 | 5.5 | Cr(VI) | 35 | 150 | - | 39.06 | 0.615 | HSDM (simulation) | 50 | - | - | 27–73 | >95 | - | [79] |
| Watermelon rind (Citrullus lanatus) | - | - | Pb(II) | Pb(II) | 5 | 1 | 55.00 | 0.265 | BA, Tho, YN | - | 3 | 0.265 | - | - | HCl | [114] |
| Rice husk (Oryza sativa) | - | 8.0 | As(V) | 0.070 | 28 | 7.0 | 0.417 | 5.57 × 10−3 | BA, Tho, YN | - | - | 60–95 | - | - | - | [52] |
| Olive tree pruning (Olea europaea) | - | 4 | Pb(II) | 150 | 5 | 6 | 5.38 | 0.026 | - | 75 | 5 | 40 | - | - | HCl | [83] |
| H2SO4 | 6.48 | 0.313 | 76 | 50 | - | - | ||||||||||
| HNO3 | 31.56 | 0.152 | 65 | 45 | - | - | ||||||||||
| NaOH | 34.42 | 0.166 | 57 | 53 | 60–99 | >51 | ||||||||||
| Sesame | - | 5.5 | Cd(II) | 60 | 2.0 | 2.5 | 22.88 | 0.204 | - | 56 | 4 | 74 | 72–94 | >55 | HNO3 | [115] |
| Tururi fibers (Manicaria saccifera Gaertn.) | - | 5.5 | Cu(II) | 276.72 | 9.5 | 4 | 104.03 | 1.64 | HSDM | 16–50 | - | >90 | - | - | - | [82] |
| Cd(II) | 299.53 | 126.75 | 1.13 | |||||||||||||
| Ni(II) | 306.53 | 48.83 | 0.832 | |||||||||||||
| Pb(II) | 303.7 | 52.59 | 0.254 | |||||||||||||
| Grapefruit peel (Citrus maxima) | - | 6 | Pb(II) | 300 | 3 | 2.5 | 160 | 0.772 | Tho | 25–56 | - | - | - | - | - | [44] |
| Cd(II) | 132 | 1.17 | ||||||||||||||
| Cu(II) | 84 | 1.32 | ||||||||||||||
| Ni(II) | 60.7 | 1.03 | ||||||||||||||
| Passion fruit shell (Passiflora edulis) | - | 6 | Pb(II) | 300 | 3 | 2.5 | 98.4 | 0.475 | ||||||||
| Cd(II) | 48.6 | 0.432 | ||||||||||||||
| Cu(II) | 40 | 0.629 | ||||||||||||||
| Ni(II) | 25.8 | 0.440 | ||||||||||||||
| Sugarcane bagasse (Saccharum officinarum) | - | 6 | Pb(II) | 300 | 3 | 2.5 | 49.8 | 0.240 | ||||||||
| Cd(II) | 26.3 | 0.234 | ||||||||||||||
| Cu(II) | 23 | 0.362 | ||||||||||||||
| Ni(II) | 16.1 | 0.274 | ||||||||||||||
| Sunflower biomass (Helianthus annuus) | - | 6.5 | Co(II) | 40 | 5 | 8 | 11.68 | 0.198 | - | >90 | - | - | - | - | - | [116] |
| Citrus peels (Vitis vinifera) | HNO3 | 4.0 | Pb(II) | 10.36 | 24 | 9 | 85 | 0.410 | Tho | 42 | - | 30–100 | 74–100 | - | HNO3 | [76] |
| Cd(II) | 5.62 | 44 | 0.391 | 31 | ||||||||||||
| Zn(II) | 3.27 | 20 | 0.306 | 30 | ||||||||||||
| Green coconut shells (Cocos nucifera) | NaOH | 5.5–5.7 | Cu(II) | 200 | 100 | 200 | 47.41 | 0.746 | Tho, EBCT | 30–60 | - | 50–99 | - | - | HNO3 | [48] |
| Ni(II) | 26.53 | 0.452 | ||||||||||||||
| Zn(II) | 25.76 | 0.394 | ||||||||||||||
| Waste phoenix tree leaf (Phoenix dactylifera) | PMDA | 6 | Cu(II) | 50 | - | 4.5 | 34.5 | 0.543 | YN, modified YN, Wol | 40–60 | - | 40–70 | - | - | - | [60] |
| Cd(II) | 38.6 | 0.343 | ||||||||||||||
| Zn(II) | 28.5 | 0.436 | ||||||||||||||
| Coconut husk (Cocos nucifera) | - | 7 | Cu(II) | 10 | 20 | 10 | 7.25 | 0.114 | BDST, YN, Ck | 45 | - | 52 | - | - | - | [41] |
| Grape stalks (Vitis vinifera) | - | 5.2 | Cu(II) | 12.71 | 6.7 | 0.5 | 11.69 | 0.184 | HSDM | 40–75 | - | - | - | - | - | [39] |
| Cd(II) | 22.48 | 26.87 | 0.239 | |||||||||||||
| Ni(II) | 11.74 | 13.81 | 0.228 | |||||||||||||
| Pb(II) | 41.44 | 54.29 | 0.262 | |||||||||||||
| Green bean husk (Phaseolus vulgaris) | - | 4 | Sb(III) | 5 | 50 | 5.0 | 20.6 | 0.1692 | Tho | 20–30 | 7 | >99 | >97 | >90 | HCl | [54] |
| Hemp fiber (Cannabis sativa) | - | 5 | Co(II) | 50 | 7 | - | 15.44 | 0.2620 | Tho, YN | 90 | - | 40–83 | - | - | - | [81] |
| Rice straw (Oryza sativa) | NaOH | - | Ni(II) | 75 | 2 | 0.5 | 43 | 0.7327 | Tho, BA, YN | - | - | - | - | - | - | [55] |
| Residue of allspice (Pimenta dioica) | - | 5.75 | Pb(II) | 15 | 15 | 20 | 16.2 | 0.0782 | Tho, BDST | 81 | - | >99 | - | - | - | [117] |
| Oil cake (Brassica juncea) | - | 8 | Ni(II) | 10 | - | 1 | 9.5 | 0.1619 | - | 5 | 7 | 69 | >99 | >99 | HCl | [118] |
| Olive pit (Olea europaea) | H2SO4 | 5 | Pb(II) | 150 | 4.4 | 6 | 17.7 | 0.0854 | - | 75 | 14 | 49 | 86–100 | >80 | HCl | [119] |
| Sugarcane bagasse (Saccharum officinarum) | ECH TEPA | 5 | Cu(II) | 20 | - | 6.25 | 18.43 | 0.29 | BA, YN | 42 | - | 61 | - | - | EDTA-2Na | [120] |
| Almond shell (Prunus amygdalus) | - | 5 | Cu(II) | 100 | 4.4 | 6 | 32.158 | 0.155 | - | - | - | 29.29 | - | - | - | [121] |
| Pb(II) | 10.531 | 0.166 | 82.27 | |||||||||||||
| Corn stalk (Zea mays) | EPH DETA TEA | 7.2 | Cr(VI) | 200 | 1.4 | 5 | 250 | 4.81 | BA, Tho, YN | 60–80 | - | 70–94 | - | - | - | [38] |
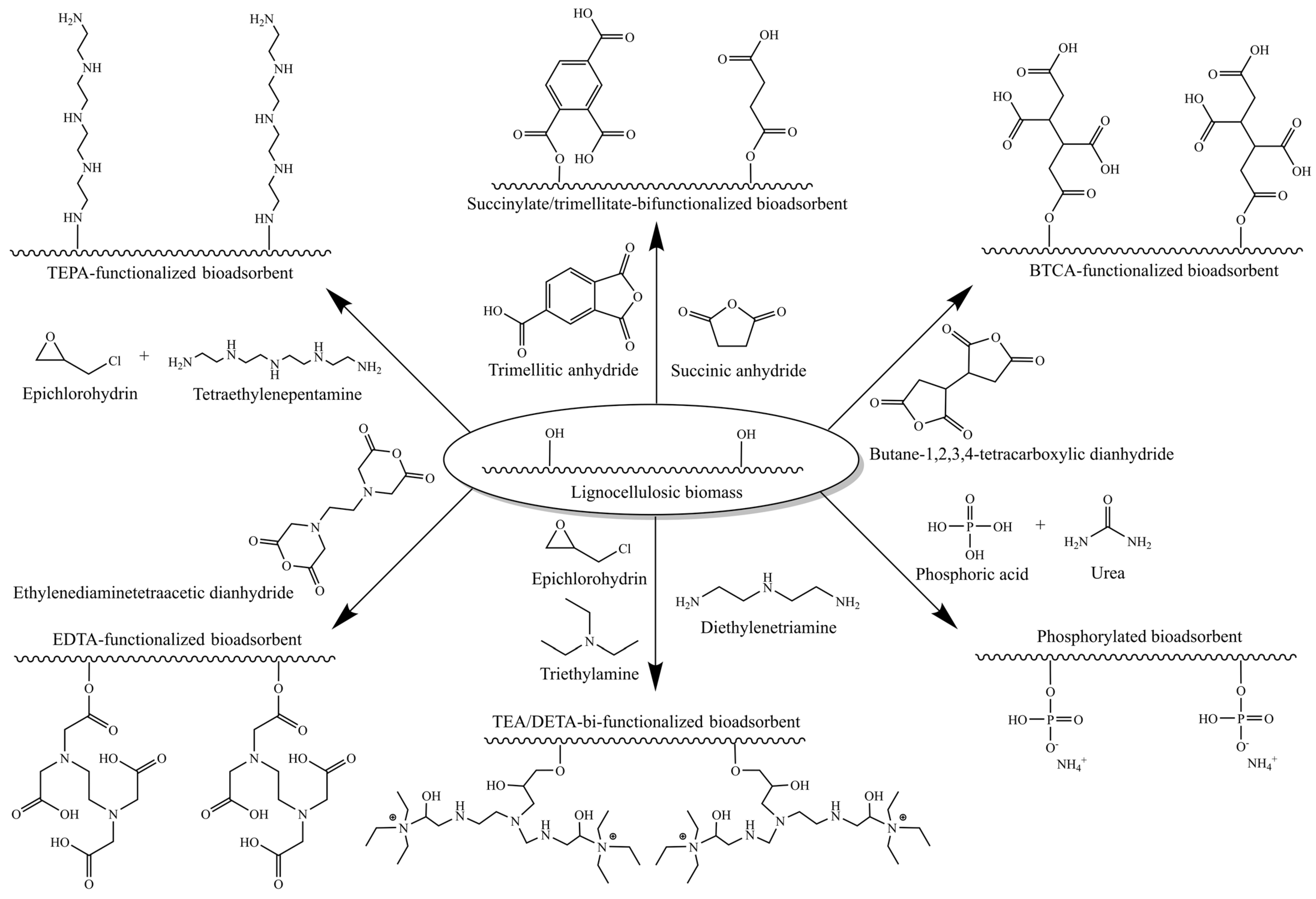
5.2. Chemically Modified Lignocellulosic Adsorbents
5.2.1. Bifunctional Adsorbents for Simultaneous Cation and Anion Removal
5.2.2. pH of the Point of Zero Charge (pHpzc)
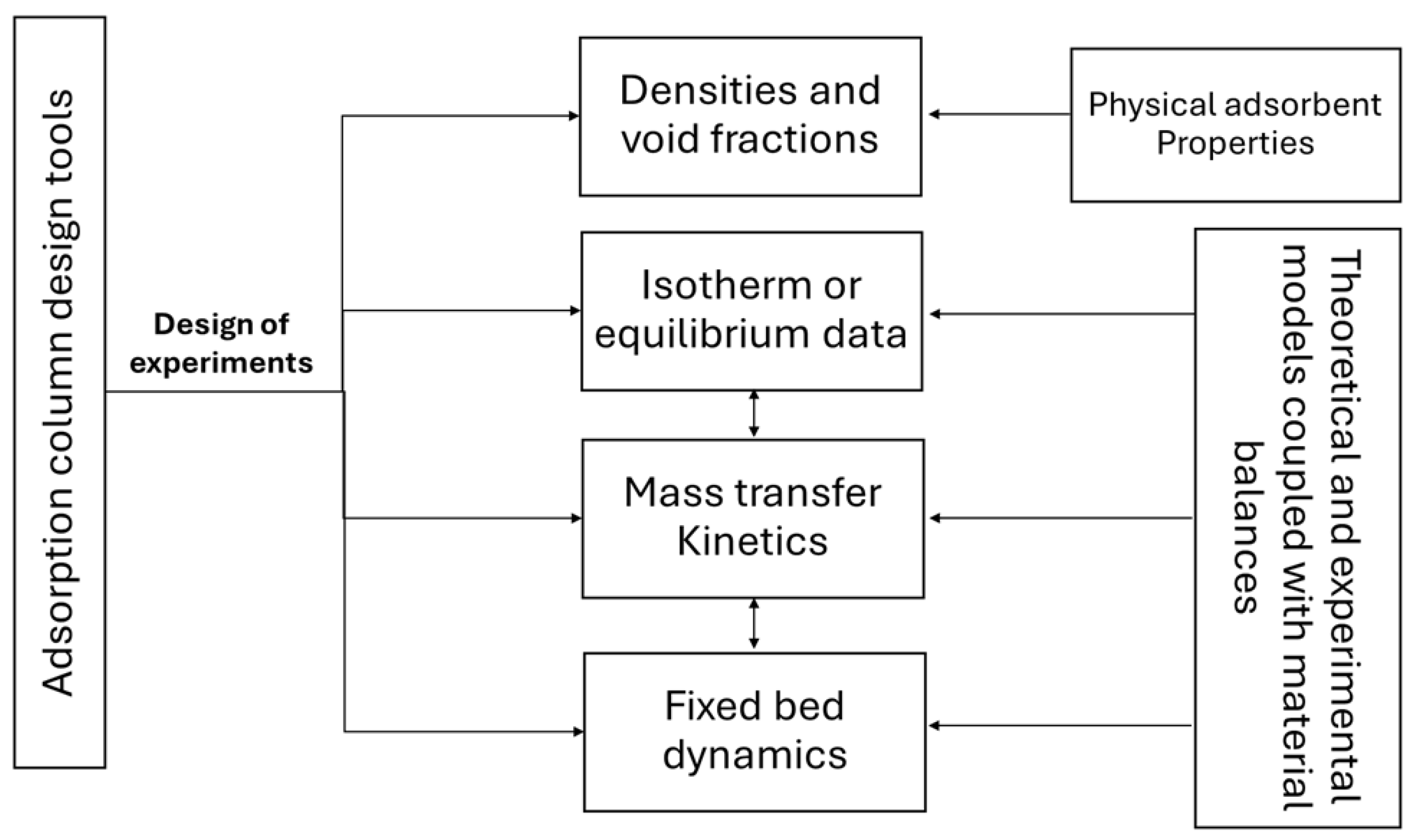
5.3. Design and Optimization of Fixed-Bed Columns
5.4. Scale-Up and Technology Maturity of Lignocellulosic Adsorbent Columns
6. Simplified Models for Monocomponent Fixed-Bed Columns
6.1. Redundant Comparisons and Misuse of Models
6.2. Data Distortion by Linearized Models
6.3. Statistical Criteria for Evaluating Adsorption Models
7. Multicomponent Adsorption in Fixed-Bed Columns
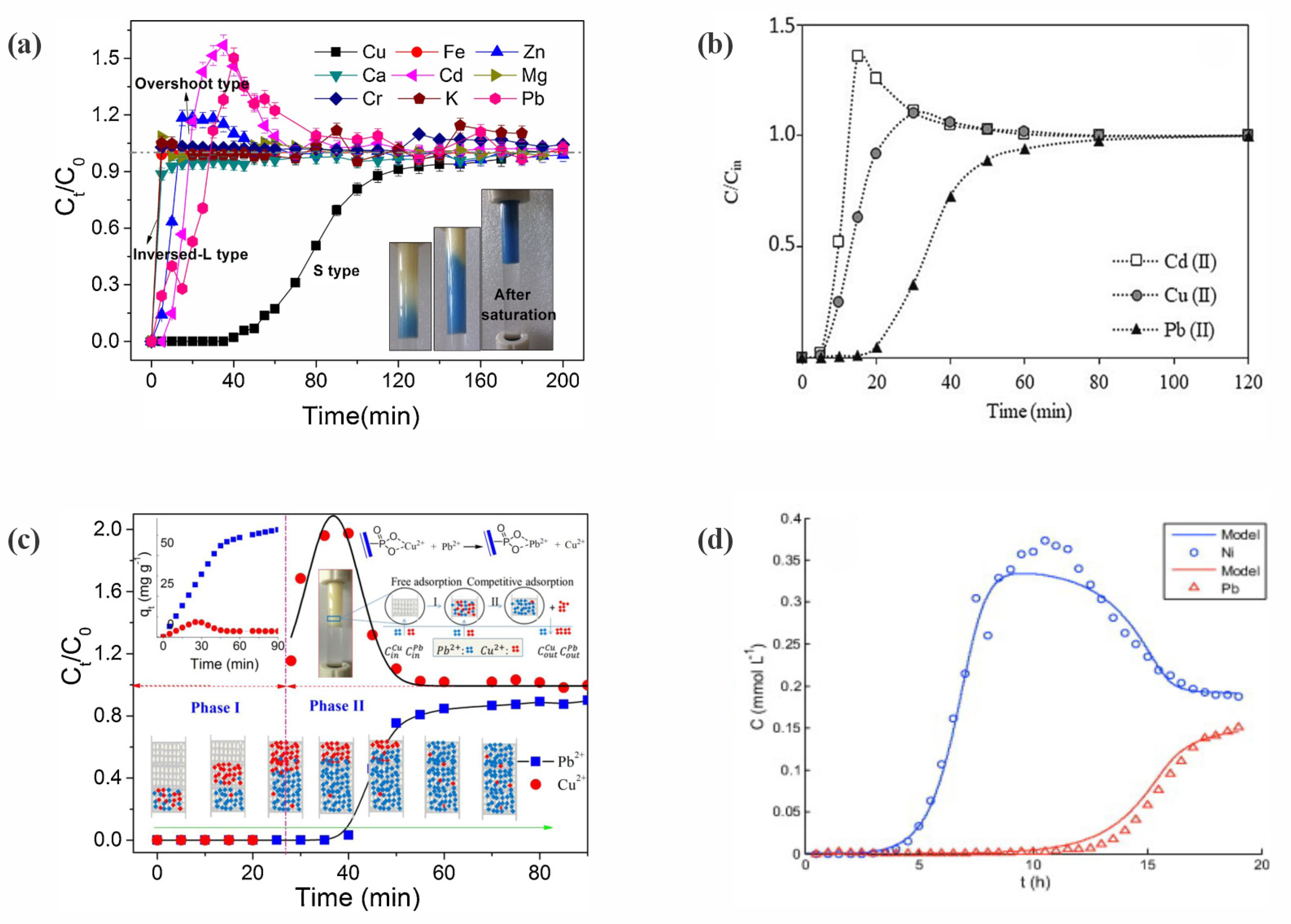
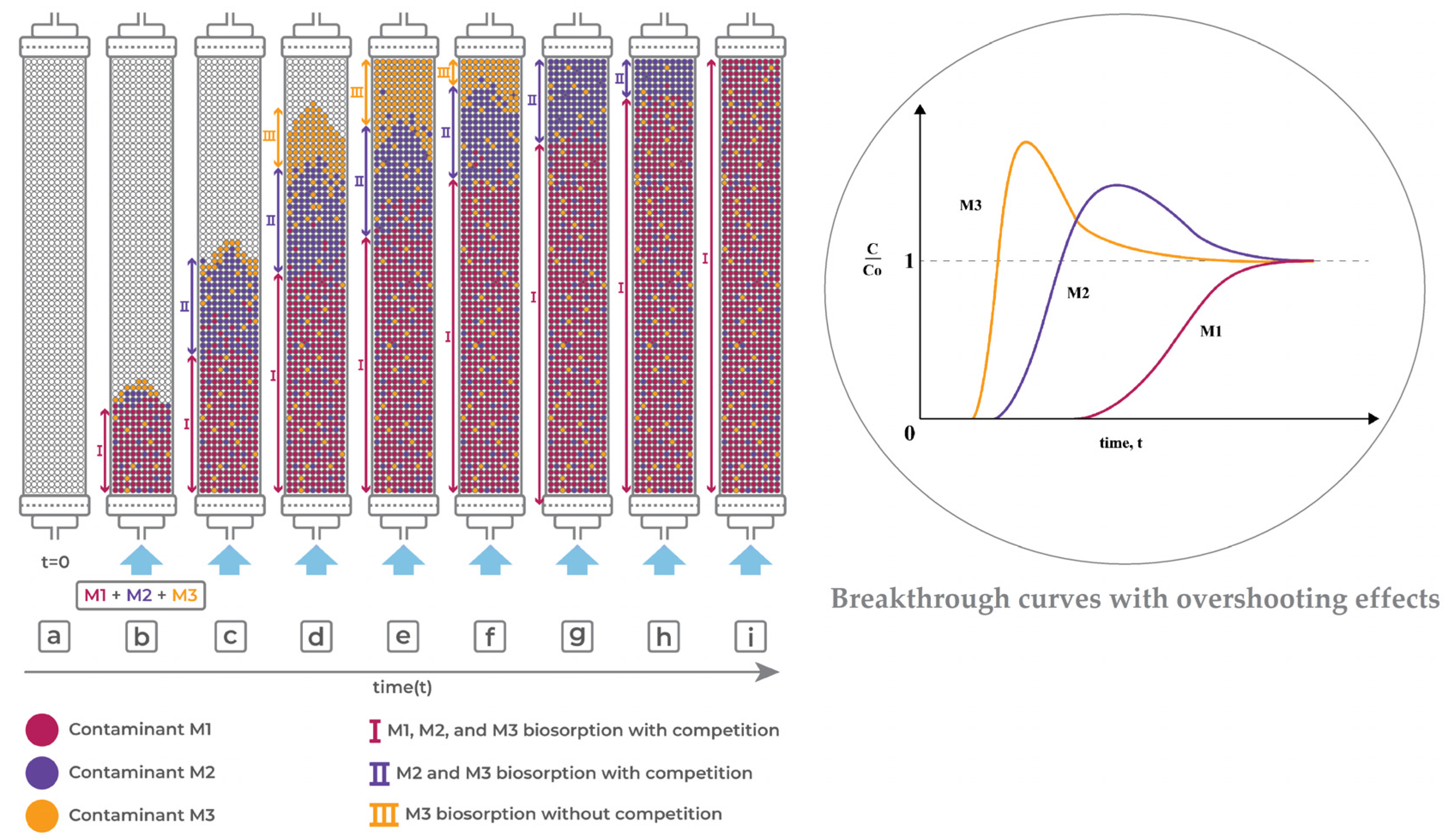
7.1. Competitive Adsorption and Overshooting Phenomenon
7.2. Evaluation of Adsorption Affinity Behavior in Fixed-Bed Columns
| Main Mechanism | Property | Explanation | Order of Affinity | Reference |
|---|---|---|---|---|
| Electrostatic interaction (electrostatic attraction and ion exchange) | Ionic radius | Ions with greater charge and smaller hydrated radius present greater polarization, facilitating electrostatic interaction | Ni(II) > Cu(II) = Co(II) > Zn(II) > Cd(II) > Hg(II) > Pb(II) | [145,152] |
| Hydrated ionic radius | Pb(II) > Ni(II) > Cu(II) > Hg(II) > Co(II) > Cd(II) > Zn(II) | [145,152] | ||
| Ionic potential (ionic charge/ionic radius) | Stronger bonds are formed with ions of higher charge/radius ratios | Pb(II) > Ni(II) > Cu(II) > Hg(II) > Co(II) > Cd(II) > Zn(II) | [145,153] | |
| Solubility product constant of phosphate salts (Ksp) | Metal ions with higher Ksp and ligand groups (e.g., PO43−) show higher affinity | Ni(II) > Zn(II) > Cd(II) > Co(II) > Pb(II) | [145,154] | |
| Covalent bond, complexation, and redox reaction | Irving–Williams series (ionic radius and second ionization potential energy) | Metal ions with smaller ionic radii form more stable complexes, but for transition metals, bond strength will depend on the radius and electron configuration | Mn(II) < Fe(II) < Co(II) < Ni(II) < Cu(II) > Zn(II) | [145,146] |
| Electronegativity (Pauling) | Metals with higher electronegativity form stronger covalent bonds with oxygen-containing ligands | Cu(II) = Hg(II) > Ni(II) > Co(II) > Pb(II) > Fe(II) > Cd(II) > Zn(II) > Mn(II) | [145,155] | |
| Standard reduction potential | Metals with higher reduction potential tend to form stronger bonds with electron-donating ligands | Hg(II) > Pb(II) > Ni(II) > Co(II) > Cu(II) > Cd(II) > Zn(II) | [145,154] | |
| Complex formation constant | Metals with higher complex formation constants form more stable complexes, similar to the Irving–Williams series but with the introduction of Pb(II) | Hg(II) > Cu(II) > Ni(II) > Co(II) > Zn(II) > Cd(II) | [145,154] |
8. Modeling Fixed-Bed Columns in Multicomponent Systems
8.1. Mass Transfer Models for Fixed-Bed Columns
- represents solute convective transport along the column in the Z direction over time;
- describes the rate of change (accumulation) in solute concentration in the liquid phase;
- represents the rate of adsorption of the solute on the solid phase;
- accounts for solute dispersion along the flow direction, due to velocity variations and diffusion effects.
8.1.1. HSDM and LDF Models
8.1.2. Multicomponent Isotherm Equations
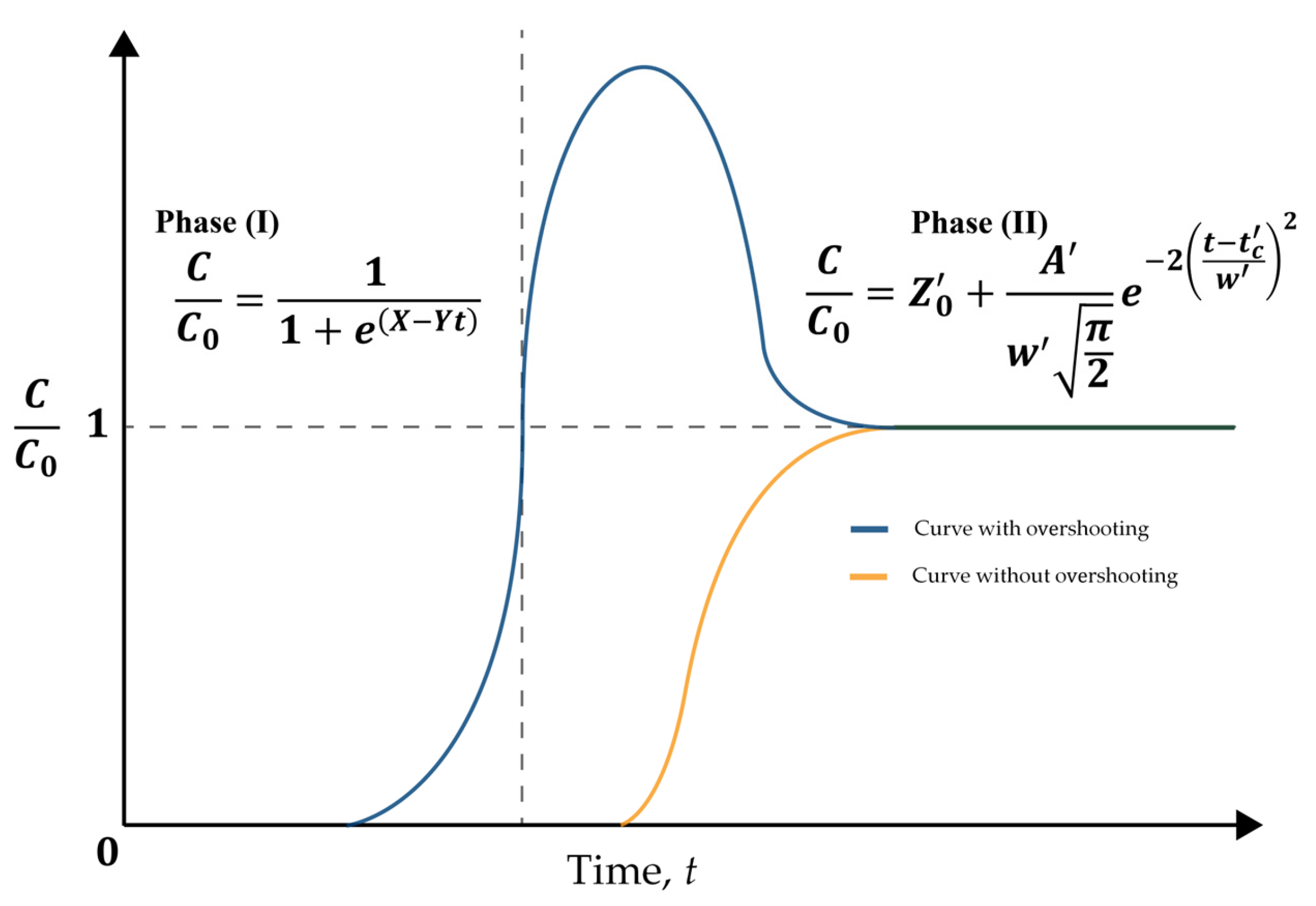
8.2. Bell-Shaped Curve Modeling
8.3. Quantitative Structure–Activity Relationship (QSAR) Approach
8.4. Modeling Using Artificial Neural Networks (ANNs)
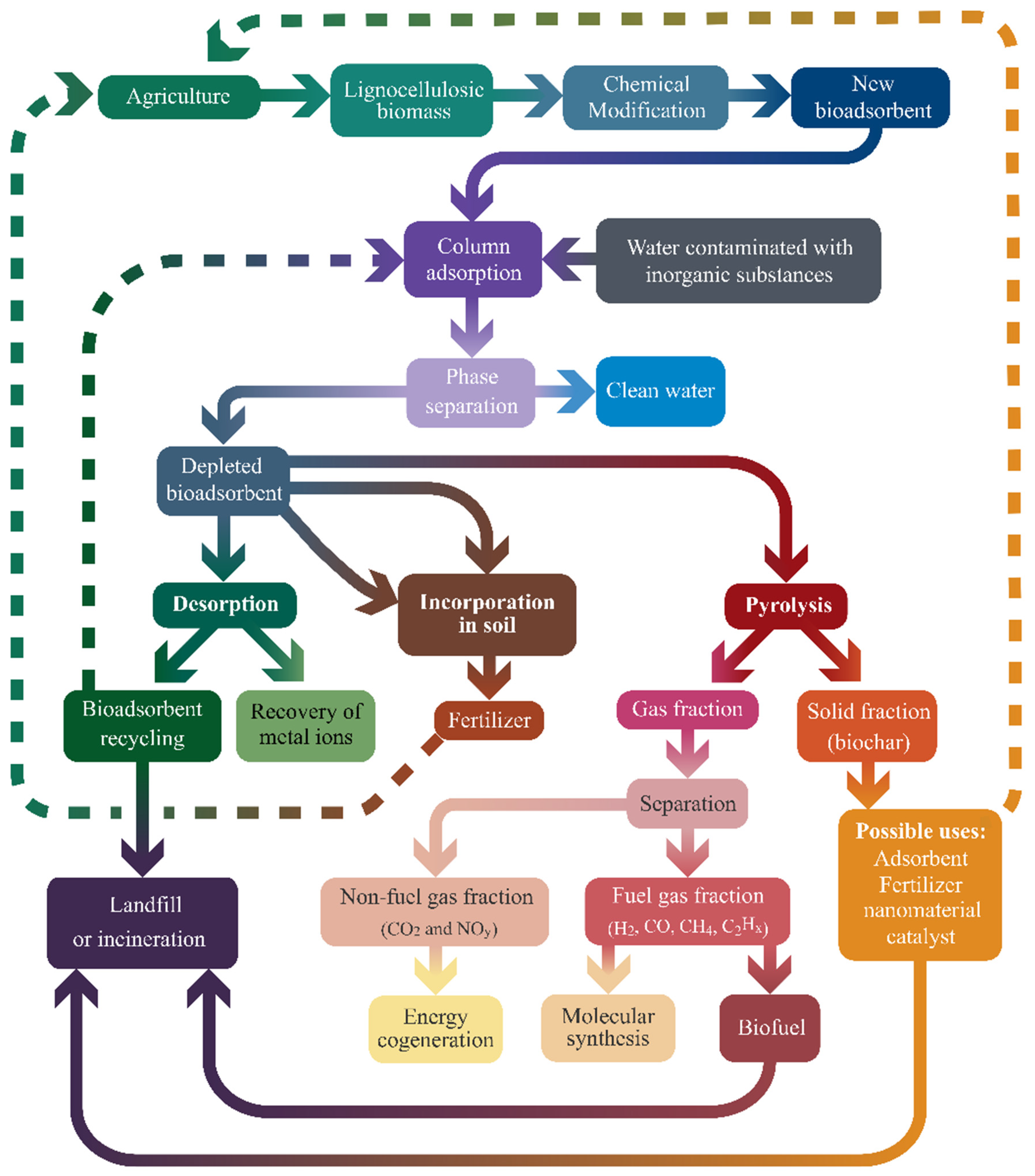
9. Future Prospects for Use of Depleted Lignocellulosic Bioadsorbents
9.1. Bioadsorbent Regeneration and Reuse
9.2. Depleted Bioadsorbents: Disposal Concerns
9.3. Incineration and Pyrolysis Evaluation
9.4. Second Uses of Depleted Bioadsorbents as Fertilizers and Catalysts
10. Future Perspectives
- Early identification of which type of contaminant will be removed, the existence of competing contaminants, and the operating mode (batch or continuous) and conditions necessary to optimize its removal (including flow rate, volume to be treated, contaminant concentration, and permissible limits according to legislation) are essential criteria for defining the synthesis route, before carrying out any chemical modification.
- The type of chemical modification and ligand(s) introduced into the structure of the lignocellulosic material should be based on the Williams–Irving series, considering the ionic character, electronegativity, and hydrated ionic radius of the metal ion, to ensure that the bioadsorbent is suitable for removing the target pollutant, in the presence of competing contaminants.
- The cost-effectiveness of the bioadsorbent must be evaluated using a preliminary life-cycle analysis and a business model (TRL > 6) to ensure an efficient and economically viable product/process.
- Comparison must be made between activated carbon and lignocellulosic bioadsorbents with specific functionalization for the removal of target pollutants, since these materials compete for similar applications.
- Regeneration studies must not only evaluate different eluent solutions, from technical, economic, and environmental perspectives, but also consider the effects on the pollutant removal efficiency and the service life of the bioadsorbent.
- Multicomponent column adsorption data modeling is still scarce in the literature, especially for systems containing three or more components. Due to the high computational cost, the use of emerging tools such as artificial neural networks and machine learning should be considered.
- Tests in relevant environments and mini-pilot plants are essential to validate the business model and the life cycle analysis.
- Environmentally safe disposal of depleted bioadsorbents and/or their second use is another crucial topic that should not be neglected, considering the concepts of a bio-based circular economy.
11. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Area of the “desorption curve peak” (min) | |
| A, B | Fitting parameters (min−2) |
| ANN | Artificial neural network |
| ANFIS | Artificial neural–fuzzy inference system |
| AIC | Akaike Information Criterion |
| BDST | Bed Depth Service Time |
| C0 | Initial adsorbate concentration (mmol L−1 or mg L−1) |
| C | Column effluent concentration at time t (mmol L−1 or mg L−1) |
| Ce | Equilibrium concentration (mmol L−1 or mg L−1) |
| D | Adsorption column diameter (cm) |
| Axial dispersion coefficient (cm2 min−1) | |
| Eads | Adsorption efficiency (%) |
| Edes | Desorption efficiency (%) |
| Ere-ads | Re-adsorption efficiency (%) |
| GA | Genetic algorithm |
| Hb | Column bed height (cm) |
| Hunb | Unused bed height (cm) |
| HSAB | Hard and Soft Acids and Bases |
| HSDM | Homogeneous Surface Diffusion Model |
| IAST | Ideal Adsorbed Solution Theory |
| kBA | Bohart–Adams rate constant (L mg−1 min−1 or L mmol−1 min−1) |
| Ksp | Solubility product constant |
| kTh | Thomas rate constant (L mg−1 min−1 or L mmol−1 min−1) |
| kYN | Yoon–Nelson rate constant (min−1) |
| JCR | Journal citation reports |
| L | Bed depth (cm) |
| LDF | Linear Driving Force |
| M | Mass of the adsorbent in the column (mg or g) |
| N0 | Adsorption capacity of the adsorbent per unit volume of the bed (mg L−1 or mmol L−1) |
| NC | Number of citations |
| MTZ | Mass transfer zone (cm) |
| P | Particle size (μm) |
| pKf | Complex formation constants |
| PSO | Particle swarm optimization |
| q0 | Maximum adsorption capacity of the adsorbent (mg g−1 or mmol g−1) |
| Q | Volumetric flow rate (L min−1) |
| Qe | Solid loading per unit weight of adsorbent at equilibrium condition (mg g−1 or mmol g−1) |
| Qe,est | Estimated adsorption capacity (mg g−1 or mmol g−1) |
| Qe,exp | Experimental adsorption capacity (mg g−1 or mmol g−1) |
| Qmono | Solid loading per unit weight of adsorbent in a monocomponent system (mg g−1 or mmol g−1) |
| Qmulti | Solid loading per unit weight of adsorbent in a multicomponent system (mg g−1 or mmol g−1) |
| RAST | Real Adsorbed Solution Theory |
| R2 | Coefficient of determination |
| R2adj | Adjusted coefficient of determination |
| T | Temperature (ºC) |
| t | Time (min) |
| tb | Breakthrough time (min) |
| Center of the “desorption curve peak” (min) | |
| ts | Saturation time (min) |
| TRL | Technology readiness level |
| u | Linear velocity of the fluid through the column (m s−1 or cm min−1) |
| w | Weight of adsorbent (mg or g) |
| Z | Distance along column length (cm) |
| Offset (equal to (1.0)) | |
| Ze | Effective use of the bed (%) |
| Half width of the “desorption curve peak”(min) | |
| α | Fitting parameter for InOrdinatio equation |
| β | External mass transfer coefficient (min−1) |
| βL | Stability constant |
| ƞ | Absolute hardness |
| χ2 | Chi-square |
| χ2red | Reduced chi-square |
| Bed porosity | |
| Empty fraction of the column | |
| Interstitial velocity (cm min−1) | |
| ρp | Particle density (g mL−1) |
References
- Ballesteros, L.F.; Michelin, M.; Vicente, A.A.; Teixeira, J.A.; Cerqueira, M.A. Lignocellulosic Materials and Their Use in Bio-Based Packaging, 1st ed.; Springer: Cham, Switzerland, 2018. [Google Scholar]
- O’Connell, D.W.; Birkinshaw, C.; O’Dwyer, T.F. Heavy metal adsorbents prepared from the modification of cellulose: A review. Bioresour. Technol. 2008, 99, 6709–6724. [Google Scholar] [CrossRef] [PubMed]
- Fomina, M.; Gadd, G.M. Biosorption: Current perspectives on concept, definition and application. Bioresour. Technol. 2014, 160, 3–14. [Google Scholar] [CrossRef] [PubMed]
- Maia, L.C.; Soares, L.C.; Gurgel, L.V.A. A review on the use of lignocellulosic materials for arsenic adsorption. J. Environ. Manag. 2021, 288, 112397. [Google Scholar] [CrossRef]
- Reddy, D.H.K.; Vijayaraghavan, K.; Kim, J.A.; Yun, Y.S. Valorisation of post-sorption materials: Opportunities, strategies, and challenges. Adv. Coll. Int. Sci. 2017, 242, 35–58. [Google Scholar] [CrossRef]
- Thirunavukkarasu, A.; Nithya, R.; Sivashankar, R. Continuous fixed-bed biosorption process: A review. Chem. Eng. J. Adv. 2021, 8, 100188. [Google Scholar] [CrossRef]
- Thirunavukkarasu, O.S.; Viraraghavan, T.; Subramanian, K.S.; Chaalal, O.; Islam, M.R. Arsenic removal in drinking water—Impacts and novel removal technologies. Energy Sources 2005, 27, 209–219. [Google Scholar] [CrossRef]
- Patel, H. Fixed-bed column adsorption study: A comprehensive review. Appl. Water Sci. 2019, 9, 45. [Google Scholar] [CrossRef]
- Ruthven, D.M. Principles of Adsorption and Adsorption Processes, 1st ed.; Wiley: New York, NY, USA, 1984; p. 464. [Google Scholar]
- Gu, T. Mathematical Modeling and Scale-Up of Liquid Chromatography: With Application Examples, 2nd ed.; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Bohart, G.S.; Adams, E.Q. Some aspects of the behavior of charcoal with respect to chlorine.1. J. Am. Chem. Soc. 1918, 42, 523–544. [Google Scholar] [CrossRef]
- Thomas, H.C. Heterogeneous ion exchange in a flowing system. J. Am. Chem. Soc. 1944, 66, 1664–1666. [Google Scholar] [CrossRef]
- Yoon, Y.H.; Nelson, J.H. Application of gas adsorption kinetics. I. A theoretical model for respirator cartridge service life. Am. In. Hyg. Assoc. J. 1984, 45, 509–516. [Google Scholar] [CrossRef]
- Wolborska, A. Adsorption on activated carbon of p-nitrophenol from aqueous solution. Water Res. 1989, 23, 85–91. [Google Scholar] [CrossRef]
- Chu, K.H. Breakthrough curve analysis by simplistic models of fixed bed adsorption: In defense of the century-old Bohart-Adams model. Chem. Eng. J. 2020, 380, 122513. [Google Scholar] [CrossRef]
- Shafeeyan, M.S.; Daud, W.M.A.W.; Shamiri, A. A review of mathematical modeling of fixed-bed columns for carbon dioxide adsorption. Chem. Eng. Res. Des. 2014, 92, 961–988. [Google Scholar] [CrossRef]
- Chu, K.H. Fixed bed sorption: Setting the record straight on the Bohart-Adams and Thomas models. J. Hazard. Mater. 2010, 177, 1006–1012. [Google Scholar] [CrossRef]
- Pagani, R.N.; Kovaleski, J.L.; Resende, L.M. Methodi Ordinatio: A proposed methodology to select and rank relevant scientific papers encompassing the impact factor, number of citation, and year of publication. Scientometrics 2015, 105, 2109–2135. [Google Scholar] [CrossRef]
- Bilal, M.; Shah, J.A.; Ashfaq, T.; Gardazi, S.M.H.; Tahir, A.A.; Pervez, A.; Haroon, H.; Mahmood, Q. Waste biomass adsorbents for copper removal from industrial wastewater—A review. J. Hazard. Mater. 2013, 263, 322–333. [Google Scholar] [CrossRef]
- Fu, F.; Wang, Q. Removal of heavy metal ions from wastewaters: A review. J. Environ. Manag. 2011, 92, 407–418. [Google Scholar] [CrossRef]
- Ferreira Junior, J.E.G.; Maia, L.C.; dos Santos, G.R.; Soares, L.C.; Gurgel, L.V.A. An affordable bioadsorbent system to treat arsenic-contaminated drinking water in the developing world: Prototyping and economic assessment. J. Environ. Chem. Eng. 2023, 11, 111199. [Google Scholar] [CrossRef]
- Afroze, S.; Sen, T.K. A Review on heavy metal ions and dye adsorption from water by agricultural solid waste adsorbents. Water Air Soil Pollut. 2018, 229, 225. [Google Scholar] [CrossRef]
- Myers, A.L.; Prausnitz, J.M. Thermodynamics of mixed-gas adsorption. AIChE J. 1965, 11, 121–127. [Google Scholar] [CrossRef]
- Wang, Y.; Lü, J.; Feng, D.; Guo, S.; Li, J. A Biosorption-pyrolysis process for removal of Pb from aqueous solution and subsequent immobilization of Pb in the char. Water 2020, 12, 2381. [Google Scholar] [CrossRef]
- Weber, W.J.; Smith, E.H. Activated carbon adsorption: The state of the art. Stud. Environ. Sci. 1986, 29, 455–492. [Google Scholar] [CrossRef]
- Çeçen, F.; Aktaş, Ö. Activated Carbon for Water and Wastewater Treatment: Integration of Adsorption and Biological Treatment, 1st ed.; Wiley-VCH: Weinheim, Germany, 2011. [Google Scholar]
- Malik, D.S.; Jain, C.K.; Yadav, A.K. Heavy metal removal by fixed-bed column—A review. ChemBioEng Rev. 2018, 5, 173–179. [Google Scholar] [CrossRef]
- Dai, Y.; Sun, Q.; Wang, W.; Lu, L.; Liu, M.; Li, J.; Yang, S.; Sun, Y.; Zhang, K.; Xu, J.; et al. Utilizations of agricultural waste as adsorbent for the removal of contaminants: A review. Chemosphere 2018, 211, 235–253. [Google Scholar] [CrossRef] [PubMed]
- Agarwal, A.; Upadhyay, U.; Sreedhar, I.; Singh, S.A.; Patel, C.M. A review on valorization of biomass in heavy metal removal from wastewater. J. Water Process Eng. 2020, 38, 101602. [Google Scholar] [CrossRef]
- Aksu, Z. Application of biosorption for the removal of organic pollutants: A review. Process Biochem. 2005, 40, 997–1026. [Google Scholar] [CrossRef]
- Ambaye, T.G.; Vaccari, M.; van Hullebusch, E.D.; Amrane, A.; Rtimi, S. Mechanisms and adsorption capacities of biochar for the removal of organic and inorganic pollutants from industrial wastewater. Int. J. Environ. Sci. Technol. 2020, 18, 3273–3294. [Google Scholar] [CrossRef]
- Wang, F.; Yu, J.; Zhang, Z.; Xu, Y.; Chi, R.-A. An amino-functionalized ramie stalk-based adsorbent for highly effective Cu2+ removal from water: Adsorption performance and mechanism. Process Saf. Environ. Prot. 2018, 117, 511–522. [Google Scholar] [CrossRef]
- Singh, S.; Kumar, V.; Datta, S.; Dhanjal, D.S.; Sharma, K.; Samuel, J.; Singh, J. Current advancement and future prospect of biosorbents for bioremediation. Sci. Total Environ. 2020, 709, 135895. [Google Scholar] [CrossRef]
- Nassar, M.M. Adsorption of Fe+3 and Mn+2 from groundwater onto maize cobs using batch adsorber and fixed bed column. Sep. Sci. Technol. 2006, 41, 943–959. [Google Scholar] [CrossRef]
- Taka, A.L.; Klink, M.J.; Mbianda, X.Y.; Naidoo, E.B. Chitosan nanocomposites for water treatment by fixed-bed continuous flow column adsorption: A review. Carbohydr. Polym. 2021, 255, 117398. [Google Scholar] [CrossRef] [PubMed]
- Ali, I. Water treatment by adsorption columns: Evaluation at ground level. Sep. Purif. Rev. 2013, 43, 175–205. [Google Scholar] [CrossRef]
- Amirnia, S.; Ray, M.B.; Margaritis, A. Copper ion removal by Acer saccharum leaves in a regenerable continuous-flow column. Chem. Eng. J. 2016, 287, 755–764. [Google Scholar] [CrossRef]
- Chen, S.; Yue, Q.; Gao, B.; Li, Q.; Xu, X.; Fu, K. Adsorption of hexavalent chromium from aqueous solution by modified corn stalk: A fixed-bed column study. Bioresour. Technol. 2012, 113, 114–120. [Google Scholar] [CrossRef]
- Escudero, C.; Poch, J.; Villaescusa, I. Modelling of breakthrough curves of single and binary mixtures of Cu(II), Cd(II), Ni(II) and Pb(II) sorption onto grape stalks waste. Chem. Eng. J. 2013, 217, 129–138. [Google Scholar] [CrossRef]
- Wang, L.; Xu, Z.; Fu, Y.; Chen, Y.; Pan, Z.; Wang, R.; Tan, Z. Comparative analysis on adsorption properties and mechanisms of nitrate and phosphate by modified corn stalks. RSC Adv. 2018, 8, 36468–36476. [Google Scholar] [CrossRef]
- Acheampong, M.A.; Pakshirajan, K.; Annachhatre, A.P.; Lens, P.N.L. Removal of Cu(II) by biosorption onto coconut shell in fixed-bed column systems. J. Ind. Eng. Chem. 2013, 19, 841–848. [Google Scholar] [CrossRef]
- Blazquez, G.; Calero, M.; Trujillo, C.; Martín-Lara, Á.; Ronda, A. Binary biosorption of Cu(II)-Pb(II) mixtures onto pine nuts shell in batch and packed bed systems. Environ. Eng. Manag. J. 2018, 17, 1349–1361. [Google Scholar] [CrossRef]
- Calero, M.; Ianez-Rodriguez, I.; Perez, A.; Martín-Lara, M.A.; Blázquez, G. Neural fuzzy modelization of copper removal from water by biosorption in fixed-bed columns using olive stone and pinion shell. Bioresour. Technol. 2018, 252, 100–109. [Google Scholar] [CrossRef]
- Chao, H.-P.; Chang, C.-C.; Nieva, A. Biosorption of heavy metals on Citrus maxima peel, passion fruit shell, and sugarcane bagasse in a fixed-bed column. J. Ind. Eng. Chem. 2014, 20, 3408–3414. [Google Scholar] [CrossRef]
- Li, J.; Ma, J.; Guo, Q.; Zhang, S.; Han, H.; Zhang, S.; Han, R. Adsorption of hexavalent chromium using modified walnut shell from solution. Water Sci. Technol. 2020, 81, 824–833. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Hu, C.; Huang, Q. Adsorption of Cu2+, Pb2+, and Cd2+ onto oiltea shell from water. Bioresour. Technol. 2019, 271, 487–491. [Google Scholar] [CrossRef] [PubMed]
- Martín-Lara, M.A.; Blázquez, G.; Calero, M.; Almendros, A.I.; Ronda, A. Binary biosorption of copper and lead onto pine cone shell in batch reactors and in fixed bed columns. Int. J. Miner. Process. 2016, 148, 72–82. [Google Scholar] [CrossRef]
- Raulino, G.S.; Vidal, C.B.; Lima, A.C.; Melo, D.Q.; Oliveira, J.T.; Nascimento, R.F. Treatment influence on green coconut shells for removal of metal ions: Pilot-scale fixed-bed column. Environ. Technol. 2014, 35, 1711–1720. [Google Scholar] [CrossRef] [PubMed]
- Yahya, M.D.; Abubakar, H.; Obayomi, K.S.; Iyaka, Y.A.; Suleiman, B. Simultaneous and continuous biosorption of Cr and Cu (II) ions from industrial tannery effluent using almond shell in a fixed bed column. Results Eng. 2020, 6, 100113. [Google Scholar] [CrossRef]
- Yahya, M.D.; Aliyu, A.S.; Obayomi, K.S.; Olugbenga, A.G.; Abdullahi, U.B.; Arellano-Garcia, H. Column adsorption study for the removal of chromium and manganese ions from electroplating wastewater using cashew nutshell adsorbent. Cogent Eng. 2020, 7, 1748470. [Google Scholar] [CrossRef]
- Rajeswari, M.; Agrawal, P.; Rao, N.N.; Sharma, A.; Hiremath, L.; Tippareddy, K.S.; Shivandappa. Modelling and efficiency assessment of the up flow fixed bed process packed with Moringa oleifera for continuous Cd(II) removal from drinking water. J. Mol. Struct. 2021, 1236, 130328. [Google Scholar] [CrossRef]
- Asif, Z.; Chen, Z. Removal of arsenic from drinking water using rice husk. Appl. Water Sci. 2015, 7, 1449–1458. [Google Scholar] [CrossRef]
- Basu, M.; Guha, A.K.; Ray, L. Adsorption of lead on lentil husk in fixed bed column bioreactor. Bioresour. Technol. 2019, 283, 86–95. [Google Scholar] [CrossRef]
- Iqbal, M.; Saeed, A.; Edyvean, R.G.J. Bioremoval of antimony(III) from contaminated water using several plant wastes: Optimization of batch and dynamic flow conditions for sorption by green bean husk (Vigna radiata). Chem. Eng. J. 2013, 225, 192–201. [Google Scholar] [CrossRef]
- Sharma, R.; Singh, B. Removal of Ni (II) ions from aqueous solutions using modified rice straw in a fixed bed column. Bioresour. Technol. 2013, 146, 519–524. [Google Scholar] [CrossRef] [PubMed]
- Abdolali, A.; Ngo, H.H.; Guo, W.; Zhou, J.L.; Zhang, J.; Liang, S.; Chang, S.W.; Nguyen, D.D.; Liu, Y. Application of a breakthrough biosorbent for removing heavy metals from synthetic and real wastewaters in a lab-scale continuous fixed-bed column. Bioresour. Technol. 2017, 229, 78–87. [Google Scholar] [CrossRef]
- Feisther, V.A.; Scherer Filho, J.; Hackbarth, F.V.; Mayer, D.A.; de Souza, A.A.U.; de Souza, S.M.A.G.U. Raw leaves and leaf residues from the extraction of essential oils as biosorbents for metal removal. J. Environ. Chem. Eng. 2019, 7, 103047. [Google Scholar] [CrossRef]
- Hymavathi, D.; Prabhakar, G. Modeling of cobalt and lead adsorption by Ficus benghalenesis L. in a fixed bed column. Chem. Eng. Commun. 2019, 206, 1264–1272. [Google Scholar] [CrossRef]
- Mitra, T.; Das, S.K. Cr(VI) removal from aqueous solution using Psidium guajava leaves as green adsorbent: Column studies. Appl. Water Sci. 2019, 9, 153. [Google Scholar] [CrossRef]
- Yu, J.; Feng, L.; Cai, X.; Wang, L.; Chi, R. Adsorption of Cu2+, Cd2+ and Zn2+ in a modified leaf fixed-bed column: Competition and kinetics. Environ. Earth Sci. 2014, 73, 1789–1798. [Google Scholar] [CrossRef]
- de Almeida, F.T.R.; Elias, M.M.C.; Xavier, A.L.P.; Ferreira, G.M.D.; Silva, I.A.; Filgueiras, J.G.; de Azevedo, E.R.; da Silva, L.H.M.; Gil, L.F.; Gurgel, L.V.A. Synthesis and application of sugarcane bagasse cellulose mixed esters. Part II: Removal of Co2+ and Ni2+ from single spiked aqueous solutions in batch and continuous mode. J. Colloid Interface Sci. 2019, 552, 337–350. [Google Scholar] [CrossRef]
- Chen, J.; Yu, J.; Wang, F.; Tang, J.; Zhang, Y.; Xu, Y.; Chi, R. Selective adsorption and recycle of Cu2+ from aqueous solution by modified sugarcane bagasse under dynamic condition. Environ. Sci. Pollut. Res. 2017, 24, 9202–9209. [Google Scholar] [CrossRef]
- Hoang, M.T.; Pham, T.D.; Nguyen, V.T.; Nguyen, M.K.; Pham, T.T.; Van der Bruggen, B. Removal and recovery of lead from wastewater using an integrated system of adsorption and crystallization. J. Clean. Prod. 2019, 213, 1204–1216. [Google Scholar] [CrossRef]
- Yu, J.; Xiong, W.; Sun, Q.; Zhu, J.; Chi, R.; Zhang, Y. Separation of Pb2+ from Mg2+ by modified sugarcane bagasse under batch and column conditions: Effect of initial concentration ratio. Arab. J. Chem. 2019, 12, 4438–4445. [Google Scholar] [CrossRef]
- Kausar, A.; Bhatti, H.N.; Iqbal, M. Kinetics and equilibrium of radioactive metal adsorption onto sugarcane bagasse waste: Comparison of batch and column adsorption modes. Z. Phys. Chem. 2021, 235, 281–294. [Google Scholar] [CrossRef]
- Rico, I.L.R.; Carrazana, R.J.C.; Karna, N.K.; Iáñez-Rodríguez, I.; de Hoces, M.C. Modeling the mass transfer in biosorption of Cr(VI) y Ni(II) by natural sugarcane bagasse. Appl. Water Sci. 2018, 8, 55. [Google Scholar] [CrossRef]
- Rodrigues, J.A.V.; Martins, L.R.; Furtado, L.M.; Xavier, A.L.P.; de Almeida, F.T.R.; Moreira, A.L.S.L.; Melo, T.M.S.; Gil, L.F.; Gurgel, L.V.A. Oxidized renewable materials for the removal of cobalt(II) and copper(II) from aqueous solution using in batch and fixed-Bed column adsorption. Adv. Polym. Technol. 2020, 2020, 8620431. [Google Scholar] [CrossRef]
- Tang, J.; Xi, J.; Yu, J.; Chi, R.; Chen, J. Novel combined method of biosorption and chemical precipitation for recovery of Pb2+ from wastewater. Environ. Sci. Pollut. Res. 2018, 25, 28705–28712. [Google Scholar] [CrossRef]
- Vera, L.M.; Bermejo, D.; Uguña, M.F.; Garcia, N.; Flores, M.; González, E. Fixed bed column modeling of lead(II) and cadmium(II) ions biosorption on sugarcane bagasse. Environ. Eng. Res. 2018, 24, 31–37. [Google Scholar] [CrossRef]
- Villabona-Ortíz, A.; Tejada-Tovar, C.; González-Delgado, Á.D. Elimination of chromium(VI) and nickel(II) ions in a packed column using oil palm bagasse and yam peels. Water 2022, 14, 1240. [Google Scholar] [CrossRef]
- Xiong, W.; Zhang, J.; Yu, J.; Chi, R. Competitive adsorption behavior and mechanism for Pb2+ selective removal from aqueous solution on phosphoric acid modified sugarcane bagasse fixed-bed column. Process Saf. Environ. Prot. 2019, 124, 75–83. [Google Scholar] [CrossRef]
- Teodoro, F.S.; Soares, L.C.; Filgueiras, J.G.; de Azevedo, E.R.; Patiño-Agudelo, Á.J.; Adarme, O.F.H.; da Silva, L.H.M.; Gurgel, L.V.A. Batch and continuous adsorption of Cu(II) and Zn(II) ions from aqueous solution on bi-functionalized sugarcane-based biosorbent. Environ. Sci. Pollut. Res. 2022, 29, 26425–26448. [Google Scholar] [CrossRef]
- Xu, Y.-L.; Song, S.-Y.; Chen, J.-D.; Chi, R.-A.; Yu, J.-X. Simultaneous recovery of Cu2+ and Pb2+ from metallurgical wastewater by two tandem columns fixed respectively with tetraethylenepentamine and phosphoric acid modified bagasse. J. Taiwan Inst. Chem. Eng. 2019, 99, 132–141. [Google Scholar] [CrossRef]
- Manikandan, N.A.; Alemu, A.K.; Goswami, L.; Pakshirajan, K.; Pugazhenthi, G. Waste Litchi peels for Cr(VI) removal from synthetic wastewater in batch and continuous systems: Sorbent characterization, regeneration and reuse study. J. Environ. Eng. 2016, 142, C4016001. [Google Scholar] [CrossRef]
- Basu, M.; Guha, A.K.; Ray, L. Adsorption of cadmium ions by cucumber peel in continuous mode. Int. J. Environ. Sci. Technol. 2017, 16, 237–248. [Google Scholar] [CrossRef]
- Chatterjee, A.; Schiewer, S. Effect of competing cations (Pb, Cd, Zn, and Ca) in fixed-bed column biosorption and desorption from citrus peels. Water Air Soil Pollut. 2014, 225, 1854. [Google Scholar] [CrossRef]
- Mora, B.P.; Bertoni, F.A.; Mangiameli, M.F.; González, J.C.; Bellú, S.E. Batch and fixed-bed column studies of selenite removal from contaminated water by orange peel-based sorbent. Water Sci. Eng. 2020, 13, 307–316. [Google Scholar] [CrossRef]
- Romero-Cano, L.A.; González-Gutiérrez, L.V.; Baldenegro-Pérez, L.A.; Carrasco-Marín, F. Grapefruit peels as biosorbent: Characterization and use in batch and fixed bed column for Cu(II) uptake from wastewater. J. Chem. Technol. Biotechnol. 2017, 92, 1650–1658. [Google Scholar] [CrossRef]
- Rosales, E.; Meijide, J.; Tavares, T.; Pazos, M.; Sanromán, M.A. Grapefruit peelings as a promising biosorbent for the removal of leather dyes and hexavalent chromium. Process Saf. Environ. Prot. 2016, 101, 61–71. [Google Scholar] [CrossRef]
- Du, Z.; Zheng, T.; Wang, P. Experimental and modelling studies on fixed bed adsorption for Cu(II) removal from aqueous solution by carboxyl modified jute fiber. Powder Technol. 2018, 338, 952–959. [Google Scholar] [CrossRef]
- Tofan, L.; Teodosiu, C.; Paduraru, C.; Wenkert, R. Cobalt(II) removal from aqueous solutions by natural hemp fibers: Batch and fixed-bed column studies. Appl. Surf. Sci. 2013, 285, 33–39. [Google Scholar] [CrossRef]
- Vidal, C.B.; Melo, D.Q.; Raulino, G.S.C.; da Luz, A.D.; da Luz, C.; Nascimento, R.F. Multielement adsorption of metal ions using Tururi fibers (Manicaria saccifera): Experiments, mathematical modeling and numerical simulation. Desalin. Water Treat. 2015, 57, 9001–9008. [Google Scholar] [CrossRef]
- Ronda, A.; Calero, M.; Blázquez, G.; Pérez, A.; Martín-Lara, M.A. Optimization of the use of a biosorbent to remove heavy metals: Regeneration and reuse of exhausted biosorbent. J. Taiwan Inst. Chem. Eng. 2015, 51, 109–118. [Google Scholar] [CrossRef]
- Jain, C.K.; Malik, D.S.; Yadav, A.K. Applicability of plant based biosorbents in the removal of heavy metals: A review. Environ. Process. 2016, 3, 495–523. [Google Scholar] [CrossRef]
- Hasan, S.H.; Ranjan, D.; Talat, M. Agro-industrial waste ’wheat bran’ for the biosorptive remediation of selenium through continuous up-flow fixed-bed column. J. Hazard. Mater. 2010, 181, 1134–1142. [Google Scholar] [CrossRef] [PubMed]
- Gawas, A.S.; Sutar, P.R.; Gokhale, J.S. Biosorption of vanadium(V) and chromium(VI) using abscised coconut leaves powder: Equilibrium and continuous packed bed column studies. Environ. Chem. Ecotoxicol. 2025, 7, 50–61. [Google Scholar] [CrossRef]
- Recepoglu, Y.K.; Arar, Ö.; Yuksel, A. Breakthrough curve analysis of phosphorylated hazelnut shell waste in column operation for continuous harvesting of lithium from water. J. Chromatogr. A 2024, 1713, 464510. [Google Scholar] [CrossRef] [PubMed]
- Amar, M.B.; Mallek, M.; Valverde, A.; Monclus, H.; Myers, T.G.; Salvado, V.; Cabrera-Codony, A. Competitive heavy metal adsorption on pinecone shells: Mathematical modelling of fixed-bed column and surface interaction insights. Sci. Total Environ. 2024, 917, 170398. [Google Scholar] [CrossRef]
- Gagnon-Poirier, S.; Zagury, G.J.; Robert, T.; Courcelles, B. Pilot-scale removal of metals from iron-rich contaminated groundwater using phosphorylated lignocellulosic fibers. Water Air Soil Pollut. 2023, 235, 39. [Google Scholar] [CrossRef]
- Elias, M.M.C.; Soares, L.C.; Maia, L.C.; Taylor, J.G.; Adarme, O.F.H.; Ferreira, G.M.D.; de Azevedo, E.R.; de Siervo, A.; da Silva, L.H.M.; Gurgel, L.V.A. Batch and continuous adsorption of Cd(II) and Pb(II) on polycarboxylated sugarcane bagasse. J. Water Process Eng. 2023, 54, 103947. [Google Scholar] [CrossRef]
- Safardastgerdi, M.; Ardejani, F.D.; Mahmoodi, N.M. Lignocellulosic biomass functionalized with EDTA dianhydride for removing Cu(II) and dye from wastewater: Batch and fixed-bed column adsorption. Min. Eng. 2023, 204, 108423. [Google Scholar] [CrossRef]
- Wang, F.; Hu, X.; Tang, C.; Liu, C.; Zhu, Z. Phosphate-functionalized ramie stalk adsorbent for efficient removal of Zn2+ from water: Adsorption performance, mechanism, and fixed-bed column treatment of real wastewater. Environ. Sci. Pollut. Res. 2023, 30, 6245–6261. [Google Scholar] [CrossRef]
- Basu, M.; Guha, A.K. Separation of lead from aqueous phase by cucumber peel in column bioreactor: A phenomenon of interaction between biological and chemical system and its ecological importance. J. Environ. Manag. 2023, 337, 117738. [Google Scholar] [CrossRef]
- Dovi, E.; Aryee, A.A.; Kani, A.N.; Mpatani, F.M.; Li, J.; Qu, L.; Han, R. High-capacity amino-functionalized walnut shell for efficient removal of toxic hexavalent chromium ions in batch and column mode. J. Environ. Chem. Eng. 2022, 10, 107292. [Google Scholar] [CrossRef]
- Tejada-Tovar, C.; Villabona-Ortíz, A.; Ortega-Toro, R. Batch and packed bed column study for the removal of Cr(VI) and Ni(II) using agro-industrial wastes. Appl. Sci. 2021, 11, 9355. [Google Scholar] [CrossRef]
- Nithya, K.; Sathish, A.; Kumar, P.S. Packed bed column optimization and modeling studies for removal of chromium ions using chemically modified Lantana camara adsorbent. J. Water Process Eng. 2020, 33, 101069. [Google Scholar] [CrossRef]
- Petrella, A.; Spasiano, D.; Rizzi, V.; Cosma, P.; Race, M.; De Vietro, N. Thermodynamic and kinetic investigation of heavy metals sorption in packed bed columns by recycled lignocellulosic materials from olive oil production. Chem. Eng. Commun. 2019, 206, 1715–1730. [Google Scholar] [CrossRef]
- Priyantha, N.; Kotabewatta, P.A. Biosorption of heavy metal ions on peel of Artocarpus nobilis fruit: 1—Ni(II) sorption under static and dynamic conditions. Appl. Water Sci. 2019, 9, 37. [Google Scholar] [CrossRef]
- Cherdchoo, W.; Nithettham, S.; Charoenpanich, J. Removal of Cr(VI) from synthetic wastewater by adsorption onto coffee ground and mixed waste tea. Chemosphere 2019, 221, 758–767. [Google Scholar] [CrossRef] [PubMed]
- Gondhalekar, S.C.; Shukla, S.R. Enhanced adsorption performance of oxidised coconut coir for removal of Cd(II) ions by multi-column arrangement in series. Environ. Sci. Pollut. Res. 2019, 26, 28022–28030. [Google Scholar] [CrossRef]
- Arim, A.L.; Quina, M.J.; Gando-Ferreira, L.M. Uptake of trivalent chromium from aqueous solutions by xanthate pine bark: Characterization, batch and column studies. Process Saf. Environ. Prot. 2019, 121, 374–386. [Google Scholar] [CrossRef]
- Fernández-González, R.; Martín-Lara, M.Á.; Blázquez, G.; Pérez, A.; Calero, M. Recovering metals from aqueous solutions by biosorption onto hydrolyzed olive cake. Water 2019, 11, 2519. [Google Scholar] [CrossRef]
- Jangde, V.; Umathe, P.; Antony, P.S.; Shinde, V.; Pakade, Y. Fixed-bed column dynamics of xanthate-modified apple pomace for removal of Pb(II). Int. J. Environ. Sci. Technol. 2018, 16, 6347–6356. [Google Scholar] [CrossRef]
- Arim, A.L.; Neves, K.; Quina, M.J.; Gando-Ferreira, L.M. Experimental and mathematical modelling of Cr(III) sorption in fixed-bed column using modified pine bark. J. Clean. Prod. 2018, 183, 272–281. [Google Scholar] [CrossRef]
- Xavier, A.L.P.; Adarme, O.F.H.; Furtado, L.M.; Ferreira, G.M.D.; da Silva, L.H.M.; Gil, L.F.; Gurgel, L.V.A. Modeling adsorption of copper(II), cobalt(II) and nickel(II) metal ions from aqueous solution onto a new carboxylated sugarcane bagasse. Part II: Optimization of monocomponent fixed-bed column adsorption. J. Colloid Interface Sci. 2018, 516, 431–445. [Google Scholar] [CrossRef] [PubMed]
- Shanmugaprakash, M.; Venkatachalam, S.; Rajendran, K.; Pugazhendhi, A. Biosorptive removal of Zn(II) ions by Pongamia oil cake (Pongamia pinnata) in batch and fixed-bed column studies using response surface methodology and artificial neural network. J. Environ. Manag. 2018, 227, 216–218. [Google Scholar] [CrossRef]
- Mathangi, J.B.; Kalavathy, M.H. Study of mathematical models for the removal of Ni2+ from aqueous solutions using Citrullus lanatus rind, an agro-based waste. Water Environ. J. 2018, 33, 276–291. [Google Scholar] [CrossRef]
- Zaidi, N.A.H.M.; Lim, L.B.L.; Usman, A. Enhancing adsorption of Pb(II) from aqueous solution by NaOH and EDTA modified Artocarpus odoratissimus leaves. J. Environ. Chem. Eng. 2018, 6, 7172–7184. [Google Scholar] [CrossRef]
- Petrella, A.; Spasiano, D.; Acquafredda, P.; De Vietro, N.; Ranieri, E.; Cosma, P.; Rizzi, V.; Petruzzelli, V.; Petruzzelli, D. Heavy metals retention (Pb(II), Cd(II), Ni(II)) from single and multimetal solutions by natural biosorbents from the olive oil milling operations. Process Saf. Environ. Prot. 2018, 114, 79–90. [Google Scholar] [CrossRef]
- Khan, U.; Rao, R.A.K. A high activity adsorbent of chemically modified Cucurbita moschata (a novel adsorbent) for the removal of Cu(II) and Ni(II) from aqueous solution: Synthesis, characterization and metal removal efficiency. Process Saf. Environ. Prot. 2017, 107, 238–258. [Google Scholar] [CrossRef]
- Castro, L.; Blazquez, M.L.; González, F.; Muñoz, J.A.; Ballester, A. Biosorption of Zn(II) from industrial effluents using sugar beet pulp and F. vesiculosus: From laboratory tests to a pilot approach. Sci. Total Environ. 2017, 598, 856–866. [Google Scholar] [CrossRef]
- Borna, M.O.; Pirsaheb, M.; Niri, M.V.; Mashizie, R.K.; Kakavandi, B.; Zare, M.R.; Asadi, A. Batch and column studies for the adsorption of chromium(VI) on low-cost Hibiscus Cannabinus kenaf, a green adsorbent. J. Taiwan Inst. Chem. Eng. 2016, 68, 80–89. [Google Scholar] [CrossRef]
- Davila-Guzman, N.E.; Cerino-Córdova, F.J.; Loredo-Cancino, M.; Rangel-Mendez, J.R.; Gómez-González, R.; Soto-Regalado, E. Studies of Adsorption of Heavy Metals onto Spent Coffee Ground: Equilibrium, Regeneration, and Dynamic Performance in a Fixed-Bed Column. Int. J. Chem. Eng. 2016, 2016, 9413879. [Google Scholar] [CrossRef]
- Lakshmipathy, R.; Sarada, N.C. A fixed bed column study for the removal of Pb2+ ions by watermelon rind. Environ. Sci. Water Res. Technol. 2015, 1, 244–250. [Google Scholar] [CrossRef]
- Cheraghi, E.; Ameri, E.; Moheb, A. Adsorption of cadmium ions from aqueous solutions using sesame as a low-cost biosorbent: Kinetics and equilibrium studies. Int. J. Environ. Sci. Technol. 2015, 12, 2579–2592. [Google Scholar] [CrossRef]
- Oguz, E.; Ersoy, M. Biosorption of cobalt(II) with sunflower biomass from aqueous solutions in a fixed bed column and neural networks modelling. Ecotoxicol. Environ. Saf. 2014, 99, 54–60. [Google Scholar] [CrossRef] [PubMed]
- Cruz-Olivares, J.; Pérez-Alonso, C.; Barrera-Díaz, C.; Ureña-Nuñez, F.; Chaparro-Mercado, M.C.; Bilyeu, B. Modeling of lead (II) biosorption by residue of allspice in a fixed-bed column. Chem. Eng. J. 2013, 228, 21–27. [Google Scholar] [CrossRef]
- Khan, M.A.; Ngabura, M.; Choong, T.S.; Masood, H.; Chuah, L.A. Biosorption and desorption of nickel on oil cake: Batch and column studies. Bioresour. Technol. 2012, 103, 35–42. [Google Scholar] [CrossRef]
- Martín-Lara, M.A.; Blázquez, G.; Ronda, A.; Rodríguez, I.L.; Calero, M. Multiple biosorption–desorption cycles in a fixed-bed column for Pb(II) removal by acid-treated olive stone. J. Ind. Eng. Chem. 2012, 18, 1006–1012. [Google Scholar] [CrossRef]
- Hang, Y.; Shan, J.; Jun-Xia, Y.; Ru-An, C. Effects of Ca2+ initial concentration on Cu2+ selective adsorption from aqueous solution by modified sugarcane bagasse under batch and column condition. Int. J. Environ. Anal. Chem. 2019, 100, 1610–1623. [Google Scholar] [CrossRef]
- Ronda, A.; Martín-Lara, M.A.; Dionisio, E.; Blázquez, G.; Calero, M. Effect of lead in biosorption of copper by almond shell. J. Taiwan Inst. Chem. Eng. 2013, 44, 466–473. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, M.; Cheng, Q.; Wang, C.; Li, H.; Han, X.; Fan, Z.; Su, G.; Pan, D.; Li, Z. Research progress of adsorption and removal of heavy metals by chitosan and its derivatives: A review. Chemosphere 2021, 279, 130927. [Google Scholar] [CrossRef]
- Zhang, S.; Ding, J.; Tian, D.; Kang, R.; Zhao, X.; Chang, M.; Yang, W.; Xie, H.; Lu, M. As(V) removal from aqueous environments using quaternary ammonium modified ZIF-8/chitosan composite adsorbent. Appl. Surf. Sci. 2023, 614, 156179. [Google Scholar] [CrossRef]
- Sun, R.C. Cereal Straw as a Resource for Sustainable Biomaterials and Biofuels: Chemistry, Extractives, Lignins, Hemicelluloses and Cellulose, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2010. [Google Scholar]
- Bukva, M.; Soares, L.C.; Maia, L.C.; Costa, C.S.D.; Gurgel, L.V.A. A review on the design and application of bi-functionalized adsorbents to remove different pollutants from water. J. Water Process Eng. 2023, 53, 103636. [Google Scholar] [CrossRef]
- Hoang, A.T.; Nižetić, S.; Cheng, C.K.; Luque, R.; Thomas, S.; Banh, T.L.; Pham, V.V.; Nguyen, X.P. Heavy metal removal by biomass-derived carbon nanotubes as a greener environmental remediation: A comprehensive review. Chemosphere 2022, 287, 131959. [Google Scholar] [CrossRef] [PubMed]
- Afroze, S.; Sen, T.K.; Ang, H.M. Adsorption removal of zinc (II) from aqueous phase by raw and base modified Eucalyptus sheathiana bark: Kinetics, mechanism and equilibrium study. Process Saf. Environ. Prot. 2016, 102, 336–352. [Google Scholar] [CrossRef]
- Ahmed, M.J.; Hameed, B.H. Removal of emerging pharmaceutical contaminants by adsorption in a fixed-bed column: A review. Ecotoxicol. Environ. Saf. 2018, 149, 257–266. [Google Scholar] [CrossRef] [PubMed]
- da Costa, T.B.; da Silva, M.G.C.; Vieira, M.G.A. Recovery of rare-earth metals from aqueous solutions by bio/adsorption using non-conventional materials: A review with recent studies and promising approaches in column applications. J. Rare Earths 2020, 38, 339–355. [Google Scholar] [CrossRef]
- Worch, E. Adsorption Technology in Water Treatment: Fundamentals, Processes, and Modeling, 1st ed.; De Gruyter: Berlin, Germany, 2012. [Google Scholar] [CrossRef]
- Mankins, J.C. Technology Readiness Levels—A White Paper; Advanced Concepts Office, NASA: Huntsville, AL, USA, 1995. [Google Scholar]
- Taty-Costodes, V.C.; Fauduet, H.; Porte, C.; Ho, Y. Removal of lead(II) ions from synthetic and real effluents using immobilized Pinus sylvestris sawdust: Adsorption on a fixed-bed column. J. Hazard. Mater. 2005, 123, 135–144. [Google Scholar] [CrossRef]
- Wolborska, A.; Pustelnik, P. A simplified method for determination of the break-through time of an adsorbent layer. Water Res. 1996, 30, 2643–2650. [Google Scholar] [CrossRef]
- González-López, M.E.; Laureano-Anzaldo, C.M.; Pérez-Fonseca, A.A.; Arellano, M.; Robledo-Ortíz, J.R. Chemically modified polysaccharides for hexavalent chromium adsorption. Sep. Purif. Rev. 2020, 50, 333–362. [Google Scholar] [CrossRef]
- Wang, J.; Guo, X. Adsorption kinetic models: Physical meanings, applications, and solving methods. J. Hazard. Mater. 2020, 390, 122156. [Google Scholar] [CrossRef]
- El-Khaiary, M.I.; Malash, G.F. Common data analysis errors in batch adsorption studies. Hydrometallurgy 2011, 105, 314–320. [Google Scholar] [CrossRef]
- Osmari, T.A.; Gallon, R.; Schwaab, M.; Barbosa-Coutinho, E.; Severo, J.B., Jr.; Pinto, J.C. Statistical analysis of linear and non-linear regression for the estimation of adsorption isotherm parameters. Adsorpt. Sci. Technol. 2013, 31, 433–458. [Google Scholar] [CrossRef]
- McCuen, R.H.; Surbeck, C.Q. An alternative to specious linearization of environmental models. Water Res. 2008, 42, 4033–4040. [Google Scholar] [CrossRef] [PubMed]
- Pagnanelli, F.; Esposito, A.; Vegliò, F. Multi-metallic modelling for biosorption of binary systems. Water Res. 2002, 36, 4095–4105. [Google Scholar] [CrossRef]
- Majd, M.M.; Kordzadeh-Kermani, V.; Ghalandari, V.; Askari, A.; Sillanpaa, M. Adsorption isotherm models: A comprehensive and systematic review (2010–2020). Sci. Total Environ. 2022, 812, 151334. [Google Scholar] [CrossRef]
- Neris, J.B.; Luzardo, F.H.M.; da Silva, E.G.P.; Velasco, F.G. Evaluation of adsorption processes of metal ions in multi-element aqueous systems by lignocellulosic adsorbents applying different isotherms: A critical review. Chem. Eng. J. 2019, 357, 404–420. [Google Scholar] [CrossRef]
- Mohan, S.; Sreelakshmi, G. Fixed bed column study for heavy metal removal using phosphate treated rice husk. J. Hazard. Mater. 2008, 153, 75–82. [Google Scholar] [CrossRef]
- Xie, Y.; Xiong, W.; Yu, J.; Tang, J.; Chi, R. Recovery of copper from metallurgical sludge by combined method of acid leaching and biosorption. Process Saf. Environ. Prot. 2018, 116, 340–346. [Google Scholar] [CrossRef]
- Kleinübing, S.J.; Guibal, E.; da Silva, E.A.; da Silva, M.G.C. Copper and nickel competitive biosorption simulation from single and binary systems by Sargassum filipendula. Chem. Eng. J. 2012, 184, 16–22. [Google Scholar] [CrossRef]
- Holmberg, J.P. Competitive Adsorption and Displacement Behaviour of Heavy Metals on Peat. Master’s Thesis, Chalmers University of Technology, Göteborg, Sweden, 2006. [Google Scholar]
- Irving, H.; Williams, R.J.P. Order of stability of metal complexes. Nature 1948, 162, 746–747. [Google Scholar] [CrossRef]
- Varadwaj, P.R.; Varadwaj, A.; Jin, B. Ligand(s)-to-metal charge transfer as a factor controlling the equilibrium constants of late first-row transition metal complexes: Revealing the Irving-Williams thermodynamical series. Phys. Chem. Chem. Phys. 2015, 17, 805–811. [Google Scholar] [CrossRef]
- Xu, H.; Xu, D.C.; Wang, Y. Natural indices for the chemical hardness/softness of metal cations and ligands. ACS Omega 2017, 2, 7185–7193. [Google Scholar] [CrossRef]
- Pearson, R.G. Hard and soft acids and bases. J. Am. Chem. Soc. 1963, 85, 3533–3539. [Google Scholar] [CrossRef]
- Parr, R.G.; Pearson, R.G. Absolute hardness: Companion parameter to absolute electronegativity. J. Am. Chem. Soc. 1986, 105, 7512–7516. [Google Scholar] [CrossRef]
- Pereira, A.R.; Soares, L.C.; Teodoro, F.S.; Elias, M.M.C.; Ferreira, G.M.D.; Savedra, R.M.L.; Siqueira, M.F.; Martineau-Corcos, C.; da Silva, L.H.M.; Prim, D.; et al. Aminated cellulose as a versatile adsorbent for batch removal of As(V) and Cu(II) from mono- and multicomponent aqueous solutions. J. Colloid Interface Sci. 2020, 576, 158–175. [Google Scholar] [CrossRef]
- Goel, J.; Kadirvelu, K.; Rajagopal, C. Competitive sorption of Cu(II), Pb(II) and Hg(II) ions from aqueous solution using coconut shell-based activated carbon. Adsorp. Sci. Technol. 2016, 22, 257–273. [Google Scholar] [CrossRef]
- Nightingale, E.R., Jr. Phenomenological theory of ion solvation. Effective radii of hydrated ions. J. Phys. Chem. 2002, 63, 1381–1387. [Google Scholar] [CrossRef]
- Speight, J.G. Lange’s Handbook of Chemistry, 16th ed.; McGraw-Hill Professional: New York, NY, USA, 2005. [Google Scholar]
- Huheey, J.E.; Keiter, E.A.; Keiter, R.L. Inorganic Chemistry: Principles of Structure and Reactivity, 4th ed.; HarperCollins College Publishers: New York, NY, USA, 1993. [Google Scholar]
- Ballesteros-Plata, D.; Zhang, Y.; Rodríguez-Castellón, E.; Vincent, T.; Guibal, E. Brown algal residue for the recovery of metal ions—Application to La(III), Cd(II), and Ni(II) sorption. Adv. Sustain. Syst. 2023, 7, 2200420. [Google Scholar] [CrossRef]
- Yu, J.; Wang, L.; Chi, R.; Zhang, Y.; Xu, Z.; Guo, J. Adsorption of Pb2+, Cd2+, Cu2+, and Zn2+ from aqueous solution by modified sugarcane bagasse. Res. Chem. Intermed. 2013, 41, 1525–1541. [Google Scholar] [CrossRef]
- Inglezakis, V.J.; Fyrillas, M.M.; Park, J. Variable diffusivity homogeneous surface diffusion model and analysis of merits and fallacies of simplified adsorption kinetics equations. J. Hazard. Mater. 2019, 367, 224–245. [Google Scholar] [CrossRef]
- Amrutha; Jeppu, G.; Girish, C.R.; Prabhu, B.; Mayer, K. Multi-component adsorption isotherms: Review and modeling studies. Environ. Process. 2023, 10, 38. [Google Scholar] [CrossRef]
- Butler, J.A.V.; Ockrent, C. Studies in electrocapillarity. III. J. Phys. Chem. 1930, 34, 2841–2859. [Google Scholar] [CrossRef]
- Bellot, J.C.; Condoret, J.S. Modelling of liquid chromatography equilibria. Process Biochem. 1993, 28, 365–376. [Google Scholar] [CrossRef]
- Teodoro, F.S.; Adarme, O.F.H.; Gil, L.F.; Gurgel, L.V.A. Synthesis and application of a new carboxylated cellulose derivative. Part II: Removal of Co2+, Cu2+ and Ni2+ from bicomponent spiked aqueous solution. J. Colloid Interface Sci. 2017, 487, 266–280. [Google Scholar] [CrossRef] [PubMed]
- Soetaredjo, F.E.; Kurniawan, A.; Ki, O.L.; Ismadji, S. Incorporation of selectivity factor in modeling binary component adsorption isotherms for heavy metals-biomass system. Chem. Eng. J. 2013, 219, 137–148. [Google Scholar] [CrossRef]
- Schay, G.J.; Fejes, F.P.; Szethmary, J. Adsorption of gases and Gas Mixtures. Acta Chim. Acad. Sci. Hung. 1957, 12, 299–308. [Google Scholar]
- Ho, Y.S.; McKay, G. Pseudo-second order model for sorption processes. Process Biochem. 1999, 34, 451–465. [Google Scholar] [CrossRef]
- Fritz, W.; Schluender, E.U. Simultaneous adsorption equilibria of organic solutes in dilute aqueous solutions on activated carbon. Chem. Eng. Sci. 1974, 29, 1279–1282. [Google Scholar] [CrossRef]
- Sheindorf, C.; Rebhun, M.; Sheintuch, M. A Freundlich-type multicomponent isotherm. J. Colloid Interface Sci. 1981, 79, 136–142. [Google Scholar] [CrossRef]
- McKay, G.; Al Duri, B. Simplified model for the equilibrium adsorption of dyes from mixtures using activated carbon. Chem. Eng. Process. Process Intensif. 1987, 22, 145–156. [Google Scholar] [CrossRef]
- Ramos, S.N.C.; Xavier, A.L.P.; Teodoro, F.S.; Gil, L.F.; Gurgel, L.V.A. Removal of cobalt(II), copper(II), and nickel(II) ions from aqueous solutions using phthalate-functionalized sugarcane bagasse: Mono- and multicomponent adsorption in batch mode. Ind. Crops Prod. 2016, 79, 116–130. [Google Scholar] [CrossRef]
- Costa, E.; Sotelo, J.L.; Calleja, G.; Marrón, C. Adsorption of binary and ternary hydrocarbon gas mixtures on activated carbon: Experimental determination and theoretical prediction of the ternary equilibrium data. AIChE J. 1981, 27, 5–12. [Google Scholar] [CrossRef]
- Reynel-Avila, H.E.; Mendoza-Castillo, D.I.; Olumide, A.A.; Bonilla-Petriciolet, A. A survey of multi-component sorption models for the competitive removal of heavy metal ions using bush mango and flamboyant biomasses. J. Mol. Liq. 2016, 224, 1041–1054. [Google Scholar] [CrossRef]
- Cho, B.; Mun, S.; Lim, C.; Kang, S.B.; Cho, C.; Yun, Y. Adsorption modeling of microcrystalline cellulose for pharmaceutical-based micropollutants. J. Hazard. Mater. 2022, 426, 128087. [Google Scholar] [CrossRef]
- Jin, S.; Cho, B.; Mun, S.; Kim, S.; Cho, C. Investigation of the adsorption affinity of organic micropollutants on seaweed and its QSAR study. Environ. Res. 2023, 232, 116349. [Google Scholar] [CrossRef] [PubMed]
- Sun, M.; Wang, X.; Xiong, R.; Chen, X.; Zhai, L.; Wang, S. High-performance biochar-loaded MgAl-layered double oxide adsorbents derived from sewage sludge towards nanoplastics removal: Mechanism elucidation and QSAR modeling. Sci. Total Environ. 2023, 901, 165971. [Google Scholar] [CrossRef]
- Pauletto, P.S.; Dotto, G.L.; Salau, N.P.G. Optimal artificial neural network design for simultaneous modeling of multicomponent adsorption. J. Mol. Liq. 2020, 320, 114418. [Google Scholar] [CrossRef]
- Fagundez, J.L.S.; Salau, N.P.G. Optimization-based artificial neural networks to fit the isotherm models parameters of aqueous-phase adsorption systems. Environ. Sci. Pollut. Res. 2022, 29, 79798–79807. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Kramer, O. Genetic Algorithm Essentials, 1st ed.; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Oguz, E.; Ersoy, M. Removal of Cu2+ from aqueous solution by adsorption in a fixed bed column and Neural Network Modelling. Chem. Eng. J. 2010, 164, 56–62. [Google Scholar] [CrossRef]
- Setzu, M.; Guidotti, R.; Monreale, A.; Turini, F.; Pedreschi, D.; Giannotti, F. GLocalX—From local to global explanations of black box AI models. Artif. Intell. 2021, 294, 103457. [Google Scholar] [CrossRef]
- Bădescu, I.S.; Bulgariu, D.; Ahmad, I.; Bulgariu, L. Valorisation possibilities of exhausted biosorbents loaded with metal ions—A review. J. Environ. Manag. 2018, 224, 288–297. [Google Scholar] [CrossRef]
- Cherubini, F.; Bargigli, S.; Ulgiati, S. Life cycle assessment (LCA) of waste management strategies: Landfilling, sorting plant and incineration. Energy 2009, 34, 2116–2123. [Google Scholar] [CrossRef]
- Chojnacka, K. Biosorption and bioaccumulation—The prospects for practical applications. Environ. Int. 2010, 36, 299–307. [Google Scholar] [CrossRef] [PubMed]
- ABNT NBR 1004; Solid Waste—Classification. Associação Brasileira de Normas Técnicas (ABNT): Rio de Janeiro, Brazil, 2004.
- Daskalopoulos, E.; Badr, O.; Probert, S.D. Economic and environmental evaluations of waste treatment and disposal technologies for municipal solid waste. Appl. Energy 1997, 58, 209–255. [Google Scholar] [CrossRef]
- Guedes, R.E.; Luna, A.S.; Torres, A.R. Operating parameters for bio-oil production in biomass pyrolysis: A review. J. Anal. Appl. Pyrolysis 2018, 129, 134–149. [Google Scholar] [CrossRef]
- Blázquez, G.; Martín-Lara, M.A.; Dionisio-Ruiz, E.; Tenorio, G.; Calero, M. Copper biosorption by pine cone shell and thermal decomposition study of the exhausted biosorbent. J. Ind. Eng. Chem. 2012, 18, 1741–1750. [Google Scholar] [CrossRef]
- Torres, F.G.; Teodoro, F.S.; Gurgel, L.V.A.; Bourdreux, F.; Zayene, O.; Gaucher, A.; Gil, L.F.; Prim, D. Application of raw and chemically modified biomasses for heterogeneous Cu-catalysed conversion of aryl boronic acids to phenols derivatives. Catalysts 2022, 12, 92. [Google Scholar] [CrossRef]
- Myers, R.H.; Montgomery, D.C.; Anderson-Cook, C.M. Response Surface Methodology Process and Product Optimization Using Designed Experiments, 4th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2016; pp. 1–12. [Google Scholar]
- Yang, R.T. Gas Separation by Adsorption Processes; Butterworth-Heinemann: Stoneham, MA, USA, 1987; pp. 49–100. [Google Scholar] [CrossRef]
- Sips, R. On the Structure of a Catalyst Surface. J. Chem. Phys. 1948, 16, 490–495. [Google Scholar] [CrossRef]
- Redlich, O.; Peterson D., L. A Useful Adsorption Isotherm. J. Phys. Chem. 1959, 63, 1024. [Google Scholar] [CrossRef]
- Hutchins, R.A. New simplified design of activated carbon systems. Chem. Eng. 1973, 80, 133–138. [Google Scholar]



| T/°C | Column Dimensions | Characteristics of the Bed | Reference | |||
|---|---|---|---|---|---|---|
| H/cm | D/cm | P/μm | Hb/cm | w/g | ||
| - | 1.5 | 30.0 | 355 | 10, 15, 20 | - | [86] |
| 25 | 0.7 | 12 | - | 1.0, 1.5, 2.0 | - | [87] |
| 22 | 20 | 1.2 | <200 | 0.5, 0.7, 1.0 | 0.15, 0.22, 0.33 | [88] |
| - | 90 | 54 | - | 60 | 3550 | [89] |
| 25 | 10 | 1 | 500 | 3.1 | - | [90] |
| 25 | 51 | 3 | <210 | 3.0, 7.0, 15.0 | 0 | [91] |
| - | 20 | 1.00 | - | 5.0, 10.0, 15.0 | 0.24, 0.44, 0.70 | [92] |
| - | 20 | 1 | <500 | 5.0, 6.5, 8.0 | - | [93] |
| 30 | 30 | 1.3 | 200–400 | 3.0, 6.0, 9.0 | 0.93, 1.86, 2.64 | [94] |
| 30–80 | 15 | 4.1 | 100–1220 | 0.61, 3, 6.5, 10, 12.4 | - | [70] |
| 33–76 | - | - | 1000 | 1.6, 3.0, 6.0, 10.0, 11.5 | - | [95] |
| 29 | 10 | 3.0 | <600 | 11.3, 20.9, 32.1 | 2.0, 4.0, 6.0 | [51] |
| - | 43 | 2 | <300 | 1, 2, 3 | - | [65] |
| 25 | 10 | 1.00 | <150 | 3.8 | - | [67] |
| - | 15 | 1.4 | 2000–3000 | 3.0, 6.0, 9.0 | - | [77] |
| - | 30 | 2.4 | 850 | 2, 3, 4 | - | [96] |
| - | 30 | 3 | 250–350 | 3, 5, 7 | - | [49] |
| - | 30 | 1.6 | 250–350 | 4, 8,10 | - | [50] |
| - | 25 | 1 | 250–400 | 2 | 1.03 | [45] |
| 30–35 | 20 | 1 | 149 | - | 0.5 | [62] |
| - | 20 | 2.54 | <150 | - | 0.5 | [73] |
| 25 | 50 | 1.0 | 1000–3000 | 5.1, 6.4, 9.2 | 4.0, 5.5, 8.0 | [97] |
| - | 10 | 1.0 | 710–1000 | 2.5, 5.0, 7.5, 10.0 | 0.75, 1.50, 2.25, 3.00 | [98] |
| - | 20 | 1.00 | - | - | 0.5 | [71] |
| - | 20 | 1.00 | <150 | 12.1 | 1.0 | [64] |
| 28–30 | 25 | 6.25 | - | - | 200 | [99] |
| 25 | 10 | 1.00 | - | 3.1 | 0.5 | [61] |
| - | 30 | 2.00 | 100–500 | 7.0 | 3 | [63] |
| - | 50 | 1.8 | 290–350 | 4, 6, 10 | - | [59] |
| - | 20.3 | 2 | <2000 | - | 5 | [46] |
| 25 | 35 | 2.5 | 2580 | 24 | 24 | [57] |
| - | 24 | 3.00 | - | 21.0 | - | [100] |
| - | 1.5 | - | 128 | 2.5 | 1.8 | [101] |
| - | 23 | 1.5 | 420, 960, 1500 | - | 18 | [102] |
| - | 20 | 1 | <520 | 5.0, 8.0, 10.0 | 2.10, 2.75, 3.20 | [53] |
| - | - | - | <63 | 2.0, 3.0, 4.0 | 0.44, 0.66, 0.88 | [58] |
| 25 | 1.5 | 23 | <1000 | 3.8, 11.5 | 5.0, 15.0 | [42] |
| 17 | 50 | 1.60 | 594 | 28.0 | 7.15 | [69] |
| 30 | - | 1.10 | <150 | 5.0, 10.0, 15.0 | - | [32] |
| - | 28 | 0.8 | 500–1000 | 5, 7, 10, 15 | 0.5, 0.6, 0.75, 1.0 | [103] |
| 25 | 12 | 0.15 | 88–149 | 2.5, 5.0, 7.5 | - | [104] |
| 25 | 10 | 1.0 | <250 | 3.20 | 0.5 | [105] |
| - | 20 | 1.00 | <150 | - | 0.5 | [68] |
| 30 | 45 | 2 | - | 5.0, 10, 15 | - | [106] |
| 30 | 1 | - | 2.5, 5.0, 7.5, 10 | - | [107] | |
| - | - | 1 | <350 | 2.5, 5.0, 10 | - | [108] |
| - | 25 | 4 | - | 2, 4, 6 | 4, 8, 12 | [80] |
| - | 20 | 1.00 | 500–100 | - | - | [66] |
| - | 50 | 1 | 1000–3000 | - | 5.5 | [109] |
| - | - | 0.6 | 150–300 | - | 0.5 | [110] |
| 25 | - | - | <1000 | 5.0, 15.0 | 4.4, 13.4 | [43] |
| - | 16 | 1 | 1000–2000 | 4, 6, 12, 16 | 1.24, 1.99, 4.07, 5.09 | [78] |
| - | 100 | 22.00 | 425–600 | 9.5, 21, 31 | 5, 10, 15 | [56] |
| - | 30 | 1.00 | <500 | 5.0, 6.5, 8.0 | 1.5, 1.92, 2.25 | [75] |
| - | 100 | 7.5 | 500–1500 | 66 | 350 | [111] |
| - | 23 | 1.5 | <1000 | 14.3, 4.4 | 15, 5 | [47] |
| 30 | 5 | 2.5 | 244–355 | 2, 4, 5 | 0.120, 0.2341, 0.3426 | [74] |
| - | 27 | 3.42 | 500–1000 | 21.0–23.0 | 40.0 | [37] |
| - | 25 | 0.55 | - | 15 | 2.2 | [112] |
| 25 | 30 | 1 | 217–324.7 | 7, 14, 21 | 2, 4, 8 | [113] |
| - | 30 | 150 | <500 | 150 | 75,000 | [79] |
| - | 15 | 1.00 | 500–1000 | 1.0, 3.0, 5.0 | 0.28, 0.84, 1.39 | [114] |
| - | 150 | 2.5, 5.0 | 710–1180 | 28.0, 15.0 | 47.5, 25.5 | [52] |
| 25 | 23 | 1.5 | <1000 | - | 5 | [83] |
| 25 | 30 | 2.2 | <210 | 2.0 | 4.0 | [115] |
| - | 9.5 | 1.00 | - | - | 2 | [82] |
| 25 | 10 | 2.54 | <840 | 3 | 4.5 | [44] |
| 15 | - | 1.00 | 200–250 | 5.0, 10.0, 15.0 | - | [116] |
| - | 100, 160 | 62.00 | 200–250 | - | 480 | [48] |
| - | 20 | 1.00 | <150 | - | 2 | [60] |
| 30 | 80 | 25.40 | 500–1400 | 20.0 | 972 | [41] |
| 20 | 10 | 1 | 250–500 | 6.7 | 0.5 | [39] |
| - | 55 | 1.70 | 1000–2000 | 50 | 25 | [54] |
| - | 15 | 1.5 | - | 7.0 | 0.7 | [81] |
| - | 30 | 2 | 300–500 | 1.5, 2.0 | 1.5, 2.0 | [55] |
| - | 30 | 1.78 | <840 | 8.0, 15.0 | - | [117] |
| - | 25 | 1.14 | 250–500 | - | 1 | [118] |
| 25 | 23 | 1.50 | <1000 | 4.4 | 5 | [119] |
| - | 20 | 1 | 75–150 | - | 0.5 | [120] |
| 25 | 23 | 1.5 | <1000 | 4.41, 13.4 | 15, 5 | [121] |
| 23 | 29 | 2.20 | 300–500 | 1.4, 2.2, 2.9 | 2, 3, 4 | [38] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Coelho, R.S.; Soares, L.C.; Adarme, O.F.H.; Maia, L.C.; Costa, C.S.D.; Guibal, E.; Gurgel, L.V.A. A Review on Advances in the Use of Raw and Modified Agricultural Lignocellulosic Residues in Mono- and Multicomponent Continuous Adsorption of Inorganic Pollutants for Upscaling Technologies. Polymers 2025, 17, 953. https://doi.org/10.3390/polym17070953
Coelho RS, Soares LC, Adarme OFH, Maia LC, Costa CSD, Guibal E, Gurgel LVA. A Review on Advances in the Use of Raw and Modified Agricultural Lignocellulosic Residues in Mono- and Multicomponent Continuous Adsorption of Inorganic Pollutants for Upscaling Technologies. Polymers. 2025; 17(7):953. https://doi.org/10.3390/polym17070953
Chicago/Turabian StyleCoelho, Ricardo Silva, Liliane Catone Soares, Oscar Fernando Herrera Adarme, Luisa Cardoso Maia, Camila Stéfanne Dias Costa, Eric Guibal, and Leandro Vinícius Alves Gurgel. 2025. "A Review on Advances in the Use of Raw and Modified Agricultural Lignocellulosic Residues in Mono- and Multicomponent Continuous Adsorption of Inorganic Pollutants for Upscaling Technologies" Polymers 17, no. 7: 953. https://doi.org/10.3390/polym17070953
APA StyleCoelho, R. S., Soares, L. C., Adarme, O. F. H., Maia, L. C., Costa, C. S. D., Guibal, E., & Gurgel, L. V. A. (2025). A Review on Advances in the Use of Raw and Modified Agricultural Lignocellulosic Residues in Mono- and Multicomponent Continuous Adsorption of Inorganic Pollutants for Upscaling Technologies. Polymers, 17(7), 953. https://doi.org/10.3390/polym17070953











