Monte Carlo Simulations of Polymer Collapse in an Explicit Solvent of Varying Quality
Abstract
1. Introduction
2. The Model and the Method
3. Results and Discussion
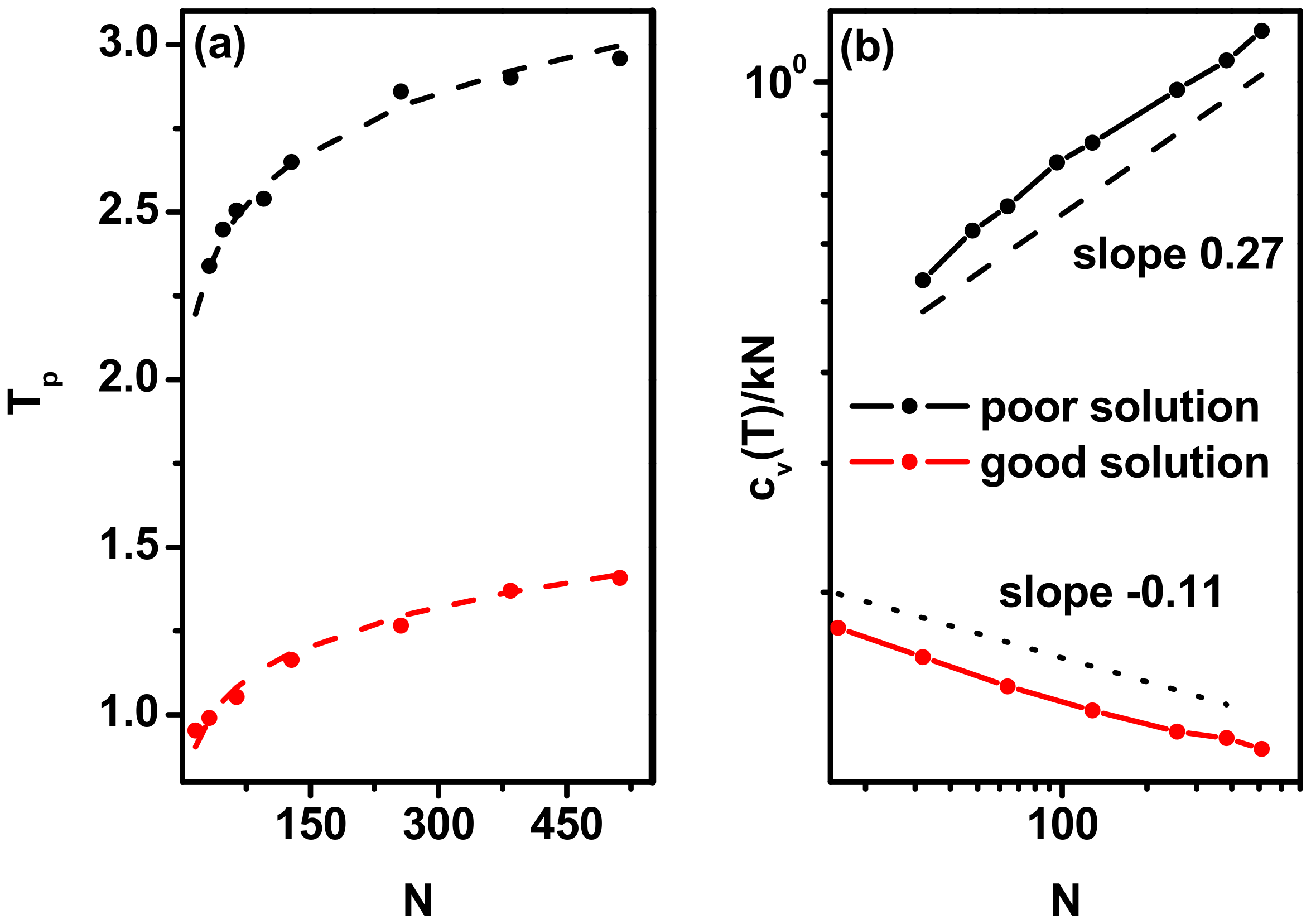
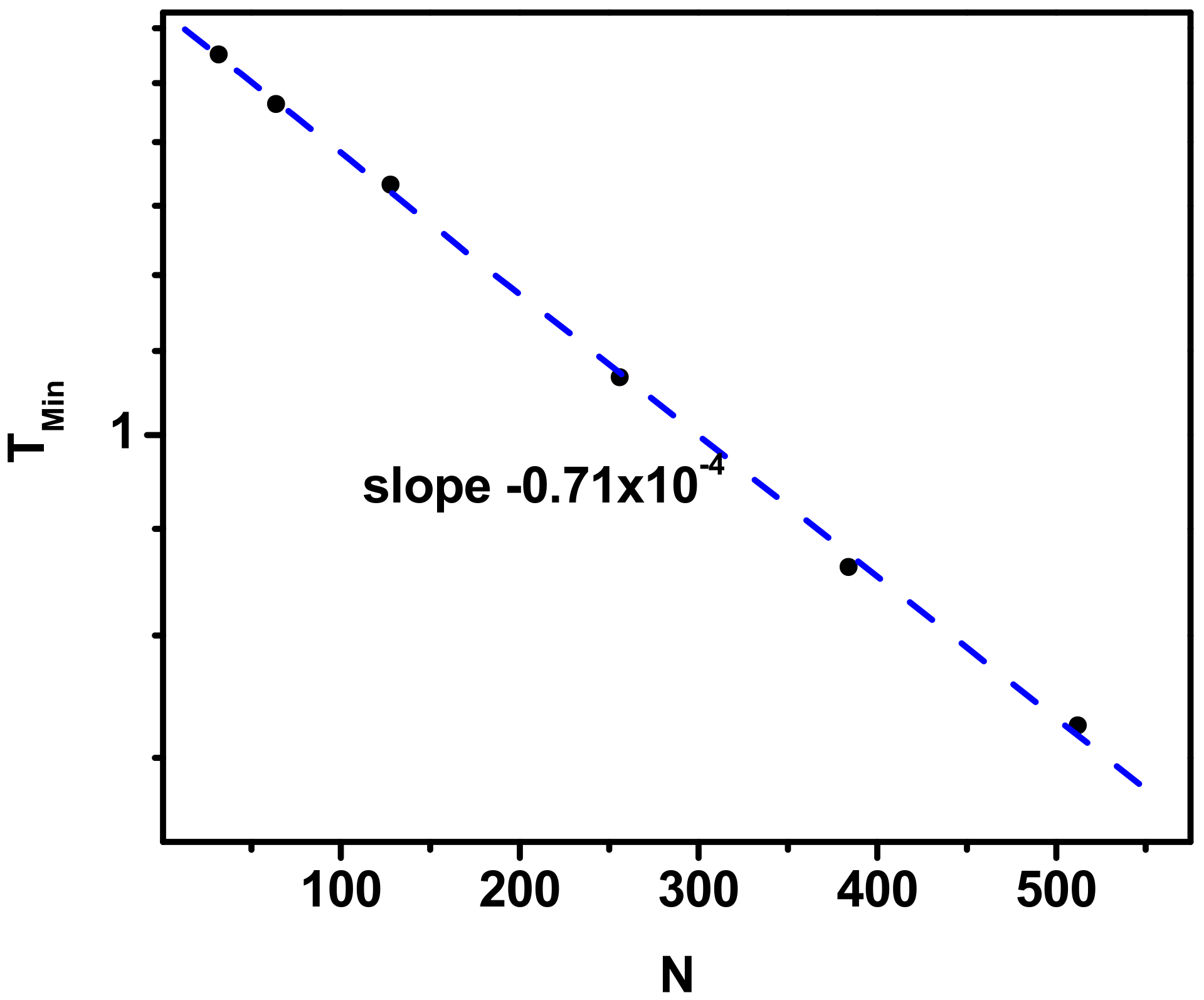
3.1. Phase Transitions
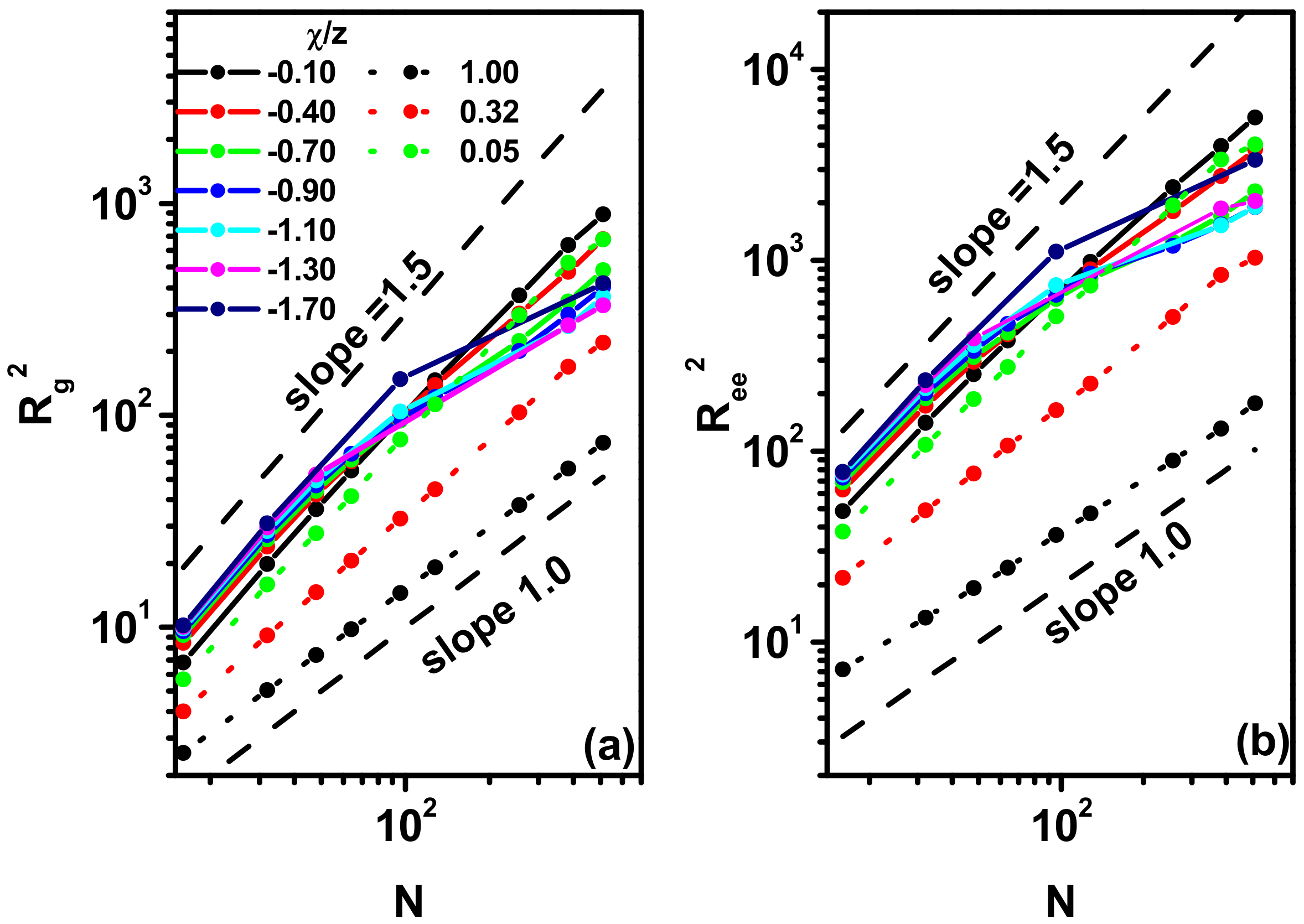
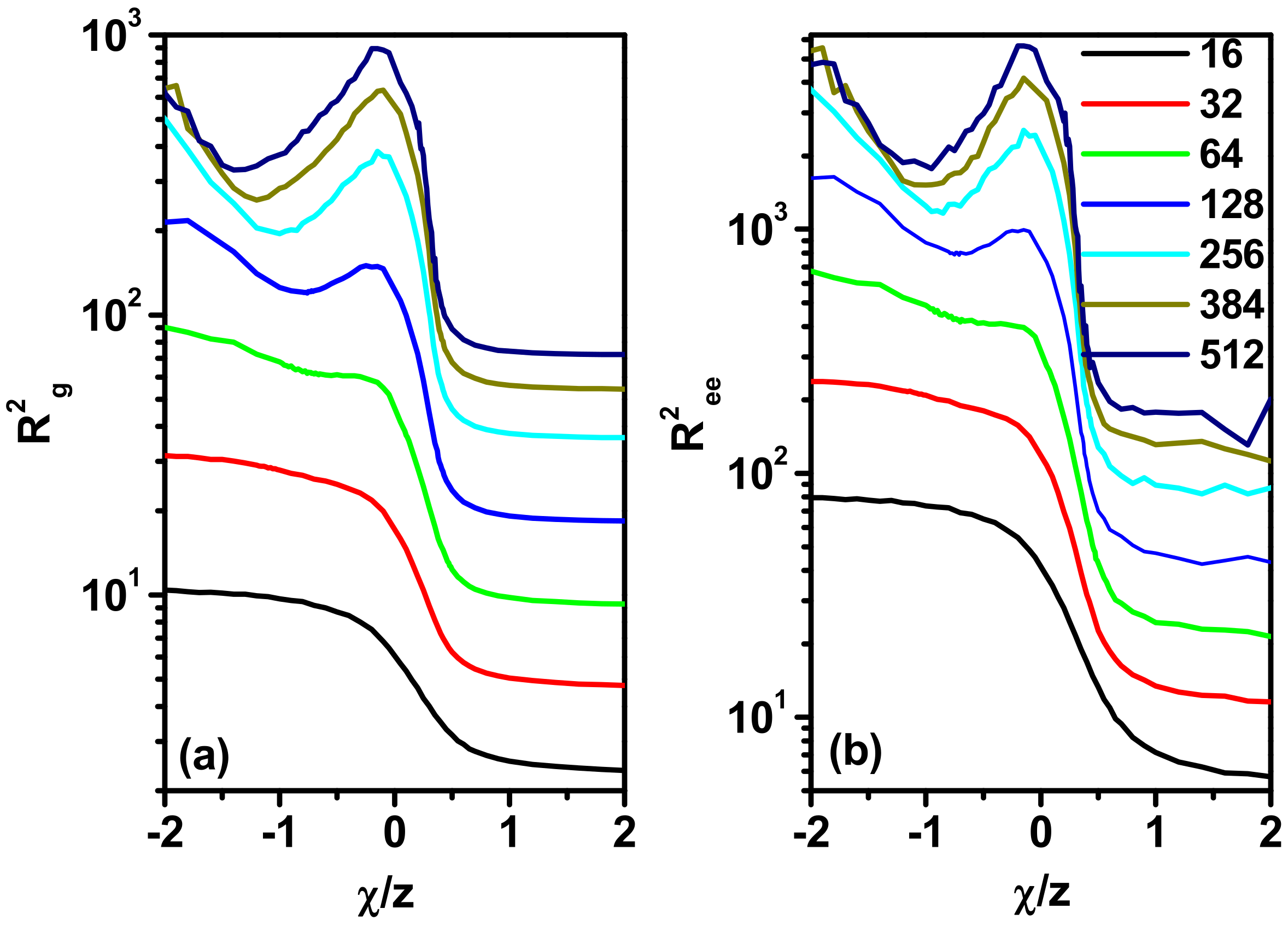
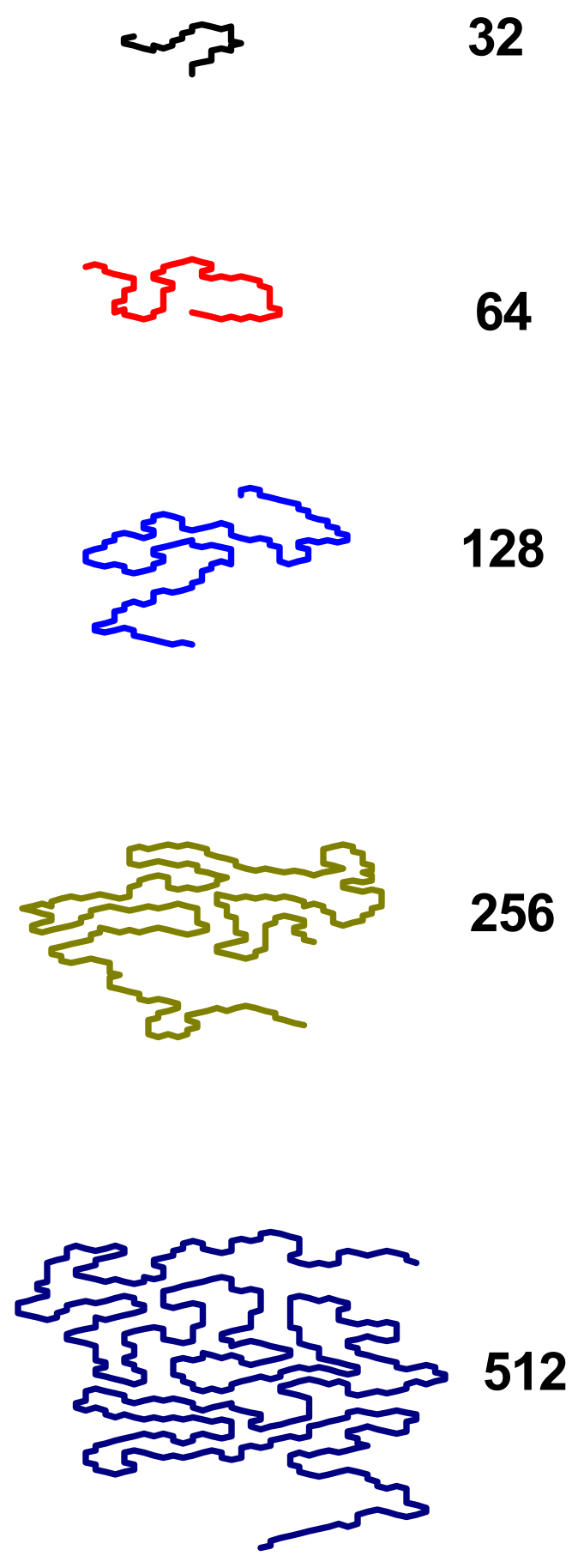
3.2. Size and Shape of the Chain
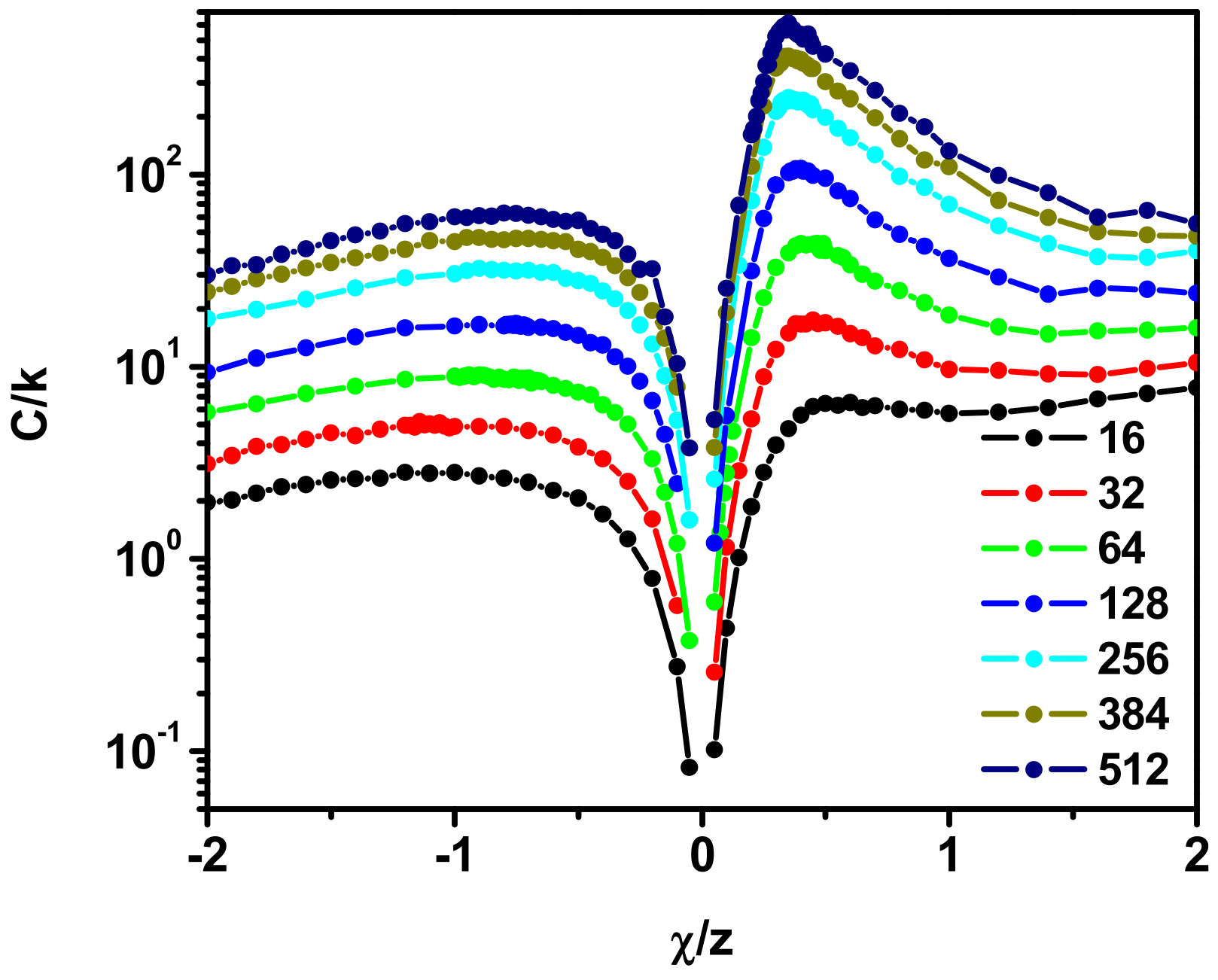
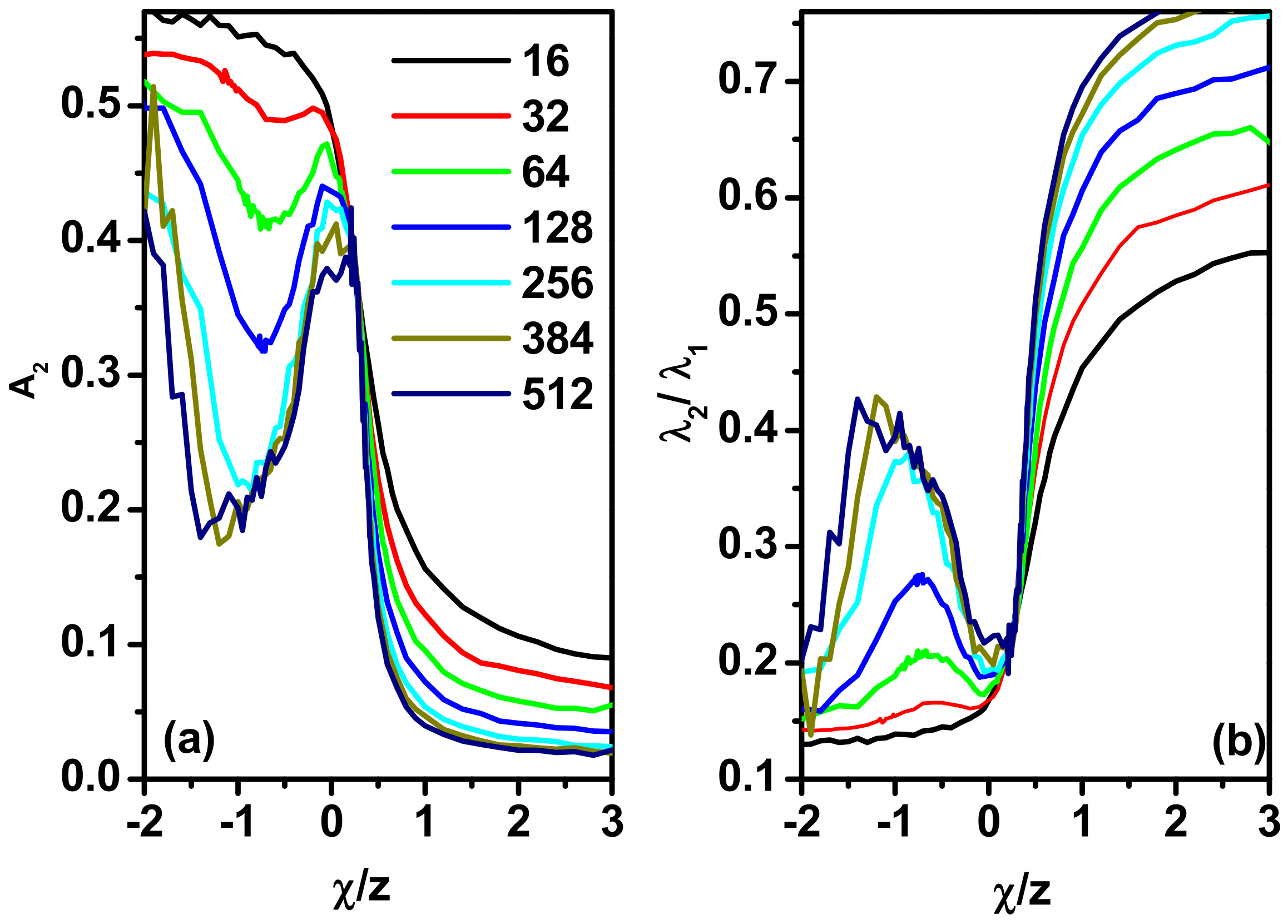
3.3. Scattering Properties
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Ziv, G.; Thirumalai, D.; Haran, G. Collapse transition in proteins. Phys. Chem. Chem. Phys. 2009, 11, 83–93. [Google Scholar] [CrossRef] [PubMed]
- Baysal, B.M.; Karasz, F.E. Coil-globule collapse in flexible macromolecule. Macromol. Theory Simul. 2003, 12, 627–646. [Google Scholar] [CrossRef]
- Chu, B.; Ying, Q.C.; Grosberg, A.Y. 2-stage kinetics of single-chain collapse—Polystyrene in cyclohexane. Macromolecules 1995, 28, 180–189. [Google Scholar] [CrossRef]
- Chu, B.; Ying, Q.C. Single-chain expansion from the collapsed globule of polystyrene in cyclohexane to the Θ coil. Macromolecules 1996, 29, 1824–1826. [Google Scholar] [CrossRef]
- Nakamura, Y.; Sasaki, N.; Nakata, M. Kinetics of the coil–globule transition of poly(methyl methacrylate) in a mixed solvent. Macromolecules 2001, 34, 5992–6002. [Google Scholar] [CrossRef]
- Kayaman, N.; Gürel, E.E.; Baysal, B.M.; Karasz, F.E. Kinetics of coil–globule collapse in poly(methyl methacrylate) in dilute solutions below ϑ temperatures. Macromolecules 1999, 32, 8399–8403. [Google Scholar] [CrossRef]
- Xu, J.; Zhu, Z.; Luo, S.; Wu, C.; Liu, S. First observation of two-stage collapsing kinetics of a single synthetic polymer chain. Phys. Rev. Lett. 2006, 96, 027802. [Google Scholar] [CrossRef]
- Ye, X.; Lu, Y.; Shen, L.; Ding, Y.; Liu, S.; Zhang, G.; Wu, C. How many stages in the coil-to-globule transition of linear homopolymer chains in a dilute solution? Macromolecules 2007, 40, 4750–4752. [Google Scholar] [CrossRef][Green Version]
- Wu, C.; Zhou, S. First observation of the molten globule state of a single homopolymer chain. Phys. Rev. Lett. 1996, 77, 3053–3055. [Google Scholar] [CrossRef]
- Nakata, M.; Nakagawa, I. Coil-globule transition of poly(methyl methacrylate) in isoamyl acetate. Phys. Rev. E 1997, 56, 3338–3340. [Google Scholar] [CrossRef]
- Baysal, B.M.; Kayaman, N. Coil–globule transition of poly(methyl methacrylate) by intrinsic viscosity. J. Chem. Phys. 1998, 109, 8701–8707. [Google Scholar]
- Kayaman, N.; Gürel, E.E.; Baysal, B.M.; Karasz, F.E. Coil to globule transition behaviour of poly(methyl methacrylate) in isoamyl acetate. Polymer 2000, 41, 1461–1468. [Google Scholar]
- Spěváček, J. NMR investigations of temperature-induced phase transition in aqueous polymer solutions. Macromol. Symp. 2011, 305, 18–25. [Google Scholar]
- Chakraborty, I.; Mukherjee, K.; De, P.; Bhattacharyya, R. Monitoring coil–globule transitions of thermoresponsive polymers by using NMR solvent relaxation. J. Phys. Chem. B 2018, 122, 6094–6100. [Google Scholar]
- Coca-Hidalgo, J.J.; Recillas-Mota, M.; Fernández-Quiroz, D.; Lizardi-Mendoza, J.; Peniche-Covas, C.; Goycoolea, F.M.; Argüelles-Monal, W.M. Study of the thermal phase transition of poly(N,N-diethylacrylamide-co-N-ethylacrylamide) random copolymers in aqueous solution. Polymers 2024, 16, 1575. [Google Scholar] [CrossRef]
- Hu, J.; Wang, D.; Xu, J.; Zhu, Z.; Liu, S. Contraction and collapsing kinetics of single synthetic polymer chains at small quench cepths. Macromol. Chem. Phys. 2010, 211, 2573–2584. [Google Scholar]
- Wu, C.; Wang, X. Globule-to-coil transition of a single homopolymer chain in solution. Phys. Rev. Lett. 1998, 80, 4092–4094. [Google Scholar] [CrossRef]
- Ming, X.; Wu, C. A Method to determine Θ condition of a polymer solution. Macromolecules 2018, 51, 4608–4614. [Google Scholar]
- Lifshitz, M.; Grosberg, A.Y.; Khokhlov, A.R. Some problems of the statistical physics of polymer chains with volume interactions. Rev. Mod. Phys. 1978, 50, 683–713. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, Z.-G. Coil-to-globule transition in polymeric solvents. Macromolecules 2021, 54, 10984–10993. [Google Scholar]
- Wang, Z.-G. 50th Anniversary Perspective: Polymer conformation—A pedagogical review. Macromolecules 2017, 50, 9073–9114. [Google Scholar]
- Grosberg, A.Y.; Kuznetsov, D.V. Quantitative theory of the globule-to-coil transition. 1. Link density distribution in a globule and its radius of gyration. Macromolecules 1992, 25, 1970–1979. [Google Scholar] [CrossRef]
- Wang, R.; Wang, Z.-G. Theory of polymer chains in poor solvent: Single-chain structure, solution thermodynamics, and Θ point. Macromolecules 2014, 47, 4094–4102. [Google Scholar] [CrossRef]
- Yang, D.; Wang, Q. Unified view on the mean-field order of coil–globule transition. ASC Macro Lett. 2013, 2, 952–954. [Google Scholar] [CrossRef]
- Crooks, G.E.; Ostrovsky, B.; Bar-Yam, Y. Mesostructure of polymer collapse and fractal smoothing. Phys. Rev. E 1999, 60, 4559–4563. [Google Scholar] [CrossRef]
- Rosa, A.; Marenduzzo, D.; Kumar, S. Stretching a self-interacting semiflexible polymer. Europhys. Lett. 2006, 75, 818–824. [Google Scholar]
- Brak, R.; Owczarek, A.L.; Prellberg, T. A scaling theory of the collapse transition in geometric cluster models of polymers and vesicles. J. Phys. A Math. Gen. 1993, 26, 4565–4579. [Google Scholar]
- de Gennes, P.G. Collapse of a polymer chain in poor solvents. J. Phys. Lett. 1975, 36, 55–57. [Google Scholar] [CrossRef]
- Daoud, M.; Jannink, G. Temperature-concentration diagram of polymer solutions. J. Phys. 1976, 37, 973–979. [Google Scholar] [CrossRef]
- Duplantier, B.; Saleur, H. Exact tricritical exponents for polymers at the Θ point in two dimensions. Phys. Rev. Lett. 1987, 59, 539–542. [Google Scholar]
- Duplantier, B.; Saleur, H. Stability of the polymer Θ point in two dimensions. Phys. Rev. Lett. 1989, 62, 1368–1371. [Google Scholar] [CrossRef] [PubMed]
- Hu, W. Structural transformation in the collapse transition of the single flexible homopolymer model. J. Chem. Phys. 1998, 109, 3686–3690. [Google Scholar] [CrossRef]
- Sikorski, A. Molten globule state in homopolymers. A Monte Carlo study. Macromol. Theory Simul. 2000, 9, 564–569. [Google Scholar]
- Binder, K.; Paul, W. Recent developments in Monte Carlo simulations of lattice models for polymer systems. Macromolecules 2008, 41, 4537–4550. [Google Scholar] [CrossRef]
- Wittkop, M.; Kreitmeier, S.; Göritz, D. The collapse transition of a sing le polymer chain in two and three dimensions: A Monte Carlo study. J. Chem. Phys. 1996, 104, 3373–3385. [Google Scholar]
- Polson, J.M.; Zuckermann, M.J. Simulation of short-chain polymer collapse with an explicit solvent. J. Chem. Phys. 2002, 116, 7244–7254. [Google Scholar]
- Antypov, D.; Elliott, J.A. Computer simulation study of a single polymer chain in an attractive solvent. J. Chem. Phys. 2008, 129, 174901. [Google Scholar] [CrossRef]
- Steinhauser, M.O. A molecular dynamics study on universal properties of polymer chains in different solvent qualities. Part I. A review of linear chain properties. J. Chem. Phys. 2005, 122, 094901. [Google Scholar]
- Torres, A.M.; Rubio, A.M.; Freire, J.J.; Bishop, M.; Clarke, J.H.R. Theta state and collapse of off-lattice chains in two dimensions. J. Chem. Phys. 1994, 100, 7754–7758. [Google Scholar] [CrossRef]
- Werlich, B.; Taylor, M.P.; Shakirov, T.; Paul, W. On the pseudo phase diagram of single semi-flexible polymer chains: A flat-histogram Monte Carlo study. Polymers 2017, 9, 38. [Google Scholar] [CrossRef]
- Kuriata, A.; Sikorski, A. Structure of adsorbed linear and cyclic block copolymers: A computer simulation study. J. Mol. Liq. 2023, 379, 121664. [Google Scholar] [CrossRef]
- Schram, R.D.; Barkema, G.T.; Schiessel, H. On the stability of fractal globules. J. Chem. Phys. 2013, 138, 224901. [Google Scholar] [CrossRef]
- Kremer, K.; Baumgärtner, A.; Binder, K. Collapse transition and crossover scaling for self-avoiding walks on the diamond lattice. J. Phys. A 1982, 15, 2879–2897. [Google Scholar] [CrossRef]
- Dhabal, D.; Jiang, Z.; Pallath, A.; Patel, A.J. Characterizing the interplay between polymer solvation and conformation. J. Phys. Chem. B 2021, 125, 5434–5442. [Google Scholar] [CrossRef]
- Terada, E.; Isono, T.; Satoh, T.; Yamamoto, T.; Kakuchi, T.; Sato, S. All-atom Molecular Dynamics simulations of the temperature response of poly(glycidyl ether)s with oligooxyethylene side chains terminated with alkyl groups. Polymers 2023, 13, 1628. [Google Scholar] [CrossRef]
- Michel, A.; Kreitmeier, S. Molecular dynamics simulation of the collapse of a single polymer chain. Comput. Theor. Polym. Sci. 1997, 7, 113–120. [Google Scholar] [CrossRef]
- Kikuchi, N.; Gent, A.; Yeomans, J.M. Polymer collapse in the presence of hydrodynamic interactions. Eur. Phys. J. E 2002, 9, 63–66. [Google Scholar] [CrossRef]
- Zhou, Y.; Hall, C.K.; Karplus, M. First-order disorder-to-order transition in an isolated homopolymer model. Phys. Rev. Lett. 1996, 77, 2822–2825. [Google Scholar] [CrossRef]
- Huang, Y.; Cheng, S. Chain conformations and phase separation in polymer solutions with varying solvent quality. J. Polym. Sci. 2021, 59, 2819–2831. [Google Scholar] [CrossRef]
- Garg, H.; Rajesh, R.; Vemparala, S. The conformational phase diagram of neutral polymers in the presence of attractive crowders. J. Chem. Phys. 2023, 158, 114903. [Google Scholar] [CrossRef]
- Pham, T.T.; Bajaj, M.; Prakash, J.R. Brownian dynamics simulation of polymer collapse in a poor solvent: Influence of implicit hydrodynamic interactions. Soft Matter 2008, 4, 1196–1207. [Google Scholar] [CrossRef] [PubMed]
- Pham, T.T.; Dünweg, B.; Prakash, J.R. Collapse dynamics of copolymers in a poor solvent: Influence of hydrodynamic interactions and chain sequence. Macromolecules 2010, 43, 10084–10095. [Google Scholar] [CrossRef][Green Version]
- Lappala, A.; Terentjev, E.M. Raindrop coalescence of polymer chains during coil-globule transition. Macromolecules 2013, 46, 1239–1247. [Google Scholar] [CrossRef]
- Heyda, J.; Muzdalo, A.; Dzubiella, J. Rationalizing polymer swelling and collapse under attractive cosolvent conditions. Macromolecules 2013, 46, 1231–1238. [Google Scholar] [CrossRef]
- Brackley, C.A. Polymer compaction and bridging-induced clustering of protein-inspired patchy particles. J. Phys. Condens. Matter 2020, 32, 314002. [Google Scholar] [CrossRef]
- Chertovich, A.; Kos, P. Crumpled globule formation during collapse of a long flexible and semiflexible polymer in poor solvent. J. Chem. Phys. 2014, 141, 134903. [Google Scholar] [CrossRef]
- Guo, J.; Liang, H.; Wang, Z.-G. Coil-to-globule transition by dissipative particle dynamics simulation. J. Chem. Phys. 2011, 134, 244904. [Google Scholar] [CrossRef]
- Schneider, J.; Meinel, M.K.; Dittmar, H.; Müller-Plathe, F. Different stages of polymer-chain collapse following solvent quenching–scaling relations from Dissipative Particle Dynamics simulations. Macromolecules 2020, 53, 8889–8900. [Google Scholar] [CrossRef]
- Rampf, F.; Paul, W.; Binder, K. On the first-order collapse transition of a three-dimensional, flexible homopolymer chain model. Europhys. Lett. 2005, 70, 628–634. [Google Scholar] [CrossRef]
- Parsons, D.F.; Williams, D.R.M. An off-lattice Wang-Landau study of the coil-globule and melting transitions of a flexible homopolymer. J. Chem. Phys. 2006, 124, 221103. [Google Scholar] [CrossRef]
- Taylor, M.P.; Paul, W.; Binder, K. Phase transitions of a single polymer chain: A Wang–Landau simulation study. J. Chem. Phys. 2009, 131, 114907. [Google Scholar] [CrossRef] [PubMed]
- Parsons, D.F.; Williams, D.R.M. Globule transitions of a single homopolymer: A Wang-Landau Monte Carlo study. Phys. Rev. E 2006, 74, 041804. [Google Scholar]
- Polson, J.M.; Moore, N.E. Simulation study of the coil-globule transition of a polymer in solvent. J. Chem. Phys. 2005, 122, 024905. [Google Scholar]
- Taylor, M.P.; Vinci, C.; Suzuki, R. Effects of macromolecular crowding on the folding of a polymer chain: A Wang–Landau simulation study. J. Chem. Phys. 2020, 153, 174901. [Google Scholar]
- Marenduzzo, D.; Maritan, A.; Rosa, A.; Seno, F. Stretching of a polymer below the θ point. Phys. Rev. Lett. 2003, 90, 088301. [Google Scholar]
- Zhou, H.; Zhou, J.; Ou-Yang, Z.-C.; Kumar, S. Collapse transition of two-dimensional flexible and semiflexible polymers. Phys. Rev. Lett. 2006, 97, 158302. [Google Scholar]
- Lee, J.H.; Kim, S.-Y.; Lee, J. Collapse transition of a square-lattice polymer with next nearest-neighbor interaction. J. Chem. Phys. 2011, 135, 204102. [Google Scholar]
- Zhou, J.; Ou-Yang, Z.-C.; Zhou, H. Simulating the collapse transition of a two-dimensional semiflexible lattice polymer. J. Chem. Phys. 2008, 128, 124905. [Google Scholar]
- Grassberger, P.; Hsu, H.-P. Stretched polymers in a poor solvent. Phys. Rev. E 2002, 65, 031807. [Google Scholar]
- Doukas, J.; Owczarek, A.L.; Prellberg, T. Identification of a polymer growth process with an equilibrium multicritical collapse phase transition: The meeting point of swollen, collapsed, and crystalline polymers. Phys. Rev. E 2010, 82, 031103. [Google Scholar]
- Bradly, C.J.; Owczarek, A.L. Polymer collapse of a self-avoiding trail model on a two-dimensional inhomogeneous lattice. Phys. A 2022, 604, 127688. [Google Scholar]
- Yethiraj, A. Computer simulation study of two-dimensional polymer solutions. Macromolecules 2003, 36, 5854–5862. [Google Scholar]
- Polanowski, P.; Jeszka, J.K.; Sikorski, A. Dynamic properties of linear and cyclic chains in two dimensions. Computer simulation studies. Macromolecules 2014, 47, 4830–4839. [Google Scholar] [CrossRef]
- Polanowski, P.; Jeszka, J.K.; Sikorski, A. Monte-Carlo studies of two-dimensional polymer-solvent systems. J. Mol. Model. 2017, 23, 63. [Google Scholar] [CrossRef]
- Meyer, H.; Wittmer, J.P.; Kreer, T.; Johner, A.; Baschnagel, J. Static properties of polymer melts in two dimensions. J. Chem. Phys. 2010, 132, 184904. [Google Scholar]
- Nelson, P.H.; Hatton, T.A.; Rutledge, G.C. General reptation and scaling of 2d athermal polymers on close-packed lattices. J. Chem. Phys. 1997, 107, 1269–1278. [Google Scholar]
- Liang, H. Observation of the molten globule state in a Monte Carlo simulation of the coil-to-globule transition of a homopolymer chain. J. Chem. Phys. 1999, 110, 10212–10215. [Google Scholar]
- Polanowski, P.; Sikorski, A. Coil-globule transition in two-dimensional polymer chains in an explicit solvent. Soft Matter 2023, 19, 7979–7987. [Google Scholar]
- Pakula, T. Simulation on the completely occupied lattice. In Simulation Method for Polymers; Kotelyanski, M., Theodorou, D.N., Eds.; Marcel Dekker: New York, NY, USA; Basel, Switzerland, 2004; pp. 147–176. [Google Scholar]
- Pakula, T. Cooperative relaxations in condensed macromolecular systems. 1. A model for computer simulation. Macromolecules 1987, 20, 679–682. [Google Scholar] [CrossRef]
- Vanderzande, C. Superconformal invariance in the tricritical O(N) model. Phys. Rev. B 1988, 38, 2865–2867. [Google Scholar]
- Šolc, K.; Stockmayer, W.H. Shape of a random-flight chain. J. Chem. Phys. 1970, 54, 2756–2757. [Google Scholar] [CrossRef]
- Šolc, K. Statistical mechanics of random-flight chains. IV. Size and shape parameters of cyclic, star-like, and comb-like chains. Macromolecules 1973, 6, 378–385. [Google Scholar] [CrossRef]
- Rudnick, J.; Gaspari, G. The aspherity of random walks. J. Phys. A Math. Gen. 1986, 19, L191–L193. [Google Scholar] [CrossRef]
- Aronovitz, J.A.; Nelson, D.R. Universal features of polymer shapes. J. Phys. 1986, 47, 1445–1456. [Google Scholar] [CrossRef]
- Maier, B.; Rädler, J.O. DNA on fluid membranes: A model polymer in two dimensions. Macromolecules 2000, 33, 7185–7194. [Google Scholar] [CrossRef]
- Maier, B.; Rädler, J.O. Shape of self-avoiding walks in two dimensions. Macromolecules 2001, 34, 5723–5724. [Google Scholar] [CrossRef]
- Burger, V.M.; Arenas, D.J.; Stultz, C.M. A structure-free method for quantifying conformational flexibility in proteins. Sci. Rep. 2016, 6, 29040. [Google Scholar] [CrossRef]
- Banks, A.; Qin, S.; Weiss, K.L.; Stanley, C.B.; Zhou, H.-X. Intrinsically disordered protein exhibits both compaction and expansion under macromolecular crowding. Biophys. J. 2018, 114, 1067–1079. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Polanowski, P.; Sikorski, A. Monte Carlo Simulations of Polymer Collapse in an Explicit Solvent of Varying Quality. Polymers 2025, 17, 978. https://doi.org/10.3390/polym17070978
Polanowski P, Sikorski A. Monte Carlo Simulations of Polymer Collapse in an Explicit Solvent of Varying Quality. Polymers. 2025; 17(7):978. https://doi.org/10.3390/polym17070978
Chicago/Turabian StylePolanowski, Piotr, and Andrzej Sikorski. 2025. "Monte Carlo Simulations of Polymer Collapse in an Explicit Solvent of Varying Quality" Polymers 17, no. 7: 978. https://doi.org/10.3390/polym17070978
APA StylePolanowski, P., & Sikorski, A. (2025). Monte Carlo Simulations of Polymer Collapse in an Explicit Solvent of Varying Quality. Polymers, 17(7), 978. https://doi.org/10.3390/polym17070978






