Effects of Molecular Structure on the Physical Properties of Fully Substituted Cellulose Esters of Aliphatic Acids
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Preparation of SCEs
2.3. Preparation of MCEs
2.4. Chemical Characterization
2.5. Thermal Properties
2.6. Preparation of Hot-Pressed Films
2.7. Mechanical Properties
3. Results and Discussion
3.1. Esterification of Cellulose and Determination of DS
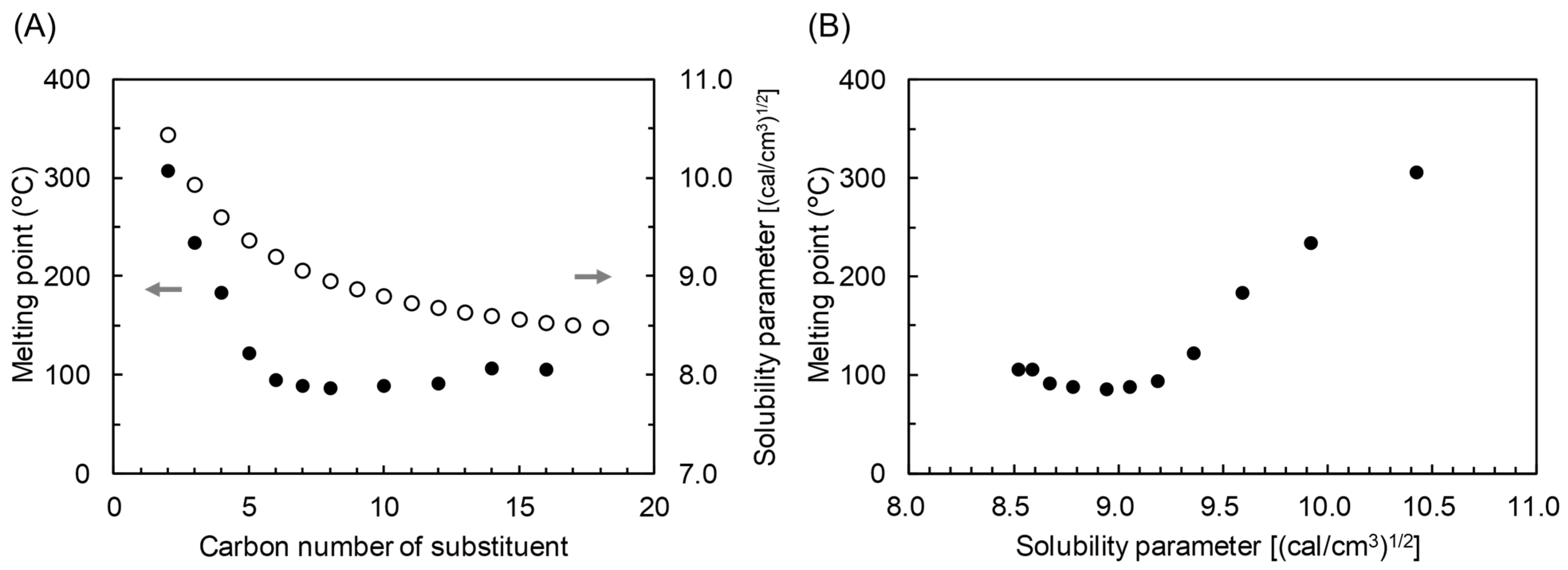
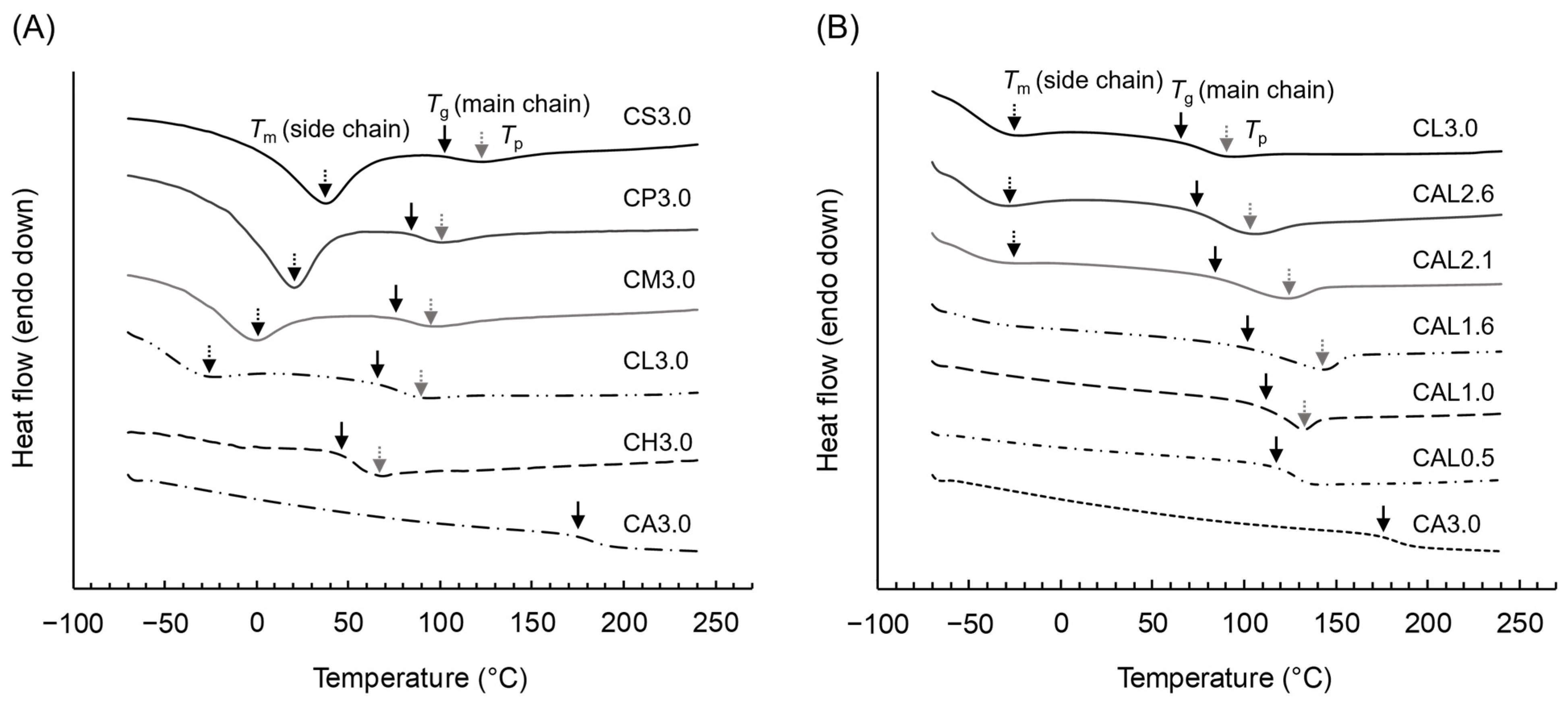
3.2. Thermal Properties of MCEs
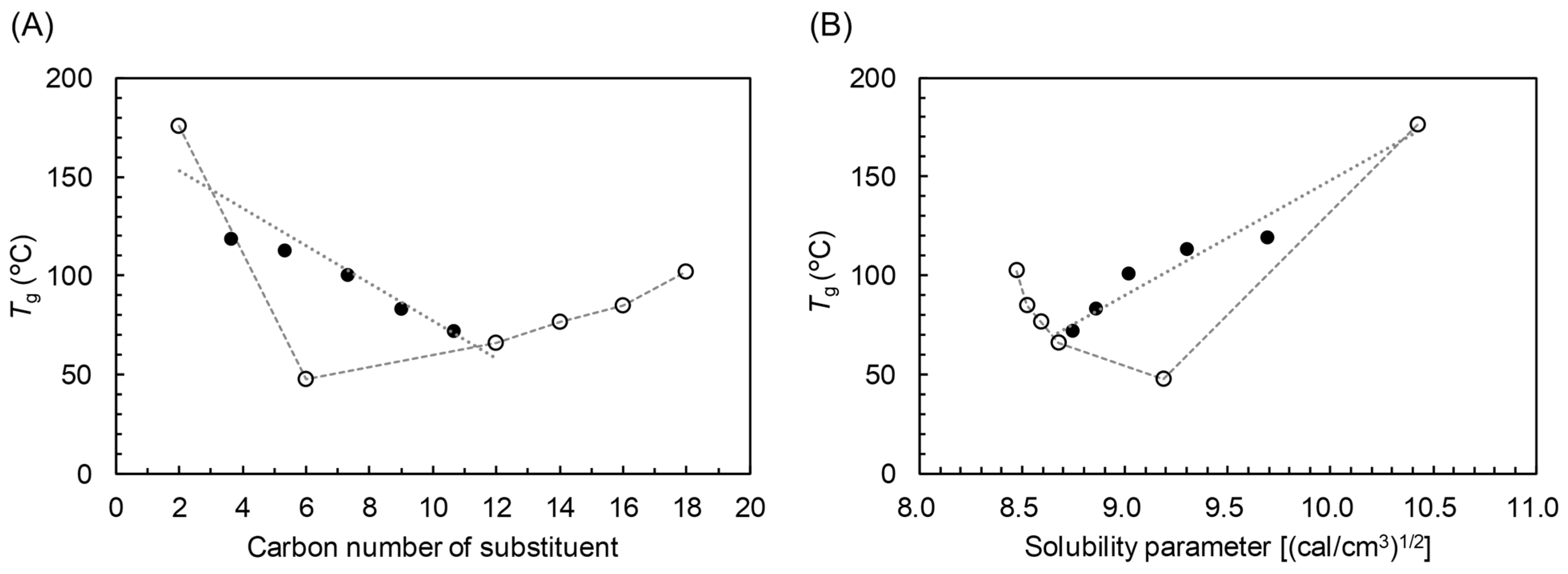
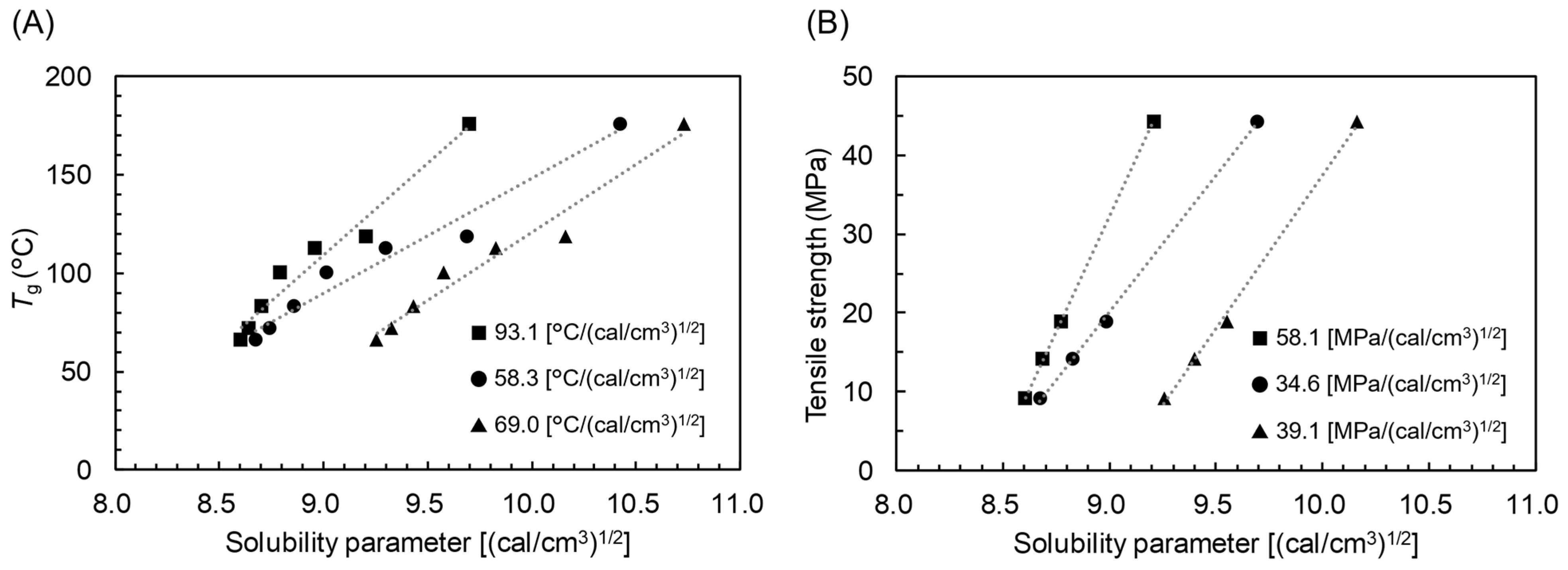
3.3. SP–Thermal Properties Relationship of CEs
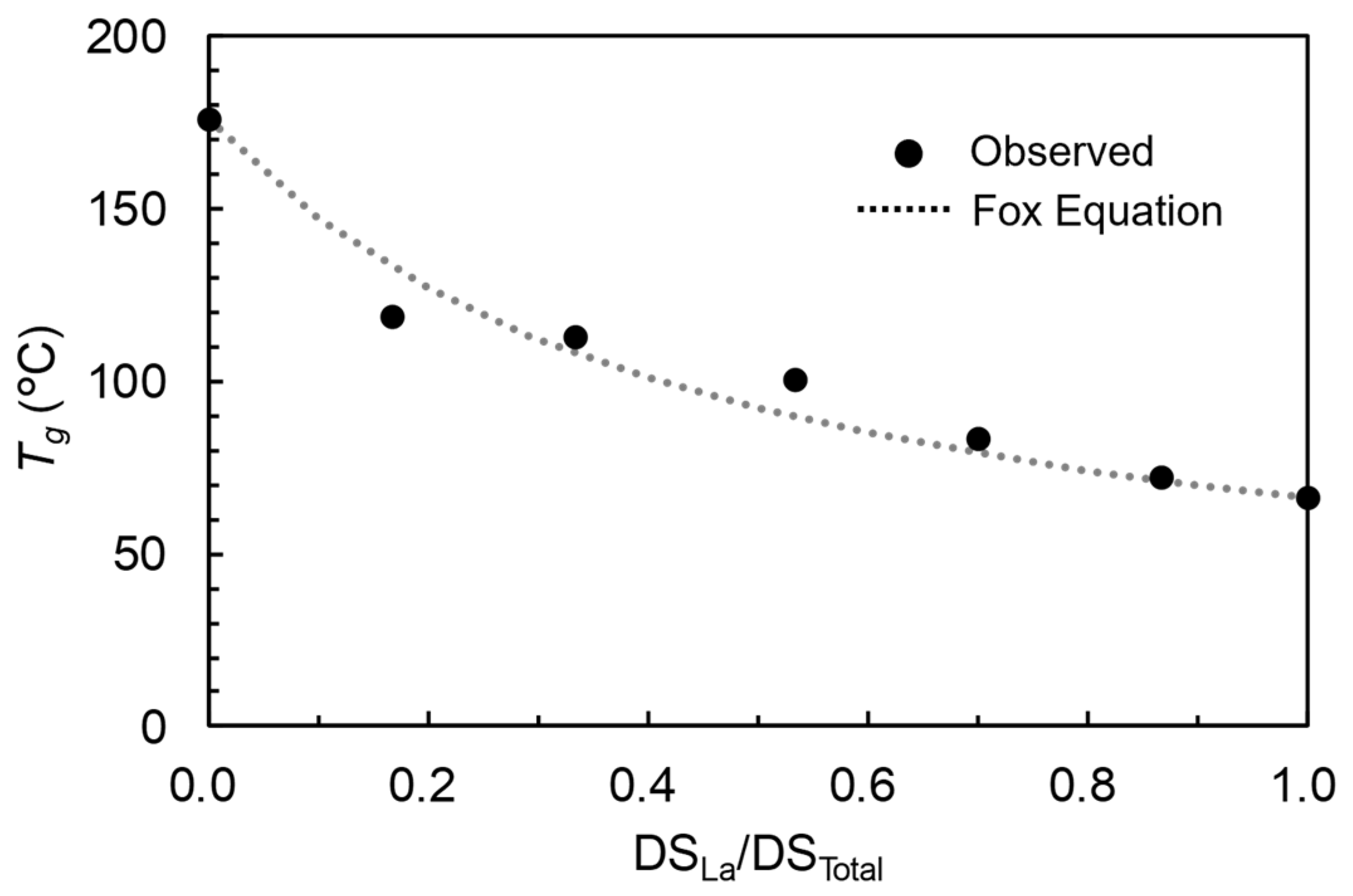
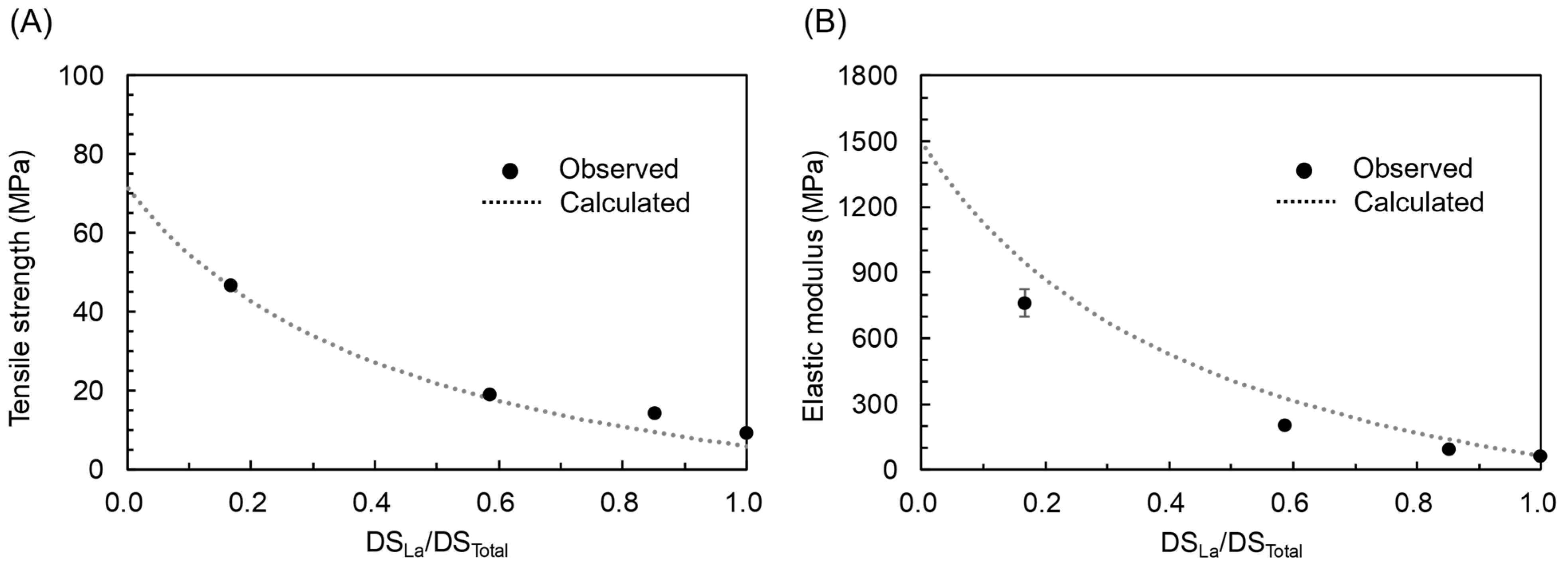
3.4. Prediction of the Physical Properties of MCEs
4. Conclusions
- The correlation between SP and physical properties exists only for MCE. There is no such correlation for SCE. The origin of such difference between MCE and SCE has yet to be further studied.
- Even for MCE, the empirical relationship involving SP varies from acyl group to acyl group; there is no universal relationship.
- In spite of the aforementioned limitation, the empirical relationship with SP is useful for the property prediction of MCE as long as acyl groups are specified. The Fox equation and Voigt model could also be utilized for the prediction based only on the properties of the corresponding SCEs. The observed root mean squared errors for prediction were 8.0 °C (Tg based on SP), 13.2 °C (Tg based on Fox equation), 3.0 MPa (tensile strength based on SP), and 3.5 MPa (tensile strength based on Voigt model).
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Organisation for Economic Co-Operation and Development. Global Plastics Outlook: Policy Scenarios to 2060. Available online: https://www.oecd.org/en/publications/global-plastics-outlook_aa1edf33-en.html (accessed on 18 November 2024).
- Plastics Europe. Plastics—The Fast Facts 2023. Available online: https://plasticseurope.org/knowledge-hub/plastics-the-fast-facts-2023/ (accessed on 18 November 2024).
- Thakur, S.; Chaudhary, J.; Sharma, B.; Verma, A.; Tamulevicius, S.; Thakur, V.K. Sustainability of bioplastics: Opportunities and challenges. Curr. Opin. Green Sustain. Chem. 2018, 13, 68–75. [Google Scholar] [CrossRef]
- Organisation for Economic Co-Operation and Development. Global Material Resources Outlook to 2060: Economic Drivers and Environmental Consequences. Available online: https://www.oecd.org/en/publications/global-material-resources-outlook-to-2060_9789264307452-en.html (accessed on 26 November 2024).
- Janaswamy, S.; Yadav, M.P.; Hoque, M.; Bhattarai, S.; Ahmed, S. Cellulosic fraction from agricultural biomass as a viable alternative for plastics and plastic products. Ind. Crops Prod. 2022, 179, 114692. [Google Scholar] [CrossRef]
- Wang, J.; Wang, L.; Gardner, D.J.; Shaler, S.M.; Cai, Z. Towards a cellulose-based society: Opportunities and challenges. Cellulose 2021, 28, 4511–4543. [Google Scholar] [CrossRef]
- Heinze, T. Cellulose: Structure and properties. In Cellulose Chemistry and Properties: Fibers, Nanocelluloses and Advanced Materials. Advances in Polymer Science; Rojas, O., Ed.; Springer: Cham, Switzerland, 2015; Volume 271, pp. 1–52. [Google Scholar] [CrossRef]
- Edgar, K.J.; Buchanan, C.M.; Debenham, J.S.; Rundquist, P.A.; Seiler, B.D.; Shelton, M.C.; Tindall, D. Advances in cellulose ester performance and application. Prog. Polym. Sci. 2001, 26, 1605–1688. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X.; Xie, Y.; Zhang, K. Functional nanomaterials through esterification of cellulose: A review of chemistry and application. Cellulose 2018, 25, 3703–3731. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, J.; Xiao, P.; Tian, W.; Zhang, J. Novel thermoplastic cellulose esters containing bulky moieties and soft segments. ACS Sustain. Chem. Eng. 2018, 6, 4931–4939. [Google Scholar] [CrossRef]
- Sata, H.; Murayama, M.; Shimamoto, S. Properties and applications of cellulose triacetate film. Macromol. Symp. 2004, 208, 323–334. [Google Scholar] [CrossRef]
- Candido, R.G.; Godoy, G.G.; Gonçalves, A. Characterization and application of cellulose acetate synthesized from sugarcane bagasse. Carbohydr. Polym. 2017, 167, 280–289. [Google Scholar] [CrossRef]
- Kamide, K.; Saito, M. Thermal analysis of cellulose acetate solids with total degrees of substitution of 0.49, 1.75, 2.46, and 2.92. Polym. J. 1985, 17, 919–928. [Google Scholar] [CrossRef]
- Charvet, A.; Vergelati, C.; Long, D.R. Mechanical and ultimate properties of injection molded cellulose acetate/plasticizer materials. Carbohydr. Polym. 2019, 204, 182–189. [Google Scholar] [CrossRef]
- Bonifacio, A.; Bonetti, L.; Piantanida, E.; Nardo, L. Plasticizer design strategies enabling advanced applications of cellulose acetate. Eur. Polym. J. 2023, 197, 112360. [Google Scholar] [CrossRef]
- Fordyce, C.R.; Meyer, L.W.A. Plasticizers for cellulose acetate and cellulose acetate butyrate. Ind. Eng. Chem. 1940, 32, 1053–1060. [Google Scholar] [CrossRef]
- Richardson, E.; Truffa Giachet, M.; Schilling, M.; Learner, T. Assessing the physical stability of archival cellulose acetate films by monitoring plasticizer loss. Polym. Degrad. Stab. 2014, 107, 231–236. [Google Scholar] [CrossRef]
- Fujii, M.; Shinohara, N.; Lim, A.; Otake, T.; Kumagai, K.; Yanagisawa, Y. A study on emission of phthalate esters from plastic materials using a passive flux sampler. Atmos. Environ. 2003, 37, 5495–5504. [Google Scholar] [CrossRef]
- Bui, T.T.; Giovanoulis, G.; Cousins, A.P.; Magnér, J.; Cousins, I.T.; de Wit, C.A. Human exposure, hazard and risk of alternative plasticizers to phthalate esters. Sci. Total Environ. 2016, 541, 451–467. [Google Scholar] [CrossRef]
- Vidéki, B.; Klébert, S.; Pukánszky, B. External and internal plasticization of cellulose acetate with caprolactone: Structure and properties. J. Polym. Sci. Part B Polym. Phys. 2007, 45, 873–883. [Google Scholar] [CrossRef]
- Teramoto, Y. Functional thermoplastic materials from derivatives of cellulose and related structural polysaccharides. Molecules 2015, 20, 5487–5527. [Google Scholar] [CrossRef]
- Malm, C.J.; Mench, J.W.; Kendall, D.L.; Hiatt, G.D. Aliphatic acid esters of cellulose. Properties. Ind. Eng. Chem. 1951, 43, 688–691. [Google Scholar] [CrossRef]
- Morooka, T.; Norimoto, M.; Yamada, T.; Shiraishi, N. Dielectric properties of cellulose acylates. J. Appl. Polym. Sci. 1984, 29, 3981–3990. [Google Scholar] [CrossRef]
- Wang, P.; Tao, B.Y. Synthesis of cellulose-fatty acid esters for use as biodegradable plastics. J. Environ. Polym. Degrad. 1995, 3, 115–119. [Google Scholar] [CrossRef]
- Sealey, J.E.; Samaranayake, G.; Todd, J.G.; Glasser, W.G. Novel cellulose derivatives. IV. Preparation and thermal analysis of waxy esters of cellulose. J. Polym. Sci. Part B Polym. Phys. 1996, 34, 1613–1620. [Google Scholar] [CrossRef]
- Glasser, W.G.; Samaranayake, G.; Dumay, M.; Davé, V. Novel cellulose derivatives. III. Thermal analysis of mixed esters with butyric and hexanoic acid. J. Polym. Sci. Part B Polym. Phys. 1995, 33, 2045–2054. [Google Scholar] [CrossRef]
- Edgar, K.J.; Pecorini, T.J.; Glasser, W.G. Long-chain cellulose esters: Preparation, properties, and perspective. ACS Symp. Ser. 1998, 688, 38–60. [Google Scholar] [CrossRef]
- Vaca-Garcia, C.; Thiebaud, S.; Borredon, M.E.; Gozzelino, G. Cellulose esterification with fatty acids and acetic anhydride in lithium chloride/N, N-dimethylacetamide medium. J. Am. Oil Chem. Soc. 1998, 75, 315–319. [Google Scholar] [CrossRef]
- Tanaka, S.; Iwata, T.; Iji, M. Long/short chain mixed cellulose esters: Effects of long acyl chain structures on mechanical and thermal properties. ACS Sustain. Chem. Eng. 2017, 5, 1485–1493. [Google Scholar] [CrossRef]
- Tedeschi, G.; Guzman-Puyol, S.; Paul, U.C.; Barthel, M.J.; Goldoni, L.; Caputo, G.; Heredia-Guerrero, J.A. Thermoplastic cellulose acetate oleate films with high barrier properties and ductile behaviour. Chem. Eng. J. 2018, 348, 840–849. [Google Scholar] [CrossRef]
- Boulven, M.; Quintard, G.; Cottaz, A.; Joly, C.; Charlot, A.; Fleury, E. Homogeneous acylation of Cellulose diacetate: Towards bioplastics with tuneable thermal and water transport properties. Carbohydr. Polym. 2019, 206, 674–684. [Google Scholar] [CrossRef]
- Coleman, M.M.; Serman, C.J.; Bhagwagar, D.E.; Painter, P.C. A practical guide to polymer miscibility. Polymer 1990, 31, 1187–1203. [Google Scholar] [CrossRef]
- McCormick, C.L. Novel Cellulose Solutions. U.S. Patent 4,278,790, 14 July 1981. [Google Scholar]
- Dawsey, T.R.; McCormick, C.L. The lithium chloride/dimethylacetamide solvent for cellulose: A literature review. Rev. Macromol. Chem. Phys. 1990, 30, 405–440. [Google Scholar] [CrossRef]
- Diamantoglou, M.; Kuhne, H. Reaktionen von Cellulose in homogener Loesung. Das Pap. 1988, 42, 690–696. [Google Scholar]
- Samaranayake, G.; Glasser, W.G. Cellulose derivatives with low DS. I. A novel acylation system. Carbohydr. Polym. 1993, 22, 1–7. [Google Scholar] [CrossRef]
- Samaranayake, G.; Glasser, W.G. Cellulose derivatives with low DS. II. Analysis of alkanoates. Carbohydr. Polym. 1993, 22, 79–86. [Google Scholar] [CrossRef]
- Shimizu, Y.; Hayashi, J. Acylation of cellulose with carboxylic acids. Cellul. Chem. Technol. 1987, 23, 661–670. Available online: http://pascal-francis.inist.fr/vibad/index.php?action=getRecordDetail&idt=19765050 (accessed on 6 November 2024).
- Crépy, L.; Miri, V.; Joly, N.; Martin, P.; Lefebvre, J.M. Effect of side chain length on structure and thermomechanical properties of fully substituted cellulose fatty esters. Carbohydr. Polym. 2011, 83, 1812–1820. [Google Scholar] [CrossRef]
- ISO527-3:1995; Plastics—Determination of Tensile Properties—Part 3: Test Conditions for Films and Sheets. ISO: Geneva, Switzerland, 1995.
- Maim, C.J.; Mench, J.W.; Kendall, D.L.; Hiatt, G.D. Aliphatic acid esters of cellulose. Preparation by acid-chloride-pyridine procedure. Ind. Eng. Chem. 1951, 43, 684–688. [Google Scholar] [CrossRef]
- Wen, X.; Wang, H.; Wei, Y.; Wang, X.; Liu, C. Preparation and characterization of cellulose laurate ester by catalyzed transesterification. Carbohydr. Polym. 2017, 168, 247–254. [Google Scholar] [CrossRef]
- Cao, X.; Peng, X.; Zhong, L.; Sun, S.; Yang, D.; Zhang, X.; Sun, R. A novel transesterification system to rapidly synthesize cellulose aliphatic esters. Cellulose 2014, 21, 581–594. [Google Scholar] [CrossRef]
- Yamagishi, T.; Fukuda, T.; Miyamoto, T. Thermotropic cellulose derivatives with flexible substituents IV. Columnar liquid crystals from ester-type derivatives of cellulose. Liq. Cryst. 1991, 10, 467–473. [Google Scholar] [CrossRef]
- Milotskyi, R.; Szabó, L.; Fujie, T.; Sakata, K.; Wada, N.; Takahashi, K. Low waste process of rapid cellulose transesterification using ionic liquid/DMSO mixed solvent: Towards more sustainable reaction systems. Carbohydr. Polym. 2021, 256, 117560. [Google Scholar] [CrossRef]
- Danjo, T.; Iwata, T. Syntheses of cellulose branched ester derivatives and their properties and structure analyses. Polymer 2018, 137, 358–363. [Google Scholar] [CrossRef]
- Watanabe, J.; Goto, M.; Nagase, T. Thermotropic polypeptides. 3. Investigation of cholesteric mesophase properties of poly (gamma.-benzyl L-glutamate-co-.gamma.-dodecyl L-glutamates) by circular dichroic measurements. Macromolecules 1987, 20, 298–304. [Google Scholar] [CrossRef]
- Fedors, R.F. A method for estimating both the SPs and molar volumes of liquids. Poly. Eng. Sci. 1974, 14, 147–154. [Google Scholar] [CrossRef]
- Brandrup, J.; Immergut, E.H.; Grulke, E.A. (Eds.) Polymer Handbook, 4th ed.; Wiley: Hoboken, NJ, USA, 1999. [Google Scholar]
- Fox, T.G. Influence of diluent and of copolymer composition on the glass temperature of a polymer system. Bull. Am. Phs. Soc. 1952, 1, 123. [Google Scholar]
- Johnston, N.W. Sequence distribution-glass transition effects. J. Macromol. Sci. Rev. Macromol. Chem. 1976, 14, 215–250. [Google Scholar] [CrossRef]
- Bonardelli, P.; Moggi, G.; Turturro, A. Glass transition temperatures of copolymer and terpolymer fluoroelastomers. Polymer 1986, 27, 905–909. [Google Scholar] [CrossRef]
- Erdmann, R.; Kabasci, S.; Heim, H.P. Thermal properties of plasticized cellulose acetate and its β-relaxation phenomenon. Polymers 2021, 13, 1356. [Google Scholar] [CrossRef]
- Bao, C.Y.; Long, D.R.; Vergelati, C. Miscibility and dynamical properties of cellulose acetate/plasticizer systems. Carbohydr. Polym. 2015, 116, 95–102. [Google Scholar] [CrossRef]
- Vaca-Garcia, C.; Gozzelino, G.; Glasser, W.G.; Borredon, M.E. Dynamic mechanical thermal analysis transitions of partially and fully substituted cellulose fatty esters. J. Polym. Sci. Part B Polym. Phys. 2003, 41, 281–288. [Google Scholar] [CrossRef]
- Voigt, W. Űber die Beziehung zwischen den beiden Elastizi ä tskonstanten isotroper Körper. Wied. Ann. 1889, 38, 573–587. [Google Scholar] [CrossRef]
- Joseph, S.; Thomas, S. Modeling of tensile moduli in polystyrene/polybutadiene blends. J. Polym. Sci. Part B Polym. Phys. 2002, 40, 755–764. [Google Scholar] [CrossRef]
- Bulıcek, M.; Málek, J.; Rajagopal, K.R. On Kelvin–Voigt model and its generalizations. Evol. Equ. Control. Theory 2012, 1, 17–42. [Google Scholar] [CrossRef]
- Mark, J.E. (Ed.) Physical Properties of Polymers Handbook, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
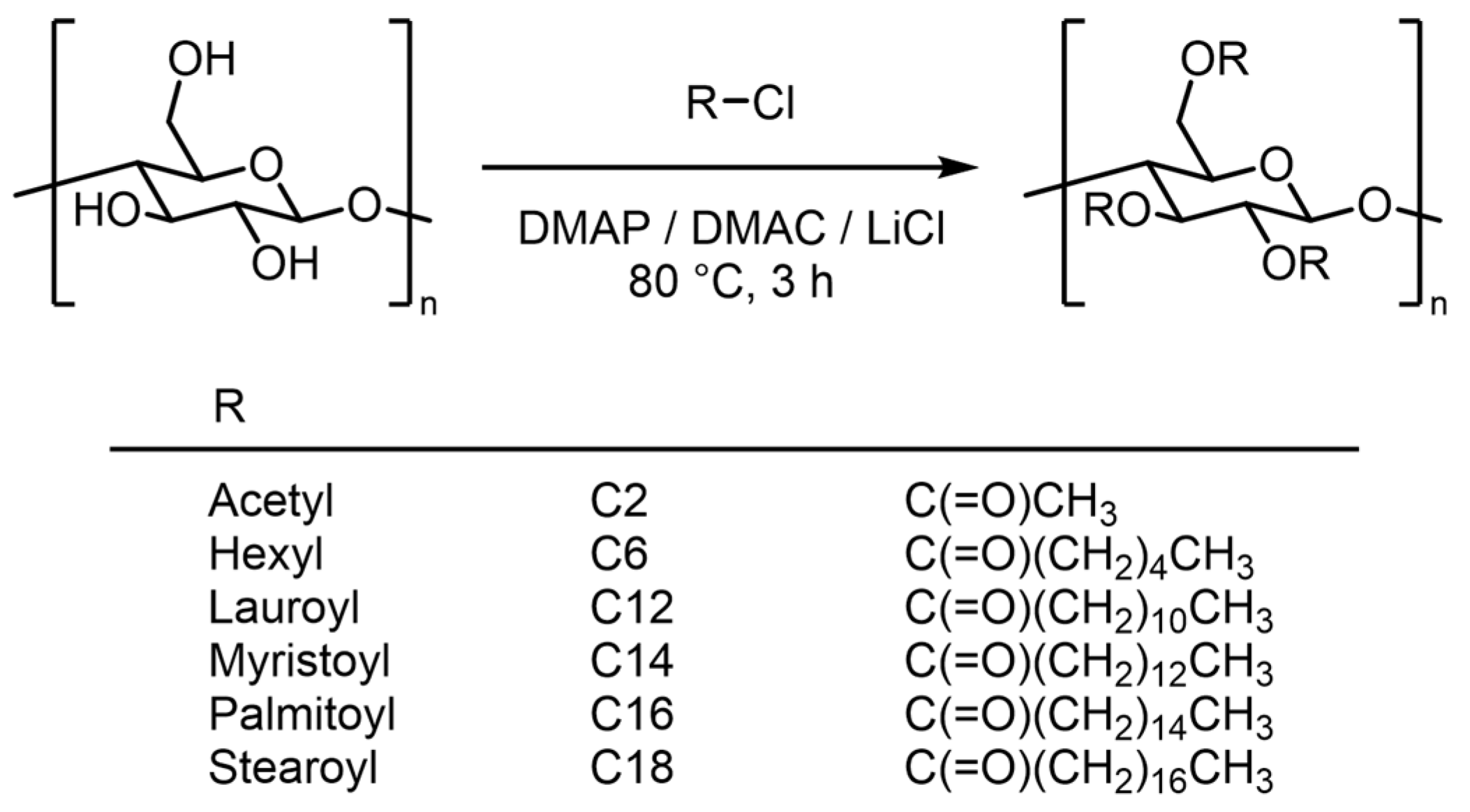

| CE | Substituent I | Substituent II | Molar Mass 4 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| ID | Name | Carbon Number | DSx 1 | Carbon Number | DSAc | DSTotal | DSx/DSTotal 2 | MAGU3 | Mn/10−3 | Mw/10−3 | DPw 5 |
| (g/mol) | (g/mol) | (g/mol) | |||||||||
| Simple cellulose ester (SCE) | |||||||||||
| CS3.0 | Cellulose stearate | 18 | 3.0 | - | - | 3.0 | 1.0 | 961.5 | 85 | 281 | 292 |
| CP3.0 | Cellulose palmitate | 16 | 3.0 | - | - | 3.0 | 1.0 | 877.4 | 86 | 338 | 385 |
| CM3.0 | Cellulose myristate | 14 | 3.0 | - | - | 3.0 | 1.0 | 793.2 | 89 | 422 | 532 |
| CL3.0 | Cellulose laurate | 12 | 3.0 | - | - | 3.0 | 1.0 | 709.0 | 94 | 536 | 776 |
| CH3.0 | Cellulose hexanoate | 6 | 3.0 | - | - | 3.0 | 1.0 | 456.6 | 161 | 347 | 760 |
| CA3.0 | Cellulose acetate | - | - | 2 | 3.0 | 3.0 | 0.0 | 288.2 | 116 | 360 | 1248 |
| Mixed cellulose ester (MCE) | |||||||||||
| CAL2.6 | Cellulose acetate laurate | 12 | 2.6 | 2 | 0.4 | 3.0 | 0.9 | 652.9 | 86 | 539 | 849 |
| CAL2.1 | Cellulose acetate laurate | 12 | 2.1 | 2 | 0.9 | 3.0 | 0.7 | 582.8 | 85 | 427 | 738 |
| CAL1.6 | Cellulose acetate laurate | 12 | 1.6 | 2 | 1.4 | 3.0 | 0.5 | 512.7 | 66 | 333 | 655 |
| CAL1.0 | Cellulose acetate laurate | 12 | 1.0 | 2 | 2.0 | 3.0 | 0.3 | 428.5 | 68 | 295 | 695 |
| CAL0.5 | Cellulose acetate laurate | 12 | 0.5 | 2 | 2.5 | 3.0 | 0.2 | 358.4 | 61 | 243 | 686 |
| CE | DS | TG-DTA 1 | DSC 2 | |||||
|---|---|---|---|---|---|---|---|---|
| ID | DSX | DSAc | Td5% | Tm | ΔHm | Tg | Tp | ΔHp |
| (°C) | (°C) | (J/g) | (°C) | (°C) | (J/g) | |||
| SCE | ||||||||
| CS3.0 | 3.0 | - | 349.2 | 37.8 | 66.1 | 102.3 | 123.7 | 7.4 |
| CP3.0 | 3.0 | - | 323.8 | 20.8 | 50.0 | 85.0 | 101.1 | 6.9 |
| CM3.0 | 3.0 | - | 320.8 | 0.1 | 32.7 | 76.5 | 95.6 | 9.9 |
| CL3.0 | 3.0 | - | 317.4 | −26.6 | 16.5 | 66.1 | 90.1 | 10.1 |
| CH3.0 | 3.0 | - | 331.8 | - | - | 47.7 | 68.7 | 6.8 |
| CA3.0 | - | 3.0 | 317.3 | - | - | 175.9 | - | - |
| MCE | ||||||||
| CAL2.6 | 2.6 | 0.4 | 324.6 | −28.9 | 7.4 | 72.1 | 104.1 | 14.9 |
| CAL2.1 | 2.1 | 0.9 | 325.4 | −27.7 | 6.9 | 83.1 | 125.7 | 16.0 |
| CAL1.6 | 1.6 | 1.4 | 324.0 | - | - | 100.5 | 142.4 | 16.6 |
| CAL1.0 | 1.0 | 2.0 | 317.9 | - | - | 112.9 | 132.7 | 15.6 |
| CAL0.5 | 0.5 | 2.5 | 320.4 | - | - | 118.8 | - | - |
| CE | DS | Mechanical Property | |||
|---|---|---|---|---|---|
| ID | DSX | DSAc | Tensile Strength | Elongation at Break | Tensile Modulus |
| (MPa) | (%) | (MPa) | |||
| CL3.0 | 3.0 | - | 9.2 ± 0.4 | 282.5 ± 13.4 | 63.2 ± 3.3 |
| CAL2.3 | 2.3 | 0.4 | 14.2 ± 1.6 | 188.7 ± 30.0 | 96.9 ± 6.9 |
| CAL1.7 | 1.7 | 1.2 | 18.9 ± 1.9 | 154.5 ± 20.6 | 203.0 ± 14.0 |
| CAL0.5 | 0.5 | 2.5 | 44.3 ± 4.2 | 79.5 ± 14.0 | 749.1 ± 82.7 |
| MCE | Tg from δ by First Order Regression 1 | Tg from Dr by Fox Equation 2 | |||||
|---|---|---|---|---|---|---|---|
| Carbon Number of Substituent | Abbreviation | Intercept a | Slope b | RMSE 3 (°C) | TgCA3.0 (°C) | TgCX3.0 (°C) | RMSE 3 (°C) |
| C2 and C6 | CAH | −905.1 | 103.7 | N.A. | 175.9 | 47.7 | N.A. |
| C2 and C12 | CAL | −477.6 | 62.7 | 8.0 | 175.9 | 66.1 | 13.2 |
| C2 and C14 | CAM | −388.3 | 54.1 | N.A. | 175.9 | 76.5 | N.A. |
| C2 and C16 | CAP | −322.2 | 47.8 | N.A. | 175.9 | 85.0 | N.A. |
| C2 and C18 | CAS | −216.5 | 37.6 | N.A. | 175.9 | 102.3 | N.A. |
| MCE | σR from δ by First Order Regression 1 | σR from Dr by Voigt Model 2 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Carbon Number of Substituent | Abbreviation | Intercept a | Slope b | RMSE 3 (MPa) | σRCA3.0 (MPa) | σRCX (MPa) | ρCA3.0 (g/cm3) | ρCX3.0 (g/cm3) | RMSE 3 (MPa) |
| C2 and C6 | CAH | −416.3 | 46.8 | N.A. | 71.6 | 13.7 | 1.28 | 1.10 | N.A. |
| C2 and C12 | CAL | −319.5 | 37.5 | 3.0 | 71.6 | 5.9 | 1.28 | 1.00 | 3.5 |
| C2 and C14 | CAM | −301.4 | 35.8 | N.A. | 71.6 | 5.9 | 1.28 | 0.99 | N.A. |
| C2 and C16 | CAP | −293.8 | 35.0 | N.A. | 71.6 | 4.9 | 1.28 | 0.99 | N.A. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mori, T.; Nagai, K.; Shimamoto, S. Effects of Molecular Structure on the Physical Properties of Fully Substituted Cellulose Esters of Aliphatic Acids. Polymers 2025, 17, 1053. https://doi.org/10.3390/polym17081053
Mori T, Nagai K, Shimamoto S. Effects of Molecular Structure on the Physical Properties of Fully Substituted Cellulose Esters of Aliphatic Acids. Polymers. 2025; 17(8):1053. https://doi.org/10.3390/polym17081053
Chicago/Turabian StyleMori, Taro, Kanji Nagai, and Shu Shimamoto. 2025. "Effects of Molecular Structure on the Physical Properties of Fully Substituted Cellulose Esters of Aliphatic Acids" Polymers 17, no. 8: 1053. https://doi.org/10.3390/polym17081053
APA StyleMori, T., Nagai, K., & Shimamoto, S. (2025). Effects of Molecular Structure on the Physical Properties of Fully Substituted Cellulose Esters of Aliphatic Acids. Polymers, 17(8), 1053. https://doi.org/10.3390/polym17081053







