A Hybrid Artificial Neural Network Approach for Modeling the Behavior of Polyethylene Terephthalate (PET) Under Conditions Applicable to Stretch Blow Molding
Abstract
:1. Introduction
2. Experimental Procedure
2.1. Material and Specimens
2.2. Free Stretch Blow Test
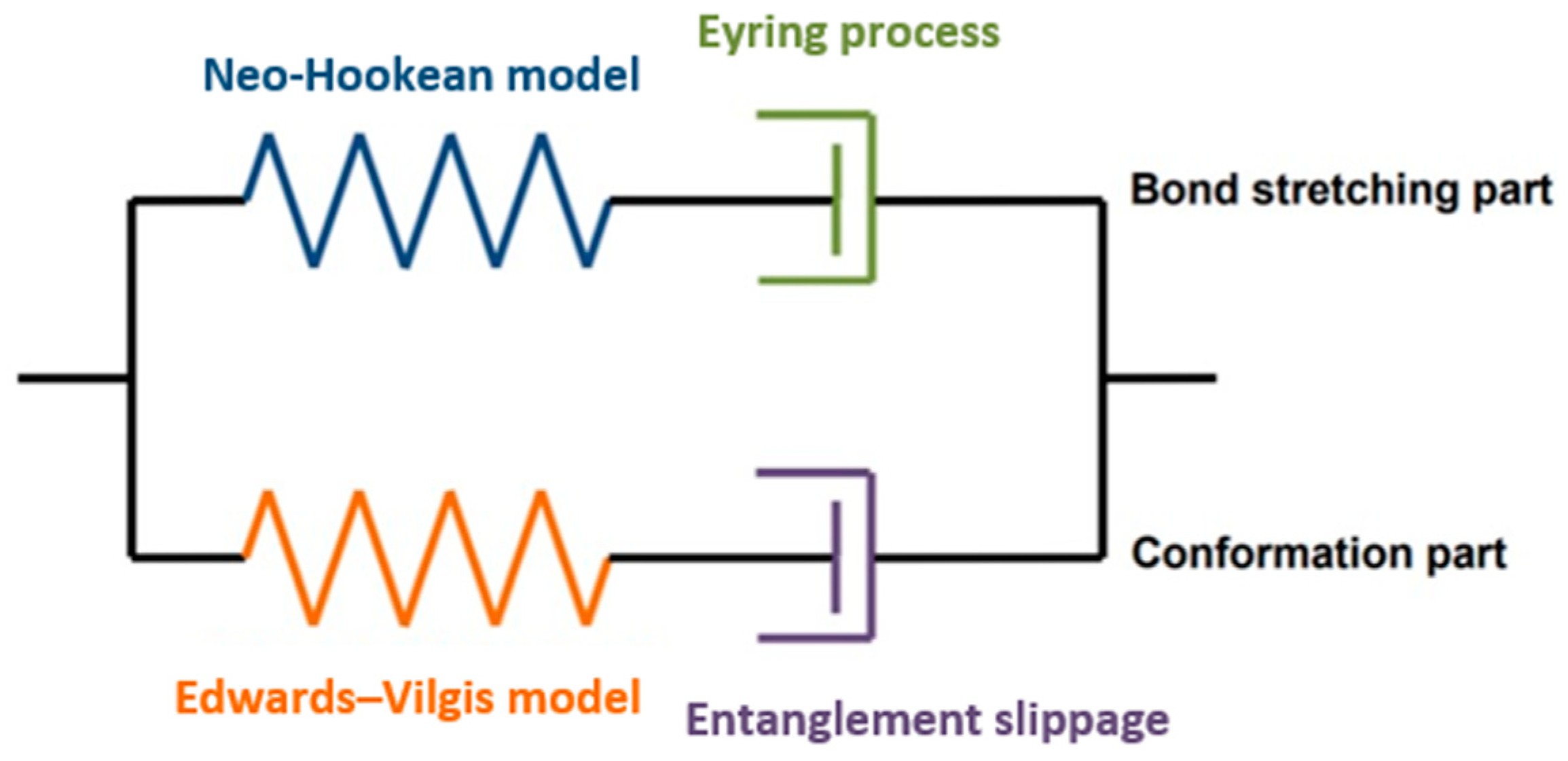
3. Brief Description of Buckley Model
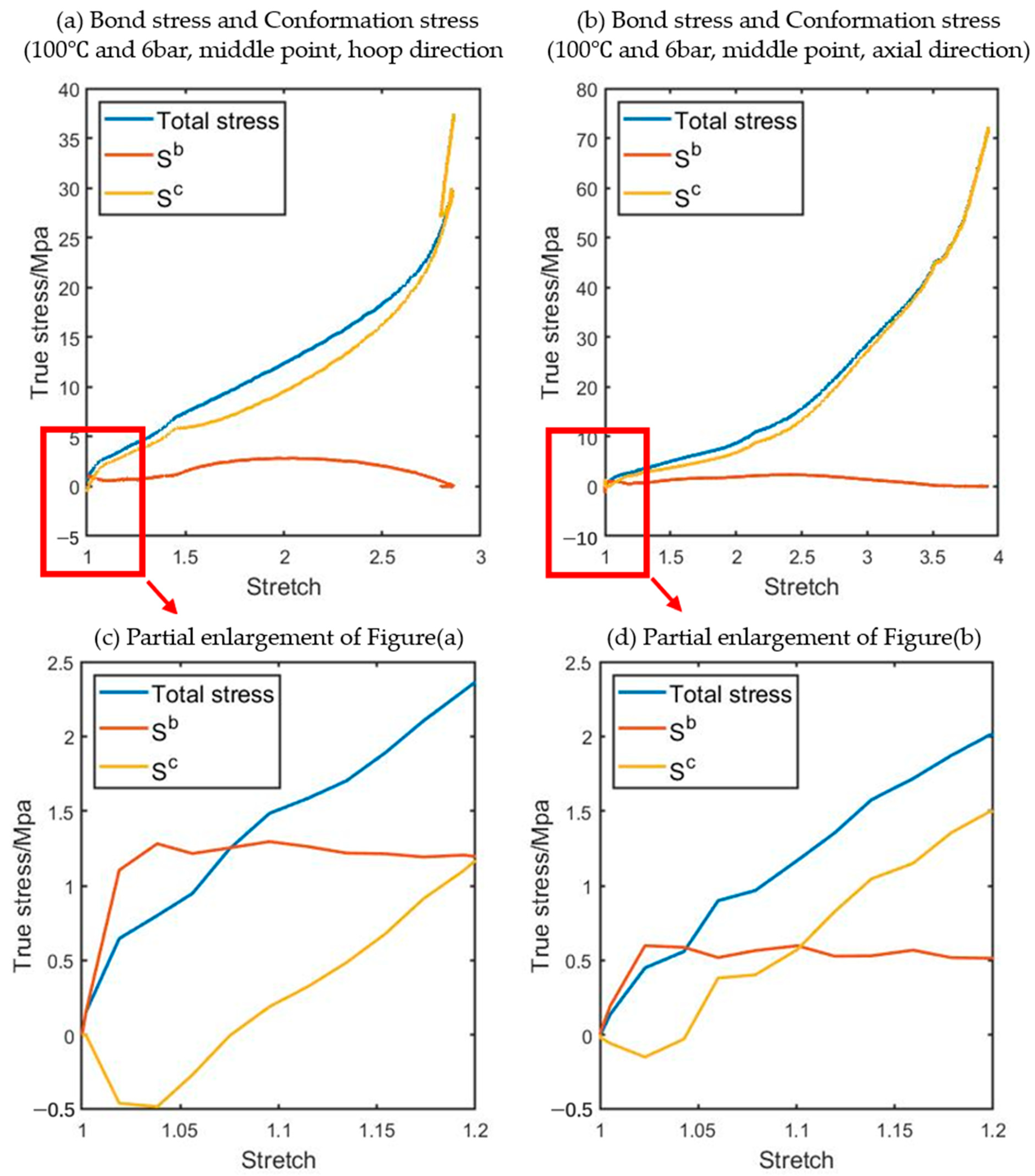
3.1. Bond Stretching Part
3.2. Conformation Part
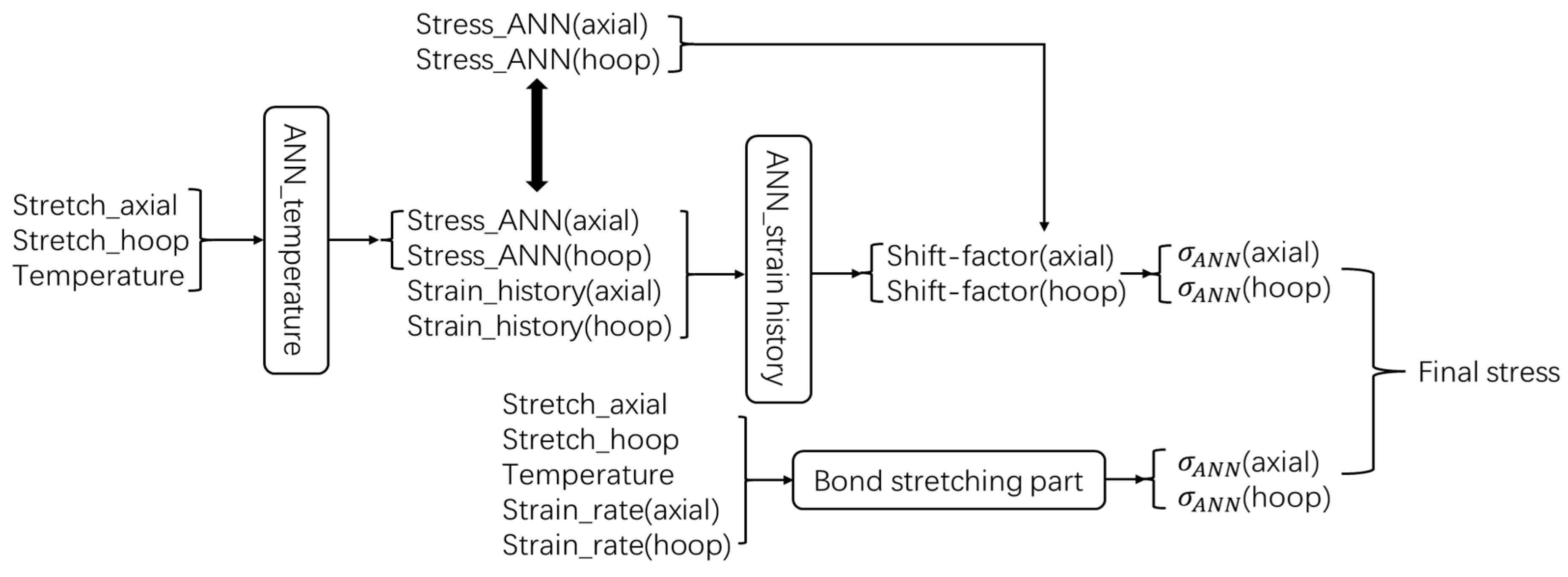
4. Hybrid ANN-Based Constitutive Model
4.1. Algorithm Selection and Overall Architecture Selection
4.2. Calculation of Bond Stretching Stress
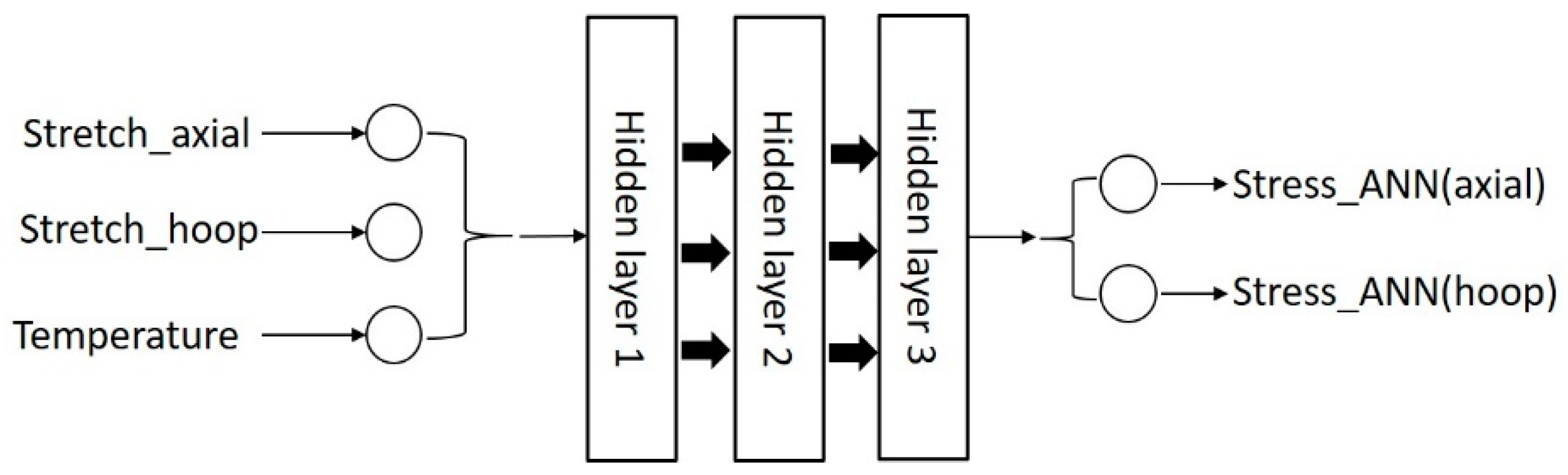
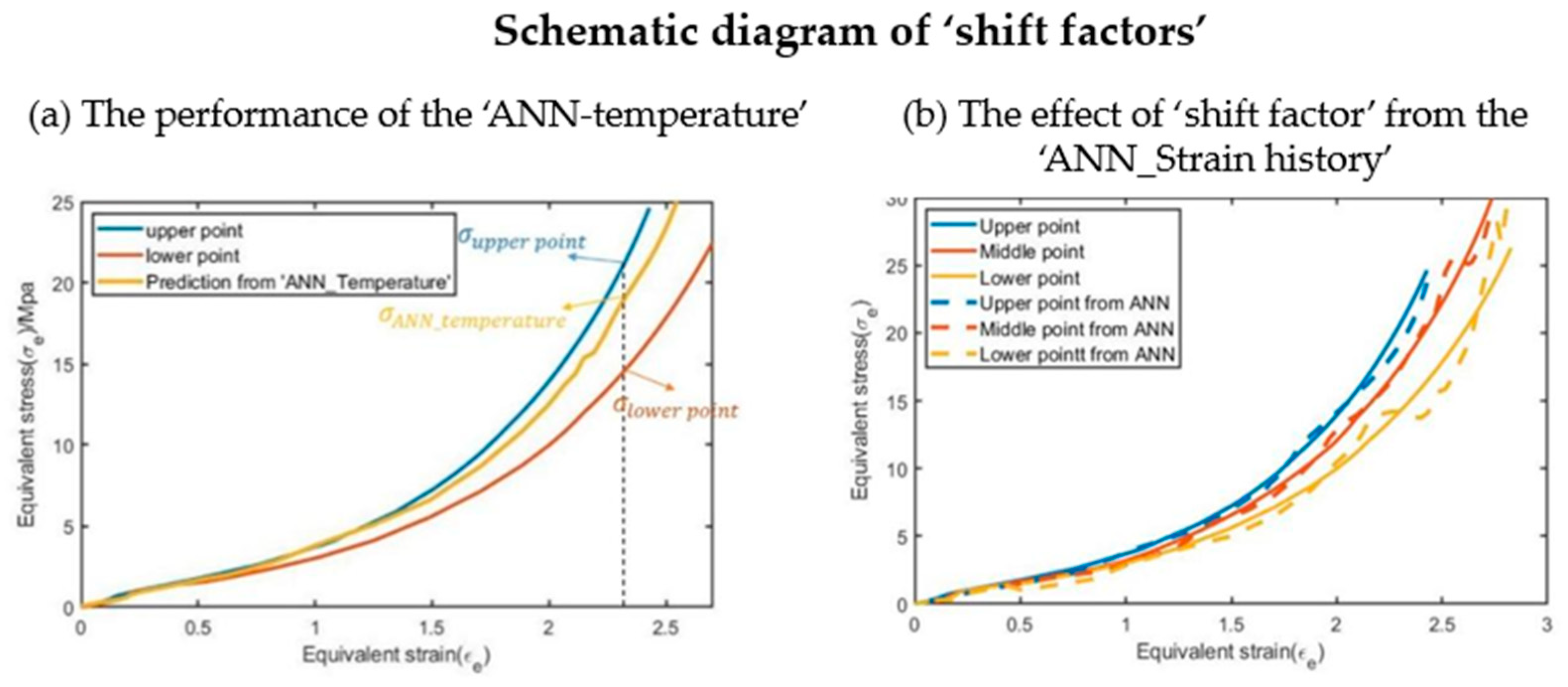
4.3. ANN_Temperature
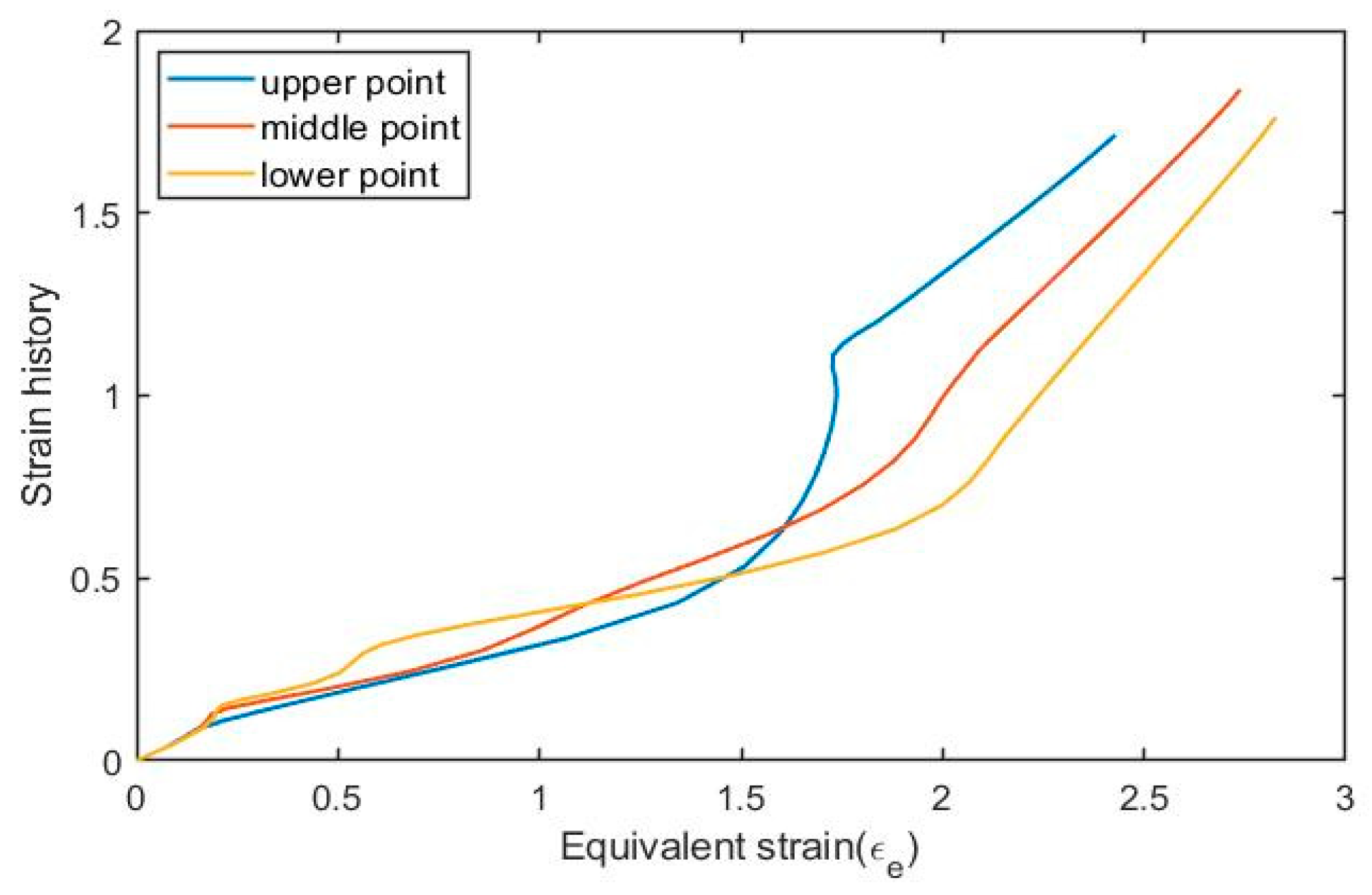
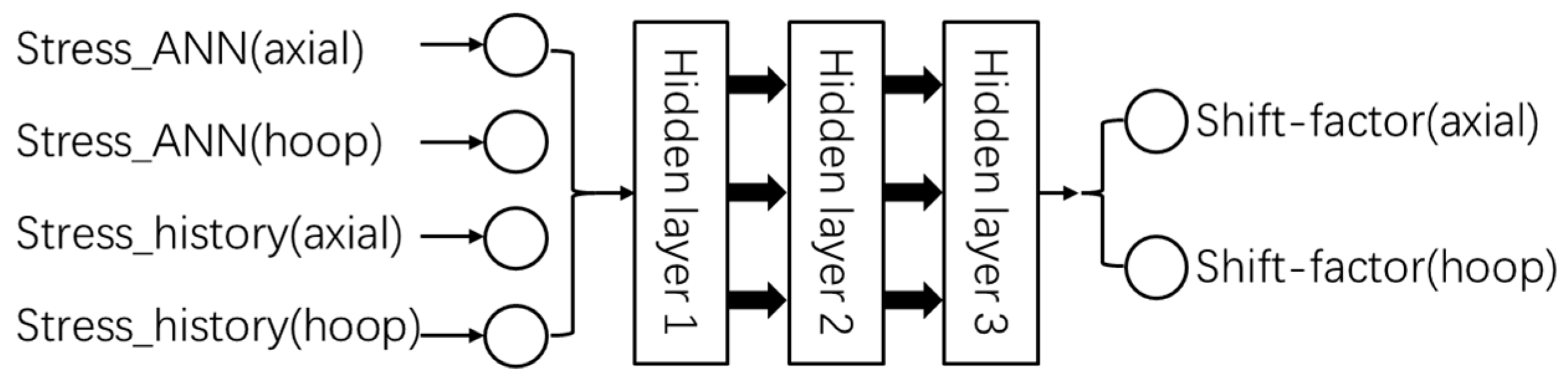
4.4. ANN_Strain History
4.5. A Walk-Through of the Hybrid ANN-Based Constitutive Model
5. Training the ANN Part of the Constitutive Model
5.1. Detailed Training Settings
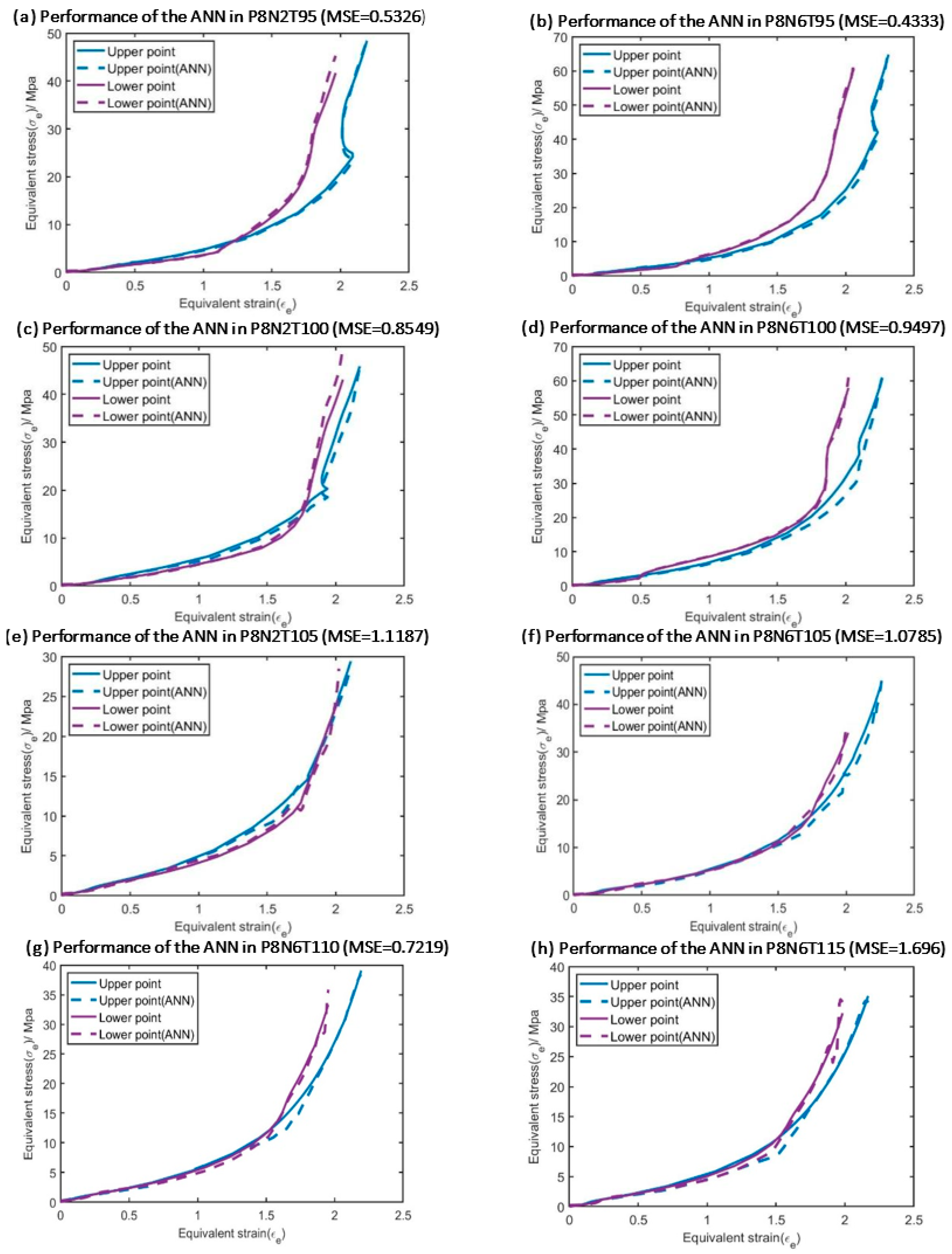
5.2. Validation in Testing Database
6. Validation and Comparison
6.1. Implementation in Abaqus
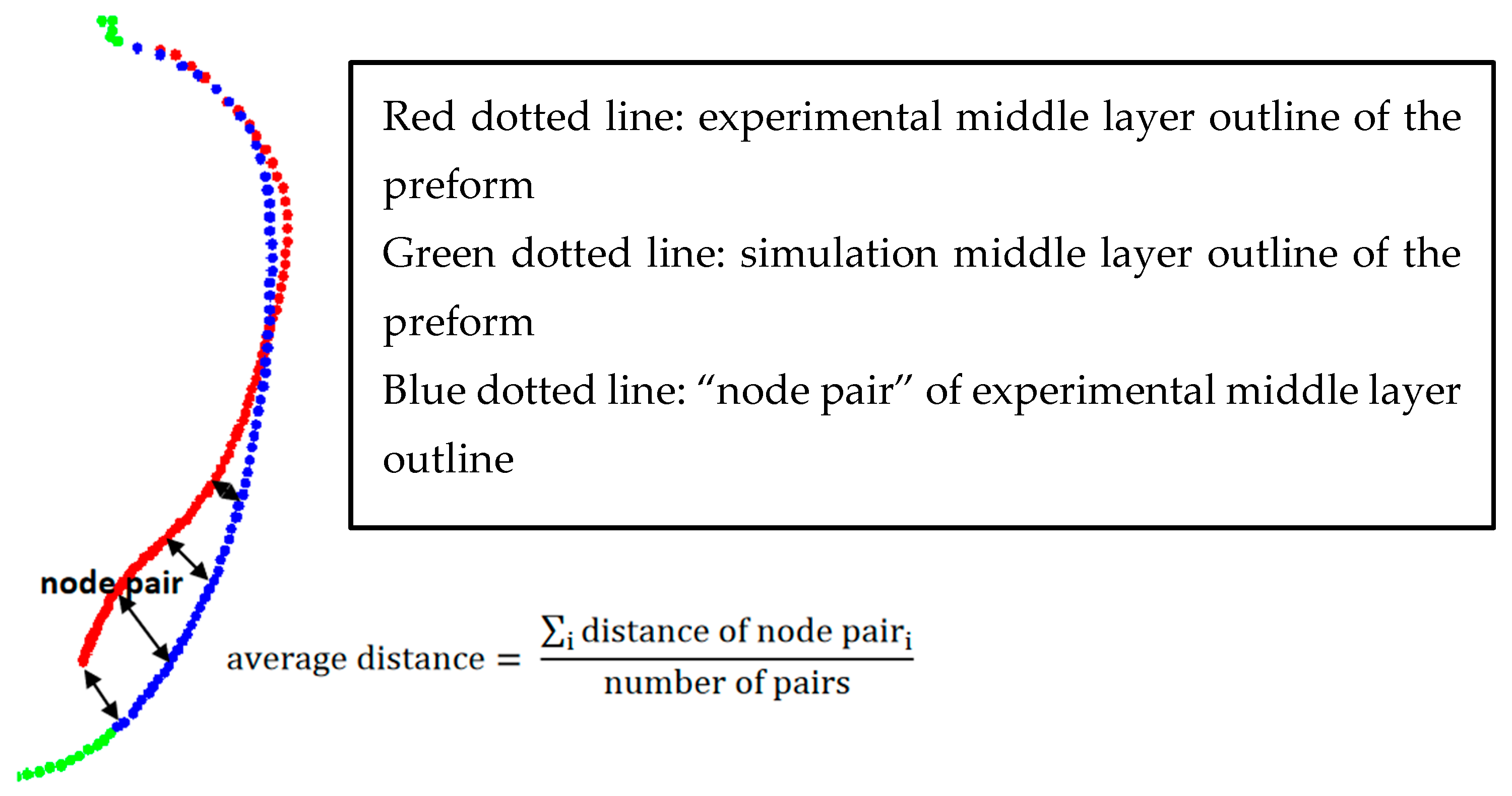
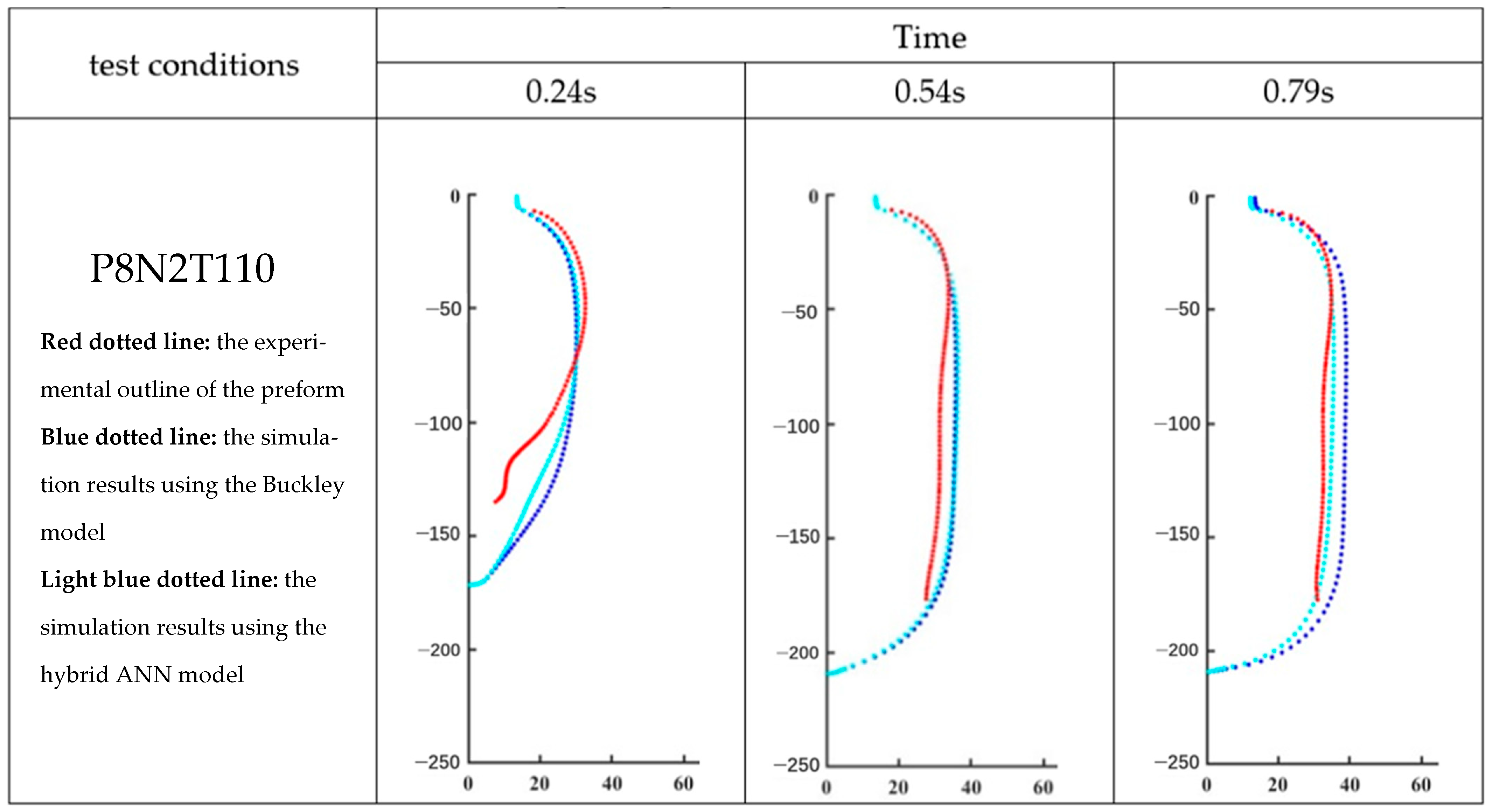
6.2. Free Blow Validation
7. Discussion
8. Conclusions
- A new semi-automatic experimental rig has been developed enabling a rich data set of stress–strain curves (850 strain–stress curves) directly from preforms under conditions representative of the stretch blow molding process.
- A hybrid ANN combining an Eyring function proposed by Buckley et al. for capturing the small-strain behavior in parallel with an ANN model for capturing the temperature-dependent large-strain nonlinear viscoelastic behavior of PET has been developed and validated over a range of conditions typically used in the stretch blow molding process.
- The ANN has demonstrated the ability to be utilized in a simulation of stretch blow molding (without mold), thus validating its stability in a load-controlled scenario and its ability to predict the blowing behavior of a preform.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Bond stretching part | shear activation volume Vs (m3 mol−1) | 2.814 × 10−3 |
| pressure activation volume Vp (m3 mol−1) | 0.526 × 10−3 | |
| reference viscosity (Mpa) | 1.8165 | |
| limiting temperature (K) | 342.61 | |
| viscosity constant Cv (K) | 56.09 |
References
- Buckley, C.P.; Jones, D.C.; Jones, D.P. Hot-drawing of poly(ethylene terephthalate) under biaxial stress: Application of a three-dimensional glass-rubber constitutive model. Polymer 1996, 37, 2403–2414. [Google Scholar] [CrossRef]
- Buckley, C.P. Glass-rubber constitutive model for amorphous polymers near the glass transition. Polymer 1995, 36, 3301–3312. [Google Scholar] [CrossRef]
- Adams, A.M.; Buckley, C.P.; Jones, D.P. Biaxial hot drawing of poly(ethylene terephthalate): Measurements and modelling of strain-stiffening. Polymer 2000, 41, 771–786. [Google Scholar] [CrossRef]
- Yan, S. Modelling the Constitutive Behaviour of Poly (ethylene terephthalate) for the Stretch Blow Moulding Process. Ph.D. Thesis, Queen’s University Belfast, Belfast, Northern Ireland, 2014. [Google Scholar]
- Buckley, C.P.; Lew, C.Y. Biaxial hot-drawing of poly(ethylene terephthalate): An experimental study spanning the processing range. Polymer 2011, 52, 1803–1810. [Google Scholar] [CrossRef]
- Tan, C.W. Biaxial deformation of PET at conditions applicable to stretch blow moulding and the subsequent effect on mechanical properties. Ph.D. Thesis, Queen’s University Belfast, Belfast, Northern Ireland, 2008. [Google Scholar]
- Teng, F.; Menary, G.; Malinov, S.; Yan, S.; Stevens, J.B. Predicting the multiaxial stress-strain behavior of polyethylene terephthalate (PET) at different strain rates and temperatures above Tg by using an Artificial Neural Network. Mech. Mater. 2022, 165, 104175. [Google Scholar] [CrossRef]
- Teng, F.; Menary, G.; Malinov, S.; Yan, S. Estimation of Stress-Strain behavior of polyethylene terephthalate(PET) at differerent strain rates by Artificial Neural Network under simultaneous stretch scenario. In Proceedings of the 24th International Conference on Material Forming, Online, 14–16 April 2021; pp. 1–11. [Google Scholar] [CrossRef]
- Menary, G.H.; Tan, C.W.; Armstrong, C.G.; Martin, P.J. Biaxial Deformation and Experimental Study of PET at Conditions Applicable to Stretch Blow Molding. Polym. Eng. Sci. 2012, 52, 671–688. [Google Scholar] [CrossRef]
- Liu, X.; Gasco, F.; Goodsell, J.; Yu, W. Initial failure strength prediction of woven composites using a new yarn failure criterion constructed by deep learning. Compos. Struct. 2019, 230, 111505. [Google Scholar] [CrossRef]
- Zhang, A.; Mohr, D. Using neural networks to represent von Mises plasticity with isotropic hardening. Int. J. Plast. 2020, 132, 102732. [Google Scholar] [CrossRef]
- Ghaboussi, J.; Garrett, J.H., Jr.; Wu, X. Knowledge-Based Modeling of material behavior with neural network. J. Eng. Mech. 1991, 117, 132–153. [Google Scholar] [CrossRef]
- Settgast, C.; Hütter, G.; Kuna, M.; Abendroth, M. A hybrid approach to simulate the homogenized irreversible elastic-plastic deformations and damage of foams by neural networks. Int. J. Plast. 2020, 126, 102624. [Google Scholar] [CrossRef]
- Pandya, K.S.; Roth, C.C.; Mohr, D. Strain rate and temperature dependent fracture of aluminum alloy 7075: Experiments and neural network modeling. Int. J. Plast. 2020, 135, 102788. [Google Scholar] [CrossRef]
- Li, X.; Roth, C.C.; Mohr, D. Machine-learning based temperature- and rate-dependent plasticity model: Application to analysis of fracture experiments on DP steel. Int. J. Plast. 2019, 118, 320–344. [Google Scholar] [CrossRef]
- Li, X.; Roth, C.C.; Bonatti, C.; Mohr, D. Counterexample-trained neural network model of rate and temperature dependent hardening with dynamic strain aging. Int. J. Plast. 2022, 151, 103218. [Google Scholar] [CrossRef]
- Bonatti, C.; Mohr, D. On the importance of self-consistency in recurrent neural network models representing elasto-plastic solids. J. Mech. Phys. Solids. 2022, 158, 104697. [Google Scholar] [CrossRef]
- Diamantopoulou, M.; Karathanasopoulos, N.; Mohr, D. Stress-strain response of polymers made through two-photon lithography: Micro-scale experiments and neural network modeling. Addit. Manuf. 2021, 47, 102266. [Google Scholar] [CrossRef]
- Jordan, B.; Gorji, M.B.; Mohr, D. Neural network model describing the temperature- and rate-dependent stress-strain response of polypropylene. Int. J. Plast. 2020, 135, 102811. [Google Scholar] [CrossRef]
- Jang, D.P.; Fazily, P.; Yoon, J.W. Machine learning-based constitutive model for J2- plasticity. Int. J. Plast. 2021, 138, 102919. [Google Scholar] [CrossRef]
- Kessler, B.S.; El-Gizawy, A.S.; Smith, D.E. Incorporating neural network material models within finite element analysis for rheological behavior prediction. J. Press. Vessel Technol. Trans. ASME 2007, 129, 58–65. [Google Scholar] [CrossRef]
- Simo, J.C.; Taylor, R.L. A return mapping algorithm for plane stress elastoplasticity. Int. J. Numer. Methods Eng. 1986, 22, 649–670. [Google Scholar] [CrossRef]
- Salomeia, Y.M.; Menary, G.H.; Armstrong, C.G. Instrumentation and modelling of the stretch blow moulding process. Int. J. Mater. Form. 2010, 3, 591–594. [Google Scholar] [CrossRef]
- Benham, P.P.; Crawford, R.J.; Armstrong, C.G. Mechanics of Engineering Materials, 2nd ed.; Longman Group: London, UK, 1996. [Google Scholar]
- Salomeia, Y.; Menary, G.H.; Armstrong, C.G.; Nixon, J.; Yan, S. Measuring and modelling air mass flow rate in the injection stretch blow moulding process. Int. J. Mater. Form. 2016, 9, 531–545. [Google Scholar] [CrossRef]
- Menary, G.H.; Armstrong, C.G.; Crawford, R.J.; Mcevoy, J.P. Modelling of poly (ethylene terephthalate) in injection stretch–blow moulding. Plast. Rubber Compos. 2013, 8011, 360–370. [Google Scholar] [CrossRef]
- Buckley, C.P.; Dooling, P.J.; Harding, J.; Ruiz, C. Deformation of thermosetting resins at impact rates of strain. Part 2: Constitutive model with rejuvenation. J. Mech. Phys. Solids 2004, 52, 2355–2377. [Google Scholar] [CrossRef]
- Halsey, G.; White, H.J.; Eyring, H. Mechanical Properties of Textiles, I. Text. Res. J. 1945, 15, 295–311. [Google Scholar] [CrossRef]
- Tammann, G.; Hesse, W. Die Abhängigkeit der Viscosität von der Temperatur bie unterkühlten Flüssigkeiten. Z. Für Anorg. Und Allg. Chem. 1926, 156, 245–257. [Google Scholar] [CrossRef]
- Fulcher, G.S. Analysis of Recent Measurements of the Viscosity of Glasses. J. Am. Ceram. Soc. 1925, 8, 339–355. [Google Scholar] [CrossRef]
- Arrhenius, S. Über die Reaktionsgeschwindigkeit bei der Inversion von Rohrzucker durch Säuren. Z. Für Phys. Chem. 1889, 4U, 226–248. [Google Scholar] [CrossRef]
- Li, H.X.; Buckley, C.P. Evolution of strain localization in glassy polymers: A numerical study. Int. J. Solids Struc. 2009, 46, 1607–1623. [Google Scholar] [CrossRef]
- Edwards, S.F.; Vilgis, T. The effect of entanglements in rubber elasticity. Polymer 1986, 27, 483–492. [Google Scholar] [CrossRef]
- Zhang, P.; Yin, Z.Y.; Jin, Y.F. State-of-the-Art Review of Machine Learning Applications in Constitutive Modeling of Soils. Arch. Comput. Methods Eng. 2021, 28, 3661–3686. [Google Scholar] [CrossRef]
- Hagan, M.T.; Demuth, H.B.; Beale, M.H. Neural Networks Design, 2nd ed. 2006. Available online: https://hagan.okstate.edu/nnd.html?utm_source (accessed on 13 November 2024).
- Mehrpouya, M.; Gisario, A.; Rahimzadeh, A.; Barletta, M. An artificial neural network model for laser transmission welding of biodegradable polyethylene terephthalate/polyethylene vinyl acetate (PET/PEVA) blends. Int. J. Adv. Manuf. Technol. 2019, 102, 1497–1507. [Google Scholar] [CrossRef]
- Lefik, M.; Schrefler, B.A. Artificial neural network as an incremental non-linear constitutive model for a finite element code. Comput. Methods Appl. Mech. Eng. 2003, 192, 3265–3283. [Google Scholar] [CrossRef]
- Hashash, Y.M.A.; Jung, S.; Ghaboussi, J. Numerical implementation of a neural network based material model in finite element analysis. Int. J. Numer. Methods Eng. 2004, 59, 989–1005. [Google Scholar] [CrossRef]
- Gorji, M.B.; Mohr, D. Towards neural network models for describing the large deformation behavior of sheet metal. IOP Conf. Ser. Mater. Sci. Eng. 2019, 651, 012102. [Google Scholar] [CrossRef]
- Tao, F.; Liu, X.; Du, H.; Yu, W. Learning composite constitutive laws via coupling Abaqus and deep neural network. Compos. Struct. 2021, 272, 114137. [Google Scholar] [CrossRef]
- Le, V.; Caracoglia, L. A neural network surrogate model for the performance assessment of a vertical structure subjected to non-stationary, tornadic wind loads. Comput. Struct. 2020, 231, 106208. [Google Scholar] [CrossRef]
- Pal, S.; Naskar, K. Machine learning model predict stress-strain plot for Marlow hyperelastic material design. Mater. Today Commun. 2021, 27, 102213. [Google Scholar] [CrossRef]
- Kim, K.G. Deep learning book review. Nature 2019, 29, 1–73. [Google Scholar] [CrossRef]
- Nixon, J.; Menary, G.H.; Yan, S. Free-stretch-blow investigation of poly(ethylene terephthalate) over a large process window. Int. J. Mater. Form. 2017, 10, 765–777. [Google Scholar] [CrossRef]
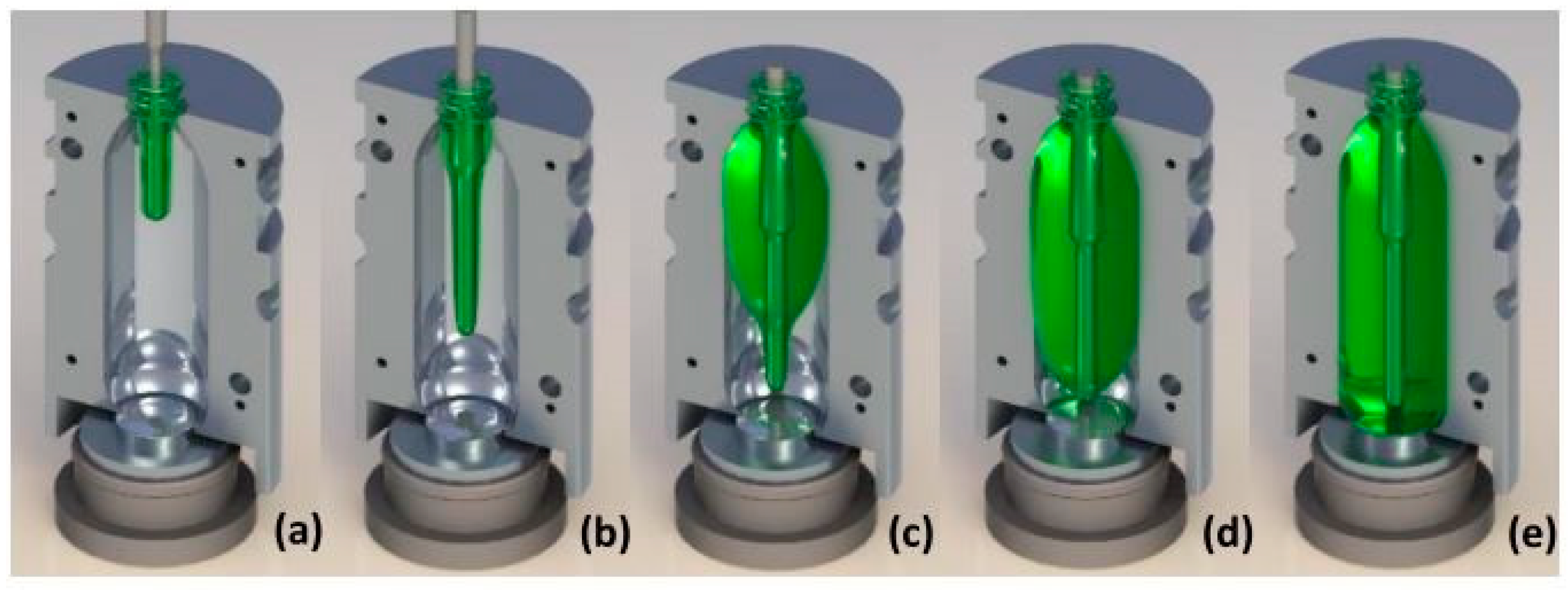
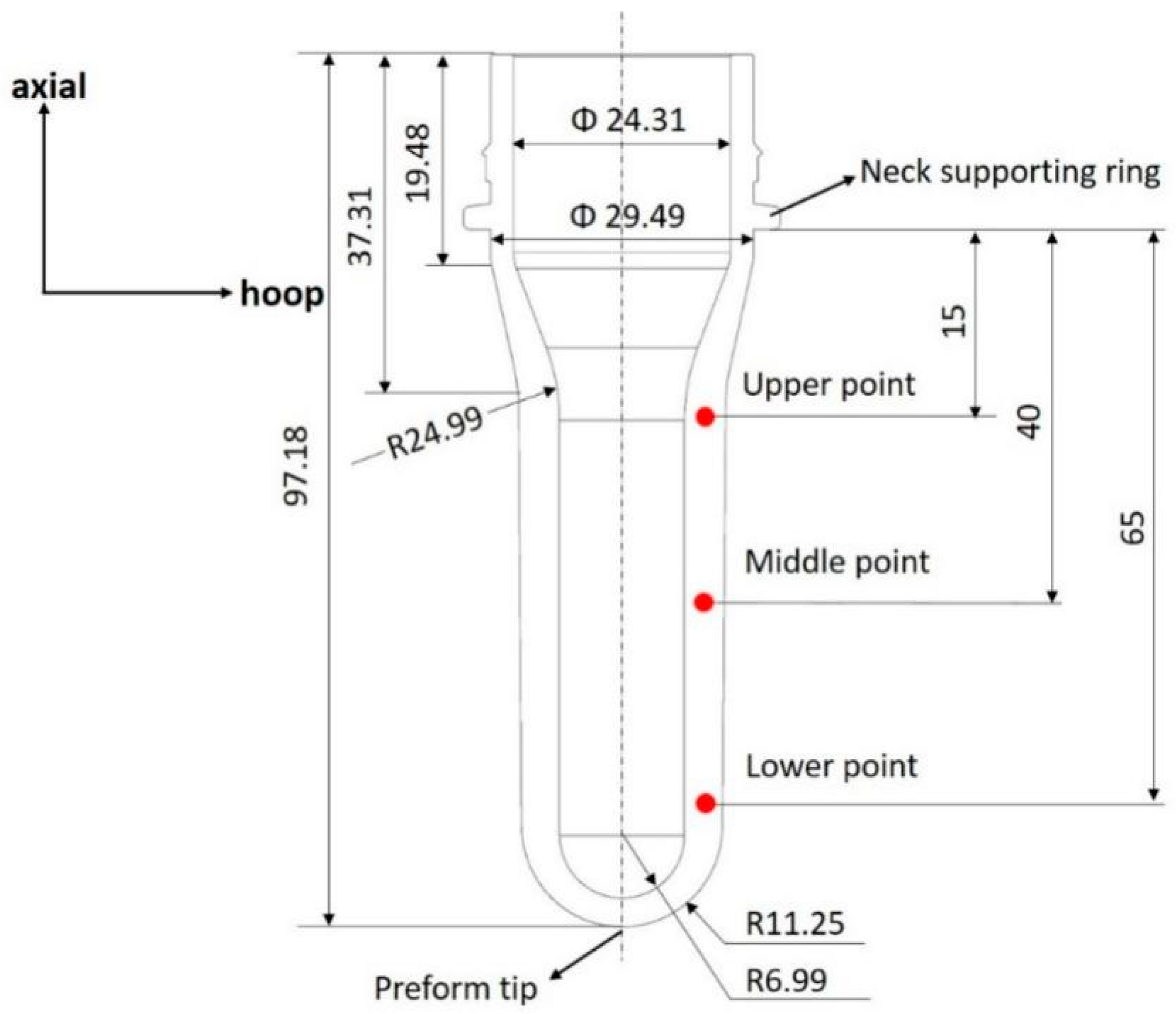

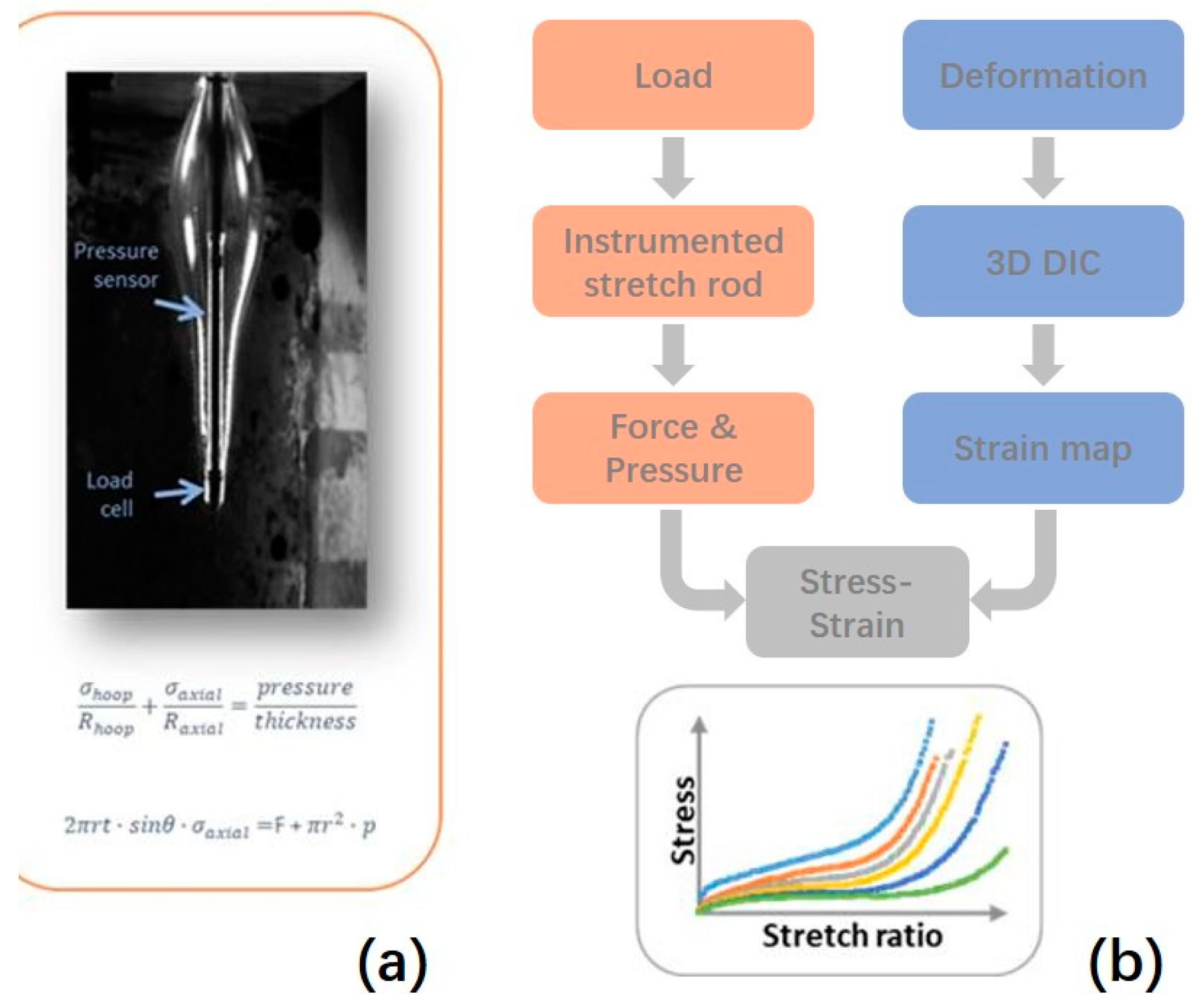

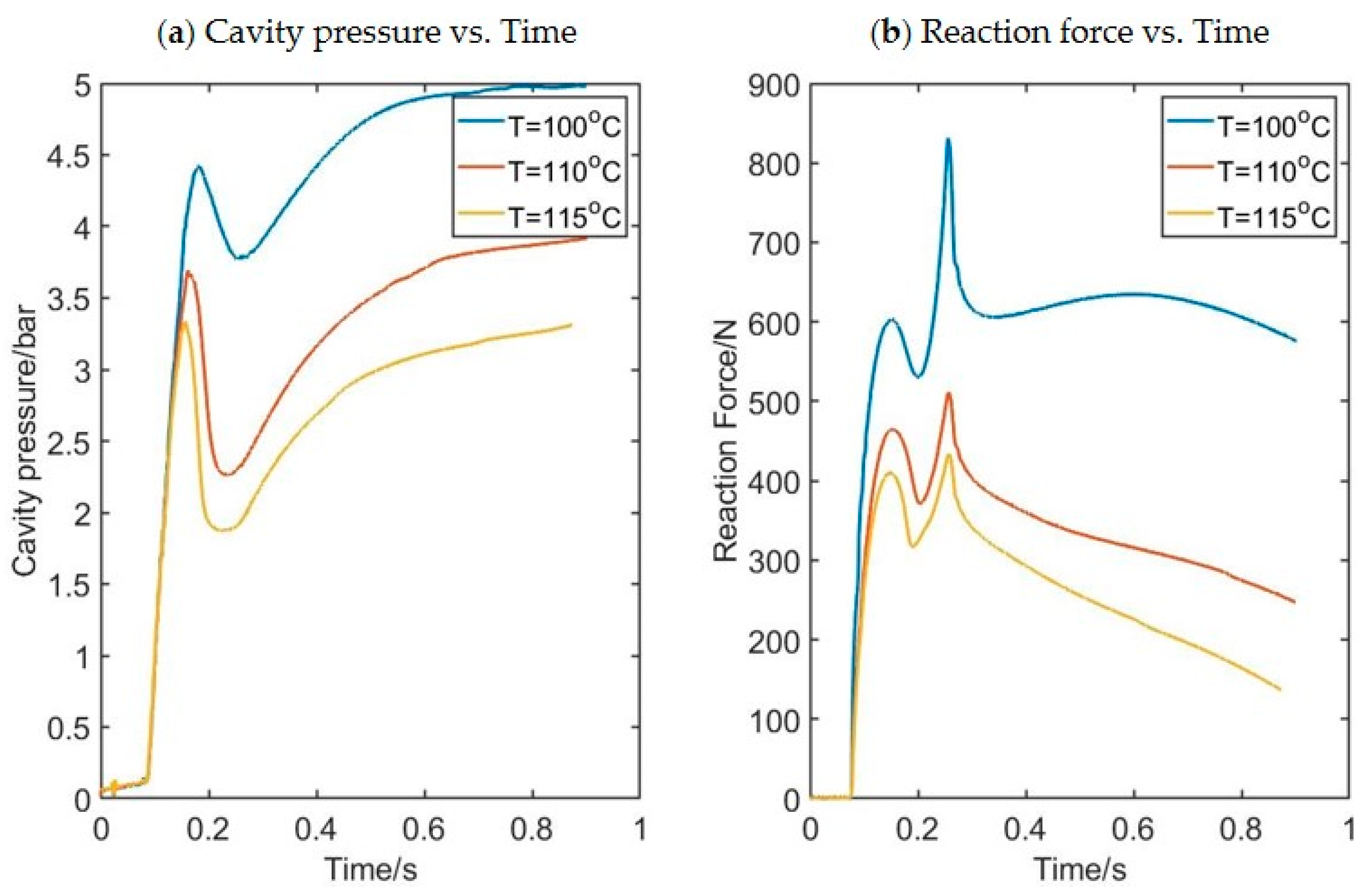
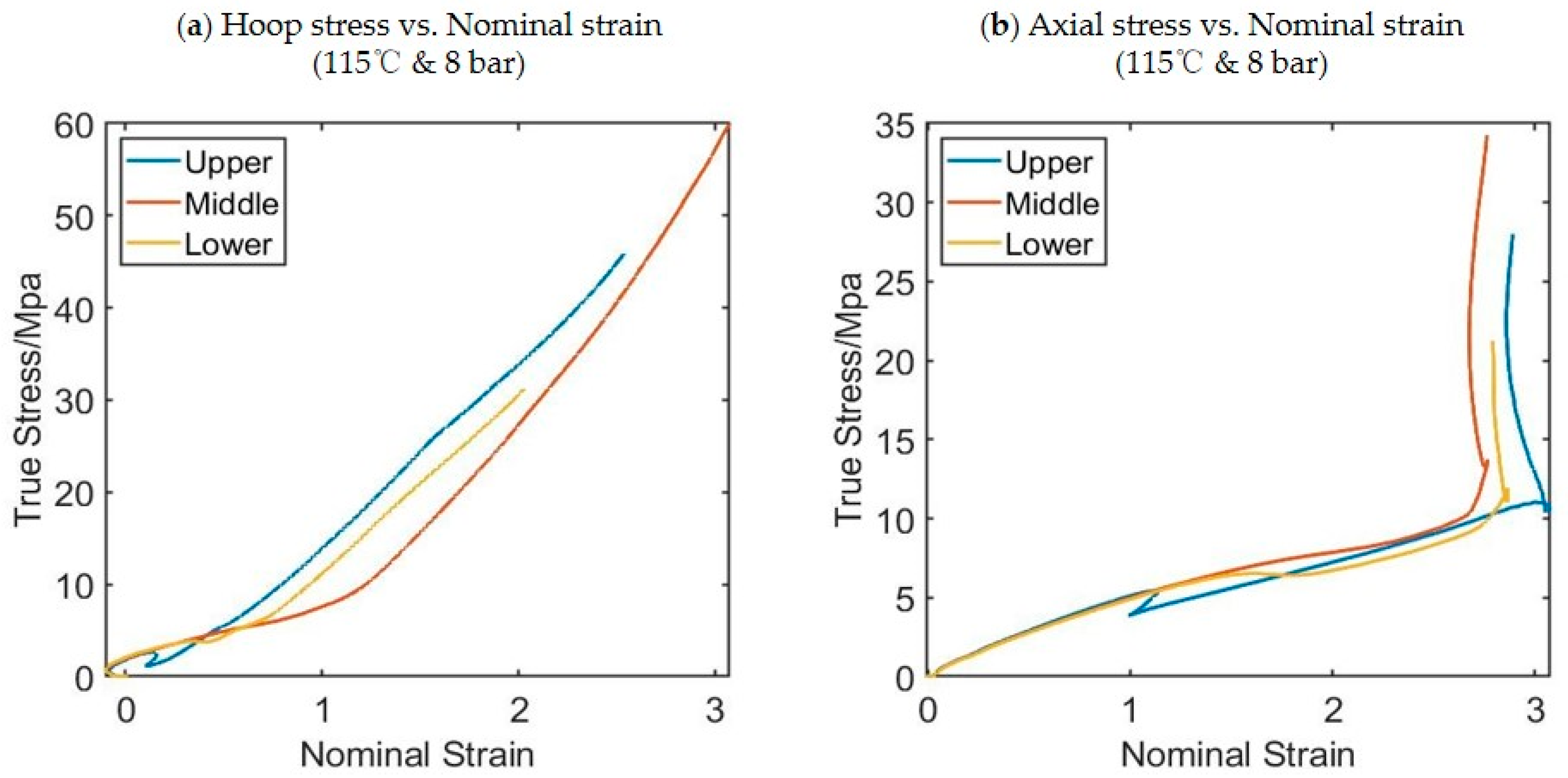
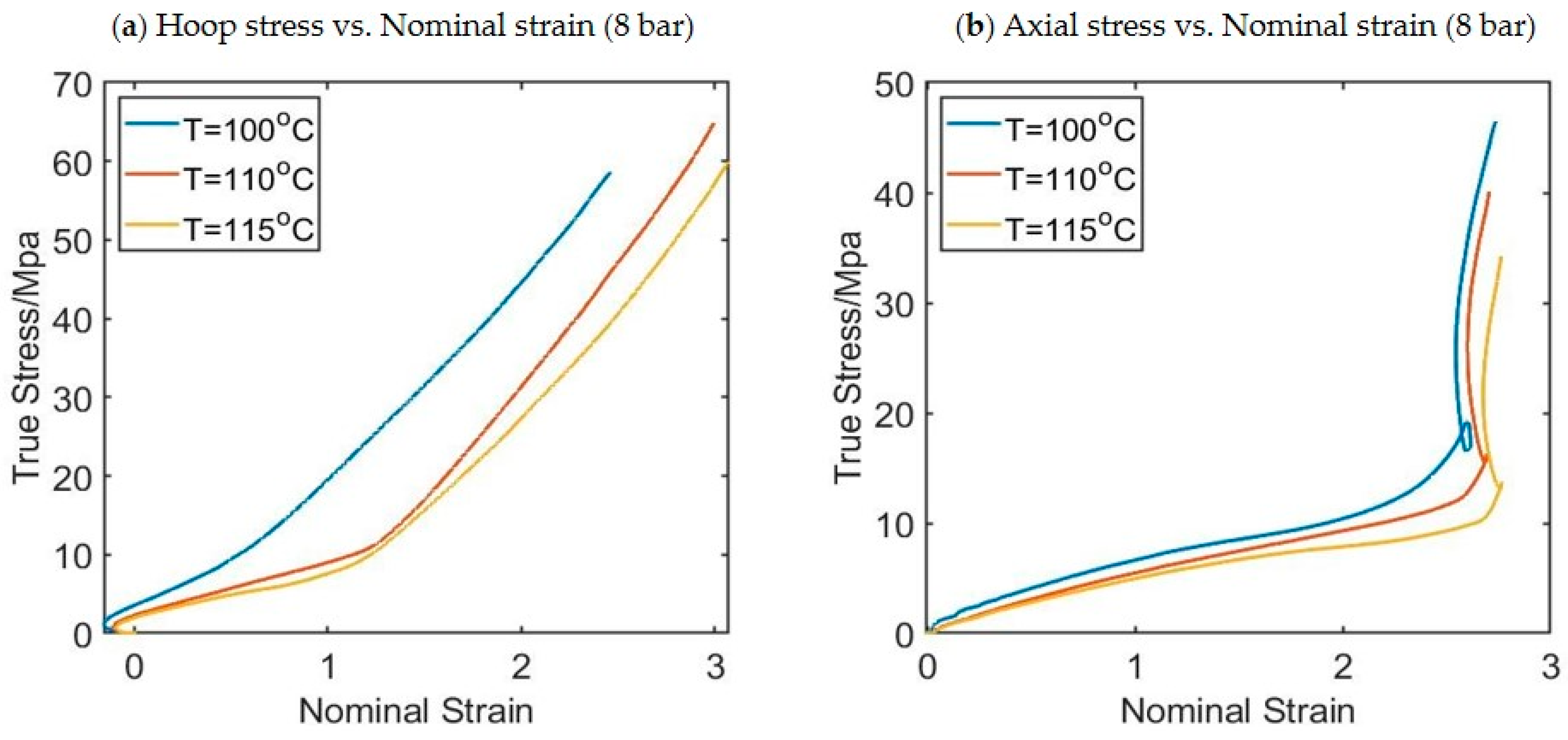







| Experiment Label (Press/Flow/Temp) | Pressure, P (bar) | Flow Index, N (1–6) | Temperature Setting of Oil Bath (°C) |
|---|---|---|---|
| P8N2T95 | 8 | 2 | 95 |
| P8N6T95 | 8 | 6 | 95 |
| P8N2T100 | 8 | 2 | 100 |
| P8N6T100 | 8 | 6 | 100 |
| P8N2T105 | 8 | 2 | 105 |
| P8N6T105 | 8 | 6 | 105 |
| P8N2T110 | 8 | 2 | 110 |
| P8N6T110 | 8 | 6 | 110 |
| P8N2T115 | 8 | 2 | 115 |
| P8N6T115 | 8 | 6 | 115 |
| Experiment Label | Mean Relative Error |
|---|---|
| P8N2T95 | 1.37% |
| P8N6T95 | 1.16% |
| P8N2T100 | 2.14% |
| P8N6T100 | 2.42% |
| P8N2T105 | 2.57% |
| P8N6T110 | 2.00% |
| P8N6T115 | 4.14% |
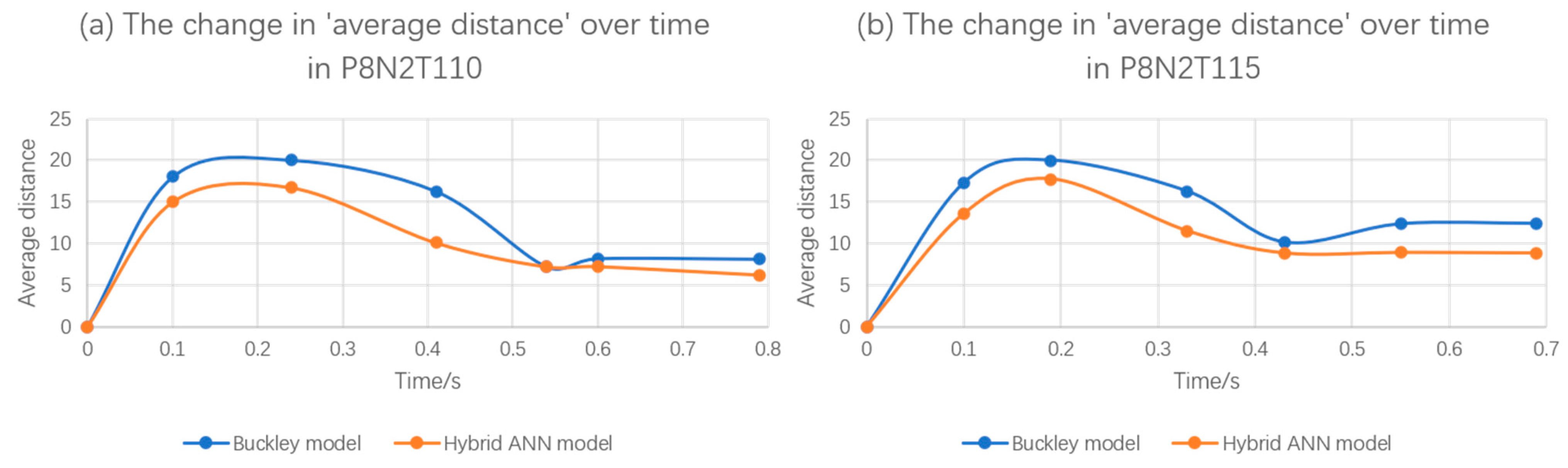
| Buckley Model Simulation | Hybrid ANN-Based Constitutive Model Simulation | |
|---|---|---|
| P8N2T110 | 8.11 | 6.21 |
| P8N2T115 | 12.39 | 8.83 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Teng, F.; Menary, G.; Yan, S.; Nixon, J.; Stevens, J.B. A Hybrid Artificial Neural Network Approach for Modeling the Behavior of Polyethylene Terephthalate (PET) Under Conditions Applicable to Stretch Blow Molding. Polymers 2025, 17, 1067. https://doi.org/10.3390/polym17081067
Teng F, Menary G, Yan S, Nixon J, Stevens JB. A Hybrid Artificial Neural Network Approach for Modeling the Behavior of Polyethylene Terephthalate (PET) Under Conditions Applicable to Stretch Blow Molding. Polymers. 2025; 17(8):1067. https://doi.org/10.3390/polym17081067
Chicago/Turabian StyleTeng, Fei, Gary Menary, Shiyong Yan, James Nixon, and John Boyet Stevens. 2025. "A Hybrid Artificial Neural Network Approach for Modeling the Behavior of Polyethylene Terephthalate (PET) Under Conditions Applicable to Stretch Blow Molding" Polymers 17, no. 8: 1067. https://doi.org/10.3390/polym17081067
APA StyleTeng, F., Menary, G., Yan, S., Nixon, J., & Stevens, J. B. (2025). A Hybrid Artificial Neural Network Approach for Modeling the Behavior of Polyethylene Terephthalate (PET) Under Conditions Applicable to Stretch Blow Molding. Polymers, 17(8), 1067. https://doi.org/10.3390/polym17081067






