Analysis on Adhesively-Bonded Joints of FRP-steel Composite Bridge under Combined Loading: Arcan Test Study and Numerical Modeling
Abstract
:1. Introduction
2. Tensile-Shear Loading Device (Arcan Test Device)
- Shear stress τ: due to the composite action between FRP deck and steel girder in the longitudinal direction of bridge, the deck and steel girder trend to bend together to carry the traffic load. Thus, the adhesive joints are under the shear stress condition to transfer the load from the FRP deck to the steel girder, as shown in Figure 1a;
- Tensile stress σ: in the transverse direction of bridge, loading on other traffic lanes causes up-lift forces on adhesive joints, which results in the tensile stress (peeling stress), as shown in Figure 1b;
- Combination of shear stress and tensile stress with different contribution ratios.


| Product name | Total weight (g/m2) | Weight uniformity (g/m2) | ||||
|---|---|---|---|---|---|---|
| Yarn roving | Knit yarn | |||||
| 0° | +45° | 90° | −45° | |||
| EQX 1200 | 1,193 | 283 | 300 | 300 | 300 | 10 |


3. Experiment

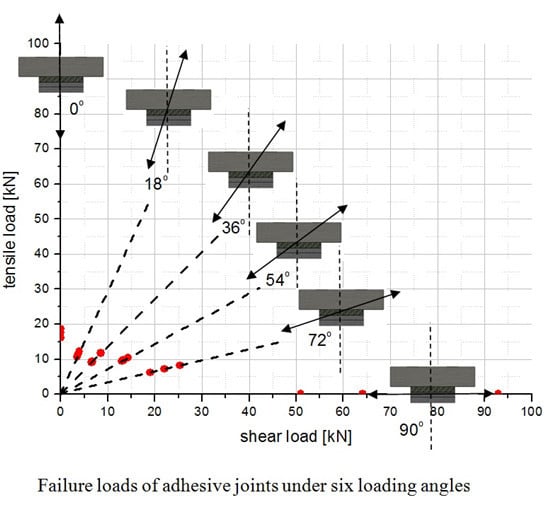
4. Results and Discussion
| Loading angle | Failure load (MPa) | Average | Deviation | ||
|---|---|---|---|---|---|
| Specimen01 | Specimen02 | Specimen03 | |||
| Pure tensile | 17.53 | 16.05 | 18.72 | 17.43 | 7.94% |
| 18° angle | 12.7 | 11.2 | 11.8 | 11.9 | 6.72% |
| 36° angle | 11.2 | 14.6 | 11.8 | 12.53 | 16.5% |
| 54° angle | 16.5 | 17.7 | 16.1 | 16.77 | 5.55% |
| 72° angle | 26.6 | 20.0 | 23.2 | 23.27 | 14.3% |
| Pure shear | 51.0 | 92.9 | 64.1 | 69.3 | 34.0% |








5. FE Analysis
5.1. FE Model



| Property | FRP Laminates |
|---|---|
| Elastic modulus 11 (MPa) | 16,609 |
| Elastic modulus 22 (MPa) | 16,609 |
| Elastic modulus 33 (MPa) | 11,000 |
| Poisson ratio 12 | 0.33 |
| Poisson ratio 23 | 0.3 |
| Poisson ratio 13 | 0.18 |
| Shear modulus 12 (MPa) | 6,986 |
| Shear modulus 23 (MPa) | 1,200 |
| Shear modulus 31 (MPa) | 1,200 |
| Adhesive | |
| Elastic modulus (MPa) | 3,400 |
| Poisson ratio | 0.37 |
| Core material | |
| Elastic modulus 11 (MPa) | 86 |
| Elastic modulus 22 (MPa) | 265 |
| Elastic modulus 33 (MPa) | 5,759 |
| Poisson ratio 12 | 0.23 |
| Poisson ratio 23 | 0.23 |
| Poisson ratio 13 | 0.49 |
| Shear modulus 12 (MPa) | 29 |
| Shear modulus 13 (MPa) | 213 |
| Shear modulus 23 (MPa) | 309 |
| Steel | |
| Elastic modulus (MPa) | 206,000 |
| Poisson ratio | 0.3 |
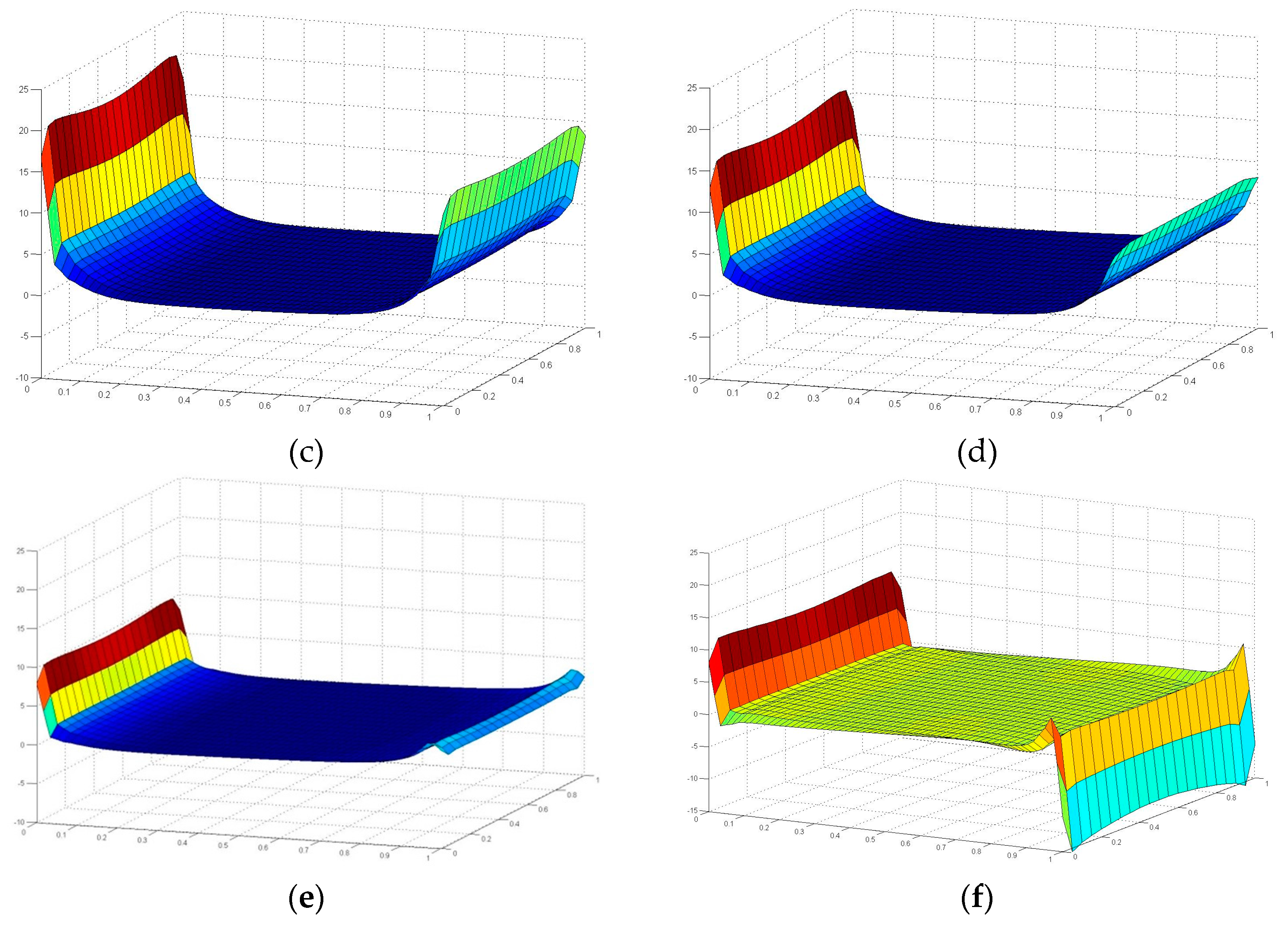
5.2. FE Results and Discussion





6. Conclusions
- (1)
- The load-bearing capacities of adhesive joints under combined loading are much lower than those of the pure tensile and pure shear loading conditions.
- (2)
- According to failure loads of adhesive joints under the four combined loading conditions, the modified failure criterion of the adhesive joint is addressed by using aquadratic ellipsoid function, which is conservative and practical for the real application of an adhesive joint between FRP decks and steel girders in bridges.
- (3)
- For adhesive joints under the shear loading condition, the failure mode is the cohesive failure (near the interface between the adhesive layer and the steel support) in the adhesive layer. However, for adhesive joints under the tensile loading and four combined loading conditions, the fracture plane is through the interface between the FRP sandwich deck element and the adhesive layer, combining with fiber breaking or FRP delamination in the FRP laminates.
- (4)
- The controllable adhesive bonding technique is essential to guarantee the reliable mechanical performance of adhesive joints.
- (5)
- The stress states on the interface between the FRP laminate and the adhesive layer under six loading angles are characterized using Finite Element modeling method, which gives a brief indication on crack initiation location and failure mode of the tested adhesive joints.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Knippers, J.; Pelke, E.; Gabler, M.; Berger, D. Bridges with glass fibre-reinforced polymer decks: The road bridge in friedberg. Struct. Eng. Int. 2010, 20, 400–404. [Google Scholar] [CrossRef]
- Sebastian, W.M.; Ross, J.; Keller, T.; Luke, S. Load response due to local and global indeterminacies of FRP-deck bridges. Compos. Eng. 2012, 43, 1727–1738. [Google Scholar] [CrossRef]
- Luke, S.; Canning, L.; Collins, S.; Knudsen, E.; Brown, P.; Taljsten, B.; Olofsson, I. Advanced composite bridge decking system—project ASSET. Struct. Eng. Int. 2002, 12, 76–79. [Google Scholar] [CrossRef]
- Keller, T.; Rothe, J.; de Castro, J.; Osei-Antwi, M. GFRP-balsa sandwich bridge deck: Concept, design, and experimental validation. J. Compos. Construct. 2014, 18, 04013043-1-6. [Google Scholar]
- Adams, R.D. Adhesive Bonding: Science, Technology And Applications; Woodhead Publishing Limited and CRC Press LLC: New York, NY/Washington, DC, USA, 2005. [Google Scholar]
- Hollaway, L.C. A review of the present and future utilisation of FRP composites in the civil infrastructure with reference to their important in-service properties. Construct. Build. Mater. 2010, 24, 2419–2445. [Google Scholar]
- Keller, T.; Vallee, T. Adhesively bonded lap joints from pultruded GFRP profiles. Part I: stress-strain analysis and failure modes. Compos. Eng. 2005, 36, 331–340. [Google Scholar] [CrossRef]
- Keller, T.; Vallee, T. Adhesively bonded lap joints from pultruded GFRP profiles. Part II: Joint strength prediction. Compos. Eng. 2005, 36, 341–350. [Google Scholar] [CrossRef]
- Vallee, T.; Keller, T. Adhesively bonded lap joints from pultruded GFRP profiles. Part III: Effects of chamfers. Compos. Eng. 2006, 37, 328–336. [Google Scholar] [CrossRef]
- Vallee, T.; Correia, J.R.; Keller, T. Probabilistic strength prediction for double lap joints composed of pultruded GFRP profiles part I: Experimental and numerical investigations. Compos. Sci. Technol. 2006, 66, 1903–1914. [Google Scholar] [CrossRef]
- Vallee, T.; Correia, J.R.; Keller, T. Probabilistic strength prediction for double lap joints composed of pultruded GFRP profiles—Part II: Strength prediction. Compos. Sci. Technol. 2006, 66, 1915–1930. [Google Scholar] [CrossRef]
- Berthet, J.F.; Yurtdas, I.; Delmas, Y.; Li, A. Evaluation of the adhesion resistance between steel and concrete by push out test. Int. J. Adhes. Adhes. 2011, 31, 75–83. [Google Scholar] [CrossRef]
- Bouazaoui, L.; Perrenot, G.; Delmas, Y.; Li, A. Experimental study of bonded steel concrete composite structures. J. Constr. Steel Res. 2007, 63, 1268–1278. [Google Scholar] [CrossRef]
- Larbi, A.S.; Ferrier, E.; Hamelin, P. Concrete to steel lap joint failure criteria under combined shear and peeling stress. J. Construct. Steel Res. 2009, 65, 386–394. [Google Scholar] [CrossRef]
- Jurkiewiez, B.; Meaud, C.; Michel, L. Non linear behaviour of steel-concrete epoxy bonded composite beams. J. Construct. Steel Res. 2011, 67, 389–397. [Google Scholar] [CrossRef]
- Bouazaoui, L.; Jurkiewiez, B.; Delmas, Y.; Li, A. Static behaviour of a full-scale steel-concrete beam with epoxy-bonding connection. Eng. Struct. 2008, 30, 1981–1990. [Google Scholar] [CrossRef]
- Meaud, C.; Jurkiewiez, B.; Ferrier, E. Steel-concrete bonding connection: An experimental study and non-linear finite element analysis. Int. J. Adhesion Adhes. 2014, 54, 131–142. [Google Scholar] [CrossRef]
- 3A Composites product data sheet. Available online: http://www.3acomposites.com/ (accessed on 3 February 2013).
- Nauticexpo Product Data Sheet. Available online: http://pdf.nauticexpo.com/pdf/vetrotex-ocv-reinforcements/quadraxial-fabrics/27891–13674-_2.html (accessed on 3 February 2013).
- Composite bridge decks. Available online: http://www.infracomposites.com (accessed on 3 February 2013).
- Créac'hcadec, R.; Sohier, L.; Cellard, C.; Gineste, B. A stress concentration-free bonded arcan tensile compression shear test specimen for the evaluation of adhesive mechanical response. Int. J. Adhes. Adhes. 2015, 61, 81–92. [Google Scholar] [CrossRef]
- El-Hajjar, R.; Haj-Ali, R. In-plane shear testing of thick-section pultruded FRP composites using a modified Arcan fixture. Compos. Eng. 2004, 35, 421–428. [Google Scholar] [CrossRef]
- Dos Santos, D.J.; Batalha, G.F.; Polimeros-Ciencia, E. Failure criterion for adhesively bonded joints using Arcan’s experimental method. Tecnologia 2014, 24, 441–445. [Google Scholar]
- Jiang, X.; Kolstein, M.H.; Bijlaard, F.S.K. Experimental and numerical study on mechanical behavior of an adhesively-bonded joint of FRP-steel composite bridge under shear loading. Compos. Struct. 2014, 108, 387–399. [Google Scholar] [CrossRef]
- Qiang, X.; Jiang, X.; Kolstein, H.; Bijlaard, F.S.K. Mechanical degradation on flexural property of glass-fiber-reinforced polymer laminates under hot/wet environment. Compos. Eng. 2015. Under review. [Google Scholar]
- Wood Handbook, Wood as an Engineering Material. Available online: http://www.woodweb.com/Resources/wood_eng_handbook/wood_handbook_fpl_2010.pdf (accessed on 3 February 2013).
- GB50017-2003 Code for Design of Steel Structures. Ministry of Construction of the People’s Republic of China: Beijing, China, 2003. (In Chinese)
© 2016 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, X.; Qiang, X.; Kolstein, H.; Bijlaard, F. Analysis on Adhesively-Bonded Joints of FRP-steel Composite Bridge under Combined Loading: Arcan Test Study and Numerical Modeling. Polymers 2016, 8, 18. https://doi.org/10.3390/polym8010018
Jiang X, Qiang X, Kolstein H, Bijlaard F. Analysis on Adhesively-Bonded Joints of FRP-steel Composite Bridge under Combined Loading: Arcan Test Study and Numerical Modeling. Polymers. 2016; 8(1):18. https://doi.org/10.3390/polym8010018
Chicago/Turabian StyleJiang, Xu, Xuhong Qiang, Henk Kolstein, and Frans Bijlaard. 2016. "Analysis on Adhesively-Bonded Joints of FRP-steel Composite Bridge under Combined Loading: Arcan Test Study and Numerical Modeling" Polymers 8, no. 1: 18. https://doi.org/10.3390/polym8010018
APA StyleJiang, X., Qiang, X., Kolstein, H., & Bijlaard, F. (2016). Analysis on Adhesively-Bonded Joints of FRP-steel Composite Bridge under Combined Loading: Arcan Test Study and Numerical Modeling. Polymers, 8(1), 18. https://doi.org/10.3390/polym8010018