Assessing the Sensitivity of Site-Specific Lime and Gypsum Recommendations to Soil Sampling Techniques and Spatial Density of Data Collection in Australian Agriculture: A Pedometric Approach
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Design
2.2. Investigation Site
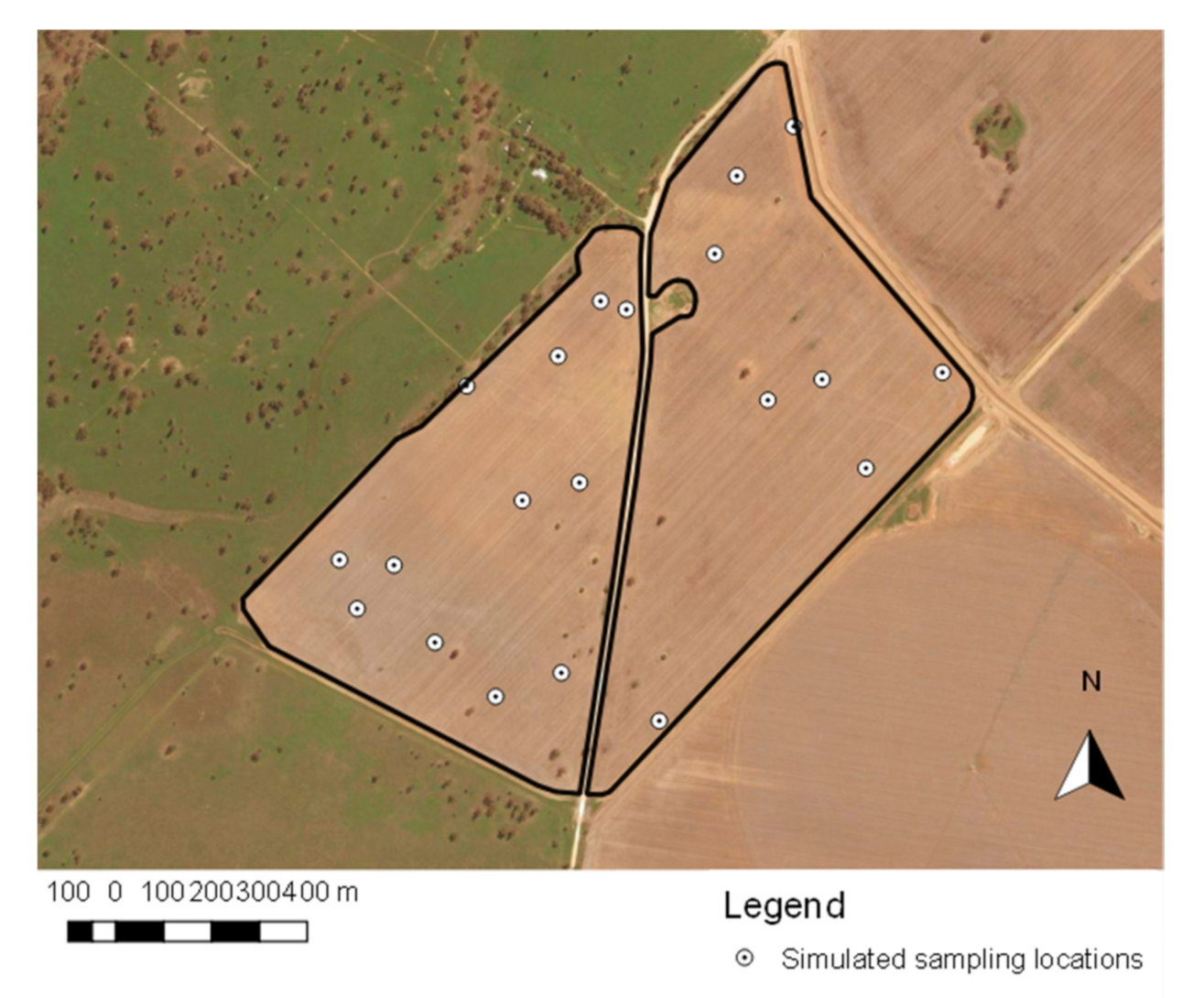
2.3. Sampling Methods
2.4. Proximally Sensed Environmental Covariates
2.5. Spatial Prediction Methods
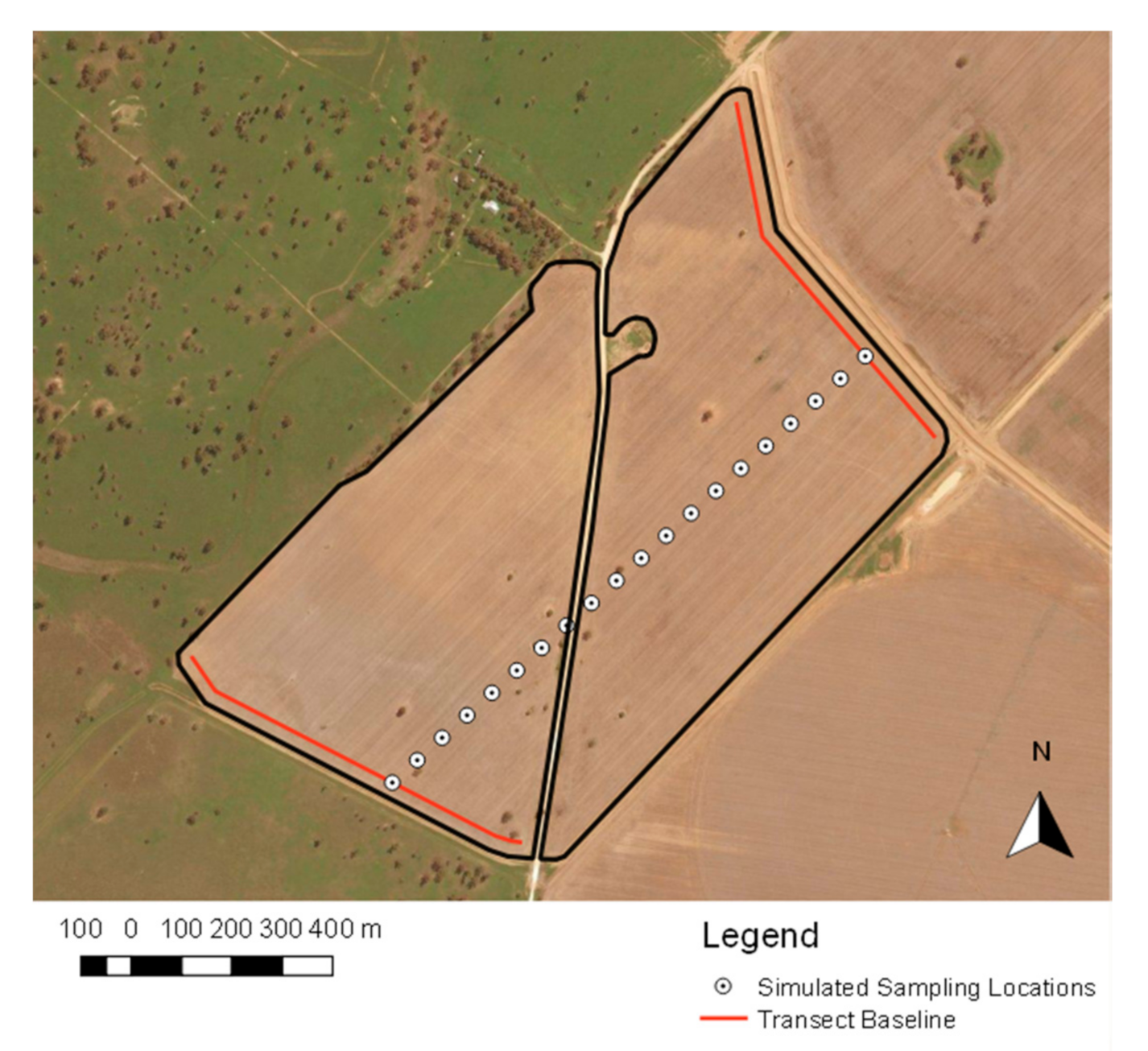
2.5.1. Random Transect Sampling
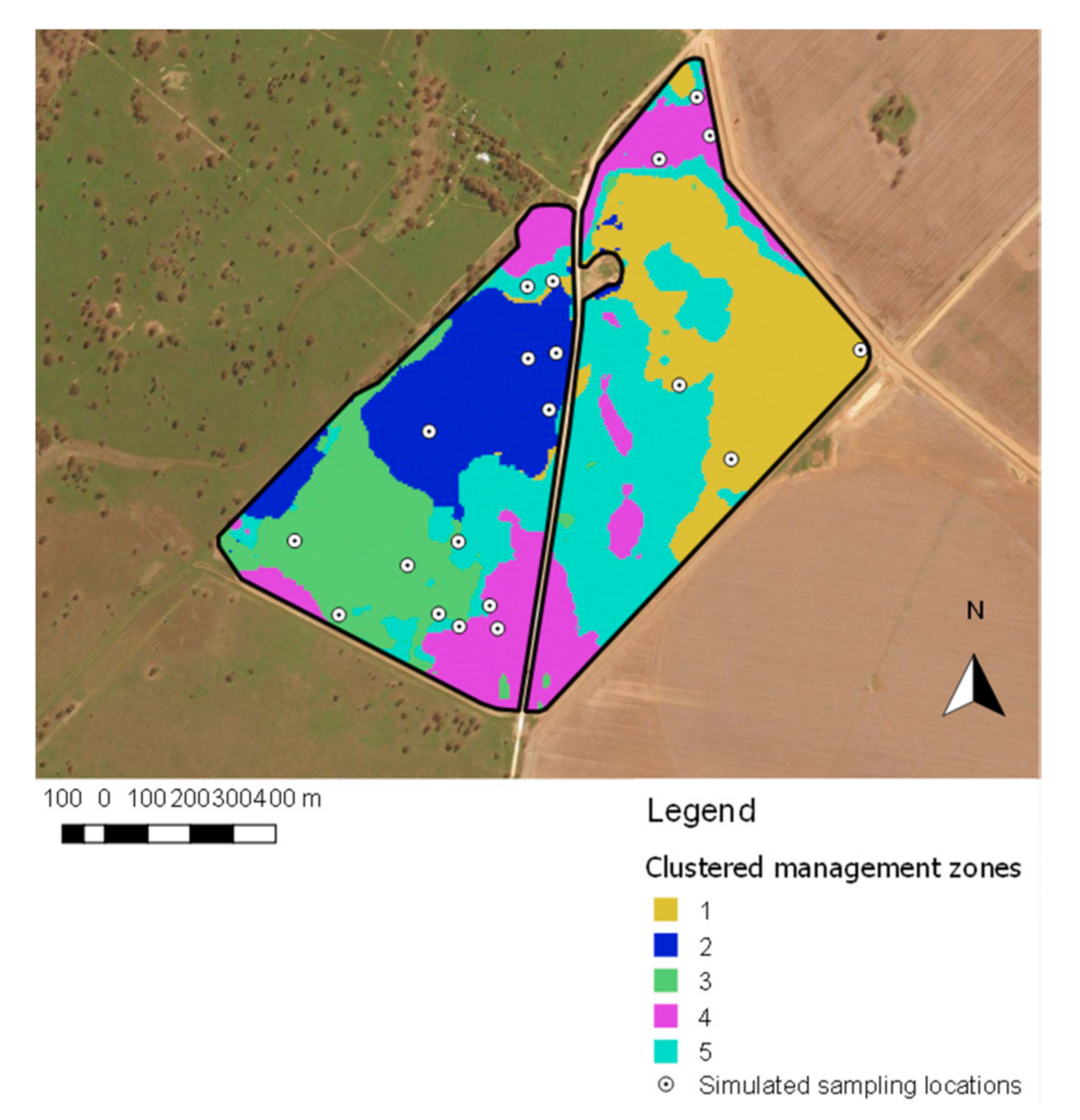
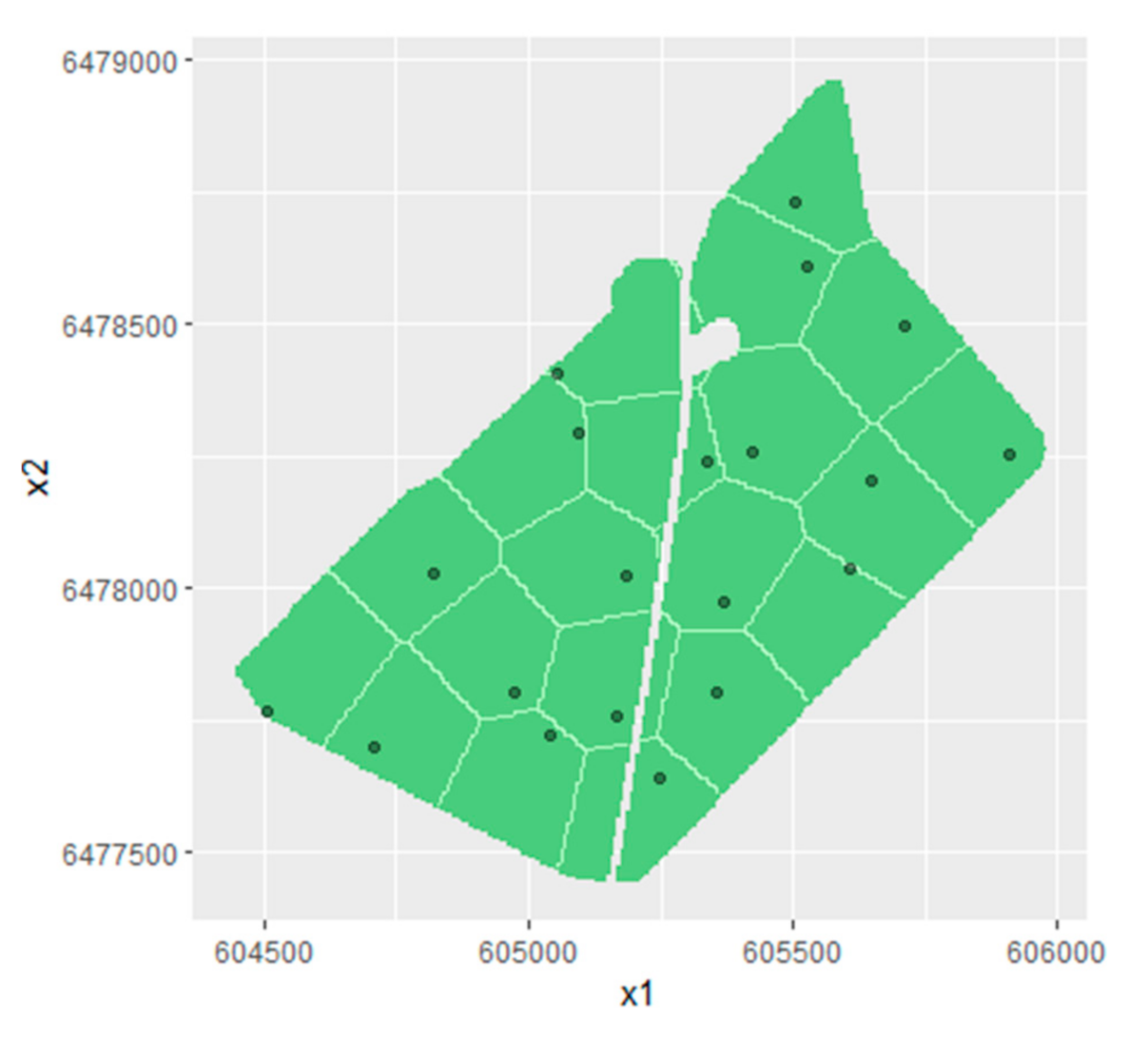
2.5.2. Management Zone Sampling
2.5.3. Ordinary Kriging
2.5.4. Regression Kriging
2.6. Amendment Requirement Calculations
3. Results
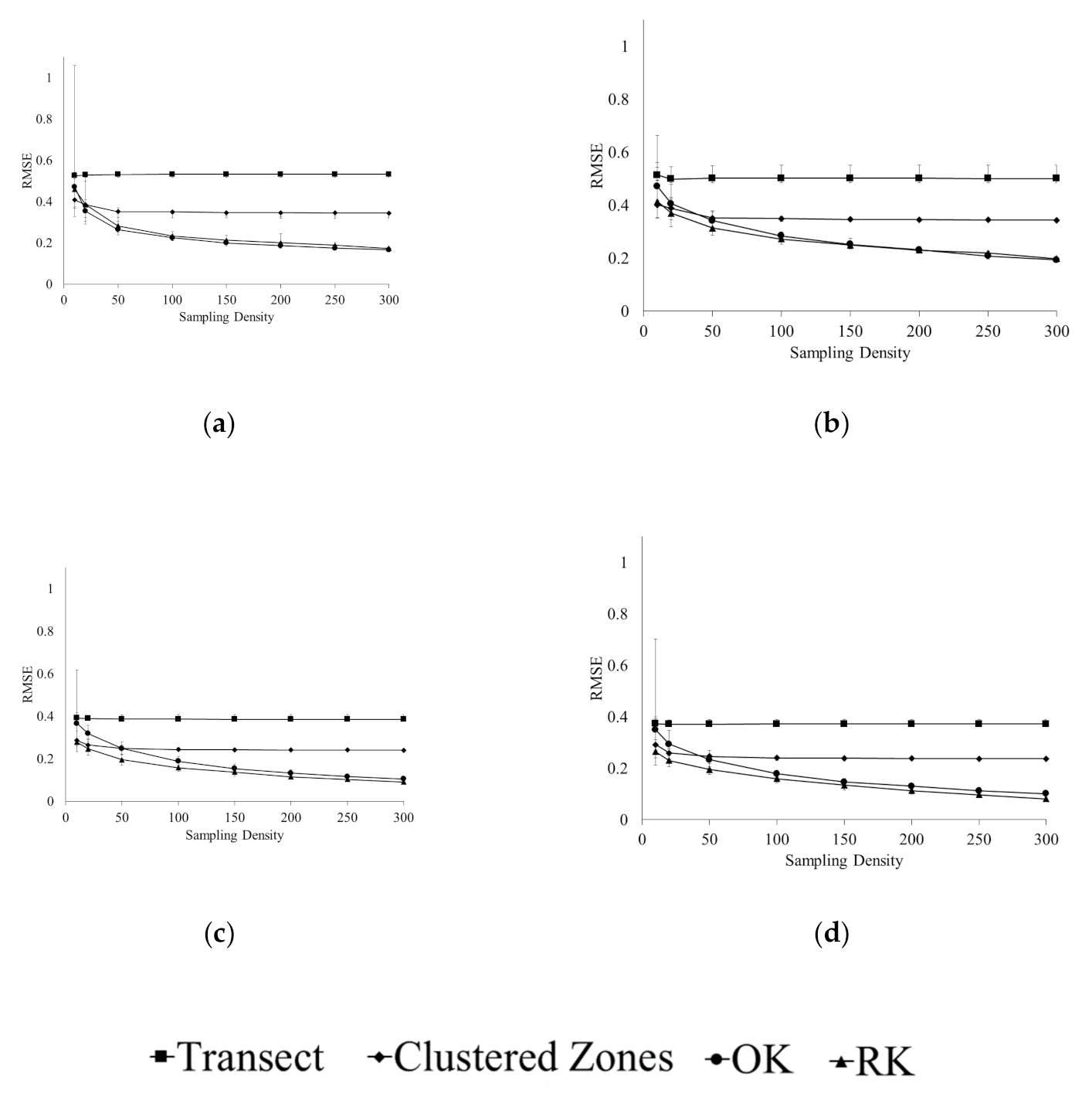
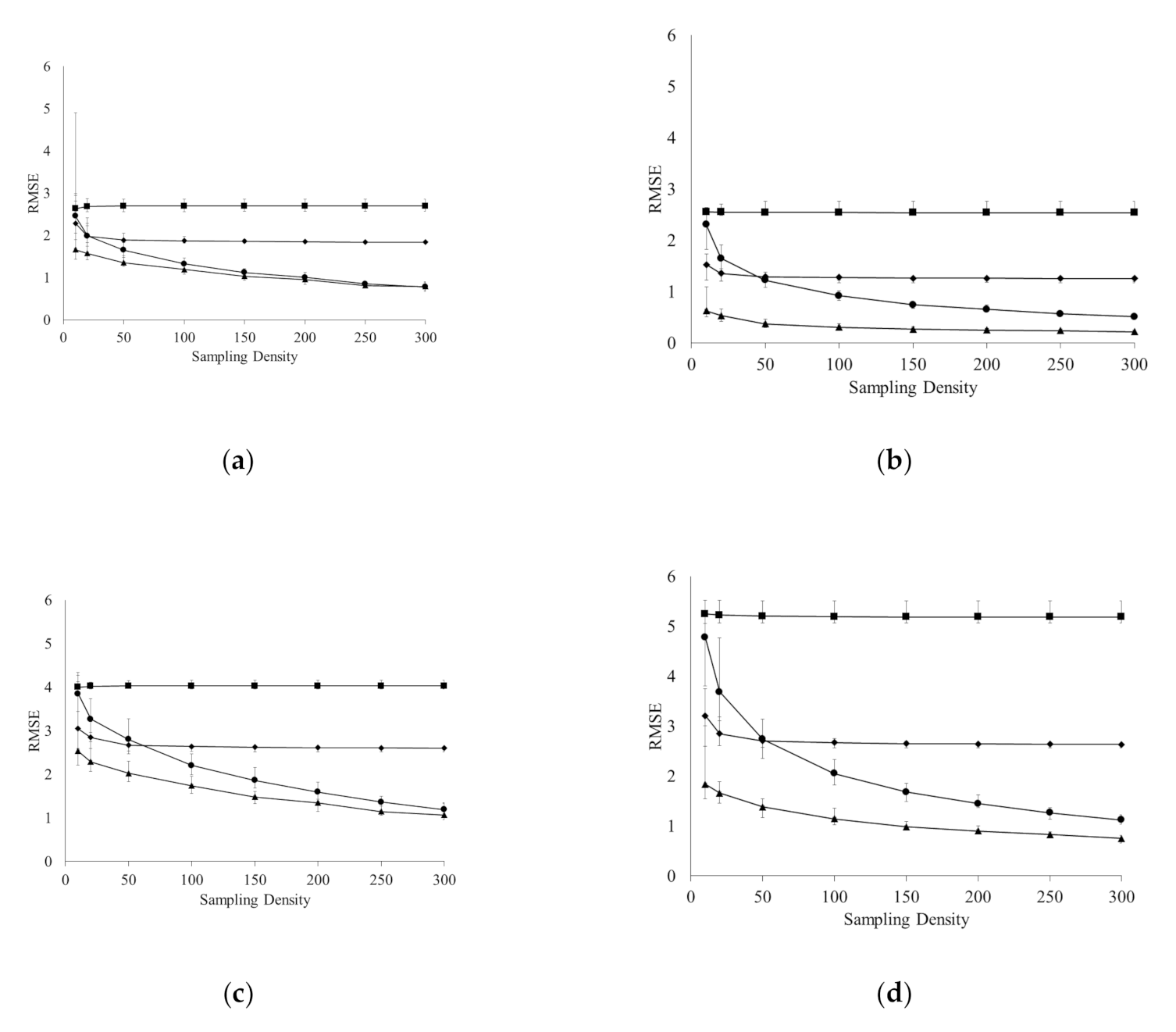
3.1. Accuracy of Spatial Prediction Methods
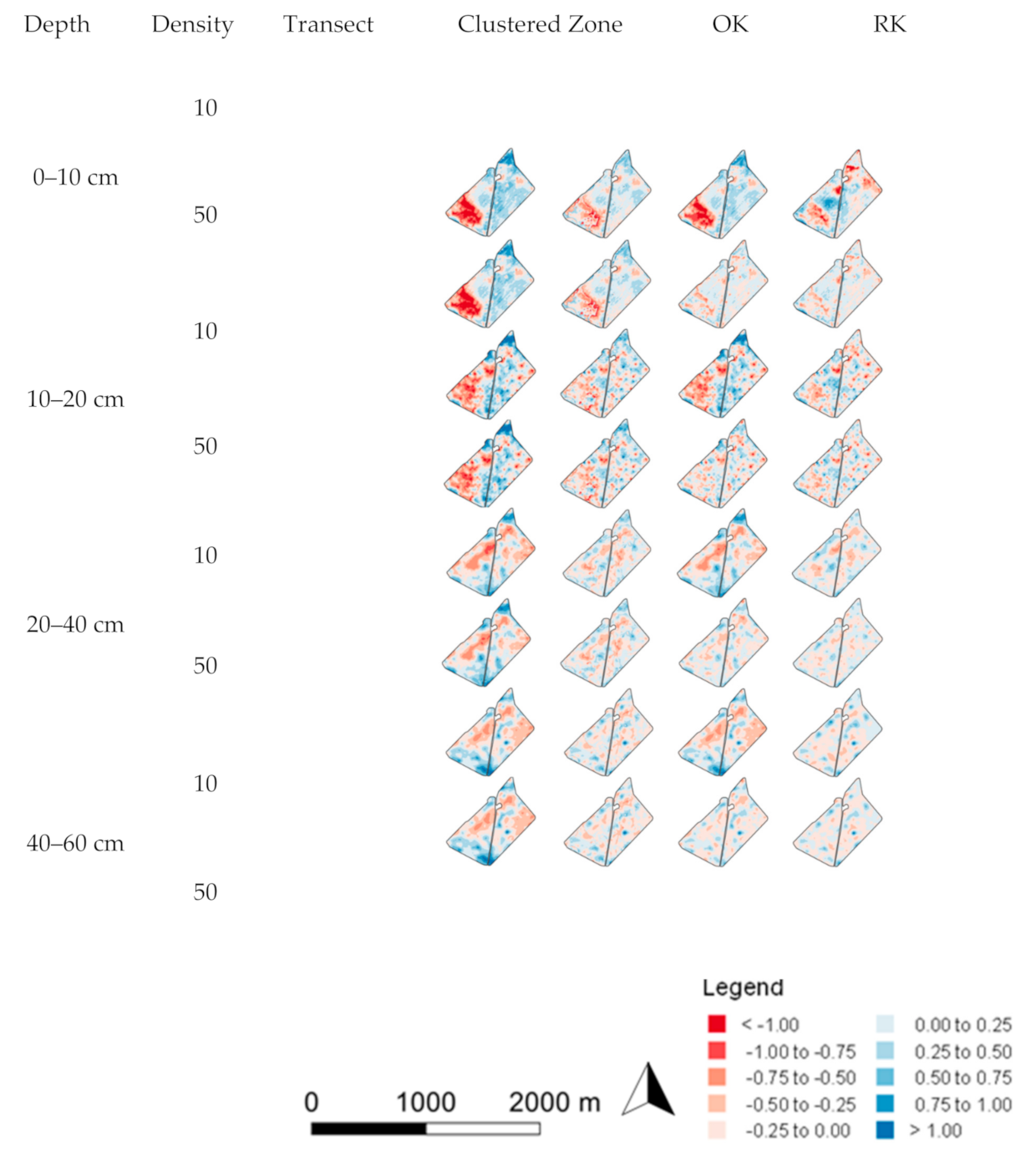
3.2. Spatial Prediction Errors
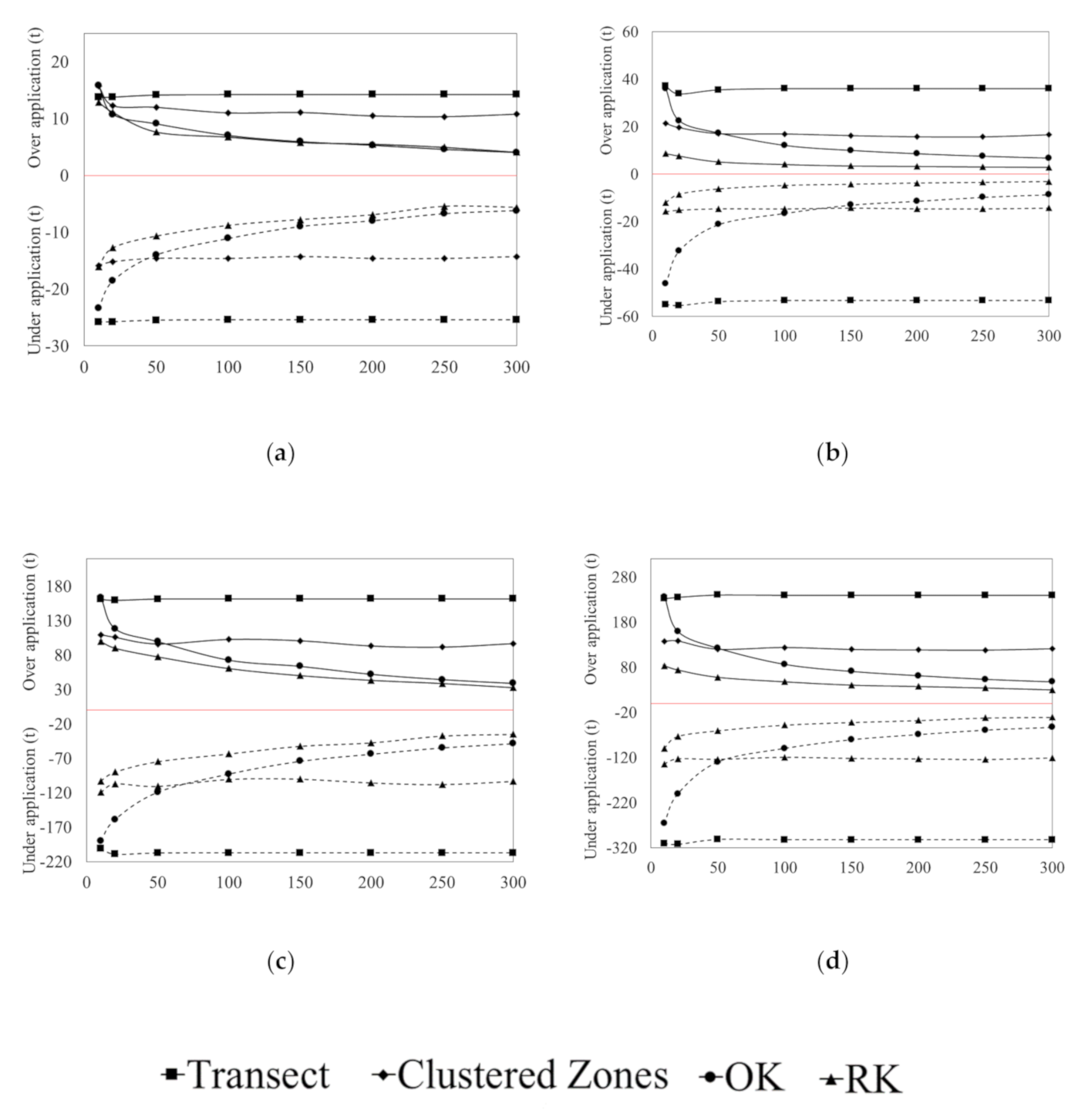
3.3. Error of Agronomic Recommendations
4. Discussion
4.1. Agronomic Consequences of Data Limited Recommendations
4.2. Improving Recommendations through Advanced Spatial Prediction Methods with Increased Sampling Requirements
4.3. The Effect of Sample Selection on Prediction Uncertainty
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lobry de Bruyn, L.; Andrews, S. Are Australian and United States farmers using soil information for soil health management? Sustainability 2016, 8, 304. [Google Scholar] [CrossRef] [Green Version]
- Bennett, J.M.; Cattle, S. Adoption of soil health improvement strategies by Australian farmers: I. Attitudes, management and extension implications. J. Agric. Educ. Ext. 2013, 19, 407–426. [Google Scholar] [CrossRef]
- Bennett, J.M.; Cattle, S. Adoption of soil health improvement strategies by Australian farmers: II. Impediments and incentives. J. Agric. Educ. Ext. 2014, 20, 107–131. [Google Scholar] [CrossRef]
- Bennett, J.M.; Cattle, S.; Singh, B. The efficacy of lime, gypsum and their combination to ameliorate sodicity in irrigated cropping soils in the Lachlan Valley of New South Wales. Arid Land Res. Manag. 2015, 29, 17–40. [Google Scholar] [CrossRef]
- Bennett, J.M.; Marchuk, A.; Raine, S.R.; Dalzell, S.A.; Macfarlane, D.C. Managing land application of coal seam water: A field study of land amendment irrigation using saline-sodic and alkaline water on a Red Vertisol. J. Environ. Manag. 2016, 184, 178–185. [Google Scholar] [CrossRef]
- Heath, R. Editorial to John Ralph Essay Competition 2018: Should society determine the right to farm? Farm Policy J. 2018, 15, 2–3. [Google Scholar]
- Lush, D. Should society determine the right to farm? Farm Policy J. 2018, 15, 4. [Google Scholar]
- Bennett, J.M.; Bennett, J.M.; McBratney, A.; Field, D.; Kidd, D.; Stockmann, U.; Liddicoat, C.; Grover, S. Soil Security for Australia. Sustainability 2019, 11, 3416. [Google Scholar] [CrossRef] [Green Version]
- De Gruijter, J.J. Numerical Classification of Soils and Its Application in Survey; Pudoc: Wageningen, The Netherlands, 1977. [Google Scholar]
- Boydell, B.; McBratney, A. Identifying potential within-field management zones from cotton-yield estimates. Precis. Agric. 2002, 3, 9–23. [Google Scholar] [CrossRef]
- Fu, Q.; Wang, Z.; Jiang, Q. Delineating soil nutrient management zones based on fuzzy clustering optimized by PSO. Math. Comput. Model. 2010, 51, 1299–1305. [Google Scholar] [CrossRef]
- Taylor, J.; McBratney, A.; Whelan, B. Establishing management classes for broadacre agricultural production. Agron. J. 2007, 99, 1366–1376. [Google Scholar] [CrossRef]
- Li, Y.; Shi, Z.; Li, F.; Li, H.-Y. Delineation of site-specific management zones using fuzzy clustering analysis in a coastal saline land. Comput. Electron. Agric. 2007, 56, 174–186. [Google Scholar] [CrossRef]
- McBratney, A.; Whelan, B.; Ancev, T.; Bouma, J. Future directions of precision agriculture. Precis. Agric. 2005, 6, 7–23. [Google Scholar] [CrossRef]
- Robertson, M.J.; Llewellyn, R.S.; Mandel, R.; Lawes, R.; Bramley, R.G.V.; Swift, L.; Metz, N.; O’Callaghan, C. Adoption of variable rate fertiliser application in the Australian grains industry: Status, issues and prospects. Precis. Agric. 2012, 13, 181–199. [Google Scholar] [CrossRef]
- Burgess, T.; Webster, R. Optimal interpolation and isarithmic mapping of soil properties: I. The semivariogram and punctual kriging. J. Soil Sci. 1980, 31, 315–331. [Google Scholar] [CrossRef]
- Brus, D.J.; Heuvelink, G.B. Optimization of sample patterns for universal kriging of environmental variables. Geoderma 2007, 138, 86–95. [Google Scholar] [CrossRef]
- Heuvelink, G.B.; Brus, D.J.; de Gruijter, J.J. Optimization of sample configurations for digital mapping of soil properties with universal kriging. Dev. Soil Sci. 2006, 31, 137–151. [Google Scholar]
- Vašát, R.; Heuvelink, G.; Borůvka, L. Sampling design optimization for multivariate soil mapping. Geoderma 2010, 155, 147–153. [Google Scholar] [CrossRef]
- Walvoort, D.J.; Brus, D.; De Gruijter, J. An R package for spatial coverage sampling and random sampling from compact geographical strata by k-means. Comput. Geosci. 2010, 36, 1261–1267. [Google Scholar] [CrossRef]
- Odeh, I.; McBratney, A.; Chittleborough, D. Spatial prediction of soil properties from landform attributes derived from a digital elevation model. Geoderma 1994, 63, 197–214. [Google Scholar] [CrossRef]
- Odeh, I.O.; McBratney, A.; Chittleborough, D. Further results on prediction of soil properties from terrain attributes: Heterotopic cokriging and regression-kriging. Geoderma 1995, 67, 215–226. [Google Scholar] [CrossRef]
- Hengl, T.; Heuvelink, G.B.; Stein, A. A generic framework for spatial prediction of soil variables based on regression-kriging. Geoderma 2004, 120, 75–93. [Google Scholar] [CrossRef] [Green Version]
- Bishop, T.; McBratney, A. A comparison of prediction methods for the creation of field-extent soil property maps. Geoderma 2001, 103, 149–160. [Google Scholar] [CrossRef]
- McBratney, A.; Mendonça Santos, M.L.; Minasny, B. On digital soil mapping. Geoderma 2003, 117, 3–52. [Google Scholar] [CrossRef]
- Minasny, B.; McBratney, A.B. A conditioned Latin hypercube method for sampling in the presence of ancillary information. Comput. Geosci. 2006, 32, 1378–1388. [Google Scholar] [CrossRef]
- IUSS Working Group WRB. World Reference Base for Soil Resources 2014, Update 2015: International Soil Classification System for Naming Soils and Creating Legends for Soil Maps; FAO: Rome, Italy, 2015; p. 192. [Google Scholar]
- Rayment, G.E.; Lyons, D.J. Soil Chemical Methods: Australasia; CSIRO Publishing: Collingwood, Australia, 2011; Volume 3. [Google Scholar]
- Hiemstra, P.; Hiemstra, M.P. Package ‘Automap’; Carnegie-Mellon University Institute for Software Research: Pittsburgh, PA, USA, 2013; Volume 105, p. 10. [Google Scholar]
- Webster, R.; Oliver, M.A. Sample adequately to estimate variograms of soil properties. J. Soil Sci. 1992, 43, 177–192. [Google Scholar] [CrossRef]
- Minasny, B.; McBratney, A. Latin hypercube sampling as a tool for digital soil mapping. Dev. Soil Sci. 2006, 31, 153–606. [Google Scholar]
- Roudier, P.; Beaudette, D.; Hewitt, A.A. A conditioned Latin hypercube sampling algorithm incorporating operational constraints. In Digital Soil Assessments and Beyond: Proceedings of the 5th Global Workshop on Digital Soil Mapping, Sydney, Australia, 10–13 April 2012; Taylor & Francis: Sydney, Australia, 2012; pp. 227–231. [Google Scholar]
- Oster, J.; Jayawardane, N. Agricultural Management of Sodic Soils, In Sodic Soil: Distribution, Management and Envrionmental Consequences; Oxford University Press: New York, NY, USA, 1998. [Google Scholar]
- Shainberg, I.; Rhoades, J.; Prather, R. Effect of Low Electrolyte Concentration on Clay Dispersion and Hydraulic Conductivity of a Sodic Soil 1. Soil Sci. Soc. Am. J. 1981, 45, 273–277. [Google Scholar] [CrossRef]
- Helyar, K.R.; Porter, W. Soil acidification, its measurement and the processes involved. In Soil Acidity and Plant Growth; Academic Press: Marrickvlle, Australia, 1989; pp. 61–102. [Google Scholar]
- Doerge, T. Defining management zones for precision farming. Crop Insights 1999, 8, 1–5. [Google Scholar]
- Whelan, B.; McBratney, A. Definition and interpretation of potential management zones in Australia. In Proceedings of the 11th Australian Agronomy Conference, Geelong, VIC, Australia, 2–6 February 2003. [Google Scholar]
- Florinsky, I.V.; Eilers, R.G.; Manning, G.R.; Fuller, L.G. Prediction of soil properties by digital terrain modelling. Environ. Model. Softw. 2002, 17, 295–311. [Google Scholar] [CrossRef]
- McKenzie, N.J.; Ryan, P.J. Spatial prediction of soil properties using environmental correlation. Geoderma 1999, 89, 67–94. [Google Scholar] [CrossRef]
- Minasny, B.; McBratney, A. Conditioned Latin hypercube sampling for calibrating soil sensor data to soil properties. In Proximal Soil Sensing; Springer: Dordrecht, The Netherlands, 2010; pp. 111–119. [Google Scholar]
- Henderson, B.L.; Bui, E.N.; Moran, C.J.; Simon, D.A.P. Australia-wide predictions of soil properties using decision trees. Geoderma 2005, 124, 383–398. [Google Scholar] [CrossRef]
- Lacoste, M.; Minasny, B.; McBratney, D.; Michot, D.; Viaud, V.; Walter, C. High resolution 3D mapping of soil organic carbon in a heterogeneous agricultural landscape. Geoderma 2014, 213, 296–311. [Google Scholar] [CrossRef]
- Ballabio, C. Spatial prediction of soil properties in temperate mountain regions using support vector regression. Geoderma 2009, 151, 338–350. [Google Scholar] [CrossRef]
- Were, K.; Bui, D.T.; Dick, Ø.B.; Singh, B.R. A comparative assessment of support vector regression, artificial neural networks, and random forests for predicting and mapping soil organic carbon stocks across an Afromontane landscape. Ecol. Indic. 2015, 52, 394–403. [Google Scholar] [CrossRef]
- Dai, X.; Huo, Z.; Wang, H. Simulation for response of crop yield to soil moisture and salinity with artificial neural network. Field Crops Res. 2011, 121, 441–449. [Google Scholar] [CrossRef]
- Behrens, T.; Förster, H.; Scholten, T.; Steinrücken, U.; Spies, E.D.; Goldschmitt, M. Digital Soil Mapping using Artificial Neural Networks. J. Plant Nutr. Soil Sci. 2005, 168, 21–33. [Google Scholar] [CrossRef]
- Chang, D.-H.; Islam, S. Estimation of soil physical properties using remote sensing and artificial neural network. Remote Sens. Environ. 2000, 74, 534–544. [Google Scholar] [CrossRef]
- Brus, D.; Kempen, B.; Heuvelink, G. Sampling for validation of digital soil maps. Eur. J. Soil Sci. 2011, 62, 394–407. [Google Scholar] [CrossRef]



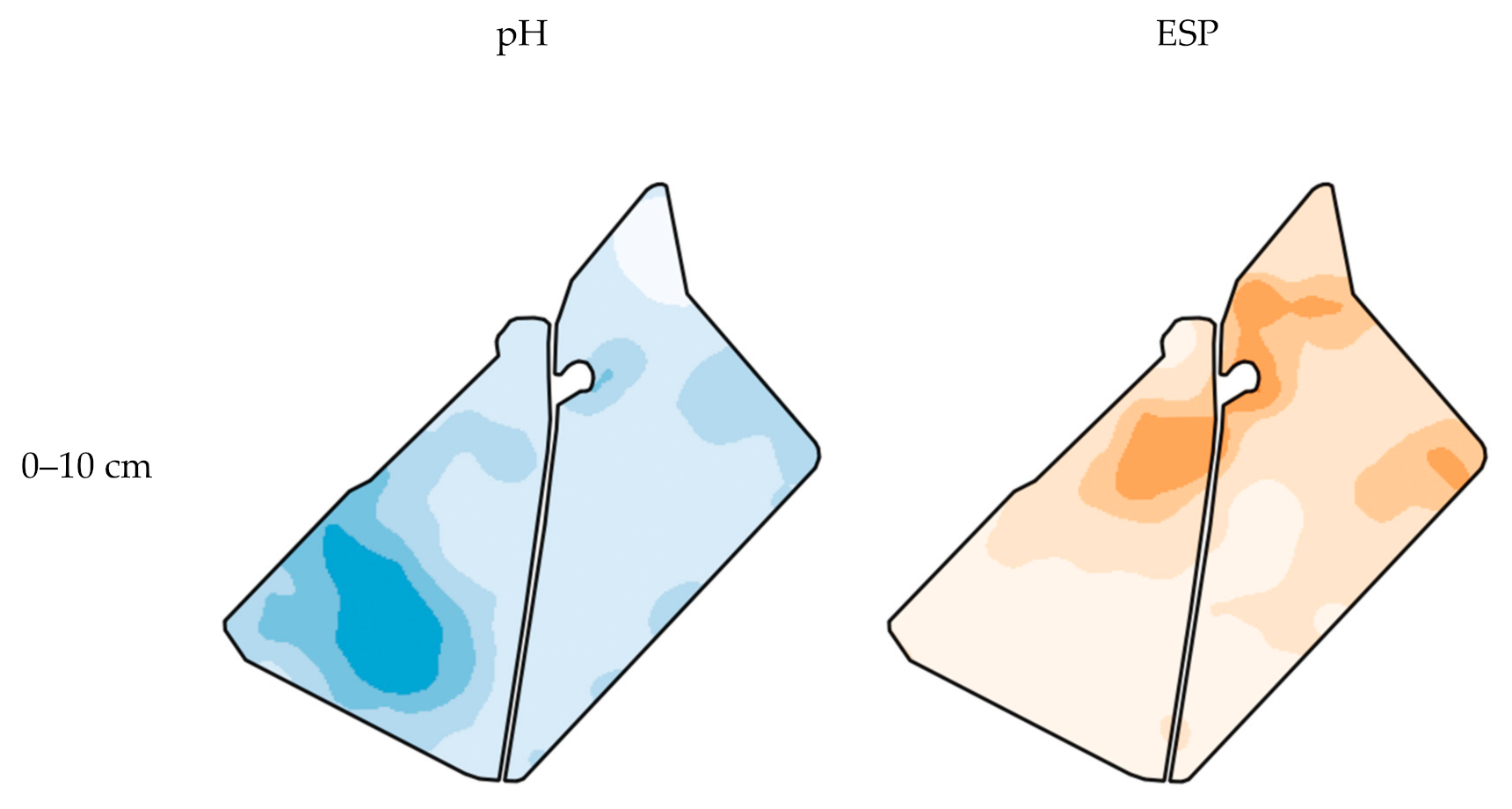
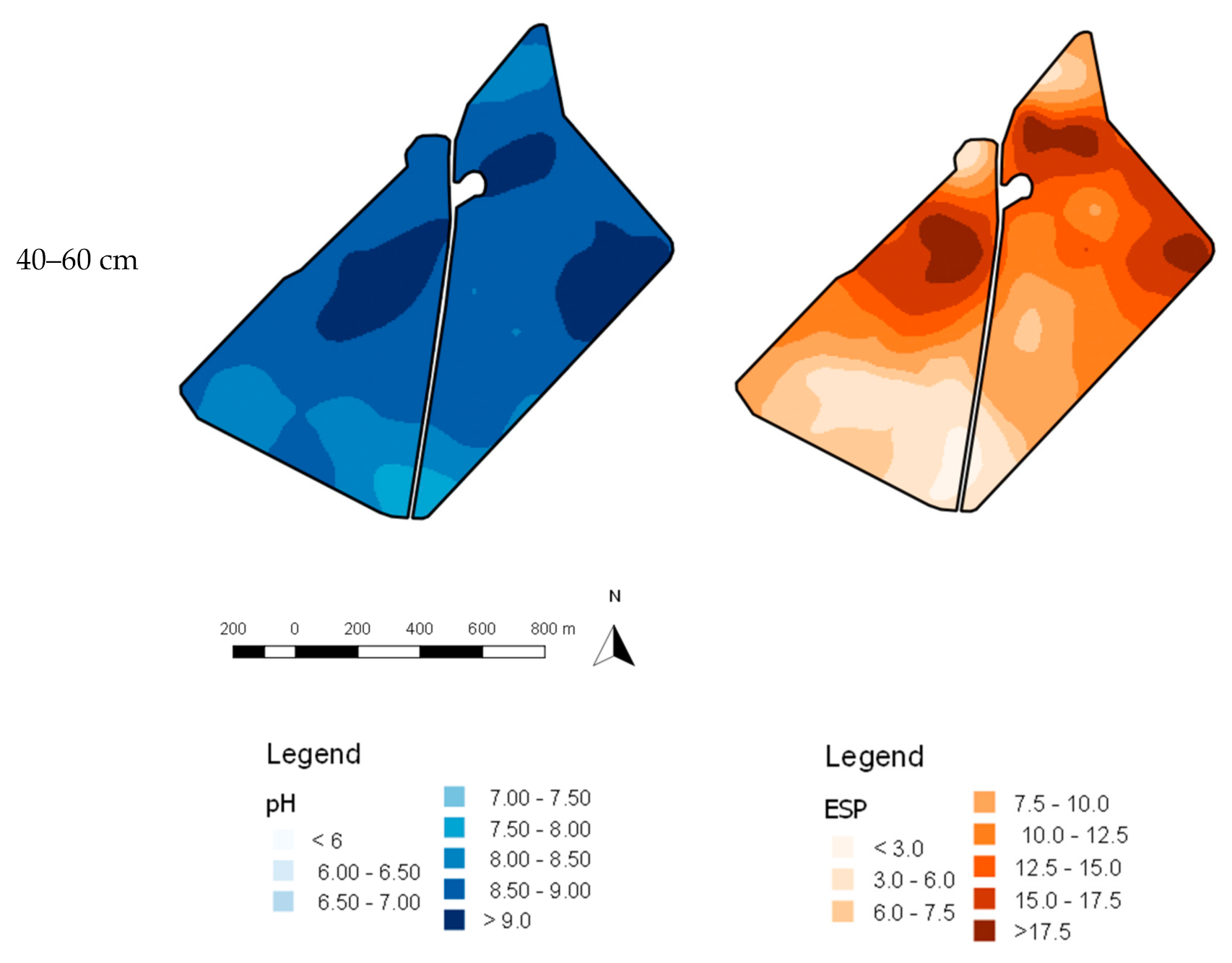
| 0–10 cm | 10–20 cm | 20–40 cm | 40–60 cm | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Min | Max | Average | SD | Min | Max | Average | SD | Min | Max | Average | SD | Min | Max | Average | SD | |
| pH | 5.27 | 9.15 | 6.58 | 0.64 | 5.98 | 9.23 | 7.52 | 0.68 | 6.55 | 9.45 | 8.23 | 0.57 | 5.98 | 9.65 | 8.72 | 0.56 |
| BD | 1.18 | 1.83 | 1.47 | 0.11 | 1.37 | 1.84 | 1.61 | 0.08 | 1.01 | 1.85 | 1.64 | 0.08 | 1.1 | 1.91 | 1.68 | 0.07 |
| CEC | 5.78 | 38.28 | 16.55 | 6.39 | 7.64 | 39.21 | 23.31 | 6.16 | 10.07 | 66.5 | 28.24 | 5.46 | 11.05 | 41.98 | 29.57 | 4.53 |
| ESP | 0.03 | 20.86 | 4.01 | 3.17 | 0.13 | 26.21 | 5.32 | 3.75 | 0.05 | 30.33 | 7.36 | 4.69 | 0.14 | 34 | 10.48 | 5.9 |
| Depth | Total (t) |
|---|---|
| 0–10 cm | 36.5 |
| 10–20 cm | 109.7 |
| 20–40 cm | 517.05 |
| 40–60 cm | 952.85 |
| pH1 | pH2 | pH3 | pH4 | ESP1 | ESP2 | ESP3 | ESP4 | |
|---|---|---|---|---|---|---|---|---|
| 2013 Yield | 0.47 | 0.48 | 0.37 | 0.27 | 0.20 | 0.27 | 0.23 | 0.33 |
| 2014 Yield | 0.41 | 0.25 | 0.13 | 0.03 | 0.05 | 0.02 | 0.04 | 0.08 |
| 2015 Yield | 0.32 | 0.26 | 0.18 | 0.01 | 0.18 | 0.13 | 0.13 | 0.17 |
| 2016 Yield | 0.39 | 0.22 | 0.06 | 0.16 | 0.16 | 0.14 | 0.14 | 0.19 |
| 0–25 cm ECa | 0.07 | 0.36 | 0.49 | 0.49 | 0.58 | 0.63 | 0.68 | 0.78 |
| 0–75 cm ECa | 0.04 | 0.33 | 0.49 | 0.51 | 0.57 | 0.63 | 0.68 | 0.78 |
| 0–125 cm ECa | 0.07 | 0.35 | 0.50 | 0.52 | 0.55 | 0.61 | 0.66 | 0.77 |
| 0–275 cm ECa | 0.03 | 0.31 | 0.49 | 0.52 | 0.52 | 0.59 | 0.64 | 0.74 |
| Elevation | 0.52 | 0.27 | 0.08 | 0.24 | 0.44 | 0.36 | 0.40 | 0.41 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roberton, S.D.; Bennett, J.M.; Lobsey, C.R.; Bishop, T.F.A. Assessing the Sensitivity of Site-Specific Lime and Gypsum Recommendations to Soil Sampling Techniques and Spatial Density of Data Collection in Australian Agriculture: A Pedometric Approach. Agronomy 2020, 10, 1676. https://doi.org/10.3390/agronomy10111676
Roberton SD, Bennett JM, Lobsey CR, Bishop TFA. Assessing the Sensitivity of Site-Specific Lime and Gypsum Recommendations to Soil Sampling Techniques and Spatial Density of Data Collection in Australian Agriculture: A Pedometric Approach. Agronomy. 2020; 10(11):1676. https://doi.org/10.3390/agronomy10111676
Chicago/Turabian StyleRoberton, Stirling D., John McL. Bennett, Craig R. Lobsey, and Thomas F. A. Bishop. 2020. "Assessing the Sensitivity of Site-Specific Lime and Gypsum Recommendations to Soil Sampling Techniques and Spatial Density of Data Collection in Australian Agriculture: A Pedometric Approach" Agronomy 10, no. 11: 1676. https://doi.org/10.3390/agronomy10111676
APA StyleRoberton, S. D., Bennett, J. M., Lobsey, C. R., & Bishop, T. F. A. (2020). Assessing the Sensitivity of Site-Specific Lime and Gypsum Recommendations to Soil Sampling Techniques and Spatial Density of Data Collection in Australian Agriculture: A Pedometric Approach. Agronomy, 10(11), 1676. https://doi.org/10.3390/agronomy10111676





