Abstract
Computer-Generated Imagery (CGI) has received increasing interest in both research and the entertainment industry. Recent advancements in computer graphics allowed researchers and companies to create large-scale virtual environments with growing resolution and complexity. Among the different applications, the generation of biological assets is a relevant task that implies challenges due to the extreme complexity associated with natural structures. An example is represented by trees, whose composition made by thousands of leaves, branches, branchlets, and stems with oriented directions is hard to be modeled. Realistic 3D models of trees can be exploited for a wide range of applications including decision-making support, visualization of ecosystem changes over time, and for simple visualization purposes. In this review, we give an overview of the most common approaches used to generate 3D tree models, discussing both methodologies and available commercial software. We focus on strategies for modeling and rendering of plants, highlighting their accordance or not with botanical knowledge and biological models. We also present a proof of concept to link biological models and 3D rendering engines through Ordinary Differential Equations.
1. Introduction
Computer simulations of plant growth have a long history. Botanists and computer scientists have tried to develop methods to generate natural objects synthetically for over forty years [,]. The first method for branching structure simulation using a computer called a cellular automaton was proposed by Ulam [] in 1966: an arrangement of square cells on a grid, directed by a computer program that had the ability to adapt to different conditions. Greene [] extended the cellular automaton to a three-dimensional space called voxel space automata trying to simulate growing processes with reactions and adaptations to the environment. Simpler models, which ignored even fundamental factors such as branch collisions, were developed later. Honda [] proposed a model in which a variety of tree-like shapes was obtained by changing few numeric parameters. Lindenmayer [] proposed a string rewriting system for cellular interaction commonly called the L-system, later adopted to generate plants and trees with the contribution of Prusinkiewicz []. Oppenheimer [] used fractals to form trees with more advanced parameters such as branching angle, branch-to-parent size ratio, stem taper rates, helical twist, and branches per stem segment. Oppenheimer introduced random variations to alleviate some of the self-similarities intrinsic in fractal models (same specifications for every recursive level). Other models were developed during the years, following the needs of both 3D artists or professionals and botanists []. Following the development of these pioneering methodologies, the field has been revolutionized in the last two decades thanks to the exponential rise of computational capabilities and the integration with mathematical-biological models. The Functional–Structural Plant Models (FSPMs) in the last two decades have been developed by scientists in order to explore and integrate the structure and the underlying processes of a plant []. Nowadays, the complexity of digital design has reached elevated levels of quality standards allowing the use of 3D structure as output of FSPMs in order to characterize plant phenotypes [] or as feedback to assess and calculate light partitioning []. 3D plants can be part of several modeling systems, being main components of many digital representations of landscapes or natural scenarios []. As proposed by Pirk et al. [], a 3D tree can be used in different scientific applications, such as synthetic silviculture [], generic digital representation of real world [], flow dynamics [] and, as mentioned, in botany to determine physiological parameters []. In botany, models are used to determine physiological parameters [,,]. Geometrical plant modeling allows researchers to validate visually biological processes, such as the interaction of plants with light and environment. In ecology, plant models are of interest to visualize information of deep-lying processes, allowing scientists to see “invisible” things []. Examples are represented by how plants develop in reaction to disease or stress and how plants grow after pruning [,]. This is critical to study the competition of plants for light or to estimate field crop canopy photosynthesis [,,] or carbon and water flows [], making an observer aware of the system’s mechanism. In this paper, we aim to review the different modeling approaches of tree generation using FSPM that have 3D output to understand the state-of-the-art of current modeling approaches and how these models can benefit, if any and if functional to the model, from the generated 3D structure. We decided to focus the review on models that describe the epigeal part of the plant by excluding those that model only the root system. In Section 2, we present and review the FSPM methods with 3D output, grouped in three categories, depending on model category: FSPM (Functional–Structural Plant Model, Section 2.1), FPM (Functional Plant Model, Section 2.2), SPM (Structural Plant Model, Section 2.3). In Section 2.4, we compared the models described according to their applications in agronomy: which plant organs were modeled and considered, whether plant–plant interaction in community is modeled, whether plant-soil interaction is modeled, what processes were considered (e.g., carbon allocation, photosynthesis, and so on), and the various agronomic and scientific applications. As stated by Louarn and Song [], one of the most promising horizons and opportunities of FSPMs is the use of non-invasive imaging and modeling-based methods. We give particular emphasis on their use of 3D model, how the 3D models generated are validated, what the scientific applications are. In Section 3, we provide a brief description of 3D rendering techniques used to generate synthetic trees and how these are used in commercial software. We also provide a proof of concept in Section 4 for a link between a biological mathematical model based on Ordinary Differential Equations (ODE) and a 3D rendering engine. This link can operate in both ways, i.e., by rendering a tree using parameters from ODE solutions or by considering geometrical 3D data (e.g., the amount of light from the scene) as input to solve ODEs. The in-depth development, validation, and more detailed results of the model are provided in the companion paper [], part II of this research.
2. Plant and Crop Models
The development of computer models of plant functioning and growth has been in scientists’ interests in the last 40 years []. During the last 20 years, scientists approached a new method to model plants by creating and developing FSPMs []. The main idea of this approach is to describe and model the plant as a population of interconnected parts, ranging from the smallest scale (organism prospective and genetic models) to the biggest one (community of plants and ecological models) []. Achieving this goal required a number of studies that made concepts such as those of plant architecture widely recognized in botany and the scientific community [,]. In parallel to the development of globally recognized models, the advancement of computing power by personal computers has allowed the development of the first methods and standards. The FSPM models allow a creation of “virtual” plants thanks also to the possibility, given the presence of architecture models, to have as output 3D models of plants []. This output, in addition to being visually immediate for the evaluation of the biological model itself [], allows a more precise calculation of a series of interactions both with the external environment (virtual and not) such as the amount of light intercepted [,], the competition of plants in the community [] or external mechanical actions (e.g., pruning) [] and with other parts of the model of smaller scale [], such as the reaction of the plant to diseases []. The present study focuses the attention on functional–structural models with 3D plant architecture output. The studies reviewed in this work are grouped in three categories, according to their modeling goal: (i) FSPM for models that have both functional and structural modeling; (ii) FPM for models that have functional modeling; and (iii) SPM for models that have only structural modeling. All the models reviewed have a 3D plant output. The objective of this review is to assess how the 3D output of models is generated, how it is useful for the development of the model itself, how the 3D structure could be improved, and how it could be a new opportunity for the further development of FSPM models. All the models reviewed are shown in Table 1 with their names, the programming language used, and the modeling environment. The works reviewed have been selected through a search on major public databases (Scopus, Web of Science, ScienceDirect, SpringerLink, ACM Digital Library), among those that have 3D output and that have a particular feedback in the scientific community in terms of citations and applications. Another table (Table 2) will be presented in Section 2.4 to summarize the agronomic applications, modeling objectives, modeled organs, and whether plant–plant and plant–soil interactions are present in order to have an overview of the described models and proceed to critically compare them.

Table 1.
Plant and crop models reviewed in this work categorized in model types.

Table 2.
Overview of reviewed model characteristics, aims, and agronomic applications.
2.1. Functional–Structural Plant Models (FSPM)
Barczi et al. proposed in 2008 a structural whole-plant architecture simulator called AMAPsim []. The main goal of AMAPsim model is to combine architectural and physiological models, including both a general botanic framework and plug-in functions. The model and software, written in C++ language, is mostly based on those proposed by Bouchon et al. []. At its core, AMAPsim is a model designed to reconstruct a 3D plant structure (SPM) using a set of botanical parameters and concepts as growth engine. It has been classified in this work as an FSPM since, thanks to its modular structure, it is possible to use plug-ins for modeling the functional part of plants, becoming in all respects an FSPM. AMAPsim describes the plant as a set of hierarchical levels starting from the axis, annual shoot, growing unit, zone, and internode. The model considers the bud as a potential growth point. Once the topology is determined, the plant components are placed in the 3D space according to the method proposed by Jaeger [] by associating geometric shapes to each plant component, e.g., a cylinder to the internode and polygonal surfaces to the leaves. These 3D components are placed in the environment according to geometric rules. The curvature of the branches by their own weight is modeled according to beam theory. The initial direction of the axes is defined according to phyllotaxis, and the initial length and diameter vary over time according to proportion rules. In its basic form as SPM, AMAPsim does not consider effects such as heliotropism or epitony. However, due to the possibility of using plug-ins, these features were included later as external module. The authors showed an example of their FSPM based on the AMAPsim core, using tomato plants. Figure 1a shows the results of this simulation: on the left (A) is shown a complete shape with detailed leaves; on the right (B), a simplified shape with leaves is approximated to an equivalent area. As shown in Figure 1a, the 3D output can be defined by to the computational power and the wanted precision; however, it is not a real-time 3D rendering, and it is not possible to modify environmental variables’ runtime except at the end of every time-step of simulation. The modularity of the AMAPsim model, as well as the possibility of being able to use it without knowing programming languages, allows its use by non-programmers simply by calibrating the input parameters.
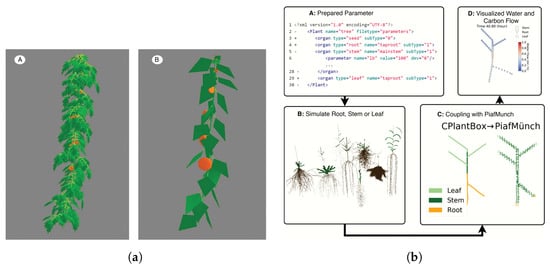
Figure 1.
AMAPsim model output (a) and CPlantBox framework (b). (a) 3D output of AMAPsim model. Tomato plant modeled with complete shape (A) and simplified leaves shape (B), Barczi et al. [], with permission from Oxford University Press, 2021 license 5200260057623; (b) major steps, as flow chart, in CPlantBox framework coupled with PiafMunch. Zhou et al. [] 2020. Published by Oxford University Press on behalf of the Annals of Botany Company. Distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0/, 28 September 2021).
In 2020, Zhou et al. [] introduced CPlantBox, a whole-plant functional–structural modeling framework. The authors proposed a model that can simulate both root and plant shoot as full plant structure and as a single topological network of organs. The model is written in Python language, and the input parameter file are XML-based to increase flexibility. As output, CPlantbox generates a one-dimensional graph with 3D topological coordinates. The nodes of this output graph have properties such as 3D coordinates, radius, organ type, water potential, and others. The workflow of the model is shown in Figure 1b. The model is capable of generating a 3D plant architecture for both the hypogeal and epigeal parts. For the epigeal part, CPlantBox is able to generate different patterns of leaf orientation, depending on the parameters set. The different structures are generated by changing the input parameters. CPlantBox is also capable of calculating the impact on the plant of a heterogeneous environment. In this case, the input parameters are assigned manually and punctually and cannot be varied during the run-time of the simulation. The novelty introduced by CPlantBox consists in simulating as a single network both the roots and the shoot and the possibility to couple it to water and carbon flow models, making it a full FSPM. While having a 3D output of the plant architecture, we believe that an improvement of this aspect can bring several benefits to the model itself: a better 3D representation of the leaves and of the plant structure itself, as well as an improved calculation of the ambient light input, can lead to a more accurate calculation of the photosynthesis process, improving the water and carbon flux model data. In addition, improved 3D structure can be useful for calculating competition between adjacent plants for both light and resources.
The GreenLab mathematical model proposed by de Reffye et al. [] is based on the architectural foundations of trees, identifying the basic components of plant development. A key assumption is that axes of the same type are duplicated at different stages of development. GreenLab is an FSPM that integrates the functional and structural part of metabolic processes with a phytomere-level structure. The model has been developed over the years in different development environments and programming languages. The development of the plant structure and its formalism is based on a double-scale stochastic automaton. The 3D output provides the entire topological basis, having a recursive system of equations as its basis (Figure 2a). In addition to the graph visualization, GreenLab can also produce simple 3D structures (Figure 2a), which are purely geometric since photosynthesis is not contemplated. As stated by de Reffye et al. [], compared to FSPM and crop models, GreenLab falls “in the middle”, as a voluntarily simplified model both from the geometric and structural point of view and from the physiological one. It is a “source–sink solver”: a tool capable of solving source–sink dynamics during growth. Moreover, as stated by the authors, unlike other FSPMs, GreenLab does not provide a fine description of physiological processes. Its strength lies in the fact that it can be used both as a solver of source–sink relationships and to model individual plants up to stand level. In addition to further developments that are underway by the authors, the possibility of integrating GreenLab with a more performant and precise 3D geometric structure could be a further step towards improving the model.

Figure 2.
The GreenLab (a) and L-PEACH models with their 3D structure output (b). (a) Various geometrical structures of trees generated by GreenLab model, de Reffye et al. [], with permission from Oxford University Press, 2021 license 5200260511673. (b) Two peach trees structures with different water intake made by L-PEACH model, Allen et al. [], with permission from John Wiley and Sons, 2021 license 5200251150244.
The L-PEACH model proposed by Allen et al. [] is based on the PEACH model by Grossman and DeJong [] which models carbohydrate source–sink dynamics of vegetative growth of fruit trees. While making it possible to avoid the use of empirical allocation coefficients, functional balance rules, or fixed allometric relationships, the PEACH model completely ignored the relationship between architecture and carbon allocation. In addition, it was not possible to evaluate differences in organ size based on its position on the structure. The integration with L-systems allowed these limitations to be overcome. L-PEACH was written in L+C language and implemented in L-studio []. The plant model is also sensitive to variation in water concentration, affecting carbohydrate production and flux. Figure 2b shows how the simulated plant reacts to different concentrations of water: the tree on the left has been simulated under conditions of full irrigation and the one on the right with mild water stress during growth. The L-systems used in the L-PEACH model facilitates the integration of individual organ models into a branched growth structure as well as dynamically updating the system of equations governing carbon partitioning. It also allows the interface between the plant model itself and the ambient light partitioning model, as well as the water concentration model. L-PEACH attempts to overcome some of the limitations that tree growth models based on carbon partitioning have had, as reviewed by []. However, the authors declare that more testing is needed to have sufficient data to fully calibrate the model []. The flexibility given by the L-systems allows to adapt the studied model to different case studies. Integration between the two fields is promising and possible, as discussed in the following sections.
An integration between FSPM models and 3D rendering is introduced by Bailey in 2019 [] as a framework for plant and environmental modeling called Helios. The author pointed out some important trade-offs in plant systems models and proposed Helios as a different framework in which the mentioned trade-offs are prioritized. The complexity of the model is one of these trade-offs: simple models such as the “big leaf” model proposed by Sinclair et al., Raupach and Finnigan, Friend [,,] can lead to very low computational effort but introduce inherent errors and biases into the model approximation. On the other hand, more precise models that simulate each individual leaf [,] are more accurate but computationally heavier. Another trade-off pointed out by Bailey is the choice between ease of use and flexibility. Increasing the ability of the end user to have more control over the configuration of the software inevitably results in a decrease in the ease of use of the model framework. By automating some of the tedious and technical tasks, developers can increase ease of use but also create multiple limitations for advanced users. An example is given by the non-sequentiality of processes: the simulation of the photosynthesis, as an example, is based on cyclical processes linked between them. Coupling these processes into a model requires iterations, which requires flexibility when incorporated into a generalized modeling framework. This problem was also discussed by Pradal et al. in the development of the OpenALEA model [], where some of the flexibility was sacrificed in the name of ease of use for the end user. The author used C++ language as more efficient and flexible sacrificing some of the usability [,]. Sacrificing ease of use, the model is formulated to allow maximum user control over plugins (submodels), data flow, and execution. Helios is capable of using complex biophysical models, utilizing the parallel computing capability of GPUs to reduce computational weight. The core of the model is represented by a class called Context, which manages the data and geometry of the model. The output of the model is a 3D representation of the plant that can be exported as standard OBJ or PLY files, coupled with XML files for simulation data. This way, coupling of geometric data with other models such as GroIMP or OpenAlea is possible. The generation of 3D tree structure in Helios is possible thanks to the procedural tree generation submodel. This plug-in allows to create semirandom tree geometries through the algorithm proposed by Weber and Penn []. The woody architecture of trees is generated by recursive sets of branching levels with a random perturbation. The procedural tree generation plug-in comes in Helios with predefined tree geometries as shown in Figure 3a. The final tree is similar to ones generated with L-systems approach. Although the Helios model has the ability to procedurally generate the 3D structure of the tree, this function appears limited, having a defined number of trees (predefined tree geometries). There is no possibility to generalize the procedure, as in the other plug-ins, to generate the architecture according to a mathematical biological model; additionally, it is not in real-time. We believe that an improvement in the tree structure generation part could improve the calculation of these submodel parameters by allowing the user to appreciate any differences caused by the different architectures generated, differences in light interception, competition between nearby trees, and more.

Figure 3.
(a) Different 3D trees generated with procedural tree generation plug-in in Helios. Copyright © 2019 Bailey []. Distributed under the terms of the Creative Commons Attribution License (CC BY). (b) GroIMP application on a 3D generated maple tree. Reproduced with Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Netherlands from Kniemeyer et al. [].
The concept of relational growth grammars (RGG) proposed by Kurth et al. [] features a combination of L-systems and graph structures, using a generic programming language. This concept was introduced to make the L-system formalism more suitable for FSPMs since a plant is not the sum of individual parts and shows graph structures that cannot be represented with L-systems which are a linear string of symbols. The formalization of these concepts is exactly the concept of RGG, and its implementation is the XL programming language. The linear sequence of symbols of the L-systems is replaced by a real graph having a series of connected nodes and edges. Typical FSPM relationships can be represented by the graphs and their connections between nodes. The graphs themselves can be transformed by applying rules, such as the rule-based paradigm of L-systems. Kniemeyer et al. [] put together relational growth grammars in an interactive modeling platform, based on the XL language, called GroIMP, with the aim of making the concepts of relational growth grammars usable to the end user. GroIMP has a module for modeling 3D parts, using geometric classes that include primitive shapes such as spheres, cones, boxes, splines, surfaces, and lights, as well as a library of materials applicable to shapes and surfaces. The generated 3D structure is rendered using the POV-Ray engine []. On the 3D structure, the user can apply some modifications such as the deletion of parts by interacting directly on the shape. The implementation of relational growth grammars in GroIMP was done via the XL programming language. It is defined as an extension of the Java language and allows to maintain the syntax of the L-system rules. The language also allows queries and peforms mathematical operations on data sets. All of this allows an implementation of the process-based part of the plant models and links it with the structure. The structure visualization is shown in Figure 3b with a basic example of a maple tree. RGG is not the only extension of the L-system formalism: in the literature, it is possible to find several extensions that take different directions, such as context-sensitive ones that allow the modeling of local transport [], global-sensitive ones that take into account the global environment by interfacing the L-system with an external program [], and those of implementation of different programming languages, such as L+C that adds the rules of L-systems to the programming language C++ []. These extentions remain in the framework of the L-system, and relational growth grammars extend the formalism of L-systems towards the graph grammars to model the complex FSPM in a natural way. Kniemeyer et al. [] argue that the advantages of RGG are that it can store tree- and graph-like structures as data instead of a sequence of symbols that is inadequate for FSPM modeling of graph-like structures. The representation of structures is also immediate, avoiding the interpretation of turtle steps as an algorithm, simplifying the interpretation of global and local rules. Moreover, the use of a generic programming language is useful to implement the process-based part of FSPM. L-systems have this kind of integration, for example with the already mentioned L+C language with the L-PEACH model aforementioned [], but does not define any syntactic support for accessing and calculating on the entire structure. The calculated graph is exportable to be modeled in 3D software such as CINEMA 4D or Maya. However, the 3D structure is only a graphical representation and not a functional object for the model itself. Such a use could be in our opinion an important step to further extend the model. The authors also pointed out that GroIMP cannot solve systems of differential equations that are often the basis of FSPMs. GroIMP has been implemented for modeling different plants and performing functional–structural calculations, as shown by Zhu et al. in GrapeVineXL [].
An example of the application of FSPM as an agronomic tool for crop practice design is V-MANGO proposed by Boudon et al. []. The model is based on a representative FSPM of the mango tree (Mangifera indica L.) that reproduces the vegetative and reproductive development of the tree and their interactions. The main goal of the authors has been to create an integrative FSPM model of mango tree development and fruit production to demonstrate that an FSPM can be used to formalize the development of the complex architecture of mango trees also phenologically, to show how the introduction of some temporal and structural factors can simulate the complex interactions between vegetative and reproductive growth, to create a first basis for a model that can be used for the design of cultural practices. V-MANGO is based on the architecture model proposed by Hallè el al. [], described as a series of growth units, inflorescences and fruits organized as an arborescent structure. Growth units are composed of a series of internodes and leaves organized in a spiral pattern. Boudon el al. [] modeled several sub-models to integrate these different scales and combined them consistently. A plant architecture model was first defined simulating the visual part of the different entities (growth units and inflorescence) by decomposing morphogenesis into elementary stochastic processes. Growth unit geometry is defined by several variables such as axis length and diameter, number of leaves, leaf length, width and area, internode length, and phyllotaxis (see Figure 4a). Using all of these parameters, the authors have been able to accurately represent the geometry and location of each individual growth unit. All these growth unit, fruit, and inflorescence models have been assembled by the authors into a complete architecture using an L-Py [] module of the OpenaAlea [] platform, using L-system formalism with the Python language. The visualization of the structure is then entrusted to the L-system formalism and rules. Although V-MANGO is a complete FPSM, which models both the structural and functional part of the mango tree and has as output a 3D structure of the tree, it has further integrations and updates to be implemented, according to the authors. The 3D structure generated by V-MANGO lacks a module to calculate the amount of intercepted light, and the introduction of this module would allow a more accurate calculation of photosynthesis in fruit production. Finally, the introduction of modules that take into account agronomic practices, such as pruning, would allow the V-MANGO model to be used as a tool for precision agriculture.
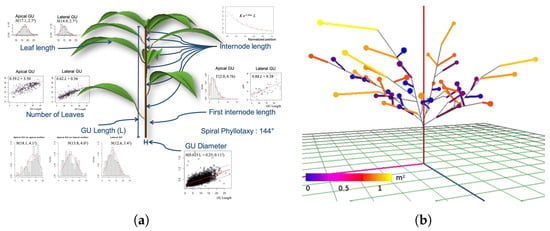
Figure 4.
(a) Mango tree structures, parameters, and model calculations in V-Mango FSPM. Boudon et al. [] 2020. Published by Oxford University Press on behalf of the Annals of Botany Company. Distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0/, 28 September 2021). (b) Fruit tree simulated in QualiTree with representation of Fruits Units (FU—colored lines) and old wood (black lines). Reproduced with permission from Lescourret et al. [], published by Springer, 2011, license number 5198331325727.
A more generic model aimed at modeling fruit trees is QualiTree, presented by Lescourret et al. []. The authors presented QualiTree as a model that can simulate the effects of different agronomic practices on fruit tree development, particularly on the quality of fruits produced. The proposed model is highly targeted towards the study and modeling of the quality of the fruits produced, focusing on some functional aspects of their growth. The modeling of the tree was done considering only the characteristic traits of the quality of the fruits produced (Figure 4b), leaving the other parts of the tree separate as different compartments. From a level of detail point of view, QualiTree falls in the middle between compartmental models and those that use the description of individual organs to represent the architecture of the tree, such as the other FSPMs described in this study. The hierarchical structure has been developed with UML language which, through a representation based on object/class programming paradigm, allows the hierarchical modeling proposed. The functions (mathematical operations) encoded in the model have been classified as specialized models and generalized models. According to the authors, specialized models include all mathematical equations describing carbon allocation according to source–sink systems and their balances, while generalized models include those describing leaf photosynthesis, carbon assimilation by fruits, mobility of carbon reserves, daily growth requirements and others. Some of the improvements proposed by the authors for QualiTree are the extension of the fruit quality parameters, the amplification of the effects on the cultivation practices model, but above all the integration with QualiTree of light interception models for a more precise calculation of photosynthesis. In this regard, we believe that the implementation of a generic model such as QualiTree with a 3D rendering system of the structure, thus overcoming the fact that the structure is already defined as input data, can improve the calculation of light interception and consequently the calculation of photosynthesis and all processes related to it. The authors also propose to scale the model in the future from a tree scale to a tree group scale in addition to increasing the time scale from one growing season to multiple consequential and consecutive seasons.
2.2. Functional Plant Models (FPM)
The ARCHIMED model proposed by Dauzat et al. [] integrates biophysical modules to model the complex interactions between leaf, plant, and plot scales. The authors’ choice was to use a single-leaf scale for most processes such as photosynthesis, leaf radiation, and energy balances. The modules present in ARCHIMED allow the calculation of several biophysical processes such as the radiative balance of organs, their transpiration, and their carbon assimilation. The ARCHIMED platform includes two sub-platforms called ARCHIMED-φ and ARCHIMED-ψ, respectively specialized in biophysical modeling and in 3D plant growth modeling. The processes of photosynthesis and transpiration are controlled by stomatal conductance parameter which can limit photosynthesis by reducing carbon dioxide influx and indirectly modulates leaf temperature through evaporation. In order to be able to calculate all the parameters involved in the simulation, ARCHIMED presents a system of modeling of the light and its quantity that arrives on the structure (in particular on the leaves) as photosynthetic active radiation (PAR). The light input is not calculated in real time by the 3D environment, but it is a prior measurement. The internal behavior of the leaves is governed by the water potential calculated according to a sap flow model. ARCHIMED is capable of modeling interactions between neighboring plants in the same plot. Each plant modifies its own environment either due to its proximity to another plant or due to external elements such as wind. The model used by ARCHIMED to calculate the light flux in the plot is the MMR (Mir-Musc-RadBal) model as described in Dauzat et al. []. As shown in Figure 5a, through the XPlo component of the AMAPstudio platform, it is possible to generate and render 3D tree structures from ARCHIMED model data. In the Figure 5a, a coffee tree was generated and rendered. Through AMAPstudio, it is possible to modify the architecture, evaluate data, and visualize the structure. The modularity of the simulation platform allows the future integration of other models to extend and refine the system, as proposed by the authors themselves.
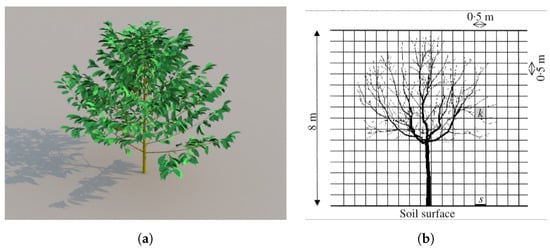
Figure 5.
(a) Coffee tree simulated in ARCHIMED with XPlo AMAPstudio’s module and Sunflow integrated renderer; (b) walnut tree structure with division in 3D cells made by RATP model, Sinoquet et al. [], with permission from John Wiley and Sons, 2021 license 5200250775819.
The functional tree model presented by Sinoquet et al. in 2001 [] called RATP (Radiation Absorption, Transpiration, Photosyntesis) allows the simulation of the spatial distribution of radiation and leaf gas exchange within the vegetation as a function of its structure and microclimate. The model has as input tree geometry, microclimate variables, and properties of tree components. In the research proposed by Sinoquet et al., the model was calibrated on a walnut tree on which all input parameters were measured. The RATP model does not allow a structure generation per se, but the structure itself is input data. RATP according to the authors can be used to study the allocation of resources between vegetative components and between organs in the same plant. The model does not simulate the microclimate inside the canopy except for radiation and wind speed in small scale according to empirical relationships. As proposed, RATP is a model used to study water and carbon exchanges at the interface between the plant and the atmosphere. It does not have the ability to generate a 3D model of the plant, and the input model of the structure is given by field measurements of real trees. Thus, there is no exchange of information between the virtual environment and the model with its parameters. Being a generalized FPM model, it would be possible to integrate it with 3D rendering engines to increase the accuracy of some calculations such as absorption and interception of solar radiation, leaf distribution on the canopy structure, leaf irradiance measurement and so on, relying on a precise architecture of synthetic tree.
FPM models can also be used on non-tree plants. The applications in the literature are numerous, such as modeling the functionality of the tomato plant. In particular, some studies have been performed using a virtual plant model to optimize certain growth conditions. For example, De Visser et al. [] used in their study a 3D model of tomato plant coupled to a ray-tracing model of lighting for the optimization of the light itself showing that illumination efficiency increases when the lamp light is directed at most to leaves that have a high photosynthetic potential. Dieleman et al. [] have instead demonstrated how, by conducting tests in a 3D virtual environment, dynamic light spectra may offer perspectives to increase growth and production in high-value production systems such as greenhouse horticulture and vertical farming.
2.3. Structural Plant Models (SPM)
The main feature offered by the OpenALEA model is to provide researchers with a visual and interactive interface to an FSPM application. OpenALEA due to these features has been used as the basis for several models, some of which are mentioned in this paper [,,,]. The visual programming environment was conceived by the authors as a way to integrate and connect the model rather than model feedback and retroaction, which can still be done using specific dataflow nodes and biophysical solvers (Figure 6a). The intricate interactions between plant functions, such as hormonal control, resource partitioning, and water flow, are partially modeled and require the definition and sharing of generic data structures representing different plant processes at different scales and in parallel. Due to the fact that OpenALEA is a general purpose model, the authors have chosen to develop it in an open-source, object-oriented, platform-independent language with an easy-to-learn syntax such as Python []. OpenALEA is based on the “component framework” principles introduced by Councill and Heineman [] that allow the dynamic combination of independent pieces of software into a workflow. The authors have also developed a visual programming environment, VisuAlea, that allows scientists to create complex models without having to learn a programming language. In VisuAlea, it is possible to graphically combine the different modules, nodes, and components provided by the OpenALEA library and then run the model. Thanks to its modularity, OpenALEA presents basic components already integrated for the modeling and analysis of plant architecture, geomentric plant modeling, ecophysiological processes, and meristem modeling and its simulation. VPlants is the successor of AMAPmod and is a package for the modeling and analysis of the plant architecture, while for the modeling of the geometry, there is the PlantGL graphics library that uses the procedural rendering method proposed by Weber and Penn []. As described, the integration of modules in the OpenALEA model allows the creation of 3D structures of plants aimed both at the visualization of the model and at a functional use such as for the calculation of light and rain interception. The procedural methods of shape generation used in OpenALEA will be described in Section 3.
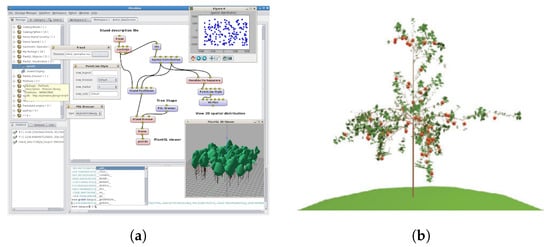
Figure 6.
(a) Overview of OpenALEA software interface with dataflow and interconnectind nodes. On the lower right, the 3D viewer is shown. Screenshot from software. Main research by Pradal et al. []. (b) A five-year-old apple tree modeled with MAppleT. Adapted from Costes et al. [] with permission from CSIRO Publishing, 2021 license 1165429-1.
An example of OpenALEA application is given by the MAppleT model presented by Costes et al. [], which aims to model the apple tree using biomechanical properties and mixed stochastic models. The integration of topology and geometry models in a single simulation in order to make the architecture of an apple tree emerge from the interactions between the processes was achieved by the authors using L-systems. At the time of its publication, MAppleT, together with L-PEACH already described in this paper [], was one of the first approaches to the simulation of fruit trees with development over the years and responsive to gravity. The 3D output turns out to be only visual, used by the authors as a comparison with data measured on real trees for model validation. It is not used as input to the biological model, e.g., for calculating light interception, as well as in other models described in this work.
FSPM, SPM, and FPM models are also used to evaluate how the structure of a plant can modify its characteristics, understood as the ability to intercept light, fruit distribution, production, gas exchange, water transport, and so on. These solutions are also adopted for high-revenue species such as fruit trees and vineyards. In the case of the vineyard, several studies have used these models to simulate the plant in its functions and structure. An example is given by Top-Vine, proposed in 2005 by Louarn et al. []. This model is proposed as a topiary approach based on an architectural model to simulate vine canopy structure with a 3D distribution of leaf area for contrasted vine training systems. Leaf area is an input to the model that operates at the shoot level and considers each shoot to have the same leaf area. The volume is refined by the inputs which are field measurements of real vines using a 3D electromagnetic digitizer. Top-Vine has been implemented on the ALEA/OpenALEA platform. The authors noted a close relationship between the field data and the model results at both the canopy and organ level, allowing, once the model is calibrated, to be able to generate a structure at any desired time-step and allowing a light interception calculation. Thus, as in the model proposed by Louarn et al., other authors have also used FSPM, SPM, and FPM models to virtually recreate the vine. Models such as the one proposed by Zhu et al. [], thanks to a 3D reconstruction of the plant, allow the calculation of gas exchange, coupling it to the dynamics of water transport.
2.4. Critical Comparison of Modeling Systems in Agronomical Applications
The development of FSPMs has matured significantly over the past 20 years and has already provided significant results at different levels of organization and in different fields of plant science. FSPM models are now at the core of fundamental questions in plant biology and predictive ecology. The models studied in this work exhibit specialization on a single plant or are generic frameworks on which specific models have been developed. In particular, FSPMs present a more holistic modeling, often of the whole plant or part of it (shoot or root), both the functional and the structural part. The variety of model applications has also allowed the development of SPM and FPM models, as a branch of FSPM models, which are specialized in a particular aspect: structural only or functional only, by choice of the modeler and for the aims of the development. Table 2 shows the differences between the various models analyzed in terms of model aims, agronomic applications, the presence or absence of plant–plant and plant–soil interactions, and the organs and processes modeled.
As shown in Table 2, among the various models reviewed, there is a large heterogeneity between the processes considered, the organs modeled, and the agronomic applications. AMAPsim uses the processes of carbon allocation and photosynthesis, modeling buds, stems, fruits, and leaves. The carbon allocation is managed by external modules, which is possible thanks to the possibility of connection with external modules specialized in particular functions. In the case of AMAPsim, the external module of carbon allocation is a specialization of the one already used in GreenLab [,] that calculates the storage of biomass, photosynthesis and biomass allocation for each time unit according to current climate and current plant shape, the length according to allometry on biomass, and the diameter according to allometry on biomass. The allocated carbon is used to determine the size of the organs, which in the case of AMAPsim are buds, stems, fruits, and leaves. CPlantBox, unlike AMAPsim, considers the plant as a single connected network of organs and models the allocation of water and carbon not as a redistribution of the data calculated according to the topology but as a flow generated by the potential difference between the various organs of the plant according to the Münch theory []. In this way, the model is able to simulate plant and roots as a single network, generalizing the parameters so that they can be adapted to field measurements. The difference in modeling approach and modeled organs leads to a number of different agronomic applications. Applications of AMAPsim have been found in the literature in several areas such as studying the response of trees to wind, as shown by Sellier et al. [], quantitative analysis of branching patterns [], and how planting density and density can affect plant architecture []. These applications have been made possible, as described in the previous section, by the integration of specialized external modules into AMAPsim. The different modeling approach of CPlantBox has allowed its application in other agronomic fields such as in-field phenotyping. Magistri et al. [] used CPlantBox to rely on synthetically generated models instead of scanning real plants in a controlled environment and use them to measure phenotypic traits in an automated fashion without intensive manual work. GreenLab, as described in Section 2.1, is presented as a model that starts from a concise mathematical representation at the phytomer level of metabolic processes to describe plant growth and development at the individual level up to the stand level []. Carbon allocation was assessed by computing, according to the source–sink concept, the strength of source organs and sink organs, calculating the plant demand as the sum of all active sink organs at a given time t. The root system is considered as a simple, single compartment, focusing only on the epigeal structure. The equation governing the model has the form of a discrete dynamic system, as a function of time, set parameters, allocated biomass, and environmental conditions over time. The development of the botanical structure was developed in GreenLab by describing the physiological rules of each new phytomer produced, using a graph notation approach. The structures produced can be simple or complex depending on the characteristics of the meristems. Random events that alter the development of the plant architecture are introduced into the model as stochastic functions that modify the automaton transition rules. The validation of the model was found to be satisfactory for about 20 plant species (herbaceous, shrubs, and trees) showing stability of the estimated parameters in different climatic conditions. Being a deliberately simplified generic model, both from the point of view of ecophysiology and of representation of the structure, the agronomic applications are different, even with the necessary approximations. Feng et al. [] used GreenLab to calculate the 3D structure of maize after evaluating and calculating the various parameters at a given planting density, showing good adherence to the measured data. In plant breeding, Letort et al. [] considered the growth parameters, in first approximation, as invariants leading to an efficient selection in the search of ideotypes. Moving from individual plant to stand, the approximation of parameters increases as parameters are partitioned using a production area parameter, a function of density. Baey et al. [] used this approach to estimate stand biomass as a function of density, showing comparable performance to other specific models. GreenLab, according to their authors, has a modeling rigidity given the fact that feedback between growth and development is ignored in addition to the lack of mortality models, things that will be supported in future developments. Carbon allocation modeling has also been used in the literature to estimate fruit production and quality, as shown in L-PEACH, V-Mango, and QualiTree among the models analyzed in this work. MAppleT also models carbon allocation, but in this case it is not targeted to fruit production and quality but to plant architecture by simulating gravitrophism and light interception. Returning to the models for estimating the production and quality of the fruit, L-PEACH is proposed as a model aimed at studying the effects of crop load, in this case for the peach tree. The model, like GreenLab, estimates carbon allocation through source–sink interactions and the calculation of their potential. L-PEACH simulates the effects of management and genetic and environmental factors that may affect the plant through complex interactions between plant organs, obtained by manipulating and adjusting parameters such as fruit number, fruit behavior, and the stems’ storage capacity. The model is structured by modules, each for individual plant organs. Each individual organ can be evaluated as a source or sink of carbohydrates. The physiological parameters used were treated as electrical counterparts in that the calculation of carbohydrate storage, flux, and partitioning (amount (mass) of carbohydrate, carbohydrate concentration, carbohydrate flux, rate of photosynthesis, source/sink strength, resistance to concentration-driven flow) was done using equations studied in principle for the calculation of linear electrical circuits. The model is also interfaced with a method for calculating light distribution using a quasi-Monte Carlo method. The proposed model works well in a variety of agronomic applications such as canopy management. As shown by Lopez et al. [], L-PEACH has been used to guide experimental research by helping to identify or develop quantitative hypotheses of potential yield-limiting processes that can be measured in the field, as well as the reaction of trees to external manipulations such as pruning. L-PEACH is a good example of how architectural growth, carbohydrate assimilation and partitioning, and organ growth can simulate tree growth and physiology to provide integrated understanding of the environmental physiology of trees, in this case peach trees []. While also modeling the allocation of carbon in fruit trees, QualiTree has a different approach from L-PEACH because it does not generate the structure of the tree with architecture algorithms but needs data for initialization of the model that are the numbers of leafy shoots and fruits for each FU (Fruiting Unit). The model, after getting also as inputs the environmental parameters such as temperature, humidity, and PPFD for photosynthesis calculation, proceeds to the estimation of fruit quality. Agronomic practices influence the status of various classes such as winter or summer pruning. Pruning changes the shape to the structure of the tree, and QualiTree takes this into account by recalculating the source–sink balance and carbon exchange depending on the number of fruiting units and the distances between them. The main application of this model is crop management. Miras-Avalos et al. [] used QualiTree to model peach tree reactions to a pest attack in different domains: on different cultivars (Alexandra or Suncrest), thinning intensity, and presence or absence of pest attack, showing a difference in the results of the fruit quality calculation and offering satisfactory results. The model is limited only to the size, quality, and yield of fruits and needs to be expanded with other quality parameters and other modules such as the estimation of water absorption (to simulate irrigation practices). Designed to be a specific model for estimating fruit quality and quantity, V-Mango uses carbon and water allocation processes for fruits only. The modeled organs are fruits and flowers along with what the authors call Growth Units (GU), modeled using empirical distributions and thermal time. Fruit growth was determined using an ecophysiological model that simulated carbon and water-related processes at the fruiting branch scale. The generated 3D models are used to accurately calculate light interception and require several variables: axis length and diameter; number of leaves; individual leaf length, width, and area; internode length; and phyllotaxy. The values of these variables were measured from experimental data. The fruit growth model simulated the daily increase of fresh mass of each individual fruit and was calculated by dividing it into two growth phases: the first corresponding to cell division and the second to cell expansion. The mass of the fruit is calculated every day as a combination of the masses calculated in the two phases of cell growth considering also the external environmental conditions such as temperature, humidity, and light conditions. Although it is a specialized model on a single type of fruit tree, V-Mango lends itself to several agronomic applications such as studying phenology and how, for example, the tree under certain conditions reacts to a pest attack, as shown by Boudon et al. []. V-Mango, despite being applied in several crop management applications, has not yet implemented the effects of agronomic practices such as pruning that is instead present in other models reviewed in this work (e.g., L-PEACH cited earlier). Another specialized model on a fruit tree is MAppleT. Unlike the previous ones, although modeling the carbon allocation through the representation of the bud organs, stems, and leaves, being an SPM (Structural Plant Model), it is aimed only at the study of the structure of the tree (apple) influenced by gravity (gravitrophism). To do this, the authors have used stochastic topology models, on a Growth Unit (GU) scale, modeling their succession according to Markov chains. In order to estimate the effects of gravity on the structure, the authors also modeled the secondary growth of GUs and generated the shape of individual branches according to the biomechanical component of the model that estimates the bending and twisting of the branch itself. The generated 3D tree models were compared with empirical measurements on real trees, showing similarity between the real and modeled data. The effect of gravity on branches is also very similar to what the authors measured on real trees; however, the effect of gravity on morphogenesis, i.e., simulated gravitropism, is partially implemented. The authors note that there are discrepancies between the measured and model data of branch inclinations that are found to be incorrectly simulated. While MAppleT has limitations, it is the first model to simulate the effect of gravity on structure and has been used subsequently for crop management applications and biomechanics studies. For example, Han et al. [] used MAppleT to estimate the efficiency of light interception as a function of tree geometric trait. A different approach was proposed by Bailey with the FSPM Helios model []. The proposed model does not simulate carbon allocation but focuses more on the photosynthetic, energy balance, radiation pattern, and stomatal conductance part. To do this, the author built the model by separating it into “contexts”, “primitives” (defined as basic forms of individual plant elements), and separate, specialized “plug-ins” where the user has full control over parameters and processes. The plug-in (or module) for modeling radiation transfer was developed by Bailey in 2018 using a reverse ray-tracing method for modeling the net radiative flux in leaves []. The surface energy balance module was developed by considering the surface area of the single primitive and some parameters such as Stefan–Boltzmann constant, emissivity, and surface temperature, as well as external environmental parameters. The energy module depends on the estimated position of the sun based on Gueymard’s [] study. The stomatal conductance module is based on the studies of Buckley et al. [] where stomatal conductance is given by a hyperbolic function of photosynthetically active photon flux density and local vapor pressure deficit. The module for photosynthesis is given by the studies of Johnson [], and the mechanistic biochemical model of Farquhar et al. [] for C3 photosynthesis. One of the results that this model shows is that there are minimal differences in simulations of radiation absorption, transpiration, and photosynthesis through most of the day and in daily integrated distributions between isolated and dense canopy trees, raising questions about the representation of trees using simplified biophysical models. The Helios model was primarily used to model grapevine and vineyard management. As shown by Bahr et al. [], Helios allows the estimation of sunburn damage to berry in the vineyard as a function of leaf structure, density, and position, as well as vineyard architecture. Another use of the model was that proposed by Salter et al. [] in phenotyping using a virtual chickpea plant as support for validation of a 3D reconstruction system using structure from motion (SFM) algorithms. Radiative processes have also been modeled in other works analyzed in this paper, such as the GroIMP model, which is proposed as a generic model by combining L-systems with a graph structure and uses an inverse ray tracing system: the scene consists of a series of light sources and objects that absorb (or reflect) radiation. The ray is traced from the source to the target, in an inverse mode to what happens in a classical ray tracing system. The amount of light calculated at each point is used to estimate photosynthesis as the amount of carbon assimilated into the leaves, given the calculated radiation and leaf area. The carbon thus assimilated is redistributed among the organs, which in the case of GroIMP are buds and stems, via the carbon allocation model proposed by De Reffye et al. []. Being a generic model, GroIMP has been used in several agronomic applications: Vermeiren et al. [] studied how the shape of the leaves of a tomato plant affects light interception, Kang et al. [] characterized genotypically and phenotypically sunflower plantations based on differences in water budget, Streit et al. [] studied with GroIMP modeling how light interception changes when the geometry of Scots pine trees changes, and Kniemeyer et al. [] studied how different carrot plants compete with each other by self-shadowing processes and how planting can be optimized to maximize yield. Another generic model that exploits the potential of radiation processes is OpenALEA. This model simulates, by using specialized single-function modules interconnected with each other, the organs buds, stems and leaves, combining radiation processes with carbon and water allocation processes. Specifically, to analyze branching patterns and architecture, OpenALEA relies on the models proposed by Durand et al. [] and Guedon et al. [] based on statistical models of Markov chains and change point detection. For the ecophysiological study, OpenALEA relies on the models already proposed by Chelle and Andrieu [] and Sinoquet et al. [] Specifically, the radiation is calculated according to a radiosity algorithm where two surfaces, one emitting and the other receiving, are linked according to an equation that takes into account their transmittance, reflectance, and relative geometric position (how much they are exposed in front of each other in terms of surface area). Photosynthesis and relative carbon gain are computed for sunlit and shaded leaves of each vegetation component in each 3D cell. Photosynthetic rates are simulated according to C3 theory, as already seen for Helios. This model was used without including the potential limitation arising from triose phosphate utilization. The agronomic applications of OpenALEA range from biomechanical studies on fruit trees to crop management of vines, as shown by Louarn et al. []. The analyzed models RATP, Tomato, and Top-Vine share the modeling structure with OpenALEA, using the same carbon and water allocation processes in addition to radiation absorption processes. While RATP models bud organs, stems, and fruits, Top-Vine and Tomato model only stems and leaves. Again, the agronomic applications are different. As for RATP, the model was used for studies of plant response to drought. The geometry of the tree canopy was described as an array of 3D cells of defined size on the three axes. Each cell can contain different parts of the tree or be empty (Figure 5b), while the soil was discretized into a series of zones that exchange radiation with the vegetation. The plant properties are physical, such as angles of orientation of branches and leaves, and physiological (reactions to environmental conditions of the photosynthesis process if there are leaves). The model has as output the radiative balance, organ temperatures, carbon, and water balance in shaded and illuminated areas in each 3D cell. Ngao et al. [] used RATP to study the variability of leaf temperature and stomatal conductance enhanced by drought in apple tree. With Tomato, instead, Sarlikioti et al. [] studied how plant architecture affects light absorption and photosynthesis in tomato plants, using as a model for the photosynthesis process the one already analyzed and proposed by Farquhar et al. [], while the light input module is given by the studies of Chelle and Andrieu [] by calculating it with the inputs being the amount of light absorbed by each plant organ, the leaf transmittance and reflectance coefficients for the upper and lower side of the leaf, and the light from the light sources that were used to simulate the sky. The experiments were carried out in a virtual greenhouse at the variation of the 3D architecture of the plant. The ARHIMED model has a different approach in modeling the photosynthesis process: it is controlled together with transpiration by stomatal conductance parameter which can limit photosynthesis by reducing carbon dioxide influx and indirectly modulates leaf temperature through evaporation. Light exchange has been modeled by Vezy et al. [] as a discretized model along the directions, alternative to ray tracing and radiosity models, while the internal behavior of the leaves is governed by the water potential calculated according to a sap flow model. Perez et al. [] used ARHIMED to study architectural plasticity in response to planting density of oil palm. Dauzat et al. [] used ARHIMED to study ecophysiological processes on 3D Virtual Stands.
In the review of these works, a fragmentary nature of the approaches emerged, both from the model design point of view and more in depth, such as the choice of programming languages. It is sufficient to note that, just taking into account the works reviewed in this review, there are five different frameworks and ten programming languages, in addition to the fact that each model has its own set of processes, modules, organs, and applications. Many reuse modules already extensively validated in previous years, such as the C3 module of photosynthesis, while some propose new approaches but remain to be validated with field data. A greater uniformity of the models can be achieved by improving the standard of integration of the models, without losing a limited generality, as discussed by Louarn and Song []. The fragmentary nature of the proposed solutions can also be seen in the 3D output of the studied models: all of them present a non real-time 3D rendering, with different techniques. Only a few models use the 3D model as a functional part of the model itself, for example, to calculate the amount of light collected in photosynthesis processes. We believe that an improvement in this aspect can benefit the development of FSPM models, such as in the paper by Zhu et al. [], in which the 3D architecture of plants in the field is derived from photography of real plants. Their study applies this method to assess light distribution throughout the growing season. The 3D outputs of FSPMs could also be involved in the development of deep learning methods used for automatic image analysis: the realistic representation of plant architecture that FSPMs can generate could serve as a novel way to provide inexpensive datasets of rendered images for a wide range of phenotypes [,,].
3. 3D Tree-Rendering Techniques
As discussed in the previous sections, the analyzed models allow a 3D reconstruction of the results. The 3D model is generated using computer graphics techniques that can be generally classified in four categories: particle system and procedural methods, rule-based methods, and hybrid methods []. These methods are the most used and are based on the most recent and advanced techniques of 3D modeling. In this section, we provide a brief description of the rendering methodologies to get a clearer picture of the potential they can have by coupling them to a functional–structural model.
3.1. Particle Systems and Procedural Methods
The particle systems for the generation of trees were created by Reeves [] to represent in synthetic images the remarkable variety of irregular shapes and random variations exhibited by natural objects. Instead of using classical representations based on surfaces such as polygons, patches and quadratic surfaces, particle systems represent objects as a cloud of primitive particles that occupy the volume []. The algorithm consists of two successive steps. First, the general characteristics of the object are specified through a database; then, the generation of details comes in to describe the object completely. Details such as branches, buds, twigs, and leaves are generated in this phase. In the particle systems that shape trees, each tree is traced as a set of segments and small circles representing the branches and leaves, respectively. A set of initial features and dimensions, such as the height of the tree, is stochastically assigned before invoking the recursive branch generation procedure. The values of these parameters are randomly determined by distributions associated with the type of tree, according to phyllotaxis. Particle systems can model solid objects that are conventionally modeled with surface-based techniques. An example of the use of particle system technique to generate vegetation and trees is the SpeedTree® commercial software []. This software is made specifically for video game and movie development, and the graphic rendering is photorealistic. The focus is more on the visual results than on the biological modeling, although the generated trees appear very realistic. Weber and Penn [] proposed in 1995 a new approach to tree rendering based on particle systems with the goal of creating synthetic trees as realistically as possible. Weber and Penn’s procedure needs a set of approximately 50 input parameters such as stem splits, stem children, stem radius, leaves, pruning, vertical attraction, leaf orientation, and degradation at a certain range. The approximation of the model refers to simplification of tree shape and structure in order to minimize the number of parameters. The general appearance and the lower part size of the tree are the main parameters needed to start with tree generation. Then, branching levels are considered as well as trunk foot shapes. The algorithm continues for every maximal tree branching level using an average value in a range variation (i.e., child branch angle, deviation angle, length relative to father branch, number of branches, photropism) []. One of the most popular softwares using this approximate approach is Arbaro [].
3.2. Rule-Based Methods
Rule-based methods differ from procedural algorithms by implementing a formal rule in order to transform a primary state into a final one with the application of a number of changes. This supplies a compact description of complex final conditions, even if generating geometric data from a set of rules is an intensive computational task. Only recent computational advancements made it possible to work with the vast amount of data associated with large objects in near real time. Lindenmayer systems (L-systems) for the generation of tree geometry, described thoroughly in [], are widely used as rule-based method as described in the previous section (L-PEACH [], V-Mango [], MAppleT []). In addition to the models already described, L-systems are also used in commercial 3D modeling software such as OnyxTree from Onyx Computing []. Trees generated by this software are used only as visual elements in 3D art productions: they are visually very similar to trees, but they are lacking from the point of view of adherence to biological rules and interaction with the virtual environment, since this is not their purpose. However, they express all the potential that these technologies can put at the service of the FSPM models already analyzed. Another rule-based technique is the combination of the latter and procedural techniques, generating the shape as a combination of unitary components such as leaves, trunk and branch parts, and fruits. The distributions are produced using multiplication components that have built-in parameters defining the number of objects to be generated, their distribution characteristics, and their orientation. By connecting the components, the plant is defined as a directional graph. The graph represents the system of rules, and its edges describe the production dependencies. After the geometry of a parent component is generated, the production of the geometry for all the children is invoked [] until the entire descriptive graph is processed. In this way, the components can be interlinked freely, and recursions are also possible. One software that uses this generation method is XFrog from XFrog Inc. []. Nevertheless, as in other software, XFrog lacks a biological rule base. The positive thing about rule-based object production methods is that most plants on earth can be generated with a small number of components or parameters providing a user-friendly interface, being a good base for a future link between 3D rendering systems and FSPMs.
3.3. Hybrid Methods
Hybrid 3D modeling methods are those that attempt a link between biological growth rules and 3D shape generation rules. Some FSPM models discussed in this review can be considered as hybrids in a broad sense as they combine a functional–structural model with a 3D modeling part of the results obtained. From a 3D modeling software point of view, there are some noteworthy ones that try to create this link between biological rules (minimal and often not scientifically correct) and 3D modeling, showing the potential of the method. Laubwerk software developed Plants Kit 14, a 3D rendering plug-in for commercial software that claims to be based on botanical/biological rules []. In Plants Kit 14, the operator has the control only on 3D rendering parameters such as level of details (LOD), polygon density, and switching between “summer, fall, winter, spring” tree presets. Despite the claim of being based on botanical/biological rules, the operator has no control on these rules. The extensive research by Pirk et al. and the University of Kostanz [,] on 3D modeling of vegetation has led to the creation of a method to model synthetic trees to be interactive with surroundings (e.g., obstacles) or extract plausible growing steps. The generated trees can be used in 3D rendering software such as Maya, 3DS Max, and Houdini but are not for scientific applications. TheGrove3D is a commercial plug-in for Blender (Blender Foundation) [] open-source 3D rendering software. It can be considered as based on hybrid method because of the use of both procedural rendering techniques and biological models. Trees are generated according to some pre-set parameters (e.g., internode growth length, branch angle), with some of them that are species-specific. The biological model is based on a simulation of tree growth mechanisms such as branch elongation. The model considers the number of nodes and growing buds regulate their own growth by controlling the flow of sugars and hormones. The plug-in can grow and modify trees according to spatial occlusion or regulate growth in presence or absence of light and shadow. Hybrid models are the proof that an interface between the world of photorealistic 3D rendering and mathematical biological models is possible. The potentialities, as discussed, are numerous for both fields. For the modelers, it is possible to visualize the result of their models in a satisfying way, besides having a more precise feedback from the virtual environment, thanks to a structure very adherent to the reality, and besides the not less important calculation of some environmental parameters, such as the quantity of light, which is possible to calculate in a more precise way with a 3D model. For the 3D artists, it is possible on the other hand to have even more realistic trees because they are strictly adherent to biological rules of growth.
4. VISmaF: Synthetic Tree for Immersive Virtual Visualization in Smart Farming Model Porposal
In this section, we provide a proof of concept for a link between a biological mathematical model based on Ordinary Differential Equations (ODE) and a 3D real-time rendering engine and the results of first experiments with the model, showing how a synthetic tree reacts to different light amounts in a 3D real-time environment, first with a simple simulation of an internode growing in different light conditions (different growing rate), then expanding the model to the whole tree, showing how it grows differently under different virtual environmental light conditions. This link can operate in both ways, i.e., by rendering a tree using parameters from ODE solutions or by considering geometrical 3D data (e.g., the amount of light from the virtual scene) as input to solve the ODEs. We also provide the starting mathematical biological model in Simile [] and how we linked this model to the real-time 3D rendering engine. The proposed model is presented in more detail, with its validation, development, and detailed results in the companion paper []. In particular, the final tree is made up of several independent and interconnected modules, following object-oriented programming (OOP) paradigms:
- A biological mathematical model to simulate the internode and branch growth;
- A 3D structure module to render the tree.
The mathematical model is a set of ordinary differential equations able to simulate the internode elongation and the rules for stopping growth. The internode elongation is a function of environmental parameters (temperature and light) and some species parameters (growth rate and max length). Stopping rules of internode growth are simulated according to the concentration of an inhibitory substance produced during the internode elongation. Internodes grow until a given inhibitor concentration is reached; then, the tree enters a seasonal growth stop and starts growing again after the inhibitor concentration reaches a minimum (Figure 7). Restarting the growth, the system will generate one or more branches depending on the species-specific parameters set. Figure 8 shows the stock and flow model representation in the system dynamics tool Simile [].
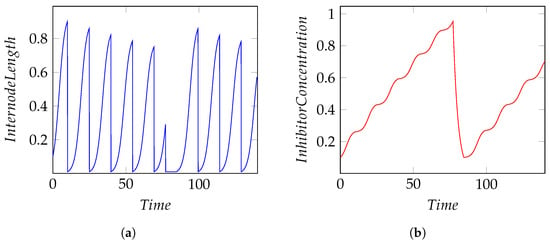
Figure 7.
Internode length and inhibitor concentration simulations. (a) Internode length; (b) inhibitor concentration.
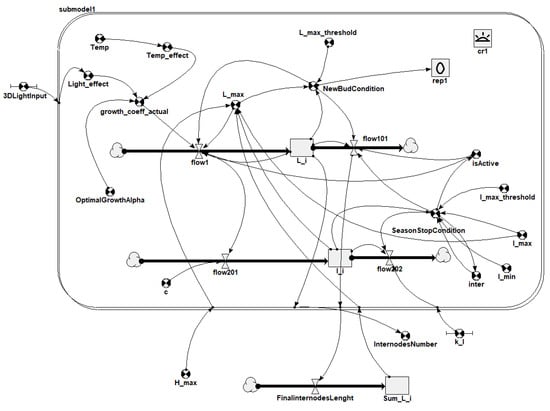
Figure 8.
Stock and flow model of internode growth in the system dynamics tool Simile.
The 3D module is composed by two different sub-modules: (a) internode module, finalized with the creation of the internode geometry (length and width) thanks to the data calculated by the integrator, which contains the stop-growth rules (maximum length reached) and the positioning of the apical bud; (b) bud module, modeled as a particular internode of unitary length, which stores information about the number of children to be generated, the branching angle, and the state of the bud (asleep/awake). A particular bud module called seed stores species-specific information about the tree and is hierarchically the first bud from which all subsequent buds, branches, and internodes descend. The modeling mathematical part is independent from the rendering part due to its modularity: the change of mathematical model does not affect the 3D generation part. The simulation is capable of calculating the amount of light in the virtual environment to be used as a parameter in the mathematical model of growth. Global illumination, radiosity, and ray-tracing solutions have been tested, each with their own precision and computational performance, leading to the conclusion to use a custom shader for the calculation of the amount of light. This solution is a balance between accuracy and computational performance, sufficient for the purpose of simulation. An ambient light sensor has been programmed that renders a temporary texture on the surface of the sensor itself, extracting an array of RGB values and converting them into brightness values (lux). The calculated value of the amount of light is used as a parameter in the calculation of the length of the internode in the relative module. A higher light amount leads to higher internode growth, and vice versa—lower light amount leads to lower internode growth, as shown in the first results (Figure 9). More detailed results and development of the model are provided in the companion paper []. The results of the first tests with the model are shown in Figure 9. A first simulation was performed with a simple one-child internode model at two different light conditions. In Figure 9a, it can be seen that internodes grow differently depending on the amount of ambient light in which they grow. The left internode has a shorter total length than the right internode as it grew in a low light environment. The result will be different with different amounts of light in terms of single internode length and total length. In the presence of branches, as shown in Figure 9b,c, even a simple tree behaves differently. Specifically, it was set as number of children equal to 2 and branching angle of 30° (the model allows to set species-specific parameters depending on the tree to be modeled, with the number of children and branching angle being some of them). From Figure 9b,c, it can be seen that the amount of light affects the total length of the tree and the lengths of individual internodes. Branching is triggered when the calculation of the inhibitor concentration, referred to the individual branch, reaches its maximum value. Once the maximum concentration is reached, the tree enters a seasonal growth stop phase until the inhibitor concentration reaches a minimum value. Upon reaching the minimum value, the tree resumes growth by generating the number of new branches set oriented according to the branching angle (Figure 7b). In addition, the length of the single internode decreases as the total height of the tree increases, in accordance with the model. Internodes at the top of the tree will be shorter than those on the main trunk (the first to grow from seed) because they are closer to the maximum height of the tree.
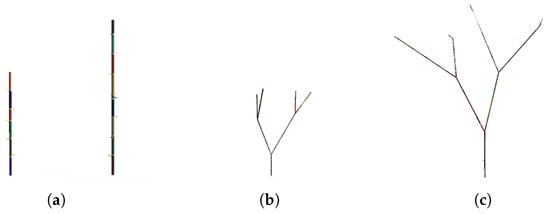
Figure 9.
Different growing rate and ramification of internodes under different light conditions. (a) Different amount of annual growth; (b) growth under low light; (c) growth under full light. Different internodes are rendered in different colors for showing purpose. (a) Amount of annual growth under different light conditions, with low ambient light (in shadow) on the left, and full ambient light on the right; (b) ramification process in low light conditions, with different colors used to show different internodes; (c) ramification process in full light conditions, with colors used to show different internodes.
5. Conclusions
As seen in previous sections, FSPM models can be used as a basis for creating 3D models of trees that are consistent with biological rules. However, not all models analyzed have 3D structure output that can be satisfactory from a visual or functional point of view. Techniques for 3D modeling of photorealistic trees do exist, as analyzed in Section 3, and we believe that an integration between the two worlds may be possible that can enhance both the field of mathematical biological modeling by being able to calculate some parameters more precisely, and the field of 3D modeling that can make use of a strong scientific basis to generate even more likely trees. A proof of concept of this integration has been presented in this paper, showing how it is possible to create a synthetic tree in a 3D real-time modeling environment from a mathematical biological model. The flexibility of the model is given by the use of interconnected modules according to the object-oriented programming (OOP) paradigm. The use of a proprietary shader for calculating the amount of light in the virtual environment provides further flexibility to the model. It is possible, in fact, to use the calculated amount of light to modify the main growth parameters such as branching angles and amount of growth. In this way, it is also possible to model the competition for light between near trees in addition to the change in branching direction caused by a tree’s own shadow. The proposed model is presented in more detail, with its validation, development, and detailed results in the companion paper [].
Author Contributions
Conceptualization, M.C.; methodology, M.C. and F.G.; investigation, M.C.; proof of concept, F.G., F.C. and M.C.; resources, M.C.; writing—original draft preparation, M.C.; writing—review and editing, M.C. and F.G.; supervision, F.G.; funding acquisition, F.G. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported and funded by the P.O.R. Campania FSE 2014/2020 “Dottorati di ricerca con caratterizzazione industriale” grant.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| FSPM | Functional–Structural Plant Model |
| FPM | Functional Plant Model |
| SPM | Sctructural Plant Model |
| ODE | Ordinary Differential Equation |
| RGG | Relational Growth Grammars |
| GU | Growth Units |
| FU | Fruiting Units |
References
- Zhang, Q.L.; Pang, M.Y. A survey of Modeling and Rendering Trees; Springer: Berlin/Heidelberg, Germany, 2008; pp. 757–764. [Google Scholar]
- Boudon, F.; Meyer, A.; Godin, C. Survey on Computer Representations of Trees for Realistic and Efficient Rendering. Research Report 2301, LIRIS UMR CNRS 5205. 2006. Available online: https://hal.inria.fr/hal-00830069/file/LIRIS-RR-2006-003.pdf (accessed on 1 September 2021).
- Ulam, S. Patterns of growth of figures: Mathematical aspects. In Module, Proportion, Symmetry, Rhythm; G. Braziller: New York, NY, USA, 1966; pp. 64–74. [Google Scholar]
- Greene, N. Voxel space automata: Modeling with stochastic growth processes in voxel space. In SIGGRAPH’89: Proceedings of the 16th Annual Conference on Computer Graphics and Interactive Techniques; Association for Computing Machinery: New York, NY, USA, 1989. [Google Scholar]
- Honda, H. Description of the form of trees by the parameters of the tree-like body: Effects of the branching angle and the branch length on the shape of the tree-like body. J. Theor. Biol. 1971, 31, 331–338. [Google Scholar] [CrossRef]
- Lindenmayer, A. Mathematical models for cellular interactions in development I. Filaments with one-sided inputs. J. Theor. Biol. 1968, 18, 280–299. [Google Scholar] [CrossRef]
- Prusinkiewicz, P.; Lindenmayer, A. The Algorithmic Beauty of Plants; Springer: New York, NY, USA, 1996. [Google Scholar]
- Oppenheimer, P. Real time design and animation of fractal plants and trees. In ACM Siggraph Computer Graphics; Association for Computing Machinery: New York, NY, USA, 1986; Volume 20, pp. 55–64. [Google Scholar]
- Deussen, O.; Lintermann, B. Digital Design of Nature: Computer Generated Plants and Organics; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Louarn, G.; Song, Y. Two decades of functional–structural plant modelling: Now addressing fundamental questions in systems biology and predictive ecology. Ann. Bot. 2020, 126, 501–509. [Google Scholar] [CrossRef]
- Zhu, B.; Liu, F.; Xie, Z.; Guo, Y.; Li, B.; Ma, Y. Quantification of light interception within image-based 3-D reconstruction of sole and intercropped canopies over the entire growth season. Ann. Bot. 2020, 126, 701–712. [Google Scholar] [CrossRef] [Green Version]
- Che, Y.; Wang, Q.; Xie, Z.; Zhou, L.; Li, S.; Hui, F.; Wang, X.; Li, B.; Ma, Y. Estimation of maize plant height and leaf area index dynamics using an unmanned aerial vehicle with oblique and nadir photography. Ann. Bot. 2020, 126, 765–773. [Google Scholar] [CrossRef]
- Lama, G.F.C.; Crimaldi, M.; Pasquino, V.; Padulano, R.; Chirico, G.B. Bulk Drag Predictions of Riparian Arundo donax Stands through UAV-Acquired Multispectral Images. Water 2021, 13, 1333. [Google Scholar] [CrossRef]
- Pirk, S.; Niese, T.; Deussen, O.; Neubert, B. Capturing and animating the morphogenesis of polygonal tree models. ACM Trans. Graph. TOG 2012, 31, 169. [Google Scholar] [CrossRef] [Green Version]
- Makowski, M.; Hädrich, T.; Scheffczyk, J.; Michels, D.L.; Pirk, S.; Pałubicki, W. Synthetic silviculture: Multi-scale modeling of plant ecosystems. ACM Trans. Graph. 2019, 38, 131. [Google Scholar] [CrossRef]
- Magnor, M.A.; Grau, O.; Sorkine-Hornung, O.; Theobalt, C. Digital Representations of the Real World: How to Capture, Model, and Render Visual Reality; AK Peters/CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Lama, G.F.C.; Errico, A.; Francalanci, S.; Solari, L.; Preti, F.; Chirico, G.B. Evaluation of Flow Resistance Models Based on Field Experiments in a Partly Vegetated Reclamation Channel. Geosciences 2020, 10, 47. [Google Scholar] [CrossRef] [Green Version]
- Millar, A.J.; Urquiza, U.; Freeman, P.L.; Hume, A.; Plotkin, G.D.; Sorokina, O.; Zardilis, A.; Zielinski, T. Practical steps to digital organism models, from laboratory model species to ‘Crops in silico. J. Exp. Bot. 2019, 70, 2403–2418. [Google Scholar] [CrossRef] [Green Version]
- Henke, M.; Kurth, W.; Buck-Sorlin, G. FSPM-P: Towards a general functional-structural plant model for robust and comprehensive model development. Front. Comput. Sci. 2016, 10, 1103–1117. [Google Scholar] [CrossRef]
- Cournède, P.H.; Kang, M.Z.; Mathieu, A.; Barczi, J.F.; Yan, H.P.; Hu, B.G. Structural Factorization of Plants to Compute Their Functional and Architectural Growth. Funct. Archit. Growth 2006, 82, 427–438. [Google Scholar] [CrossRef]
- Room, P.; Hanan, J.; Prusinkiewicz, P. Virtual plants: New perspectives for ecologists, pathologists and agricultural scientists. Trends Plant Sci. 1996, 1, 33–38. [Google Scholar] [CrossRef]
- Gumbau, J.; Chover, M.; Remolar, I.; Rebollo, C. View-dependent pruning for real-time rendering of trees. Comput. Graph. 2011, 35, 364–374. [Google Scholar] [CrossRef]
- Boudon, F.; Persello, S.; Jestin, A.; Briand, A.S.; Grechi, I.; Fernique, P.; Guédon, Y.; Léchaudel, M.; Lauri, P.E.; Normand, F. V-Mango: A functional–structural model of mango tree growth, development and fruit production. Ann. Bot. 2020, 126, 745–763. [Google Scholar] [CrossRef]
- Vries, J. How Plants Balance Competitive Growth and Defence: An Analysis of Virtual Plants in Dynamic Interactions. Ph.D. Dissertation, Wageningen University, Wageningen, The Netherlands, 2019. [Google Scholar]
- Lecarpentier, C.; Barillot, R.; Blanc, E.; Abichou, M.; Goldringer, I.; Barbillon, P. WALTer: A three-dimensional wheat model to study competition for light through the prediction of tillering dynamics. Ann. Bot. 2019, 123, 961–975. [Google Scholar] [CrossRef]
- Wu, A.; Doherty, A.; Farquhar, G.D.; Hammer, G.L. Simulating daily field crop canopy photosynthesis: An integrated software package. Funct. Plant Biol. 2018, 45, 362–377. [Google Scholar] [CrossRef] [Green Version]
- Zhou, X.; Schnepf, A.; Lacointe, A.; Vanderborght, J.; Leitner, D.; Vereecken, H.; Lobet, G. Presentation of CPlantBox: A whole functional-structural plant model (root and shoot) coupled with a mechanistic resolution of carbon and water flows. In Proceedings of the 2018 6th International Symposium on Plant Growth Modeling, Simulation, Visualization and Applications (PMA), Hefei, China, 4–8 November 2018; pp. 147–151. [Google Scholar] [CrossRef]
- Crimaldi, M.; Cartenì, F.; Giannino, F. VISmaF: Synthetic Tree for Immersive Virtual Visualization in Smart Farming. Part II: Model Development, Validation and Results. Available online: https://sciforum.net/manuscripts/9880/manuscript.pdf (accessed on 28 September 2021).
- DeJong, T.M.; Da Silva, D.; Vos, J.; Escobar-Gutiérrez, A.J. Using functional–structural plant models to study, understand and integrate plant development and ecophysiology. Ann. Bot. 2011, 108, 987–989. [Google Scholar] [CrossRef] [Green Version]
- Godin, C.; Sinoquet, H. Functional–structural plant modelling. New Phytol. 2005, 166, 705–708. [Google Scholar] [CrossRef]
- Godin, C. Representing and encoding plant architecture: A review. Ann. For. Sci. 2000, 57, 413–438. [Google Scholar] [CrossRef]
- Chaudhury, A.; Godin, C. Geometry Reconstruction of Plants. In Intelligent Image Analysis for Plant Phenotyping; CRC Press: Boca Raton, FL, USA, 2020; pp. 119–142. [Google Scholar]
- Kahlen, K.; Chen, T.W. Predicting Plant Performance Under Simultaneously Changing Environmental Conditions—The Interplay Between Temperature, Light, and Internode Growth. Front. Plant Sci. 2015, 6, 1130. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, N.; Van Westreenen, A.; Anten, N.P.; Evers, J.B.; Marcelis, L.F. Disentangling the effects of photosynthetically active radiation and red to far-red ratio on plant photosynthesis under canopy shading: A simulation study using a functional–structural plant model. Ann. Bot. 2020, 126, 635–646. [Google Scholar] [CrossRef] [PubMed]
- Lam, Z.; King, S.A. Simulating tree growth based on internal and environmental factors. In Proceedings of the 3rd International Conference on Computer Graphics and Interactive Techniques in Australasia and South East Asia, Dunedin, New Zealand, 29 November–2 December 2005; Association for Computing Machinery: Dunedin, New Zealand, 2005. GRAPHITE’05. pp. 99–107. [Google Scholar] [CrossRef]
- Barczi, J.F.; Rey, H.; Caraglio, Y.; de Reffye, P.; Barthélémy, D.; Dong, Q.X.; Fourcaud, T. AmapSim: A Structural Whole-plant Simulator Based on Botanical Knowledge and Designed to Host External Functional Models. Ann. Bot. 2008, 101, 1125–1138. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhou, X.R.; Schnepf, A.; Vanderborght, J.; Leitner, D.; Lacointe, A.; Vereecken, H.; Lobet, G. CPlantBox, a whole-plant modelling framework for the simulation of water- and carbon-related processes. Silico Plants 2020, 2, diaa001. [Google Scholar] [CrossRef] [Green Version]
- De Reffye, P.; Hu, B.; Kang, M.; Letort, V.; Jaeger, M. Two decades of research with the GreenLab model in Agronomy. Ann. Bot. 2020. [Google Scholar] [CrossRef]
- Allen, M.T.; Prusinkiewicz, P.; DeJong, T.M. Using L-systems for modeling source-sink interactions, architecture and physiology of growing trees: The L-PEACH model. New Phytol. 2005, 166, 869–880. [Google Scholar] [CrossRef] [Green Version]
- Bailey, B.N. Helios: A Scalable 3D Plant and Environmental Biophysical Modeling Framework. Front. Plant Sci. 2019, 10, 1185. [Google Scholar] [CrossRef] [PubMed]
- Kniemeyer, O.; Buck-Sorlin, G.; Kurth, W. GroIMP as a platform for functional-structural modelling of plants. Frontis 2007, 22, 43–52. [Google Scholar]
- Lescourret, F.; Moitrier, N.; Valsesia, P.; Génard, M. QualiTree, a virtual fruit tree to study the management of fruit quality. I. Model development. Trees 2011, 25, 519–530. [Google Scholar] [CrossRef]
- Dauzat, J.; Franck, N.; Rapidel, B.; Luquet, D.; Vaast, P. Simulation of ecophysiological processes on 3D virtual stands with the ARCHIMED simulation platform. In Proceedings of the 2006 Second International Symposium on Plant Growth Modeling and Applications, Beijing, China, 13–17 November 2006; pp. 101–108. [Google Scholar] [CrossRef]
- Sinoquet, H.; Le Roux, X.; Adam, B.; Ameglio, T.; Daudet, F.A. RATP: A model for simulating the spatial distribution of radiation absorption, transpiration and photosynthesis within canopies: Application to an isolated tree crown. Plant Cell Environ. 2001, 24, 395–406. [Google Scholar] [CrossRef]
- Sarlikioti, V.; de Visser, P.H.B.; Buck-Sorlin, G.H.; Marcelis, L.F.M. How plant architecture affects light absorption and photosynthesis in tomato: Towards an ideotype for plant architecture using a functional–structural plant model. Ann. Bot. 2011, 108, 1065–1073. [Google Scholar] [CrossRef] [Green Version]
- Pradal, C.; Dufour-Kowalski, S.; Boudon, F.; Fournier, C.; Godin, C. OpenAlea: A visual programming and component-based software platform for plant modelling. Funct. Plant Biol. 2008, 35, 751–760. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Costes, E.; Smith, C.; Renton, M.; Guédon, Y.; Prusinkiewicz, P.; Godin, C. MAppleT: Simulation of apple tree development using mixed stochastic and biomechanical models. Funct. Plant Biol. 2008, 35, 936–950. [Google Scholar] [CrossRef] [Green Version]
- Louarn, G.; Lebon, E.; Lecoeur, J. “Top-vine”, a topiary approach based architectural model to simulate vine canopy structure. In Proceedings of the XIV International GESCO Viticulture Congress, Geisenheim, Germany, 23–27 August 2005; pp. 464–470. [Google Scholar]
- Leroy, C.; Sabatier, S.; Wahyuni, N.S.; Barczi, J.F.; Dauzat, J.; Laurans, M.; Auclair, D. Virtual trees and light capture: A method for optimizing agroforestry stand design. Agrofor. Syst. 2009, 77, 37–47. [Google Scholar] [CrossRef]
- Xia, N.; Li, A.; Lin, W. Simulation and Quantitative Analysis of Branching Patterns of the Plum Tree. J. Comput. Sci. Technol. Updat. 2014, 1, 9–18. [Google Scholar] [CrossRef]
- Sellier, D.; Fourcaud, T. Crown structure and wood properties: Influence on tree sway and response to high winds. Am. J. Bot. 2009, 96, 885–896. [Google Scholar] [CrossRef] [PubMed]
- Griffon, S.; de Coligny, F. AMAPstudio: An editing and simulation software suite for plants architecture modelling. Ecol. Model. 2014, 290, 3–10. [Google Scholar] [CrossRef]
- Duchemin, L.; Eloy, C.; Badel, E.; Moulia, B. Tree crowns grow into self-similar shapes controlled by gravity and light sensing. J. R. Soc. Interface 2018, 15, 20170976. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rakocevic, M.; Matsunaga, F.T.; Novaes, M.P.; Oyamada, R.S.; Scholz, M.B.D.S.; Griffon, S.; Dauzat, J.; Costes, E. How density and planting pattern affect coffee plant structure and berry distribution in first production year? In Proceedings of the 25th International Conference on Coffee Science, ASIC 2014, Armenia, Colombia, 8–13 September 2014; Association Scientifique Internationale du Café: Paris, France, 2014. [Google Scholar]
- Momo Takoudjou, S.; Ploton, P.; Sonké, B.; Hackenberg, J.; Griffon, S.; de Coligny, F.; Kamdem, N.G.; Libalah, M.; Mofack, G.I.; Le Moguédec, G.; et al. Using terrestrial laser scanning data to estimate large tropical trees biomass and calibrate allometric models: A comparison with traditional destructive approach. Methods Ecol. Evol. 2018, 9, 905–916. [Google Scholar] [CrossRef]
- Magistri, F.; Chebrolu, N.; Behley, J.; Stachniss, C. Towards In-Field Phenotyping Exploiting Differentiable Rendering with Self-Consistency Loss. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 13960–13966. [Google Scholar] [CrossRef]
- Ahmed, M.; Aslam, M.A.; Fayyaz-ul-Hassan; Hayat, R.; Nasim, W.; Akmal, M.; Mubeen, M.; Hussain, S.; Ahmad, S. Nutrient Dynamics and the Role of Modeling. In Building Climate Resilience in Agriculture: Theory, Practice and Future Perspective; Jatoi, W.N., Mubeen, M., Ahmad, A., Cheema, M.A., Lin, Z., Hashmi, M.Z., Eds.; Springer International Publishing: Cham, Switzerland, 2022; pp. 297–316. [Google Scholar] [CrossRef]
- Schnepf, A.; Leitner, D.; Landl, M.; Lobet, G.; Mai, T.H.; Morandage, S.; Sheng, C.; Zörner, M.; Vanderborght, J.; Vereecken, H. CRootBox: A structural–functional modelling framework for root systems. Ann. Bot. 2018, 121, 1033–1053. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kang, M.; Heuvelink, E.; Carvalho, S.M.P.; Reffye, P.d. A virtual plant that responds to the environment like a real one: The case for chrysanthemum. New Phytol. 2012, 195, 384–395. [Google Scholar] [CrossRef] [PubMed]
- Cournède, P.H.; Mathieu, A.; Houllier, F.; Barthélémy, D.; de Reffye, P. Computing Competition for Light in the GREENLAB Model of Plant Growth: A Contribution to the Study of the Effects of Density on Resource Acquisition and Architectural Development. Ann. Bot. 2007, 101, 1207–1219. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Feng, L.; Mailhol, J.C.; Rey, H.; Griffon, S.; Auclair, D.; De Reffye, P. Comparing an empirical crop model with a functional structural plant model to account for individual variability. Eur. J. Agron. 2014, 53, 16–27. [Google Scholar] [CrossRef]
- Letort, V.; Mahe, P.; Cournède, P.H.; De Reffye, P.; Courtois, B. Quantitative genetics and functional–structural plant growth models: Simulation of quantitative trait loci detection for model parameters and application to potential yield optimization. Ann. Bot. 2008, 101, 1243–1254. [Google Scholar] [CrossRef] [PubMed]
- Baey, C.; Didier, A.; Lemaire, S.; Maupas, F.; Cournède, P.H. Parametrization of five classical plant growth models applied to sugar beet and comparison of their predictive capacity on root yield and total biomass. Ecol. Model. 2014, 290, 11–20. [Google Scholar] [CrossRef] [Green Version]
- Da Silva, D.; Qin, L.; DeBuse, C.; DeJong, T.M. Measuring and modelling seasonal patterns of carbohydrate storage and mobilization in the trunks and root crowns of peach trees. Ann. Bot. 2014, 114, 643–652. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lopez, G.; Favreau, R.R.; Smith, C.; Costes, E.; Prusinkiewicz, P.; DeJong, T.M. Integrating simulation of architectural development and source–sink behaviour of peach trees by incorporating Markov chains and physiological organ function submodels into L-PEACH. Funct. Plant Biol. 2008, 35, 761–771. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fei, Z.; Olenskyj, A.G.; Bailey, B.N.; Earles, M. Enlisting 3D crop models and GANs for more data efficient and generalizable fruit detection. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV) Workshops, Virtual, 24–26 November 2021; pp. 1269–1277. [Google Scholar]
- Ponce de León, M.A.; Bailey, B.N. A 3D model for simulating spatial and temporal fluctuations in grape berry temperature. Agric. For. Meteorol. 2021, 306, 108431. [Google Scholar] [CrossRef]
- Salter, W.T.; Shrestha, A.; Barbour, M.M. Open source 3D phenotyping of chickpea plant architecture across plant development. Plant Methods 2021, 17, 95. [Google Scholar] [CrossRef] [PubMed]
- Bahr, C.; Schmidt, D.; Kahlen, K. Missing Links in Predicting Berry Sunburn in Future Vineyards. Front. Plant Sci. 2021, 12, 2178. [Google Scholar] [CrossRef] [PubMed]
- Qu, H.; Zhu, Q.; Guo, M.; Lu, Z. Simulation of carbon-based model for virtual plants as complex adaptive system. Simul. Model. Pract. Theory 2010, 18, 677–695. [Google Scholar] [CrossRef]
- Coussement, J.R.; De Swaef, T.; Lootens, P.; Roldán-Ruiz, I.; Steppe, K. Introducing turgor-driven growth dynamics into functional–structural plant models. Ann. Bot. 2018, 121, 849–861. [Google Scholar] [CrossRef] [PubMed]
- Kang, F.; Cournède, P.H.; Lecoeur, J.; Letort, V. SUNLAB: A functional–structural model for genotypic and phenotypic characterization of the sunflower crop. Ecol. Model. 2014, 290, 21–33. [Google Scholar] [CrossRef] [Green Version]
- Henke, M.; Huckemann, S.; Kurth, W.; Sloboda, B. Reconstructing Leaf Growth Based on Non-Destructive Digitizing and Low-Parametric Shape Evolution for Plant Modelling over a Growth Cycle. Silva Fenn. 2014, 48. [Google Scholar] [CrossRef] [Green Version]
- Streit, K.; Henke, M.; Bayol, B.; Cournède, P.H.; Sievänen, R.; Kurth, W. Impact of geometrical traits on light interception in conifers: Analysis using an FSPM for Scots pine. In Proceedings of the 2016 IEEE International Conference on Functional-Structural Plant Growth Modeling, Simulation, Visualization and Applications (FSPMA), Qingdao, China, 7–11 November 2016; pp. 194–203. [Google Scholar] [CrossRef]
- Auzmendi, I.; Hanan, J. Using L-studio to Visualize Data and Modify Plant Architecture for Agronomic Purposes: Visualization and modification of plant architecture with L-studio. In Proceedings of the 2018 6th International Symposium on Plant Growth Modeling, Simulation, Visualization and Applications (PMA), Hefei, China, 4–8 November 2018; pp. 43–49. [Google Scholar] [CrossRef]
- Anderson, N.T.; Walsh, K.B.; Wulfsohn, D. Technologies for Forecasting Tree Fruit Load and Harvest Timing—From Ground, Sky and Time. Agronomy 2021, 11, 1409. [Google Scholar] [CrossRef]
- Zheng, J.; Tarin, M.W.K.; Jiang, D.; Li, M.; Zhang, M.; Chen, L.; He, T.; Hong, X.; Zheng, Y. Various distances and orientations influenced the branching traits of Dendrocalamus minor var. amoenus in Dongshan Island, China. Glob. Ecol. Conserv. 2021, 26, e01468. [Google Scholar] [CrossRef]
- Lauri, P.E. Tree architecture and functioning facing multispecies environments: We have gone only halfway in fruit-trees. Am. J. Bot. 2021, 108, 3–7. [Google Scholar] [CrossRef] [PubMed]
- Mirás-Avalos, J.M.; Egea, G.; Nicolás, E.; Génard, M.; Vercambre, G.; Moitrier, N.; Valsesia, P.; González-Real, M.M.; Bussi, C.; Lescourret, F. QualiTree, a virtual fruit tree to study the management of fruit quality. II. Parameterisation for peach, analysis of growth-related processes and agronomic scenarios. Trees 2011, 25, 785–799. [Google Scholar] [CrossRef]
- Vezy, R.; Perez, R.P.; Grand, F.; Dauzat, J. Light Exchanges in Discrete Directions as an Alternative to Raytracing and Radiosity. 2020. Available online: https://www.researchgate.net/publication/344340475_Light_exchanges_in_discrete_directions_as_an_alternative_to_raytracing_and_radiosity?channel=doi&linkId=5f6a4ee6458515b7cf46d473&showFulltext=true (accessed on 1 August 2021).
- Leroy, C.; Laurans, M.; Dauzat, J.; Sabatier, S.A.; Auclair, D. Simulation of light transmission under Acacia mangium Willd. and Tecton grandis L. canopies and comparison with in situ measurements. In Proceedings of the International Worhshop on Smallholder Agroforestry Option for Degraded Soils, Malany, Indonesia, 18–21 August 2005. [Google Scholar]
- Prieto, J.A.; Louarn, G.; Perez Peña, J.; Ojeda, H.; Simonneau, T.; Lebon, E. A functional–structural plant model that simulates whole-canopy gas exchange of grapevine plants (Vitis vinifera L.) under different training systems. Ann. Bot. 2020, 126, 647–660. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bouchon, J.; De Reffye, P.; Barthélémy, D. Modélisation et Simulation de l’Architecture des végéTaux. In Proceedings of the Colloque sur l’architecture des Arbres Fruitiers et Forestiers, Montpellier, France, 10 December 1997. [Google Scholar]
- Jaeger, M.; De Reffye, P.H. Basic concepts of computer simulation of plant growth. J. Biosci. 1992, 17, 275–291. [Google Scholar] [CrossRef]
- Grossman, Y.L.; DeJong, T.M. PEACH: A simulation model of reproductive and vegetative growth in peach trees. Tree Physiol. 1994, 14, 329–345. [Google Scholar] [CrossRef] [PubMed]
- Karwowski, R.; Prusinkiewicz, P. The L-system-based plant-modeling environment L-studio 4.0. In Proceedings of the 4th International Workshop on Functional-Structural Plant Models, Montpellier, France, 7–11 June 2004; pp. 403–405. [Google Scholar]
- Le Roux, X.; Lacointe, A.; Escobar-Gutiérrez, A.; Le Dizès, S. Carbon-based models of individual tree growth: A critical appraisal. Ann. For. Sci. 2001, 58, 469–506. [Google Scholar] [CrossRef] [Green Version]
- Sinclair, T.; Murphy, C.; Knoerr, K. Development and evaluation of simplified models for simulating canopy photosynthesis and transpiration. J. Appl. Ecol. 1976, 13, 813–829. [Google Scholar] [CrossRef]
- Friend, A. Modelling canopy CO2 fluxes: Are ‘big-leaf’simplifications justified? Glob. Ecol. Biogeogr. 2001, 10, 603–619. [Google Scholar] [CrossRef]
- Raupach, M.; Finnigan, J. ‘Single-layer models of evaporation from plant canopies are incorrect but useful, whereas multilayer models are correct but useless’: Discuss. Aust. J. Plant Physiol. 1988, 15, 705–716. [Google Scholar] [CrossRef]
- Hemmerling, R.; Kniemeyer, O.; Lanwert, D.; Kurth, W.; Buck-Sorlin, G. The rule-based language XL and the modelling environment GroIMP illustrated with simulated tree competition. Funct. Plant Biol. 2008, 35, 739–750. [Google Scholar] [CrossRef] [PubMed]
- Weber, J.; Penn, J. Creation and Rendering of Realistic Trees. In Proceedings of the SIGGRAPH’95: Proceedings of the 22nd Annual Conference on Computer Graphics and Interactive Techniques, Los Angeles, CA, USA, 6–11 August 1995; pp. 119–128. [Google Scholar]
- Kurth, W.; Kniemeyer, O.; Buck-Sorlin, G. Relational Growth Grammars – A Graph Rewriting Approach to Dynamical Systems with a Dynamical Structure. In Unconventional Programming Paradigms; Banâtre, J.P., Fradet, P., Giavitto, J.L., Michel, O., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2005; pp. 56–72. [Google Scholar] [CrossRef]
- Plachetka, T. POV Ray: Persistence of vision parallel raytracer. In Proceedings of the Spring Conference on Computer Graphics, Budmerice, Slovakia, 23–25 April 1998; Volume 123. [Google Scholar]
- Měch, R.; Prusinkiewicz, P. Visual models of plants interacting with their environment. In Proceedings of the 23rd Annual Conference on Computer Graphics and Interactive Techniques, New Orleans, Louisiana, 4–9 August 1996; pp. 397–410. [Google Scholar]
- Karwowski, R.; Prusinkiewicz, P. Design and Implementation of the L+C Modeling Language. In Proceedings of the 4th International Workshop, RULE 2003 (Connected RDP’03 Federated. Conference on Rewriting, Deduction, and Programming), Valencia, Spain, 9 June 2003; Volume 86, pp. 134–152. [Google Scholar] [CrossRef] [Green Version]
- Zhu, J.; Dai, Z.; Vivin, P.; Gambetta, G.A.; Henke, M.; Peccoux, A.; Ollat, N.; Delrot, S. A 3-D functional–structural grapevine model that couples the dynamics of water transport with leaf gas exchange. Ann. Bot. 2018, 121, 833–848. [Google Scholar] [CrossRef]
- Hallé, F.; Oldeman, R.A.; Tomlinson, P.B. Tropical Trees and Forests: An Architectural Analysis; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Boudon, F.; Pradal, C.; Cokelaer, T.; Prusinkiewicz, P.; Godin, C. L-Py: An L-system simulation framework for modeling plant architecture development based on a dynamic language. Front. Plant Sci. 2012, 3, 76. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dauzat, J.; Rapidel, B.; Berger, A. Simulation of leaf transpiration and sap flow in virtual plants: Model description and application to a coffee plantation in Costa Rica. Agric. For. Meteorol. 2001, 109, 143–160. [Google Scholar] [CrossRef]
- De Visser, P.H.B.; van der Heijden, G.; Buck-Sorlin, G. Optimizing illumination in the greenhouse using a 3D model of tomato and a ray tracer. Front. Plant Sci. 2014, 5, 48. [Google Scholar] [CrossRef] [Green Version]
- Dieleman, J.A.; De Visser, P.H.B.; Meinen, E.; Grit, J.G.; Dueck, T.A. Integrating Morphological and Physiological Responses of Tomato Plants to Light Quality to the Crop Level by 3D Modeling. Front. Plant Sci. 2019, 10, 839. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Louarn, G.; Lecoeur, J.; Lebon, E. A Three-dimensional Statistical Reconstruction Model of Grapevine (Vitis vinifera) Simulating Canopy Structure Variability within and between Cultivar/Training System Pairs. Ann. Bot. 2008, 101, 1167–1184. [Google Scholar] [CrossRef] [Green Version]
- Barillot, R.; Huynh, P.; Gutiérrez, A.E.; Combes, D. L-Pea: An architectural model of pea (Pisum sativum) development. In Proceedings of the 7th International Conference on Functional Structure PLANT models, Saariselkä, Finland, 9–14 June 2013; p. 371. [Google Scholar]
- Ascher, D.; Lutz, M. Learning Python; O’Reilly: Newton, MA, USA, 1999. [Google Scholar]
- Councill, B.; Heineman, G.T. Definition of a software component and its elements. In Component-Based Software Engineering: Putting the Pieces Together; Springer: Berlin/Heidelberg, Germany, 2001; pp. 5–19. [Google Scholar]
- Yan, H.P.; Kang, M.Z.; De Reffye, P.; Dingkuhn, M. A dynamic, architectural plant model simulating resource-dependent growth. Ann. Bot. 2004, 93, 591–602. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lacointe, A.; Minchin, P.E.H. A Mechanistic Model to Predict Distribution of Carbon Among Multiple Sinks. In Phloem: Methods and Protocols; Liesche, J., Ed.; Methods in Molecular Biology; Springer: New York, NY, USA, 2019; pp. 371–386. [Google Scholar] [CrossRef]
- Han, L.; Costes, E.; Boudon, F.; Cokelaer, T.; Pradal, C.; Da Silva, D.; Faivre, R. Investigating the influence of geometrical traits on light interception efficiency of apple trees: A modelling study with MAppleT. In Proceedings of the 2012 IEEE 4th International Symposium on Plant Growth Modeling, Simulation, Visualization and Applications, Shanghai, China, 31 October–3 November 2012; pp. 152–159. [Google Scholar] [CrossRef] [Green Version]
- Bailey, B.N. A reverse ray-tracing method for modelling the net radiative flux in leaf-resolving plant canopy simulations. Ecol. Model. 2018, 368, 233–245. [Google Scholar] [CrossRef] [Green Version]
- Gueymard, C.A. Direct solar transmittance and irradiance predictions with broadband models. Part I: Detailed theoretical performance assessment. Solar Energy 2003, 74, 355–379. [Google Scholar] [CrossRef]
- Buckley, T.N.; Turnbull, T.L.; Adams, M.A. Simple models for stomatal conductance derived from a process model: Cross-validation against sap flux data. Plant Cell Environ. 2012, 35, 1647–1662. [Google Scholar] [CrossRef] [PubMed]
- Johnson, I. PlantMod: Exploring the Physiology of Plant Canopies; IMJ Software: Armidale, NSW, Australia, 2010. [Google Scholar]
- Farquhar, G.D.; von Caemmerer, S.v.; Berry, J.A. A biochemical model of photosynthetic CO2 assimilation in leaves of C3 species. Planta 1980, 149, 78–90. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- De Reffye, P.; Houllier, F.; Blaise, F.; Fourcaud, T. Essai sur les relations entre l’architecture d’un arbre et la grosseur de ses axes végétatifs. In Modélisation et Simulation de L’architecture des Végétaux; INRA, CIRAD-GERDAT-AMAP: Paris, France, 1997. [Google Scholar]
- Vermeiren, J.; Villers, S.L.Y.; Wittemans, L.; Vanlommel, W.; van Roy, J.; Marien, H.; Coussement, J.R.; Steppe, K. Quantifying the importance of a realistic tomato (Solanum lycopersicum) leaflet shape for 3-D light modelling. Ann. Bot. 2020, 126, 661–670. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Durand, J.B.; Caraglio, Y.; Heuret, P.; Nicolini, E. Segmentation-based approaches for characterising plant architecture and assessing its plasticity at different scales. In Proceedings of the FSPM07—5th International Workshop on Functional-Structural Plant Models, Napier, New Zealand, 4–9 November 2007; pp. 1–3. [Google Scholar]
- Guédon, Y.; Caraglio, Y.; Heuret, P.; Lebarbier, E.; Meredieu, C. Identifying and characterizing the ontogenetic component in tree development. In Proceedings of the 5th International Workshop on Functional-Structural Plant Models, Napier, New Zealand, 4–9 November 2007; pp. 1–5. [Google Scholar]
- Chelle, M.; Andrieu, B. The nested radiosity model for the distribution of light within plant canopies. Ecol. Model. 1998, 111, 75–91. [Google Scholar] [CrossRef]
- Ngao, J.; Adam, B.; Saudreau, M. Intra-crown spatial variability of leaf temperature and stomatal conductance enhanced by drought in apple tree as assessed by the RATP model. Agric. For. Meteorol. 2017, 237–238, 340–354. [Google Scholar] [CrossRef]
- Perez, R.; Vezy, R.; Brancheriau, L.; Boudon, F.; Raharjo, D.A.; Caliman, J.P.; Dauzat, J. Toward a functional-structural model of oil palm accounting for architectural plasticity in response to planting density. In Proceedings of the FSPM 2020: Towards Computable Plants. 9th International Conference on Functional-Structural Plant Models, Allemagne, Germany, 5–9 October 2020. [Google Scholar]
- Liu, Z.; Shen, C.; Li, Z.; Weng, T.; Deussen, O.; Cheng, Z.; Wang, D. Interactive modeling of trees using VR devices. In Proceedings of the 2019 International Conference on Virtual Reality and Visualization (ICVRV), Hong Kong, China, 21–22 November 2019; pp. 69–75. [Google Scholar] [CrossRef]
- Ubbens, J.; Cieslak, M.; Prusinkiewicz, P.; Stavness, I. The use of plant models in deep learning: An application to leaf counting in rosette plants. Plant Methods 2018, 14, 6. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Reeves, W.T. Particle systems—A technique for modeling a class of fuzzy objects. ACM Trans. Graph. 1983, 2, 91–108. [Google Scholar] [CrossRef]
- IDV. SpeedTree® [Computer Program]. Available online: https://store.speedtree.com/ (accessed on 1 August 2021).
- de la Re, A.; Abad, F.; Camahort, E.; Juan, M.C. Tools for Procedural Generation of Plants in Virtual Scenes; Springer: Berlin/Heidelberg, Germany, 2009; pp. 801–810. [Google Scholar]
- Diestel, W. Arbaro Tree Generation for Povray [Computer Program]. Available online: http://arbaro.sourceforge.net/ (accessed on 1 September 2021).
- OnyxComputing. OnyxTree [Computer Program]. Available online: http://www.onyxtree.com/ (accessed on 1 September 2021).
- XFrog. XFrog Plants [Computer Program]. Available online: http://xfrog.com/ (accessed on 1 September 2021).
- Laubwerk. Plants Kit 14® [Computer Program]. Available online: https://www.laubwerk.com/ (accessed on 1 August 2021).
- Pirk, S.; Stava, O.; Kratt, J.; Said, M.A.M.; Neubert, B.; Měch, R.; Benes, B.; Deussen, O. Plastic trees: Interactive self-adapting botanical tree models. ACM Trans. Graph. TOG 2012, 31, 50. [Google Scholar] [CrossRef]
- van Keulen, F.W. TheGrove3D© [Computer Program]. Available online: https://www.thegrove3d.com/ (accessed on 1 July 2021).
- Simulistics. Simile [Computer Program]. Available online: https://www.simulistics.com/products/simile.php (accessed on 1 June 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).