Genomic Selection and Genome-Wide Association Studies for Grain Protein Content Stability in a Nested Association Mapping Population of Wheat
Abstract
:1. Introduction
2. Materials and Methods
2.1. Plant Material and Trait Measurement
2.2. Statistical Analysis
2.3. Stability Analysis
2.4. Genotyping
2.5. Population Structure and Genome-Wide Association Studies
2.6. Genomic Selection
3. Results
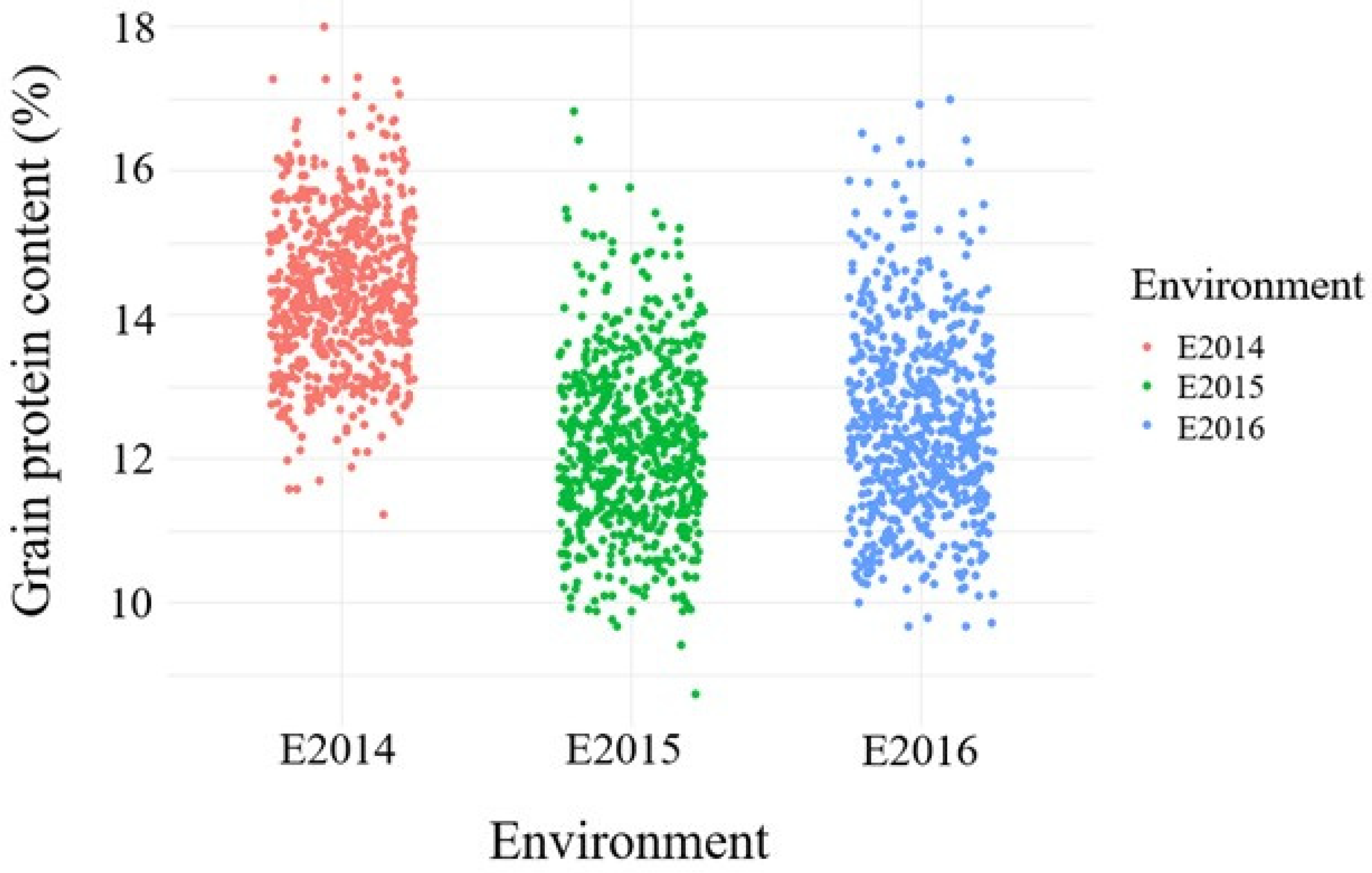
3.1. Variation of Grain Protein Content across Environments
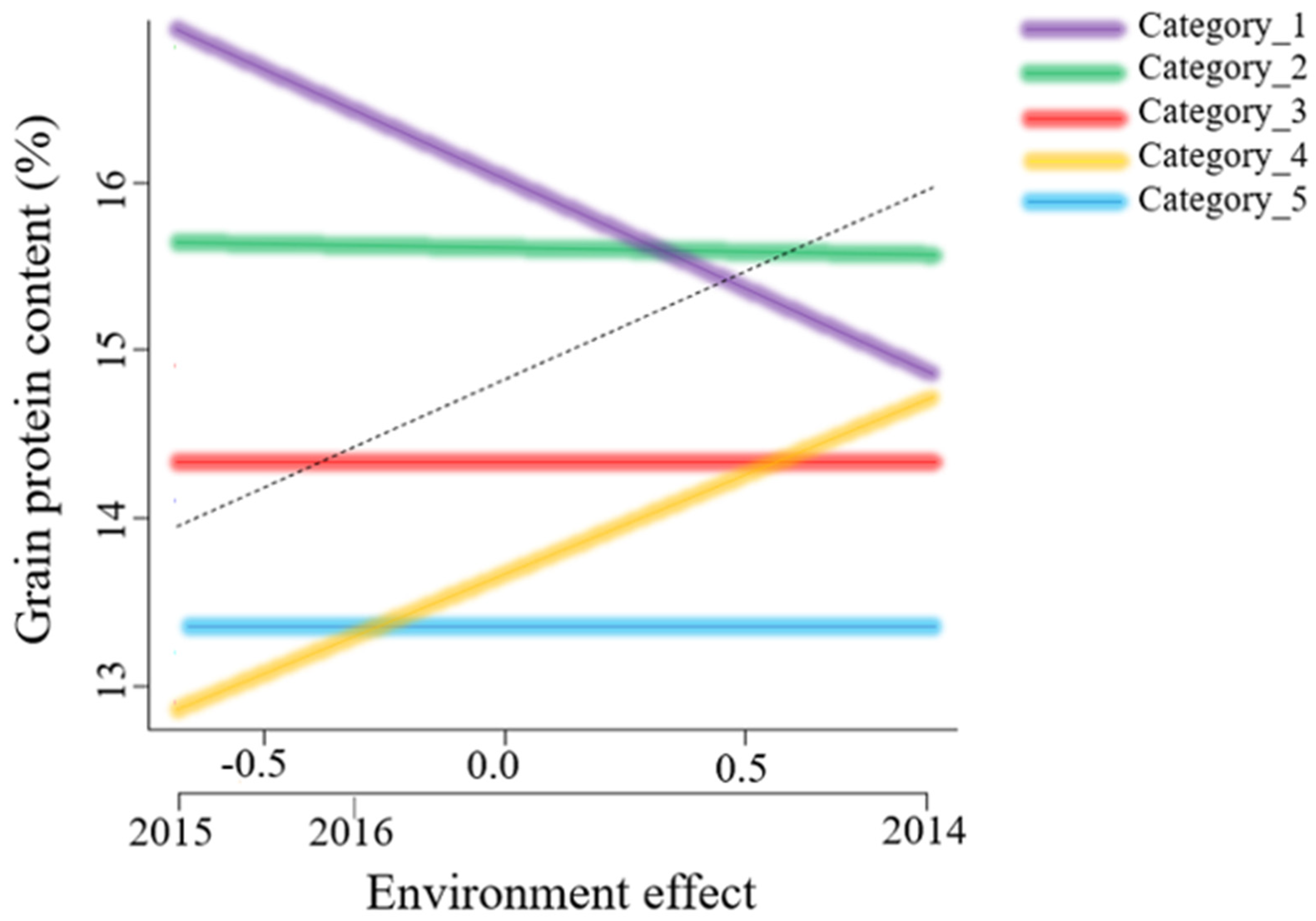
3.2. Stability Analysis
3.3. Population Structure Analysis
3.4. Marker–Trait Associations for the Stability of Grain Protein Content
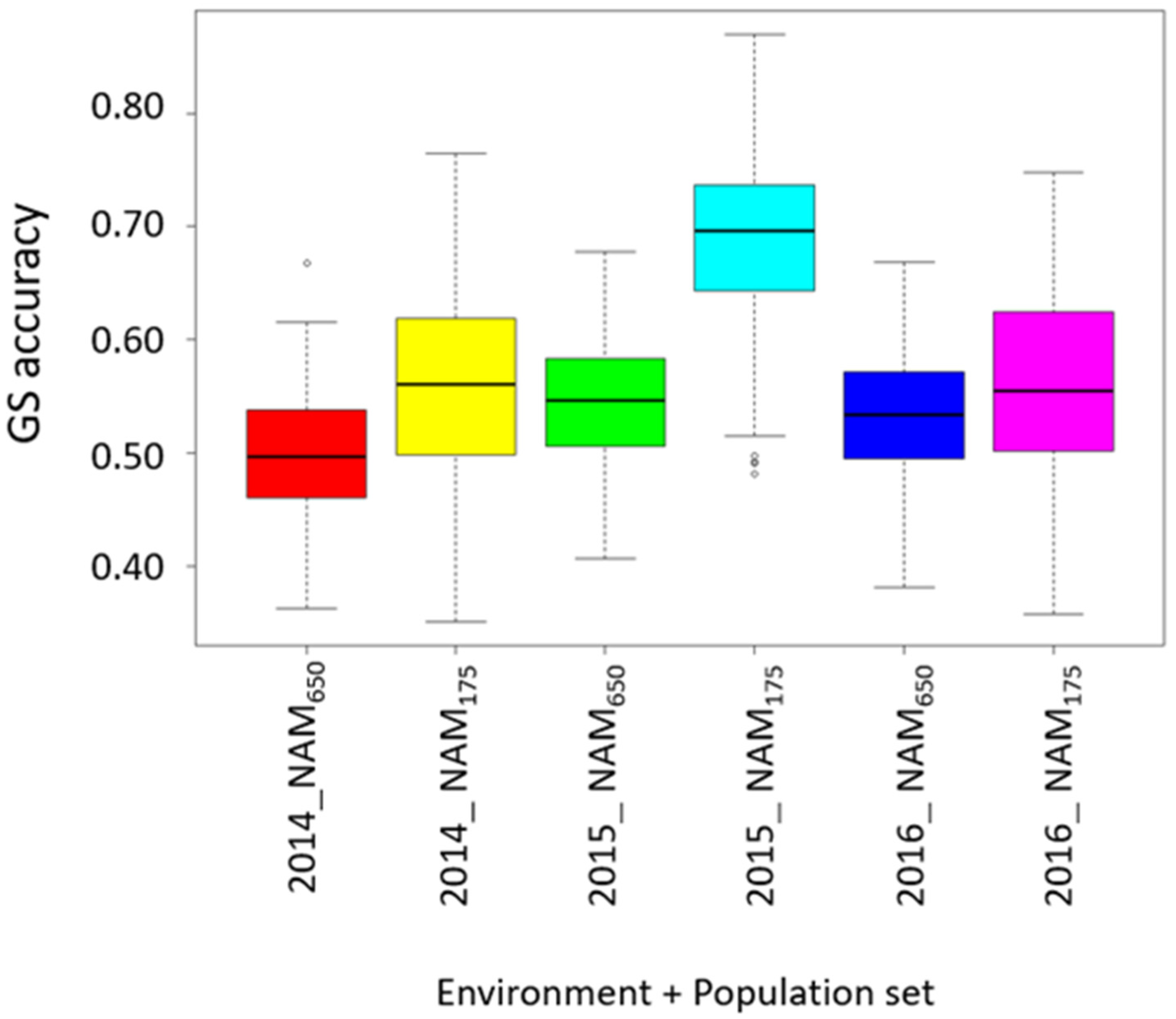
3.5. Prediction for Grain Protein Content and Stability
4. Discussion
4.1. Stability of Genotypes across Environments
4.2. Genomic Regions Controlling Stability of GPC
4.3. Accuracy for Predicting GPC and GPC Stability
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Shewry, P.R.; Halford, N.G. Cereal seed storage proteins: Structures, properties and role in grain utilization. J. Exp. Bot. 2002, 53, 947–958. [Google Scholar] [CrossRef] [Green Version]
- Shewry, P.R. Improving the protein content and composition of cereal grain. J. Cereal Sci. 2007, 46, 239–250. [Google Scholar] [CrossRef]
- Vogel, K.P.; Johnson, V.A.; Mattern, P.J. Protein and Lysine Content of Grain, Endosperm, and Bran of Wheats from the USDA World Wheat Collection. Crop Sci. 1976, 16, 655–660. [Google Scholar] [CrossRef] [Green Version]
- Löffler, C.M.; Busch, R.H. Selection for Grain Protein, Grain Yield, and Nitrogen Partitioning Efficiency in Hard Red Spring Wheat. Crop Sci. 1982, 22, 591–595. [Google Scholar] [CrossRef]
- DePauw, R.M.; Knox, R.E.; Clarke, F.R.; Wang, H.; Fernandez, M.R.; Clarke, J.M.; McCaig, T.N. Shifting undesirable correlations. In Proceedings of the Euphytica. Euphytica 2007, 157, 409–415. [Google Scholar] [CrossRef]
- De Kroon, H.; Huber, H.; Stuefer, J.F.; Van Gorenendael, J.M. A modular concept of phenotypic plasticity in plants. New Phytol. 2005, 166, 73–82. [Google Scholar] [CrossRef] [PubMed]
- Kusmec, A.; Srinivasan, S.; Nettleton, D.; Schnable, P.S. Distinct genetic architectures for phenotype means and plasticities in Zea mays. Nat. Plants 2017, 3, 715–723. [Google Scholar] [CrossRef] [PubMed]
- Kliebenstein, D.J.; Figuth, A.; Mitchell-olds, T. Genetic Architecture of Plastic Methyl Jasmonate Responses in Arabidopsis thaliana. Genetics 2002, 1696, 1685–1696. [Google Scholar] [CrossRef] [PubMed]
- Eberhart, S.A.; Russell, W.A. Stability Parameters for Comparing Varieties. Crop Sci. 1966, 6, 36–40. [Google Scholar] [CrossRef] [Green Version]
- Lin, C.S.; Binns, M.R.; Lefkovitch, L.P. Stability Analysis: Where Do We Stand? Crop Sci. 1986, 26, 894–900. [Google Scholar] [CrossRef] [Green Version]
- Finlay, K.W.; Wilkinson, G.N. The analysis of adaptation in a plant-breeding programme. Aust. J. Agric. Res. 1963, 14, 742–754. [Google Scholar] [CrossRef] [Green Version]
- Lian, L.; de los Campos, G. GENOMIC SELECTION FW: An R Package for Finlay—Wilkinson Regression that Incorporates Genomic/Pedigree Information and Covariance Structures Between Environments. G3 Genes Genomes Genet. 2016, 6, 589–597. [Google Scholar] [CrossRef] [Green Version]
- Ordas, B.; Malvar, R.A.; Hill, W.G. Genetic variation and quantitative trait loci associated with developmental stability and the environmental correlation between traits in maize. Genet. Res. (Camb) 2008, 90, 385–395. [Google Scholar] [CrossRef] [Green Version]
- Blanco, A.; De Giovanni, C.; Laddomada, B.; Sciancalepore, A.; Simeone, R.; Devos, K.M.; Gale, M.D. Quantitative trait loci influencing grain protein content in tetraploid wheats. Plant Breed. 1996, 115, 310–316. [Google Scholar] [CrossRef]
- Huang, X.; Wei, X.; Sang, T.; Zhao, Q.; Feng, Q.; Zhao, Y.; Li, C.; Zhu, C.; Lu, T.; Zhang, Z.; et al. Genome-wide asociation studies of 14 agronomic traits in rice landraces. Nat. Genet. 2010, 42, 961–967. [Google Scholar] [CrossRef]
- Zhu, C.; Gore, M.; Buckler, E.S.; Yu, J. Status and Prospects of Association Mapping in Plants. Plant Genome J. 2008, 1, 5–20. [Google Scholar] [CrossRef]
- Kaur, B.; Sandhu, K.S.; Kamal, R.; Kaur, K.; Singh, J.; Röder, M.S.; Muqaddasi, Q.H. Omics for the Improvement of Abiotic, Biotic, and Agronomic Traits in Major Cereal Crops: Applications, Challenges, and Prospects. Plants 2021, 10, 1989. [Google Scholar] [CrossRef]
- Yu, J.; Buckler, E.S. Genetic association mapping and genome organization of maize. Curr. Opin. Biotechnol. 2006, 17, 155–160. [Google Scholar] [CrossRef]
- Saade, S.; Maurer, A.; Shahid, M.; Oakey, H.; Schmöckel, S.M.; Negrão, S.; Pillen, K.; Tester, M. Yield-related salinity tolerance traits identified in a nested association mapping (NAM) population of wild barley. Sci. Rep. 2016, 6, 32586. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gage, J.L.; Monier, B.; Giri, A.; Buckler, E.S. Ten years of the maize nested association mapping population: Impact, limitations, and future directions. Plant Cell 2020, 32, 2083–2093. [Google Scholar] [CrossRef] [PubMed]
- Fragoso, C.A.; Moreno, M.; Wang, Z.; Heffelfinger, C.; Arbelaez, L.J.; Aguirre, J.A.; Franco, N.; Romero, L.E.; Labadie, K.; Zhao, H.; et al. Genetic architecture of a rice nested association mapping population. G3 Genes Genomes Genet. 2017, 7, 1913–1926. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, H.; Bradbury, P.; Ersoz, E.; Buckler, E.S.; Wang, J. Joint QTL linkage mapping for multiple-cross mating design sharing one common parent. PLoS ONE 2011, 6, e0017573. [Google Scholar] [CrossRef] [Green Version]
- Blanc, G.; Charcosset, A.; Mangin, B.; Gallais, A.; Moreau, L. Connected populations for detecting quantitative trait loci and testing for epistasis: An application in maize. Theor. Appl. Genet. 2006, 113, 206–224. [Google Scholar] [CrossRef]
- Samantara, K.; Shiv, A.; de Sousa, L.L.; Sandhu, K.S.; Priyadarshini, P.; Mohapatra, S.R. A Comprehensive Review on Epigenetic Mechanisms and Application of Epigenetic Modifications for Crop Improvement. Environ. Exp. Bot. 2021, 188, 104479. [Google Scholar] [CrossRef]
- Mcmullen, M.D.; Kresovich, S.; Villeda, H.S.; Bradbury, P.; Li, H.; Sun, Q.; Flint-Garcia, S.; Thornsberry, J.; Acharya, C.; Bottoms, C.; et al. Genetic Properties of the Maize Nested Association Mapping Population. Science 2009, 325, 737–740. [Google Scholar] [CrossRef] [Green Version]
- Würschum, T.; Liu, W.; Gowda, M.; Maurer, H.P.; Fischer, S.; Schechert, A.; Reif, J.C. Comparison of biometrical models for joint linkage association mapping. Heredity (Edinb) 2012, 108, 332–340. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tian, F.; Bradbury, P.J.; Brown, P.J.; Hung, H.; Sun, Q.; Flint-garcia, S.; Rocheford, T.R.; Mcmullen, M.D.; Holland, J.B.; Buckler, E.S. Genome-wide association study of leaf architecture in the maize nested association mapping population. Nat. Genet. 2011, 43, 159–162. [Google Scholar] [CrossRef] [PubMed]
- Korte, A.; Ashley, F. The advantages and limitations of trait analysis with GWAS: A review. Plant Methods 2013, 9, 29. [Google Scholar] [CrossRef] [Green Version]
- Meuwissen, T.H.E.; Hayes, B.J.; Goddard, M.E. Prediction of Total Genetic Value Using Genome-Wide Dense Marker Maps. Genetics 2001, 157, 1819–1829. [Google Scholar] [CrossRef] [PubMed]
- Crossa, J.; Pérez, P.; Hickey, J.; Burgueño, J.; Ornella, L.; Cerón-Rojas, J.; Zhang, X.; Dreisigacker, S.; Babu, R.; Li, Y.; et al. Genomic prediction in CIMMYT maize and wheat breeding programs. Heredity (Edinb) 2014, 112, 48–60. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Robertsen, C.D.; Hjortshøj, R.L.; Janss, L.L. Genomic Selection in Cereal Breeding. Agronomy 2019, 9, 95. [Google Scholar] [CrossRef] [Green Version]
- Larkin, D.L.; Lozada, D.N.; Mason, R.E. Genomic Selection—Considerations for Successful Implementation in Wheat Breeding Programs. Agronomy 2019, 9, 479. [Google Scholar] [CrossRef] [Green Version]
- Sandhu, K.S.; Mihalyov, P.D.; Lewien, M.J.; Pumphrey, M.O.; Carter, A.H. Combining Genomic and Phenomic Information for Predicting Grain Protein Content and Grain Yield in Spring Wheat. Front. Plant Sci. 2021, 12, 170. [Google Scholar] [CrossRef]
- Rutkoski, J.E.; Heffner, E.L.; Sorrells, M.E. Genomic selection for durable stem rust resistance in wheat. Euphytica 2011, 179, 161–173. [Google Scholar] [CrossRef]
- Heffner, E.L.; Jannink, J.-L.; Iwata, H.; Souza, E.; Sorrells, M.E. Genomic Selection Accuracy for Grain Quality Traits in Biparental Wheat Populations. Crop Sci. 2011, 51, 2597–2606. [Google Scholar] [CrossRef] [Green Version]
- Huang, M.; Cabrera, A.; Hoffstetter, A.; Griffey, C.; Van Sanford, D.; Costa, J.; McKendry, A.; Chao, S.; Sneller, C. Genomic selection for wheat traits and trait stability. Theor. Appl. Genet. 2016, 129, 1697–1710. [Google Scholar] [CrossRef]
- Blake, N.K.; Pumphrey, M.; Glover, K.; Chao, S.; Jordan, K.; Jannick, J.L.; Akhunov, E.A.; Dubcovsky, J.; Bockelman, H.; Talbert, L.E. Registration of the triticeae-cap spring wheat nested association mapping population. J. Plant Regist. 2019, 13, 294–297. [Google Scholar] [CrossRef] [Green Version]
- Sandhu, K.; Patil, S.S.; Pumphrey, M.; Carter, A. Multitrait machine- and deep-learning models for genomic selection using spectral information in a wheat breeding program. Plant Genome 2021, e20119. [Google Scholar] [CrossRef] [PubMed]
- Sandhu, K.S.; Lozada, D.N.; Zhang, Z.; Pumphrey, M.O.; Carter, A.H. Deep Learning for Predicting Complex Traits in Spring Wheat Breeding Program. Front. Plant Sci. 2021, 11, 613325. [Google Scholar] [CrossRef] [PubMed]
- Jordan, K.W.; Wang, S.; He, F.; Chao, S.; Lun, Y.; Paux, E.; Sourdille, P.; Sherman, J.; Akhunova, A.; Blake, N.K.; et al. The genetic architecture of genome-wide recombination rate variation in allopolyploid wheat revealed by nested association mapping. Plant J. 2018, 95, 1039–1054. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lanning, S.P.; Talbert, L.E.; McGuire, C.F.; Bowman, H.F.; Carlson, G.R.; Jackson, G.D.; Eckhoff, J.L.; Kushnak, G.D.; Stougaard, R.N.; Stallknecht, G.F.; et al. Registration of ‘McNeal’ Wheat. Crop Sci. 1994, 34, 1126. [Google Scholar] [CrossRef]
- Delwiche, S.R. Single Wheat Kernel Analysis by Near-Infrared Transmittance: Protein Content. 1995. Available online: https://www.cerealsgrains.org/publications/cc/backissues/1995/Documents/72_11.pdf (accessed on 23 November 2021).
- Delwiche, S.R. Protein Content of Single Kernels of Wheat by Near-Infrared Reflectance Spectroscopy. J. Cereal Sci. 1998, 27, 241–254. [Google Scholar] [CrossRef]
- Olmos, S.; Distelfeld, A.; Chicaiza, O.; Schlatter, A.R.; Fahima, T.; Echenique, V.; Dubcovsky, J. Precise mapping of a locus affecting grain protein content in durum wheat. Theor. Appl. Genet. 2003, 107, 1243–1251. [Google Scholar] [CrossRef] [Green Version]
- Distelfeld, A.; Uauy, C.; Fahima, T.; Dubcovsky, J. Physical map of the wheat high-grain protein content gene Gpc-B1 and development of a high-throughput molecular marker. New Phytol. 2006, 169, 753–763. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- R Development Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2020; p. 201. ISBN 978-0792305866. [Google Scholar]
- Rodríguez, F.; Alvarado, G.; Pacheco, Á.; Burgueno, J. ACBD-R. Augmented Complete Block Design with R for Windows. Version 4.0. CIMMYT Res. Data Softw. Repos. Netw. 2018. [Google Scholar]
- Monaghan, J.M.; Snape, J.W.; Chojecki, A.J.S.; Kettlewell, P.S. The use of grain protein deviation for identifying wheat cultivars with high grain protein concentration and yield. Euphytica 2001, 122, 309–317. [Google Scholar] [CrossRef]
- Mosleth, E.F.; Lillehammer, M.; Pellny, T.K.; Wood, A.J.; Riche, A.B.; Hussain, A.; Griffiths, S.; Hawkesford, M.J.; Shewry, P.R. Genetic variation and heritability of grain protein deviation in European wheat genotypes. Field Crops. Res. 2020, 255, 107896. [Google Scholar] [CrossRef]
- Marcussen, T.; Sandve, S.R.; Heier, L.; Pfeifer, M.; Kugler, K.G.; Sandve, S.R.; Zhan, B. A chromosome-based draft sequence of the hexaploid bread wheat (Triticum aestivum) genome Ancient hybridizations among the ancestral genomes of bread wheat Genome interplay in the grain transcriptome of hexaploid bread wheat Structural and functional pa. Science 2014, 345, 6194. [Google Scholar]
- Lipka, A.E.; Tian, F.; Wang, Q.; Peiffer, J.; Li, M.; Bradbury, P.J.; Gore, M.A.; Buckler, E.S.; Zhang, Z. GAPIT: Genome association and prediction integrated tool. Bioinformatics 2012, 28, 2397–2399. [Google Scholar] [CrossRef] [Green Version]
- Vanraden, P.M. Efficient Methods to Compute Genomic Predictions. J. Dairy Sci. 2008, 91, 4414–4423. [Google Scholar] [CrossRef] [Green Version]
- Price, A.L.; Patterson, N.J.; Plenge, R.M.; Weinblatt, M.E.; Shadick, N.A.; Reich, D. Principal components analysis corrects for stratification in genome-wide association studies. Nat. Genet. 2006, 38, 904–909. [Google Scholar] [CrossRef] [PubMed]
- SAS Institute Inc. SAS® 9.3 System Options: Reference; SAS Institute Inc.: Cary, NC, USA, 2011. [Google Scholar]
- Yu, J.; Pressoir, G.; Briggs, W.H.; Bi, I.V.; Yamasaki, M.; Doebley, J.F.; McMullen, M.D.; Gaut, B.S.; Nielsen, D.M.; Holland, J.B.; et al. A unified mixed-model method for association mapping that accounts for multiple levels of relatedness. Nat. Genet. 2006, 38, 203–208. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Ersoz, E.; Lai, C.; Todhunter, R.J.; Tiwari, H.K.; Gore, M.A.; Bradbury, P.J.; Yu, J.; Arnett, D.K.; Ordovas, J.M.; et al. Mixed linear model approach adapted for genome-wide association studies. Nat. Genet. 2010, 42, 355–360. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Huang, M.; Fan, B.; Buckler, E.S.; Zhang, Z. Iterative Usage of Fixed and Random Effect Models for Powerful and Efficient Genome-Wide Association Studies. PLoS Genet. 2016, 12, e1005767. [Google Scholar] [CrossRef] [PubMed]
- Huang, M.; Liu, X.; Zhou, Y.; Summers, R.M.; Zhang, Z. BLINK: A package for the next level of genome-wide association studies with both individuals and markers in the millions. Gigascience 2018, 8, 1–12. [Google Scholar] [CrossRef]
- Holm, S. A Simple Sequentially Rejective Multiple Test Procedure. Scand. J. Stat. 1978, 6, 65–70. [Google Scholar]
- Endelman, J.B. Ridge Regression and Other Kernels for Genomic Selection with R Package rrBLUP. Plant Genome 2011, 4, 250–255. [Google Scholar] [CrossRef] [Green Version]
- Berke, T.G.; Baenziger, P.S.; Morris, R. Chromosomal location of wheat quantitative trait loci affecting agronomic performance of seven traits, using reciprocal chromosome substitutions. Crop Sci. 1992, 32, 621–627. [Google Scholar] [CrossRef]
- Tollenaar, M.; Lee, E.A. Yield potential, yield stability and stress tolerance in maize. Field Crops Res. 2002, 75, 161–169. [Google Scholar] [CrossRef]
- Kraakman, A.T.W.; Niks, R.E.; Van Den Berg, P.M.M.M.; Stam, P.; Van Eeuwijk, F.A. Linkage disequilibrium mapping of yield and yield stability in modern spring barley cultivars. Genetics 2004, 168, 435–446. [Google Scholar] [CrossRef] [Green Version]
- Sehgal, D.; Autrique, E.; Singh, R.; Ellis, M.; Singh, S.; Dreisigacker, S. Identification of genomic regions for grain yield and yield stability and their epistatic interactions. Sci. Rep. 2017, 7, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Blanco, A.; Simeone, R.; Gadaleta, A. Detection of QTLs for grain protein content in durum wheat. Theor. Appl. Genet. 2006, 112, 1195–1204. [Google Scholar] [CrossRef]
- Groos, C.; Robert, N.; Bervas, E.; Charmet, G. Genetic analysis of grain protein-content, grain yield and thousand-kernel weight in bread wheat. Theor. Appl. Genet. 2003, 106, 1032–1040. [Google Scholar] [CrossRef] [PubMed]
- Joppa, L.R.; Hareland, G.A.; Du, C.; Hart, G.E. Mapping gene(s) for grain protein in tetraploid wheat (Triticum turgidum L.) using a population of recombinant inbred chromosome lines. Crop Sci. 1997, 37, 1586–1589. [Google Scholar] [CrossRef]
- Perretant, M.R.; Cadalen, T.; Charmet, G.; Sourdille, P.; Nicolas, P.; Boeuf, C.; Tixier, M.H.; Branlard, G.; Bernard, S.; Bernard, M. QTL analysis of bread-making quality in wheat using a doubled haploid population. Theor. Appl. Genet. 2000, 100, 1167–1175. [Google Scholar] [CrossRef]
- Prasad, M.; Kumar, N.; Kulwal, P.L.; Röder, M.S.; Balyan, H.S.; Dhaliwal, H.S.; Gupta, P.K. QTL analysis for grain protein content using SSR markers and validation studies using NILs in bread wheat. Theor. Appl. Genet. 2003, 106, 659–667. [Google Scholar] [CrossRef]
- Mahjourimajd, S.; Taylor, J.; Rengel, Z.; Khabaz-Saberi, H.; Kuchel, H.; Okamoto, M.; Langridge, P. The genetic control of grain protein content under variable nitrogen supply in an Australian wheat mapping population. PLoS ONE 2016, 11, e0159371. [Google Scholar] [CrossRef] [Green Version]
- Rapp, M.; Lein, V.; Lacoudre, F.; Lafferty, J.; Müller, E.; Vida, G.; Bozhanova, V.; Ibraliu, A.; Thorwarth, P.; Piepho, H.P.; et al. Simultaneous improvement of grain yield and protein content in durum wheat by different phenotypic indices and genomic selection. Theor. Appl. Genet. 2018, 131, 1315–1329. [Google Scholar] [CrossRef]
- Heo, H.; Sherman, J. Identification of QTL for Grain Protein Content and Grain Hardness from Winter Wheat for Genetic Improvement of Spring Wheat. Plant Breed. Biotechnol. 2013, 1, 347–353. [Google Scholar] [CrossRef] [Green Version]
- He, F.; Pasam, R.; Shi, F.; Kant, S.; Keeble-Gagnere, G.; Kay, P.; Forrest, K.; Fritz, A.; Hucl, P.; Wiebe, K.; et al. Exome sequencing highlights the role of wild-relative introgression in shaping the adaptive landscape of the wheat genome. Nat. Genet. 2019, 51, 896–904. [Google Scholar] [CrossRef]
- Schulthess, A.W.; Wang, Y.; Miedaner, T.; Wilde, P.; Reif, J.C.; Zhao, Y. Multiple-trait- and selection indices-genomic predictions for grain yield and protein content in rye for feeding purposes. Theor. Appl. Genet. 2016, 129, 273–287. [Google Scholar] [CrossRef] [PubMed]
- Michel, S.; Löschenberger, F.; Ametz, C.; Pachler, B.; Sparry, E.; Bürstmayr, H. Simultaneous selection for grain yield and protein content in genomics-assisted wheat breeding. Theor. Appl. Genet. 2019, 132, 1745–1760. [Google Scholar] [CrossRef]
- Heffner, E.L.; Jannink, J.; Sorrells, M.E. Genomic Selection Accuracy using Multifamily Prediction Models in a Wheat Breeding Program. Plant Genome 2011, 4, 65–75. [Google Scholar] [CrossRef] [Green Version]
- Poland, J.; Endelman, J.; Dawson, J.; Rutkoski, J.; Wu, S.; Manes, Y.; Dreisigacker, S.; Crossa, J.; Sánchez-Villeda, H.; Sorrells, M.; et al. Genomic Selection in Wheat Breeding using Genotyping-by-Sequencing. Plant Genome J. 2012, 5, 103–113. [Google Scholar] [CrossRef] [Green Version]
- Windhausen, V.S.; Atlin, G.N.; Hickey, J.M.; Crossa, J.; Jannink, J.-L.; Sorrells, M.E.; Raman, B.; Cairns, J.E.; Tarekegne, A.; Semagn, K.; et al. Effectiveness of Genomic Prediction of Maize Hybrid Performance in Different Breeding Populations and Environments. G3 Genes Genomes Genet. 2012, 2, 1427–1436. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Battenfield, S.D.; Guzmán, C.; Chris Gaynor, R.; Singh, R.P.; Peña, R.J.; Dreisigacker, S.; Fritz, A.K.; Poland, J.A. Genomic selection for processing and end-use quality traits in the CIMMYT spring bread wheat breeding program. Plant Genome 2016, 9. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Asoro, F.G.; Newell, M.A.; Beavis, W.D.; Scott, M.P.; Jannink, J. Accuracy and Training Population Design for Genomic Selection on Quantitative Traits in Elite North American Oats. Plant Genome 2011, 4, 132–144. [Google Scholar] [CrossRef] [Green Version]
- Piepho, H.-P. Methods for Comparing the Yield Stability of Cropping Systems. J. Agron. Crop Sci. 1998, 180, 193–213. [Google Scholar] [CrossRef]
- Sandhu, K.S.; Aoun, M.; Morris, C.F.; Carter, A.H. Genomic Selection for End-Use Quality and Processing Traits in Soft White Winter Wheat Breeding Program with Machine and Deep Learning Models. Biology 2021, 10, 689. [Google Scholar] [CrossRef]
- Isidro, J.; Jannink, J.L.; Akdemir, D.; Poland, J.; Heslot, N.; Sorrells, M.E. Training set optimization under population structure in genomic selection. Theor. Appl. Genet. 2015, 128, 145–158. [Google Scholar] [CrossRef] [Green Version]
- Lorenz, A.J.; Chao, S.; Asoro, F.G.; Heffner, E.L.; Hayashi, T.; Iwata, H.; Smith, K.P.; Sorrells, M.E.; Jannink, J. Genomic Selection in Plant Breeding: Knowledge and Prospects. Adv. Agron. 2011, 110, 77–123. [Google Scholar]
- Lorenzana, R.E.; Bernardo, R. Accuracy of genotypic value predictions for marker-based selection in biparental plant populations. Theor. Appl. Genet. 2009, 120, 151–161. [Google Scholar] [CrossRef] [PubMed]
- Heffner, E.L.; Lorenz, A.J.; Jannink, J.L.; Sorrells, M.E. Plant breeding with Genomic selection: Gain per unit time and cost. Crop Sci. 2010, 50, 1681–1690. [Google Scholar] [CrossRef]
- Lorenz, A.J.; Smith, K.P. Adding genetically distant individuals to training populations reduces genomic prediction accuracy in Barley. Crop Sci. 2015, 55, 2657–2667. [Google Scholar] [CrossRef] [Green Version]


| Marker Description ∆ | Allelic Effect ∫ | Significance Values | ||||||
|---|---|---|---|---|---|---|---|---|
| SNP name | Chromosome | Position on Chromosome | Alleles ↄ | Parental Line with Bolded Allele | Model Providing Significant Results | Minor Allele Frequency | Cumulative R2 | p-Value (Bonf.) |
| SpringWheatNAM_tag_81337:59 | 1A | 50917564 | C/T | Berkut, Dharwar Dry | BLINK, MLM, CMLM | 0.40 | +1.15 | 7.91 × 10−8 |
| SpringWheatNAM_tag_302718 | 1B | 381359110 | A/G | CItr15144 | BLINK | 0.12 | −4.19 | 1.32 × 10−7 |
| SpringWheatNAM_tag_94853 | 2A | 569963539 | T/G | CItr15144, PI210945, PI92001, Dharwar Dry | BLINK, MLM, CMLM | 0.36 | +3.68 | 1.06 × 10−6 |
| SpringWheatNAM_tag_272313 | 2A | 196126844 | C/G | Berkut, Dharwar Dry | FarmCPU | 0.15 | +1.58 | 9.39 × 10−7 |
| SpringWheatNAM_tag_269074 | 2B | 155136626 | A/C | PI210945, PI43355 | BLINK | 0.11 | −3.62 | 5.67 × 10−12 |
| BS00036168_51 | 3A | 6.89 × 108 | T/C | CItr15144 | FarmCPU | 0.17 | −2.01 | 2.16 × 10−7 |
| SpringWheatNAM_tag_84633 | 3B | 23359725 | A/T | PI92569 | BLINK, MLM, CMLM | 0.14 | −3.98 | 1.05 × 10−8 |
| SpringWheatNAM_tag_7037 | 3B | 508522245 | G/T | Berkut, Dharwar Dry, PI92569 | BLINK, MLM, CMLM | 0.42 | −1.27 | 2.84 × 10−9 |
| SpringWheatNAM_tag_75584 | 3B | 6.77 × 108 | T/G | Berkut, CItr15144, PI210945, PI92569 | MLM and CMLM | 0.29 | +2.53 | 0.000218 |
| SpringWheatNAM_tag_281164 | 4A | 309647389 | T/C | Berkut, Dharwar Dry, CItr15144, PI210945, | BLINK | 0.30 | −0.51 | 2.84 × 10−9 |
| SpringWheatNAM_tag_75584 | 4D | 6.77 × 108 | A/G | CItr15144, PI210945, PI92001, Dharwar Dry, Berkut | MLM and CMLM | 0.43 | +1.68 | 0.000218 |
| SpringWheatNAM_tag_17034 | 5B | 4.31 × 108 | T/C | PI210945, PI43355, PI92569 | MLM and CMLM | 0.41 | −0.74 | 0.000399 |
| SpringWheatNAM_tag_18817:22 | 7B | 100166484 | C/A | Berkut, Dharwar Dry | FarmCPU | 0.27 | +2.13 | 2.81 × 10−8 |
| SpringWheatNAM_tag_108839 | 7B | 98739595 | T/G | CItr15144, PI210945 | FarmCPU | 0.32 | +1.06 | 2.43 × 10−7 |
| SpringWheatNAM_tag_37074 | 7B | 720870596 | C/G | CItr15144, PI210945, PI92001 | FarmCPU | 0.25 | −2.70 | 9.39 × 10−7 |
| SpringWheatNAM_tag_72025 | 7B | 721085362 | A/C | Berkut, Dharwar Dry | FarmCPU | 0.17 | +0.43 | 6.48 × 10−7 |
| SpringWheatNAM_tag_37362 | 7B | 720892406 | G/T | PI92569 | FarmCPU | 0.20 | +1.89 | 2.00 × 10−7 |
| SpringWheatNAM_tag_280095 | 7D | 57137544 | A/C | Dharwar Dry, Berkut | MLM and CMLM | 0.15 | +0.25 | 0.000187 |
| Marker Description ∆ | Allelic Effect ∫ | Significance Values | ||||||
|---|---|---|---|---|---|---|---|---|
| SNP Name | Chromosome | Position on Chromosome (cM) | Alleles ↄ | Parental Line with Bolded Allele | Model Providing Significant Results | Minor Allele Frequency | Cumulative R2 | p-Value |
| SpringWheatNAM_tag_190170 | 1A | 1.24 × 108 | T/C | Berkut, Dharwar Dry | BLINK | 0.49 | +6.78 | 1.60 × 10−8 |
| SpringWheatNAM_tag_127808 | 1A | 3.66 × 108 | T/A | Berkut, Dharwar Dry | FarmCPU | 0.14 | +3.02 | 6.07 × 10−17 |
| SpringWheatNAM_tag_82306 | 2B | 7.17 × 108 | A/T | CItr4175 | MLM, CMLM | 0.16 | +0.44 | 4.33 × 10−5 |
| SpringWheatNAM_tag_32264 | 3B | 125543693 | A/T | Berkut, PI43355 | BLINK | 0.34 | −7.30 | 1.26 × 10−6 |
| SpringWheatNAM_tag_82154 | 4A | 6.4 × 108 | C/A | CItr15144, PI210945, CItr4175. | BLINK | 0.26 | −2.34 | 1.23 × 10−7 |
| SpringWheatNAM_tag_124206 | 6B | 7.07 × 108 | A/G | PI43355 | FarmCPU | 0.14 | −1.02 | 1.74 × 10−15 |
| SpringWheatNAM_tag_136322 | 7A | 6.67 × 108 | T/G | Berkut, PI43355 | BLINK, MLM, CMLM | 0.41 | −0.32 | 1.55 × 10−8 |
| SpringWheatNAM_tag_122369 | 7B | 6.19 × 108 | C/G | Berkut, Dharwar Dry | MLM, CMLM | 0.16 | +3.59 | 5.31 × 10−5 |
| Marker Description ∆ | Allelic Effect ∫ | Significance Values | ||||
|---|---|---|---|---|---|---|
| SNP Name | Chromosome | Position on Chromosome (cM) | Model Providing Significant Results | Minor Allele Frequency | Cumulative R2 | p-Value |
| SpringWheatNAM_tag_127808 | 1A | 3.66 × 108 | FarmCPU | 0.14 | +3.53 | 7.26 × 10−8 |
| BS00022409_51 | 2A | 745092365 | FarmCPU | 0.11 | +2.18 | 1.06 × 10−10 |
| SpringWheatNAM_tag_40957:20 | 2B | 2737380 | FarmCPU, BLINK | 0.22 | −1.83 | 1.64 × 10−7 |
| SpringWheatNAM_tag_252336 | 2B | 534836257 | FarmCP, BLINK, MLM, CMLM | 0.17 | +2.76 | 3.01 × 10−13 |
| SpringWheatNAM_tag_69709 | 4A | 118275776 | FarmCPU | 0.48 | −3.05 | 2.25 × 10−8 |
| Kukri_c20822_1029 | 4B | 106973454 | FarmCPU | 0.12 | −2.70 | 3.34 × 10−8 |
| SpringWheatNAM_tag_84935 | 4B | 5.92 × 108 | BLINK | 0.13 | +1.85 | 1.43 × 10−7 |
| SpringWheatNAM_tag_218381 | 5A | 6.87 × 108 | BLINK | 0.21 | +0.89 | 2.70 × 10−8 |
| SpringWheatNAM_tag_53378 | 6A | 543101208 | FarmCPU | 0.20 | +1.54 | 4.08 × 10−7 |
| SpringWheatNAM_tag_101029 | 6B | 4.76 × 108 | MLM, CMLM | 0.12 | −2.88 | 1.56 × 10−5 |
| SpringWheatNAM_tag_94821 | 6B | 517508015 | FarmCPU | 0.42 | +1.69 | 5.57 × 10−11 |
| SpringWheatNAM_tag_38314 | 6B | 659974659 | FarmCPU | 0.16 | −2.73 | 2.22 × 10−7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sandhu, K.S.; Mihalyov, P.D.; Lewien, M.J.; Pumphrey, M.O.; Carter, A.H. Genomic Selection and Genome-Wide Association Studies for Grain Protein Content Stability in a Nested Association Mapping Population of Wheat. Agronomy 2021, 11, 2528. https://doi.org/10.3390/agronomy11122528
Sandhu KS, Mihalyov PD, Lewien MJ, Pumphrey MO, Carter AH. Genomic Selection and Genome-Wide Association Studies for Grain Protein Content Stability in a Nested Association Mapping Population of Wheat. Agronomy. 2021; 11(12):2528. https://doi.org/10.3390/agronomy11122528
Chicago/Turabian StyleSandhu, Karansher S., Paul D. Mihalyov, Megan J. Lewien, Michael O. Pumphrey, and Arron H. Carter. 2021. "Genomic Selection and Genome-Wide Association Studies for Grain Protein Content Stability in a Nested Association Mapping Population of Wheat" Agronomy 11, no. 12: 2528. https://doi.org/10.3390/agronomy11122528
APA StyleSandhu, K. S., Mihalyov, P. D., Lewien, M. J., Pumphrey, M. O., & Carter, A. H. (2021). Genomic Selection and Genome-Wide Association Studies for Grain Protein Content Stability in a Nested Association Mapping Population of Wheat. Agronomy, 11(12), 2528. https://doi.org/10.3390/agronomy11122528






