Climate Projections for Precipitation and Temperature Indicators in the Douro Wine Region: The Importance of Bias Correction
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Region
2.2. Climate Data
2.3. Climatic Indices
2.4. Bias Correction and Future Projections
3. Results
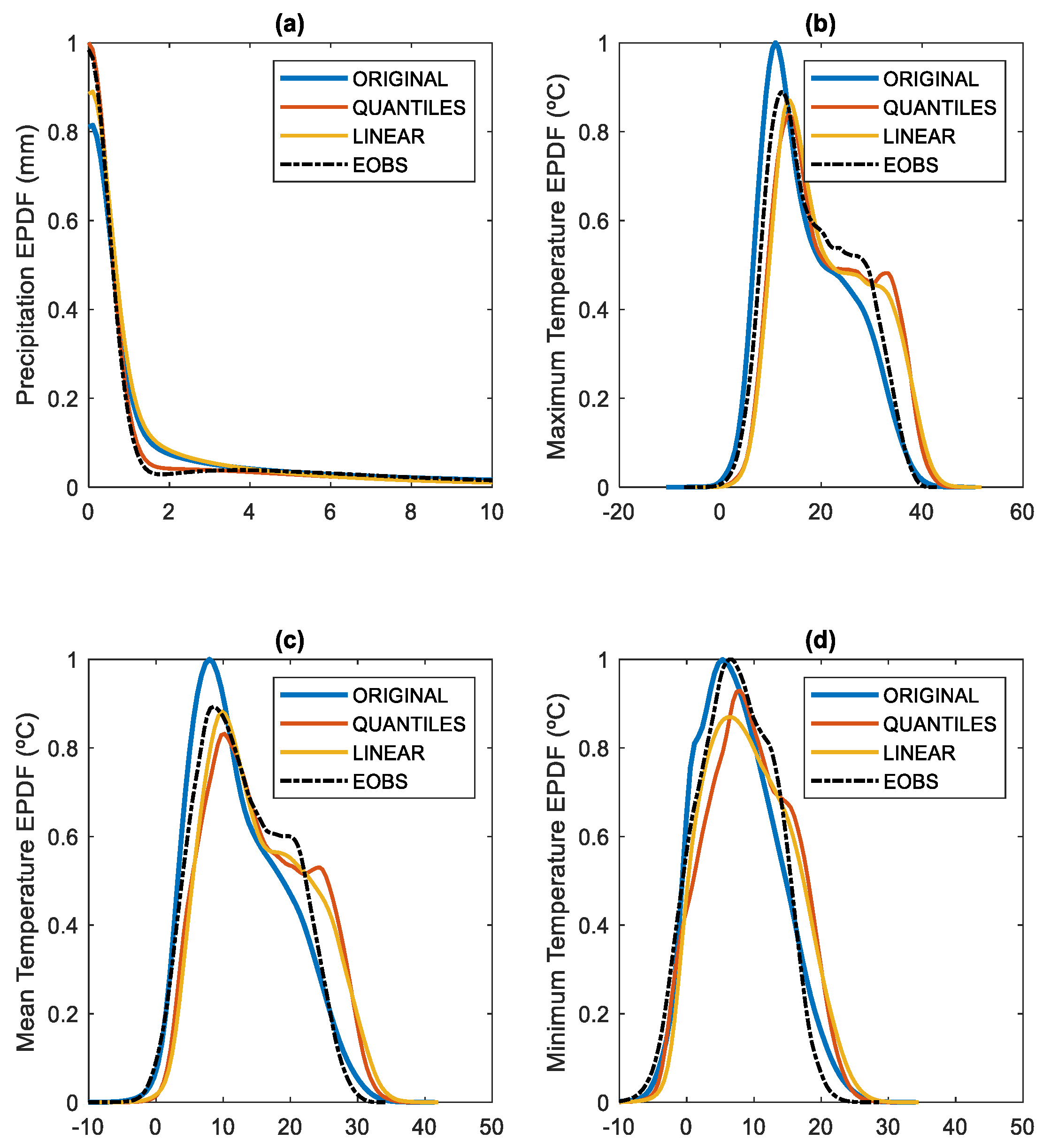
3.1. Comparison of Bias Correction Methods
3.2. Indices: Linear vs. Quantile Corrections
3.3. Climate Change Assessments
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- IPCC. Climate Change 2014: Synthesis Report, Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; IPCC: Geneva, Switzerland, 2014; Volume 218, ISBN 9789291691432. [Google Scholar]
- Frich, P.; Alexander, L.V.; Della-Marta, P.; Gleason, B.; Haylock, M.; Tank Klein, A.M.G.; Peterson, T. Observed coherent changes in climatic extremes during the second half of the twentieth century. Clim. Res. 2002, 19, 193–212. [Google Scholar] [CrossRef] [Green Version]
- Klein Tank, A.M.G.; Wijngaard, J.B.; Können, G.P.; Böhm, R.; Demarée, G.; Gocheva, A.; Mileta, M.; Pashiardis, S.; Hejkrlik, L.; Kern-Hansen, C.; et al. Daily dataset of 20th-century surface air temperature and precipitation series for the European Climate Assessment. Int. J. Climatol. 2002, 22, 1441–1453. [Google Scholar] [CrossRef]
- Alexander, L.V.; Zhang, X.; Peterson, T.C.; Caesar, J.; Gleason, B.; Klein Tank, A.M.G.; Haylock, M.; Collins, D.; Trewin, B.; Rahimzadeh, F.; et al. Global observed changes in daily climate extremes of temperature and precipitation. J. Geophys. Res. Atmos. 2006, 111, 1–22. [Google Scholar] [CrossRef] [Green Version]
- Della-Marta, P.M.; Haylock, M.R.; Luterbacher, J.; Wanner, H. Doubled length of western European summer heat waves since 1880. J. Geophys. Res. Atmos. 2007, 112, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Moberg, A.; Jones, P.D.; Lister, D.; Walther, A.; Brunet, M.; Jacobeit, J.; Alexander, L.V.; Della-Marta, P.M.; Luterbacher, J.; Yiou, P.; et al. Indices for daily temperature and precipitation extremes in Europe analyzed for the period 1901–2000. J. Geophys. Res. Atmos. 2006, 111. [Google Scholar] [CrossRef] [Green Version]
- Peings, Y.; Cattiaux, J.; Douville, H. Evaluation and response of winter cold spells over Western Europe in CMIP5 models. Clim. Dyn. 2013, 41, 3025–3037. [Google Scholar] [CrossRef]
- Russo, S.; Sillmann, J.; Fischer, E.M. Top ten European heatwaves since 1950 and their occurrence in the coming decades. Environ. Res. Lett. 2015, 10. [Google Scholar] [CrossRef]
- Cardoso, R.M.; Soares, P.M.M.; Lima, D.C.A.; Miranda, P.M.A. Mean and extreme temperatures in a warming climate: EURO CORDEX and WRF regional climate high-resolution projections for Portugal. Clim. Dyn. 2019, 52, 129–157. [Google Scholar] [CrossRef]
- Sillmann, J.; Kharin, V.V.; Zwiers, F.W.; Zhang, X.; Bronaugh, D. Climate extremes indices in the CMIP5 multimodel ensemble: Part 2. Future climate projections. J. Geophys. Res. Atmos. 2013, 118, 2473–2493. [Google Scholar] [CrossRef]
- Karagiannidis, A.F.; Karacostas, T.; Maheras, P.; Makrogiannis, T. Climatological aspects of extreme precipitation in Europe, related to mid-latitude cyclonic systems. Theor. Appl. Climatol. 2012, 107, 165–174. [Google Scholar] [CrossRef]
- Costa, A.C.; Soares, A. Trends in extreme precipitation indices derived from a daily rainfall database for the South of Portugal. Int. J. Climatol. 2009, 29, 1956–1975. [Google Scholar] [CrossRef]
- De Lima, M.I.P.; Santo, F.E.; Ramos, A.M.; Trigo, R.M. Trends and correlations in annual extreme precipitation indices for mainland Portugal, 1941–2007. Theor. Appl. Climatol. 2015, 119, 55–75. [Google Scholar] [CrossRef]
- Rajczak, J.; Schär, C. Projections of Future Precipitation Extremes Over Europe: A Multimodel Assessment of Climate Simulations. J. Geophys. Res. Atmos. 2017, 122, 10–773. [Google Scholar] [CrossRef]
- de Melo-Gonçalves, P.; Rocha, A.; Santos, J.A. Robust inferences on climate change patterns of precipitation extremes in the Iberian Peninsula. Phys. Chem. Earth 2016, 94, 114–126. [Google Scholar] [CrossRef]
- Santos, M.; Fonseca, A.; Fragoso, M.; Santos, J.A. Recent and future changes of precipitation extremes in mainland Portugal. Theor. Appl. Climatol. 2019, 137, 1305–1319. [Google Scholar] [CrossRef]
- Costa, A.C.; Santos, J.A.; Pinto, J.G. Climate change scenarios for precipitation extremes in Portugal. Theor. Appl. Climatol. 2012, 217–234. [Google Scholar] [CrossRef]
- Cardoso Pereira, S.; Marta-Almeida, M.; Carvalho, A.C.; Rocha, A. Extreme Precipitation Events under Climate Change in the Iberian Peninsula. Int. J. Climatol. 2018, 40, 1255–1278. [Google Scholar] [CrossRef]
- Santos, J.A.; Pinto, J.G.; Ulbrich, U. On the development of strong ridge episodes over the eastern North Atlantic. Geophys. Res. Lett. 2009, 36, L17804. [Google Scholar] [CrossRef] [Green Version]
- Viceto, C.; Pereira, S.C.; Rocha, A. Climate change projections of extreme temperatures for the Iberian Peninsula. Atmosphere 2019, 10, 229. [Google Scholar] [CrossRef] [Green Version]
- Serrano, J.P.; Díaz, F.J.A.; García, J.A.G. Analysis of extreme temperature events over the Iberian Peninsula during the 21st century using dynamic climate projections chosen using max-stable processes. Atmosphere 2020, 11, 506. [Google Scholar] [CrossRef]
- Drobinski, P.; Da Silva, N.; Bastin, S.; Mailler, S.; Muller, C.; Ahrens, B.; Christensen, O.B.; Lionello, P. How warmer and drier will the Mediterranean region be at the end of the twenty-first century? Reg. Environ. Chang. 2020, 20. [Google Scholar] [CrossRef]
- Yu, H.; Wu, D.; Piao, X.; Zhang, T.; Yan, Y.; Tian, Y.; Li, Q.; Cui, X. Reduced impacts of heat extremes from limiting global warming to under 1.5 °C or 2 °C over Mediterranean regions. Environ. Res. Lett. 2021, 16. [Google Scholar] [CrossRef]
- Fraga, H.; Pinto, J.G.; Viola, F.; Santos, J.A. Climate change projections for olive yields in the Mediterranean Basin. Int. J. Climatol. 2020, 40, 769–781. [Google Scholar] [CrossRef] [Green Version]
- Van Leeuwen, C.; Friant, P.; Choné, X.; Tregoat, O.; Koundouras, S.; Dubourdieu, D. Influence of climate, soil, and cultivar on terroir. Am. J. Enol. Vitic. 2004, 55, 207–217. [Google Scholar]
- Santos, J.A.; Fraga, H.; Malheiro, A.C.; Moutinho-Pereira, J.; Dinis, L.T.; Correia, C.; Moriondo, M.; Leolini, L.; Dibari, C.; Costafreda-Aumedes, S.; et al. A review of the potential climate change impacts and adaptation options for European viticulture. Appl. Sci. 2020, 10, 3092. [Google Scholar] [CrossRef]
- Parker, A.K.; De Cortázar-Atauri, I.G.; Van Leeuwen, C.; Chuine, I. General phenological model to characterise the timing of flowering and veraison of Vitis vinifera L. Aust. J. Grape Wine Res. 2011, 17, 206–216. [Google Scholar] [CrossRef]
- Lereboullet, A.L.; Beltrando, G.; Bardsley, D.K.; Rouvellac, E. The viticultural system and climate change: Coping with long-term trends in temperature and rainfall in Roussillon, France. Reg. Environ. Chang. 2014, 14, 1951–1966. [Google Scholar] [CrossRef]
- Fraga, H.; Molitor, D.; Leolini, L.; Santos, J.A. What Is the Impact of Heatwaves on European Viticulture? A Modelling Assessment. Appl. Sci. 2020, 10, 3030. [Google Scholar] [CrossRef]
- Van Leeuwen, C.; Tregoat, O.; Choné, X.; Bois, B.; Pernet, D.; Gaudillére, J.P. Vine water status is a key factor in grape ripening and vintage quality for red bordeaux wine. How can it be assessed for vineyard management purposes? J. Int. Sci. Vigne Vin 2009, 43, 121–134. [Google Scholar] [CrossRef]
- Ollé, D.; Guiraud, J.L.; Souquet, J.M.; Terrire, N.; Ageorges, A.; Cheynier, V.; Verries, C. Effect of pre- and post-veraison water deficit on proanthocyanidin and anthocyanin accumulation during Shiraz berry development. Aust. J. Grape Wine Res. 2011, 17, 90–100. [Google Scholar] [CrossRef]
- Le Menn, N.; Van Leeuwen, C.; Picard, M.; Riquier, L.; De Revel, G.; Marchand, S. Effect of Vine Water and Nitrogen Status, as Well as Temperature, on Some Aroma Compounds of Aged Red Bordeaux Wines. J. Agric. Food Chem. 2019. [Google Scholar] [CrossRef] [PubMed]
- Picard, M.; van Leeuwen, C.; Guyon, F.; Gaillard, L.; de Revel, G.; Marchand, S. Vine Water Deficit Impacts Aging Bouquet in Fine Red Bordeaux Wine. Front. Chem. 2017, 5, 56. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guilpart, N.; Metay, A.; Gary, C. Grapevine bud fertility and number of berries per bunch are determined by water and nitrogen stress around flowering in the previous year. Eur. J. Agron. 2014, 54, 9–20. [Google Scholar] [CrossRef]
- Huglin, M.P. Nouveau mode d’évaluation des possibilités héliothermiques d’un milieu viticole. Comptes Rendus Académie Agric. Fr. 1978, 64, 1117–1126. [Google Scholar]
- Solomon, S.; Qin, D.; Manning, M.; Chen, Z.; Marquis, M.; Averyt, K.B.; Tignor, M.; Miller, H.L.; IPCC (Eds.) Climate Change 2007: The Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2007. [Google Scholar]
- Casanueva, A.; Kotlarski, S.; Herrera, S.; Fernández, J.; Gutiérrez, J.M.; Boberg, F.; Colette, A.; Christensen, O.B.; Goergen, K.; Jacob, D.; et al. Daily precipitation statistics in a EURO-CORDEX RCM ensemble: Added value of raw and bias-corrected high-resolution simulations. Clim. Dyn. 2016, 47, 719–737. [Google Scholar] [CrossRef] [Green Version]
- Velasquez, P.; Messmer, M.; Raible, C.C. A new bias-correction method for precipitation over complex terrain suitable for different climate states: A case study using WRF ( version 3. 8. 1). Geosci. Model Dev. 2020, 13, 5007–5027. [Google Scholar] [CrossRef]
- Ishizaki, N.N.; Nishimori, M.; Iizumi, T.; Shiogama, H. Evaluation of Two Bias-Correction Methods for Gridded Climate Scenarios over Japan. SOLA 2020, 16, 80–85. [Google Scholar] [CrossRef] [Green Version]
- Singh, D.; Mohite, A.R.; Pratyasha, P.; Khatun, A. Impact of climate change on streamflow regime of a large Indian river basin using a novel monthly hybrid bias correction technique and a conceptual modeling framework. J. Hydrol. 2020, 590, 125448. [Google Scholar] [CrossRef]
- François, B.; Vrac, M.; Cannon, A.J.; Robin, Y.; Allard, D.; Cnrs, E.L.; Uvsq, C.E.A. Multivariate bias corrections of climate simulations: Which benefits for which losses? Earth Syst. Dyn. 2020, 11, 537–562. [Google Scholar] [CrossRef]
- Passow, C. Regression-based distribution mapping for bias correction of climate model outputs using linear quantile regression. Stoch. Environ. Res. Risk Assess. 2020, 34, 87–102. [Google Scholar] [CrossRef]
- Fraga, H.; Pinto, J.; Santos, J. Climate change projections for chilling and heat forcing conditions in European vineyards and olive orchards: A multi-model assessment. Clim. Chang. 2019, 152, 179–193. [Google Scholar] [CrossRef]
- Wang, Z.; Wen, X.; Lei, X.; Tan, Q.; Fang, G.; Zhang, X. Effects of different statistical distribution and threshold criteria in extreme precipitation modelling over global land areas. Int. J. Climatol. 2020, 40, 1838–1850. [Google Scholar] [CrossRef]
- Chen, W.; Zhu, D.; Ciais, P.; Huang, C.; Viovy, N.; Kageyama, M. Response of vegetation cover to CO2 and climate changes between Last Glacial Maximum and pre-industrial period in a dynamic global vegetation model. Quat. Sci. Rev. 2019, 218, 293–305. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, Y.L.; Guo, Z.T.; Fang, K.Y.; Li, Q.; Cao, X.Y. Abrupt vegetation shifts caused by gradual climate changes in central Asia during the Holocene. Sci. China Earth Sci. 2017, 60, 1317–1327. [Google Scholar] [CrossRef]
- Maraun, D. Bias Correcting Climate Change Simulations–A Critical Review. Curr. Clim. Chang. Rep. 2016, 2, 211–220. [Google Scholar] [CrossRef] [Green Version]
- Fraga, H.; García de Cortázar Atauri, I.; Malheiro, A.C.; Moutinho-Pereira, J.; Santos, J.A. Viticulture in Portugal: A review of recent trends and climate change projections. Oeno One 2017, 51, 61–69. [Google Scholar] [CrossRef] [Green Version]
- Real, A.C.; Borges, J.; Cabral, J.S.; Jones, G.V. Partitioning the grapevine growing season in the Douro Valley of Portugal: Accumulated heat better than calendar dates. Int. J. Biometeorol. 2015, 59, 1045–1059. [Google Scholar] [CrossRef]
- Santos, J.A.; Ceglar, A.; Toreti, A.; Prodhomme, C. Performance of seasonal forecasts of Douro and Port wine production. Agric. For. Meteorol. 2020, 291, 108095. [Google Scholar] [CrossRef]
- Fraga, H.; Santos, J.A.; Malheiro, A.C.; Oliveira, A.A.; Moutinho-Pereira, J.; Jones, G.V. Climatic suitability of Portuguese grapevine varieties and climate change adaptation. Int. J. Climatol. 2016, 36, 1–12. [Google Scholar] [CrossRef]
- Santos, J.A.; Grätsch, S.D.; Karremann, M.K.; Jones, G.V.; Pinto, J.G. Ensemble projections for wine production in the Douro Valley of Portugal. Clim. Chang. 2013, 117, 211–225. [Google Scholar] [CrossRef]
- Santos, J.A.; Malheiro, A.C.; Karremann, M.K.; Pinto, J.G. Statistical modelling of grapevine yield in the Port Wine region under present and future climate conditions. Int. J. Biometeorol. 2011, 55, 119–131. [Google Scholar] [CrossRef] [PubMed]
- Santos, M.; Fonseca, A.; Fraga, H.; Jones, G.V.; Santos, J.A. Bioclimatic conditions of the Portuguese wine denominations of origin under changing climates. Int. J. Climatol. 2019, 1–15. [Google Scholar] [CrossRef]
- Fonseca, A.R.; Santos, J.A. High-resolution temperature datasets in Portugal from a geostatistical approach: Variability and extremes. J. Appl. Meteorol. Climatol. 2018, 57, 627–644. [Google Scholar] [CrossRef]
- Fraga, H.; Santos, J.A. Daily prediction of seasonal grapevine production in the Douro wine region based on favourable meteorological conditions. Aust. J. Grape Wine Res. 2017, 23, 296–304. [Google Scholar] [CrossRef]
- Blanco-Ward, D.; Monteiro, A.; Lopes, M.; Borrego, C.; Silveira, C.; Viceto, C.; Rocha, A.; Ribeiro, A.; Andrade, J.; Feliciano, M.; et al. Climate change impact on a wine-producing region using a dynamical downscaling approach: Climate parameters, bioclimatic indices and extreme indices. Int. J. Climatol. 2019, 39, 5741–5760. [Google Scholar] [CrossRef]
- Fraga, H.; Malheiro, A.C.; Moutinho-Pereira, J.; Cardoso, R.M.; Soares, P.M.M.; Cancela, J.J.; Pinto, J.G.; Santos, J.A. Integrated analysis of climate, soil, topography and vegetative growth in iberian viticultural regions. PLoS ONE 2014, 9. [Google Scholar] [CrossRef]
- Fraga, H.; Costa, R.; Santos, J.A. Multivariate clustering of viticultural terroirs in the Douro winemaking region. Cienc. Tec. Vitivinic. 2017, 32, 142–153. [Google Scholar] [CrossRef] [Green Version]
- Cornes, R.C.; van der Schrier, G.; van den Besselaar, E.J.M.; Jones, P.D. An Ensemble Version of the E-OBS Temperature and Precipitation Data Sets. J. Geophys. Res. Atmos. 2018, 123, 9391–9409. [Google Scholar] [CrossRef] [Green Version]
- Klein Tank, A.M.G.; Können, G.P. Trends in Indices of daily temperature and precipitation extremes in Europe, 1946–1999. J. Clim. 2003, 16, 3665–3680. [Google Scholar] [CrossRef]
- Jacob, D.; Petersen, J.; Eggert, B.; Alias, A.; Christensen, O.B.; Bouwer, L.M.; Braun, A.; Colette, A.; Déqué, M.; Georgievski, G.; et al. EURO-CORDEX: New high-resolution climate change projections for European impact research. Reg. Environ. Chang. 2014, 14, 563–578. [Google Scholar] [CrossRef]
- Christensen, J.H.; Kjellström, E.; Giorgi, F.; Lenderink, G.; Rummukainen, M. Weight assignment in regional climate models. Clim. Res. 2010, 44, 179–194. [Google Scholar] [CrossRef]
- Jacob, D.; Teichmann, C.; Sobolowski, S.; Katragkou, E.; Anders, I.; Belda, M.; Benestad, R.; Boberg, F.; Buonomo, E.; Cardoso, R.M.; et al. Regional climate downscaling over Europe: Perspectives from the EURO-CORDEX community. Reg. Environ. Chang. 2020, 20. [Google Scholar] [CrossRef]
- Peterson, T.C.; Folland, C.; Gruza, G.; Hogg, W.; Mokssit, A.; Plummer, N. Report on the Activities of the Working Group on Climate Change Detection and Related Rapporteurs; Report on the Activities of the Working Group on Climate Change Detection and Related Rapporteurs Methods with emphasis on analyses of extreme events; World Meteorological Organization: Geneva, Switzerland, 2001; p. 144. [Google Scholar]
- Karl, T.R.; Nicholls, N.; Ghazi, A. Clivar/GCOS/WMO Workshop on Indices and Indicators for Climate Extremes Workshop Summary. Clim. Chang. 1999, 42, 3–7. [Google Scholar] [CrossRef]
- Riou, C.; European Union. Le Déterminisme Climatique de la Maturation du Raisin: Application au Zonage de la Teneur en Sucre Dans la Communauté Européenne; Publications Office of the European Union: Luxembourg, 1994. [Google Scholar]
- Hardie, W.J.; Martin, S.R. Shoot growth on de-fruited grapevines: A physiological indicator for irrigation scheduling. Aust. J. Grape Wine Res. 2000, 6, 52–58. [Google Scholar] [CrossRef]
- Amengual, A.; Homar, V.; Romero, R.; Alonso, S.; Ramis, C. A statistical adjustment of regional climate model outputs to local scales: Application to Platja de Palma, Spain. J. Clim. 2012, 25, 939–957. [Google Scholar] [CrossRef] [Green Version]
- Miao, C.; Su, L.; Sun, Q.; Duan, Q. A nonstationary bias-correction technique to remove bias in GCM simulations. J. Geophys. Res. Atmos. 2016, 121, 5718–5735. [Google Scholar] [CrossRef]
- Fowler, H.J.; Ekström, M.; Blenkinsop, S.; Smith, A.P. Estimating change in extreme European precipitation using a multimodel ensemble. J. Geophys. Res. Atmos. 2007, 112. [Google Scholar] [CrossRef] [Green Version]
- Malheiro, A.C.; Santos, J.A.; Fraga, H.; Pinto, J.G. Climate change scenarios applied to viticultural zoning in Europe. Clim. Res. 2010, 43, 163–177. [Google Scholar] [CrossRef] [Green Version]
- Fraga, H.; Malheiro, A.C.; Moutinho-Pereira, J.; Jones, G.V.; Alves, F.; Pinto, J.G.; Santos, J.A. Very high resolution bioclimatic zoning of Portuguese wine regions: Present and future scenarios. Reg. Environ. Chang. 2014, 14, 295–306. [Google Scholar] [CrossRef]
- Santos, J.A.; Belo-Pereira, M. A comprehensive analysis of hail events in Portugal: Climatology and consistency with atmospheric circulation. Int. J. Climatol. 2019, 39, 188–205. [Google Scholar] [CrossRef] [Green Version]
- Collins, M.; Knutti, R.; Arblaster, J.; Dufresne, J.-L.; Fichefet, T.; Friedlingstein, P.; Gao, X.; Gutowski, W.J.; Johns, T.; Krinner, G.; et al. Long-term Climate Change: Projections, Commitments and Irreversibility. In Climate Change 2013-The Physical Science Basis: Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2013; pp. 1029–1136. [Google Scholar]
- Volosciuk, C.; Maraun, D.; Semenov, V.A.; Park, W. Extreme precipitation in an atmosphere general circulation model: Impact of horizontal and vertical model resolutions. J. Clim. 2015, 28, 1184–1205. [Google Scholar] [CrossRef] [Green Version]
- Soriano, E.; Mediero, L.; Garijo, C. Selection of Bias Correction Methods to Assess the Impact of Climate Change on Flood Frequency Curves. Water 2019, 11, 2266. [Google Scholar] [CrossRef] [Green Version]
- Luo, M.; Liu, T.; Meng, F.; Duan, Y.; Frankl, A.; Bao, A.; Maeyer, P. De Comparing Bias Correction Methods Used in Downscaling Precipitation and Temperature from Regional Climate Models: A Case Study from the Kaidu River Basin in Western China. Water 2018, 10, 1046. [Google Scholar] [CrossRef] [Green Version]
- Mosedale, J.R.; Wilson, R.J.; Maclean, I.M.D. Climate Change and Crop Exposure to Adverse Weather: Changes to Frost Risk and Grapevine Flowering Conditions. PLoS ONE 2015, 10, e0141218. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Molitor, D.; Keller, M. Yield of Müller-Thurgau and Riesling grapevines is altered by meteorological conditions in the current and previous growing seasons. Oeno One 2016, 50, 245–258. [Google Scholar] [CrossRef] [Green Version]
- Greer, D.H.; Weedon, M.M. The impact of high temperatures on Vitis vinifera cv. Semillon grapevine performance and berry ripening. Front. Plant Sci. 2013, 4, 491. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Robinson, A.L.; Boss, P.K.; Solomon, P.S.; Trengove, R.D.; Heymann, H.; Ebeler, S.E. Origins of grape and wine aroma. Part 1. Chemical components and viticultural impacts. Am. J. Enol. Vitic. 2014, 65, 1–24. [Google Scholar] [CrossRef] [Green Version]
- Savoi, S.; Wong, D.C.J.; Arapitsas, P.; Miculan, M.; Bucchetti, B.; Peterlunger, E.; Fait, A.; Mattivi, F.; Castellarin, S.D. Transcriptome and metabolite profiling reveals that prolonged drought modulates the phenylpropanoid and terpenoid pathway in white grapes (Vitis vinifera L.). BMC Plant Biol. 2016, 16, 67. [Google Scholar] [CrossRef] [Green Version]
- Vilanova, M.; Fandiño, M.; Frutos-Puerto, S.; Cancela, J.J. Assessment fertigation effects on chemical composition of Vitis vinifera L. cv. Albariño. Food Chem. 2019, 278, 636–643. [Google Scholar] [CrossRef]
- Hardie, W.J.; Considine, J.A. Response of Grapes to Water-Deficit Stress in Particular Stages of Development. Am. J. Enol. Vitic. 1976, 27, 55–61. [Google Scholar]
- Ramos, M.C.; Jones, G.V.; Martínez-Casasnovas, J.A. Structure and trends in climate parameters affecting winegrape production in northeast Spain. Clim. Res. 2008, 38, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Kenny, G.J.; Harrison, P.A. The Effects of Climate Variability and Change on Grape Suitability in Europe. J. Wine Res. 1992, 3, 163–183. [Google Scholar] [CrossRef]
- Fraga, H.; García de Cortázar Atauri, I.; Santos, J.A. Viticultural irrigation demands under climate change scenarios in Portugal. Agric. Water Manag. 2018, 196, 66–74. [Google Scholar] [CrossRef]


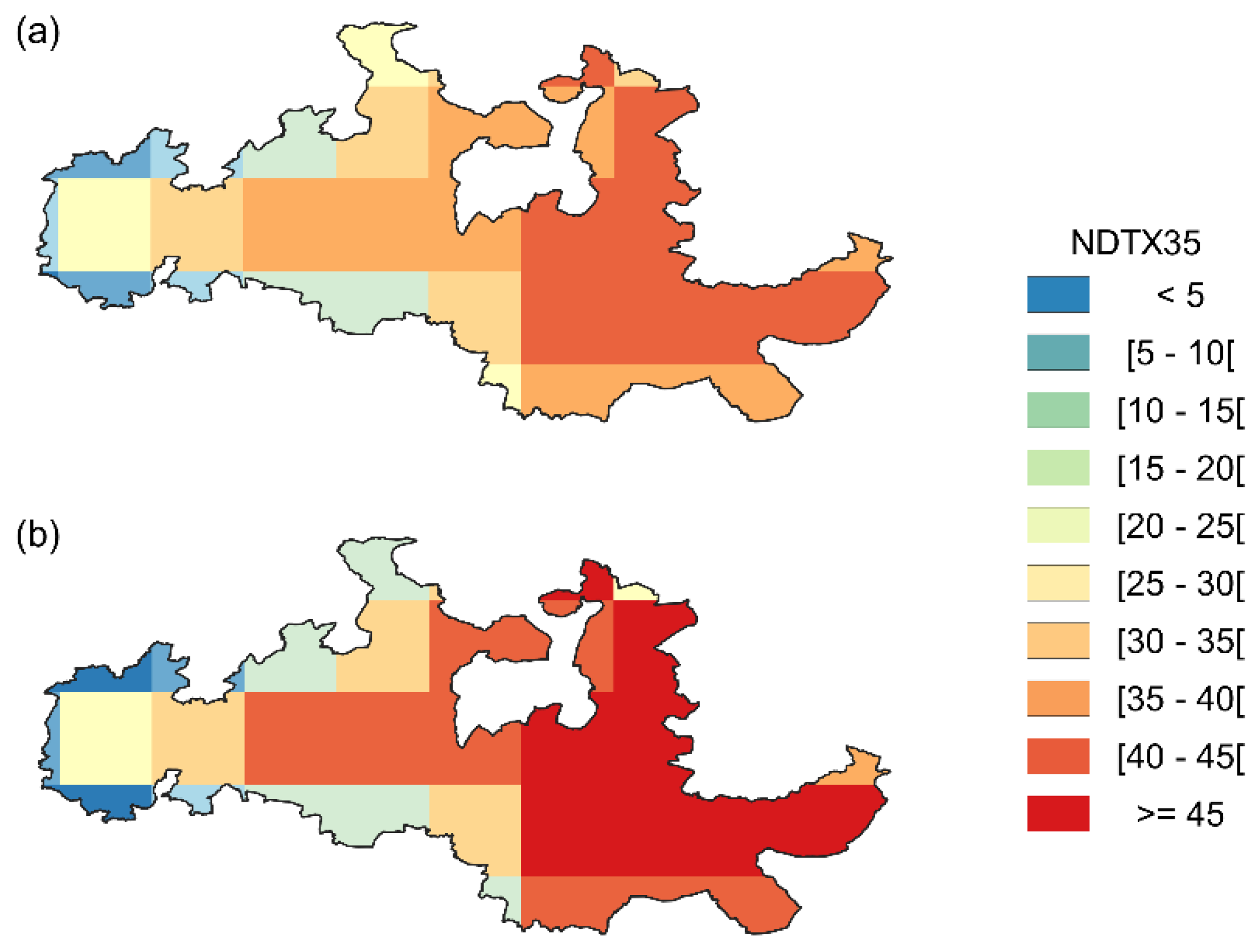









| NDTX35 | NDTX20-30 | NWS | WSDI90 | CDD | NDS | HI | DI | GSP |
|---|---|---|---|---|---|---|---|---|
| 13.4% | 4.7% | 12.3% | 19.7% | 19.5% | 1.9% | 3.3% | 29.3% | 22.7% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martins, J.; Fraga, H.; Fonseca, A.; Santos, J.A. Climate Projections for Precipitation and Temperature Indicators in the Douro Wine Region: The Importance of Bias Correction. Agronomy 2021, 11, 990. https://doi.org/10.3390/agronomy11050990
Martins J, Fraga H, Fonseca A, Santos JA. Climate Projections for Precipitation and Temperature Indicators in the Douro Wine Region: The Importance of Bias Correction. Agronomy. 2021; 11(5):990. https://doi.org/10.3390/agronomy11050990
Chicago/Turabian StyleMartins, Joana, Helder Fraga, André Fonseca, and João Andrade Santos. 2021. "Climate Projections for Precipitation and Temperature Indicators in the Douro Wine Region: The Importance of Bias Correction" Agronomy 11, no. 5: 990. https://doi.org/10.3390/agronomy11050990
APA StyleMartins, J., Fraga, H., Fonseca, A., & Santos, J. A. (2021). Climate Projections for Precipitation and Temperature Indicators in the Douro Wine Region: The Importance of Bias Correction. Agronomy, 11(5), 990. https://doi.org/10.3390/agronomy11050990









